Куб — свойства, виды и формулы

Примеры применения куба

1. Архитектура: В современной архитектуре кубы используются для создания современных и уникальных зданий. Кубические формы могут быть использованы в качестве основной структурной единицы или как декоративный элемент.

2. Математика: Кубы играют важную роль в геометрии и линейной алгебре. Они помогают изучить различные аспекты трехмерного пространства, такие как объемы, площади поверхностей и диагонали куба.

3. Разработка компьютерных игр: Кубы широко используются в разработке компьютерных игр для создания игровых объектов и сценариев. Они могут быть использованы для создания архитектуры игрового мира или в качестве основных элементов геймплея.

4. Упаковка и хранение: Кубы могут использоваться для упаковки и хранения различных предметов. Их регулярная форма и одинаковые размеры делают их удобными для создания стопок или контейнеров.

5. Мебель и домашний декор: Кубическая форма может использоваться для создания мебели и элементов декора, таких как столы, полки и светильники. Кубические элементы дизайна могут придать комнате современный и стильный вид.

Это только некоторые примеры применения куба. Этот геометрический объект оказывает непосредственное влияние на множество аспектов нашей жизни и может использоваться в самых разных областях.

Математика. 4 класс

Конспект урока

Перечень вопросов, рассматриваемых в теме:

Как распознавать и называть куб, его грани, ребра, вершины.?

Куб — это многогранник, поверхность которого состоит из шести квадратов.

Грани куба – это стороны куба, которые представляют собой квадрат.

Ребра куба – это стороны граней куба.

Вершина куба— это точка, где сходятся три грани или точка, в которой сходятся три ребра куба.

Площадь фигуры – это часть плоскости, ограниченная замкнутой ломаной или кривой линией.

Периметр фигуры — это сумма длин всех сторон фигуры.

Основная и дополнительная литература по теме урока:

1. Моро М.И., Бантова М.А. и др. Математика 4 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 110
2. Математика: Рабочая тетрадь для 4 класса/ О.А. Рыдзе, К.А. Краснянская. – М.; СПб.: Просвещение, 2012. – с. 26-32

Теоретический материал для самостоятельного изучения

Подумайте, на какие две группы можно разделить фигуры?

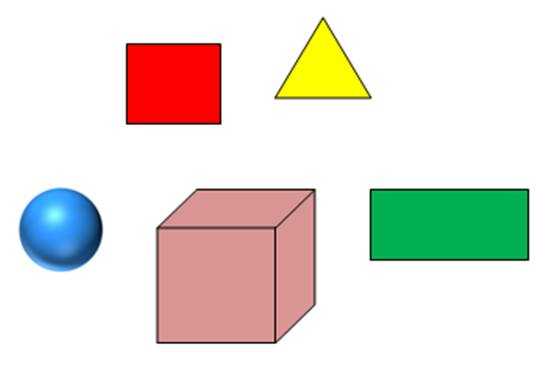
Верно, на плоские и объемные.

Назовите плоские геометрические фигуры.

Верно, квадрат, треугольник, прямоугольник.

Объемные фигуры называются – геометрическими телами.

Вы видите геометрическое тело «шар» и геометрическое тело «куб».

Внимательно посмотрите и скажите, из какой фигуры состоит поверхность куба?

Верно, поверхность куба состоит из квадратов, их называют гранями куба.

Посчитайте, сколько граней у куба.

Правильно, у куба 6 граней.

Стороны граней (квадратов) называют ребрами куба.

Посчитайте, сколько ребер у куба?

Вершины граней – это вершины куба.

Посчитайте, сколько вершин у куба.

Правильно, у куба 8 (восемь) вершин.

Таким образом, у куба 6 граней, 12 ребер, 8 вершин.

Для того чтобы изготовить модель куба необходимо построить развертку куба.

И какого бы куб ни был роста, сшить костюм для него очень просто. Для начала же, сделав разметку, изготовьте раскройку – развертку. Шесть квадратов! Нехитрое дело. Но расклеить их надо умело.

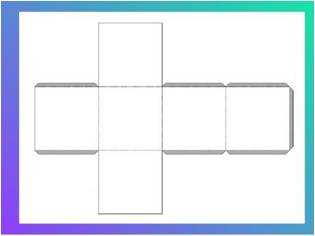
Где можно встретить куб? Здания чаше всего имеют кубическую форму, так что можно просто выглянуть в окно, и вы сразу увидите куб.

Самая знаменитая игрушка-головоломка «кубик-рубик».

Кристаллы поваренной соли имеют форму куба.

Выполним несколько тренировочных заданий.

1. Найдите и напишите номер того куба, который сделан из данной развёртки.

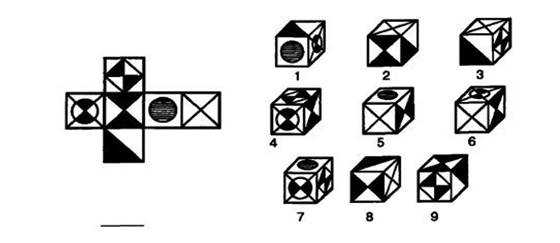
Правильный вариант/варианты (или правильные комбинации вариантов): 4

2. Выберите правильное утверждение.

а) площадь круга больше площади квадрата;

б) площадь круга меньше площади квадрата;

Правильные варианты: б) площадь круга меньше площади квадрата.

Геометрические фигуры. Куб.

Куб или правильный гексаэдр – это правильный многогранник, у которого все грани это квадраты.

Куб является частным случаем параллелепипеда и призмы. 4 сечения куба имеют вид правильных

шестиугольников — это сечения через центр куба перпендикулярно 4-м главным диагоналям.

В кубе насчитывается шесть квадратов. Все вершины куба являются вершинами 3-х квадратов. То есть,

сумма плоских углов у каждой вершины = 270º.

Число рёбер примыкающих к вершине – 3;

Предположим, что а – длина стороны куба, а d — диагональ, тогда:

Диагональ куба – это отрезок, который соединяет 2 вершины, которые симметричны относительно центра

Свойства куба.

4 сечения куба имеют вид правильных шестиугольников — они проходят сквозь центр куба

перпендикулярно четырём его главным диагоналям.

В куб вписывают тетраэдр 2-мя способами. В любом из них 4-ре вершины тетраэдра всегда

совмещены с 4-мя вершинами куба и каждое из шести ребер тетраэдра принадлежат граням куба. В 1-м

случае каждая вершина тетраэдра принадлежит граням трехгранного угла, вершиной совпадающего с одной

из вершин куба. Во 2-м случае ребра тетраэдра, которые попарно скрещиваются принадлежат попарно

противоположным граням куба. Такой тетраэдр будет правильным, а его объём будет составлять треть от

В куб вписывают октаэдр, при этом все 6 вершин октаэдра совмещаются с центрами 6-ти граней

Куб вписывают в октаэдр, при этом все 8 вершин куба располагаются в центрах 8-ми граней

В куб вписывают икосаэдр, притом 6 взаимно параллельных рёбер икосаэдра располагаются на

6-ти гранях куба, следующие 24 ребра располагаются внутри куба. Каждая из 12 вершин икосаэдра

располагается на 6-ти гранях куба.

Элементы симметрии куба.

Ось симметрии куба может пролегать или сквозь середины ребер, которые

параллельны, не принадлежащих одной из граней, или сквозь точку

пересечения диагоналей противолежащих граней. Центром симметрии

куба будет точка пересечения диагоналей куба.

Сквозь центр симметрии куба проходят 9 осей симметрии.

Плоскостей симметрии у куба тоже 9, они пролегают или

через противолежащие ребра (таких плоскостей 6), или

через середины противолежащих ребер (таких 3).

Куб — свойства, виды и формулы » Kupuk.

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.

Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

• многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;

• прямая призма, все грани которой есть квадраты;

•  прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

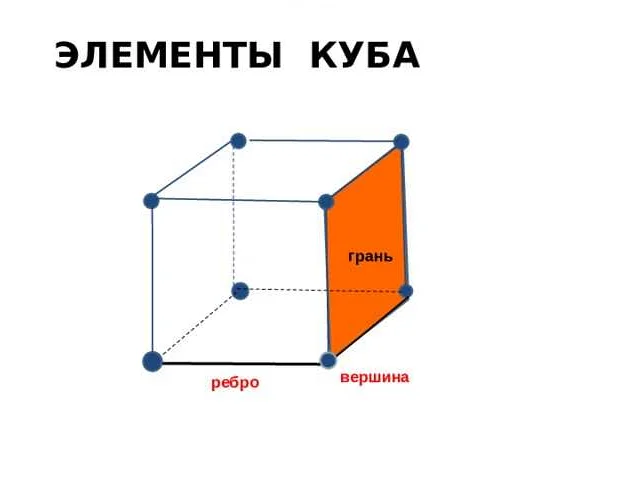
Элементы куба

Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю. 

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника. 

Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Диагональ куба — одна из осей симметрии.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Диагональ грани куба

Длина диагонали грани в √2 раз больше ребра, то есть:

Эта формула доказывается также с помощью теоремы Пифагора.

Такая сфера имеет центр, совпадающий с центром куба. 

Радиус равен половине ребра:

Координаты вершин куба

В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.

Наиболее часто используют следующий способ.

Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).

Свойства куба

Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.

Построение сечений необходимо для решения многих задач.

Прочие свойства:

• у куба все грани равны, являются квадратами;

• у куба все рёбра равны;

• один центр и несколько осей симметрии.

Как обозначить ребро куба в математических формулах?

Ребро куба — это одна из его важнейших характеристик, в математических формулах она обозначается разными способами в зависимости от контекста.

В задачах, связанных с расстояниями между точками в пространстве, ребро куба иногда обозначается как d. Это обозначение происходит от английского слова «distance», что означает «расстояние», что является подходящим обозначением в этом контексте.

Кроме того, в некоторых задачах, где речь идет о построении пространственных объектов, ребро куба может быть обозначено наряду с другими характеристиками объекта, такими как высота и ширина. В этом случае обозначение может зависеть от конкретной нотации, используемой автором формулы.

Независимо от обозначения ребра куба в математической формуле, важно помнить, что оно является критически важной характеристикой этой фигуры и является ключом к пониманию многих ее свойств

Где в жизни можно увидеть куб и его ребро?

Куб и его ребро встречаются в жизни достаточно часто. Начиная от элементарных игрушек для детей до сложной научной техники, кубы и их рёбра являются неотъемлемой частью нашей повседневной жизни.

Одно из наиболее очевидных применений кубов — это игральные кости. Кубики используются во многих настольных играх, таких как «Монополия», «Кости», «Мафия» и многие другие.

Еще одним примером является строительство. Дома, архитектурные сооружения и здания часто имеют форму кубов или прямоугольных параллелепипедов, а ребра используются в качестве стен и перегородок.

Также куб и его ребро используются в изучении математики и науки. Например, в физике, куб используется для измерения объема, площади поверхности и длины ребер.

В искусстве куб может использоваться как символ и форма. Объекты и скульптуры в форме куба можно увидеть и в музеях современного искусства, на площадях и в парках.

В общем, куб и его ребро присутствуют в нашей жизни настолько широко, что мы просто не замечаем их. Однако, полное понимание свойств и качеств куба может дать большое преимущество при решении математических задач и в жизни в целом.

Куб — свойства, виды и формулы

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.

Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;

прямая призма, все грани которой есть квадраты;

прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

Вариант развертки

Куб можно изготовить самостоятельно. Бумага или картон самый подходящий вариант. Для сборки потребуется бумажная развёртка — единая деталь с линиями сгибов.

Древнегреческий философ Платон ассоциировал гексаэдр с землёй – одним из базовых «земных» элементов, поэтому для построения модели этого правильного многогранника мы выбрали коричневый цвет.

На рис.2 представлена развертка гексаэдра:

Для построения модели Вы можете скачать развертку в формате pdf и распечатать на листе формата А4:— если Вы предполагаете распечатать на цветном принтере — цветная развертка (pdf) — если Вы предполагаете использовать для сборки цветной картон — разверткa (pdf)

Куб из набора «Волшебные грани»

Вы можете изготовить модель додекаэдра воспользовавшись деталями для сборки из набора «Волшебные грани».

Пять правильных многогранников

Тетраэдр

Тетраэдр состоит из четырёх равносторонних треугольников.

Фигура имеет 4 грани, 4 вершины и 6 ребер(a).

Площадь поверхности тетраэдра:

Объем тетраэдра:

Радиус описанной вокруг тетраэдра сферы:

Радиус вписанной в тетраэдр сферы:

Куб (Гексаэдр)

Куб состоит из шести квадратов.

Фигура имеет 6 граней, 8 вершин и 12 ребер (a).

Площадь поверхности куба:

Радиус описанной вокруг куба сферы:

Радиус вписанной в куб сферы:

Октаэдр

Октаэдр составлен из восьми равносторонних треугольников.

Фигура имеет 8 граней, 6 вершин и 12 ребер (a).

Площадь поверхности октаэдра:

Объем октаэдра:

Радиус описанной вокруг октаэдра сферы:

Радиус вписанной в октаэдр сферы:

Икосаэдр

Икосаэдр составлен из двадцати равносторонних треугольников.

Фигура имеет 20 граней, 12 вершин и 30 ребер (a).

Площадь поверхности икосаэдра:

Объем икосаэдра:

Радиус описанной вокруг икосаэдра сферы:

Радиус вписанной в икосаэдр сферы:

Додекаэдр

Додекаэдр составлен из двенадцати равносторонних пятиугольников.

Фигура имеет 12 граней, 20 вершин и 30 ребер (a).

Площадь поверхности додекаэдра:

Объем додекаэдра:

Радиус описанной вокруг додекаэдра сферы:

Радиус вписанной в додекаэдр сферы:

Cube Formula — Что такое Cube Formula? Примеры

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Куб числа непосредственно отражает объем куба, имеющего длину ребра, равную данному числу.

Что такое формула куба?

Куб является одним из пяти платоновых тел и также известен как правильный шестигранник.

Формула куба

Объем куба

Объем куба можно рассчитать с использованием различных формул на основе заданных параметров. Его можно рассчитать, используя длину стороны, а также размер диагонали куба.

• Объем куба (на основе длины стороны) = a 3  кубических дюймов, где a – длина стороны куба
• Объем куба (по диагонали) = (√3×d 3 )/9кубических дюймов, где d — длина диагонали куба

Боковая площадь куба

Боковая площадь куба равна сумме площадей всех боковых граней куба.

LSA куба = 4a 2

, где a — длина стороны.

Общая площадь куба

Общая площадь поверхности куба будет равна сумме площади основания и площади вертикальных поверхностей куба. Поскольку все грани куба состоят из квадратов одинакового размера, то общая площадь поверхности куба будет равна площади поверхности одной грани, сложенной с самой собой в пять раз. Таким образом, формула для нахождения площади поверхности куба:

Общая площадь поверхности (TSA) куба = 6a 2

, где a — длина стороны.

Диагональ куба

Куб имеет диагонали двух разных длин, более короткие лежат на квадратных гранях, а более длинные проходят через центр. Главной диагональю куба называется та, которая проходит через центр, который можно найти, умножив длину одной стороны на квадратный корень из 3.

Диагональ куба = a√3

Давайте лучше разберемся с формулами куба на нескольких решенных примерах.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запись на бесплатный пробный урок

Примеры с использованием формулы куба

Пример 1: Найдите объем кубика Рубика длиной 4 дюйма. Решение:

Чтобы найти объем кубика Рубика: кубик Рубика0003

Длина стороны куба = 4 дюйма (дано)

Используя формулу куба, объем = с × с × с = с 3

Поместите значения,

объем = 4 × 4 × 4 = 4 3  = 64

Ответ: Объем кубика Рубика составляет 64 кубических дюйма.

Пример 2: Размеры куба – 64 дюйма. Найдите его диагональ по формуле куба. Решение: 

Чтобы найти диагональ куба:

Размеры куба: длина (l) = ширина (w) = высота (h) = 64 дюйма (данные)

Используя формулу куба,

диагональ = a√3 

Поместите значения,

Диагональ = 64√3 = 110,848 дюйма

Ответ: Диагональ куба равна 110,848 дюйма

Пример 3: Найдите общую площадь поверхности куба, если длина стороны куба равна 25 дюймам.

Решение:

Длина стороны куба, a = 25 дюймов 

Используя формулу площади куба, а именно: A = 6a 2

Поместите значения,

A = 6 × 25 × 25 = 3750 квадратных дюймов

Ответ: Площадь поверхности куб равен 3750 квадратных дюймов.

Часто задаваемые вопросы о формуле куба

Что такое формула куба?

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Это простые формулы, зависящие в основном от одного параметра — длины ребра или стороны куба.

Как рассчитать диагональ куба по формуле куба?

Главную диагональ куба , пересекающую центр, можно найти, умножив длину одной стороны на квадратный корень из 3. Таким образом, диагональ куба = a√3, где a – ребро куба. .

Что такое s в формуле куба?

В формуле куба s относится к ребру куба. Все формулы куба — объем, площадь поверхности и диагонали — зависят от ребра куба, представленного как s, так и a.

Как вывести формулу куба?

Чтобы вычислить объем по формуле куба,

• Шаг 1: Рассмотрим любой квадратный лист бумаги.
• Шаг 2: Теперь площадь, покрытая этим квадратным листом, будет равна площади его поверхности, т. е. его длине, умноженной на его ширину. Оба одинаковы в случае куба. Таким образом, площадь поверхности будет равна «s 2 ».
• Шаг 3: Куб получается путем складывания нескольких квадратных листов таким образом, чтобы высота стала равной длине и ширине, т. е. единицам «s». Таким образом, высота или толщина куба равна «s».

Таким образом, можно сделать вывод, что общее пространство, занимаемое кубом, то есть объем, равно площади основания, умноженной на высоту. Объем куба = s 2  × s = s 3

Чтобы вывести формулу поверхности куба,

• Шаг 1. Рассмотрим любой лист бумаги квадратной формы.
• Шаг 2: В случае квадрата, поскольку длина и ширина равны, площадь поверхности будет равна «s 2 » (длина, умноженная на ширину).
• Шаг 3: Поскольку у куба 6 граней, общая площадь поверхности куба равна площади одной грани, умноженной на 6 = 6s 2

Свойства граней в кубе

1. Грани куба являются квадратными. У них все стороны равны между собой и все углы прямые.
2. Куб имеет три пары параллельных граней. Пара граней называется «боковыми», а третья пара – «верхней» и «нижней».
3. Грани куба смежны друг с другом, то есть они имеют общие стороны, но не пересекаются.
4. Все грани куба являются плоскими и чередуются по цвету при изображении в двумерном пространстве.
5. Каждая грань куба ограничена ребрами. У каждой грани куба есть четыре ребра.

Свойства граней куба являются основными характеристиками этой геометрической фигуры. Они определяют его форму и структуру. Знание этих свойств позволяет легче понимать и работать с кубом и решать задачи, связанные с его конструкцией и параметрами.

Формула куба – объяснение, свойства и примеры решения

Нас окружают разные предметы, которые состоят из разных геометрических форм. Подумайте о детской игре с кубиками, игральными костями или кубиком льда. Что вы замечаете общего среди всего этого? Все они имеют форму куба, не так ли? В этой статье мы изучим, что такое куб? Объем формулы куба, площадь формулы куба, площадь поверхности формулы куба. Некоторыми из распространенных примеров кубика являются кубик льда, игральные кости, кубик Рубика.

Введение. Что такое куб?

Куб — это трехмерная фигура, состоящая из граней квадратной формы одинакового размера.

На приведенном ниже рисунке изображен куб, где l — длина, b — ширина, h — высота, и l = b = h. Длина, ширина и высота представляют ребра куба. И когда три ребра встречаются в точке, это называется вершиной.

(Изображение будет загружено в ближайшее время)

Свойства куба

1.  Все грани куба имеют квадратную форму.

2. Все грани и ребра равны.

3. Углы куба прямые.

4. Каждая из граней встречается с четырьмя соседними гранями.

5. Каждая из вершин встречается с тремя гранями и тремя ребрами.

6. Ребра, противоположные друг другу, параллельны и также равны.

7. Все 12 диагоналей на поверхности имеют площадь одинаковой величины

8. Все 4 внутренние диагонали равны

Например, куб имеет шесть граней. Следовательно, площадь его поверхности будет равна сумме площадей всех шести граней.

В основном площадь поверхности можно классифицировать как:

Площадь изогнутой поверхности объекта – это площадь всех криволинейных поверхностей объекта.

Боковая поверхность предмета – это площадь всех граней предмета, за исключением площади его основания и вершины. Для куба площадь боковой поверхности будет равна сумме площадей четырех сторон, то есть умноженной на 4 стороны.

Площадь боковой поверхности = 4 × (край) 2

902

Куб — это трехмерный объект, поэтому пространство, занимаемое кубом, будет трехмерным.

Куб ограничен шестью квадратными гранями, поэтому площадь поверхности будет вычисляться путем сложения площадей всех шести квадратных граней. Следовательно, площадь поверхности куба по формуле равна 9.0003

Площадь поверхности куба = 6 (сторона) 2

Внутренняя часть полого объекта может быть заполнена воздухом или какой-либо жидкостью, которая принимает форму объекта. В таких случаях объем вещества, который может вместить внутренность предмета, называется вместимостью полого предмета. Таким образом, мы можем сказать, что объем объекта — это мера занимаемого им пространства, а вместимость объекта — это объем вещества, которое может вместить его внутренность.

А объем куба — это занимаемое им пространство. Объем формулы куба будет рассчитан как:

Volume = (side) 3

Length of Diagonal of Face of the Cube = √2(edge)

Длина диагонала из куба = √3 (Edge)

3

3

3

3 9000

Периметр = 12 (ребро)

Решаемые примеры

Пример 1. Найдите площадь поверхности куба, длина стороны которого равна 7 см.

Решение:

Указанная длина = края = 7 см

Ум.

        = 6 × 49

        =  294 см 2

Пример 2: Сторона кубического ящика равна 9 м. Найдите объем кубического ящика.

Решение:

DED, сторона = A = 9m

по формуле объема A Cube, мы знаем, что

V = A 3 11963

9

v = 3 1113

9

v = 3 1113

9

v = 3 1113

V = 3 111996469

v = 3 11996469

v = 3 113

V = 3 x 9 x 9

V = 729 кв.

2

Значение кубов в математике

Кубы — это трехмерные квадраты, которые многие считают символом геометрического совершенства. С какой стороны на него ни посмотри, он выглядит одинаково. Это часть геометрии в математике и чрезвычайно важна как глава. Понимание этого является ключом к пониманию других связанных концепций. Учащиеся должны быть внимательны при изучении кубиков, так как из этой главы возникнет много вопросов. Они могут перейти к формуле куба — объяснение, свойства и примеры решений и подробно разобраться в этом. На этой странице Веданту каждая концепция упрощена для понимания учеником.

Урок математики в 3-м классе «Куб. Элементы куба: грани, ребра, вершины. Развертка куба»

Нехитрое дело. Но расклеить их надо умело. Куб в жизни человека. Где можно встретить куб? Здания чаше всего имеют кубическую форму, так что можно просто выглянуть в окно, и вы сразу увидите куб.

Самая знаменитая игрушка-головоломка «кубик-рубик». Кристаллы поваренной соли имеют форму куба. Выполним несколько тренировочных заданий. Найдите и напишите номер того куба, который сделан из данной развёртки.

Выберите правильное утверждение.

Они помогают определить объем куба, площадь его поверхности, а также являются основой для решения различных задач и заданий. Свойства ребра куба Основные свойства ребра куба: 1. Длина: Ребро куба представляет собой отрезок прямой линии, который соединяет две соседние вершины. Длина каждого ребра куба равна. Направление: Ребро куба направлено от одной вершины к другой.

Оно является вектором, который задаётся начальной и конечной точками. Равноправность: Все рёбра куба идентичны между собой и имеют одинаковое значение. Независимо от положения ребра в пространстве, оно будет иметь одну и ту же длину и направление. Соединительная функция: Рёбра куба соединяют вершины и образуют грани этого геометрического тела. Они играют важную роль в определении формы и структуры куба.

Существует несколько вариантов определения ребра куба. Грань куба представляет собой квадрат со стороной, равной ребру куба. Соответственно, её площадь равняется квадрату ребра куба.

Топографические карты, схемы, рисунки информируют о месте расположения точки по определенным линиям, меридианам, каналам. Так, на спине таких линий — 3, на грудной клетке спереди — 4, а пересечение вертикальных линий с поперечными на уровне позвонка, ребра или углов лопаток, их остей и по другим ориентирам дает возможность сравнительно легко локализовать искомую точку. Владимир Васичкин, Лечебные точки организма: нормализуем давление и облегчаем невралгию, 2015 Связанные понятия продолжение Многоугольник Петри для правильного многогранника в размерности n — это пространственный многоугольник, такой что любые n-1 последовательных ребра но не n принадлежат одной n-1 -мерной грани. В каждой из его 24 одинаковых вершин сходятся одна квадратная грань и четыре треугольных. Треугольные грани делятся на две группы: 8 из них окружены только другими треугольными, остальные 24 — квадратной и двумя треугольными. Диэдр — вид многогранника, состоящего из двух многоугольных граней, имеющих общий набор рёбер. В трёхмерном евклидовом пространстве он является вырожденным, если его грани плоские, в то время как в трёхмерном сферическом пространстве диэдр с плоскими гранями может рассматриваться как линза, примером которой является фундаментальная область линзового пространства L p,q. Как правило, рассматриваются множества точек n-мерного евклидова пространства и движения этого пространства, но понятие группы симметрии сохраняет свой смысл и в более общих случаях. В евклидовой геометрии спрямление или полное усечение — это процесс усечения многогранника путём пометки середины всех его рёбер и отсечения всех вершин вплоть до этих точек. Получающийся многогранник будет ограничен фасетами гранями размерности n-1, в трёхмерном пространстве это многоугольники вершинных фигур и усечёнными фасетами исходного многогранника. Операции спрямления даётся однобуквенный символ r. Подробнее: Полное усечение геометрия В геометрии пространственный многоугольник — это многоугольник, вершины которого не компланарны. Пространственные многоугольники должны иметь по меньшей мере 4 вершины. Внутренняя поверхность таких многоугольников однозначно не определяется. В геометрии построение Витхоффа , или конструкция Витхоффа — это метод построения однородных многогранников или мозаик на плоскости. Метод назван по имени математика В. Часто метод построения Витхоффа называют калейдоскопным построением. Выпуклым многоугольником называется многоугольник , все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Соты обычно рассматриваются в обычном евклидовом «плоском» пространстве. Их можно также построить в неевклидовых пространствах, например, гиперболические соты. Любой конечный однородный многогранник можно спроецировать на его описанную сферу, что даст однородные соты в сферическом пространстве.

Что такое куб: определение, свойства, формулы

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Что такое куб: определение, свойства, формулы

В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).

• Определение куба
• Свойства куба
  • Свойство 1
  • Свойство 2
  • Свойство 3
• Формулы для куба
  • Диагональ
  • Диагональ грани
  • Площадь полной поверхности
  • Периметр ребер
  • Объем
  • Радиус описанного вокруг шара
  • Радиус вписанного шара

Определение куба

Куб – это правильный многогранник, все грани которого являются квадратами.

• Вершины куба – это точки, являющиеся вершинами его граней.Всего их 8: A, B, C, D, A₁, B₁, C₁ и D₁.
• Ребра куба – это стороны его граней.Всего их 12: AB, BC, CD, AD, AA₁, BB₁ , CC₁, DD₁, A₁B₁, B₁C₁, C₁D₁ и A₁D₁.
• Грани куба – это квадраты, из которого состоит фигура.Всего их 6: ABCD, A₁B₁C₁D₁, AA₁B₁B, BB₁C₁C, CC₁D₁D и AA₁D₁D.

Примечание: куб является частным случаем параллелепипеда или призмы.

Свойства куба

Свойство 1

Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.

• ABCD || A₁B₁C₁D₁
• AA₁B₁B || CC₁D₁D
• BB₁C₁C || AA1D₁D

Свойство 2

Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.

• AC₁ = BD₁ = A₁C = B₁D (диагонали куба).
• О – точка пересечения диагоналей:AO = OC₁ = BO = OD₁ = A₁O = OC = B₁O = OD.

Свойство 3

Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.

Например, на рисунке выше угол между гранями ABCD и AA₁B₁B является прямым.

Формулы для куба

Примем следующие обозначения, которые будут использоваться далее:

• a – ребро куба;
• d – диагональ куба или его грани.

Площадь полной поверхности

Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Прямоугольный параллелепипед. Куб. Объем. Единицы объема

У каждого угла куба 3 смежных грани, и сумма мер трех углов каждой грани, сходящихся в угле куба, также составляет 360 градусов. Правильные углы в кубе: определение и примеры Куб — это правильный многогранник, имеющий 6 граней, равных между собой и образующих прямые углы друг с другом. Каждая грань куба является квадратом, и грани встречаются по ребрам. В точках соединения ребер образуются углы, которые и называются углами куба. Всего в кубе можно выделить 8 таких углов.

Пример угла в кубе можно наблюдать на каждом его ребре, где сходятся две плоскости квадратных граней. Каждый из этих углов равен 90 градусов и является прямым углом

Углы в кубе имеют важное значение при изучении его свойств и применении в различных областях науки и техники. Знание об устройстве куба и его углах позволяет решать задачи по геометрии, а также применять его в архитектуре, дизайне и строительстве

Объемный угол в кубе: как рассчитать и его применение Сколько у куба углов? В кубе всего 8 углов. Каждый из них является прямым углом, то есть равен 90 градусам. Рассчитать объемный угол в кубе очень просто.

Куб дров. Сосуд для перегонки или кипячения жилкостей в форме шара или цилиндра с… … Толковый словарь Ушакова КУБ — 1. Сосуд для перегонки или кипячения жилкостей в форме шара или цилиндра с… … Толковый словарь Ушакова КУБ — от латинского cubus, от греческого kybos игральная кость , 1 один из 5 типов правильных многогранников, имеющий гранями квадраты, 12 ребер, 8 вершин, в каждой вершине сходятся 3 ребра.

Куб иногда называют гексаэдром. Таким образом, кубом числа а является произведение а х а х а, что записывается как а3.

Конусы различаются между собой: например, если основанием конуса является круг, то это может быть прямой круговой конус. Цилиндр по своей форме напоминает валик.

В его основании находятся круги, а между ними — часть цилиндрической поверхности. Куб — это многогранная фигура , каждая грань которой представляет собой квадрат. При этом у него 6 граней, 12 ребер и 8 вершин. Куб также можно назвать правильным гексаэдром , или шестигранником.

Пирамида — это многогранник , у которого в основании находится многоугольник, а грани представлены треугольниками, имеющими общую вершину. Призма — это многогранник , 2 грани которого являются равными многоугольниками, располагающимися в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. На картинке выше частный пример — шестиугольная призма. У нее 8 граней, 18 ребер и 12 вершин.

Если выпуклый многогранник состоит из одинаковых правильных многоугольников и обладает пространственной симметрией, то его называют правильным многогранником , или платоновым телом. В трехмерном пространстве различают 5 таких правильных многогранников. Название каждого из них происходит от греческого наименования количества его граней: Тетраэдр, или треугольная пирамида. У этого многогранника гранями являются 4 треугольника.

Гексаэдр, или куб. Октаэдр — многогранник, чьими гранями являются 8 равносторонних треугольников.

Angellru 29 июн. Islamabzhanov 28 июн. Tarasovasofa3 28 июн. Ответ : скорость пешехода 30 км ч… Расстояние 1 км? Nikigood25 28 июн.