Закон кулона, определение и формула

Направление сил в законе Кулона

Тем самым, отличаясь от похожего правила гравитационного взаимодействия, при котором объекты только способны притягиваться.

Радиус-вектор – это сила, направленная вдоль прямой, которая проведена между двумя зарядами. Эта величина имеет следующее обозначение —  r12.

В том случае, когда два заряда имеют противоположные знаки, то тогда направление сил будет от центральной части одного заряда к противоположному заряду по всей проведенной прямой этими зарядами.

Однако, если они имеют одинаковые знаки, то направление будет в противоположную сторону.

Величина силы, приложенной кq1со стороны q2имеет обозначение следующего вида — F12. Чтобы определить силу, которая прикладывается на второй разряд применяют следующие символы -F21 и R21.

В случае, когда объект обладает сложной формой и большими размерами, что с заданным расстоянием оно не считается точечным, тогда объект разделяют на небольшие разделы и принимают каждый раздел за одиночный заряд.

Проведя все геометрические расчёты векторов выводят итоговое значение силы.

Прямая и обратная пропорциональность

Под пропорциональностью в данном случае необходимо понимать зависимость одной действующей силы от иной. Взаимодействие между телами производно от их текущего заряда (чем выше — тем больше сила действует). Обратная же пропорциональность актуальна по отношению к расстоянию: чем оно больше, тем сила меньше. Но это актуально только для тех расстояний, при котором закон действует. Если выполняется расчет для зарядов, расположенных в веществе или диэлектрике, то здесь тоже наблюдается обратная пропорциональность. Чем выше показатель диэлектрической проницаемости — тем сила меньше, так как среда «поглощает» часть электромагнитного поля и рассеивает его.

Модель упрочняющегося грунта

Разумной альтернативой модели Мора-Кулона является модель «Hardening Soil» (модель упрочняющегося грунта). Эта модель отлично подходит для описания поведения песков, нормально- и переуплотнённых глин.

От классической модели Мора-Кулона эта модель отличается, в первую очередь, тем, что описывает гиперболическую зависимость между вертикальной относительной деформацией и девиатором напряжений при первичном трёхосном нагружении, то есть описывает нелинейную работу грунта в допредельной области. Модель характерна тем, что использует три модуля деформаций: 1-ый секущий модуль при 50%-ой прочности, 2-ой одометрический модуль, 3-ий модуль разгрузки и повторного нагружения (линейная зависимость). Значение всех трёх модулей меняется в зависимости от величины наименьшего главного напряжения. Соответственно, модуль меняется как по глубине, так и с изменением нагрузки без участия инженера. Также модель позволяет учесть коэффициент предуплотнения. Таким образом, используя метод K0 как метод формирования начальных напряжений, уже учитывается и предуплотнение грунта (подробнее в статье Коэффициент бокового давления грунта К0). Метод гравитационного загружения для модели упрочняющегося грунта, напротив, применять нельзя, поскольку модель в качестве входного параметра имеет коэффициент Пуассона разгрузки, тогда как в формуле, заложенной в алгоритме гравитационного загружения, описан обычный коэффициент Пуассона.

Модель «Hardening Soil» является более сложной и требует больше параметров, чем классические модели. Однако в виду своего более сложного математического описания она позволяет точнее моделировать поведение грунта основания, анализировать его работу в зоне пластических деформаций и корректно оценивать величину выпора грунта благодаря модулю деформации разгрузки/повторного загружения. Характер работы грунта, описываемый этой моделью, представлен на рисунке 3.

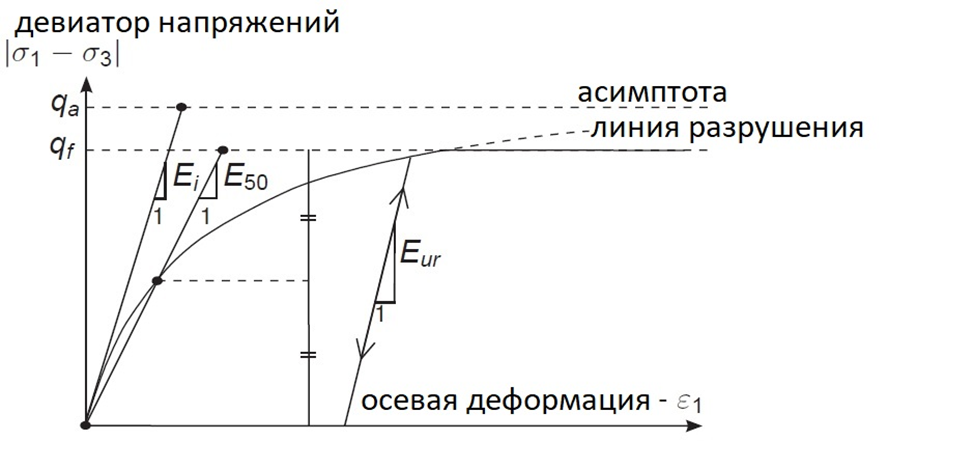Рисунок 3. Поведение материала в соответствии с моделью «Hardening Soil»

Модель «Hardening Soil» требует следующие параметры для работы:

• Модуль деформации при 50% прочности E_50ref;
• Модуль деформации одометрический E_oedref;
• Модуль разгрузки/повторного нагружения E_urref;
• Коэффициент Пуассона разгрузки/повторного нагружения V_ur;
• Удельный вес γ;
• Коэффициент разрушения R_f;
• Опорное давление P_ref;
• Степенной показатель жесткости m Power of Stress Level Dependency;
• Угол внутреннего трения Friction Angle;
• Коэффициент бокового давление нормальной консолидации K_0nc;
• Угол дилатансии ψ;
• Удельное сцепление С;
• Коэффициент переуплотнения OCR;
• Давление предуплотнения POP.

Почти все параметры, которые необходимы для модели «Hardening Soil», фигурируют в нормативных документах. А именно, ГОСТ 12248.3–2020 описывает параметры удельного сцепления, угла внутреннего трения, секущего модуля деформации E50, модуля деформации разгрузки/повторного загружения Eur, коэффициент Пуассона разгрузки, угол дилатансии. Одометрический модуль деформации описан в ГОСТ 12248.4–2020. Коэффициент переуплотнения присутствует в ГОСТ Р 58326–2018.

Есть параметры, которые не описаны в ГОСТ, а именно, степенной показатель m. Его можно получить либо по имеющимся результатам трёхосных испытаний, либо по результатам одометрических в зависимости от преобладающей работы грунта. Многие лаборатории определяют его самостоятельно при дополнительном запросе. Также в модели присутствует параметр опорного давления. Этот параметр является давлением начального всестороннего обжатия при трёхосном испытании. Его принимает инженер и передаёт в лабораторию. Также одометрический модуль будет получен по этому давлению. Обычно этот параметр принимается в диапазоне от бытового давления до эксплуатационного для каждого слоя. Параметр коэффициента разрушения также не описан в ГОСТ. Это отношение предела прочности по Мору-Кулону к асимптоте, к которой стремится гиперболическая зависимость. Этот параметр помогает откалибровать модель в midas GTS NX.

Таким образом, несмотря на большое количество входных параметров модели, не возникает проблем при её практическом применении, тогда как описываемое моделью поведение гораздо точнее.

Закон сохранения электрического заряда

Согласно принципам закона сохранения электрического заряда, алгебраическая сумма электрических зарядов каждой частицы из изолированной системы останется неизменной, несмотря на происходящие в ней процессы.

Электрический заряд абсолютно любой частицы (системы частиц) считается целым кратным элементарному электрическому заряду (по величине равному заряду электрона) или приобретает нулевое значение.

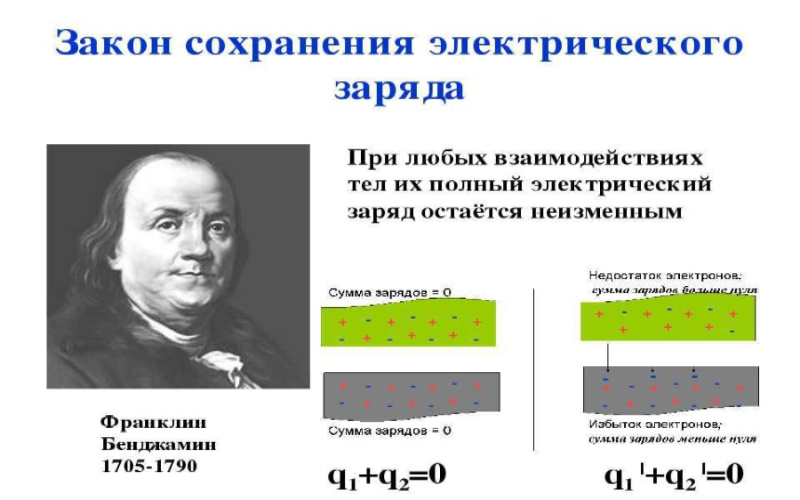Рисунок 2. Закон сохранения электрического заряда. Автор24 — интернет-биржа студенческих работ

В качестве одного из подтверждений закона по сохранению электрического заряда выступает строгое равенство электрических зарядов (по абсолютной величине) электрона и протона. Исследование движения атомов (молекул), а также микроскопических тел в электрических полях только подтверждает электрическую нейтральность вещества и непосредственно равенство зарядов протона и электрона.

Закон сохранения заряда также подтверждают и простые опыты с электризацией тел. Так, если закрепить на стержне электрометра металлический диск, положить на него прослойку из сукна и поставить сверху такой же диск, с ручкой из диэлектрика, можно наблюдать следующий результат. При совершении нескольких движений верхним диском по изоляционной прослойке можно заметить, что стрелка электрометра отклоняется, свидетельствуя таким образом о появлении на сукне и диске, соприкасающимся с ним, электрического заряда.

Если прикоснуться потом вторым диском (потертым о сукно) к стержню второго электрометра, можно наблюдать отклонение стрелки электрометра приблизительно на такой же угол, что и стрелка первого электрометра. Это будет означать, что при электризации каждый диск получил равный по модулю заряд. Если далее соединить электрометры металлическим стержнем, то можно увидеть, как стрелки приборов каются вниз. Нейтрализация зарядов стала свидетельством того, что они были равными по модулю, но противоположными по знаку (и поэтому в сумме давали нулевое значение).

Закон сохранения заряда в 1750 г. установил Б. Франклин. Им же было введено понятие об отрицательных и положительных зарядах.

Элементарные частицы могут рождаться и исчезать, претерпевая различные превращения. При этом возникновение и исчезновение элементарных частиц происходит всегда парным образом (парами с противоположными зарядами). Согласно многочисленным наблюдениям превращений элементарных частиц, закон сохранения заряда постоянно находит свое подтверждение. Таким образом, он служит выражением одного из фундаментальных свойств электрического заряда.

Расчет электростатических сил с использованием закона Кулона Мора

Один из основных принципов электростатики – закон Кулона Мора – позволяет рассчитывать силы взаимодействия между заряженными частицами. Согласно этому закону, электростатическая сила прямо пропорциональна произведению зарядов частиц и обратно пропорциональна квадрату расстояния между ними.

При расчете электростатических сил с использованием закона Кулона Мора необходимо знать величину зарядов частиц и расстояние между ними. Заряды частиц обычно выражаются в кулонах (C) и имеют знаки, обозначающие тип заряда – положительный или отрицательный. Расстояние между частицами измеряется в метрах (м).

Формула для расчета электростатической силы с использованием закона Кулона Мора выглядит следующим образом:

F = k * (|q1 * q2|) / r^2,

где F – электростатическая сила, k – электростатическая постоянная, q1 и q2 – заряды частиц, r – расстояние между частицами.

Значение электростатической постоянной k равно приблизительно 8,99 * 10^9 Н·м^2/Кл^2. Силу F можно выразить в ньютонах (Н).

Расчет электростатических сил с использованием закона Кулона Мора позволяет определить силу взаимодействия между заряженными частицами и предсказать их поведение при различных сценариях. Этот закон широко применяется в физике, электротехнике и других науках, где изучаются электростатические явления и взаимодействие зарядов.

Формулировка закона Кулона Мора

Закон Кулона Мора формулирует связь между главными напряжениями, возникающими на поверхности тела в результате работы электрического поля. Закон гласит, что сила электрического поля, действующая на единичный положительный заряд, пропорциональна произведению модулей заряда и градиента напряжения. Таким образом, главные напряжения на поверхности тела возникают под действием электрического поля и являются пропорциональными градиенту напряжения.

Формула для вычисления главных напряжений на поверхности тела в зависимости от электрического поля выглядит следующим образом:

1. σ_xx = εε (∂V/∂x)
2. σ_yy = εε (∂V/∂y)
3. σ_zz = εε (∂V/∂z)

Где σ_xx, σ_yy, σ_zz – главные напряжения вдоль трех осей координат, ε – удельная электрическая проводимость, ε – электрическая постоянная, V – потенциал электрического поля, x, y, z – координаты точки на поверхности тела.

История открытия закона

Взаимодействия двух точечных зарядов рассмотренным выше законом в первый раз были доказаны в 1785 Шарлем Кулоном. Доказать правдивость сформулированного закона физику удалось с использованием крутильных весов, принцип действия которых также был представлен в статье.

Кулон также доказал, что внутри сферического конденсатора нет электрического заряда. Так он пришёл к утверждению, что величину электростатических сил можно менять путём изменения расстояния между рассматриваемыми телами.

Таким образом, закон Кулона по-прежнему является главнейшим законом электростатики, на основе которого было сделано немало величайших открытий. В рамках данной статьи была представлена официальная формулировка закона, а также подробно описаны его составляющие части.

Сила Лоренца и правило левой руки. Движение заряженных частиц в магнитном поле

Закон Ома: формулировка, формулы, графическая интерпретация и применение

Закон Джоуля-Ленца: формулировка, вывод формулы и применение

Что такое диэлектрическая проницаемость

Что такое потенциал и разность потенциалов между двумя точками

Как правильно расположить точечные светильники на натяжном потолке

Принцип Кулона простыми словами: формула, описание, практическое применение и его значение

В физике есть раздел, изучающий электрические разряды и их взаимодействие с электрическим полем в состоянии покоя, и называется он электростатикой. В этой главе основным принципом оказывается правило Кулона.

Это правило используется для определения силы, с которой взаимодействуют два покоящихся электрических заряда, или расстояния одного заряда от другого. Закон Кулона ни от чего не зависит и ни от чего не зависит. Это фундаментальный закон. Таким образом, тип рассматриваемого объекта не влияет на силу и ее значение.

Ниже мы объясним простыми словами, что такое правило и закон Кулона и где они применяются.

¯left(|q| ; |Q|) ¯left( ¯textПоля являются величинами зарядов;

Электрическое поле. Напряженность электрического поля

Всякое взаимодействие между зарядами, называемое также кулоновским взаимодействием (по названию закона Кулона) происходит при помощи электростатического поля, которое является неизменяющимся по времени электрическим полем неподвижных зарядов. Электрическое поле является частью электромагнитного поля и создаётся оно электрическим зарядами или заряженными телами. Электрическое поле воздействует на заряды и заряженные тела независимо от того движутся ли они или находятся в состоянии покоя.

Одним из фундаментальных понятий электрического поля является его напряженность, которая определяется как отношение силы действующей на заряд в электрическом поле к величине этого заряда. Для раскрытия данного понятия необходимо ввести такое понятие как «пробный заряд».

«Пробным зарядом», называется такой заряд, который не участвует в создании электрического поля, а также имеет очень маленькую величину и поэтому своим присутствием не вызывает перераспределение зарядов в пространстве, тем самым не искажая электрическое поле создаваемое электрическим зарядами.

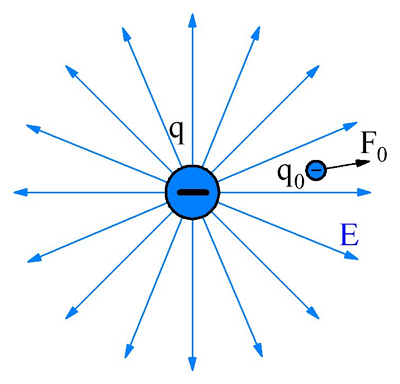
Заряд в электрическом поле.

Таким образом, если внести «пробный заряд» q в точку, находящуюся на некотором расстоянии от заряда q, то на «пробный заряд» q_П будет действовать некоторая сила F, обусловленная присутствием заряда q. Отношение силы F действующей на пробный заряд, в соответствии с законом Кулона, к величине «пробного заряда», называется напряженностью электрического поля. Напряженность электрического поля обозначается Е и имеет разрядность Н/Кл

Электрическая емкость. Конденсатор

Потенциал электрического поля. Разность потенциалов

Потенциал – скалярная физическая величина, равная отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.

Обозначение – ​\( \varphi \)​, единица измерения в СИ – вольт (В).

Потенциал \( \varphi \) является энергетической характеристикой электростатического поля.

Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:

Обозначение – ​\( \Delta\varphi \)​, единица измерения в СИ – вольт (В).

Иногда разность потенциалов обозначают буквой ​\( U \)​ и называют напряжением.

Важно!
Разность потенциалов \( \Delta\varphi=\varphi_1-\varphi_2 \), а не изменение потенциала \( \Delta\varphi=\varphi_2-\varphi_1 \). Тогда работа электростатического поля равна:

Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле. В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки

В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал поля точечного заряда ​\( q \)​ в точке, удаленной от него на расстояние ​\( r \)​, вычисляется по формуле:

Для наглядного представления электрического поля используют эквипотенциальные поверхности.

Важно!
Внутри проводящего шара потенциал всех точек внутри шара равен потенциалу поверхности шара и вычисляется по формуле потенциала точечного заряда (​\( r =R \)​, где ​\( R \)​ – радиус шара). Напряженность поля внутри шара равна нулю

Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение.

Свойства эквипотенциальных поверхностей

• Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону убывания потенциала.
• Работа по перемещению заряда по эквипотенциальной поверхности равна нулю.

В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Для точечного заряда эквипотенциальные поверхности представляют собой концентрические окружности.

Разность потенциалов и напряженность связаны формулой:

Из принципа суперпозиции полей следует принцип суперпозиции потенциалов:

Потенциал результирующего поля равен сумме потенциалов полей отдельных зарядов.

Важно!
Потенциалы складываются алгебраически, а напряженности – по правилу сложения векторов. Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил.

Алгоритм решения таких задач:

• установить характер и особенности электростатических взаимодействий объектов системы;
• ввести характеристики (силовые и энергетические) этих взаимодействий, сделать рисунок;
• записать законы сохранения и движения для объектов;
• выразить энергию электростатического взаимодействия через заряды, потенциалы, напряженности;
• составить систему уравнений и решить ее относительно искомой величины;
• проверить решение.

МЕТОД ОПРЕДЕЛЕНИЯ ПРОЧНОСТНЫХ ХАРАКТЕРИСТИК ГРУНТА

Сопротивление грунта сдвигу может быть установлено различными способами, среди которых наиболее простым и распространённым является способ испытания образца на прямой сдвиг (срез). Последовательность испытания:

1. Цилиндрический образец грунта помещается в «срезыватель» 1 так, чтобы одна его половина оставалась неподвижной, а другая могла перемещаться горизонтально под действием прикладываемой к ней горизонтальной сдвигающей нагрузки (рис. 3);

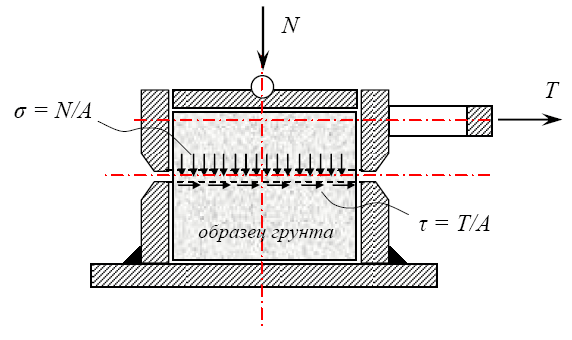
Рис. 3. N – сжимающая сила; T – сдвигающая сила; Площадь поперечного сечения образца — A

2. К образцу прикладывается нормальная к поверхности среза сжимающая нагрузка N;

3. Сдвигающую касательную к поверхности среза нагрузку T прикладывают к срезывателю ступенями до тех пор, пока не произойдёт срез и скольжение одной части грунта по другой;

4. одновременно с приложением нагрузки и во всё время испытания производятся замеры горизонтальных деформаций (смещений) грунта δ (рис. 4);

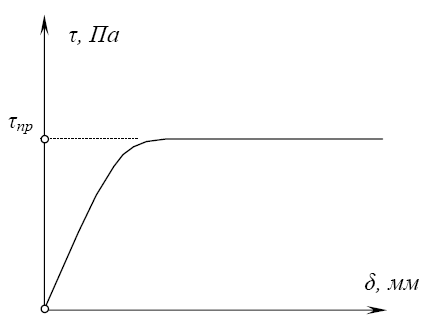
5. Проводят несколько испытаний на срез (i штук 2 ) при различных значениях вертикальной (сжимающей) нагрузки N. То есть каждой ступени нагрузки σ_i будет соответствовать своё сопротивление сдвигу τ_i.

6. Данные опытов наносят на график, выражающий зависимость между нормальным напряжением σ и касательным напряжением τ. Опыты показывают, что в общем случае зависимость оказывается линейной.

Литература

• Сивухин Д. В. Общий курс физики. — М.: Наука, 1979. — Т. I. Механика. — С. 101—102. — 520 с.
• Справочник по триботехнике / Под ред. М.Хебды, А. В. Чичинадзе. Т.1. — М.: Машиностроение, 1989. С.19, 118.
• Крагельский И. В., Виноградова И. Э. Коэффициенты трения. Справочное пособие. — М.: Машгиз, 1962. С.9, 11.
• Словарь-справочник по трению, износу и смазке деталей машин / В. Д. Зозуля, Е. Л. Шведков, Д. Я. Ровинский, Э. Д. Браун. АН УССР. Ин-т проблем материаловедения. — 2-е изд., пере-раб. и доп. — Киев : Наук, думка, 1990. С. 66.
• Первозванский А. А. Трение — сила знакомая, но таинственная. Соросовский образовательный журнал, 1998, № 2, с. 129—134.
• Минаков А. П. Немного о трении. ИТФВестник № 2. myreset.narod.ru

Калибровка модели «Hardening Soil» перед использованием в midas GTS NX

Перед использованием модели «Hardening Soil» необходимо выполнить калибровку модели, то есть некоторое редактирование исходных параметров. Целью этой процедуры является точное моделирование поведения в интересующем диапазоне нагрузок. Для выполнения калибровки в midas GTS NX предусмотрен инструмент «Soil Test» (виртуальная лаборатория).

Принцип выполнения калибровки следующий: инженер должен сопоставить график, полученный по результату выполненного лабораторного испытания (в качестве исходных данных у инженера имеются протоколы лабораторных испытаний образцов грунта, в том числе, графики результатов этих испытаний) с графиком моделирования этого испытания в виртуальной лаборатории midas GTS NX с последующим редактированием параметров материала.

В качестве примера возьмём лабораторные графики трёхосного испытания.

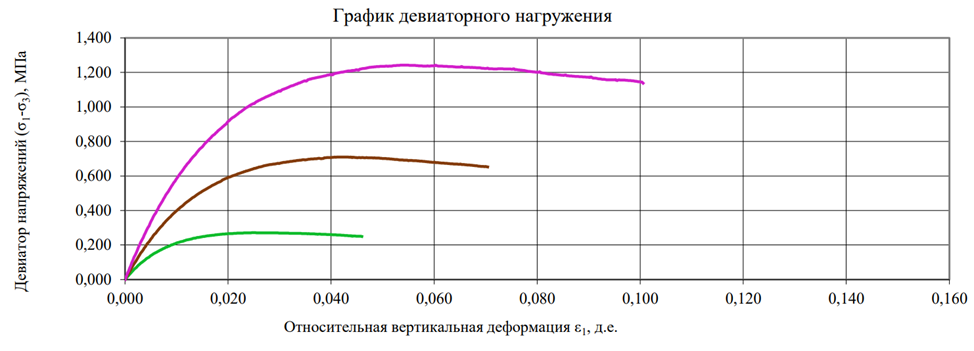Рисунок 6. График лабораторного трёхосного испытания

Воссоздадим это испытание в инструменте «Soil Test».

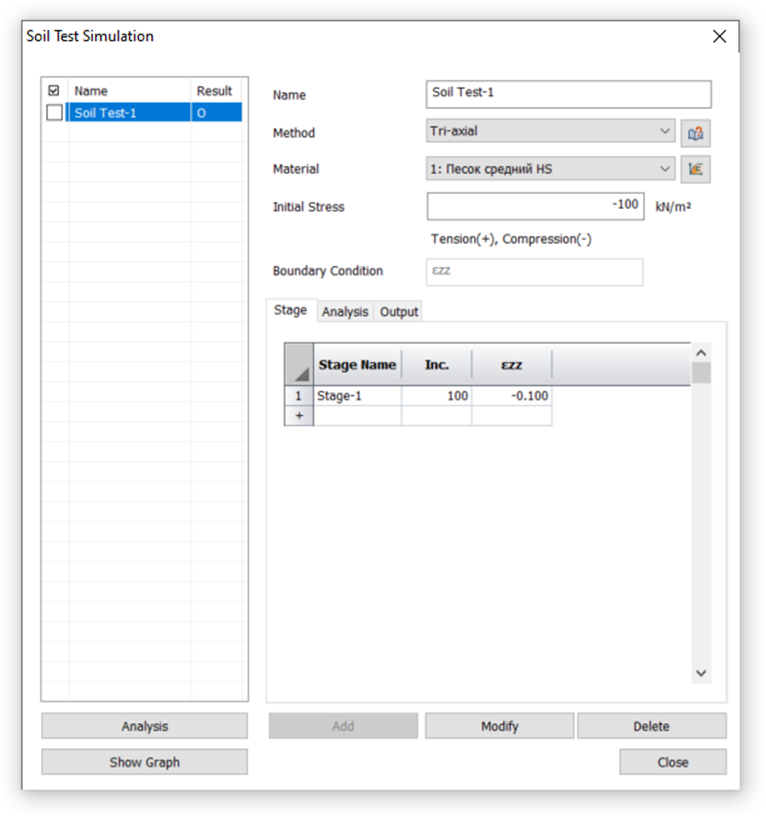Рисунок 7. Настройка виртуального испытания в midas GTS NX

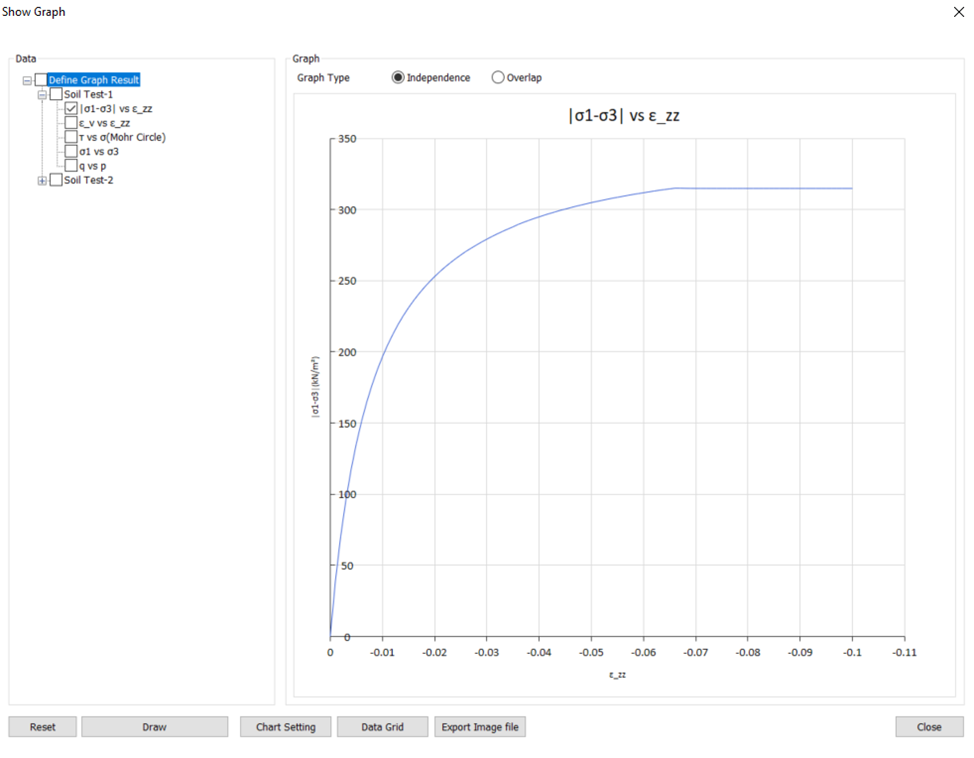Рисунок 8. Результат виртуального испытания в midas GTS NX

После того, как данные получены, нужно любым доступным способом выполнить наложение графиков и сравнить, насколько моделируемое поведение соотносится с реальным, наблюдаемым в лаборатории.

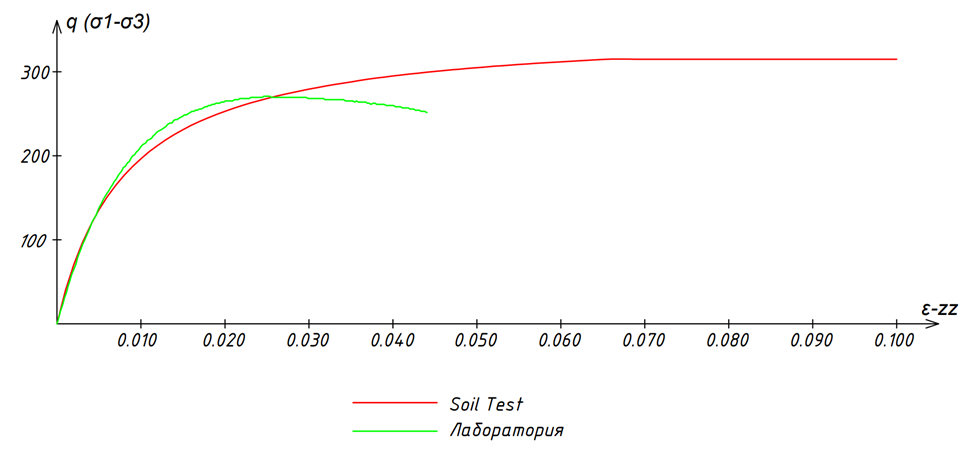Рисунок 9. Сопоставление результатов

Теперь, когда у инженера есть данные по отличиям работы, можно выполнить изменение параметров модели в программе, чтобы добиться максимальной сходимости графиков в диапазоне предполагаемых нагрузок. Этот процесс итерационный, но у опытного инженера не уйдёт много времени на выполнения этих действий.

Для примера выберем диапазон работы грунта от σ1 = 250 кН/м2 до σ1 = 325 кН/м2.

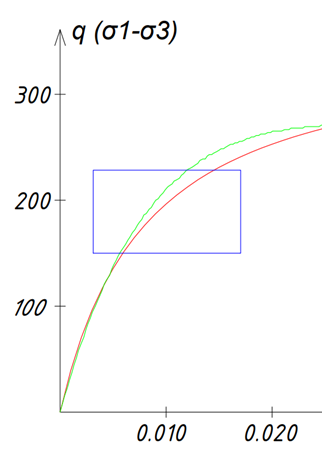Рисунок 10. Интересующий диапазон

Первостепенным во время выполнения калибровки является достижение сходимости именно для выбранного диапазона. На практике не всегда получится добиться полного наложения графиков по всей длине.

Для достижения сходимости нужно изменять параметры материала. Для рассматриваемого примера достаточно немного увеличить модуль деформации при 50% прочности и понизить значение коэффициента разрушения.

Рисунок 11. Изменения параметров при калибровке

В результате, финальный график полностью ложится на лабораторный в заданном диапазоне.

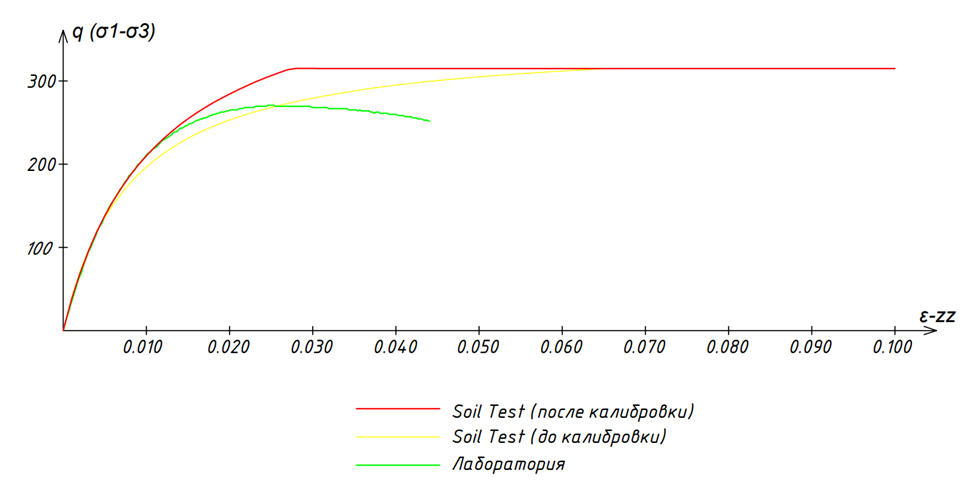Рисунок 12. Результат калибровки

Калибровку модели можно проводить и при конечно-элементном моделировании испытания, будь то одометр или стабилометр. Разницы подходов в сравнении с «Soil Test» нет. Однако при использовании инструмента «Soil Test» процесс значительно ускоряется.

Потенциальность электростатического поля

Электрическое поле с напряженностью ​\( \vec{E} \)​ при перемещении заряда ​\( q \)​ совершает работу. Работа ​\( A \)​ электростатического поля вычисляется по формуле:

где ​\( d \)​ – расстояние, на которое перемещается заряд,
​\( \alpha \)​ – угол между векторами напряженности электрического поля и перемещения заряда.

Важно!
Эта формула применима для нахождения работы только в однородном электростатическом поле. Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда.

Потенциальным называется поле, работа сил которого по перемещению заряда по замкнутой траектории равна нулю.

Важно!
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Электростатическое поле является потенциальным

Работа электростатического поля по перемещению заряда равна изменению потенциальной энергии, взятому с противоположным знаком. В электродинамике энергию принято обозначать буквой ​\( W \)​, так как буквой ​\( E \)​ обозначают напряженность поля:

Потенциальная энергия заряда ​\( q \)​, помещенного в электростатическое поле, пропорциональна величине этого заряда. Потенциальная энергия взаимодействия зарядов вычисляется относительно нулевого уровня (аналогично потенциальной энергии поля силы тяжести). Выбор нулевого уровня потенциальной энергии определяется исходя из соображений удобства при решении задачи.

Формулировка

Текущее формулирование закона Кулона звучит следующим образом:

Но есть условия, при которых получается рассчитать взаимодействие двух точечных зарядов по закону:

1. В пространстве расстояние между зарядами должно существенно превышать их физические габариты.
2. Тела — статичны относительно окружающей среды.
3. Тела расположены в вакууме (нивелируется возможное воздействие окружающей среды).

Но в теории, закон Кулона можно применять и для расчета электростатического взаимодействия между двумя точечными движущимися телами. В итоговую формулу лишь потребуется добавить вектор от заряда q1 к q2. Но расчет взаимодействия между собой точечных зарядов актуален только если тела находятся в условиях вакуума. Для движущихся тел, находящихся в окружении определенной среды, применять радиус-вектор не представляется возможным, так как при смене положения меняется также и направление внешних действующих сил. То есть в данном случае невозможно определить статический коэффициент зависимости.

Закон Кулона для связных и несвязных грунтов.

Грунты оснований зданий и сооружений испытывают воздействие не только нормальных, но и касательных напряжений. Когда касательные напряжения по какой-либо поверхности в грунте достигают его предельного сопротивления, то происходит сдвиг одной части массива грунта по другой.

Сопротивлений грунта сдвигу характеризуется его прочностными свойствами и используется в расчетах оснований по первому предельному стоянию (прочности).

Прочностью грунта называют способность его воспринимать силы внешнего воздействия, не разрушаясь. Прочность грунта определяется его сопротивляемостью сдвигу и оценивается показателем, который называется предельным сопротивлением сдвигу

Внутренним сопротивлением, препятствующим сдвигу частиц, в песчаных грунтах будет лишь трение, возникающее в точках контакта частиц. В связных же грунтах перемещению частиц будут сопротивляться внутренние структурные связи.

Предельное сопротивление грунтов сдвигу может быть установлено по испытанию его образцов на прямой плоскостной срез, трехосное сжатие, по результатам среза грунта крыльчаткой и др. способами. При испытаниях на прямой плоскостной срез используют односрезный прибор. При этом цилиндрический образец грунта помещают в срезыватель так, чтобы одна его половина оставалась неподвижной, а другая могла перемещаться горизонтально под действием сдвигающей нагрузке. К образцу прикладывается так же вертикальная сжимающая нагрузка.

Рис.10. Схема сдвигового прибора.

Многочисленными экспериментами установлено, что график зависимости предельного сопротивления сдвигу сыпучих грунтов от давления представляет собой прямую, исходящую из начала координат и наклоненную под углом φ к оси давлений.

Рис.11. График сопротивления сдвигу сыпучего грунта.

Эта зависимость может быть выражена уравнением:

где φ – угол внутреннего трения грунта.

Это и есть закон Кулона для сыпучих грунтов (1773 г.) — предельное сопротивление сыпучих грунтов сдвигу есть сопротивление трению, прямо пропорциональное нормальному давлению.

Основными видами испытаний связных грунтов на сдвиг будут испытания по закрытой (неконсолидированные испытания) и открытой (консолидированные) системам. Испытания грунтов по первой схеме выполняются таким образом, что плотность и влажность грунта в процессе опыта не меняются, и поэтому такие опыты носят название быстрого сдвига. Испытания по открытой схеме производят после предварительного уплотнения образцов вертикальной нагрузкой до стабилизации осадки, а горизонтальное усилие на образец передается ступенями, при этом каждая ступень выдерживается до стабилизации горизонтальной деформации. Испытания сыпучих грунтов производят по первой схеме, а связных по второй.

Диаграмма испытания глинистых грунтов на сдвиг приведена на рис.12.

Рис.12. График сопротивления сдвигу связного грунта.

Опыты показывают, что диаграмму консолидированного сдвига глинистых грунтов, несмотря на кривизну начального участка, без особых погрешностей можно описать уравнением прямой линии:

.

Это уравнение выражает закон Кулона для связных грунтов: предельное сопротивление связных грунтов сдвигу при завершенной консолидации есть функция первой степени от нормального давления.

Т.о. для связных грунтов сопротивление сдвигу характеризуется двумя параметрами: углом внутреннего трения φ и удельным сцеплением с. Если прямую аb продлить влево до пересечения с осью абсцисс, то она отсечет на ней отрезок р_ε. Величину р_ε – называют давлением связности. Используя это давление, параметр сцепления (связности) грунта можно представить в виде:

Характеристики сопротивления грунтов сдвигу могут быть так же определены по результатам опытов на трехосное сжатие. Прибор для таких испытаний называется – стабилометром.

Т.о., для расчета оснований зданий и сооружений необходимо определить вышеуказанные прочностные характеристики, а именно: угол внутреннего трения и удельное сцепление грунта.

Коэффициент пропорциональности k и электрическая постоянная

В формуле закона Кулона есть параметры k — коэффициент пропорциональности или — электрическая постоянная. Электрическая постоянная представлена во многих справочниках, учебниках, интернете, и её не нужно считать! Коэффициент пропорциональности в вакууме на основе можно найти по известной формуле:

Здесь — электрическая постоянная,

— число пи,

— коэффициент пропорциональности в вакууме.

Чтобы подытожить вышесказанное, необходимо привести официальную формулировку главного закона электростатики. Она принимает вид:

Сила взаимодействия двух покоящихся точечных зарядов в вакууме прямо пропорциональна произведению этих зарядов и обратно пропорциональна квадрату расстояния между ними. Причём произведение зарядов необходимо брать по модулю!

В данной формуле q₁ и q₂ — это точечные заряды, рассматриваемые тела; r2 — расстояние на плоскости между этими телами, взятое в квадрате; k — коэффициент пропорциональности ( для вакуума).

ВНУТРЕННЕЕ СОПРОТИВЛЕНИЕ ГРУНТА СДВИГУ

Внутреннее сопротивление грунта сдвигу происходит в результате действия сил трения между частицами и сцепления между ними:

1. Силы трения. Характеризуют внутреннее сопротивление в идеально сыпучих телах (чистые пески). Трение возникает в точках контакта частиц и зависит от многих факторов, среди которых основными являются: — минеральный состав грунта; — величина зёрен грунта; — форма зёрен (окатанная, пластинчатая, игольчатая); — состояние поверхности (округлая, угловатая); — плотность грунта, степень водонасыщенности и др. Показатель, характеризующий внутреннее трение в грунтах – это угол внутреннего трения (обозначается символом φ , измеряется в градусах).

2. Силы сцепления. Характеризуют сопротивление структурных связей всякому перемещению связываемых ими частиц, независимо от величины внешнего давления. Сцепление (связность) в грунте определяется: — наличием капиллярного давления в грунте; — силами молекулярного притяжения между частицами грунта; — наличием в грунте вяжущих веществ (известь, минеральные смолы, соли). Показатель, характеризующий сцепление в грунтах – удельное сцепление (обозначается символом c , измеряется в паскалях). Каким образом определить внутреннее сопротивление грунта сдвигу, характеризуемое показателями φ и c?

Слайд 413. ОСОБЕННОСТИ ТЕОРИИ ПРОЧНОСТИ КУЛОНА-МОРА Теория прочности Мора имеет две особенности.

Первая заключается в том, что абсолютные значения нормального и касательного

напряжений по площадке сами по себе не оказывают влияния на прочность, а решающее значение имеет отношение этих напряжений. В самом деле, т.к. τ = σ tgp; если увеличить пропорционально значения τ и σ, то отношение τ/σ остается без изменений и будет равно тангенсу угла p (отклонения равнодействующей напряжений р от нормали к площадке). Этот угол p называют углом отклонения. Очевидно, что чем больше угол отклонения, тем меньше при том же p величина σ, и больше τ, и тем ближе состояние грунта к моменту разрушения будет. Значение угла p, при которой наступает сдвиг, называется предельным углом отклонения (обычно обозначается φ). Вторая особенность: проекция напряжений, нормальных к плоскости чертежа на эту плоскость, равна нулю. Поэтому эти напряжения не оказывают влияния на величины τ и σ в рассматриваемой плоскости, а следовательно, и не влияют на их отношение.

Выводы из закона Кулона

Ученый экспериментировал с различной величиной зарядов, проверяя взаимодействие между телами с различной величиной заряда. Разумеется, измерить электрический заряд в каких-либо единицах он не мог – не хватало ни знаний, ни соответствующих приборов. Шарль Кулон смог разделять снаряд, прикасаясь к заряженному шарику незаряженным. Так он получал дробные значения исходного заряда. Ряд опытов показал, что электрический заряд сохраняется, происходит обмен без увеличения или уменьшения количества заряда. Этот фундаментальный принцип лег в основу закона сохранения электрического заряда. В настоящее время доказано, что этот закон соблюдается и в микромире элементарных частиц и в макромире звезд и галактик.