Электромагнитные волны. гипотеза максвелла

3.1 Интегральная по спектру плотность энергии

Проинтегрируем формулу (4.7) главы 2 по всему интервалу

частот:

Переходя, как обычно, к безразмерной

переменной

получим, что плотность энергии

пропорциональна четвёртой степени температуры:

Вычислим безразмерный интеграл в

правой части последней формулы. Он является частным случаем интегралов вида

соответствующим n = 4. Разложим дробь в подынтегральном выражении:

Искомый интеграл представляется в

виде ряда

каждое слагаемое

которого аналитически выражается через гамма-функцию

Следовательно,

Сумма в последней формуле известна

как дзета–функция Римана:

Выпишем ряд её значений, некоторые

из которых понадобятсянам в дальнейшем:

n	z(n)
	аналитич.	число
2	π2/6	1.645
3		1.202
4	π4/90	1.082
5		1.037

Функция z(n)

имеет аналитическое выражение при чётных значениях аргумента. Итак, множитель

пропорциональности в формуле, выражающей зависимость плотности энергии U от температуры T:

(1.1)U = a·T4,

равен

В последней формуле присутствует постоянная Больцмана

= 1.3802·10–16 эрг/К,

означающая, что температура в ней

выражена в градусах Кельвина.

Иногда множитель a называют постоянной Стефана–Больцмана для плотности

энергии. Используется также другая форма закона Стефана–Больцмана, связывающая

полный поток F и температуру чёрного тела:

F = sT4.

Чтобы определить величину s,

необходимо сформулировать модель, в которой поток от чёрного тела отличен от

нуля. Такая модель будет изложена в следующих разделах, а сейчас вычислим

полное число квантов N_ф в единичном объёме

чёрного тела. Для этого проинтегрируем по всем частотам формулу (4.8) второй

главы:

Если измерять температуру в градусах

Кельвина, то

(1.3)N_ф ≈ 20.3·T3.

В качестве примера оценим плотность числа фотонов

реликтового излучения, температура которого, как известно, равна 2.73 К:

Последняя величина значительно

превышает среднюю плотность частиц во Вселенной, которая по разным оценкам

лежит в диапазоне от 10–3 см–3 до 10–6 см–3.

Сфера применения

Где-то начиная с конца XIX столетия, весь человеческий прогресс был связан с практическим применением электромагнитных волн.

Первое о чем стоит упомянуть – радиосвязь. Она дала возможность людям общаться, даже если они находились далеко друг от друга.

Именно эти технологии сформировали информационный облик современного общества.

Источниками электромагнитного излучения следует рассматривать как крупные промышленные объекты, так и различные линии электропередач.

Электромагнитные волны активно используются в военном деле (радары, сложные электрические устройства). Также без их применения не обошлась и медицина. Для лечения многих болезней могут использовать инфракрасное излучение.

С помощью лазеров проводят ряд операций, требующих ювелирной точности.

Важность электромагнитного излучения в практической жизни человека сложно переоценить. Советское видео о электромагнитном поле:

Советское видео о электромагнитном поле:

Точечный источник Телесный угол

При изучении физики мы уже использовали ряд идеализированных моделей (материальная точка, идеальный газ и др.), которые помогали нам при рассмотрении физических явлений и законов. В фотометрии удобно использовать еще одну идеализацию — точечный источник.

Считается, что такой источник равномерно излучает свет во все стороны, а размеры его много меньше расстояния до освещаемой поверхности. Например, если лампа диаметром 10 см освещает поверхность на расстоянии 100 м, то эту лампу можно считать точечным источником. Но если расстояние до поверхности

50 см, то такое предположение сделать нельзя. Типичный пример точечных источников света — звезды. Их размеры огромны (диаметры звезд составляют десятки и сотни тысяч километров), но расстояние от них до Земли на много порядков больше. Понятие телесного угла было введено в десятом классе, при формулировке теоремы Гаусса. Кратко напомним смысл этого понятия. Телесный угол характеризует область пространства, ограниченную конической поверхностью. Для измерения телесного угла следует найти отношение площади поверхности шарового сегмента Soк квадрату радиуса сферы с центром в вершине конуса:

W = SR2

Единица телесного угла — стерадиан(ср). 1 ср равен телесному углу с вершиной в центре сферы, вырезающему на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы. Зная площадь поверхности сферы, можно определить полный телесный угол вокруг точки:

W = 4pR2R2 = 4pср

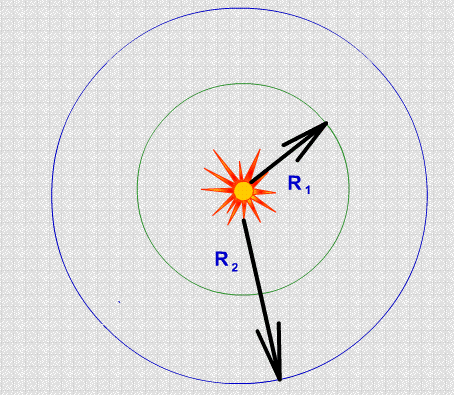
Зависимость интенсивности волны от расстояния до источника и угла падения. Определим, как интенсивность волны зависит от расстояния точечного источника до облучаемой поверхности. Пусть точечный источник находится в центре двух концентрических сфер радиусами R₁и R₂.

Если среда не поглощает (например, вакуум), то полная энергия, переносимая в единицу времени через поверхностьи этих сфер, будет одной и той же. Поэтому

I₁=W/(4pR₁2t), I₂=W/(4pR₂2t),

откуда следует:

I₁/I₂=R₂2/R₁2

В астрономии расстояния до звезд определяют, сравниваяинтенсивностиихизлучения(т.е.ихсветимости).

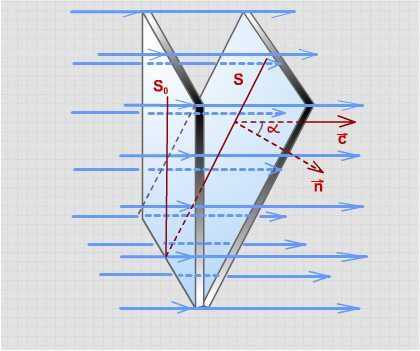
Для целого ряда практических случаев важна зависимость поверхностной плотности потока излучения от угла между направлением распространения волны и нормалью к освещаемой поверхности.

Из рисунка следует, что через поверхности площадью Sи S_oпереносится волной одинаковая энергия. Поэтому I=W/(S_ot) и I=W/(St) и отношение интенсивностей

I/I=S/S=cosa,

откуда

I= Icosa.

Именно этой формулой и пользуются в большей части случаев для расчетов, ведь крайне редко поверхность расположена перпендикулярно световому потоку.

Формула зависимости плотности потока излучения от расстояния до источника

§ 50 ПЛОТНОСТЬ ПОТОКА ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ

Излучаемые электромагнитные волны несут с собой энергию.

Плотность потока излучения. Рассмотрим поверхность площадью S, через которую электромагнитные волны переносят энергию. На рисунке 7.5 изображена такая площадка.

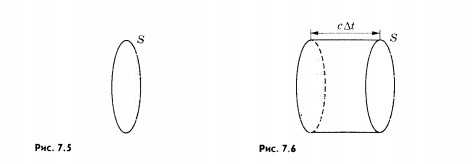
Прямые линии указывают направления распространения электромагнитных волн. Это лучи —линии, перпендикулярные поверхностям, во всех точках которых колебания происходят в одинаковых фазах. Такие поверхности называются волновыми поверхностями (см. § 46). Плотностью потока электромагнитного излучения / называют отношение электромагнитной энергии

Фактически это мощность электромагнитного излучения (энергия в единицу времени), проходящего через единицу площади поверхности. Плотность потока излучения в СИ выражают в ваттах на квадратный метр (Вт/м 2 ). Иногда эту величину называют интенсивностью волны.

Выразим I через плотность электромагнитной энергии и скорость ее распространения с. Выберем поверхность площадью S, перпендикулярную лучам, и построим на ней как на основании цилиндр с образующей c

т. е. плотность потока излучения равна произведению плотности электромагнитной энергии на скорость ее распространения.

Найдем зависимость плотности потока излучения от расстояния до источника. Для этого надо ввести еще одно новое понятие.

Точечный источник излучения. Источники излучения электромагнитных волн могут быть весьма разнообразными. Простейшим является точечный источник.

Источник излучения считается точечным, если его размеры много меньше расстояния, на котором оценивается его действие. Кроме того, предполагается, что такой источник посылает электромагнитные волны по всем направлениям с одинаковой интенсивностью. Точечный источник — такая же идеализация реальных источников, как и другие модели принятые в физике: материальная точка, идеальный газ и т. д.

Звезды излучают свет, т. е. электромагнитные волны Так как расстояния до звезд в огромное число раз превы шают их размеры, то именно звезды представляют собой лучшее реальное воплощение точечных источников.

Зависимость плотности потока излучения от расстояния до точечного источника. Энергия, которую переносят электромагнитные волны, с течением времени распределяется по все большей и большей поверхности. Поэтому энергия, передаваемая через поверхность единичной площадки за единицу времени, т. е. плотность потока излучения, уменьшается по мере удаления от источника.

Поместим точечный источник в центр сферы радиусом R. Площадь поверхности сферы S = 4

Плотность потока излучения от точечного источника убывает обратно пропорционально квадрату расстояния до источника.

Зависимость плотности потока излучения от частоты. Излучение электромагнитных волн происходит при ускоренном движении заряженных частиц (см. § 48). Напряженность электрического поля

Плотность энергии электрического поля пропорциональна квадрату напряженности поля. Энергия магнитного поля, как это можно показать, пропорциональна квадрату магнитной индукции. Полная плотность энергии электромагнитного поля равна сумме плотностей энергий электрического и магнитного полей. С учетом формулы (7.2) плотность потока излучения

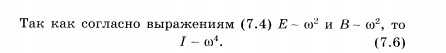Плотность потока излучения пропорциональна четвертой степени частоты.

При увеличении частоты колебаний заряженных частиц в 2 раза излучаемая энергия возрастает в 16 раз! В антеннах радиостанций поэтому возбуждают колебания больших частот: от десятков тысяч до десятков миллионов герц.

Электромагнитные волны переносят энергию. Плотность потока излучения (интенсивность волны) равна произведению плотности энергии на скорость ее распространения. Интенсивность волны пропорциональна четвертой степени частоты и убывает обратно пропорционально квадрату расстояния от источника.

Мякишев Г. Я., Физика. 11 класс : учеб. для общеобразоват. учреждений : базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 17-е изд., перераб. и доп. — М. : Просвещение, 2008. — 399 с : ил.

_{Планирование по физике, учебники и книги онлайн, курсы и задачи по физике для 11 класса скачать}

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.

Физика 9 класс?

120) определите период, частоту и амплитуду колебаний силы переменного тока.

Закон сохранения энергии Ер1 = Ек2 + Ер2 mgh1 = Ek2 + mgh2 3×10×5 = 60 + 3×10h2 150 — 60 = 30h2 h2 = 90 / 30 = 3м Ответ 3м.

R = ρL / S ; S = ρL / R ; ρалюминия = 0. 028 Ом * мм ^ 2 / м ; Uпад = IR ; R = Uпад / I ; R = 1. 5 / 1 = 1. 5 Ом ; S = 0. 028 * 2100 / 1. 5 = 39. 2 мм ^ 2 = 39. 2 * 10 ^ — 6 м ^ 2 ; S = (pi * d ^ 2) / 4 ; d = sqrt(4S / pi) ; d = sqrt(4 * 39. ..

S = (V — V0) ^ 2 / 2 * a = (0 — 6, 94 ^ 2) / — 2 * 2 = 12 м.

Что тут обїяснять, задача в одну формулу ))в последнем віражении под корнем 10 в степени 9, а не в степени — 9. Ответ верній.

L = 40 * 10 ^ — 3 Гн W = 1 Дж I = ? = = = W = L * I² / 2 I = √(2 * W / L) = √(2 * 1 / 0. 04)≈7. 1 A = = = = = = = = = = = = = = = = = = = = = = = = = = = =.

T = 2 * pi * sqrt(L / g) T ^ 2 * g = 4 * pi ^ 2 * L L = T ^ 2 * g / 4 * pi ^ 2 = 1 ^ 2 * 3, 7 / 4 * 9, 86 = 0, 094 м = 9, 4 см.

По формуле периодаТ = 2П * корень квадратный из L * C. ( C — ёмкость, L — индуктивность = 1, 5 * 10 ^ ( — 3)Гн. П = 3, 14, Т — период) . Так как периодТ = лямбда / c. ( лямбда — дина волны, с — скорость света = 3 * 10 ^ 8м / c. ) подставимлямбда..

А = Fs A = 2Н * 0. 5м = 1Дж. Ответ : 1 Дж.

Если брусок двигался равномерно, то пружина действовала с силой 2 Н и брусок переместился на 50см = 0. 5м. А = Fs A = 2Н * 0. 5м = 1Дж. Ответ : 1 Дж.

F = 27 H a = 0. 9 м / с2 m = ? = = = F = m * a m = F / a = 27 / 0. 9 = 30 кг = = = = = = = = = = = = = = = = = = = = = = = = = = = =.

Источник

Среда распространения

Среда распространения — это пространство, в котором проявляются волновые особенности электромагнитного поля. Электромагнитное поле может распространяться в следующих средах.

1. В свободном пространстве, характеризуемом диэлектрической проницаемостью $$\begin{equation} \varepsilon_0=\left(\frac{1}{36\pi}\right)\cdot{10^{-9}}\approx{8,854\cdot{10^{-12}}} \end{equation}\tag{2.1}$$

и магнитной проницаемостью $$\begin{equation} \mu_0=4\pi\cdot{10^{-7}} \end{equation}\tag{2.2}$$

2. В идеальном диэлектрике , характеризуемом относительной диэлектрической проницаемостью ε_r и относительной магнитной проницаемостью μ_r, для которого, следовательно, электрическая проницаемость $$\begin{equation} \varepsilon={\varepsilon_r}{\varepsilon_0} \end{equation}\tag{2.3}$$

а магнитная проницаемость $$\begin{equation} \mu={\mu_r}{\mu_0} \end{equation}\tag{2.4}$$

3. В средах с потерями, обусловленными наличием проводимости, характеризуемых относительной проницаемостью $$\begin{equation} \varepsilon_r^\prime=\varepsilon_r-{I}{60}{\lambda_0}{\sigma} \end{equation}\tag{2.5}$$ где λ — длина волны в вакууме. Для этих сред ε’_r носит комплексный характер.

В табл. 2.1 приведены значения величин ε_rμ_r и σ для некоторых сред. Эти значения справедливы в диапазоне УКВ.

4. В средах с большой проводимостью (частный случай п. 3). характеризуемых большим значением комплексной части ε’_r.

Таблица 2.1. Значения параметров ε_r, μ_r и σ для некоторых сред
Среда распространения	ε_r	μ_r	σ
Воздух	1 ,0005	1
Вода пресная	81	1	10-3
Вода морская	80	1	4
Почва влажная	10	1	10-2
Почва сухая, песок	4	1	10-3
Скалистый грунт	10	1	10-3
Снег	1,4	1	10-3
Лед	3,2	1	10-3
Лесной массив	10	1	10-3
Городской массив	3	1	10-4

Среда распространения является однородной, если ее параметры ε, μ и σ не меняются вдоль направления распространения электромагнитной энергии. Среду распространения, для которой параметры ε, μ и σ не зависят от направления распространения электромагнитной энергии, принято называть изотропной. В противоположность этому, среду, параметры которой зависят от направления распространения волны, называют анизотропной средой.Примером последней может служить ионосфера.

Кроме того, следует отличать дисперсионные и недисперсионные среды, т. е среды, для которых параметры ε_r, σ и μ зависят или не зависят соответственно от частоты электромагнитного колебания. Примером дисперсионной среды также может служить ионосфера.

Волновая, фазовая и групповая скорости

Волновая скорость v — скорость, определенная уравнением (2.10). Для синусоидальной волны точка постоянной фазы перемещается по лучу в направлении распространения волны с волновой скоростью v.

Фазовая скорость v_ф — скорость перемещения точки с постоянной фазой, перемещение которой не обязательно совпадает с направлением распространения волны. Фазовая скорость равна или больше волновой скорости: v_ф ≥ v.

Групповая скорость v_г — скорость перемещения энергии и информации, содержащейся в волне несущей частоты. Ее значение находится в пределах 0 ≤ v_г ≤ v.

Понятия фазовой и групповой скоростей связаны с дисперсионными свойствами среды и играют большую роль при анализе некоторых антенн.

Предположим, что источник S излучает электромагнитную волну частотой f. На рис. 2.4а показано, каким образом происходит распространение волны от источника: сплошными линиями показаны фазовые фронты, отличающиеся друг от друга на 2π, а пунктирными линиями — фазовые фронты, фаза которых отличается от фазы первых фронтов на π. Точка В отстоит от источника S на расстоянии $R=m\lambda$ (на рисунке т = 8). Волна от источника S достигает точки В за время $t_1=\frac{R}{v}=\frac{m\lambda}{v}$. В данной ситуации скорость v совпадает с фазовой скоростью v_ф.

Теперь установим на пути распространения волны SB препятствие, не пропускающее прямую волну (рис. 2.4б). Дополнительно установим по обе стороны от прямой SB два экрана, перпендикулярные плоскости R и целиком отражающие волну. Энергия, излученная источником S под углом α в направлении экранов, после отражения в точках A₃ проходит в точку В. В точке В обе волны складываются и их равнодействующая в направлении SB такова, как если бы преграды не было.

Рассмотрим теперь явления, происходящие на поверхностях экранов Р — Р. Очередные гребни волн частотой f и длиной λ достигают одновременно нескольких точек A₁, A₂, A₃, A₄, … поверхности Р—Р. Расстояния между этими точками составляют l₁₂, l₂₃, l₃₄, … соответственно. Из рисунка видно, что l₁₂ > l₂₃ > l₃₄ и т. д. Напомним, что частота колебания для любой точки на поверхности экранов постоянна.

В начальный момент времени до точки A₃ дойдет гребень волны, обозначенный на рисунке цифрой 5, до точки A₄ — гребень 6. Через время $T=\frac{1}{f}$ до точки A₃ дойдет гребень 4, а до точки A₄ — гребень 5. Следовательно, за время Т гребень 5 прошел вдоль поверхности экрана Р — Р отрезок l₃₄ со скоростью v_ф34= l₃₄/T = l₃₄f. Это и есть фазовая скорость. Можно просто показать, что $$\begin{equation} v_ф=\frac{v}{\cos\alpha} \end{equation}\tag{2.15а}$$

Заметим, что эта скорость различна в разных местах экрана и при α→0 приближается к волновой скорости v.

Понятие фазовой скорости можно проиллюстрировать, рассмотрев распространение волн на воде. Предположим, что линия Р—Р есть линия берега моря. По морю бежит волна, падающая на берег под углом α. Предположим также, что перед нами стоит такая задача: во-первых, плыть строго вдоль прямой линии берега и, во-вторых, удерживаться все время на гребне волны. Рассмотрим ряд случаев. Первая ситуация: волна перпендикулярна линии берега, т. е. α=90°. Для того чтобы выполнить сформулированную выше задачу, необходимо плыть вдоль линии берега с бесконечно большой скоростью. Вторая ситуация: волна параллельна линии берега, т. е α=0°. Теперь для того чтобы выполнить ту же задачу, достаточно плыть со скоростью перемещения волны. Первая ситуация является аналогом распространения с бесконечно большой фазовой скоростью, а вторая — с фазовой скоростью, равной скорости перемещения.

Перейдем теперь к рассмотрению луча, отраженного от точки A₃. Из физики (в частности, из оптики) хорошо известно, что угол падения равен углу отражения. Поэтому можно записать, что SA₃=A₃B. На каждом отрезке полупути укладывается n длин волн, т. е. на всем пути — 2п длин волн (на рисунке п=5). Ранее на прямом пути умещалось m длин волн и этот путь волна проходила за время t₁ = mλ/v (рис. 2.4а). При переотражении время распространения составляет t₂ = nλ/v, а так как т<п, то t₂>t₁. Скорость распространения волны от точки S до точки В равна v_г=SB/t₂. Можно легко показать, что групповая скорость $$\begin{equation} v_г=v\cos\alpha \end{equation}\tag{2.15б}$$

Из приведенной формулы следует, что значение групповой скорости зависит от угла α, и в предельных случаях групповая скорость может быть равна волновой скорости (v_г=v) или нулю (v_г=0).

Из формул (2.13) и (2.14) следует, что $$\begin{equation} {v_г}{v_ф}=v^2 \end{equation}\tag{2.15в}$$

Фотометрические величины

Наряду с энергетическими характеристиками важную роль в науке, технике и практической деятельности играют фотометрические характеристики, описывающие видимое излучение, т. е. ту часть спектра электромагнитных волн, которая воспринимается нашим глазом. Так, с потоком излучения непосредственно связана субъективная характеристика света — световой поток: мощность оптического излучения, оцениваемая по вызываемому им световому ощущению. Световой поток обозначается буквой Ф_v. Единицей светового потока в СИ служит люмен (лм).

Важнейшая характеристика любого источника света — сила света I_v. Она определяется отношением светового потока Ф_v к телесному углу W, внутри которого этот поток распространяется:

I_v = Ф_vW.

Так как телесный угол вокруг точки равен 4p, то сила света точечного источника определяется из соотношения:

I_v = Ф_v4p

В Международной системе единиц единица силы света — к а н д е л а (кд) — является основной. Кандела равна силе света в заданном направлении источника, испускающего монохроматическое излучение частотой 5,40*1014 Гц, энергетическая сила света которого в этом направлении составляет 1,683 Вт/ср. Заметим, что данная частота соответствует максимальной чувствительности человеческого глаза, т. е. длине волны в вакууме, равной 555 нм.

Все остальные фотометрические единицы выражаются через канделу. Так, люмен равен световому потоку, испускаемому точечным источником силой света 1 кд в телесном угле, равном 1 ср.

Пусть на некоторую поверхность падает световой поток Ф. Очевидно, чем больше площадь этой поверхности, тем меньшая часть светового потока попадает на каждый участок, тем темнее этот участок. Освещенность E_vсвязывает световой поток с площадью той поверхности, на которую этот поток падает. Освещенность в данной точке поверхности равна отношению светового потока, падающего на элемент поверхности, к площади этого элемента:

E_v = DФ_v/DS

Единица освещенности в СИ — л ю к с (лк) — равен освещенности поверхности площадью 1 м2 при падающем на нее световом потоке1лм, равномерно распределенном по этой поверхности.

Защита от электромагнитных излучений

Если вы проводите много времени за компьютером, запомните одно правило: расстояние между лицом и монитором должно быть около метра.
Уровень электромагнитного излучения бытовой техники, которую вы покупаете, не должен доходить до о. Обратитесь к продавцу-консультанту. Он поможет выбрать наиболее безопасную технику.
Ваша кровать не должна находиться рядом с местом, где проложена электропроводка. Расположите спальное место в противоположном конце комнаты.
Установите защитный экран на компьютер. Он выполнен в виде мелкой металлической сетки и действует по принципу Фарадея: вбирает в себя все излучение, защищая пользователя.
Сократите пребывание в электрифицированном общественном транспорте. Отдавайте предпочтение пешей ходьбе, велосипеду.

Что такое электромагнитное излучение?

Электромагнитное излучение – это колебания электрического и магнитного полей. Скорость распространения в вакууме равна скорости света (около 300 000 км/с). В других средах скорость распространения излучения меньше. Электромагнитное излучение классифицируется по частотным диапазонам. Границы между диапазонами весьма условны, в них нет резких переходов.

Видимый свет. Это самый узкий диапазон во всем спектре. Человек может воспринимать только его. Видимый свет сочетает в себе цвета радуги: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый. За красным цветом находится инфракрасное излучение, за фиолетовым – ультрафиолетовое, но они уже не различимы человеческим глазом.

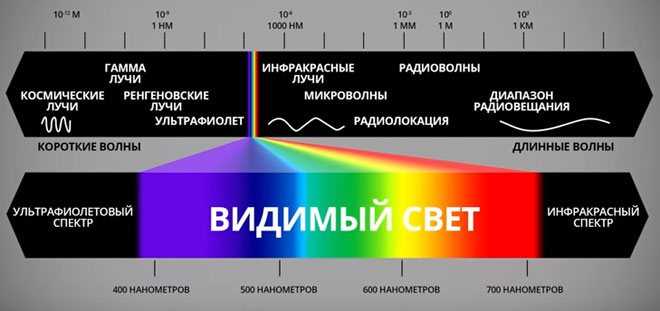
Волны видимого света очень короткие и высокочастотные. Длина таких волн – одна миллиардная часть метра или один миллиард нанометров. Видимый свет от Солнца – своеобразный коктейль, в котором смешаны три основных цвета: красный, желтый и синий.

Ультрафиолетовое излучение – часть спектра между видимым светом и рентгеном. Ультрафиолетовое излучение используется для создания световых эффектов на сцене театра, дискотеках; банкноты некоторых стран содержат защитные элементы, видимые только при ультрафиолете.
Инфракрасное излучение является частью спектра между видимым светом и короткими радиоволнами. Инфракрасное излучение – это скорее тепло, чем свет: каждое нагретое твердое или жидкое тело испускает непрерывный инфракрасный спектр. Чем выше температура нагревания, тем короче длина волны и выше интенсивность излучения.
Рентгеновское излучение (рентген). Волны рентгеновского излучения обладают свойством проходить сквозь вещество и не поглощаться слишком сильно. Видимый свет такой способностью не обладает. Благодаря рентгену некоторые кристаллы могут светиться.
Гамма-излучение – это наиболее короткие электромагнитные волны, которые проходят сквозь вещество без поглощения: они могут преодолеть однометровую стену из бетона и свинцовую преграду толщиной в несколько сантиметров.

Виды электромагнитных волн

Все электромагнитное излучение делят по частоте.

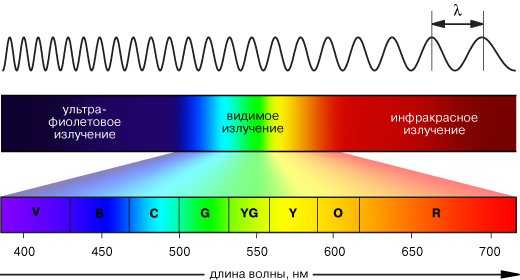
1. Радиоволны. Бывают короткими, ультракороткими, сверхдлинными, длинными, средними.

Их источниками может быть как деятельность человека, так и различные естественные атмосферные явления.

2. Инфракрасное излучение. Длина волны лежит в пределах 1мм — 780нм, а частота может доходить до 429 ТГц. Инфракрасное излучение еще называют тепловым. Основа всей жизни на нашей планете.

3. Видимый свет. Длина 400 — 760/780нм. Соответственно частота колеблется в пределах 790-385 ТГц. Сюда относят весь спектр излучения, которое можно увидеть человеческим глазом.

4. Ультрафиолет. Длина волны меньше, чем в инфракрасного излучения.

5. Рентгеновские лучи. частота волны 6х10^19 Гц, а длина порядка 10нм — 5пм.

6. Гамма волны. Сюда относят любое излучение, частота которого больше, чем в рентгеновских лучах, а длина – меньше. Источником таких электромагнитных волн являются космические, ядерные процессы.

Интенсивность плоской электромагнитной волны

Допустим, что плоская монохроматическая волна распространяется в вакууме по оси X. Это означает, что напряженности этой волны можно записать при помощи уравнений:

$E=E_0\sin{\left(\omega{}t-kx\right),}$

$H=H_0\sin{\left(\omega{}t-kx\right)\ \left(12\right),}$

где $k=\frac{2\pi{}}{\lambda{}}$ .

Мгновенная величина вектора Умова – Пойнтинга равна:

$P=EH=E_0H_0{sin}^2\left(\omega{}t-kx\right)\left(13\right).$

От полученной в (13) величины мы должны взять среднее по времени:

$I=\left\langle{}\vec{P}\right\rangle{}=\frac{1}{T}\left\vert{}\int_0^TPdt\right\vert{}=\frac{E_0H_0}{2}\left(14\right).$

Наша волна распространяется в вакууме ($\epsilon{}=1;\ \mu{}=1$) и

$\sqrt{{\epsilon{}}_0}E=\sqrt{{\mu{}}_0}H\left(15\right),$

Окончательно имеем:

$I=\sqrt{\frac{{\epsilon{}}_0}{{\mu{}}_0}}\frac{E_0^2}{2}\ \left(16\right).$

Выражение (16) показывает, что интенсивность плоской, линейно поляризованной волны пропорциональна квадрату амплитуды напряженности поля.

Для произвольной плоской волны в однородной среде при отсутствии поглощения интенсивность электромагнитной волны постоянна.
В стоячей электромагнитной волне интенсивность равна нулю.
Для сферической электромагнитной волны в среде без поглощения интенсивность волны изменяется только в зависимости от расстояния от ее центра ($r$) и можно считать, что:

$I=\frac{const}{r^2}\left(17\right).$

Определение понятия

Электромагнитное излучение определяется как изменённое состояние электромагнитного поля. Оно порождается движением электрических зарядов и способно воздействовать на человека вдали от источника, уменьшая своё воздействие с увеличением расстояния.

Излучение представляет собой волны, которые подразделяются на следующие виды:

радиоизлучение;
инфракрасное;
терагерцовое;
ультрафиолет;
видимый свет;
рентген.

Первым признаком повышения нормы электромагнитного излучения в квартире или производственном помещении являются неправильная работа бытовых приборов (их поломка и сбои), помехи при воспроизведении изображения и звука на телевизоре, неправильная работа персональных компьютеров, помехи в радиосвязи.

План

1. Вступление ……………………………………………………… 3

2. Понятие волна и ее характеристики…………………………… 4

3. Электромагнитные волны……………………………………… 5

4. Экспериментальное доказательство существования электромагнитных волн………………………………………… 6

5. Плотность потока электромагнитного излучения ……………. 7

6. Изобретение радио …………………………………………….… 9

7. Свойства электромагнитных волн ………………………………10

8. Модуляция и детектирование…………………………………… 10

9. Виды радиоволн и их распространение………………………… 13

Вступление

Волновые процессы чрезвычайно широко распространены в природе. В природе существует два вида волн: механические и электромагнитные. Механические волны распространяются в веществе: газе, жидкости или твердом теле. Электромагнитные волны не нуждаются в каком-либо веществе для своего распространения, к которым, в частности, относятся радиоволны и свет. Электромагнитное поле может существовать в вакууме, т. е. в пространстве, не содержащем атомов. Несмотря на существенное отличие электромагнитных волн от механических, электромагнитные волны при своем распространении ведут себя подобно механическим. Но подобно колебаниям все виды волн описываются количественно одинаковыми или почти одинаковыми законами. В своей работе я постараюсь рассмотреть причины возникновения электромагнитных волн, их свойства и применение в нашей жизни.

Установленные нормы ЭМИ для человека

Каждый орган в нашем теле вибрирует. Благодаря вибрации вокруг нас создается электромагнитное поле, содействующее гармоничной работе всего организма. Когда на наше биополе воздействуют другие магнитные поля, это вызывает в нем изменения. Иногда организм справляется с влиянием, иногда – нет. Это становится причиной ухудшения самочувствия.

Даже большое скопление людей создает электрический заряд в атмосфере. Полностью изолироваться от электромагнитного излучения невозможно. Есть допустимый уровень ЭМИ, который лучше не превышать.

Вот безопасные для здоровья нормы:

30-300 кГц, возникающие при напряженности поля 25 Вольт на метр (В/м),
0,3-3 МГц, при напряженности 15 В/м,
3-30 МГц – напряженность 10 В/м,
30-300 МГц – напряженность 3 В/м,
300 МГц-300 ГГц – напряженность 10 мкВт/см2.

При таких частотах работают гаджеты, радио- и телеаппаратура.

Презентация на тему: » Сегодня четверг, 12 марта 2015 г. Интенсивность волны Поток энергии электромагнитной волны энергия электромагнитного излучения, проходящего в единицу.» — Транскрипт:

Сегодня четверг, 12 марта 2015 г.

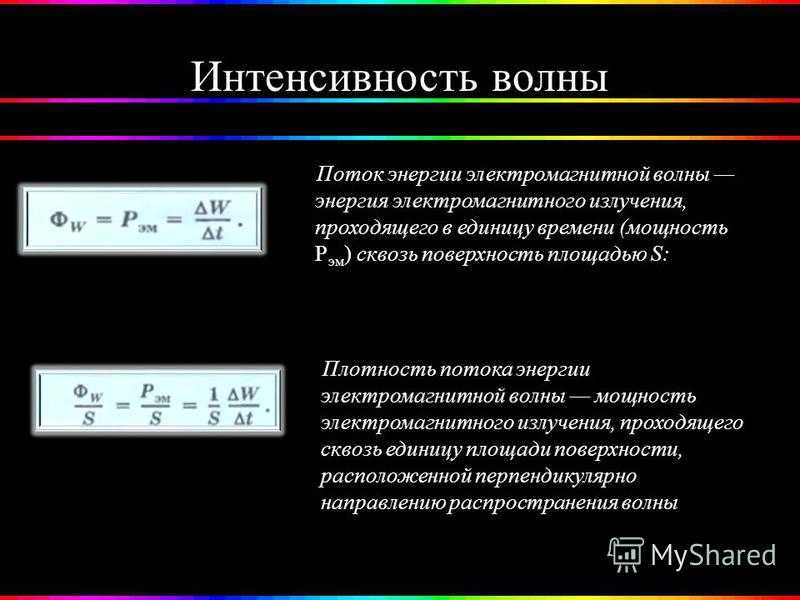
Интенсивность волны Поток энергии электромагнитной волны энергия электромагнитного излучения, проходящего в единицу времени (мощность Р эм ) сквозь поверхность площадью S: Плотность потока энергии электромагнитной волны мощность электромагнитного излучения, проходящего сквозь единицу площади поверхности, расположенной перпендикулярно направлению распространения волны

интенсивность электромагнитной волны интенсивность гармонической электромагнитной волны пропорциональна квадрату амплитуды напряженности электрического поля

Интенсивность излучения точечного источника убывает обратно пропорционально квадрату расстояния до источника.

энергия излучаемой электромагнитной Средняя энергия излучаемой электромагнитной волны (и соответственно ее интенсивность) прямо пропорциональна среднему квадрату ускорения излучающей заряженной частицы Интенсивность гармонической электромагнитной волны прямо пропорциональна четвертой степени ее частоты.

задача

Задача ЕГЭ

вопросы 1. Как определяют поток и плотность потока энергии электромагнитной волны? Ответ Поток энергии электромагнитной волны – это энергия электромагнитного излучения, которое проходит сквозь поверхность площадью S в единицу времени. Плотность потока энергии электромагнитной волны – это мощность электромагнитного излучения, которое проходит через единицу площади поверхности, расположенной перпендикулярно направлению распространения волны.

вопросы 2. Какая физическая величина характеризует перенос средней мощности электромагнитной волной? Ответ Перенос средней мощности электромагнитной волной характеризуется интенсивностью электромагнитной волны.

вопросы 3. Как интенсивность гармонической электромагнитной волны зависит от амплитуды напряженности электрического поля в волне? Ответ Интенсивность гармонической электромагнитной волны прямо пропорциональна квадрату амплитуды напряженности электрического поля.

вопросы 4. Как интенсивность электромагнитной волны зависит от расстояния до источника? Что можно сказать о зависимости напряженности электрического поля от этого расстояния? Ответ Интенсивность электромагнитной волны обратно пропорциональна квадрату расстояния до источника. Напряженность электрического поля обратно пропорциональна расстоянию до источника.

вопросы 5. Как интенсивность электромагнитной волны зависит от ее частоты? Объясните, почему энергетически выгодно излучение электромагнитных волн больших частот. Ответ Интенсивность гармонической электромагнитной волны пропорциональна четвертой степени ее частоты. Так как излучение электромагнитных волн больших частот требует меньшей мощности передатчика, то оно энергетически более выгодно.