Энергетическая светимость

Световой поток

Световой поток F является одной из основных световых величин
и представляет собой тот же лучистый поток, но оценивается по световому
ощущению, которое он производит на глаз человека. Т. е. световой поток —
это величина, образуемая от лучистого потока путем умножения
на коэффициенты спектральной чувствительности глаза по каждой из длин
волн видимого спектра.

Если энeргия излучается только на одной из длин волн λ,
то световой поток этого монохроматического излучения будет равен:

F_λ = F_eλ·V(λ)

При таком представлении световой поток измеряется в ваттах, как
и лучистый. Чтобы различать эти потоки, для обозначения светового потока
добавляется слово «световой», т. е. получается световой ватт. Правда,
такая размерность светового потока практически не используется,
поскольку система СИ рекомендует в качестве единиц светового потока
люмены (от лат. lumen — свет).

Международным комитетом мер и весов в 1977 г. было
принято, что в фотометрии лучистый поток
1 Вт на длине волны в λ=555 нм (частота
излучения — 540.1012 Гц), обладающего наибольшей световой
эффективностью, эквивалентен световому потоку 683 лм. Почему коэффициент
для пересчета световых ватт в люмены равняется 683, будет рассказано
ниже при рассмотрении понятия силы света. С учетом этого коэффициента
формула для расчета светового потока (в люменах) для монохроматического
излучения примет вид:

F = 683·F_eλ·V(λ)

Для определения светового потока во всем диапазоне видимых излучений
(380…780 нм) необходимо просуммировать все световые потоки
монохроматических составляющих:

F = 683·∑ F_eλ·V(λ)

Таким образом, чтобы получить световой поток, излучаемый на любой
длине волны видимого спектра, необходимо умножить 683 лм/Вт
на соответствующий коэффициент относительной спектральной
чувствительности (см. рис.1 и табл.1) и на значение лучистого потока
на этой длине волны.

Например, световой поток натриевой лампы состоит из излучений
на 589 нм и 589,6 нм. Из данных, приведенных в табл. 1, следует, что при
лучистом потоке (мощности лампы), равном 10 Вт, V(589 нм) = 0,77,
V(589,6 нм) = 0,765, световой поток составит:

F = 683·5·0,77 + 683·5·0,765 = 5242,025 лм.

Значения световых потоков для некоторых источников света приведены в табл. 2.

Таблица 2. Световые потоки некоторых источников света
Источник света	Световой поток, лм
Лампа накаливания 220 В, 100 Вт	1000
Лампа накаливания 220 В, 1000 Вт	17000
Лампа накаливания 110 В, 10000 Вт	295000
Лампа накаливания 220 В, 100 Вт	400000
Поток, падающий на один квадратный метрповерхности Земли в ясный солнечный день	100000

В качестве эталона одного люмена принят световой поток, излучаемый
с поверхности абсолютно черного тела площадью 0,5305 мм² при температуре
затвердевания платины, равной 2046°К. Государственный эталон,
соответствующий международным соглашениям, был разработан профессором П.
М. Тиходеевым. Он представляет собой двойной сосуд из оксида тория,
заполненный платиной. Выходное отверстие сосуда формирует трубка
из оксида тория, погруженная в платину. При расплавлении платины (под
воздействием индукционных токов) отверстие трубки светится, как
абсолютно черное тело.

Фотометрические величины

Наряду с энергетическими харак­теристиками важную роль в науке, технике и практической дея­тельности играют фотометрические характеристики, описывающие видимое излучение, т. е. ту часть спектра электромагнитных волн, которая воспринимается нашим глазом. Так, с потоком излучения непосредственно связана субъективная характеристика света — световой поток: мощность оптического излучения, оцени­ваемая по вызываемому им световому ощущению. Световой по­ток обозначается буквой Ф_v. Единицей светового потока в СИ служит люмен (лм).

Важнейшая характеристика любого источника света — сила света I_v. Она определяется отношением светового потока Ф_v к телесному углу W, внутри которого этот поток распространяется:

I_v = Ф_vW.

Так как телесный угол вокруг точки равен 4p, то сила света точечного источника определяется из соотношения:

I_v = Ф_v4p

В Международной системе единиц единица силы света — к а н д е л а (кд) — является основной. Кандела равна силе света в заданном направлении источника, испускающего монохрома­тическое излучение частотой 5,40*1014 Гц, энергетическая сила света которого в этом направлении составляет 1,683 Вт/ср. За­метим, что данная частота соответствует максимальной чувстви­тельности человеческого глаза, т. е. длине волны в вакууме, равной 555 нм.

Все остальные фотометрические единицы выражаются через канделу. Так, люмен равен световому потоку, испускаемому точечным источником силой света 1 кд в телесном угле, равном 1 ср.

Пусть на некоторую поверхность падает световой поток Ф. Очевидно, чем больше площадь этой поверхности, тем меньшая часть светового потока попадает на каждый участок, тем темнее этот участок. Освещенность E_vсвязывает световой поток с пло­щадью той поверхности, на которую этот поток падает. Освещен­ность в данной точке поверхности равна отношению светового потока, падающего на элемент поверхности, к площади этого элемента:

E_v = DФ_v/DS

Единица освещенности в СИ — л ю к с (лк) — равен освещен­ности поверхности площадью 1 м2 при падающем на нее световом потоке1лм, равномерно распределенном по этой поверхности.

Свойства теплового излучения.

• Тепловое излучение происходит по всему спектру частот от нуля до бесконечности
• Интенсивность теплового излучения неравномерна по частотам и имеет явно выраженный максимум при определенной частоте
• C ростом температуры общая интенсивность теплового излучения возрастает
• C ростом температуры максимум излучения смещается в сторону больших частот (меньших длин волн)
• Тепловое излучение характерно для тел независимо от их агрегатного состояния
• Самым важным и отличительным свойством теплового излучения является равновесный характер излучения. Это значит что если мы поместим тело в термоизолированный сосуд, то количество поглощаемой энергии всегда будет равно количеству испускаемой энергии.

Световой аналог

В системе световых фотометрических величин аналогом энергетической светимости является светимость \displaystyle{ M_v }. По отношению к энергетической светимости светимость является редуцированной фотометрической величиной, получаемой с использованием значений относительной спектральной световой эффективности монохроматического излучения для дневного зрения \displaystyle{ V(\lambda) }:

\displaystyle{ M_v=K_m \cdot \int\limits_{380~nm}^{780~nm}M_{e,\lambda}(\lambda)V(\lambda) d\lambda, }

где \displaystyle{ K_m } — максимальная световая эффективность излучения, равная в системе СИ 683 лм/Вт. Её численное значение следует непосредственно из определения канделы.

Энергетические фотометрические величины СИ[править | править код]

Сведения о других основных энергетических фотометрических величинах и их световых аналогах приведены в таблице. Обозначения величин даны по ГОСТ 26148—84.

Энергетические фотометрические величины СИ

Наименование (синоним)	Обозначение величины	Определение	Обозначение единиц СИ	Световая величина
Энергия излучения (лучистая энергия)	Qe{\displaystyle Q_{e}} или W{\displaystyle W}	Энергия, переносимая излучением	Дж	Световая энергия
Поток излучения (лучистый поток)	Φ{\displaystyle \Phi }e или P{\displaystyle P}	Φe=dQedt{\displaystyle \Phi _{e}={\frac {dQ_{e}}{dt}}}	Вт	Световой поток
Сила излучения (энергетическая сила света)	Ie{\displaystyle I_{e}}	Ie=dΦedΩ{\displaystyle I_{e}={\frac {d\Phi _{e}}{d\Omega }}}	Вт·ср−1	Сила света
Объёмная плотность энергии излучения	Ue{\displaystyle U_{e}}	Ue=dQedV{\displaystyle U_{e}={\frac {dQ_{e}}{dV}}}	Дж·м−3	Объёмная плотность световой энергии
Энергетическая яркость	Le{\displaystyle L_{e}}	Le=d2ΦedΩdS1cos⁡ε{\displaystyle L_{e}={\frac {d^{2}\Phi _{e}}{d\Omega \,dS_{1}\,\cos \varepsilon }}}	Вт·м−2·ср−1	Яркость
Интегральная энергетическая яркость	Λe{\displaystyle \Lambda _{e}}	Λe=∫tLe(t′)dt′{\displaystyle \Lambda _{e}=\int _{0}^{t}L_{e}(t’)dt’}	Дж·м−2·ср−1	Интегральная яркость
Облучённость (энергетическая освещённость)	Ee{\displaystyle E_{e}}	Ee=dΦedS2{\displaystyle E_{e}={\frac {d\Phi _{e}}{dS_{2}}}}	Вт·м−2	Освещённость
Энергетическая экспозиция	He{\displaystyle H_{e}}	He=dQedS2{\displaystyle H_{e}={\frac {dQ_{e}}{dS_{2}}}}	Дж·м−2	Световая экспозиция
Спектральная плотность энергии излучения	Qe,λ{\displaystyle Q_{e,\lambda }}	Qe,λ=dQedλ{\displaystyle Q_{e,\lambda }={\frac {dQ_{e}}{d\lambda }}}	Дж·м−1	Спектральная плотность световой энергии

Здесь dS1{\displaystyle dS_{1}} — площадь элемента поверхности источника,
dS2{\displaystyle dS_{2}} — площадь элемента поверхности приёмника,
ε{\displaystyle \varepsilon } — угол между нормалью к элементу поверхности источника и направлением наблюдения.

Слайд 355. Яркость.Величина показывающая отношение силы света, излучаемого поверхностью, к площади её

проекции на плоскость, перпендикулярную оси наблюдения.Яркость L —величина, равная отношению потока d2Ф к геометрическому фактору dФdAcos(альфа)

Яркость, излучаемая поверхностью dS под углом альфа к нормали этой поверхности, равняется отношению силы света I, излучаемого в данном направлении, к площади проекции излучающей поверхности на плоскость, перпендикулярную данному направлению.

Здесь

— заполненный излучением телесный угол

— площадь участка, испускающего или принимающего излучение,

— угол между перпендикуляром к этому участку и направлением излучения. Из общего определения яркости следуют два практически наиболее интересных частных определения:

Энергетические фотометрические величины СИ

Сведения о других основных энергетических фотометрических величинах и их световых аналогах приведены в таблице. Обозначения величин даны по ГОСТ 26148—84.

Энергетические фотометрические величины СИ

Наименование (синоним)	Обозначение величины	Определение	Обозначение единиц СИ	Световая величина
Энергия излучения (лучистая энергия)	\displaystyle{ Q_e } или \displaystyle{ W }	Энергия, переносимая излучением	Дж	Световая энергия
Поток излучения (лучистый поток)	\displaystyle{ \Phi }e или \displaystyle{ P }	\displaystyle{ \Phi_e=\frac{dQ_e}{dt} }	Вт	Световой поток
Сила излучения (энергетическая сила света)	\displaystyle{ I_e }	\displaystyle{ I_e=\frac{d\Phi_e}{d\Omega} }	Вт·ср−1	Сила света
Объёмная плотность энергии излучения	\displaystyle{ U_e }	\displaystyle{ U_e=\frac{dQ_e}{dV} }	Дж·м−3	Объёмная плотность световой энергии
Энергетическая яркость	\displaystyle{ L_e }	\displaystyle{ L_e=\frac{d^2\Phi_e}{d\Omega\,dS_1\,\cos\varepsilon} }	Вт·м−2·ср−1	Яркость
Интегральная энергетическая яркость	\displaystyle{ \Lambda_e }	\displaystyle{ \Lambda_e=\int_0^t L_e(t’) dt’ }	Дж·м−2·ср−1	Интегральная яркость
Облучённость (энергетическая освещённость)	\displaystyle{ E_e }	\displaystyle{ E_e=\frac{d\Phi_e}{dS_2} }	Вт·м−2	Освещённость
Энергетическая экспозиция	\displaystyle{ H_e }	\displaystyle{ H_e=\frac{dQ_e}{dS_2} }	Дж·м−2	Световая экспозиция
Спектральная плотность энергии излучения	\displaystyle{ Q_{e,\lambda} }	\displaystyle{ Q_{e,\lambda}=\frac{dQ_e}{d\lambda} }	Дж·м−1	Спектральная плотность световой энергии

Здесь \displaystyle{ dS_1 } — площадь элемента поверхности источника,
\displaystyle{ dS_2 } — площадь элемента поверхности приёмника,
\displaystyle{ \varepsilon } — угол между нормалью к элементу поверхности источника и направлением наблюдения.

Спектральная плотность энергетической светимости[править | править код]

Спектральная плотность энергетической светимости Me,λ(λ){\displaystyle M_{e,\lambda }(\lambda )} — отношение величины энергетической светимости dMe(λ),{\displaystyle dM_{e}(\lambda ),} приходящейся на малый спектральный интервал dλ,{\displaystyle d\lambda ,}, заключённый между λ{\displaystyle \lambda } и λ+dλ{\displaystyle \lambda +d\lambda }, к ширине этого интервала:

Me,λ(λ)=dMe(λ)dλ.{\displaystyle M_{e,\lambda }(\lambda )={\frac {dM_{e}(\lambda )}{d\lambda }}.}

Единицей измерения Me,λ{\displaystyle M_{e,\lambda }} в системе СИ является Вт·м−3. Поскольку длины волн оптического излучения принято измерять в нанометрах, то на практике часто используется Вт·м−2·нм−1.

Иногда в литературе Me,λ{\displaystyle M_{e,\lambda }} именуют спектральной испускательной способностью.

Слайд 14Рэлееевское рассеяние — когерентное рассеяние света без изменения длины волны (называемое также

упругим рассеянием) на частицах, неоднородностях или других объектах, когда частота рассеиваемого света существенно меньше собственной частоты рассеивающего объекта или системы. Эквивалентная формулировка: рассеяние света на объектах, размеры которых меньше его длины волны.Рассеяние света сферической частицей (рассеяние крупными частицами)— классическая задача электродинамики, решённая в 1908 году Густавом Ми для сферической частицы произвольного размера. Рассеяние зависит от соотношения размеров частицы и длины волны, которая падает на частицу. В случае, когда частица намного меньше длины волны, рассеяние является частным случаем релеевского.Рассееянием Мандельштама — Бриллюэна называют рассеяние оптического излучения конденсированными средами (твердыми телами и жидкостями) в результате его взаимодействия с собственными упругими колебаниями этих сред. Оно сопровождается изменением набора частот (длин волн), характеризующих излучение, — его спектрального состава. Например, рассеяние Мандельштама — Бриллюэна монохроматического света приводит к появлению шести частотных компонент рассеянного света, в жидкостях — трёх (одна из них — неизмененной частоты).

Слайд 9ДифракцияНаряду с интерференцией другим примером общего для всех волновых процессов явления

может служить дифракция — огибание волнами препятствий. Для световых волн дифракция проявляется в отклонении от прямолинейного распространения и загибании света в область геометрической тени. Характерной особенностью дифракционных явлений в оптике оказывается то, что здесь, как правило, длина волны света почти всегда много меньше размеров преград на пути световых волн. Поэтому наблюдать дифракцию света можно только на достаточно больших расстояниях от преграды. Проявление дифракции состоит в том, что распределение освещенности отличается от простой картины, предсказываемой геометрической оптикой на основе прямолинейного распространения света. В результате дифрации мы можем наблюдать в частности появление светлых и темных участков – дифракционных полос.

Слайд 15Комбинационное рассеяние света (эффект Рамана) — неупругое рассеяние оптического излучения на молекулах

вещества (твёрдого, жидкого или газообразного), сопровождающееся заметным изменением частоты излучения. В отличие от рэлеевского рассеяния, в случае комбинационного рассеяния света в спектре рассеянного излучения появляются спектральные линии, которых нет в спектре первичного (возбуждающего) света. Число и расположение появившихся линий определяется молекулярным строением вещества.Эффект Тиндаля, рассеяние Тиндаля — оптический эффект, рассеивание света при прохождении светового пучка через оптически неоднородную среду. Обычно наблюдается в виде светящегося конуса (конус Тиндаля), видимого на тёмном фоне.

Яркость

Рис. 6. К определению яркости поверхности

Яркость поверхности изотропных излучателей для заданного
направления — это отношение силы света, излучаемого в данном
направлении, к площади проекции светящейся поверхности на плоскость,
перпендикулярную к этому направлению (рис. 6):

L = I / (S·cosφ).

При равномерном освещении диффузно отражающей поверхности уравнение,
связывающее яркость этой поверхности с ее освещенностью, будет иметь
вид:

L = ρ·E / π.

где ρ — коэффициент отражения поверхности.

Яркость — единственная из световых величин, которую глаз воспринимает
непосредственно, и при отсутствии поглощения света в среде
распространения она не зависит от расстояния. Уравнение, связывающее
яркость объекта L, освещенность E_зр, создаваемую этим
объектом на зрачке глаза, и телесный угол ω, в пределах которого глаз
видит данный объект, можно представить как:

L = E_зр / ω.

Таким образом, при удалении глаза от объекта, освещенность E_зр
на его зрачке снижается, при этом одновременно уменьшается
телесный угол ω, но значение яркости L остается неизменным
(рис. 7).

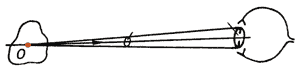Рис. 7. Восприятие глазом яркости

Единицей яркости является кандела на квадратный метр (кд / м²).
1 кд / м² — это яркость такой плоской поверхности, которая
в перпендикулярном направлении излучает силу света в 1 кд с
1 м² поверхности.

До момента принятия системы СИ в качестве основной единицы яркости
использовали нит (нт, от лат. niteo — блестеть), численно эта единица
эквивалентна кд / м².

Другой применяемой несистемной единицей является стильб (сб,
от греческого stilbio — блестящий): 1 сб = 10000 нт = 10000 кд / м².

Часто в качестве несистемной единицы для измерения и расчета яркости
отражающих свет поверхностей используется апостильб: 1 асб = 1 / π
кд / м². Один апостильб — это яркость абсолютно белой, диффузно
отражающей поверхности, имеющей освещенность, равную 1 люкс. При
расчетах яркости диффузно отражающей поверхности в апостильбах яркость
рассчитывается по формуле:

L = ρ·E.

В США в качестве несистемной единицы яркости широко используется
ламберт (лб), получившая свое название в честь немецкого ученого
И. Ламберта. Коэффициенты для пересчета различных единиц яркости
приведены в табл.3.

Таблица 3. Коэффициенты для пересчета различных единиц яркости
Единицы яркости	кд/м²	Асб	сб	лб	кд/ф²	фут-лб	мллб
Кандела/м²	1	3,14	0,0001	0,000314	0,0929	0,2919	0,3142
Апостильб	0,318	1	0,000032	0,0001	0,0296	0,0929	0,1
Стильб	10000	31416	1	3,14	929	2919	3142
Ламберт	3183	10000	0,318	1	296	929	1000
Миллиламберт	3,18	10	0,000318	0,001	0,296	0,929	1
Фут-ламберт	3,43	10,764	0,000343	0,0011	0,318	1	1,0764
Кандела/кв.фут	10,764	33,82	0,0011	0,0034	1	3,14	3,382

Александр Прядкоhttp://rus.625-net.ru

Спектральная плотность энергетической светимости

Спектральная плотность энергетической светимости \displaystyle{ M_{e,\lambda}(\lambda) } — отношение величины энергетической светимости \displaystyle{ dM_e(\lambda), } приходящейся на малый спектральный интервал \displaystyle{ d\lambda, }, заключённый между \displaystyle{ \lambda } и \displaystyle{ \lambda+d\lambda }, к ширине этого интервала:

\displaystyle{ M_{e,\lambda}(\lambda)=\frac{dM_e(\lambda)}{d\lambda}. }

Единицей измерения \displaystyle{ M_{e,\lambda} } в системе СИ является Вт·м−3. Поскольку длины волн оптического излучения принято измерять в нанометрах, то на практике часто используется Вт·м−2·нм−1.

Иногда в литературе \displaystyle{ M_{e,\lambda} } именуют спектральной испускательной способностью.

Слайд 32Фотометрические величины и единицы их измеренияСуществует энергическая система фотометрических величин и

световая, ориентированная на глаз человека.Поток излученияПолная мощность, переносимая электро-магнитным излучением. Измеряется в энергетической системе фот. величин в Вт. Мощность оптического излучения, оцениваемая по зрительному ощущению, называется световым потоком Ф. Световой поток измеряется в Лм(люменах). Световым потоком в 1 лм называется световой поток от источника силой света 1 кандела, распространяющийся в телесном угле 1 стерадиан. 2. Сила света.Сила излучения I определяет концентрацию потока излучения в пространстве. Она равна отношению потока излучения источника к телесному углу Ω, в пределах которого излучение распространяется. В энергетической системе фот. вел. измеряется в Вт/ср. В световой системе – в Кд(канделах). Сила света в 1 Кд это сила света определенного источника, принимаемого за эталон международным соглашением.

Основные понятия и характеристики теплового излучения

Энергетическая светимость тела

Энергетическая светимость тела — RT{\displaystyle ~R_{T}}- физическая величина, являющаяся функцией температуры и численно равная энергии, испускаемой телом в единицу времени с единицы площади поверхности по всем направлениям и по всему спектру частот.

RT=WtS{\displaystyle R_{T}={\frac {W}{tS}}} ;      RT={\displaystyle ~=}Дж/с·м²=Вт/м²

Спектральная плотность энергетической светимости

Спектральная плотность энергетической светимости — функция частоты и температуры, характеризующая распределение энергии излучения по всему спектру частот (или длин волн).

RT=∫1rω,Tdω{\displaystyle R_{T}=\int \limits _{0}^{\mathcal {1}}r_{\omega ,T}d\omega }

Аналогичную функцию можно написать и через длину волны

RT=∫1rλ,Tdλ{\displaystyle R_{T}=\int \limits _{0}^{\mathcal {1}}r_{\lambda ,T}d\lambda }

Можно доказать что спектральная плотность и энергетическая светимость выраженные через частоту и длину волны, связаны соотношением:

rω,T=λ22πcrλ,T{\displaystyle r_{\omega ,T}={\frac {\lambda ^{2}}{2\pi c}}r_{\lambda ,T}}

Поглощающая способность тела

Поглощающая способность тела —  aω,T{\displaystyle ~a_{\omega ,T}} — функция частоты и температуры, показывающая какая часть энергии электромагнитного излучения, падающего на тело, поглощается телом в области частот  dω{\displaystyle ~d\omega } вблизи  ω{\displaystyle ~\omega }

aω,T=dΦω,T′dΦω,T{\displaystyle a_{\omega ,T}={\frac {d\Phi ‘_{\omega ,T}}{d\Phi _{\omega ,T}}}}

где  dΦ′{\displaystyle ~d\Phi ‘} — поток энергии, поглощающейся телом.

 dΦ{\displaystyle ~d\Phi } — поток энергии, падающий на тело в области  dω{\displaystyle ~d\omega } вблизи  ω{\displaystyle ~\omega }

Отражающая способность тела

Отражающая способность тела —  bω,T{\displaystyle ~b_{\omega ,T}} — функция частоты и температуры, показывающая какая часть энергии электромагнитного излучения, падающего на тело, отражается от него в области частот  dω{\displaystyle ~d\omega } вблизи  ω{\displaystyle ~\omega }

bω,T=dΦω,T″dΦω,T{\displaystyle b_{\omega ,T}={\frac {d\Phi »_{\omega ,T}}{d\Phi _{\omega ,T}}}}

где  dΦ″{\displaystyle ~d\Phi »} — поток энергии, отражающейся от тела.

 dΦ{\displaystyle ~d\Phi } — поток энергии, падающий на тело в области  dω{\displaystyle ~d\omega } вблизи  ω{\displaystyle ~\omega }

Абсолютно черное тело

Абсолютно черное тело — это физическая абстракция(модель), под которой понимают тело, полностью поглощающее всё падающее на него электромагнитное излучение

 aω,T=1{\displaystyle ~a_{\omega ,T}=1} — для абсолютно черного цвета

Серое тело

Серое тело — это такое тело, коэффициент поглощения которого не зависит от частоты, а зависит только от температуры

 aω,T=aT<1{\displaystyle ~a_{\omega ,T}=a_{T}<1} — для серого тела

Объемная плотность энергии излучения

Объемная плотность энергии излучения —  UT{\displaystyle ~U_{T}} — функция температуры, численно равная энергии электромагнитного излучения в единицу объема по всему спектру частот

Спектральная плотность энергии

Спектральная плотность энергии —  Uω,T{\displaystyle ~U_{\omega ,T}} — функция частоты и температуры, связанная с объемной плотностью излучения формулой:

 UT=∫1dUω,Tdω{\displaystyle ~U_{T}=\int \limits _{0}^{\mathcal {1}}dU_{\omega ,T}d\omega }

Следует отметить, что спектральная плотность энергетической светимости для абсолютно черного тела связана со спектральной плотностью энергии следующим соотношением:

rω,T=f(ω,T)=c4Uω,T{\displaystyle r_{\omega ,T}=f(\omega ,T)={\frac {c}{4}}U_{\omega ,T}} — для абсолютно черного тела

Слайд 13Рассеяние светаРассеяние света — рассеяние электромагнитных волн видимого диапазона при их взаимодействии

с веществом. При этом происходит изменение пространственного распределения, частоты, поляризации оптического излучения, хотя часто под рассеянием понимается только преобразование углового распределения светового потока.

Виды рассеяния, свойственные для света:Рассеяние Рэлея — упругое рассеяние на малых частицах, размером много меньше длины волны.Рассеяние Ми — упругое рассеяние на крупных частицах.Рассеяние Мандельштама — Бриллюэна — неупругое рассеяние на колебаниях решётки.Комбинационное (рамановское) рассеяние — неупругое рассеяние на атомных колебаниях в молекуле.Рассеяние Тиндаля — упругое рассеяние света неоднородными средами.

Световой аналог[править | править код]

В системе световых фотометрических величин аналогом энергетической светимости является светимость Mv{\displaystyle M_{v}}. По отношению к энергетической светимости светимость является редуцированной фотометрической величиной, получаемой с использованием значений относительной спектральной световой эффективности монохроматического излучения для дневного зрения V(λ){\displaystyle V(\lambda )}:

Mv=Km⋅∫380 nm780 nmMe,λ(λ)V(λ)dλ,{\displaystyle M_{v}=K_{m}\cdot \int \limits _{380~nm}^{780~nm}M_{e,\lambda }(\lambda )V(\lambda )d\lambda ,}

где Km{\displaystyle K_{m}} — максимальная световая эффективность излучения, равная в системе СИ 683 лм/Вт. Её численное значение следует непосредственно из определения канделы.

Слайд 16Дисперсия светаДисперсия света (разложение света) — это совокупность явлений, обусловленных зависимостью абсолютного

показателя преломления вещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимостью фазовой скорости света в веществе от частоты (или длины волны).

Один из самых наглядных примеров дисперсии — разложение белого света при прохождении его через призму (опыт Ньютона). Сущностью явления дисперсии является различие фазовых скоростей распространения лучей света c различной длиной волны в прозрачном веществе — оптической среде (тогда как в вакууме скорость света всегда одинакова, независимо от длины волны и следовательно цвета). Обычно, чем больше частота световой волны, тем больше показатель преломления среды для неё и тем меньше фазовая скорость волны в среде (нормальная дисперсия):у света красного цвета фазовая скорость распространения в среде максимальна, а степень преломления — минимальна,у света фиолетового цвета фазовая скорость распространения в среде минимальна, а степень преломления — максимальна.

Слайд 6ИнтерференцияПрямым подтверждением волновой природы света может служить интерференция — явление наложения

нескольких волн, при котором в одних местах происходит усиление, а в других ослабление амплитуды результирующей волны. Интерференция — сложение двух когерентных волн, вследствие которого наблюдается усиление или ослабление результирующих световых колебаний в различных точках пространства.Условия интерференции: Волны должны быть когерентны (или волны, имеющие одинаковую частоту и разность фаз между ними постоянная)

Условие интерференционного максимума: разность хода равна целому числу длин волн: Условие интерференционного минимума: разность хода равна нечетному целому числу полудлин волн:

Освещенность

Освещенность представляет собой поверхностную плотность светового
потока, падающего на освещаемую поверхность. При равномерном
распределении светового потока F в пределах освещаемой поверхности
S значение освещенности можно определить как:

E = F / S.

Освещенность и сила света точечного источника света при нормальном
падении лучей (поверхность перпендикулярна лучам) связаны следующим
соотношением:

E = I / r²,

где r — расстояние от источника света до освещаемой поверхности.

Это выражение называется законом квадратов расстояний. Его
сформулировал еще в 1604 г. немецкий астроном Иоганн Кеплер. Следует
помнить, что освещенность будет оставаться постоянной вдоль пучка лучей
только тогда, когда они параллельны.

Рис. 5. К определению освещенности поверхности

Если лучи от источника падают на поверхность под углом φ к нормали
(рис. 5), то тот же световой поток F распределяется по площади, в
1 / cosφ раз большей, чем S (по площади S / cosφ), и формула примет вид:

E = I·cosφ / r²,

Закон квадратов расстояний приемлем для расчета освещенности,
создаваемой осветительными приборами, но минимальное значение r
определяется таким параметром осветительного прибора как рабочее
расстояние.

Следует добавить, что освещенность поверхности может создаваться
не одним источником, как показано на рис. 5, а любым числом произвольно
расположенных источников, посылающих свет на освещаемую поверхность (или
ее элемент) с различных направлений и под разными углами к ее нормали.
Тогда общая освещенность будет равна сумме освещенностей поверхности
в данной точке от различных источников света:

E = E₁ + E₂ + E₃ + … + E_n.

Эта формула представляет собой закон аддитивности, из которого
следует, что общая освещенность равна сумме освещенностей поверхности
в данной точке от различных источников света.

Единицей освещенности является люкс (лк, от лат. lux — свет).
То есть, 1 лк = 1 лм / 1 м². Внесистемная единица освещенности:
1 фот = 1 лм / 1 см². В США, Англии и других странах в качестве единицы
освещенности часто используется фут-кандела: 1 фут-кандела =
1 лм / 1 фут² = 10,764 лк.

Формула зависимости плотности потока излучения от расстояния до источника

§ 50 ПЛОТНОСТЬ ПОТОКА ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ

Излучаемые электромагнитные волны несут с собой энергию.

Плотность потока излучения. Рассмотрим поверхность площадью S, через которую электромагнитные волны переносят энергию. На рисунке 7.5 изображена такая площадка.

Прямые линии указывают направления распространения электромагнитных волн. Это лучи —линии, перпендикулярные поверхностям, во всех точках которых колебания происходят в одинаковых фазах. Такие поверхности называются волновыми поверхностями (см. § 46). Плотностью потока электромагнитного излучения / называют отношение электромагнитной энергии

Фактически это мощность электромагнитного излучения (энергия в единицу времени), проходящего через единицу площади поверхности. Плотность потока излучения в СИ выражают в ваттах на квадратный метр (Вт/м 2 ). Иногда эту величину называют интенсивностью волны.

Выразим I через плотность электромагнитной энергии и скорость ее распространения с. Выберем поверхность площадью S, перпендикулярную лучам, и построим на ней как на основании цилиндр с образующей c

т. е. плотность потока излучения равна произведению плотности электромагнитной энергии на скорость ее распространения.

Найдем зависимость плотности потока излучения от расстояния до источника. Для этого надо ввести еще одно новое понятие.

Точечный источник излучения. Источники излучения электромагнитных волн могут быть весьма разнообразными. Простейшим является точечный источник.

Источник излучения считается точечным, если его размеры много меньше расстояния, на котором оценивается его действие. Кроме того, предполагается, что такой источник посылает электромагнитные волны по всем направлениям с одинаковой интенсивностью. Точечный источник — такая же идеализация реальных источников, как и другие модели принятые в физике: материальная точка, идеальный газ и т. д.

Звезды излучают свет, т. е. электромагнитные волны Так как расстояния до звезд в огромное число раз превы шают их размеры, то именно звезды представляют собой лучшее реальное воплощение точечных источников.

Зависимость плотности потока излучения от расстояния до точечного источника. Энергия, которую переносят электромагнитные волны, с течением времени распределяется по все большей и большей поверхности. Поэтому энергия, передаваемая через поверхность единичной площадки за единицу времени, т. е. плотность потока излучения, уменьшается по мере удаления от источника.

Поместим точечный источник в центр сферы радиусом R. Площадь поверхности сферы S = 4

Плотность потока излучения от точечного источника убывает обратно пропорционально квадрату расстояния до источника.

Зависимость плотности потока излучения от частоты. Излучение электромагнитных волн происходит при ускоренном движении заряженных частиц (см. § 48). Напряженность электрического поля

Плотность энергии электрического поля пропорциональна квадрату напряженности поля. Энергия магнитного поля, как это можно показать, пропорциональна квадрату магнитной индукции. Полная плотность энергии электромагнитного поля равна сумме плотностей энергий электрического и магнитного полей. С учетом формулы (7.2) плотность потока излучения

Плотность потока излучения пропорциональна четвертой степени частоты.

При увеличении частоты колебаний заряженных частиц в 2 раза излучаемая энергия возрастает в 16 раз! В антеннах радиостанций поэтому возбуждают колебания больших частот: от десятков тысяч до десятков миллионов герц.

Электромагнитные волны переносят энергию. Плотность потока излучения (интенсивность волны) равна произведению плотности энергии на скорость ее распространения. Интенсивность волны пропорциональна четвертой степени частоты и убывает обратно пропорционально квадрату расстояния от источника.

Мякишев Г. Я., Физика. 11 класс : учеб. для общеобразоват. учреждений : базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 17-е изд., перераб. и доп. — М. : Просвещение, 2008. — 399 с : ил.

_{Планирование по физике, учебники и книги онлайн, курсы и задачи по физике для 11 класса скачать}

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.