Основные элементарные функции

Примеры графиков кубических функций

В этом заключительном разделе мы рассмотрим еще несколько рабочих примеров с использованием компонентов, которые мы изучили на протяжении графиков кубических функций.

Постройте график

\

учитывая, что \(x=-1\) является решением этого кубического многочлена.

Решение

Шаг 1: По теореме о факторах, если \(x=-1\) является решением этого уравнения, то \((x+1)\) должно быть фактором. Таким образом, мы можем переписать функцию в виде

\

Обратите внимание, что в большинстве случаев нам не дается ни одного решения данного кубического многочлена. Следовательно, мы должны методом проб и ошибок найти значение \(x\), при котором при решении \(y\) остаток будет равен нулю

Обычные значения \(x\), которые можно попробовать: 1, -1, 2, -2, 3 и -3.

Чтобы найти коэффициенты \(a\), \(b\) и \(c\) в квадратном уравнении \(ax^2+bx+c\), мы должны выполнить синтетическое деление, как показано ниже.

Синтетическое деление для примера 6

Рассмотрев первые три числа в последней строке, мы получим коэффициенты квадратного уравнения, и, таким образом, наш заданный кубический многочлен станет равен

\

Выражение \(x^2-x-6\) можно факторизовать как \((x-3)(x+2)\).

Таким образом, полная факторизованная форма этой функции имеет вид

\

Шаг 2: Подставляя \(y=0\), получаем

\

Решив это, мы получим три корня:

\

Шаг 3: Подставляя \(x=0\), получаем

\

Таким образом, перекресток y равен \(y = -6\).

Шаг 4: График для данного кубического многочлена изображен ниже.

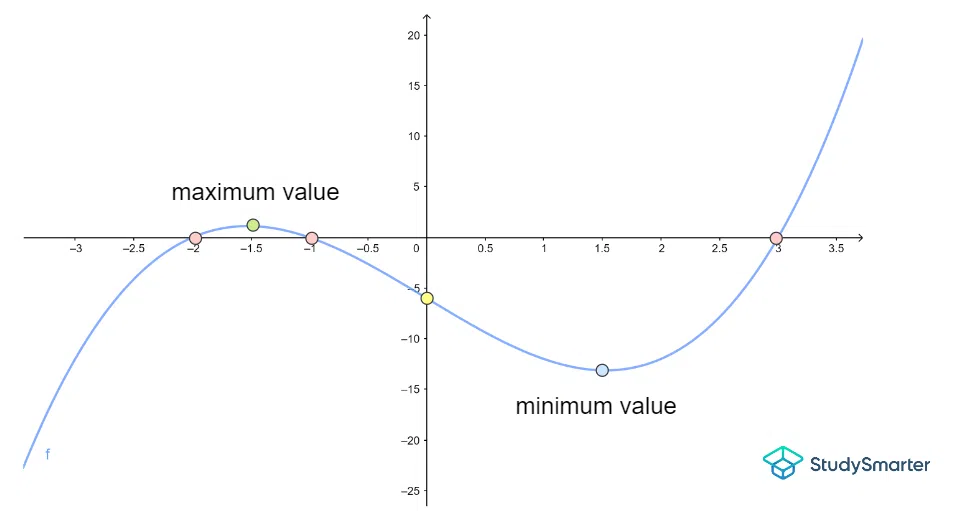
График для примера 6

Сайт розовый точки представляют собой \(x\)-пересечения.

Сайт желтый точка представляет собой \(y\)-пересечение.

И снова мы получаем две поворотные точки для этого графика:

1. максимальное значение между корнями \(x = -2\) и \(x = -1\). На это указывают зеленый точка.
2. минимальное значение между корнями \(x = -1\) и \(x = 3\). На это указывают синий точка.

Вот наш последний пример для этого обсуждения.

Постройте график

\

Решение

Во-первых, обратите внимание, что перед приведенным уравнением стоит знак минус. Это означает, что график будет иметь форму перевернутого (стандартного) кубического полинома

Другими словами, эта кривая будет сначала раскрываться вверх, а затем вниз.

Шаг 1: Сначала заметим, что бином \((x^2-1)\) является примером бинома совершенного квадрата.

Для факторизации квадратных уравнений такого рода мы можем использовать приведенную ниже формулу.

Биноминал с идеальным квадратом

\

Используя формулу выше, получаем \((x+1)(x-1)\).

Таким образом, полная разложенная форма этого уравнения имеет вид

\

Шаг 2: Подставляя \(y=0\), получаем

\

Решив это, мы получим три корня:

\

Шаг 3: Подставляя \(x=0\), получаем

\

Таким образом, перекресток y равен \(y=-1\).

Шаг 4: График данного кубического многочлена изображен ниже. Будьте внимательны и помните об отрицательном знаке в нашем исходном уравнении! График кубического многочлена здесь перевернут.

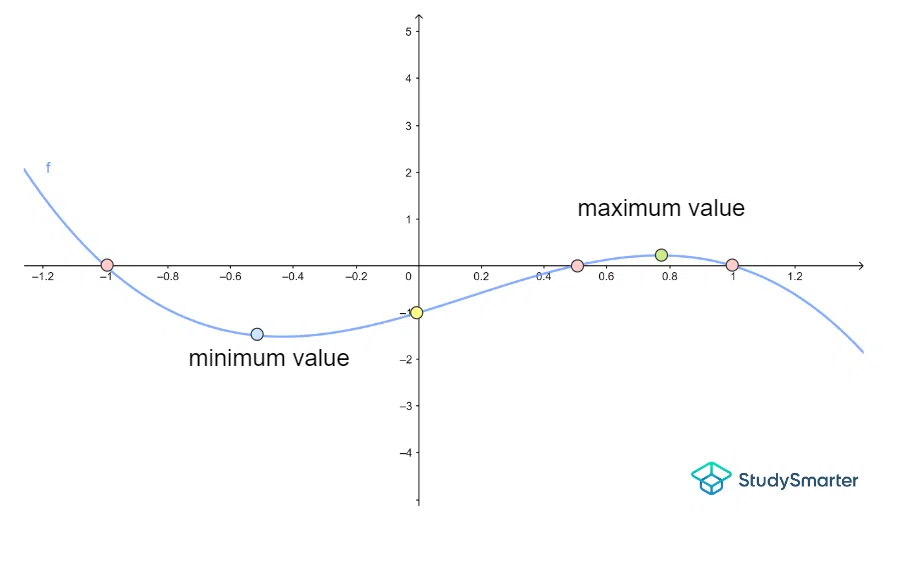
График для примера 7

Сайт розовый точки представляют собой \(x\)-пересечения.

Сайт желтый точка представляет собой \(y\)-пересечение.

В этом случае мы получаем две поворотные точки для этого графика:

1. минимальное значение между корнями \(x = -1\) и \(x=\frac{1}{2}\). На это указывает зеленый точка.
2. максимальное значение между корнями \(x=\frac{1}{2}\) и \(x = 1\). На это указывают синий точка.

График линейной функции

Линейная функция задается уравнением . График линейной функций представляет собой прямую. Для того, чтобы построить прямую достаточно знать две точки.

Пример 1

Построить график функции . Найдем две точки. В качестве одной из точек выгодно выбрать ноль.

Если , то

Берем еще какую-нибудь точку, например, 1.

Если , то

При оформлении заданий координаты точек обычно сводятся в таблицу:

 
А сами значения рассчитываются устно или на черновике, калькуляторе.

Две точки найдены, выполним чертеж:

При оформлении чертежа всегда подписываем графики.

Не лишним будет вспомнить частные случаи линейной функции:

Обратите внимание, как я расположил подписи, подписи не должны допускать разночтений при изучении чертежа. В данном случае крайне нежелательно было поставить подпись рядом с точкой пересечения прямых  ,  или справа внизу между графиками

1) Линейная функция вида  () называется прямой пропорциональностью. Например, . График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку.

2) Уравнение вида  задает прямую, параллельную оси , в частности, сама ось  задается уравнением . График функции строится сразу, без нахождения всяких точек. То есть, запись  следует понимать так: «игрек всегда равен –4, при любом значении икс».

3) Уравнение вида  задает прямую, параллельную оси , в частности, сама ось  задается уравнением . График функции также строится сразу. Запись  следует понимать так: «икс всегда, при любом значении игрек, равен 1».

Некоторые спросят, ну зачем вспоминать 6 класс?! Так-то оно, может и так, только за годы практики я встретил добрый десяток студентов, которых ставила в тупик задача построения графика вроде  или .

Построение прямой – самое распространенное действие при выполнении чертежей.

Прямая линия детально рассматривается в курсе аналитической геометрии, и желающие могут обратиться к статье Уравнение прямой на плоскости.

График квадратичной, кубической функции, график многочлена

Парабола. График квадратичной функции  () представляет собой параболу. Рассмотрим знаменитый случай:

Вспоминаем некоторые свойства функции .

Область определения – любое действительное число (любое значение «икс»). Что это значит? Какую бы точку на оси  мы не выбрали – для каждого «икс» существует точка параболы. Математически это записывается так: . Область определения любой функции стандартно обозначается через  или . Буква  обозначает множество действительных чисел или, проще говоря, «любое икс»  (когда работа оформляется в тетради, пишут не фигурную букву , а жирную букву R).    

Область значений – это множество всех значений, которые может принимать переменная «игрек». В данном случае:  – множество всех положительных значений, включая ноль. Область значений стандартно обозначается через  или .

Функция  является чётной. Если функция является чётной, то ее график симметричен относительно оси . Это очень полезное свойство, которое заметно упрощает построение графика, в чём мы скоро убедимся. Аналитически чётность функции выражается условием . Как проверить любую функцию на чётность? Нужно  вместо  подставить в уравнение . В случае с параболой проверка выглядит так: , значит, функция  является четной.

Функция  не ограничена сверху. Аналитически свойство записывается так: . Вот вам, кстати, и пример геометрического смысла предела функции: если мы будем уходить по оси  (влево или вправо) на бесконечность, то ветки параболы (значения «игрек») будут неограниченно уходить вверх  на «плюс бесконечность».

При изучении пределов функций желательно понимать геометрический смысл предела.

Я не случайно так подробно расписал свойства функции, все вышеперечисленные вещи полезно знать и помнить при построении графиков функций, а также при исследовании графиков функций.

Пример 2

Построить график функции .

В этом примере мы рассмотрим важный технический вопрос: Как быстро построить параболу? В практических заданиях необходимость начертить параболу возникает очень часто, в частности, при вычислении площади фигуры с помощью определенного интеграла. Поэтому чертеж желательно научиться выполнять быстро, с минимальной потерей времени. Я предлагаю следующий алгоритм построения.

Сначала находим вершину параболы. Для этого берём первую производную и приравниваем ее к нулю:

Если с производными плохо, следует ознакомиться с уроком Как найти производную?

Итак, решение нашего уравнения:  – именно в этой точке и находится вершина параболы. Почему это так, можно узнать из теоретической статьи о производной и урока об экстремумах функции. А пока рассчитываем соответствующее значение «игрек»:

Таким образом, вершина находится в точке

Теперь находим другие точки, при этом нагло пользуемся симметричностью параболы. Следует заметить, что функция  – не является чётной, но, тем не менее, симметричность параболы никто не отменял.

В каком порядке  находить остальные точки, думаю, будет понятно из итоговой таблицы:

Данный алгоритм построения образно можно назвать «челноком» или  принципом «туда-сюда» с Анфисой Чеховой.

Выполним чертеж:

Из рассмотренных графиков вспоминается еще один полезный признак:

Для квадратичной функции  () справедливо следующее:

Если , то ветви параболы направлены вверх.

Если , то ветви параболы направлены вниз.

Углублённые знания о кривой можно получить на уроке Гипербола и парабола.

Функция квадратного корня

Функция квадратного корня – это функция вида \(y = \sqrt{x}\), где x ≥ 0 .

\(y = \sqrt{x}\), гдеx – переменнаяx ≥ 0

В жизни такая функция часто используется для определения стороны квадрата при известной площади. Например: при проектировании дома или разбиения участка земли на квадраты.

Рассмотрим график такой функции.

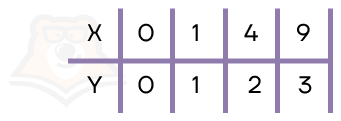
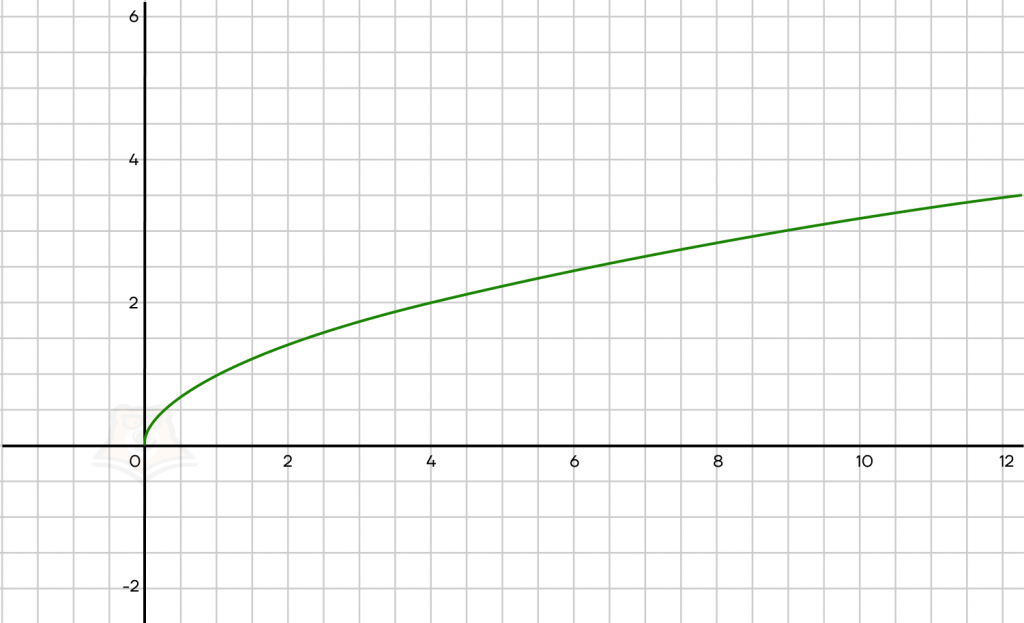
Чем отличается график функции квадратного корня от графика квадратичной функции и почему?По графику квадратного корня уже видно, что это половина параболы, изображенной вдоль оси х. А график квадратичной функции — это целая парабола, изображенная вдоль оси y.Так как корень всегда положительный, у функции квадратного корня \(y = \sqrt{x}\) , всегда y ≥ 0.  А значит не будет части параболы, где y < 0. Если возвести обе части функции квадратного корня в квадрат, то получим y2 = x. Получившаяся функция будет уже квадратичной функцией относительно y, следовательно, будет строиться относительно х.

Какие бывают сдвиги функции квадратного корня?

Сдвиг по оси Y

\(y = \sqrt{x} + n\)

При n < 0, сдвиг внизПри n > 0, сдвиг вверх

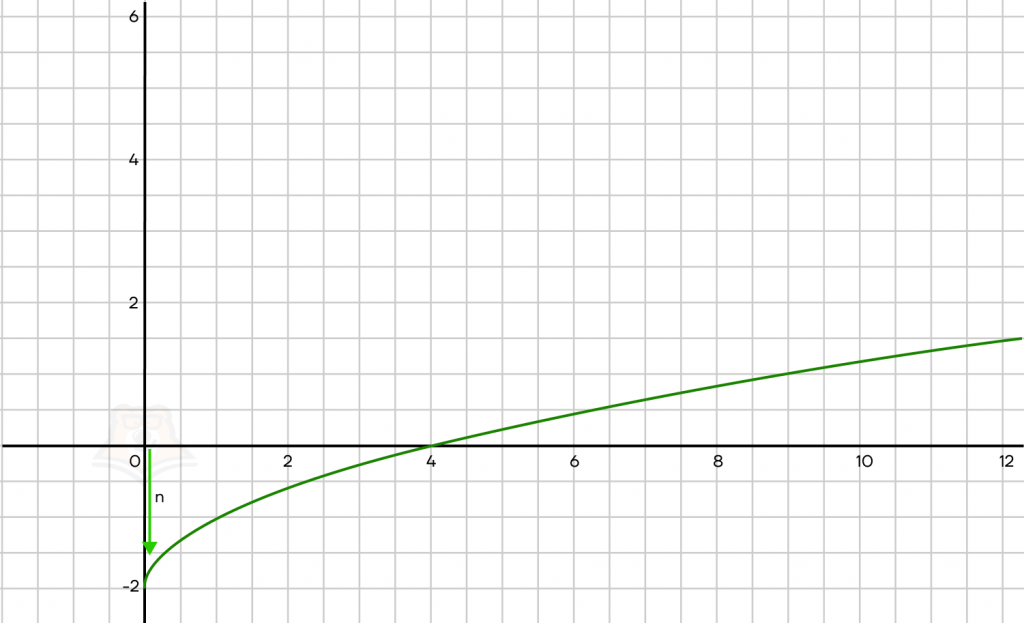
По графику выше можно утверждать, что n = -2.

Сдвиг по оси X

\(y = \sqrt{x + c}\)

При c < 0, сдвиг вправоПри c > 0, сдвиг влево

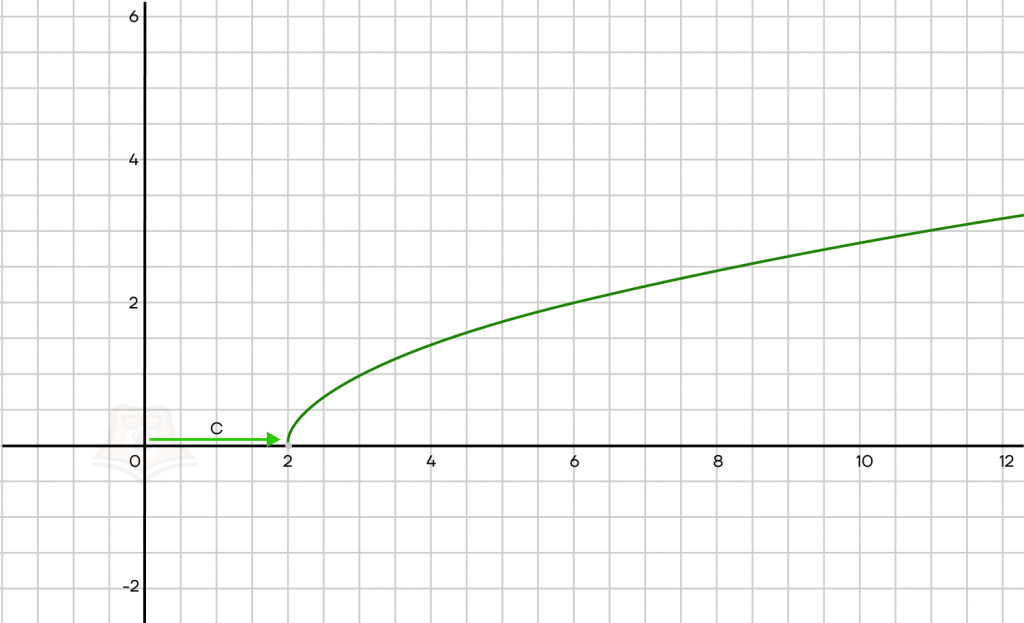
Сделаем вывод, что для рисунка выше c = -2.

Свойства функции квадратного корня:

1. Область определения: D(y) = [0; +∞)
2. Область значений функции: E(y) = [0; +∞)
3. Наименьшее значение при y = 0.
4. Непериодическая.
5. Возрастает на всей области определения.
6. Нуль функции x = 0.

Дистанционные курсы для педагогов

Выдаём документы установленного образца! Учителя о ЕГЭ: секреты успешной подготовки РДШ организовало сбор гуманитарной помощи для детей из ДНР В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей Минпросвещения России подготовит учителей для обучения детей из Донбасса Инфоурок стал резидентом Сколково Школы смогут вносить данные в портфолио школьника в «МЭШ»

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи. Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов. Источник

функций | Библиотека колледжа Дугласа

График линейной функции

График уравнения с двумя переменными — это множество всех точек, удовлетворяющих уравнению.

Если вам дали уравнение y = 3x-2 и попросили построить его график, вы должны выполнить следующие шаги. (Примечание: это уравнение представляет собой линейное уравнение , что означает, что оно будет выглядеть как прямая линия). Первый шаг — настроить таблицу из х и у .

у = 3х-2

х	г
-2
1	1
2/3

​Назначьте значения для x , затем выясните, каким будет значение для y .

x г x y x y x y y

Из приведенной выше таблицы у нас есть точки (0, -2), (1, 1) и (2/3, 0). Однако, чтобы нарисовать линию, вам нужно всего лишь нанести две точки, а затем соединить эти точки. Поскольку «линейные» уравнения дают прямую линию, вы можете использовать линейку для этой части.

Как видно на графике ниже, эти точки соединены прямой линией.

Нажмите кнопку «Воспроизвести» на панели навигации, чтобы просмотреть шаги.

Определение

Линейная функция может быть записана в виде следующего стандартного уравнения y = f(x) = bx+ a .

x y

Пример : y = 2x-1  – уравнение прямой линии, где b=2 и a= -1.

Упражнение . Перетащите точку A и изучите, как меняется уравнение линии.

Как выглядит линия, когда «b» положителен?
Как выглядит линия, когда «b» имеет отрицательное значение?
Какая связь между координатами точки «А» и уравнением прямой?
Какое уравнение линии получится, если поставить букву «А» в начало координат»?
Какое положение занимает линия, когда уравнение линии изменяется на y=a (обратите внимание, что в уравнении нет переменной x )? Как выглядит линия (параллельно какой оси)?

Изучение квадратичных функций

A Квадратичная функция имеет стандартную форму y = ax 2  + bx + c , когда наибольшая степень над переменной (переменными) x равна 2,9.

Обратите внимание, что когда «а» положительно, парабола открывается вверх, а вершина является минимальным значением функции. С другой стороны, если «а» отрицательно, график открывается вниз, а вершина является максимальным значением функции

Упражнение:

Ниже представлен интерактивный график, позволяющий изменять значения a, b и c в квадратном уравнении, и посмотреть, как изменится результирующая парабола

Обратите внимание, что начальная квадратичная функция, показанная на графике, равна y = x 2  (обновите график, чтобы вернуться к y = x 2 )

• Как ведет себя парабола, когда « a » становится положительным?
• Как ведет себя парабола, когда « a » становится отрицательным?
• Как ведет себя парабола, когда « а» приближается к ?
• Что произойдет, если «a=0»?
• Опишите, как движется парабола, когда
  1.  б = 0,
  2. б > 0  
  3. б
• Опишите, как движется парабола, когда
  1. с = 0,
  2. с > 0  
  3. с

Кубическая функция

Кубическая функция имеет стандартную форму f(x) = ax 3  + bx 2  + cx + d.

равна 3

Коэффициент «a» делает график «шире» или «тоньше» или отражает его (если он отрицательный): Константа » d» в уравнении является точкой пересечения графика по оси y.

Упражнение A:

На интерактивном графике ниже нарисуйте кубические функции, используя включенную таблицу значений. Для заданной функции и значений x вычислить и значений и изучите, как выглядит график. Нажмите кнопку «Новая проблема» для новой функции.

Саманта Круз.

Кубическая интерполяция [ править ]

Учитывая значения функции и ее производной в двух точках, существует ровно одна кубическая функция, имеющая те же четыре значения, которая называется кубическим сплайном Эрмита .

Есть два стандартных способа использовать этот факт. Во-первых, если кто-то знает, например, путем физического измерения, значения функции и ее производной в некоторых точках выборки, можно интерполировать функцию с помощью непрерывно дифференцируемой функции , которая является кусочно- кубической функцией.

Если значение функции известно в нескольких точках, кубическая интерполяция заключается в приближении функции непрерывно дифференцируемой функцией , которая является кусочно- кубической. Для однозначно определенной интерполяции необходимо добавить еще два ограничения, такие как значения производных в конечных точках или нулевая кривизна в конечных точках.

Пример решения

Существует некоторый тип задач, в которых нужно исследовать и построить график функции y = k/x. Разобрать решение можно на примере y = 5 / (x — 3). Следует воспользоваться алгоритмом:

• D(5 / (x — 3)) = (-inf;3) U (3;+inf).
• Нули функции. По ОУ: y = 5 / (0 — 3) = — 5/3. По ОХ: 5 / (x — 3) = 0. Если решить уравнения, то у него нет корней.
• Знаковые промежутки: (-inf;3) и (3;+inf).
• Непериодическая.
• Четность: 5 / (-x — 3) = — 5 / (x + 3). Нечетная: — 5 / (x + 3) не равно 5 / (x — 3).
• Экстремумы: y’ = [5 / (x — 3)] = — 5 / (x — 3)^2 = 0. Уравнение не имеет решений, а это значит, что максимума и минимума нет.
• Не является монотонной.

Чтобы построить график функции y = k / x + 3 (к = 5), нужно составить таблицу для его построения.

х	-4	-3	-2	-1	1	2	3	4
у	-5/7	-5/6	-1	-1,2	-5/3	-2,5	-5	нет	5

Таблица 1. Зависимость значения функции от ее аргумента.

После составления таблицы нужно начертить ДСК. На ней следует отмечать точки, а затем их плавно соединить (рис. 2).

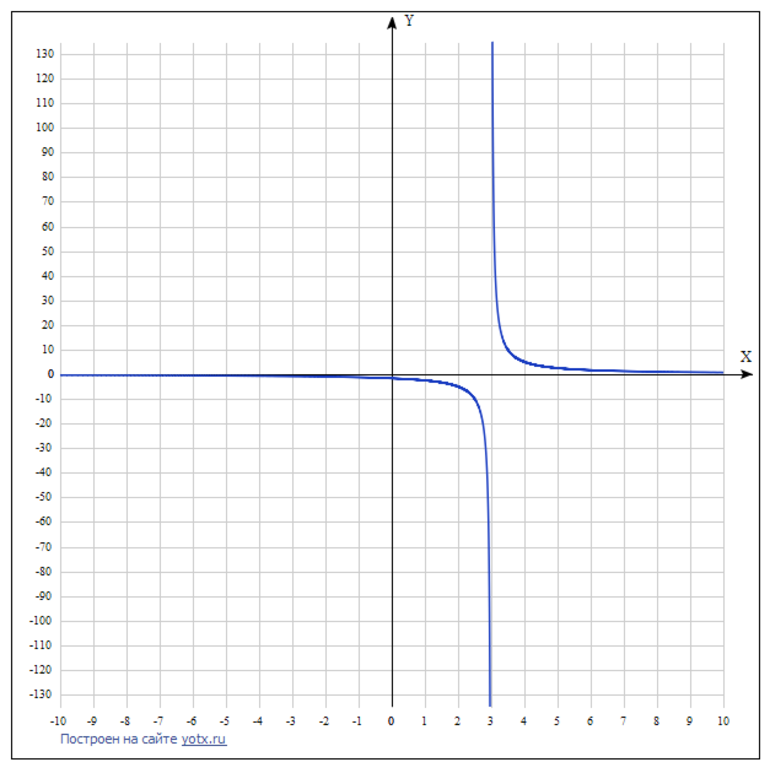
Рисунок 2. График обратной пропорциональности y = k / x — 3 при к = 5.

Таким образом, графиком обратной пропорциональности является гипербола, а прямой пропорциональности — прямая. Поведение функции исследуется по специальному алгоритму, который позволяет легко построить ее график и выяснить некоторые свойства.

характеристики

Поведение в бесконечности

Как и все полностью рациональные функции нечетной степени, применяется

LimИкс→+∞ж(Икс)знак равно+∞{\ displaystyle \ lim \ limits _ {x \ to + \ infty} f (x) = + \ infty}, ,LimИкс→-∞ж(Икс)знак равно-∞{\ displaystyle \ lim \ limits _ {x \ to — \ infty} f (x) = — \ infty}

если старший коэффициент положительный, и
а{\ displaystyle a}

LimИкс→+∞ж(Икс)знак равно-∞{\ displaystyle \ lim \ limits _ {x \ to + \ infty} f (x) = — \ infty}, ,LimИкс→-∞ж(Икс)знак равно+∞{\ displaystyle \ lim \ limits _ {x \ to — \ infty} f (x) = + \ infty}

если отрицательно.
а{\ displaystyle a}

нулевая точка

Поскольку кубическая функция непрерывна как полиномиальная функция , из поведения на бесконечности и теоремы о промежуточном значении следует, что она всегда имеет по крайней мере один действительный нуль. С другой стороны, полностью рациональная функция степени не может иметь больше нуля. Отсюда следует: кубическая функция имеет не менее одного и не более трех нулей .
п{\ displaystyle n}п{\ displaystyle n}Р.{\ Displaystyle \ mathbb {R}}

Чтобы найти нули кубической функции, см. Кубическое уравнение и Формулы Кардана . Дискриминант общей кубической функции является
ж{\ displaystyle f}

Д.знак равноб2c2-4-йаc3-4-йб3d-27а2d2+18-еабcd{\ displaystyle D = b ^ {2} c ^ {2} -4ac ^ {3} -4b ^ {3} d-27a ^ {2} d ^ {2} + 18abcd}

и подходит для классификации нулей полинома : в случае есть три разных действительных нуля, в случае только один. Верно, что существует либо одинарный и двойной действительный ноль, либо есть тройной действительный ноль.
Д.>{\ displaystyle D> 0}Д.<{\ displaystyle D <0}Д.знак равно{\ displaystyle D = 0}

Численное нахождение нулей возможно, например, методом Ньютона .

Однообразие и локальные крайности

Как полиномиальную функцию, ее можно дифференцировать сколь угодно часто ; квадратичная функция получается для ее 1-й производнойж{\ displaystyle f}ж′{\ displaystyle f ‘}

ж′(Икс)знак равно3аИкс2+2бИкс+c{\ displaystyle f ‘(x) = 3ax ^ {2} + 2bx + c}.

Их дискриминант положительный, т.е. ЧАС. это правда , тогда имеется ровно один локальный максимум и ровно один локальный минимум. В противном случае он строго монотонен , а именно строго монотонно возрастает при и строго монотонно убывает при .
4-йб2-12аc{\ displaystyle 4b ^ {2} -12ac}б2>3аc{\ displaystyle b ^ {2}> 3ac}ж{\ displaystyle f}ж{\ displaystyle f} а>{\ displaystyle a> 0}а<{\ displaystyle a <0}

Точка поворота и симметрия

Каждая кубическая функция имеет ровно одну точку поворота . Поворотный момент
ж{\ displaystyle f} (ИксW.;ж(ИксW.)){\ displaystyle (x_ {W}; f (x_ {W}))}

ИксW.знак равно-б3а{\ displaystyle x_ {W} = — {\ frac {b} {3a}}}

является однозначно определенным нулем 2-й производной .
ж″(Икс)знак равноШестойаИкс+2б{\ displaystyle f » (x) = 6ax + 2b}

Функция графа из является точкой симметрии относительно ее точки перегиба.
ж{\ displaystyle f}

Нормальная форма

Любую кубическую функцию можно преобразовать в форму
путем сдвига и масштабированияж{\ displaystyle f}

г(ты)знак равноты3+kты{\ Displaystyle г (и) = и ^ {3} + ку}

с принести.
k∈{-1,,1}{\ Displaystyle к \ в \ {- 1,0,1 \}}

Итак, вы получаете ровно три возможных случая этой нормальной формы:

1. kзнак равно-1{\ displaystyle k = -1}: График имеет две крайние точки.г{\ displaystyle g}
2. kзнак равно{\ displaystyle k = 0}: Крайние точки совпадают ровно с одной седловой точкой .
3. kзнак равно1{\ displaystyle k = 1}: График не имеет ни экстремумов, ни седловых точек, так как производная теперь положительна во всей области.г{\ displaystyle g}

Поскольку преобразование в нормальную форму не меняет существования экстремумов, эта характеристика также применима к исходной функции . Коэффициент является противоположным знаком дискриминанта производной исходной функции .
ж{\ displaystyle f}k{\ displaystyle k}ж{\ displaystyle f}

x^3=6 (уравнение)

Найду корень уравнения: x^3=6

Решение

Дано уравнение$$x^ = 6$$Т.к. степень в ур-нии равна = 3 — не содержит чётного числа в числителе, тоур-ние будет иметь один действительный корень.Извлечём корень 3-й степени из обеих частей ур-ния:Получим:$$\sqrt> = \sqrt$$или$$x = \sqrt$$Раскрываем скобочки в правой части ур-ния

Получим ответ: x = 6^(1/3)

Остальные 2 корня(ей) являются комплексными.сделаем замену:$$z = x$$тогда ур-ние будет таким:$$z^ = 6$$Любое комплексное число можно представить так:$$z = r e^$$подставляем в уравнение$$r^ e^ = 6$$где$$r = \sqrt$$— модуль комплексного числаПодставляем r:$$e^ = 1$$Используя формулу Эйлера, найдём корни для p$$i \sin + \cos = 1$$значит$$\cos = 1$$и$$\sin = 0$$тогда$$p = \frac$$где N=0,1,2,3. Перебирая значения N и подставив p в формулу для zЗначит, решением будет для z:$$z_ = \sqrt$$$$z_ = — \frac> — \frac \cdot 3^> i>$$$$z_ = — \frac> + \frac \cdot 3^> i>$$делаем обратную замену$$z = x$$$$x = z$$

Графики тригонометрических функций

С чего начинаются тригонометрические мучения в школе? Правильно. С синуса

Построим график функции

Данная линия называется синусоидой.

Напоминаю, что «пи» – это иррациональное число: , и в тригонометрии от него в глазах рябит.

Основные свойства функции :

Данная функция является периодической с периодом . Что это значит? Посмотрим на отрезок . Слева и справа от него бесконечно повторяется точно такой же кусок графика.

Область определения: , то есть для любого значения «икс» существует значение синуса.

Область значений: . Функция  является ограниченной: , то есть, все «игреки» сидят строго в отрезке .
Такого не бывает:  или , точнее говоря, бывает, но указанные уравнения не имеют решения.

Синус – это функция нечетная, синусоида симметричная относительно начала координат, и справедлив следующий факт: . Таким образом, если в вычислениях встретится, например, , то минус терять здесь ни в коем случае нельзя! Он выносится:

Как ведет себя синус на бесконечности? Попробуем провести исследование с помощью пределов:,  Чему равны такие пределы? Запомните, данных пределов не существует. По вполне понятным причинам, график синуса болтается как как неприкаянный, то дойдет единицы, то уйдет к минус единице и так до бесконечности.

Вот вам пример, когда предела не существует. В высшей математике это можно встретить не очень часто, но такое понятие, как «предела не существует» – существует!

В практических вычислениях желательно (и даже обязательно) знать и помнить следующие значения синуса: , , . Другие значения синуса (а также остальных тригонометрических функций) можно найти в методическом материале Тригонометрические таблицы.

График косинуса

Построим график функции

График косинуса – это та же самая синусоида, сдвинутая вдоль оси  на  влево
(см. также Пример 8 урока о геометрических преобразованиях графиков).

Поэтому почти все свойства синуса справедливы и для косинуса. За некоторым, но существенным исключением.

Косинус – это функция четная, ее график симметричен относительно оси  , и справедлив следующий факт: . То есть, минус перед аргументом косинуса можно безболезненно убирать (или наоборот, ставить). В отличие от синуса в косинусе минус «бесследно пропадает».

Для решения практических задач нужно знать и помнить следующие значения косинуса: , , .

Графики тангенса и котангенса

Построим график функции

Основные свойства функции :

Данная функция является периодической с периодом . То есть, достаточно рассмотреть отрезок , слева и справа от него ситуация будет бесконечно повторяться.

Область определения:  – все действительные числа, кроме …  , , , … и т. д. или коротко: , где  – любое целое число. Множество целых чисел (… -4, -3, -2, -1, 0, 1, 2, 3, 4, …) в высшей математике обозначают жирной буквой Z.

Область значений: . Функция  не ограничена. В этом легко убедиться и аналитически: – если мы приближаемся по оси  к значению  справа, то ветка тангенса уходит на минус бесконечность, бесконечно близко приближаясь к своей асимптоте . – если мы приближаемся по оси  к значению  слева, то «игреки» шагают вверх на плюс бесконечность, а ветка тангенса бесконечно близко приближается к асимптоте .

Тангенс – функция нечетная, как и в случае с синусом, минус из-под тангенса не теряется, а выносится: .

В практических вычислениях полезно помнить следующие значения тангенса: , , , а также те точки, в которых тангенса не существует (см. график).

График котангенса – это почти тот же самый тангенс, функции связаны тригонометрическим соотношением . Вот его график:

Свойства попробуйте сформулировать самостоятельно, они практически такие же, как и у тангенса.

Параболы и кубики

Параболы и кубики

На этом уроке мы познакомимся с графиками уравнений вида y   =  x 2 и y   =  ax 3 .
Мы видели ранее, что график y   = m x + b — это график линии. Что произойдет, если там
является членом x 2 в этом выражении?
Давайте сначала посмотрим на простейшее уравнение, которое имеет х 2 срок.

Пример 1

Что такое график

y   =  x 2

Раствор

Чтобы нарисовать это, мы можем придумать несколько точек. Давайте сделаем T-таблицу с
значения -3,-2,-1,0,1,2
для х .

У нас есть

(-3) 2   =  9    (-2) 2   =
4    (-1) 2   =  1

        (0) 2 =  0      (1) 2   =  1
(2) 2   =  4    (3) 2   =
9

Мы можем поместить их в Т-таблицу.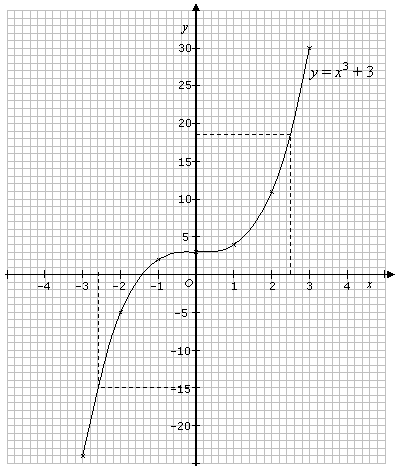

х	г
-3	9
-2	4
-1	1
1	1
2	4
3	9

Эта таблица дает нам баллы (-3,9),
(-2,4), (-1,1),
(0,0), (1,1),
(2,4) и (3,9).
Затем мы нанесем эти точки на плоскость xy .
Обратите внимание, что все эти точки имеют неотрицательное и -координата. Наконец, на графике мы можем соединить точки плавной кривой.
график показан ниже

Наконец, на графике мы можем соединить точки плавной кривой.
график показан ниже.

Обратите внимание, что график остается над осью x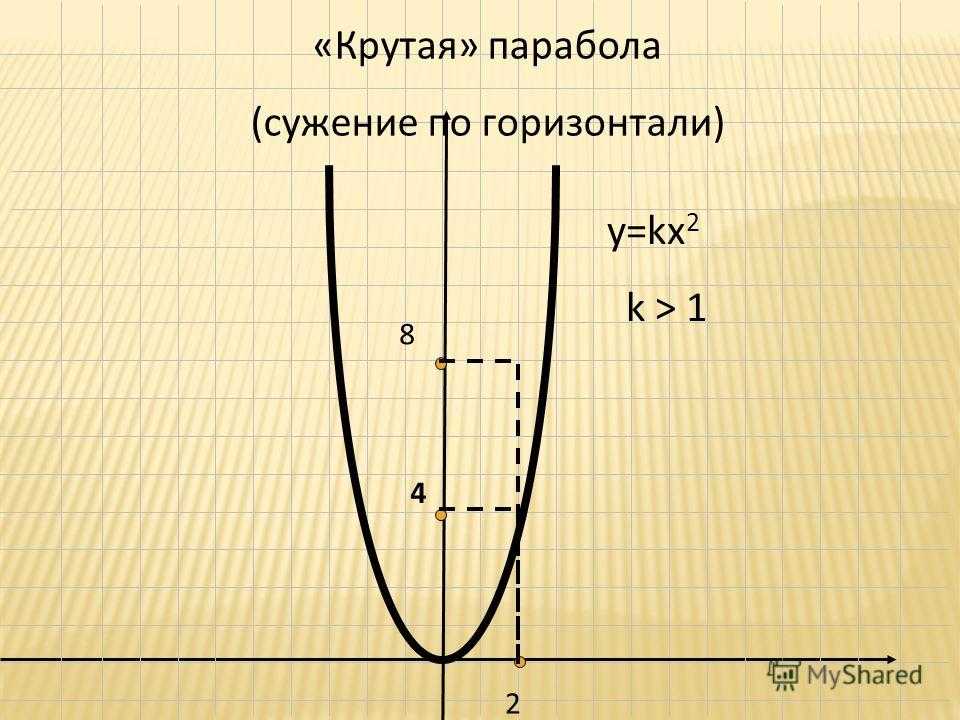. y y

y y

Теперь давайте рассмотрим другой пример построения графика уравнения, содержащего х 2 .

Пример 2

Нарисуйте график

        у   =  — x 2

Раствор

Мы следуем тому же процессу, что и в примере 1.

Создадим Т-таблицу со значениями -3,-2,-1,0,1,2
для х .

У нас есть

-(-3) 2   =  -9    -(-2) 2   =
-4    -(-1) 2   =  -1

-(0) 2   =  -0      -(1) 2 =  -1     -(2) 2   =  -4
-(3) 2   =  -9

Мы можем поместить их в Т-таблицу.

х	г
-3	-9
-2	-4
-1	-1
-0
1	-1
2	-4
3	-9

Эта таблица дает нам баллы (-3,-9),
(-2,-4), (-1,-1),
(0,-0), (1,-1),
(2,-4) и (3,-9).
Затем мы наносим эти точки на плоскость xy .
и соедините точки плавной кривой.
Обратите внимание, что все эти точки имеют неположительную координату y. Мы видим, что эта кривая имеет ту же форму, но перевернута, как хмурый взгляд

Мы видим, что эта кривая имеет ту же форму, но перевернута, как хмурый взгляд.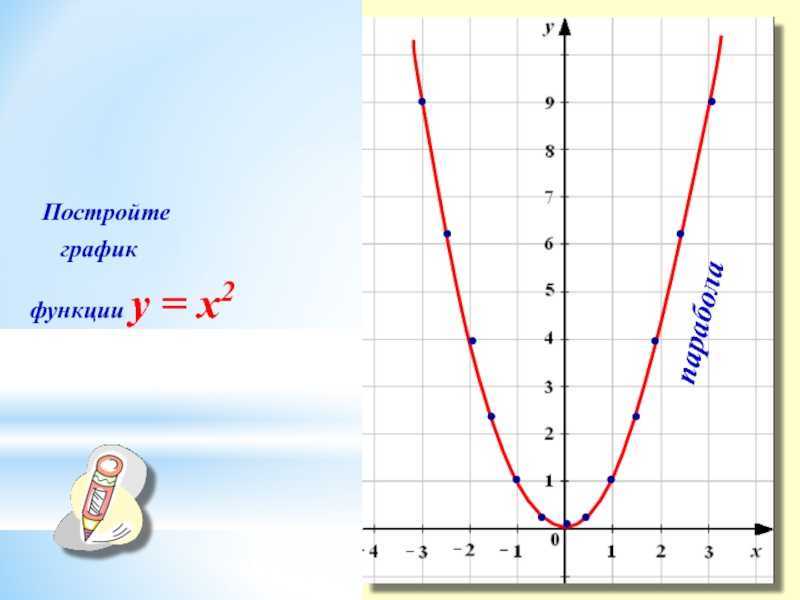

Получается, что все графики уравнений вида

        у   = ах 2

, где a — ненулевое число, имеют форму
парабола. Чтобы определить, похоже ли это на улыбку или хмурый взгляд, следуйте
принцип:

Пример 3

Графики, показанные ниже, представляют собой графики парабол

Обратите внимание, что
уравнения, которые включают отрицательный знак, имеют графики, которые «хмурятся», в то время как те
без «смайлов». Теперь попробуйте сами

Если хотите увидеть ответ, наведите мышку
на желтом прямоугольнике и появится ответ

Теперь попробуйте сами. Если хотите увидеть ответ, наведите мышку
на желтом прямоугольнике и появится ответ.

Упражнение 1

Что из следующего может быть графиком y   =  -0,4 x 2 для положительных значений х ?

Ответ

Теперь, когда мы понимаем, как распознавать графики y   =  ax 2 , посмотрим когда будем
иметь мощность 3 вместо мощности
2.

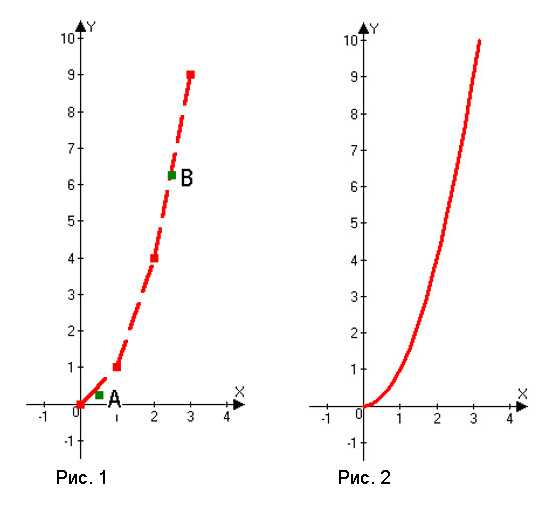
        у   =  ах 3

Пример 4

График y   =  x 3 показан ниже.

Обратите внимание, что этот график начинается снизу слева, резко движется вверх, становится плоским.
в начале координат, а затем снова резко поднимается вверх. Это описание
будет применяться ко всем графикам уравнений г   = ax 3 с положительными значениями a

Пример 5

График y   =  -x 3 показан ниже.

Обратите внимание, что этот график совпадает с графиком и .
= x 3 , но в перевернутом виде. В частности, слева
начинается высоко

Затем она резко падает, пока не выравнивается в начале координат.
Затем он возобновляет крутой спуск вправо от начала координат. Этот
описание будет применяться ко всем графикам уравнений г =  x 3 с отрицательными значениями и .

Пример 6

Ниже приведены еще несколько кубических графиков.

Обратите внимание, что при появлении отрицательного знака график идет сверху слева к
Нижний правый. В противном случае он идет снизу слева вверх справа

Теперь попробуйте сами. Если хотите увидеть ответ, наведите мышку
на желтом прямоугольнике и появится ответ.

Упражнение 2

Сопоставьте уравнение с его графиком.

A.   y   =  1/3 x 2 Б.   y   =  1/3
х 3   

C.     y   =  -1/3 x 2 Д.   г =  -1/3 x 3                  

Ответ

📌 Кубическая парабола — это… 🎓 Что такое Кубическая парабола?

Кубическая парабола

График кубической функции(кубическая парабола)

Куби́ческая фу́нкция в математике — это числовая функция вида

где Другими словами кубическая функция задаётся многочленом третьей степени.

Аналитические свойства

Производная кубической функции f(x) = ax3 + bx2 + cx + d имеет вид f‘(x) = 3ax2 + 2bx + c. В случае, когда дискриминант D = b2 − 4ac квадратного уравнения f‘(x) = 0 больше нуля, оно имеет два различных решения, которые соответствуют критическим точкам функции f. При этом, одна из этих точек является точкой локального минимума, а другая точкой локального максимума. Равенство нулю второй производной f» определяет точку перегиба x = − b / 3a.

График

График кубической функции называется куби́ческой пара́болой. В литературе часто встречаются альтернативные определения кубической параболы как графика функции y = ax3 или y = x3. Легко видеть, что применяя параллельный перенос можно привести кубическую параболу к виду, когда она будет задаватся уравнением y = ax3 − px. Путём применения аффинных преобразований плоскости можно добиться, чтобы a = 1 и p = 0. В этом смысле все определения будут эквивалентны.

Кроме того, кубическая парабола

Wikimedia Foundation.
2010.

• Кубическая гранецентрированная решётка
• Кубическая решетка

Смотреть что такое «Кубическая парабола» в других словарях:

• КУБИЧЕСКАЯ ПАРАБОЛА — алгебраическая кривая 3 го порядка: y = x3 …   Большой Энциклопедический словарь

• кубическая парабола — алгебраическая кривая 3 го порядка: у = х3. * * * КУБИЧЕСКАЯ ПАРАБОЛА КУБИЧЕСКАЯ ПАРАБОЛА, алгебраическая кривая 3 го порядка: y = x3 …   Энциклопедический словарь

• КУБИЧЕСКАЯ ПАРАБОЛА — алгебр кривая 3 го порядка (рис.): у = х3 …   Естествознание. Энциклопедический словарь

• Кубическая парабола —         плоская кривая; см. Линия …   Большая советская энциклопедия

• КУБИЧЕСКАЯ ПАРАБОЛА — плоская кривая (см, рис.), выражаемая в прямоугольной системе координат уравнением у=ах 3 …   Математическая энциклопедия

• Парабола кубическая — График кубической функции (кубическая парабола) Кубическая функция в математике это числовая функция вида где Другими словами кубическая функция задаётся многочленом третьей степени …   Википедия

• Кубическая функция — График кубической функции (кубическая парабола) Кубическая функция в математике  это числовая функция …   Википедия

• Парабола — У этого термина существуют и другие значения, см. Парабола (значения). Парабола, её фокус и директриса Коническое сечение …   Википедия

• Парабола (значения) — Парабола: Парабола геометрическое место точек, равноудалённых от данной прямой и данной точки. Кубическая парабола числовая функция, задаваемая многочленом третьей степени. Полукубическая парабола (парабола Нейла) плоская алгебраическая кривая.… …   Википедия

• Кубическая кривая Безье — Кривые Безье были разработаны в 60 х годах XX века независимо друг от друга Пьером Безье (Bézier) из автомобилестроительной компании «Рено» и Полем де Кастелье (de Casteljau) из компании «Ситроен», где применялись для проектирования кузовов… …   Википедия

Информация о свойствах

В некоторых источниках описываются свойства y = k/x и ее график. Следует отметить, что они получаются при исследовании последней. Существует два состояния. При первом коэффициент пропорциональности больше 0 (k > 0). Следовательно, она обладает такими свойствами:

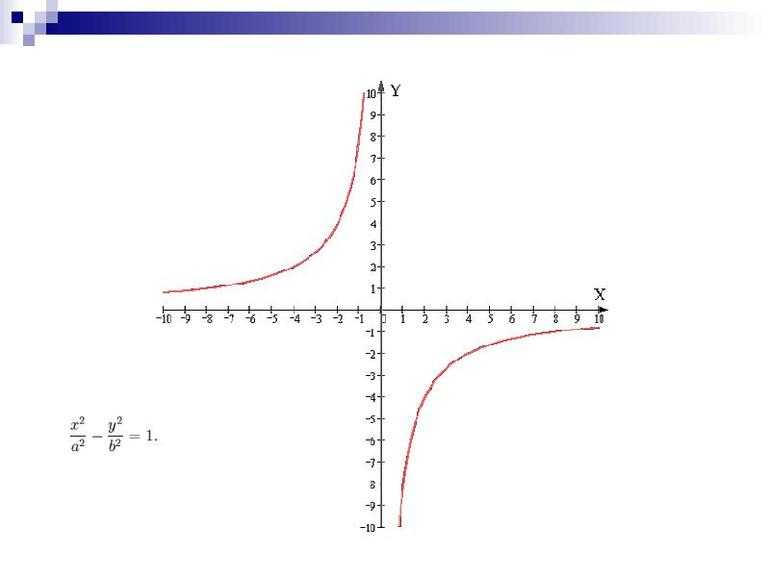
• График: кривая-гипербола.
• D(y) = (-inf;0) U (0;+inf).
• Если x > 0, то y > 0.
• При отрицательных величинах аргумента функция принимает отрицательные значения.
• Она убывает на интервалах: (-inf;0) и (0;+inf).
• Точек экстремума нет.
• Непрерывна, кроме точки х = 0.
• Непериодическая.
• Нечетная.

Когда к < 0, тогда ее свойства отличаются только в 3 и 4 пунктах: y > 0 при отрицательных значениях аргумента, а y < 0 при x > 0. Функция y = kx обладает такими свойствами (k > 0):

• График: прямая.
• D(y) = (-inf;+inf).
• Если x > 0, то y > 0. Когда x < 0, то y < 0.
• Всегда возрастает по всей D(y).
• Минимумов и максимумов нет.
• Непрерывна.
• Нечетная.
• Непериодическая.

При k < 0 она обладает такими же свойствами, но есть такие отличия в пункте 3: y > 0 при x < 0. Следует отметить, что в высшей математике уравнения гиперболы отличаются. Каноническая форма имеет такой вид: [x^2 / a] — [у^2 / b] = 1 (a и b — некоторые целые числа).

Виды и их свойства, область определения

Степенные функции обладают рядом специфических свойств, которые могут отличаться в зависимости от их вида. Рассмотрим основные из них.

Свойства функции\( y=x^{\frac{m}{n}}, (m>n)\):

• D(y)=[0;+∞);
• функцию нельзя отнести ни к четной, ни к нечетной;
• возрастает на [0;+∞);
• не имеет ограничений в верхней части, но ограничена в нижней;
• отсутствует максимальное значение, минимальное значение равно нулю;
• непрерывность;
• E(f)=[0; +∞);
• выпукла вниз.

В качестве примера можно рассмотреть случай, когда показатель степени является правильной дробью, у которой значение числителя меньше, чем знаменателя. График функции\( y=x^{\frac{m}{n}}\), \((m>n)\) напоминает график функции \(y=\sqrt{x}\):

Свойства функции\( y=x^{\frac{m}{n}}\), \(0<\frac{m}{n}<1:\)

• D(y)=[0;+∞);
• нельзя отнести ни к четной, ни к нечетной;
• возрастает на [0;+∞);
• не имеет ограничений сверху, ограничена снизу;
• максимальное значение отсутствует, наименьшее значение равно нулю;
• непрерывность;
• E(f)=[0; +∞);
• выпукла вверх.

Далее следует ознакомиться с графиком функции \(y=x^{-\frac{m}{n}}\). Можно заметить, что он похож на гиперболу. График обладает двумя асимптотами:

• горизонтальной y=0;
• вертикальной х=0.

График имеет следующий вид:

Свойства функции \(y=x^{-\frac{m}{n}}:\)

• D(y)=(0;+∞);
• не является ни четной, ни нечетной;
• убывает на (0;+∞);
• не ограничена в верхней части, обладает ограничением в нижней;
• максимальное значение отсутствует, минимальное – ноль;
• непрерывность;
• E(f)=(0; +∞);
• выпукла вниз.

В том случае, когда x>0, а r – какое-либо рациональное число, производная степенной функции \(y=x^r\) определяется, согласно формуле:

\(y’=r*x^{r-1}\)

К примеру: \((x^{1000})’=1000x^{999} \)

\((x^{-8})’=-8x^{-9}\)

\(\frac{2}{(x^3)’}=\frac{2}{3}*x^{-\frac{1}{3}}\)

\((\sqrt{(2x+5)^5})’=((2x+5)^{\frac{5}{6}})’=2*\frac{5}{6}(2x+5)^{-\frac{1}{6}}=\frac{5}{3}(2x+5)^{-\frac{1}{6}}.\)