Параллелепипед

Вместо заключения

Слово ПРИЗМА используется не только в геометрии, хотя именно это значение считается главным. И именно оно первым записано во многих словарях. Но есть и другие варианты:

1. Физика– устройство для преломления световых лучей.
2. Риторика– оценка с учетом определенных факторов. Например, «Он смотрел на нее через призму прожитых лет» или «Он общался с ними через призму своего настроения».
3. Техника– элемент металлорежущего станка, который предназначен для закрепления на нем цилиндрической заготовки.

А еще «Призма» — это кодовое название советской радиостанции 5-АК. Есть такой хоккейный клуб в Латвии – «Призма-Рига». И наконец, в Финляндии существует сеть продуктовых магазинов «PRISMA».

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

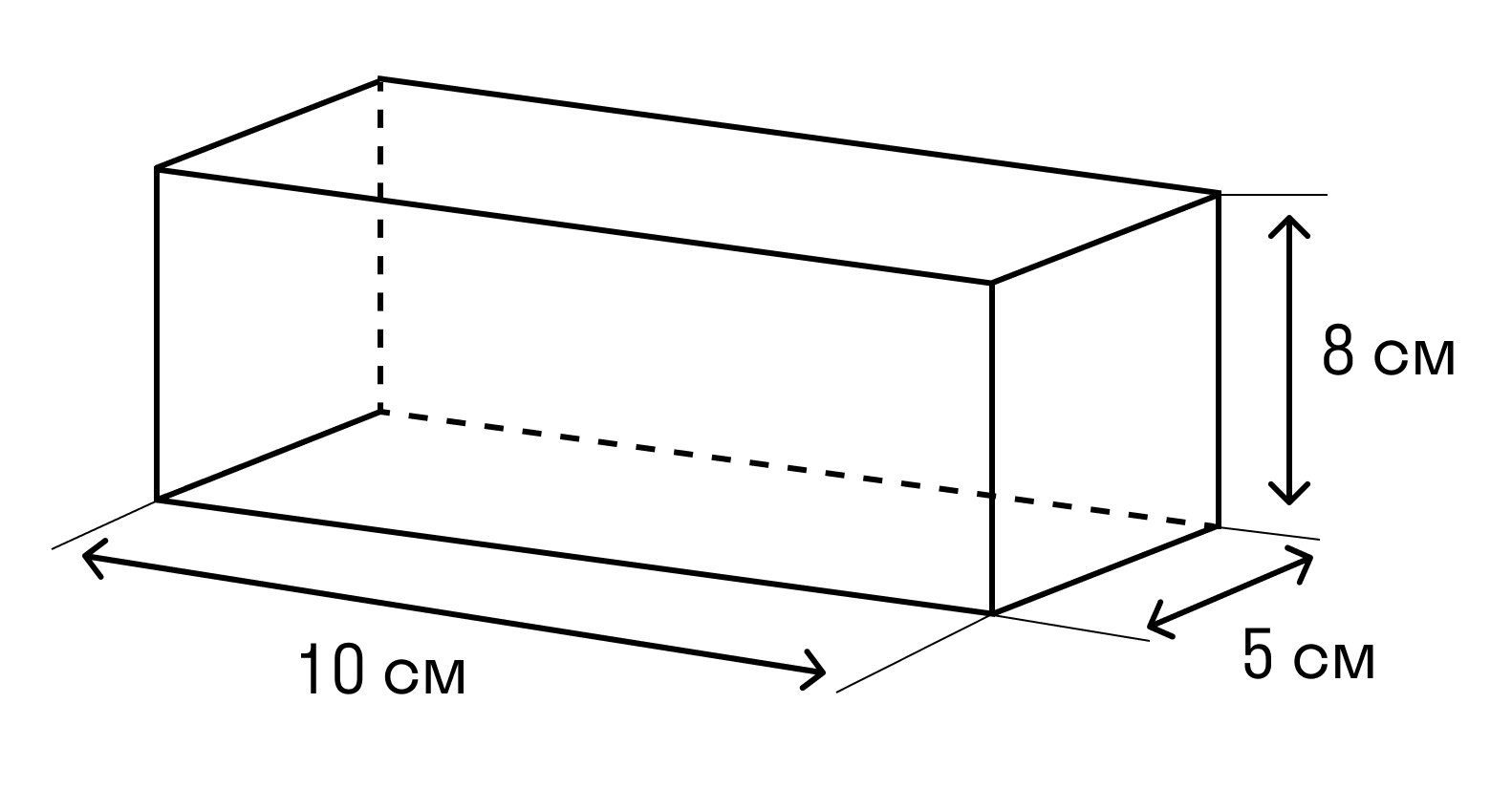
Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a — длина, b — ширина, c — высота. Тогда a = 10, b = 5, c = 8.

Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то: 1) 4 * 10 = 40 (см) — сумма длин параллелепипеда; 2) 4 * 5 = 20 (см) — суммарное значение ширины параллелепипеда; 3) 4 * 8 = 32 (см) — сумма высот параллелепипеда; 4) 40 + 20 + 32 = 92 (см) — сумма длин всех ребер прямоугольного параллелепипеда.

Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП: X = 4a + 4b + 4c (где X — сумма длин ребер).

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac). Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Нужно найти длину ребра A₁B₁.

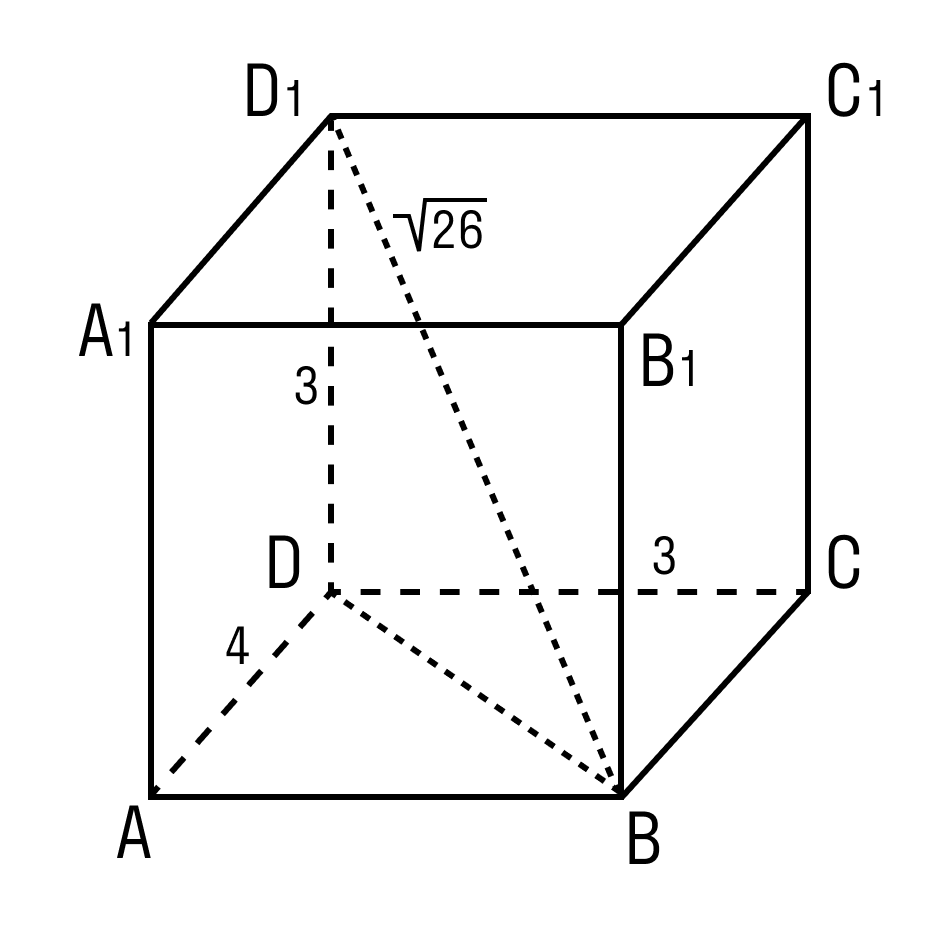
В фокусе внимания треугольник BDD1. Угол D = 90°.

По теореме Пифагора: BD₁ 2 = DD₁ 2 + BD 2 BD 2 = BD₁ 2 – DD₁ 2 BD 2 = 26 – 9 = 17 BD = √17 В треугольнике ADB угол А = 90°. BD 2 = AD 2 + AB 2 AB 2 = BD 2 — AD 2 = (√17)2 — 4 2 = 1 A₁B₁ = AB = 1.

Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4 AD = 6 AA₁= 5 Нужно найти отрезок BD₁.

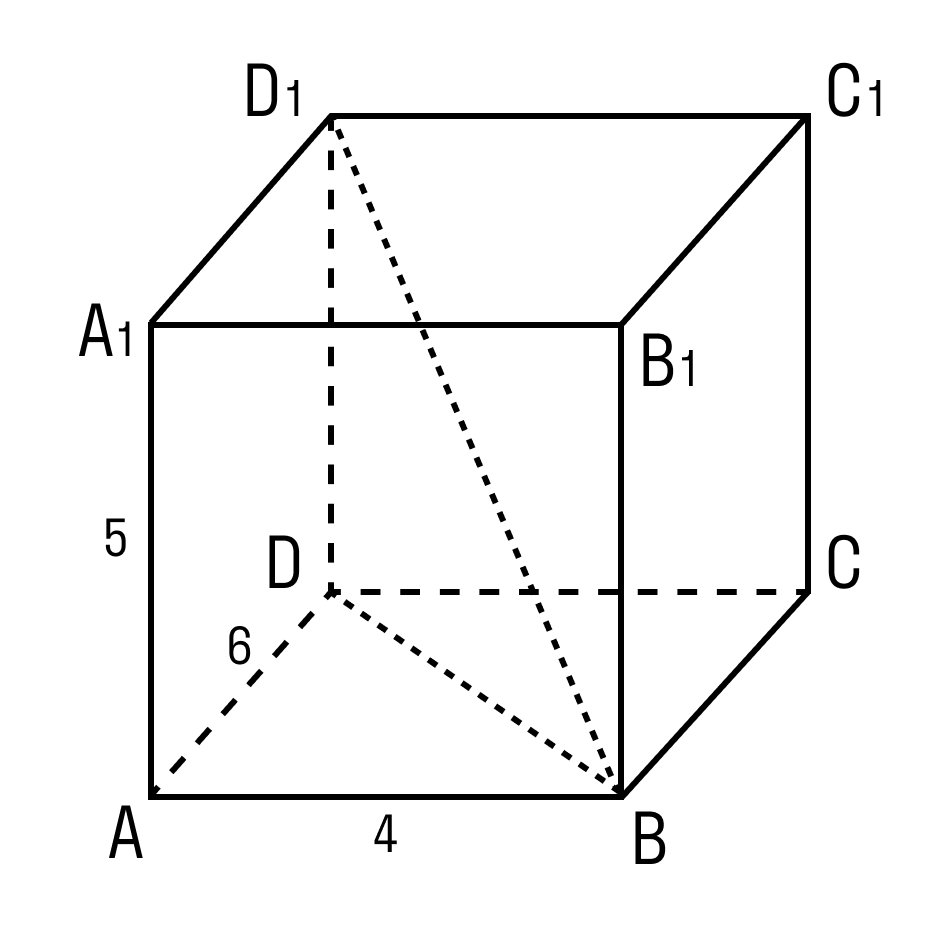
В треугольнике ADB угол A = 90°.

По теореме Пифагора: BD 2 = AB 2 +AD 2 BD 2 = 4 2 + 6 2 = 16 + 36 = 52 В треугольнике BDD₁ угол D = 90°. BD₁ 2 = 52 + 25 = 77 BD₁ = √77.

5.3.2 Параллелепипед; куб; симметрии в кубе, в параллелепипеде

Видеоурок 1: Параллелепипед

Видеоурок 2: Прямоугольный параллелепипед

Лекция: Параллелепипед; куб; симметрии в кубе, в параллелепипеде

Параллелепипед

Основной тип объемной фигуры мы выучили. Однако в зависимости от вида многоугольника, который лежит в основании, призма может видоизменяться.

Призма, в основании которой лежит параллелограмм, называется параллелепипедом.

Все, что мы изучали ранее о призме, можно использовать и при изучении параллелепипеда.

Параллелепипед имеет 6 граней, две из которых являются основаниями. У параллелепипеда все противолежащие грани равны между собой.

Параллелепипеды могут быть прямоугольными (те, у которых угол между всеми соседними ребрами прямой), а так же наклонными (те, у которых угол между соседними ребрами отличается от прямого).

Любой параллелепипед имеет вершины. Вершинами параллелепипеда являются вершины соответствующих граней.

В качестве оснований призмы можно выбрать любые параллельные грани.

Если грани параллелепипеда имеют одно общее ребро, то они называются смежными, если же таковых не имеется, то грани противоположные.

Любой отрезок, который соединяет вершины противоположных граней, называется диагональю этой призмы.

Любые три ребра, которые имеют общую вершину, называются характеристиками параллелепипеда, то есть являются его длиной, шириной и высотой.

• Какой бы параллелепипед Вы не построили бы, он должен иметь симметрию относительно любой диагонали данной фигуры.
• Если построить несколько диагоналей, то они пересекутся в точке, которая поделит их на две равные части.
• Любые две грани, которые лежат друг против друга, имеют одинаковую длину, и обязательно параллельны.
• Сумма квадратов длины, ширины и высоты равна квадрату диагонали.

Формулы полной поверхности и объема прямоугольного параллелепипеда:

Куб

Частным случаем параллелепипеда является куб. С ним все намного проще: куб – это параллелепипед, у которого все грани являются квадратами. Причем все соседние ребра перпендикулярные друг другу.

Все свойства, которые изучались для призмы и для параллелепипеда, справедливы и для куба.

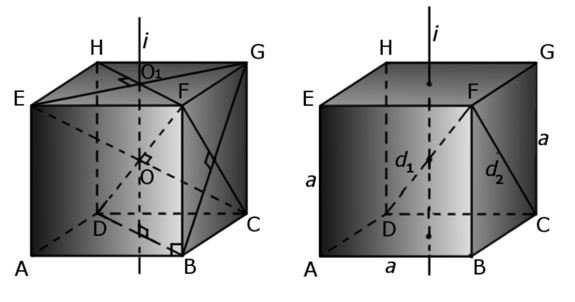
У куба все грани являются правильными четырехугольниками, которые лежат под углом 90 градусов друг к другу. При этом стоит помнить, что для того, чтобы найти площадь одной грани, необходимо воспользоваться формулой площади квадрата S = a 2 . Мы знаем, что куб состоит из 6 граней, а это значит, что для нахождения площади поверхности куба, достаточно просто площадь одной грани умножить на 6. S_общ = 6a 2

Если некоторый отрезок проходит через центр куба (место, где пересекаются все диагонали куба), через центры параллельных граней, то он будет называться осью данного куба.

С легкостью можно найти диагональ куба. Для этого достаточно воспользоваться формулой:

Объем куба можно определить по известной длине стороны или же по диагоналям:

Если провести сечение через диагонали, через центр куба, или же просто взять его ось или диагонали, то куб всегда будет симметричен относительно всего перечисленного.

Готовьтесь к ЕГЭ вместе со «Школково»!

Чтобы занятия проходили легко и максимально эффективно, выбирайте наш математический портал. Здесь вы найдете весь необходимый материал, который потребуется на этапе подготовки к единому государственному экзамену.

Специалисты образовательного проекта «Школково» предлагают пойти от простого к сложному: сначала мы даем теорию, основные формулы и элементарные задачи с решением, а затем постепенно переходим к заданиям экспертного уровня. Вы можете потренироваться, например, с .

Нужную базовую информацию вы найдете в разделе «Теоретическая справка». Вы также можете сразу приступить к решению задач по теме «Прямоугольный параллелепипед» в онлайн-режиме. В разделе «Каталог» представлена большая подборка упражнений разной степени сложности. База заданий регулярно пополняется.

Проверьте, легко ли вы сможете найти объем прямоугольного параллелепипеда, прямо сейчас. Разберите любое задание. Если упражнение дается вам легко, переходите к более сложным задачам. А если возникли определенные сложности, рекомендуем вам планировать свой день таким образом, чтобы ваше расписание включало занятия с дистанционным порталом «Школково».

| параллелепипед, параллелепипед фото
Параллелепи́пед
(др.-греч. παραλληλ-επίπεδον от др.-греч. παρ-άλληλος — «параллельный» и др.-греч. ἐπί-πεδον — «плоскость») — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них — параллелограмм
.

• 1 Типы параллелепипеда
• 2 Основные элементы
• 3 Свойства
• 4 Основные формулы
  • 4.1 Прямой параллелепипед
  • 4.2 Прямоугольный параллелепипед
  • 4.3 Куб
  • 4.4 Произвольный параллелепипед
• 5 математическом анализе
• 6 Примечания
• 7 Ссылки

Математика

Все двухгранные углы прямоугольного параллелепипеда —прямые Для следующего свойства нужно вспомнить, что в пространстве прямоугольный параллелепипед характеризуется шириной, длиной и высотой. Длины этих трех ребер назовем измерениями прямоугольного параллелепипеда На экране изображение и текст: Длины трёх рёбер, имеющих общую вершину называются измерениями прямоугольного параллелепипеда. В силу этих изменений, для основания длину и ширину можно назвать измерениями прямоугольника. И свойство диагонали прямоугольника сформулировать так: квадрат диагонали прямоугольника равен сумме квадратов двух его измерений.

Прямой параллелепипед может быть прямоугольным — основаниями являются прямоугольники. Наклонный параллелепипед — боковые грани не перпендикулярны основаниям. Куб — все грани фигуры являются равными квадратами. Если все грани параллелепипеда — это одинаковые ромбы, он называется ромбоэдром. Свойства параллелепипеда 1. Противоположные грани параллелепипеда взаимно параллельны и являются равными параллелограммами. Все диагонали параллелепипеда пересекаются в одной точке и в ней делятся пополам. Квадрат диагонали d прямоугольного параллелепипеда равен сумме квадратов трех его измерений: длины a , ширины b и высоты c. Прямоугольный параллелепипед. Что это такое? Определение параллелепипеда Начнем с того, что узнаем, что такое параллелепипед. Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

Каждый прямоугольник перпендикулярен тем, что имеет общий край. Они наиболее распространены в нашей повседневной жизни, так как это обычный способ обувных коробок и кирпичей.. Куб или правильный шестигранник Это частный случай предыдущего, где каждая из граней является квадратом. Куб также является частью геометрических тел, называемых платоновыми телами. Платоническое тело представляет собой выпуклый многогранник, так что его грани и внутренние углы равны друг другу. Эти алмазы все равны между собой, так как они имеют общие края. Romboiedro Его шесть граней — ромбоиды. Напомним, что ромбоид представляет собой многоугольник с четырьмя сторонами и четырьмя углами, которые равны от двух до двух. Ромбоиды — это параллелограммы, которые не являются ни квадратными, ни прямоугольниками, ни ромбами. С другой стороны, косые параллелепипеды — это те, в которых хотя бы одна высота не совпадает с ее краем. В эту классификацию мы можем включить ромбоэдры и ромбиэдры. Диагональный расчет Чтобы вычислить диагональ ортоэдра, мы можем использовать теорему Пифагора для R3. Напомним, что ортоэдр имеет характеристику, состоящую в том, что каждая сторона перпендикулярна сторонам, имеющим общий край. Из этого факта мы можем сделать вывод, что каждое ребро перпендикулярно тем, которые имеют общую вершину. Чтобы вычислить длину диагонали ортоэдра, действуем следующим образом: 1. Мы рассчитаем диагональ одной из граней, которую мы положим в качестве основы. Для этого мы используем теорему Пифагора.

Вот по этому в нашей задаче прямо говорится об этом. Если верить Священным Писаниям разных религий, то именно из одного такого ребра сотворены все прямоугольные параллелепипеды, задачи о которых решает вся прекрасная половина человечества. Следующая фраза «… равны 1, 2, 3» обозначает, что нам не нужно искать этот злополучный прямоугольный параллелепипед и свою линейку, чтобы измерить длины его граней, как это показано на рисунке. Тот, кто эту задачу придумал, уже сам всё измерил или выдумал эти размеры, что в данном случае принципиального значения не имеет. Кто есть кто в этом списке чисел? Где длина, ширина, высота нашего параллелепипеда? Нам это без разницы. Как бы мы этот прямоугольный параллелепипед не крутили, площадь его поверхности всегда будет оставаться неизменной. Предыдущие поколения математиков этот факт не единожды проверили. Когда мы доберемся до решения, мы сами в этом убедимся. Теперь вопрос, в чём же конкретно измеряется наш прямоугольный параллелепипед и площадь его поверхности? В каких единицах измерения? Ответ довольно прост — в любых единицах измерения длины. Англичане и американцы любят дюймы, футы, мили. Мы предпочитаем сантиметры, метры, километры. В чем измеряют длину инопланетяне? Мы вообще не знаем. Да нам эти единицы измерения и не важны. В чем бы мы не измеряли длину граней, циферки возле длин и площади будут одинаковыми. Циферки остаются, единицы измерения меняются.

Призма

Призма – это геометрическая фигура в пространстве; многогранник с двумя параллельными и равными гранями (многоугольниками), а другие грани при этом являются параллелограммами. 

• Боковое ребро – отрезок, соединяющий соответствующие друг другу вершины разных оснований (AA₁, BB₁, CC₁ и DD₁). Является общей стороной двух боковых граней.
• Высота (h) – это перпендикуляр, проведенный от одного основания к другому, т.е. расстояние между ними. Если боковые ребра расположены под прямым углом к основаниям фигуры, значит они одновременно являются и высотами призмы.
• Диагональ основания – отрезок, который соединяет две противолежащие вершины одного и того же основания (AC, BD, A₁C₁ и B₁D₁). У треугольной призмы данного элемента нет.
• Диагональ боковой грани – отрезок, который соединяет две противолежащие вершины одной и той же грани. На рисунке изображены диагонали только одной грани (CD₁ и C₁D), чтобы не перегружать его.
• Диагональ призмы – отрезок, соединяющий две вершины разных оснований, не принадлежащих одной боковой грани. Мы показали только две из четырех: AC₁ и B₁D.
• Поверхность призмы – суммарная поверхность двух ее оснований и боковых граней.

Основные свойства призмы

• Основы призмы — равные многоугольники.
• Боковые грани призмы — параллелограммы.
• Боковые ребра призмы параллельны и равны между собой.
• Перпендикулярное сечение перпендикулярно всем боковым ребрам и боковым граням.
• Высота прямой призмы равна длине бокового ребра.
• Высота наклонной призмы всегда меньше длины ребра.
• В прямой призме гранями могут быть прямоугольниками или квадратами.

Варианты сечения призмы

1. Диагональное сечение – секущая плоскость проходит через диагональ основания призмы и два соответствующих боковых ребра.

Примечание: у треугольной призмы нет диагонального сечения, т.к. основанием фигуры является треугольник, у которого нет диагоналей.

2. Перпендикулярное сечение – секущая плоскость пересекает все боковые ребра под прямым углом.

Виды призм

Рассмотрим разновидности фигуры с треугольным основанием.

1. Прямая призма– это такая геометрическая фигура, у которой боковые грани расположены под прямым углом к основаниям (т.е. перпендикулярны им). Высота такой фигуры равняется ее боковому ребру.
2. Наклонная призма– боковые грани фигуры не перпендикулярны ее основаниям.
3. Правильная призма – основаниями являются правильные многоугольники. Может быть прямой или наклонной.
4. Усеченная призма– часть фигуры, оставшаяся после пересечения ее плоскостью, не параллельной основаниям. Также может быть как прямой, так и наклонной.

Урок 31. Прямоугольный параллелепипед

Прямоугольный параллелепипед – это шестигранник, у которого все грани имеют прямоугольную форму.

Лицо — это плоская поверхность предмета, образующая угол с другой поверхностью. такой же поверхностью.

Основания параллелепипеда — верхний и нижний грани.

Обязательное чтение

Никольский С. М. Математика. 5 класс. учебное пособие для общеобразовательных учреждений // С.М. Никольский, М.К. Потапов, Н.Н. Решетников и др. — М.: Просвещение, 2017 г. — 272 с.

Дальнейшее чтение

1. математика: тематические тесты. П.В. Чулков, Е.Ф. Шершнев, О.Ф. Зарапина.

Шарыгин И. Ф. Задачи на пригеклку: 5-6 класс // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014 г. — 95 с.

Теоретический материал для самостоятельного изучения

Мир, в котором мы живем, состоит из огромного количества предметов разных форм, цветов и размеров. Исследование их свойства, Люди открывают для себя что-то новое. Например, математики изучают геометрические твердые тела в окружающей среде: цилиндры, кубы. и так далее.

Сегодня мы рассмотрим прямоугольник параллелепипед – многогранник, название которого переводится с древнегреческого как «самолеты, летящие бок о бок».

Прямоугольный параллелепипед ограничОн состоит из шести прямоугольников, а именно. гранями. Край, на котором располагается прямоугольник. параллелепипед, Край прямоугольника и его противоположность называются нижней и верхней ножкой.

Остальные четыре грани называют боковыми гранями.

Стороны граней параллелепипеда называются ребрами. Их двенадцать.

Концы ребер называются вершинами. К ним относятся. в параллелепипеде восемь.

Вершина — это общая точка трех ребер.

Длины двух ребер базовой поверхности, начиная от вершины, называются длиной и шириной прямоугольника. параллелепипеда.

Длина боковой грани называется высотой.

Таким образом, длины трех ребер, начиная от вершины, называются длиной, шириной и высотой. В противном случае длина, ширина и высота называются размерами прямоугольника параллелепипеда.

Прямоугольный параллелепипед, который имеет три равные грани, начинающиеся от вершины, называется кубом. Каждый грань куба – квадрат.

Рассмотрим свойства прямоугольного параллелепипеда и куба.

У прямоугольного параллелепипед а противоположные грани равны.

Все грани куба равны между собой.

Построим прямоугольник с заданной длиной a и высотой h.

Из каждой вершины добавьте отрезок длиной, равной половине ширины b, под углом 45 градусов. И соедините концы отрезков, невидимые. грани – пунктирной линией.

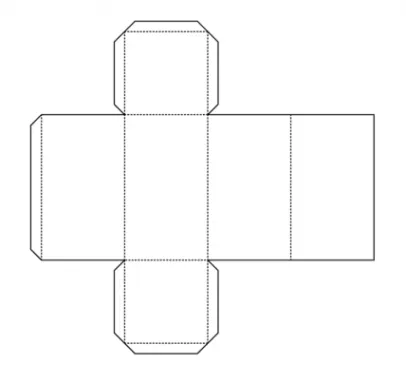
Изготовить параллелепипед Существует несколько вариантов. Например, с помощью дрели. Нарисуйте на бумаге шаблон, похожий на шаблон выше

Обратите внимание, что на рисунке припуски на швы даны с учетом возможности сварки. параллелепипед