2.2 Функция распределения
После разговора о распределении вероятностей пришло время поговорить о функции распределения. Эта функция распределения является упрощенной версией! Должно называться полное имяФункция распределения понятий。
Посмотрите на закон распределения на рисунке ниже. Закон распределения здесь явно является «функцией вероятности», о которой мы только что говорили, и это всего лишь одно. Но я знаю, что многие учебники называются законами о распределении.
Функция распределения вероятностей — это накопление функций вероятности
Давайте посмотрим на формулу на графике, где F (x) представляет собой функцию распределения вероятностей. Справа от этого символа находится длинная формула, которая напоминает функцию вероятности, но знак равенства становится формулой, которая меньше или равна знаку. Если вы посмотрите вправо, это скопление функций вероятности одна за другой!
Вы открыли секрет функции распределения вероятностей? Это совсем не новость, это совокупный результат значения функции вероятности! Поэтому ее еще называют кумулятивной функцией вероятности!
Функция вероятности и функция распределения вероятности похожи на две стороны медали, они просто разные средства описания вероятности!
3 Функция вероятности и функция распределения непрерывных случайных величин
«Функция вероятности» непрерывных случайных величин имеет другое название.Это называется «Функция плотности вероятности».
Почему это так называется? Воспользуемся словами мастера, чтобы сказать вам, что в книге Чэнь Сиру «Теория вероятностей и математическая статистика»
Если вы все еще не понимаете этот анализ, взгляните на следующую формулу:
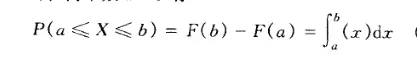
Функция плотности вероятности, выраженная математической формулой, является функцией определенного интеграла. Определенный интеграл используется для определения площади в математике, и здесь вы можете выразить вероятность как площадь!
Слева представлен график, построенный функцией распределения непрерывной случайной величины F (x), а справа — график, построенный функцией плотности вероятности непрерывной случайной величины f (x). Между ними существует следующее соотношение:Функция плотности вероятности — это производная функция функции распределения。
Сравнивая два изображения, вы обнаружите, что если вы используете область на правом рисунке для представления вероятности, вы можете использовать график, чтобы четко увидеть, какие значения имеют большую вероятность!Следовательно, когда мы выражаем вероятность непрерывной случайной величины, очень хорошо использовать функцию плотности вероятности f (x) для ее выражения!
Однако у читателей могут возникнуть такие вопросы:
В: Каково значение значения функции плотности вероятности в определенной точке?
A: Значение легче понять в определенный моментФункция плотности вероятности А именноСкорость изменения вероятности в этой точке(Или производная). В этом месте значение плотности вероятности легко принять за значение вероятности.
Например: соотношение между расстоянием (вероятностью) и скоростью (плотностью вероятности).
- Скорость определенной точки нельзя рассматривать как расстояние до определенной точки.
- Это не имеет смысла, потому что расстояние — это понятие от ХХ до ХХ.
- Следовательно, вероятность также должна иметь интервал.
- Этот интервал может быть окрестностью x (он может бесконечно приближаться к 0). Интегрируя f (x) в окрестности x, вы можете найти площадь этой окрестности, которая представляет вероятность возникновения этого события, представленного этой окрестностью.
Функции нескольких переменных
В этом разделе мы остановимся на некоторых специфических функциях п переменных и их законах распределения, часто встречающихся в приложениях и играющих важную роль в статистике.
Экстремумы и порядковые статистики
Распределение максимума n случайных величин
Очевидное обобщение рассуждений предыдущего пункта (см. (1)) дает: если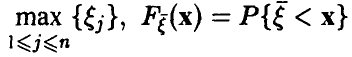 
— функция распределения то
Если вектор непрерывен с плотностью , то плотность дается соотношением
В случае независимости компонент вектора в совокупности
а в предположении непрерывности
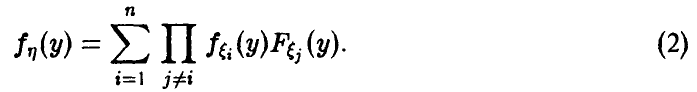
Распределение минимума n случайных величин
Обобщая соотношение (8) дословным повторением выкладок, получаем для вектора с независимыми в совокупности компонентами
Для непрерывных также непрерывна и
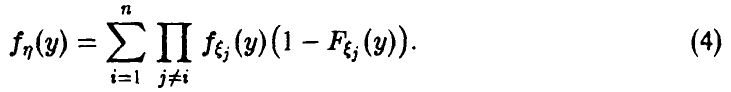
Заметим, что здесь, как и для случая двухкомпонентного вектора , из условия экспоненциальное компонент следует экспоненциальное минимума.
Если n достаточно велико, то оказывается, что этот результат — экспоненциальное минимума — слабо зависит от характера распределения компонент. Точнее, имеет место следующее утверждение.
Теорема:
Пусть случайные величины — независимы в совокупности, непрерывны на и одинаково распределены. Тогда при распределение минимума близко к экспоненциальному:
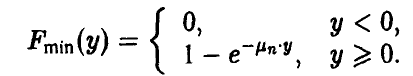
Здесь
◄ Соотношение (3) в условиях теоремы дает
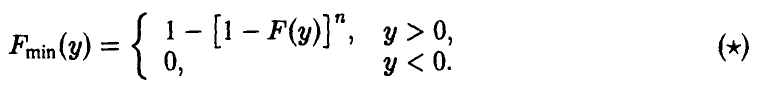
В силу непрерывности , в окрестности нуля (точнее, в правой полуокрестности) выполняется равенство
Из соотношения (*) ясно, что при 
т. е. вся информация о поведении минимума сосредоточена в окрестности нуля. Положим Тогда
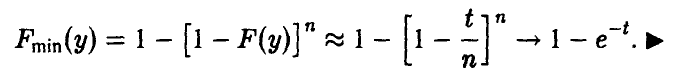
Указанное обстоятельство является теоретическим осмыслением т. н. «принципа слабого звена», широко используемого в теории надежности — надежность агрегата, функционирование которого необходимо зависит от надежности большого количества составляющих, определяется надежностью самого ненадежного из них и описывается экспоненциальным распределением.
Распределение порядковых статистик
Пусть — случайный вектор с законом распределения . Вектор назовем вектором порядковых статистик, а его компоненты —порядковыми статистиками, если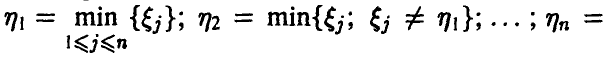 
Компоненты вектора расположены в порядке неубывания
Найдем закон распределения m-й компоненты в предположении независимости и одинаковой распределенности компонент Логику рассуждений рассмотрим на примере n = 3, m = 2.
Для того, чтобы вторая порядковая статистика приняла значение, меньшее у, нужно чтобы не менее двух из трех компонент вектора приняли значения, меньшие у. Это значит, что
Аналогично для произвольных m и n
Основные законы распределения
Биометрия (=биологическая статистика) изучает случайные события и поведение случайных величин. Вообще-то биологически явления не случайны, они закономерно вытекают из определённых причин. Но мы не может узнать и проанализировать все эти причины во всей их совокупности, поэтому конкретные биологические явления и события выглядят для нас случайными. Так мы и будем к ним относиться.
Начиная биологический эксперимент или приступая к наблюдению, невозможно точно сказать, каков будет его результат. Это, например, уровень численности животных в данном районе, вес тела ещё не отловленных особей, количество сахара в крови через час после введения препарата и т. п. В этом смысле биологические явления случайны, точно не предсказуемы. Однако любому биологу ясно, что случайность эта не абсолютна. Несмотря на сложность точного прогноза, приблизительный результат можно предугадать, в частности, предсказав, что интересующая нас величина будет находиться в пределах некоторого интервала между конкретными минимальными и максимальными значениями. Так, например, вполне предсказуемо, что рост человека, выбранного наугад из группы обычных людей, вряд ли превысит два метра или будет ниже полутора метров. Вариационная статистика может дать и более точный прогноз, ориентируясь на известные ей законы поведения случайных величин, относящихся к разным типам распределений. При этом под распределением признаков (случайных величин, объектов) понимается соотношение между их значениями и частотой встречаемости.
Распределением признаков (случайных величин, объектов) — это соотношение между их значениями и частотой их встречаемости.
В биологических исследованиях чаще всего могут встретиться шесть вариантов распределения:
- Нормальное.
- Биномиальное.
- Распределение Пуассона.
- Альтернативное.
- Полиномиальное.
- Равномерное.
Асимметричное многомерное распределение Лапласа
Типичная характеристика асимметричного многомерного распределения Лапласа имеет вид характеристическая функция:
- φ(т;μ,Σ)=11+12т′Σт−яμт.{ displaystyle varphi (t; { boldsymbol { mu}}, { boldsymbol { Sigma}}) = { frac {1} {1 + { tfrac {1} {2}} mathbf {t } ‘{ boldsymbol { Sigma}} mathbf {t} -i { boldsymbol { mu}} mathbf {t}}}.}
Как и в случае с симметричным многомерным распределением Лапласа, асимметричное многомерное распределение Лапласа имеет среднее значение μ{ displaystyle { boldsymbol { mu}}}, но ковариация становится Σ+μ′μ{ displaystyle { boldsymbol { Sigma}} + { boldsymbol { mu}} ‘{ boldsymbol { mu}}}. Асимметричное многомерное распределение Лапласа не является эллиптическим, если только μ={ displaystyle { boldsymbol { mu}} = mathbf {0}}, и в этом случае распределение сводится к симметричному многомерному распределению Лапласа с μ={ displaystyle { boldsymbol { mu}} = mathbf {0}}.
В функция плотности вероятности (pdf) для k-мерное асимметричное многомерное распределение Лапласа:
- жИкс(Икс1,…,Иксk)=2еИкс′Σ−1μ(2π)k2|Σ|0.5(Икс′Σ−1Икс2+μ′Σ−1μ)v2Kv((2+μ′Σ−1μ)(Икс′Σ−1Икс)),{ displaystyle f _ { mathbf {x}} (x_ {1}, ldots, x_ {k}) = { frac {2e ^ { mathbf {x} ‘{ boldsymbol { Sigma}} ^ {- 1} { boldsymbol { mu}}}} {(2 pi) ^ {k / 2} | { boldsymbol { Sigma}} | ^ {0.5}}} { Big (} { frac { mathbf {x} ‘{ boldsymbol { Sigma}} ^ {- 1} mathbf {x}} {2 + { boldsymbol { mu}}’ { boldsymbol { Sigma}} ^ {- 1} { boldsymbol { mu}}}} { Big)} ^ {v / 2} K_ {v} { Big (} { sqrt {(2 + { boldsymbol { mu}} ‘{ boldsymbol { Sigma}} ^ {- 1} { boldsymbol { mu}}) ( mathbf {x} ‘{ boldsymbol { Sigma}} ^ {- 1} mathbf {x})}} { Big)} ,}
куда:
v=(2−k)2{ Displaystyle v = (2-к) / 2} и Kv{ displaystyle K_ {v}} это модифицированная функция Бесселя второго рода.
Асимметричное распределение Лапласа, включая частный случай μ={ displaystyle { boldsymbol { mu}} = mathbf {0}}, является примером геометрическое устойчивое распределение. Он представляет собой предельное распределение для суммы независимые, одинаково распределенные случайные величины с конечной дисперсией и ковариацией, где количество суммируемых элементов само по себе является независимой случайной величиной, распределенной в соответствии с геометрическое распределение. Такие геометрические суммы могут возникать в практических приложениях в биологии, экономике и страховании. Распределение также может быть применимо в более широких ситуациях для моделирования многомерных данных с более тяжелыми хвостами, чем нормальное распределение, но конечным моменты.
Отношения между экспоненциальное распределение и Распределение Лапласа позволяет использовать простой метод моделирования двумерных асимметричных переменных Лапласа (в том числе для случая μ={ displaystyle { boldsymbol { mu}} = mathbf {0}}). Моделируйте двумерный нормальный вектор случайных величин Y{ displaystyle mathbf {Y}} из раздачи с μ1=μ2={ Displaystyle му _ {1} = му _ {2} = 0} и ковариационная матрица Σ{ displaystyle { boldsymbol { Sigma}}}. Независимо моделируйте экспоненциальные случайные величины W из распределения Exp (1). Икс=WY+Wμ{ displaystyle mathbf {X} = { sqrt {W}} mathbf {Y} + W { boldsymbol { mu}}} будет распределенным (асимметричным) двумерным Лапласом со средним μ{ displaystyle { boldsymbol { mu}}} и ковариационная матрица Σ{ displaystyle { boldsymbol { Sigma}}}.
Решим ещё задачи на нормальное распределение
Решить задачу самостоятельно, а затем посмотреть решение
Пример 5. Определить с точностью до двух знаков после запятой вероятность
попадания при стрельбе в полосу шириной 3,5 м, если ошибки стрельбы подчиняются нормальному закону
распределения со средним значением 0 и .
Решим ещё одну задачу вместе
Пример 6. О случайной величине X известно, что она нормально
распределена, а вероятности того, что она составит 10 или меньше и больше 25, соответственно
и
. Найти
среднее значение (математическое ожидание) случайной величины и её дисперсию.
Решение. Используем данные в условии задачи вероятности:
Пользуясь статистическими таблицами, находим:
Составляем систему из полученных равенств:
Решая систему, находим:
.
| Назад | Листать | Вперёд>>> |
Начало темы «Теория вероятностей»
Приближенный метод проверки нормальности распределения
Приближенный метод проверки нормальности распределения значений выборки основан на
следующем свойстве нормального распределения: коэффициент асимметрии
и коэффициент эксцесса равны нулю.
Коэффициент асимметрии
численно характеризует симметрию эмпирического распределения относительно среднего. Если коэффициент
асимметрии равен нулю, то среднее арифметрического значение, медиана и мода равны:
и кривая плотности
распределения симметрична относительно среднего. Если коэффициент асимметрии меньше нуля (),
то среднее арифметическое меньше медианы, а медиана, в свою очередь, меньше моды
() и кривая сдвинута
вправо (по сравнению с нормальным распределением). Если коэффициент асимметрии больше нуля (),
то среднее арифметическое больше медианы, а медиана, в свою очередь, больше моды
() и кривая сдвинута
влево (по сравнению с нормальным распределением).
Коэффициент эксцесса
характеризует концентрацию эмпирического распределения вокруг арифметического среднего в направлении
оси и степень островершинности кривой плотности распределения.
Если коэффициент эксцесса больше нуля, то кривая более вытянута (по сравнению с нормальным распределением)
вдоль оси (график более островершинный). Если коэффициент
эксцесса меньше нуля, то кривая более сплющена (по сравнению с нормальным распределением)
вдоль оси (график более туповершинный).
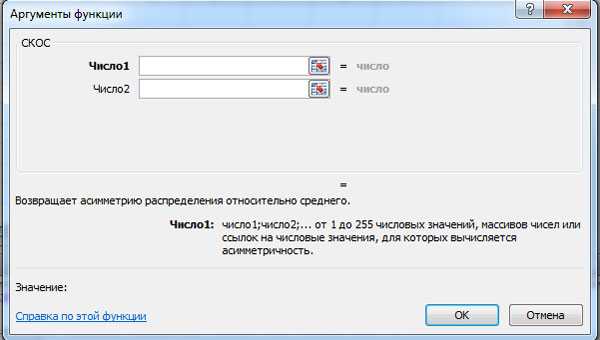
Коэффициент асимметрии можно вычислить с помощью функции MS Excel СКОС. Если вы
проверяете один массив данных, то требуется ввести диапазон данных в одно окошко «Число».
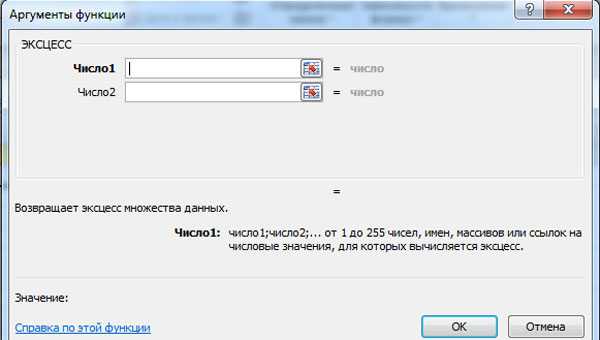
Коэффициент эксцесса можно вычислить с помощью функции MS Excel ЭКСЦЕСС. При проверке
одного массива данных также достаточно ввести диапазон данных в одно окошко «Число».
Итак, как мы уже знаем, при нормальном распределении коэффициенты асимметрии и эксцесса
равны нулю. Но что, если мы получили коэффициенты асимметрии, равные -0,14, 0,22, 0,43, а коэффициенты
эксцесса, равные 0,17, -0,31, 0,55? Вопрос вполне справедливый, так как практически мы имеем дело лишь с
приближенными, выборочными значениями асимметрии и эксцесса, которые подвержены некоторому неизбежному,
неконтролируемому разбросу. Поэтому нельзя требовать строгого равенства этих коэффициентов нулю, они
должны лишь быть достаточно близкими к нулю. Но что значит — достаточно?
Требуется сравнить полученные эмпирические значения с
допустимыми значениями. Для этого нужно проверить следующие неравенства (сравнить значения коэффициентов
по модулю с критическими значениями — границами области проверки гипотезы).
Для коэффициента асимметрии :
,
где
—
квантиль стандартного нормального распределения уровня ,
—
среднеквадратическое отклонение для выборки с числом наблюдений .
Для коэффициента эксцесса :
,
где
—
квантиль стандартного нормального распределения уровня ,
—
среднеквадратическое отклонение для выборки с числом наблюдений .
Так как коэффициенты асимметрии и эксцесса могут оказаться и положительными, и отрицательными,
то в приближенном методе проверки нормальности распределения используется двусторонний квантиль
стандартного нормального распределения; он задаёт интервал, в который случайная величина попадает
с определённой вероятностью. Приведём значения двусторонних квантилей стандартного нормального
распределения определённых уровней
(слева — уровень, справа — значение квантиля):
- 0,90: 1,645
- 0,95: 1,960
- 0,975: 2,241
- 0,98: 2,326
- 0,99: 2,576
- 0,995: 2,807
- 0,999: 3,291
- 0,9995: 3,481
- 0,9999: 3,891
Например, для выборки с числом наблюдений и
,
пользуясь этими значениями и ранее приведёнными формулами, можно получить границу области принятия гипотезы для
коэффициента асимметрии 0,62 и для коэффициента эксцесса 1,15. Поэтому приведённые ранее примеры эмпирических
значений коэффициента асимметрии -0,14, 0,22, 0,43 попадают в область принятия гипотезы. То же самое
относится к значениям коэффициента эксцесса 0,17, -0,31, 0,55. Следовательно, если получены такие
эмпирические значения, то с вероятностью 95% данные выборки подчиняются нормальному закону распределения.
Функции одного переменного
Пусть — случайная величина, закон распределения ко-торой задан функцией распределения . Если функция распределения случайной величины , то приведенные выше соображения дают
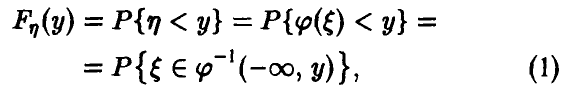
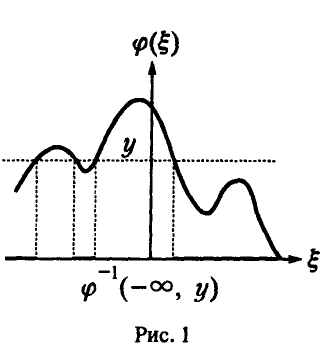
где через обозначен полный прообраз полупрямой . Соотношение (1) является очевидным следствием (*) и для рассматриваемого случая проиллюстрировано на рис. 1.
Монотонное преобразование случайной величины
Пусть — непрерывная монотонная функция (для определенности — монотонно невозрастающая) и . Для функции распределения получаем
(здесь — функция, обратная к , существование которой обеспечивается монотонностью и непрерывность. Для монотонно неубывающей аналогичные выкладки дают
В частности, если — линейна, , то при а > 0 (рис. 2)
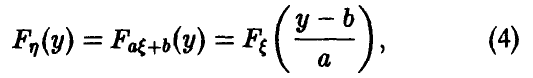
а при а < О
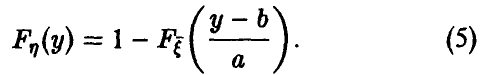
Линейные преобразования не меняют характера распределения, а сказываются лишь на его параметрах.
Линейное преобразование равномерной на случайной величины
Пусть Тогда 
Линейное преобразование нормальной случайной величины
Пусть Тогда 
, и вообще, если то
◄ Пусть, например, а > 0. Из (4) заключаем, что
Положим в последнем интеграле u = ах + b. Эта замена дает
Важное тождество, являющееся источником многих интересных приложений, может быть получено из соотношения (3) при
Лемма:
Если — случайная величина с непрерывной функцией распределения , то случайная величина — равномерна на .
Имеем
— монотонно не убывает и заключена в пределах от 0 до 1. Поэтому
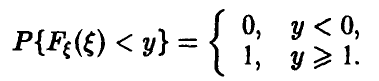
На промежутке же получаем
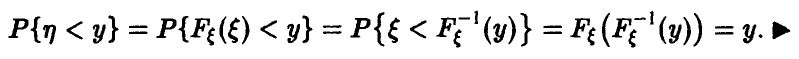
Одним из возможных путей использования доказанной леммы является, например, процедура моделирования случайной величины с произвольным законом распределения . Как следует из леммы, для этого достаточно уметь получать значения равномерной на случайной величины, тогда значения могут быть получены из тождества
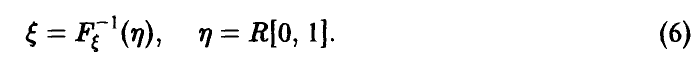
В заключение заметим, что если случайная величина непрерывна и функция не только монотонна, но и дифференцируема, то также непрерывна. При этом плотность случайной величины легко может быть получена из (2) или (3):
Если ) свойством монотонности не обладает, то результат может быть получен скрупулезным следованием логике соотношения (1), как показывают приводимые ниже примеры.
Распределение квадрата равномерной на случайной величины
Пусть . Рассмотрим (рис. 3)
Отсюда для плотности получим
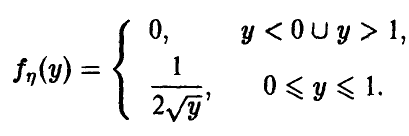
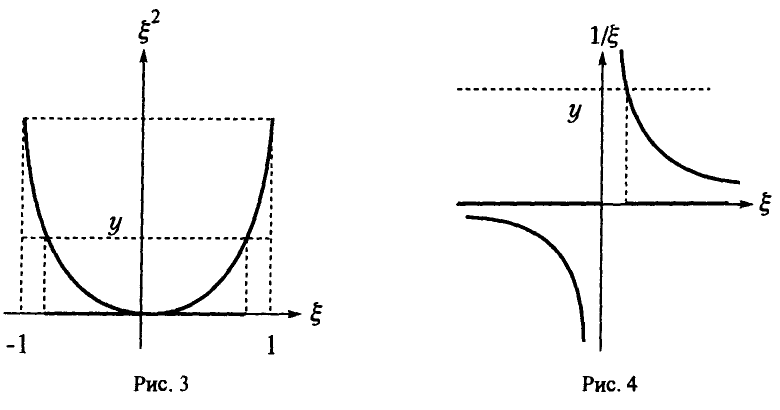
Распределение случайной величины, обратной к случайной величине с распределением Коши
Пусть — случайная величина, имеющая распределения Коши (см. п. 2.1.1) и 
Положим (рис. 4). Следуя (1), получаем:
Таким образом, если
Вопросы и ответы
Что представляет собой функция плотности вероятности (PDF)?
Функция плотности вероятности (PDF) представляет собой вероятность различных исходов в рамках распределения набора данных. Она дает представление о вероятности конкретных значений и помогает оценить риски, связанные с инвестиционной доходностью.
Как рассчитывается функция плотности вероятности (PDF)?
Расчет функции плотности вероятности (PDF) заключается в анализе распределения данных и определении вероятности появления определенных значений. Это можно сделать с помощью математических формул или специализированных статистических программных пакетов, которые выполняют необходимые расчеты и генерируют графическое представление PDF.
На что указывает асимметричная функция плотности вероятности (PDF)?
Асимметричная функция плотности вероятности (PDF) указывает на асимметричное распределение данных. Если кривая перекошена вправо (положительный перекос), это говорит о большем потенциале вознаграждения. И наоборот, если кривая перекошена влево (отрицательный перекос), это указывает на больший потенциал риска падения. Перекос дает представление о форме и характеристиках набора данных.
Как центральная предельная теорема (ЦПТ) связана с функциями плотности вероятностей (ФПВ)?
Теорема о центральной границе (CLT) — это математический принцип, который гласит, что распределение случайной переменной в выборке будет стремиться к нормальному распределению по мере увеличения размера выборки. PDF часто напоминает колоколообразную кривую, что свидетельствует о нормальном распределении. CLT позволяет нам анализировать и понимать свойства PDF-файлов, даже если основной процесс, порождающий данные, не является нормально распределенным.
Можно ли применить функции плотности вероятностей (ФПВ) к инвестициям в Россию?
Да, функции плотности вероятностей (ФПВ) могут применяться для инвестиций в России, как и в любой другой стране. Концепции и принципы, лежащие в основе ФПВ, универсальны и применимы в статистическом анализе и финансах. Понимая PDF, инвесторы в России могут оценивать риски и ожидания, связанные с доходностью инвестиций, что позволяет принимать обоснованные решения в отношении своих инвестиционных портфелей.
Свойства математического ожидания
Рассмотрим свойства математического ожидания.
Свойство 1. Математическое ожидание постоянной величины равно этой постоянной:
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:
Свойство 3. Математическое ожидание суммы (разности) случайных величин равно сумме (разности) их математических ожиданий:
Свойство 4. Математическое ожидание произведения случайных величин равно произведению их математических ожиданий:
Свойство 5. Если все значения случайной величины X уменьшить (увеличить) на одно и то же число С, то её математическое ожидание уменьшится (увеличится) на то же число:
Непараметрическое восстановление плотности
Будем считать, что общий вид функции распределения неизвестен, известны только некоторые свойства — например, функция гладкая, непрерывная. Тогда для оценки плотности применяют непараметрические методы оценивания.
Постановка задачи
Построить функцию , которая аппроксимировала бы неизвестную функцию в некотором смысле.
Гистограммный метод оценивания
Идея: если — плотность случайного вектора , то ,
где , — мера области . Если — выборка, — число значений выборки в , то
.
Поэтому .
Значит, — оценка плотности.
Построение гистограммы:
- найдем ограниченную область пространства (пространства объектов), содержащее все векторы из обучающей выборки ;
- разобьем на непересекающиеся области ;
- если — количество элементов обучающей выборки , принадлежащих области , то
, ,
где — мера области .
Оценка будет состоятельной при некотором выборе . К сожалению, нет универсального способа выбора областей таких, чтобы оценка была состоятельной.
Методы локального оценивания
Идея: оценить плотность в точке с помощью элементов обучающей выборки, попавших в некоторую окрестность .
Пусть — последовательность выборок независимых случайных векторов, — последовательность областей, содержащих точку , — число выборочных значений выборки , попавших в область .
Теорема. Если функция непрерывна в точке , все области содержат точку и удовлетворяют условиям
- ;
- ,
то функция , будет несмещенной, асимптотически эффективной и состоятельной оценкой плотности в точке .
Существуют два основных подхода к выбору областей, содержащих точку :
- метод парзеновского окна. предполагаются регулярными областями, размеры которых удовлетворяют условиям теоремы, исходя из этого определяется число .
- метод k ближайших соседей. Фиксируются не области , а число , затем для точки определяется регулярная область, содержащая ближайших к точек.
Метод оценивания с помощью аппроксимации функции плотности
Идея: функция аппроксимируется с помощью системы базисных функций — оценка ищется в виде
. (1)
Коэффициенты выбираются таким образом, чтобы погрешность аппроксимации была минимальной, т.е.
.
Реально вместо бесконечного ряда (1) рассматривается конечная сумма первых членов.
Как правило, рассматривают ортогональную систему базисных функций, при этом используют многочлены Лежандра, Чебышева, Эрмита, Лагранжа, Лагерра и т.п.
