Термодинамика: основные законы и формулы

Молекулярная физика Основные формулы

• m — масса;
• μ — молярная масса вещества;
• N — число молекул;
• NA = 6,02·1023 моль-1 — число Авогадро

1. p — давление идеального газа;
2. m — масса одной молекулы;
3. n = N/V — концентрация молекул;
4. V — объем газа;
5. N — число молекул;

1.3 Средняя квадратичная скорость молекул идеального газа

• k = 1,38·10-23 Дж/К — постоянная Больцмана;
• R = kNA = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
• T = t+273 — абсолютная температура;
• t — температура по шкале Цельсия.

p — давление;

V — объем газа.

p0 — давление газа при 0 °С;

α = 1/273 °C-1 — температурный коэффициент давления.

V0 — объем газа при 0 °С.

2.3 Первый закон термодинамики

• ΔQ — количество подведенной теплоты;
• ΔA — работа, совершаемая веществом;
• ΔU — изменение внутренней энергии вещества.

2.4 Теплоемкость идеального газа

1. ΔQ — количество переданной системе теплоты на участке процесса;
2. ΔT — изменение температуры на этом участке процесса.

Количество вещества. Молярная масса. Идеальный газ. Основные параметры газа. — физика, уроки

Просмотрсодержимого документа

Количество вещества. Молярная масса. Идеальный газ. Основные параметры газа.

В молекулярно-кинетической теории количество вещества принято считать пропорциональным числу частиц. Единица количества вещества называется молем (моль).

Моль – это количество вещества, содержащее столько же частиц (молекул), сколько содержится атомов в0,012кгуглерода12C. Молекула углерода состоит из одного атома.

• Таким образом, в одном моле любого вещества содержится одно и то же число частиц (молекул). Это число называется постоянной АвогадроNА:
• Постоянная Авогадро – одна из важнейших постоянных в молекулярно-кинетической теории.
• Количество вещества ν определяется как отношение числа N частиц (молекул) вещества к постоянной Авогадро NА:

Массу одного моля вещества принято называть молярной массойM. Молярная масса равна произведению массы m0 одной молекулы данного вещества на постоянную Авогадро:

Молярная масса выражается в килограммах на моль (кг/моль). Для веществ, молекулы которых состоят из одного атома, часто используется термин атомная масса.

За единицу массы атомов и молекул принимается 1/12 массы атома изотопа углерода 12C (с массовым числом 12). Она называется атомной единицей массы (а. е. м.):

1 а. е. м. = 1,66·10–27 кг.

Эта величина почти совпадает с массой протона или нейтрона. Отношение массы атома или молекулы данного вещества к 1/12 массы атома углерода 12C называется относительной массой.

Простейшей моделью, рассматриваемой молекулярно-кинетической теорией, является модель идеального газа. В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Суммарный объем всех молекул предполагается малым по сравнению с объемом сосуда, в котором находится газ. Модель идеального газа достаточно хорошо описывает поведение реальных газов в широком диапазоне давлений и температур. Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, объем, температура).

В результате каждого столкновения между молекулами и молекул со стенками скорости молекул могут изменяться по модулю и по направлению; на интервалах времени между последовательными столкновениями молекулы движутся равномерно и прямолинейно. В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, т. е. подчиняются законам механики Ньютона.

Используя модель идеального газа, вычислим давление газа на стенку сосуда.

В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона.

В результате проекция υx скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υy скорости, параллельная стенке, остается неизменной (рис. 3.2.1).

Поэтому изменение импульса молекулы будет равно 2m0υx, где m0 – масса молекулы.

Концентрация молекул

7. Постоянная Авогадро. Поскольку молекулы имеют малые размеры, их число в любом макроскопическом теле очень велико.

Число молекул в единице объёма называют концентрацией. Концентрация n вычисляется по формуле

где N — число молекул в теле, V — его объём.

Концентрацию молекул в теле также можно определить, зная плотность вещества ρ и массу молекулы этого вещества m. Поскольку

Если плотность воды ρ = 1000 кг/м 3 , а масса молекулы воды m = 3 • 10 -26 кг, то концентрация молекул воды равна:

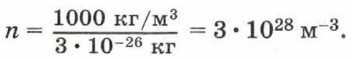
Плотность газов существенно меньше, чем плотность жидкостей, поэтому и концентрация молекул газов меньше, чем концентрация молекул жидкости. Так, если плотность водорода 9 • 10 -2 кг/м 3 , масса молекулы водорода 3,3 • 10 -27 кг, то концентрация молекул водорода равна 2,68 • 10 25 м -3 . Концентрация молекул любого газа при нормальных условиях (нормальном атмосферном давлении и температуре 0 °С) одинакова и равна приведённому для водорода значению. Это число называют постоянной Лошмидта: L = 2,68 • 10 25 м -3 .

Чтобы представить себе, насколько велико это число, предположим, что в воздушном шаре сделали настолько тонкий прокол, что за каждую секунду через него проходит 10 молекул. В этом случае, для того чтобы вышли все молекулы, потребуется 30 миллиардов лет.

Из определения моля следует, что 1 моль любого вещества содержит одинаковое число молекул (атомов). Это число называют постоянной Авогадро.

Постоянная Авогадро N_А — число молекул или атомов в количестве вещества 1 моль.

Постоянную Авогадро можно рассчитать, зная, что углероду количеством вещества 1 моль соответствует масса 0,012 кг, а масса одной молекулы углерода m 0С = 1,995 • 10 -26 кг. Тогда в одном моле углерода содержится число молекул:

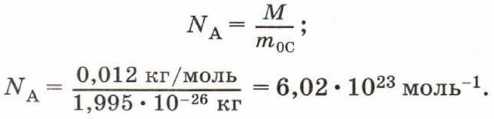
Поскольку в одном моле любого вещества содержится одинаковое число молекул, то при одинаковых условиях 1 моль любого газа занимает одинаковый объём.

Объём, занимаемый при нормальном атмосферном давлении любым газом количеством вещества 1 моль, равен 0,0224 м 3 .

1. Сформулируйте первое положение молекулярно-кинетической теории строения вещества.

2. Поясните выражение: «Молекула — мельчайшая частица вещества, сохраняющая его химические свойства».

3. Опишите опыт, позволяющий оценить размеры молекулы. Предложите способ измерения объёма капли масла.

4. Что называют относительной молекулярной массой; количеством вещества; молярной массой; концентрацией молекул; постоянной Авогадро?

6. Каков порядок значений размеров, массы молекул, их концентрации, числа молекул в одном моле вещества?

1_Д. Подготовьте краткое сообщение об исследованиях М. В. Ломоносова, результаты которых внесли вклад в развитие учения о строении вещества. Воспользуйтесь для этого интернет-ресурсами и другими источниками информации. Докажите, что результаты исследований М. В. Ломоносова имели принципиальное значение для развития взглядов на строение вещества.

2. Сравните количество вещества, содержащееся в телах равной массы из алюминия и железа.

3. Найдите число атомов в алюминиевой ложке массой 30 г.

4. Деталь площадью 30 см 2 покрыли слоем серебра толщиной 2 мкм. Сколько атомов серебра содержится в покрытии?

5. Сравните массы и объёмы двух тел, сделанных из свинца и меди, если в них содержатся равные количества вещества.

6. Вычислите постоянную Авогадро, если известно, что масса молекулы кислорода 5,312 • 10 -26 кг.

Почему мы уверены в существовании молекул и атомов, ведь мы их не видим?

Основное уравнение МКТ для модели идеального газа

Следует заметить, что основное уравнение МКТ выводилось для модели идеального газа с соответствующими допущениями:

1. Соударения молекул с окружающими объектами абсолютно упругие. Для реальных же газов это не совсем так; часть кинетической энергии молекул всё-таки переходит во внутреннюю энергию молекул и стенки.
2. Силами взаимодействия между молекулами можно пренебречь. Если же реальный газ находится при высоком давлении и сравнительно низкой температуре, эти силы становятся весьма существенными.
3. Молекулы считаем материальными точками, пренебрегая их размером. Однако размеры молекул реальных газов влияют на расстояние между самими молекулами и стенкой.
4. И, наконец, основное уравнение МКТ рассматривает однородный газ – а в действительности мы часто имеем дело со смесями газов. Как, например, воздух.

Однако для разреженных газов это уравнение дает очень точные результаты. Кроме того, многие реальные газы в условиях комнатной температуры и при давлении, близком к атмосферному, весьма напоминают по свойствам идеальный газ.

Как известно из законов динамики, кинетическая энергия любого тела или частицы . Заменив произведение массы каждой из частичек и квадрата их скорости в записанном нами уравнении, мы можем представить его в виде:

Также кинетическая энергия газовых молекул выражается формулой , что нередко используется в задачах. Здесь k – это постоянная Больцмана, устанавливающая связь между температурой и энергией. k=1,38•10 -23 Дж/К.

Основное уравнение МКТ лежит в основе термодинамики. Также оно используется на практике в космонавтике, криогенике и нейтронной физике.

Процессы в молекулярной физике и их формулы

Замечание 1

Всем понятиям и процессам присущи собственные обозначения, при этом их описывают специальные формулы, которые более наглядно отображают взаимодействия друг с другом определенных параметров. Процессы и явления будут пересекаться в своих проявлениях, различные формулы при этом могут содержать одинаковые по значению величины и выражаться посредством разных способов.

Количество вещества является определяющим для взаимосвязи веса (массы) и количества молекул, которые и будет содержать данная масса. Это обусловлено наличием разного числа минимальных частиц при одинаковой массе для различных веществ. Процессы, осуществляемые на молекулярном уровне, могут пониматься исключительно при рассмотрении количества атомных единиц – непосредственных участников взаимодействий.

Формула для определения количества вещества:

$v = \frac{N}{N_A}$, где:

• $m$ — масса,
• $N$ — число молекул,
• $N_A$ число Авогадро.

Молекулы представляют сложные системы, обладающие многоступенчатым строением. Для упрощения рассмотрим газовые частицы в сосуде в формате упругих однородных шариков, не взаимодействующих при этом друг с другом (это будет идеальный газ). Формула выглядит так:

$P = nkT$, где:

• $n$ —концентрация молекул;
• $T$ —абсолютная температура.

Определить количество частиц $d$ в данной массе вещества возможно такой формулой:

$v = \frac{N}{Na}$

Отсюда получается, что число молекул будет определять следующая формула:

$N = vNa$

Один моль всегда будет содержать равное количество минимальных частиц. Таким образом, зная массу моля, возможно разделить ее на число молекул (число Авогадро), с получением в итоге массы системной единицы:

$m = \frac{M}{Na}$

Следует учитывать отношение данной формулы исключительно к неорганическим молекулам. Что касается молекул органического типа, то их размеры намного больше, а их величине или весу свойственны совсем иные значения.

Молярная масса представляет массу в килограммах одного моля вещества. В связи с содержанием в одном моле одинакового количества структурных единиц, формулу молярной массы получаем такую:

$M = κM_r$, где:

• $k$ — коэффициент пропорциональности;
• $M_r$ — атомная масса вещества.

Молярная масса газа рассчитывается по уравнению Менделеева-Клапейрона:

$pV = \frac{mRT}{M}$

Тогда получаем такую формулу:

$M = \frac{mRT}{pV}$

Формулы, которые содержатся в термодинамике и в молекулярной физике, позволяют вычислять количественные значения для всех процессов, выполняемых в отношении твердых веществ и газов. Такие расчеты важны как для теоретических изысканий, так и в практическом применении, поскольку ориентированы на решение разноплановых задач.

Примеры решения задач

Задание	Определить скорость движения частиц воздуха в нормальных условиях.
Решение	Используем основное уравнение МКТ, считая воздух однородным газом. Так как воздух на самом деле – это смесь газов, то и решение задачи не будет абсолютно точным.

Можем заметить, что произведение

Тогда предыдущее уравнение примет вид:

В нормальных условиях давление равно 10 5 Па, плотность воздуха 1,29кг/м 3 – эти данные можно взять из справочной литературы.

Из предыдущего выражения получим скорость молекул воздуха:

Ответ м/с

Задание	Определить концентрацию молекул однородного газа при температуре 300 К и давлении 1 МПа. Газ считать идеальным.
Решение	Решение задачи начнём с основного уравнения МКТ: Кинетическая энергия молекул, как и любых материальных частичек: . Тогда наша расчетная формула примет несколько другой вид:

Однако кинетическая энергия молекул в термодинамике определяется и с помощью другого выражения, и напрямую связана с температурой газа:

Подставив эту формулу в предыдущее выражение, получим еще одну форму записи основного уравнения МКТ:

Выразим и рассчитаем концентрацию молекул газа:

Молекулярная физика

Формулы молекулярной физики

Формула концентрации молекул

Здесь n — концентрация

Формула плотности

Здесь

Формула относительной молекулярной массы

Здесь

Формула количества вещества (количества молей)

Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).

Формулы массы одной молекулы

Здесь

Формулы количества молекул

Здесь A — количество молекул (безразмерное), п — концентрация молекул

Формулы средней квадратичной скорости молекул

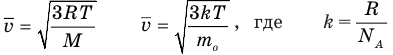
Здесь

Основное уравнение кинетической теории идеального газа

Здесь р — давление газа (Па),

Формула средней кинетической энергии молекул

Здесь

Связь шкал Цельсия и Кельвина

Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.

Связь средней кинетической энергии молекул идеального газа с абсолютной температурой

Здесь

У равнение состояния идеального газа — уравнение Клапейрона — Менделеева

Здесь р — давление газа (Па), V — объем

Объединенный газовый закон — уравнение Клапейрона

при

Здесь

Закон Бойля — Мариотта (изотермический процесс)

при

Здесь Т — абсолютная температура газа (К), m — масса газа (кг),

Закон Гей-Люссака (изобарный процесс)

при

Здесь р — давление газа (Па), m — масса газа (кг),

Закон Шарля

при

Здесь V — объем газа

Связь давления идеального газа с концентрацией его молекул и температурой

Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа

Формулы относительной влажности

Здесь

Работа при изобарном изменении объема газа

Здесь А — работа (Дж), р — давление газа (Па),

Внутренняя энергия идеального одноатомного газа

Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль),

Первый закон термодинамики

Здесь Q — количество теплоты, переданное термодинамической системе (Дж),

Применение первого закона термодинамики к термодинамическим процессам

к изотермическому: при

к изохорному: при V = const

к изобарному: при р = const

Здесь Т — абсолютная температура (К),

Формулы количества теплоты при нагревании или охлаждении тел

Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг),

Формула количества теплоты при плавлении или кристаллизации

Здесь Q — количество теплоты (Дж), т — масса тела (кг),

Формула количества теплоты при парообразовании или конденсации

Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).

Формула количества теплоты при сгорании топлива

Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).

Коэффициент полезного действия теплового двигателя

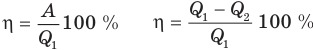
Здесь

Коэффициент полезного действия идеального теплового двигателя

Здесь

Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:

Возможно вам будут полезны эти страницы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Молекулы беспорядочно движутся

2) Молекулы находятся в непрерывном беспорядочном (тепловом) движении.

Вид теплового движения (поступательное, колебательное, вращательное) молекул зависит от характера их взаимодействия и изменяется при переходе вещества из одного агрегатного состояния в другое. Интенсивность теплового движения зависит и от температуры тела.

Приведем некоторые из доказательств беспорядочного (хаотического) движения молекул: а) стремление газа занять весь предоставленный ему объем; б) диффузия; в) броуновское движение.

Диффузия

Диффузия — самопроизвольное взаимное проникновение молекул соприкасающихся веществ, приводящее к выравниванию концентрации вещества по всему объему. При диффузии молекулы граничащих между собой тел, находясь в непрерывном движении, проникают в межмолекулярные промежутки друг друга и распределяются между ними.

Диффузия проявляется во всех телах — в газах, жидкостях, твердых телах, но в разной степени.

Диффузию в газах можно обнаружить, если, например, сосуд с пахучим газом открыть в помещении. Через некоторое время газ распространится по всему помещению.

Диффузия в жидкостях происходит значительно медленнее, чем в газах

Например, если в стакан налить сначала слой раствора медного купороса, а затем очень осторожно добавить слой воды и оставить стакан в помещении с неизменной температурой, то через некоторое время исчезнет резкая граница между раствором медного купороса и водой, а через несколько дней жидкости перемешаются

Диффузия в твердых телах происходит еще медленнее, чем в жидкостях (от нескольких часов до нескольких лет). Она может наблюдаться только в хорошо отшлифованных телах, когда расстояния между поверхностями отшлифованных тел близки к межмолекулярному расстоянию (10-8 см). При этом скорость диффузии увеличивается при повышении температуры и давления.

Диффузия играет большую роль в природе и технике. В природе благодаря диффузии, например, осуществляется питание растений из почвы. Организм человека и животных всасывает через стенки пищеварительного тракта питательные вещества. В технике с помощью диффузии, например, поверхностный слой металлических изделий насыщается углеродом (цементация) и т.д.

Разновидностью диффузии является осмос — проникновение жидкостей и растворов через пористую полупроницаемую перегородку.

Броуновское движение

Броуновское движение открыто в 1827 г. английским ботаником Р. Броуном, теоретическое обоснование с точки зрения MKT дано в 1905 г. А. Эйнштейном и М. Смолуховским.

Броуновское движение — это беспорядочное движение мельчайших твердых частиц, «взвешенных» в жидкостях (газах).

«Взвешенные» частицы — это частицы, плотность вещества которых сравнима с плотностью среды, в которой они находятся. Такие частицы находятся в равновесии, и малейшее внешнее воздействие на нее приводит к их движению.

Для броуновского движения характерно следующее:

1. броуновские частицы совершают непрерывное хаотическое движение, интенсивность которого зависит от температуры и от размеров броуновской частицы;
2. траектория движения броуновской частицы очень сложная, не зависит от природы вещества частиц и внешних условий.
   
   Рис. 2
   

   На рисунке 2 показаны положения броуновской частицы через каждые 30 с, а на врезке — положения этой частицы на участке АВ, зафиксированные через каждую секунду. Эти положения соединены прямыми линиями. Траектория же частицы еще более сложная;

3. броуновское движение наблюдается в жидкостях и газах.

Причинами броуновского движения являются:

1. тепловое хаотическое движение молекул среды, в которой находится броуновская частица;
2. отсутствие полной компенсации ударов молекул среды об эту частицу с различных сторон, так как движение молекул носит случайный характер.

Движущиеся молекулы жидкости при столкновении с какими-либо твердыми частицами передают им некоторое количество движения. Случайно с одной стороны о частицу ударит заметно большее число молекул, чем с другой, и частица придет в движение.

Если частица достаточно велика, то число молекул, налетающих на нее со всех сторон, чрезвычайно велико, их удары в каждый данный момент компенсируются, и такая частица практически остается неподвижной.

Давление идеального газа

Найдём давление, оказываемое идеальным газом на неподвижный поршень (или стенку сосуда).
Для этого рядом с поршнем выделим тонкий слой газа ширины $\Delta L$,
в котором можно пренебречь столкновениями молекул друг с другом (но их там должно быть по-прежнему много).
Если $S$ — это площадь поршня, то объём слоя равен $V=S\,\Delta L$.

Рассмотрим $N_{v}$ молекул, которые имеют примерно одинаковую компоненту скорости $v_x$
и движутся в направлении поршня $(v_x \gt 0)$.
За время $\Delta t = \Delta L/v_x$ эти молекулы из слоя шириной $\Delta L$,
успеют столкнутся с поршнем (последними — молекулы, находящиеся на границе слоя).
После упругого столкновения (поршень неподвижен),
компонента импульса $p_x$ молекул
меняет знак и полное изменение их импульса, переданное поршню, равно $\Delta p_x=2\,p_x$.
Поэтому суммарное давление со стороны этих молекул на поршень равно:
$$
P ~=~ \frac{F_x}{S} ~=~ N_{v}\,\frac{\Delta p_x}{\Delta t}\,\frac{1}{S}
~=~ N_v\,\frac{2\,p_x}{S\,\Delta t} ~=~ 2\,\frac{N_v}{V}\,p_x\,v_x.
$$

Молекулы газа движутся с различными скоростями $\mathbf{v}=\{v_x,v_y,v_z\}$, в различных направлениях.
В результате столкновений молекул друг с другом, их скорости постоянно изменяются, становясь случайными величинами.
Пусть $f(v_x)$ — это плотность распределения вероятностей для скоростей $v_x$.
Оно нормировано на единицу (интеграл от него по $dv_x$ равен $1$).
Естественно считать это распределение симметричным.
Число молекул $N_v$, имеющих компоненту скорости $v_x$ с небольшим разбросом $dv_x$, по определению,
равно $N_v~=~N\,f(v_x)\,dv_x$, где $N$ — общее число молекул (с любыми скоростями):

$$
\int\limits^\infty_{-\infty} f(v_x)\,dv_x = 1,~~~~~~~~~~~~~~~~~~~~f(-v_x)=f(v_x).
$$

Полное давление равно сумме давлений со стороны молекул, движущихся со всеми возможными скоростями $v_x$
в направлении поршня ($v_x \gt 0$):
$$
P~=~
2\,\frac{N}{V}\,\int\limits^\infty_{0} p_x\,v_x\,f(v_x)\,dv_x
~=~ \frac{N}{V}\,\int\limits^\infty_{-\infty} p_x\,v_x\,f(v_x)\,dv_x = \frac{N}{V}\,\langle p_xv_x \rangle,
$$
где учтена симметричность распределения и угловыми скобками обозначено среднее значение (интеграл).
Так как направления в пространстве равноправны:
$\langle \mathbf{p}\mathbf{v} \rangle = \langle p_x v_x + p_y v_y + p_zv_z \rangle = 3\, \langle p_xv_x \rangle$,
окончательно имеем:
$$
P ~=~ n\,\frac{\langle \mathbf{p}\mathbf{v} \rangle}{3},~~~~~~~~~~~~~~~~~~~n=\frac{N}{V}.
$$
Отношение числа молекул $N$ к объёму $n = N/V$ называется концентрацией молекул
(число в единице объёма).
Обратная величина $v=V/N$, называемая удельным объёмом,
— это часть объёма сосуда, приходящаяся на одну молекулу.
Усреднение по всем направлениям скорости производится при помощи тройного
интеграла с весами равными распределению каждой компоненты скорости: $f(v_x)f(v_y)f(v_z)\,dv_x\,dv_y\,dv_z$.

Для нерелятивистского газа импульс молекул равен $\mathbf{p}=m\mathbf{v}$, поэтому
полученное соотношение можно переписать следующим образом:
$$
P\,V ~=~\frac{2}{3}\,N\,\left\langle \frac{m\mathbf{v}^2}{2} \right\rangle,
$$
где под знаком среднего находится кинетическая энергия поступательного движения молекулы.

Определение и формула уравнения МКТ

Здесь

Основное уравнение МКТ наглядно объясняет, каким образом идеальный газ создает давление на окружающие его стенки сосуда. Молекулы все время ударяются о стенку, воздействуя на нее с некоторой силой F. Тут следует вспомнить третий закон Ньютона: когда молекула ударяется о предмет, на нее действует сила -F, вследствие чего молекула «отбивается» от стенки. При этом мы считаем соударения молекул со стенкой абсолютно упругими: механическая энергия молекул и стенки полностью сохраняется, не переходя во внутреннюю энергию тел. Это значит, что при соударениях изменяются только скорости молекул, а нагревания молекул и стенки не происходит.

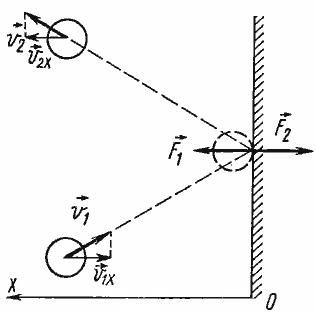
Зная, что соударение со стенкой было упругим, мы можем предсказать, как изменится скорость молекулы после столкновения. Модуль скорости останется таким же, как и до соударения, а направление движения изменится на противоположное относительно оси Ох (считаем, что Ох – это та ось, которая перпендикулярна стенке).

Молекул газа очень много, движутся они хаотично и о стенку ударяются часто. Найдя геометрическую сумму сил, с которой каждая молекула воздействует на стенку, мы узнаём силу давления газа. Чтобы усреднить скорости молекул, необходимо использовать статистические методы. Именно поэтому в основном уравнении МКТ используют усредненный квадрат скорости молекул

Теперь ясен физический смысл уравнения: чем больше молекул содержится в объеме, чем они тяжелее и чем быстрее движутся – тем большее давление они создают на стенки сосуда.

Основное уравнение МКТ для модели идеального газа

Следует заметить, что основное уравнение МКТ выводилось для модели идеального газа с соответствующими допущениями:

1. Соударения молекул с окружающими объектами абсолютно упругие. Для реальных же газов это не совсем так; часть кинетической энергии молекул всё-таки переходит во внутреннюю энергию молекул и стенки.
2. Силами взаимодействия между молекулами можно пренебречь. Если же реальный газ находится при высоком давлении и сравнительно низкой температуре, эти силы становятся весьма существенными.
3. Молекулы считаем материальными точками, пренебрегая их размером. Однако размеры молекул реальных газов влияют на расстояние между самими молекулами и стенкой.
4. И, наконец, основное уравнение МКТ рассматривает однородный газ – а в действительности мы часто имеем дело со смесями газов. Как, например, воздух.

Однако для разреженных газов это уравнение дает очень точные результаты. Кроме того, многие реальные газы в условиях комнатной температуры и при давлении, близком к атмосферному, весьма напоминают по свойствам идеальный газ.

Как известно из законов динамики, кинетическая энергия любого тела или частицы

Также кинетическая энергия газовых молекул выражается формулой

Основное уравнение МКТ лежит в основе термодинамики. Также оно используется на практике в космонавтике, криогенике и нейтронной физике.

Основные формулы молекулярной физики

Принцип актуальности формул молекулярной физики направлен на установление связи между разными параметрами системы. К основным формулам такого раздела относят:

• уравнение Клапейрона (с описанием состояния идеального газа);
• законы физиков Бойля, Гей-Люссака и Шарля.

Уравнение Клапейрона записывается таким образом:

$pV = nRT$, где:

• $р$ — давление,
• $n$ — количество вещества в молях,
• $R$ — универсальная газовая постоянная,
• $T$ — температура (в кельвинах),
• $V$ — занимаемый газом объем.

Из этой формулы посредством простых преобразований формулируются и другие законы состояния:

$pV = const$ (закон Бойля-Мариотта, применимый к изотермическому процессу)

$\frac{V}{T} = const$ (первый закон Гей-Люссака, применимый к изобарическому процессу);

$\frac{p}{T} = const$ (закон Шарля, применимый к изохорическому процессу).

Молекулярная физика Основные формулы

1. Основы молекулярно-кинетической теории. Газовые законы

μ — молярная масса вещества;

N_A = 6,02·10 23 моль -1 — число Авогадро

p — давление идеального газа;

n = N/V — концентрация молекул;

1.3 Средняя квадратичная скорость молекул идеального газа

k = 1,38·10 -23 Дж/К — постоянная Больцмана;

R = kN_A = 8,31 Дж/(моль·К) — универсальная газовая постоянная;

T = t+273 — абсолютная температура;

t — температура по шкале Цельсия.

T — абсолютная температура.

p — давление газа при 0 °С;

α = 1/273 °C -1 — температурный коэффициент давления.

p_i — парциальное давление i-й компоненты смеси газов.

2. Основы термодинамики

R = 8,31 Дж/(моль·К) — универсальная газовая постоянная;

T — абсолютная температура.

при изменении объема на бесконечно малую величину dV

2.3 Первый закон термодинамики

ΔQ — количество подведенной теплоты;

ΔA — работа, совершаемая веществом;

ΔU — изменение внутренней энергии вещества.

2.4 Теплоемкость идеального газа

ΔQ — количество переданной системе теплоты на участке процесса;

ΔT — изменение температуры на этом участке процесса.

Идеальный газ

Идеальный газ – это идеализация, как и материальная точка. Молекулы такого газа являются материальными точками, а соударения молекул – абсолютно упругие. Взаимодействием же молекул на расстоянии пренебрегаем. В задачах по термодинамике реальные газы часто принимаются за идеальные. Так гораздо легче жить, и не нужно иметь дела с массой новых членов в уравнениях.

Итак, что происходит с молекулами идеального газа? Да, они движутся! И резонно спросить, с какой скоростью? Конечно, помимо скорости молекул нас интересует еще и общее состояние нашего газа. Какое давление P он оказывает на стенки сосуда, какой объем V занимает, какая у него температура T.

Для того, чтобы узнать все это, есть уравнение состояния идеального газа, или уравнение Клапейрона-Менделеева

Здесь m – масса газа, M – его молекулярная масса (находим по таблице Менделеева), R – универсальная газовая постоянная, равная 8,3144598(48) Дж/(моль*кг).

Универсальная газовая постоянная может быть выражена через другие константы (постоянная Больцмана и число Авогадро)

Массу, в свою очередь, можно вычислить, как произведение плотности и объема.

Основное уравнение молекулярно-кинетической теории (МКТ)

Как мы уже говорили, молекулы газа движутся, причем, чем выше температура – тем быстрее. Существует связь между давлением газа и средней кинетической энергией E его частиц. Эта связь называется основным уравнением молекулярно-кинетической теории и имеет вид:

Здесь n – концентрация молекул (отношение их количества к объему), E – средняя кинетическая энергия. Найти их, а также среднюю квадратичную скорость молекул можно, соответственно, по формулам:

Подставим энергию в первое уравнение, и получим еще один вид основного уравнения МКТ

Первое начало термодинамики. Формулы для изопроцессов

Напомним Вам, что первый закон термодинамики гласит: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа U и на совершение газом работы A. Формула первого закона термодинамики записывается так:

Как известно, с газом что-то происходит, мы можем сжать его, можем нагреть. В данном случае нас интересуют такие процессы, которые протекают при одном постоянном параметре. Рассмотрим, как выглядит первое начало термодинамики в каждом из них.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы. 

Изотермический процесс протекает при постоянной температуре. Тут работает закон Бойля-Мариотта: в изотермическом процессе давление газа обратно пропорционально его объёму. В изотермическом процессе:

Изохорный процесс протекает при постоянном объеме. Для этого процесса характерен закон Шарля: При постоянном объеме давление прямо пропорционально температуре. В изохорном процессе все тепло, подведенное к газу, идет на изменение его внутренней энергии.

Изобарный процесс идет при постоянном давлении. Закон Гей-Люссака гласит, что при постоянном давлении газа его объём прямо пропорционален температуре. При изобарном процессе тепло идет как на изменение внутренней энергии, так и на совершение газом работы.

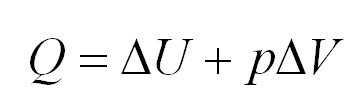
Адиабатный процесс. Адиабатный процесс – это такой процесс, который проходит без теплообмена с окружающей средой. Это значит, что формула первого закона термодинамики для адиабатного процесса выглядит так:

Теплоемкость

Удельная теплоемкость равна количеству теплоты, которое необходимо для нагревания одного килограмма вещества на один градус Цельсия.

Помимо удельной теплоемкости, есть молярная теплоемкость (количество теплоты, необходимое для нагревания одного моля вещества на один градус) при постоянном объеме, и молярная теплоемкость при постоянном давлении. В формулах ниже, i – число степеней свободы молекул газа. Для одноатомного газа i=3, для двухатомного – 5.

Тепловые машины. Формула КПД в термодинамике

Тепловая машина, в простейшем случае, состоит из нагревателя, холодильника и рабочего тела. Нагреватель сообщает тепло рабочему телу, оно совершает работу, затем охлаждается холодильником, и все повторяется вновь. Типичным примером тепловой машины является двигатель внутреннего сгорания.

Коэффициент полезного действия тепловой машины вычисляется по формуле

Вот мы и собрали основные формулы термодинамики, которые пригодятся в решении задач. Конечно, это не все все формулы из темы термодинамика, но их знание действительно может сослужить хорошую службу. А если возникнут вопросы  – помните о студенческом сервисе, специалисты которого готовы в любой момент прийти на выручку.

Примеры решения задач

Задание	Определить скорость движения частиц воздуха в нормальных условиях.
Решение	Используем основное уравнение МКТ, считая воздух однородным газом. Так как воздух на самом деле – это смесь газов, то и решение задачи не будет абсолютно точным.

Можем заметить, что произведение – это плотность газа, так как n – концентрация молекул воздуха (величина, обратная объему), а m – масса молекулы.

Тогда предыдущее уравнение примет вид:

В нормальных условиях давление равно 10 5 Па, плотность воздуха 1,29кг/м 3 – эти данные можно взять из справочной литературы.

Из предыдущего выражения получим скорость молекул воздуха:

Однако кинетическая энергия молекул в термодинамике определяется и с помощью другого выражения, и напрямую связана с температурой газа:

Подставив эту формулу в предыдущее выражение, получим еще одну форму записи основного уравнения МКТ:

Выразим и рассчитаем концентрацию молекул газа: