Кривые функции распределения вероятностей рэлея, ричиана и логнормального реализованы программным обеспечением matlab.

Генерация случайных чисел и оценка параметров

Используем обратную функцию распределения
(или p
—
quantile
,
см. статью про ), которая для распределения Вейбулла
может быть выражена в явном виде с использованием элементарных функций: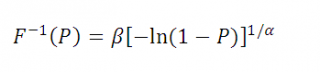

С помощью этой функции можно сгенерировать значения случайной величины, имеющей распределение Вейбулла
. Для этого нужно использовать формулу MS EXCEL:

Бета*(-LN(СЛЧИС()))^(1/альфа)

Функция СЛЧИС()
генерирует от 0 до 1, что как раз соответствует диапазону изменения вероятности (см. файл примера лист Генерация
).

Теперь имея массив случайных чисел, сгенерированных с заданными параметрами распределения альфа
и бета
(пусть их будет 200), оценим параметры распределения.

Оценку параметров альфа
и бета
можно сделать с помощью линейной регрессии. Для этого необходимо привести функцию распределения Вейбулла
к виду обычной прямой, задаваемой уравнением Y=aX+b. Для этого сделаем следующие преобразования: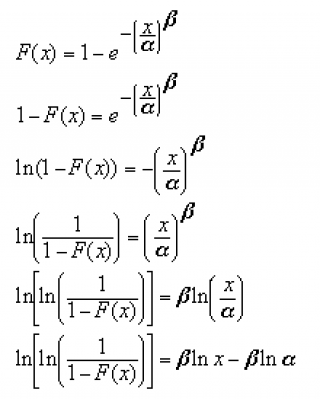

Сравнивая выражение 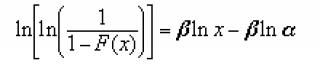с уравнением прямой Y=ax+b получим, что:

Y соответствует левая часть выражения,
X – соответствует ln(x),
параметр распределения бета
соответствует коэффициенту a
, отвечающего за наклон прямой к оси абсцисс.
выражение –бета*ln(альфа) соответствует коэффициенту b (ордината точки пересечения с осью Oy).

По сути, мы практически построили (probability plot) для распределения Вейбулла
: если ln(x), отложенные по оси Ох, лягут приблизительно вдоль прямой, то это будет означать, что значения выборки взяты из распределения Вейбулла.
Осталось модифицировать ось Оу с помощью формулы =LN(-LN(1-Ui)), где Ui=(i-0,5)/200, а i=1; 2; …; 200.

Заметим, что -LN(1-Ui) – это обратная функция распределения
с параметрами альфа=1 и бета=1. Второй логарифм нам потребовался, т.к. по оси абсцисс отложены не сами x, а ln(x).

Примечание
: Т.к. форма распределения Вейбулла
существенно зависит от его параметров, то вместо альфа=1 и бета=1 для обратной функции лучше использовать точечные оценки этих параметров
, полученные на основании выборки
. О том как вычислить оценку параметров альфа и бета см. ниже.

В файле примера на листе Генерация
построен соответствующий Вероятностный график
.

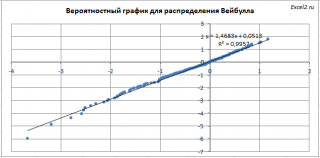
С помощью функции НАКЛОН()
вычислим наклон получившейся кривой (коэффициент прямой а,
англ. slope
), который служит оценкой параметра бета
.

Функция ОТРЕЗОК()
вернет ординату точки пересечения с Оу (коэффициент прямой b
). Выражение =EXP(-b/бета)
служит оценкой параметра альфа
.

Также можно сравнить плотности вероятностей
модельного распределения и распределения с параметрами, полученными в результате оценки.

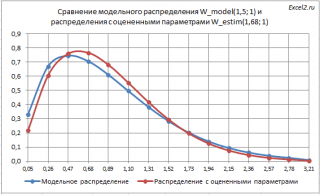
Как видно из диаграммы выше, совпадение также достаточно хорошее.

СОВЕТ

: Т.к. генерирование случайных чисел происходит с помощью функции СЛЧИС()
, то нажимая клавишу F9
, можно каждый раз получать новую выборку
и, соответственно, новую оценку параметров.

СОВЕТ

: О других распределениях MS EXCEL можно прочитать в статье .

Примечания и ссылки

(in) Эрик В. Вайстейн , на MathWorld .

Законы вероятности ( список )

Дискретные законы с конечной опорой
0 параметр формы	Дирак Радемахер
1 параметр формы	Бенфорд Бернулли сдержанная униформа
2 параметра формы	биномиальный Zipf
3 параметра формы	бета-бином гипергеометрический
N параметров формы	полиномиальный Биномиальный Пуассон

Дискретные законы с бесконечной поддержкой
0 параметр формы
1 параметр формы	геометрический логарифмический Рыбы Юл-Саймон Зета
2 параметра формы	отрицательный бином Конвей-Максвелл-Пуассон Скеллам
3 параметра формы	отрицательный бета-бином расширенный отрицательный бином Дверь

Абсолютно непрерывные законы с компактной опорой
0 параметр формы	дуговая пазуха приподнятый косинус Полукруг параболический сплошная униформа Ксенакис
1 параметр формы	Бейтс Ирвин-Холл треугольный
2 параметра формы	бета Кумарасвами логит-нормальный
3 параметра формы	внецентровая бета прямоугольная бета

Абсолютно непрерывные законы с полубесконечной поддержкой
0 параметр формы	полулогистика наполовину нормальный экспоненциальный Леви нормально сложенный Рэлей
1 параметр формы	χ χ² Дэвис Erlang Фреше Гамма обратный-χ² обратная гамма обратный гауссовский журнал-Коши лог-Лаплас логистика нормальный логарифм Накагами Парето Рис Weibull
2 параметра формы	χ не по центру χ² не по центру Benktander I Бенктандер II бета прайм Заусенец Дагум Фишер обобщенный обратный гауссовский
3 параметра формы
N параметров формы	гиперэкспоненциальный гипоэкспоненциальный

Абсолютно непрерывные законы с бесконечной поддержкой
0 параметр формы	Коши Гамбель Holtsmark Коляска Место логистика обычный гиперболический секанс слэш Voigt
1 параметр формы	Gompertz асимметричный нормальный Ученик
2 параметра формы	стабильный геометрический стабильный Фишера z

Другие виды законов

Непрерывно-дискретные смешанные законы поддержки

Законы с переменной поддержкой

законы

Дискретный	Юэнс полиномиальный
Непрерывный	Дирихле многомерный нормальный
Матрица	Wishart Обратный Уишарт

Одномерный
Двумерный сферический
Двумерные тороиды
Многомерный

эллиптический
экспоненциальная семья
функция Пирсона
параболический фрактал
усеченный

Оценка параметров [ править ]

Учитывая выборку из N независимых и одинаково распределенных случайных величин Рэлея с параметром ,xi{\displaystyle x_{i}}σ{\displaystyle \sigma }

σ^2=12N∑i=1Nxi2{\displaystyle {\widehat {\sigma }}^{2}=\!\,{\frac {1}{2N}}\sum _{i=1}^{N}x_{i}^{2}}является оценкой максимального правдоподобия и также является несмещенной .

σ^≈12N∑i=1Nxi2{\displaystyle {\widehat {\sigma }}\approx {\sqrt {{\frac {1}{2N}}\sum _{i=1}^{N}x_{i}^{2}}}} является смещенной оценкой, которую можно исправить с помощью формулы

σ=σ^Γ(N)NΓ(N+12)=σ^4NN!(N−1)!N(2N)!π{\displaystyle \sigma ={\widehat {\sigma }}{\frac {\Gamma (N){\sqrt {N}}}{\Gamma (N+{\frac {1}{2}})}}={\widehat {\sigma }}{\frac {4^{N}N!(N-1)!{\sqrt {N}}}{(2N)!{\sqrt {\pi }}}}}

Доверительные интервалы править

Чтобы найти доверительный интервал (1 — α ), сначала найдите границы, где:a,b{\displaystyle }

P(χ2N2≤a)=α2,P(χ2N2≤b)=1−α2{\displaystyle P(\chi _{2N}^{2}\leq a)=\alpha /2,\quad P(\chi _{2N}^{2}\leq b)=1-\alpha /2}

тогда параметр масштаба попадет в границы

Nx2¯b≤σ^2≤Nx2¯a{\displaystyle {\frac {{N}{\overline {x^{2}}}}{b}}\leq {\widehat {\sigma }}^{2}\leq {\frac {{N}{\overline {x^{2}}}}{a}}}

Список известных вероятностных распределений[]

Арксинуса распределение : 66 г; : 123
Бернулли распределение
Берра распределение
Бета-распределение : 65 в; : 122, 6.3.7., 130, 6.3.16
Биномиальное распределение : 164; : 109, 6.2.3
Биномиальное многомерное распределение
Биномиальное обобщённое распределение : 115, 6.2.9
Больцмана распределение
Бореля-Таннера распределение : 116, 6.2.11
Бредфорда распределение
Вейбулла-Гнеденко распределение : 68 ж; : 132: 6.3.19
Гамма-распределение : 62-63; : 121, 6.3.6
Геометрическое распределение
Гиббса распределение
Гипергеометрическое распределение : 112, 6.2.6
Гиперэкспоненциальное распределение : 118, 6.3.4
Дирихле распределение
Кантора распределение
Колмогорова распределение
Коши распределение : 66 д; : 123, 6.3.8
Лапласа распределение (второй закон, двусторонняя показательная плотность) : 65 а
Лапласа распределение (двойное экспоненциальное) : 124, 6.3.9
Логарифмическое распределение : 305 д; : 115, 6.2.10
Логистическое распределение : 68 з; : 130, 6.3.15
Логнормальное распределение : 129, 6.3.14
Максвелла-Больцмана распределение
Нормальное распределение (гауссовское) : 190 (1); : 119, 6.3.5
Нормальное многомерное распределение
Омега-квадрат-распределение (ω2-распределение)
Парето распределение : 65 в; : 122, 6.3.7., 130, 6.3.16
Паскаля распределение (отрицательное биномиальное) : 111, 6.2.4
Пирсона распределение
Пойа распределение (заболеваний) : 113, 6.2.7
Показательное распределение (экспоненциальное) : 118, 6.3.3
Полиномиальное распределение
Пуассона распределение : 114, 6.2.8
Пуассона многомерное распределение
Равномерное и треугольное распределение (Симпсона) : 65 б, : 116117, 6.3.1.,6.3.2
Рэлея распределение
Салема распределение
Стьюдента распределение (t-распределение) : 64 б; : 127, 6.3.12
Уилкса распределение (U-распределение)
Уишарта распределение (W-распределение)
Фишера распределение (z-распределение) : 64; : 131: 6.3.18
Фишера-Снедекора распределение (F-распределение) : 64 а; : 127: 6.3.13
Фреше распределение
Хи-квадрат-распределение (χ2-распределение) : 63; : 124, 6.3.10
Хи-квадрат-распределение нецентральное (χ2-распределение нецентральное)
Хи-распределение : 126, 6.3.11
Хотеллинга распределение (T2-распределение)
Шермана распределение : 130: 6.3.16, .
Эрланга распределение

Литература к списку вероятностных распределений

, В.Феллер (1984) Введение в теорию вероятностей и ее приложения. Москва: Мир, т.1 () 528 с., т.2 () 752 с.
(1985) Справочник по теории вероятностей и математической статистике. Москва: Наука, 640 с.
Хастингс Н., Дж. Пикок (1980) Справочник по статистическим распределениям. Библиотека иностранных книг для экономистов и статистиков. Москва: Статистика, 96 с. (перевод с английского: Hastings N.A.J., and J.B. Peacock (1976) Statistical Distributions. A Handbook for Students and Practitioners. London: ButterWorths.)

Связь с другими непрерывными дистрибутивами

р∼рвyлеяграммчас(σ){\ Displaystyle R \ sim \ mathrm {Рэлей} (\ sigma)}следует закону Рэлея, если , где и — две независимые гауссовские переменные , что объясняет выбор символа «σ» для параметризации закона Рэлея.рзнак равноИкс2+Y2{\ displaystyle R = {\ sqrt {X ^ {2} + Y ^ {2}}}}Икс∼НЕТ(,σ2){\ Displaystyle X \ sim {\ mathcal {N}} (0, \ sigma ^ {2})}Y∼НЕТ(,σ2){\ Displaystyle Y \ sim {\ mathcal {N}} (0, \ sigma ^ {2})}
Если , то R 2 следует закону χ² с двумя степенями свободы: что является экспоненциальным законом с параметром 1/2.р∼рвyлеяграммчас(1){\ Displaystyle R \ sim \ mathrm {Рэлей} (1)}р2∼χ22, {\ Displaystyle R ^ {2} \ sim \ chi _ {2} ^ {2}, \}
Если X следует экспоненциальному закону , то .Икс∼E(λ){\ Displaystyle X \ sim {\ mathcal {E}} (\ lambda)}Yзнак равно2Иксσ2λ∼рвyлеяграммчас(σ){\ displaystyle Y = {\ sqrt {2X \ sigma ^ {2} \ lambda}} \ sim \ mathrm {Rayleigh} (\ sigma)}
Если , и если в виде серии независимых переменных, то следует гамма — распределение параметра N и 2о 2 : .ря∼рвyлеяграммчас(σ){\ Displaystyle R_ {я} \ sim \ mathrm {Rayleigh} (\ sigma)}ря{\ displaystyle R_ {i}}∑язнак равно1НЕТря2{\ Displaystyle \ сумма _ {я = 1} ^ {N} R_ {я} ^ {2}}Yзнак равно∑язнак равно1НЕТря2∼Γ(НЕТ,2σ2){\ Displaystyle \ sim \ Gamma (N, 2 \ sigma ^ {2})}
Закон Райса является обобщением Рэлея.

Приложения [ править ]

Применение оценки σ можно найти в магнитно-резонансной томографии (МРТ). Поскольку изображения МРТ записываются как сложные изображения, но чаще всего рассматриваются как изображения магнитуды, фоновые данные распределяются по Рэлею. Следовательно, приведенная выше формула может использоваться для оценки дисперсии шума на МРТ-изображении по фоновым данным.

Распределение Рэлея также использовалось в области питания для установления связи между уровнями питательных веществ в рационе и реакциями человека и животных . Таким образом, параметр σ может использоваться для расчета зависимости отклика на питательные вещества.

Кривые функции распределения вероятностей Рэлея, Ричиана и Логнормального реализованы программным обеспечением MATLAB.

http-equiv=»Content-Type» content=»text/html;charset=UTF-8″>style=»clear:both;»>

Код функции плотности вероятности распределения Рэлея

Примечание: raylpdf (x, b) — значение функции плотности вероятности распределения Рэлея с параметром b График функции плотности вероятности распределения Рэлея Код функции плотности вероятности распределения Райса Примечание. U в программе обозначает sigmaZ = 1;

Изображение функции плотности вероятности распределения Райса Код кривой плотности вероятности логнормальной функции

Изображение кривой плотности вероятности логнормальной функции

Интеллектуальная рекомендация

Функция вероятности: плюс вероятность каждого значения в форме функции, p (x) (x = x1, x2, …). Это имеет значение только для дискретных данных. Функция распределения вероятности: дает накопленную фо…

1. Проблема Когда Matlab была запущена программное обеспечение для извлечения пленки, была запущена ошибка. 2. Справочная ссылка Решение 2. Фактическая работа После удаления этого файла вы можете рабо…

1. Установите SecureCRT Quote:Нажмите, чтобы открыть https://blog.csdn.net/hdd871532887/article/details/77994970 1.скачатьsecureCRTсsecureCRTЗарегистрировать машину(к7.3.3Версия, операционная сис…

Преступность При написании бумаги столкнулся с сценарием, который должен быть размещен на локальной кривой, поэтому Baidu ищет ответы. Результат записан в заметках, что удобно для будущего использован…

Функция Функции FPLOT: FPLOT (F, Lims, опция) Где F представляет собой функцию, обычно в форме функциональной ручки. Лимс — это диапазон значений оси x, описанный в двоичных векторах , зна…

Вам также может понравиться

1, базовое использование функций сюжета Участок (x, y): где x и y хранят x координата и координаты y. Пример кода: Результат работы: 2, самый простой формат вызова функции сюжета Участок (x): Использу…

Перепечатано: https://www.cnblogs.com/jakeylove3/p/8446798.html 1. Введение Вопрос о том, как генерировать уникальные идентификаторы в системе (например, номер заказа, партия и т. Д.) Был обеспокоен д…

В R. есть много функций вероятности. Есть функции плотности вероятности и функции распределения вероятности. Вы можете вызывать функции или генерировать случайные числа. Правила для их использо…

В этой статье мы попытаемся создать пользовательский уровень нейронной сети. Результатом обучения этого уровня является функция распределения вероятностей, а выход — это значение с наибольшей уверенно…

Функция плотности вероятности (гауссовое распределение) Соответствует Numpy: Значение параметра: Np.random.randn (size) SO -стандартный стандартный нормальное нормальное распределение (μ = 0, &sigm…

Связь с некоторыми дискретными дистрибутивами

Случайное блуждание в самолете

Три реализации изотропных случайных блужданий по сети (за 10 000 шагов). Максимальное расстояние (или конечное расстояние) обычно составляет порядка 100 шагов. Z2 {\ Displaystyle \ scriptstyle \ \ mathbb {Z} ^ {2} \}

Обратите внимание на расстояние между положением случайного пешехода в плоскости после n, а не наугад, и его начальной точкой: сходится по закону к закону Рэлея, что означает, что, пройдя расстояние n , пешеход действительно удаляется только от своей начальной точки. точки примерно ступенчато, сходимость к закону Рэлея позволяет уточнить это приближение.
Dнет{\ displaystyle D_ {n}}Dнетнет{\ displaystyle D_ {n} / {\ sqrt {n}}}нет{\ displaystyle {\ sqrt {n}}}

Расстояние между двумя случайными точками случайного дерева Кэли

Использование , мы можем показать , что закон расстояния между двумя случайными точками случайного дается, по
Dнет{\ displaystyle D_ {n}} ≤ k ≤ нет-1, {\ Displaystyle 0 \ \ Leq \ к \ \ Leq \ п-1, \}

п(Dнетзнак равноk) знак равно (k+1)×(нет)↓k+1нетk+2.{\ displaystyle \ mathbb {P} \ left (D_ {n} = k \ right) \ = \ {\ frac {(k + 1) \ times (n) _ {\ downarrow k + 1}} {n ^ { k + 2}}}.}

Мы можем показать, например, используя лемму Шеффе , которая сходится по закону к закону Рэлея, который указывает, что «типичное» расстояние между двумя точками дерева размера n имеет порядокDнетнет{\ displaystyle D_ {n} / {\ sqrt {n}}}нет.{\ displaystyle {\ sqrt {n}}.}

Циклические точки приложения

В силу биекции Joyal в число из на отображение со из ин , следует тому же закону, что и . Таким образом, сходится по закону к закону Рэлея.
ПРОТИВнет(ω) {\ Displaystyle C_ {п} (\ омега) \}1,нет{\ Displaystyle \!]}1,нет{\ Displaystyle \!]}Dнет{\ displaystyle D_ {n}}ПРОТИВнетнет{\ displaystyle C_ {n} / {\ sqrt {n}}}

Проблема дней рождения

Этот сдержанный закон проявляется и в задачах размещения (шары и урны), включая знаменитый парадокс дней рождения . Когда шары распределяются последовательно в наборе из n урн с равновероятностью, что равносильно рассмотрению вероятностной вселенной, ранг первого шара, который должен быть размещен в непустой урне, подчиняется тому же закону, что и Таким образом, сходится по закону к закону Рэлея. .
Ω знак равно 1,нетНЕТ, {\ Displaystyle \ Omega \ = \ \!] ^ {\ mathbb {N}}, \}Тнет(ω) {\ Displaystyle Т_ {п} (\ омега) \}2+Dнет. {\ displaystyle 2 + D_ {n}. \}Тнетнет{\ displaystyle T_ {n} / {\ sqrt {n}}}

Для n = 365, то есть 365 ящиков, это интерпретируется как размер группы, для которой становится вероятным, что по крайней мере два члена группы имеют одинаковую дату годовщины (мы должны представить группу, число которой постепенно увеличивается): вероятность что в группе людей все дни рождения разные, примерно
Тнет(ω) {\ Displaystyle Т_ {п} (\ омега) \}αнет {\ displaystyle \ alpha {\ sqrt {n}} \}

е-α22 знак равно ∫α+∞ж(Икс;1)dИкс,{\ Displaystyle е ^ {- \ альфа ^ {2} / 2} \ = \ \ int _ {\ alpha} ^ {+ \ infty} \, f (x; 1) \, \ mathrm {d} x,}

и поэтому стоит 1/2 для группы примерно (или 22,5) человека, или 1/10 для группы примерно (или 41) человека. Точное вычисление первого целого числа, при котором эта вероятность меньше 1/2 (соответственно 1/10), дает те же результаты: 23 (соответственно 41).
365×2пер⁡(2) {\ Displaystyle {\ sqrt {365 \ times 2 \ ln (2)}} \}365×2пер⁡(10) {\ Displaystyle {\ sqrt {365 \ times 2 \ ln (10)}} \}

§ 2. Распределения функций от случайных величин

Линейные и монотонные преобразования.

Если случайная величина имеет распределение, то для любой
величина также имеет дискретное распределение,
и таблица распределения находится просто по определению.
Поэтому мы будем рассматривать в основном преобразования случайных величин
с распределениями.

Пусть случайная величина имеет и . Построим с помощью борелевской
функции
случайную величину .
Требуется найти функцию распределения и, если существует, плотность
распределения величины .

Замечание 15.
Плотность распределения случайной величины существует далеко не при любых функциях .
Так, если функция кусочно-постоянна, то имеет
дискретное распределение, и плотность её распределения не
существует.

Упражнение 34.
Привести пример плотности распределения случайной величины
и непрерывной функции таких, что
имеет:

а) дискретное распределение;
б) дискретное распределение.

Плотность распределения величины заведомо существует, если,
например, функция (строго) монотонна.

В общем случае мы не можем просто продифференцировать функцию распределения,
поскольку не знаем, существует ли плотность.
Следует доказать, что распределение абсолютно непрерывно.
Но доказывая это, мы попутно найдём и плотность распределения.
Действительно, у нас есть следующий путь доказательства
абсолютной непрерывности распределения.
Если, согласно равенству ,
можно для любого представить функцию распределения величины в виде

то плотность распределения величины существует и
равна подынтегральной функции: .
Другой путь продифференцировать функцию распределения и уже затем убедиться, что производная
является плотностью распределения, т.е. обладает свойствами (f1) и (f2).

Теорема 23.
Пусть имеет функцию распределения и плотность
распределения , и постоянная отлична от нуля.
Тогда случайная величина имеет плотность распределения

Доказательство.
Пусть сначала .

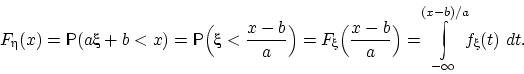
Сделаем замену переменной в последнем интеграле. Переменную заменим на
новую переменную так: . Тогда , верхняя граница области интегрирования
перейдёт в , нижняя
перейдёт в .
Получим

Функция под интегралом плотность распределения случайной величины при .

Пусть теперь .

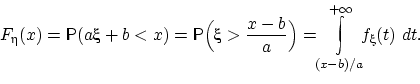
Сделаем ту же замену переменной , .
Но теперь граница интегрирования перейдёт в ,
поскольку . Получим

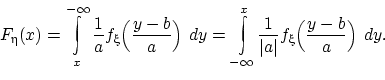
Функция под интегралом плотность распределения случайной величины при .

QED

Для произвольной монотонной функции справедливо утверждение:

Теорема 24.
Пусть имеет плотность
распределения , и функция монотонна.
Тогда случайная величина имеет плотность распределения

Здесь функция, обратная к , и её производная.

Упражнение 35.
Доказать теорему .

Из теоремы следуют уже знакомые нам утверждения:

Следствие 4.
Если , то .

Доказательство.
Действительно,

QED

Следствие 5.
Если , то
.

Следствие 6.
Если , то
при .

Следствие 7.
Если , то .

Квантильное преобразование.

Теорема 25.
Пусть функция распределения непрерывна. Тогда случайная
величина имеет на отрезке распределение.

Доказательство.
Найдём функцию распределения случайной величины .
Заметим, что всегда . Предположим сначала, что
функция всюду возрастает. Тогда она обратима, и поэтому

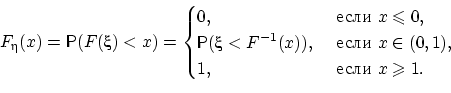(15)

Но , т.е. .

Если функция не является всюду возрастающей, то у неё есть участки постоянства.
В этом случае просто обозначим через самую левую точку из замкнутого множества
прообразов точки . При таком понимании «обратной»
функции равенства остаются справедливыми вместе с равенством
для любого .

QED

Теорему можно использовать для построения случайных величин
с заданным распределением по равномерно распределённой случайной величине
(например, по результату ДСЧ). Следующее утверждение верно не только
для непрерывных, но для любых функций распределения .
Обозначим через точную нижнюю грань множества тех , для которых
:

Для непрерывной функции это определение «обратной функции» совпадает с введённым в доказательстве
.

Теорема 26.
Пусть , а произвольная
функция распределения. Тогда случайная
величина
(«квантильное преобразование» над случайной величиной ) имеет функцию распределения .

Следствие 8.
Пусть . Верны соотношения:

Упражнение 36.

Доказать и , а также
продолжить список соотношений. Как получить случайную величину
с ?
А с распределением? (Указание: так её никто не получает).

Next:Многомерные распределения Up:Преобразования случайных величин Previous:Измеримость функций от случайных

N.Ch.

Связь со случайной длиной вектора [ править ]

Рассмотрим двумерный вектор, у которого есть компоненты, которые нормально распределены, центрированы в нуле и независимы. Тогда и имеют функции плотностиY=(U,V){\displaystyle Y=(U,V)}U{\displaystyle U}V{\displaystyle V}

fU(x;σ)=fV(x;σ)=e−x2(2σ2)2πσ2.{\displaystyle f_{U}(x;\sigma )=f_{V}(x;\sigma )={\frac {e^{-x^{2}/(2\sigma ^{2})}}{\sqrt {2\pi \sigma ^{2}}}}.}

Позвольте быть длиной . То есть тогда имеет кумулятивную функцию распределенияX{\displaystyle X}Y{\displaystyle Y}X=U2+V2.{\displaystyle X={\sqrt {U^{2}+V^{2}}}.}X{\displaystyle X}

FX(x;σ)=∬DxfU(u;σ)fV(v;σ)dA,{\displaystyle F_{X}(x;\sigma )=\iint _{D_{x}}f_{U}(u;\sigma )f_{V}(v;\sigma )\,dA,}

где дискDx{\displaystyle D_{x}}

Dx={(u,v)u2+v2<x}.{\displaystyle D_{x}=\left\{(u,v):{\sqrt {u^{2}+v^{2}}}<x\right\}.}

Записывая двойной интеграл в полярных координатах , он принимает вид

FX(x;σ)=12πσ2∫2π∫xre−r2(2σ2)drdθ=1σ2∫xre−r2(2σ2)dr.{\displaystyle F_{X}(x;\sigma )={\frac {1}{2\pi \sigma ^{2}}}\int _{0}^{2\pi }\int _{0}^{x}re^{-r^{2}/(2\sigma ^{2})}\,dr\,d\theta ={\frac {1}{\sigma ^{2}}}\int _{0}^{x}re^{-r^{2}/(2\sigma ^{2})}\,dr.}

Наконец, функция плотности вероятности для является производной ее кумулятивной функции распределения, которая согласно основной теореме исчисления равнаX{\displaystyle X}

fX(x;σ)=ddxFX(x;σ)=xσ2e−x2(2σ2),{\displaystyle f_{X}(x;\sigma )={\frac {d}{dx}}F_{X}(x;\sigma )={\frac {x}{\sigma ^{2}}}e^{-x^{2}/(2\sigma ^{2})},}

которое является распределением Рэлея. Легко обобщить на векторы размерности, отличной от 2. Существуют также обобщения, когда компоненты имеют неравную дисперсию или корреляции, или когда вектор Y следует двумерному t- распределению Стьюдента .

Свойства [ править ]

В сырые моменты определяются:

μj=σj2j2Γ(1+j2),{\displaystyle \mu _{j}=\sigma ^{j}2^{j/2}\,\Gamma \left(1+{\frac {j}{2}}\right),}

где — гамма-функция .Γ(z){\displaystyle \Gamma (z)}

Таким образом, среднее значение случайной величины Рэлея:

μ(X)=σπ2 ≈1.253 σ.{\displaystyle \mu (X)=\sigma {\sqrt {\frac {\pi }{2}}}\ \approx 1.253\ \sigma .}

Стандартное отклонение случайной величины Рэлея:

std⁡(X)=(2−π2)σ≈0.429 σ{\displaystyle \operatorname {std} (X)={\sqrt {\left(2-{\frac {\pi }{2}}\right)}}\sigma \approx {\sqrt {0.429}}\ \sigma }

Дисперсия случайной величины Рэлея:

var⁡(X)=μ2−μ12=(2−π2)σ2≈0.429 σ2{\displaystyle \operatorname {var} (X)=\mu _{2}-\mu _{1}^{2}=\left(2-{\frac {\pi }{2}}\right)\sigma ^{2}\approx 0.429\ \sigma ^{2}}

Режим является и максимальный PDF являетсяσ,{\displaystyle \sigma ,}

fmax=f(σ;σ)=1σe−12≈0.606σ.{\displaystyle f_{\max }=f(\sigma ;\sigma )={\frac {1}{\sigma }}e^{-1/2}\approx {\frac {0.606}{\sigma }}.}

Перекос определяется по формуле:

γ1=2π(π−3)(4−π)32≈0.631{\displaystyle \gamma _{1}={\frac {2{\sqrt {\pi }}(\pi -3)}{(4-\pi )^{3/2}}}\approx 0.631}

Избыточный эксцесс определяется:

γ2=−6π2−24π+16(4−π)2≈0.245{\displaystyle \gamma _{2}=-{\frac {6\pi ^{2}-24\pi +16}{(4-\pi )^{2}}}\approx 0.245}

Характеристическая функция определяется по формуле:

φ(t)=1−σte−12σ2t2π2erfi⁡(σt2)−i{\displaystyle \varphi (t)=1-\sigma te^{-{\frac {1}{2}}\sigma ^{2}t^{2}}{\sqrt {\frac {\pi }{2}}}\left}

где — функция мнимой ошибки . Функция генерирования момента задаетсяerfi⁡(z){\displaystyle \operatorname {erfi} (z)}

M(t)=1+σte12σ2t2π2erf⁡(σt2)+1{\displaystyle M(t)=1+\sigma t\,e^{{\frac {1}{2}}\sigma ^{2}t^{2}}{\sqrt {\frac {\pi }{2}}}\left}

где — функция ошибок .erf⁡(z){\displaystyle \operatorname {erf} (z)}

Дифференциальная энтропия править

Дифференциальная энтропия задаются [ править ]

H=1+ln⁡(σ2)+γ2{\displaystyle H=1+\ln \left({\frac {\sigma }{\sqrt {2}}}\right)+{\frac {\gamma }{2}}}

где — постоянная Эйлера – Маскерони .γ{\displaystyle \gamma }