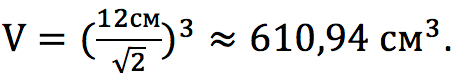Формулы нахождения площади и периметра куба

Калькулятор площади куба

Куб — это правильный шестигранник, каждая грань которого является квадратом. Кубические фигуры часто встречаются в реальной жизни, поэтому на работе или в быту вам может понадобиться вычислить объем или площадь поверхности объекта, который имеет форму кубика.

Геометрия куба

Куб или правильный гексаэдр — это частный случай шестигранной прямоугольной призмы, все грани которой представляют собой квадраты. Кроме того, куб — это и частный случай прямоугольного параллелепипеда, у которого длина, ширина и высота абсолютно равны.

Куб — уникальная фигура, существующая в разных многомерных пространствах. К примеру, нульмерный куб — это точка, одномерный — отрезок, двухмерный — квадрат, а четырехмерный — тессеракт.

В нашем родном трехмерном пространстве куб встречается повсеместно, к примеру, в форме детских кубиков, рафинированного сахара, картонных коробок, газетных киосков или предметов интерьера.

Кубы широко используются в программировании, аналитике, научных изысканиях и прочих высоких материях.

Идеальная форма геометрической фигуры позволяет при помощи разномерных кубов выражать массивы данных, измерять объемы или визуализировать данные.

Кубические фигуры часто встречаются в реальности и абстрактных задачах, поэтому вам может понадобиться рассчитать объем или площадь поверхности кубика для решения самых разных проблем.

Площадь поверхности куба

Площадь кубической фигуры — это сумма площадей всех граней. Каждая грань куба — это квадрат. Площадь квадрата, то есть одной грани, определяется по простой формуле как:

Sg = a2

Куб — это гексаэдр, то есть шестигранник. Таким образом, площадь поверхности кубической фигуры представляет собой сумму шести квадратов:

S = 6 Sg = 6 a2

Определить площадь куба можно не только при помощи длины его ребра: для расчета площади поверхности вы можете использовать диагональ самого куба или диагональ одной грани.

Диагональ куба — это отрезок, который находится внутри пространства куба и соединяет две противоположные вершины. Проведенная диагональ разделяет куб на два прямоугольных треугольника. Согласно теореме Пифагора квадрат ребра куба равен одной трети от квадрата диагонали D, следовательно, формула площади полной поверхности приобретает вид:

1. S = 2 D2

Площадь поверхности куба легко определить и с помощью диагонали одной грани. Площадь квадрата через диагональ равна:

1. S = 0,5 d2.

Так как у куба 6 граней, общая площадь поверхности составит сумму шести граней куба, то есть:

1. S = 6 × 0,5 d2 = 3 d2

Таким образом, чтобы определить площадь поверхности кубической фигуры вам достаточно ввести в форму-онлайн калькулятора всего один параметр на выбор:

• длину ребра;
• диагональ куба;
• диагональ квадрата.

Рассмотрим примеры использования данных формул в реальной жизни.

Ящик

Представьте, что вы хотите соорудить из листов ДСП ящик для хранения инструментов в форме куба. Вы знаете, что он отлично впишется в пространство на чердаке высотой 50 см.

Сколько же квадратных метров ДСП вам понадобится для создания такого контейнера? Зная высоту, равную a = 0,5 м вы можете легко подсчитать площадь общей поверхности куба, введя данный параметр в онлайн-калькулятор. Вы получите ответ в виде:

S = 1,5

Таким образом, вам понадобится всего 1,5 квадратных метра ДСП для создания ящика для инструментов. Зная всего один параметр, вы без труда порежете листы на грани куба и соорудите нужную конструкцию.

Контейнер

Допустим, вы хотите обработать антикоррозионным покрытием грузовые контейнеры, которые имеют кубическую форму. Для правильного расчета параметров покрытия вам необходимо знать площадь обрабатываемой поверхности. Вы знаете, что диагональ грани стандартного контейнера равняется d = 3 м. Зная этот параметр, вы легко рассчитаете площадь кубической поверхности, которая равна:

S = 18

Зная общую площадь покрытия, вы без проблем определите необходимое количество антикоррозионной жидкости.

Заключение

Куб встречается в реальной жизни не так часто, как призматические фигуры или параллелепипеды, однако в любом случае вам может понадобиться удобный калькулятор, при помощи которого вы определите площадь полной поверхности кубического объекта. Наш сервис поможет решить вам бытовые, производственные или школьные задачи мгновенно и без ошибок.

Понимание связи между площадью и объемом куба

Понимание связи между площадью и объемом куба важно при решении задач, связанных с геометрией и физикой. Площадь куба — это сумма площадей его граней, а объем — это произведение длины, ширины и высоты. Очевидно, что при увеличении длины, ширины и высоты куба, его объем будет увеличиваться гораздо быстрее, чем площадь его граней

И наоборот, при увеличении площади граней, объем куба будет увеличиваться медленнее

Очевидно, что при увеличении длины, ширины и высоты куба, его объем будет увеличиваться гораздо быстрее, чем площадь его граней. И наоборот, при увеличении площади граней, объем куба будет увеличиваться медленнее.

Таким образом, понимание связи между площадью и объемом куба позволяет более осознанно подходить к решению задач, например, при нахождении размеров куба по заданному объему или при определении объема куба по его площади граней.

Важно также помнить, что площадь и объем куба могут быть использованы для расчета других параметров, например, длины его диагонали или радиуса вписанной сферы

Как найти площадь поверхности куба?

Поскольку его поверхность состоит из квадратов, все его края будут иметь одинаковую длину. Поэтому, исходя из размеров высоты, его длина и ширина будут составлять 2 см. Не забудьте указать свое значение в квадратных единицах. Необходимо определить длину грани. Поскольку известна площадь поверхности, нужно считать в обратном порядке, разделив значение на 6, а затем извлечь квадратный корень. Сделав необходимые вычисления, получаем длину 3,8 см.

Допустим, что ребро куба не задано, но известен.

Так как объем данной фигуры вычисляется возведением в третью степень длины его ребра , то последнюю можно получить достаточно легко. Для этого из числа, обозначающего объем, необходимо извлечь корень третей степени. Например, для числа 27 корнем третей степени будет число 3. Ну а что делать дальше, мы уже разбирали. Таким образом, формула площади куба при известном объеме также существует, где вместо х стоит корень третей степени из объема.

Другое название — стороны. Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные — боковыми. Грани куба попарно перпендикулярны, являются квадратами, равны между собой. Ребро Линии пересечения сторон называются рёбрами. Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных. Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися. Вершина Точки пересечения рёбер называются вершинами. Их число равно восьми.

Объем присущ трехмерным объектам, таким как куб, шар, параллелепипед, призма, пирамида, конус. Объемные тела условно делят на многогранники состоят из нескольких многоугольников и поверхности вращения есть условная линия, вдоль которой вращается плоская фигура. На вычисление объема это не влияет. В таблицах представлены основные формулы объемов и площадей фигур для ЕГЭ.

Примеры задач

Задание 1
Вычислите объем куба, если его ребро равняется 5 см.

Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см 3 .

Задание 2
Известно, что объем куба равен 512 см 3 . Найдите длину его ребра.

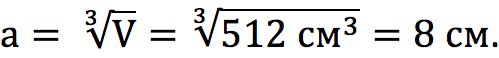
Решение:
Пусть ребро куба – это A. Выведем его длину из формулы расчета объема:

Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.

Решение:
Применим формулу, в которой используется диагональ грани:

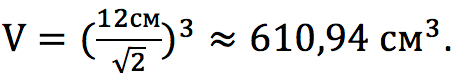
Публикации по теме:

Нахождение площади квадрата: формула и примеры Нахождение площади прямоугольника: формула и пример Нахождение площади треугольника: формула и примеры Нахождение площади круга: формула и примеры Нахождение площади ромба: формула и примеры Нахождение площади трапеции: формула и примеры Нахождение площади параллелограмма: формула и примеры Нахождение площади эллипса: формула и пример Нахождение площади выпуклого четырехугольника: формула и пример Нахождение периметра квадрата: формула и задачи Нахождение периметра треугольника: формула и задачи Нахождение периметра прямоугольника: формула и задачи Нахождение периметра трапеции: формула и задачи Нахождение периметра параллелограмма: формула и задачи Нахождение длины окружности: формула и задачи Теорема Пифагора для прямоугольного треугольника: формула и задачи Теорема косинусов для треугольника: формула и задачи Теорема синусов для треугольника: формула и задачи Теорема о сумме углов треугольника: формула и задачи Тригонометрические функции острого угла в прямоугольном треугольнике Нахождение объема конуса: формула и задачи Нахождение объема цилиндра: формула и задачи Нахождение объема шара: формула и задачи Нахождение площади правильного шестиугольника: формула и примеры Нахождение объема тетраэдра: формула и задачи Нахождение объема призмы: формула и задачи Нахождение объема параллелепипеда: формула и задачи Нахождение площади поверхности цилиндра: формула и задачи Нахождение площади поверхности конуса: формула и задачи Нахождение площади поверхности шара (сферы): формула и задачи Нахождение площади поверхности вписанного в цилиндр шара Нахождение радиуса шара: формула и примеры Нахождение радиуса цилиндра: формула и примеры Нахождение площади прямоугольного параллелепипеда: формула и пример Нахождение площади правильной пирамиды: формулы Формула Герона для треугольника Теорема Менелая: формулировка и пример с решением Теорема о внешнем угле треугольника: формулировка и задачи Теорема Чевы: формулировка и пример с решением Теорема Стюарта: формулировка и пример с решением Теорема о трех перпендикулярах Теорема Фалеса: формулировка и пример решения задачи Геометрическая фигура: треугольник Признаки равенства треугольников Признаки подобия треугольников Признаки равенства прямоугольных треугольников Свойства прямоугольного треугольника Свойства равнобедренного треугольника: теория и задача Определение и свойства медианы треугольника Определение и свойства медианы прямоугольного треугольника

Куб – это правильный многогранник, все грани которого являются квадратами.

Формулы куба

Для расчёта всех основных параметров куба воспользуйтесь калькулятором.

Части куба, свойства, определения

• У куба шесть граней
• Каждая грань куба пересекается с четырьмя другими гранями под прямым углом и параллельная противоположной грани
• Грани имеют одинаковую площадь, а так как являются квадратами, то формула площади грани S = a 2

• У куба двенадцать рёбер
• Каждое ребро перпендикулярно по отношению к примыкающим рёбрам
• Все ребра куба имеет одинаковую длину

• У куба три оси
• Оси куба взаимно перпендикулярны

• куб имеет четыре диагонали;
• диагонали куба пересекаются под прямым углом и делятся пополам в центре куба;
• диагонали куба имеют одинаковую длину;

Диагональ грани куба

• через длину ребра $$ V = a^3 $$
• через длину диагонали куба $$ V = > $$

Площадь поверхности куба

Вписанная и описанная сфера куба

Сфера, вписанная в куб

— это сфера, центр которой совпадает с центром куба и которая касается центров граней куба.

Радиус вписанной сферы через длину ребра

Объем вписанной сферы через длину ребра

Сфера, описанная вокруг куба

— это сфера, центр которой совпадает с центром куба и которая соприкасается с восьмью вершинами

• Подруга рассказала мужу о моем курортном романе

    

• Отдых в форосе уютный дворик

    

• Отдых на выходные в грузии

    

• Путешествие в тайную индию аудиокнига

    

• Закон о пребывании иностранцев в словакии

Практическое применение поверхности куба

Поверхность куба является одной из основных геометрических форм, которая нашла широкое применение в различных областях науки и техники. Поскольку куб имеет прямоугольные грани и прямые ребра, его поверхность используется для моделирования и изучения различных объектов и явлений.

Вот несколько примеров практического применения поверхности куба:

1. Архитектура: Поверхность куба может быть использована для моделирования зданий, сооружений и городской застройки. Благодаря прямоугольной форме и ребрам, куб может быть использован для определения размеров, планировки и расположения объектов в архитектурном проекте.

2. Графика и дизайн: Поверхность куба используется в компьютерной графике и дизайне для создания 3D моделей объектов и сцен. Кубические текстуры могут быть накладываются на поверхность объектов, чтобы придать им реалистичный внешний вид.

3. Математика и физика: В математике куб используется для изучения взаимосвязи между объемом, площадью и длиной ребра. В физике куб может быть использован для моделирования кристаллических структур и атомов.

4. Робототехника: Кубические формы часто используются в робототехнике для конструирования и проектирования роботов. Они позволяют легко соединять различные элементы и части робота, обеспечивая жесткость и прочность конструкции.

   

   

   

   

   

   

   

   

   

   

Это лишь некоторые примеры использования поверхности куба. Однако, в реальности кубическая форма присутствует во многих аспектах нашей жизни и имеет широкое применение в различных областях науки, техники и искусства.

Формула площади поверхности куба

П»Ã¾ÃÂðôàÿþòõÃÂÃÂýþÃÂÃÂø úÃÂñð â ÃÂÃÂþ ÃÂÃÂüüð ÿûþÃÂðôõù òÃÂõàõóþ óÃÂðýõù:

S=S1+S2+S3+S4+S5+S6S=S_1+S_2+S_3+S_4+S_5+S_6

ÃÂûþÃÂðôàúðöôþù óÃÂðýø þôøýðúþòð, ÃÂþ õÃÂÃÂÃÂ:

S1=S2=S3=S4=S5=S6=Sâ²S_1=S_2=S_3=S_4=S_5=S_6=SâÂÂ

Sâ²Sâ â ÿûþÃÂðôàûÃÂñþù óÃÂðýø úÃÂñð.

âþóôð ÿþûýðàÿûþÃÂðôàÿþòõÃÂÃÂýþÃÂÃÂø úÃÂñð ÷ðÿøÃÂõÃÂÃÂàúðú:

àðÃÂÃÂüþÃÂÃÂøü ýð ÿÃÂøüõÃÂðàÃÂð÷ýÃÂõ ÃÂÿþÃÂþñàòÃÂÃÂøÃÂûõýøàÿþûýþù ÿûþÃÂðôø ÿþòõÃÂÃÂýþÃÂÃÂø úÃÂñð.

ÃÂûþÃÂðôàúðöôþù óÃÂðýø úÃÂñð òÃÂÃÂøÃÂûÃÂõÃÂÃÂàúðú ÿûþÃÂðôàúòðôÃÂðÃÂð, ÃÂþ ÃÂÃÂþÃÂþýþù ÃÂõñÃÂð úÃÂñð ÿþ ÃÂþÃÂüÃÂûõ:

Sâ²=aâÂÂa=a2SâÂÂ=acdot a=a^2

aa â ÃÂÃÂþÃÂþýð úÃÂñð.

ÃÂÃÂÃÂÃÂôð, þúþýÃÂðÃÂõûÃÂýþ ÿûþÃÂðôàÿþòõÃÂÃÂýþÃÂÃÂø úÃÂñð:

ÃÂþ ÃÂõþÃÂõüõ ÃÂøÃÂðóþÃÂð, ôøðóþýðûàúÃÂñð ÃÂòÃÂ÷ðýýð àôûøýþù õóþ ÃÂõñÃÂð ÿþ ÃÂþÃÂüÃÂûõ:

d2=a2+a2+a2d^2=a^2+a^2+a^2d2=3âÂÂa2d^2=3cdot a^2d=3âÂÂad=sqrt{3}cdot a

ÃÂÃÂÃÂÃÂôð:

a=d3a=frac{d}{sqrt{3}}

ÃÂþôÃÂÃÂðòøü ò ÃÂþÃÂüÃÂûàôûàÿûþÃÂðôø:

S=6âÂÂa2=6âÂÂ(d3)2=2âÂÂd2S=6cdot a^2=6cdotBig(frac{d}{sqrt{3}}Big)^2=2cdot d^2

ÃÂþ ÃÂõþÃÂõüõ ÃÂøÃÂðóþÃÂð, ôøðóþýðûàúòðôÃÂðÃÂð ll ÃÂòÃÂ÷ðýýð àõóþ ÃÂÃÂþÃÂþýþù aa:

l2=a2+a2l^2=a^2+a^2l2=2âÂÂa2l^2=2cdot a^2l=2âÂÂal=sqrt{2}cdot a

âþóôð ÃÂÃÂþÃÂþýð úòðôÃÂðÃÂð:

a=l2a=frac{l}{sqrt{2}}

ÃÂþôÃÂÃÂðòûÃÂõü ò ÃÂþÃÂüÃÂûàôûàÿûþÃÂðôø ø ÿþûÃÂÃÂðõü:

S=6âÂÂa2=3âÂÂl2S=6cdot a^2=3cdot l^2

àð÷ñõÃÂõü ñþûõõ ÃÂûþöýÃÂõ ÿÃÂøüõÃÂÃÂ.

Нюансы расчета площади куба

Как и в любом другом расчете, есть определенные нюансы, которые следует учитывать при расчете площади куба:

1. Убедитесь, что все ребра куба равны.

2. Если вычисляете по диагонали, не забудьте правильно перевести ее в длину ребра.

3. Учтите, что результат будет в той же единице измерения, что и входные данные.

4. Проверьте правильность введенных вами значений перед расчетом.

5. Учитывайте округление: результат может незначительно отличаться в зависимости от количества знаков после запятой.

6. Не забудьте про погрешность измерительных инструментов, если используете их для получения данных.

7. Если используете куб в реальных проектах, учтите дополнительные факторы, такие как материал или условия окружающей среды.

8. Помните, что площадь поверхности отличается от объема куба.

9. При расчете площади для покраски или облицовки учтите запас материала на стыки и переходы.

10. Всегда проверяйте свои расчеты, особенно если они касаются значимых проектов или работ.

Задачи на нахождение площади куба

Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 40 и высота равна 15.

Площадь поверхности складывается из площади основания и площади четырех боковых граней: Высоту боковой грани найдем по теореме Пифагора: Тогда площадь поверхности пирамиды:

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 2, 4, 3 и двух площадей прямоугольников со сторонами 2, 1:

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 3, 3, 4 и двух площадей квадратов со стороной 2:

Там же «квадраты» со сторонами 2 и 3.

Мы вычитаем, только боковые грани из большого прямоугольного параллелепипеда — это как раз квадраты со сторонами 2 и 2.

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 2, 3, 5 и площади двух прямоугольников со сторонами 1, 2:

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности заданного многогранника равна сумме площадей поверхности прямоугольного параллелепипеда с ребрами 5, 4, 1 и двух прямоугольников со сторонами 1 и 2, уменьшенной на площадь двух квадратов со стороной 2:

Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Цифры на рисунке обозначают длины рёбер в сантиметрах. Найдите площадь поверхности этой детали. Ответ дайте в квадратных сантиметрах.

Площадь поверхности заданного многогранника равна сумме площадей поверхности прямоугольного параллелепипеда с ребрами 3, 5, 7 и двух прямоугольников со сторонами 1 и 5, уменьшенной на площадь двух прямоугольников со сторонами 1 и 3:

Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Цифры на рисунке обозначают длины рёбер в сантиметрах. Найдите площадь поверхности этой детали. Ответ дайте в квадратных сантиметрах.

Площадь поверхности заданного многогранника равна сумме площадей поверхности прямоугольного параллелепипеда с ребрами 4, 3, 6 и двух прямоугольников со сторонами 2 и 3, уменьшенной на площадь двух прямоугольников со сторонами 3 и 2:

Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Цифры на рисунке обозначают длины рёбер в сантиметрах. Найдите площадь поверхности этой детали. Ответ дайте в квадратных сантиметрах.

Площадь поверхности заданного многогранника равна сумме площадей поверхности прямоугольного параллелепипеда с ребрами 5, 5, 6 и двух прямоугольников со сторонами 2 и 5, уменьшенной на площадь двух прямоугольников со сторонами 2 и 3:

Как сделать процесс подготовки к аттестационному испытанию более легким и эффективным?

Наш образовательный портал предлагает выстроить занятия по-новому. Переходя от простого к сложному, выпускники смогут определить непонятные для себя темы и улучшить собственные знания.

Весь базовый материал по теме «Вычисление площадей и объемов фигур» собран в разделе «Теоретическая справка». Освежив в памяти эту информацию, учащиеся смогут попрактиковаться в решении задач. Большая подборка упражнений как простого, так и экспертного уровня представлена в разделе «Каталог». База заданий регулярно дополняется.

Решать задачи на вычисление объемов фигур или на построение сечения геометрических фигур школьники могут в режиме онлайн. Функционал образовательного сайта «Школково» позволяет сохранять упражнения в разделе «Избранное». Благодаря этому учащиеся смогут вернуться к задаче необходимое количество раз и обсудить ход ее решения со школьным учителем или репетитором.

Что такое файл cookie и другие похожие технологии

Файл cookie представляет собой небольшой текстовый файл, сохраняемый на вашем компьютере, смартфоне или другом устройстве, которое Вы используете для посещения интернет-сайтов.

Некоторые посещаемые Вами страницы могут также собирать информацию, используя пиксельные тэги и веб-маяки, представляющие собой электронные изображения, называемые одно-пиксельными (1×1) или пустыми GIF-изображениями.

Файлы cookie могут размещаться на вашем устройстве нами («собственные» файлы cookie) или другими операторами (файлы cookie «третьих лиц»).

Мы используем два вида файлов cookie на сайте: «cookie сессии» и «постоянные cookie». Cookie сессии — это временные файлы, которые остаются на устройстве пока вы не покинете сайт. Постоянные cookie остаются на устройстве в течение длительного времени или пока вы вручную не удалите их (как долго cookie останется на вашем устройстве будет зависеть от продолжительности или «времени жизни» конкретного файла и настройки вашего браузера).

Другие полезные формулы для нахождения площади поверхности геометрических фигур

1. Площадь поверхности прямоугольника

Для нахождения площади поверхности прямоугольника необходимо умножить его длину на ширину. Формула выглядит следующим образом:

Площадь поверхности прямоугольника = Длина x Ширина

2. Площадь поверхности треугольника

Для нахождения площади поверхности треугольника можно использовать несколько формул в зависимости от исходных данных:

• Если известны длины сторон треугольника, можно воспользоваться формулой Герона:

Площадь поверхности треугольника = √(p(p — a)(p — b)(p — c)), где p — полупериметр треугольника, a, b, c — длины сторон

Если известны длина основания треугольника и высота, можно воспользоваться формулой:

Площадь поверхности треугольника = 0.5 x Основание x Высота

3. Площадь поверхности круга

Для нахождения площади поверхности круга необходимо воспользоваться следующей формулой:

Площадь поверхности круга = π x Радиус²

Здесь π (пи) — постоянная, приближенное значение которой равно 3.14159.

Вычислить площадь полной и боковых поверхностей куба.

Совет полезен?

Все ребра куба равны. Куб является частным случаем параллелепипеда и призмы. В определении мы встречаем слово квадрат!

Таким же образом можно найти, например, объем куба, диагональ, длину ребра, радиус вписанного шара и т. Под калькулятором также отобразятся формулы вычислений, что весьма удобно. Введите данные: Достаточно ввести только одно значение, остальное калькулятор посчитает сам.

В зависимости от этого выбирается формула. Если по условиям задачи известна длина ребра куба , то достаточно применить простейшую формулу для нахождения площади.

Известно практически каждому, что площадь квадрата находится умножением длин двух его сторон. Грани куба — квадраты, следовательно, площадь его поверхности равна сумме площадей этих квадратов. Где х. Допустим, что ребро куба не задано, но известен.

Cookie файлы бывают различных типов:

Необходимые. Эти файлы нужны для обеспечения правильной работы сайта, использования его функций. Отключение использования таких файлов приведет к падению производительности сайта, невозможности использовать его компоненты и сервисы.

Файлы cookie, относящиеся к производительности, эффективности и аналитике. Данные файлы позволяют анализировать взаимодействие посетителей с сайтом, оптимизировать содержание сайта, измерять эффективность рекламных кампаний, предоставляя информацию о количестве посетителей сайта, времени его использования, возникающих ошибках.

Рекламные файлы cookie определяют, какие сайты Вы посещали и как часто, какие ссылки Вы выбирали, что позволяет показывать Вам рекламные объявления, которые заинтересуют именно Вас.

Электронная почта. Мы также можем использовать технологии, позволяющие отслеживать, открывали ли вы, прочитали или переадресовывали определенные сообщения, отправленные нами на вашу электронную почту. Это необходимо, чтобы сделать наши средства коммуникации более полезными для пользователя. Если вы не желаете, чтобы мы получали сведения об этом, вам нужно аннулировать подписку посредством ссылки «Отписаться» («Unsubscribe»), находящейся внизу соответствующей электронной рассылки.

Сторонние веб-сервисы. Иногда на данном сайте мы используем сторонние веб-сервисы. Например, для отображения тех или иных элементов (изображения, видео, презентации и т. п.), организации опросов и т. п. Как и в случае с кнопками доступа к социальным сетям, мы не можем препятствовать сбору этими сайтами или внешними доменами информации о том, как вы используете содержание сайта.

Примеры решения задач на нахождение площади куба

Для нахождения площади куба нужно знать длину его ребра. Площадь куба можно найти по формуле:

Площадь куба = 6 * (длина ребра)^2

Где «длина ребра» — это длина одной из сторон куба.

Пример 1:

Допустим, у нас есть куб со стороной 5 см. Чтобы найти площадь этого куба, нужно возвести длину его ребра в квадрат и умножить на 6:

Площадь куба = 6 * (5 см)^2 = 6 * 25 см^2 = 150 см^2

Таким образом, площадь куба со стороной 5 см равна 150 квадратных сантиметров.

Пример 2:

Предположим, у нас есть куб с ребром длиной 8 м. Чтобы найти его площадь, нужно выполнить следующие математические операции:

Площадь куба = 6 * (8 м)^2 = 6 * 64 м^2 = 384 м^2

Таким образом, площадь куба со стороной 8 м равна 384 квадратных метра.

Методы расчета площади куба позволяют решать разнообразные задачи, связанные с данным геометрическим телом. Найденная площадь может быть использована для дальнейших вычислений или для сравнения с другими геометрическими фигурами. Понимание данных методов поможет учащимся развивать навыки логического мышления, а также применять математические знания на практике.

Вычисление объемов фигур

Радиус первого шара в \(5\) раз больше радиуса второго шара. Во сколько раз площадь поверхности второго шара меньше площади поверхности первого шара?

Площадь поверхности шара радиуса \(R\) ищется по формуле \(S=4\pi R^2\) . Следовательно, площадь поверхности первого шара относится к площади поверхности второго шара как \ Так как радиус первого шара больше радиуса второго шара в 5 раз, то \(R_1=5R_2\) . Следовательно, \ Следовательно, площадь поверхности первого шара в 25 раз больше площади поверхности второго, значит, площадь поверхности второго в 25 раз меньше.

Даны два конуса. Радиус второго конуса в \(3\) раза больше радиуса первого конуса, а высота второго конуса в \(6\) раз меньше высоты первого конуса. Найдите объем первого конуса, если объем второго конуса равен \(18\) .

Объем конуса с высотой \(h\) и радиусом основания \(R\) вычисляется по формуле \(V=\frac13\pi R^2h\) . Следовательно, объем первого конуса относится к объему второго конуса как \ Так как радиус второго в 3 раза больше радиуса первого, то \(R_2=3R_1\) . Так как высота второго в 6 раз меньше высоты первого, то \(h_1=6h_2\) . Следовательно, \

Даны два конуса: \(K_1\) и \(K_2\) . Площадь полной поверхности \(K_1\) относится к площади полной поверхности \(K_2\) как \(4:1\) . Известно, что радиус \(K_1\) в 4 раза больше образующей \(K_1\) и в 2 раза больше радиуса \(K_2\) . Найдите отношение образующей \(K_2\) к образующей \(K_1\) .

Площадь полной поверхности конуса с образующей \(l\) и радиусом основания \(R\) ищется по формуле \(S=\pi R (R+l)\) . Тогда площадь полной поверхности \(K_1\) относится к площади полной поверхности \(K_2\) как \ Из условия следует, что \(R_1=4l_1\) , \(R_2=\frac12R_1=2l_1\) , следовательно, \

Во сколько раз радиус первого шара больше радиуса второго шара, если объем первого шара в \(343\) раза больше объема второго шара?

Объем шара радиуса \(R\) ищется по формуле \(V=\dfrac43 \pi R^3\) . Следовательно, объем первого шара относится к объему второго как \=7.\] Следовательно, радиус первого шара в 7 раз больше радиуса второго шара.

Объем первого прямоугольного параллелепипеда равен 105. Найдите объем второго прямоугольного параллелепипеда, если известно, что высота первого параллелепипеда в 7 раз больше высоты второго, ширина второго в 2 раза больше ширины первого, а длина первого в 3 раза больше длины второго.

Пусть буквы \(a\) , \(b\) и \(c\) обозначают высоту, ширину и длину соответственно. Объем прямоугольного параллелепипеда ищется по формуле \(V=abc\) . Следовательно, объем первого параллелепипеда относится к объему второго как \ Из условия следует, что \(a_1=7a_2\) , \(b_2=2b_1\) , \(c_1=3c_2\) . Тогда \

Площадь боковой поверхности первого цилиндра равна \(16\) . Найдите площадь боковой поверхности второго цилиндра, если его радиус в 4 раза больше радиуса первого, а высота в 5 раз меньше высоты первого цилиндра.

Площадь боковой поверхности цилиндра с высотой \(H\) и радиусом основания \(R\) ищется по формуле \(S=2\pi RH\) . Тогда площадь бок. поверхности первого цилиндра относится к площади бок. поверхности второго как \ Из условия следует, что \(R_2=4R_1\) , \(H_1=5H_2\) , значит, \ Следовательно, \

Площадь боковой поверхности первого конуса относится к площади боковой поверхности второго конуса как \(3:7\) . Найдите отношение образующей первого конуса к образующей второго конуса, если радиус первого конуса относится к радиусу второго как \(15:7\) .

Площадь боковой поверхности конуса с образующей \(l\) и радиусом основания \(R\) ищется по формуле \(S=\pi Rl\) . Тогда площадь бок. поверхности первого конуса относится к площади бок. поверхности второго как \ Так как радиус первого конуса относится к радиусу второго как \(15:7\) , то есть \(\frac=\frac7\) , то \

Во время подготовки к сдаче ЕГЭ по математике повторение базовых формул из школьного курса геометрии в пространстве (стереометрии), в том числе и для вычисления объемов фигур, является одним из основных этапов. И хотя на изучение этого раздела отводится достаточно большое количество времени в рамках учебной программы, многим выпускникам требуется освежить в памяти основной материал.

Понимая, как осуществляется вычисление площадей объемных фигур, учащиеся значительно повышают свои шансы на получение достойных баллов по итогам сдачи ЕГЭ.

Определение куба

Куб – это правильный многогранник, все грани которого являются квадратами.

Примечание: куб является частным случаем параллелепипеда или призмы.

как найти диагональ куба,если известна только полная площадь поверхности ?

Пусть площадь поверхности х.
тогда площадь грани х\6
тогда сторона ребро куба корень (х\6)
диагональ равна утроенный квадрат стороны, то есть 3·(х\6) = х\2
Удачи))

берете грань за х тогда площадь будет x^3 находите х а дальше и треугольника диагональ

По теореме пифагора.
Диагональ — гипотенуза
Ширина и длина у куба — катеты и они одинаковы.
И формула гипотенуза в квадрате=высота в квадрате + ширина в квадрате.
Ну площадь поверхности куба — квадрат же.
Ну вот к примеру — площадь — 16
Значит высота=ширина=4
Значит диагональ равна х^2=4^2+4^2
И равна корень из 32

я думаю, что для начала надо узнать площадь одной стороны, т. к. сторон шесть и они все равны, то и общую площадь надо поделить на шесть. дальше узнать длину грани, то есть корень квадратный и т. д.

Площадь куба, площадь сечения куба, формула, площадь куба онлайн.

1. Для того, чтобы перейти к теме «формулы площади куба» — давайте нарисуем или предоставим, что такое куб.

   Куб — это фигура с одинаковыми сторонами, угол между которыми равен 90°.

   Если сторона куба — «а».

   Площадь куба равна 6 умноженное на а²

2. Для того, чтобы доказать формулу «площади куба» Вам потребуется

   Взглянуть на куб и вы увидите, что количество сторон куба — 6. И каждая сторона куба состоит из квадрата, со стороной «а».

   Вы знаете площадь квадрата, которая выражается формулой:

   S = a²

   Выше вы уже сказали, что сторон у куба 6, то нужно площадь одного квадрата умножить на 6.

   Вы доказали, что «Площадь куба равна 6 умноженное на а²»

3. Условие задачи :

   Найдите площадь куба. если известна сторона куба, которая равна 5см.

   

   

   

   

   

   Вспоминаем уже приведенную формулу куба :

   И букву a — сторону куба заменяем на наше значение — 5см

   S = 6a² = 6 * 5² = 6 * 25 = 150Ответ:

   Если сторона куба равна 5см, то площадь куба равна 150см²

   Для проверки правильности решения задачи «найдите площадь куба, если известна сторона» — воспользуйтесь онлайн калькулятором «подсчета площади куба» — см. ниже:

4. Для того чтобы найти площадь куба онлайн, вам потребуется :

   Сторона куба — заполнить значением стороны куба.

   И нажать кнопку найти площадь куба.

5. Сформулируем «формулу площади сечения куба» начнем…

   Если сторона куба — — «а».

   То формула площади сечения куба звучит так:

   Сечение площади куба равно произведению квадрата стороны на корень из двух.

6. Выше Вы рассмотрели формулу «площади сечения куба», теперь… давайте докажем «формулу площади сечения куба».

   Нам нужно найти диагональ треугольника ABC — что будет одной из сторон сечения куба.

   Вспоминаем теорию Пифагора

   с² = а² + b²

   Если мы переведем в наши буквенные обозначения, для нашего треугольника, то:

   BC² = AB² + AC²

   В нашем случае «AB = AC= a» — из чего получаем :

   BC² = а² + а² = 2а²

   Теперь извлекаем корень с двух сторон:

   √BC² = √2а²

   Мы нашли одну сторону сечения куба:

   BC = а √2

   Мы нашли сторону сечения куба это — BC

   Теперь мы можем построить сечение куба:

   Т.е нам нужно найти площадь прямоугольника BCDE.

   Площадь прямоугольника равна :

   S = BC * CD

   Выше, мы уже нашли BC = а√2

   Как мы знаем из условия, что это куб, а у куба все стороны равны, то CD = «a».

   Заменяем BC и CD.

   S = а √2 * a = a² √2

7. Для того, чтобы найти площадь сечения куба онлайн нам понадобится формула и немного вернуться к теории, чтобы…

   добавить ясности, как видим, что в формуле присутствует корень из 2, что равно:

   1.4142135623731

   И далее к форме:

   Для того, чтобы подсчитать «площадь сечения куба» вам понадобится:

   В первом поле выбираем диапазон числа(см. выше), диапазон от 1 до 13, который будет показывать ваш выбор сколько чисел после запятой оставить!

   Во втором поле вбиваем размер стороны куба.

   И далее вам остается подсчитать площадь сечения куба онлайн! Нажимаем кнопку — «найти площадь сечения куба».

8. Условие задачи :

   Найдите площадь сечения куба, если известна сторона, которая равна 10см.

   Для решения данной задачи, нам потребуется знать

   Вспоминаем площадь сечения куба:

   S = a²√2

   Заменяем а на 10, корень квадратный из 2 округлим до 1.4 :

   S = 10²√2 = 100 * 1.4 = 140см².

   Более точные вычисления «площади сечения куба » вы можете произвести в форме выше пунктом!

Не стесняемся говорить спасибо!