Определение длины ребра куба по его объему

Что из перечисленного можно найти у куба?

Куб — это неодушевленный предмет, поэтому ни легких, ни сердца, ни почек у него быть не может. Куб является геометрической объемной фигурой, у которой имеются грани, вершины и ребра.

Поэтому правильным ответом на заданный вопрос будем считать ребра (ответ А).

Ответ А: Рёбра подсказывают мне мои знания геометрии и мое незнание анатомии.

Так смотря у какого куба-). Если взять губку Боба, так он, как персонаж одушевленный, может, точнее должен иметь легкие для дыхания, сердце для жизни и почки для. а почки для чего у нас? Но вернемся к теме вопроса. Так вот получается, что живой куб может все иметь. А графический только одним органом живых существ обладает — это ребро(а), которое(ые) под буквой «А)» в предлагаемых вариантах, вот его и выбираем.

Не нужно быть отличником по геометрии, чтобы ответить на это вопрос. Конечно же, из всего перечисленного у куба можно найти лишь РЁБРА. Рёбер у куба аж двенадцать штук! А ещё у куба есть грани и вершины.

Здравствуйте, из вышеперечисленных вариантов можно сразу же снять варианты B, C, D, куб не может иметь сердце, почки и легкие, у нас остается правильным только первый вариант » РЕБРА «, а ребер у него двенадцать штук!

Все могут представить себе правильный многогранник, который называется кубом. В этом правильном многограннике вы можете отыскать и грани, и ребра, и вершины, но никак вы не сможете найти в кубе ни сердца, ни легких, ни почек. Так что нам нужен ответ , который мы видим под буквой А : РЕБРА.

Куб — это известная геометрическая фигура, конечно, почек и сердца и легких мы там не найдем.

Вот какое определение этой фигуры есть в учебнике:

У куба есть ребра, их насчитывается у этой фигуры 12 штук, конечно, это не те ребра, которые можно найти в человеческом организме, но тем не менее в кубе они присутствуют.

Выбираем ответ А — РЕБРА.

Верным ответом на данный вопрос будет слово РЕБРА. Ещё со школы мы помним, что у куба имеются ребра. Все остальные приведенные варианты — это не то, что имеется у куба. Легкие, сердце и почки есть у человека, но никак не у геометрической фигуры куба.

Это нетрудный вопрос, ответ на который напрашивается сам собой — куб — это объёмная геометрическая фигура с равными квадратными сторонами и, стало быть, одинаковыми по длине гранями, которые имеют ещё и другое название, сходное по звучанию с названием определённого вида костей в человеческом организме — ответ: «А. Ребра».

Предложенные вами четыре варианта ответа ассоциируются с живым организмом: человек, животное, птица. Отсюда можно предположить точно, что в кубе однозначно нет легких и почек. Сердца также нет, потому что такая геометрическая фигура, начерченная на листе бумаги или имеется макет куба иметь может только равные стороны, грани и РЁБРА.

Вот и разобрались с правильным ответом.

В 2015 году журнал Hollywood Reporter сообщил, что кинокомпания Lionsgate планирует выпустить ремей Куб / Cube. Над проектом трудится Рой Ли из Vertigo Entertainment. Новая лента получит название Cubed. Выйдет не ранее 2018 года.

Куб в значении геометрического тела вы сами проиллюстрировали.

Третья степень числа тоже называется кубом.

Сюда же отнесём объёмную меру чего-нибудь, вроде, допустим, двух кубов дров. Понятно, что речь идёт о кубометрах.

Перегонный куб — если не ошибаюсь, придуманный ещё древними арабскими учёными агрегат для (ал)химических опытов и получения «воды жизни», то есть спиртяшки. Например, так не кубически выглядит перегонный куб, он же в народе «самогонный аппарат» для коньячных спиртов:

Кубами настольщики называют игральные кости. Не только шестигранники (d6), действительно являющиеся кубами, но и все прочие многогранники.

Источник

Как определить объем куба через его площадь поверхности

Куб — это геометрическое тело, у которого все грани являются квадратами одинаковой площади. Из-за такой формы куб очень прост в вычислениях объема и площади поверхности.

Если известна площадь поверхности куба, то есть два способа определить его объём. Первый способ, который является достаточно простым, — это воспользоваться формулой:

V = S2/6, где V — объем куба, а S — площадь поверхности.

Второй способ, который включает данные для трёхмерного куба, может быть получен, используя формулу:

V = ∛(S3), где V — объем куба, а S — площадь поверхности.

Какой бы способ вы не использовали, важно помнить, что объём куба не зависит от масштаба модели. Это значит, что если вы знаете значение площади поверхности, то вы сможете определить объём любого куба с одинаковой площадью поверхности

Вопрос-ответ

Вопрос: Как найти объем куба, если известна площадь одной грани?

Ответ: Чтобы найти объем куба, нужно возвести в квадрат длину стороны и умножить на нее же: V=a^3. При известной площади одной грани куба S можно найти длину стороны куба по формуле a=S^(1/2), а затем легко вычислить объем.

Вопрос: Как можно найти объем куба, если известна площадь поверхности куба?

Ответ: Если известна площадь поверхности куба S, то можно использовать формулу V=(S/6)^(3/2). Сначала находим площадь одной грани куба по формуле S=a^2, а затем подставляем площадь в формулу для нахождения объема.

Вопрос: Можно ли найти объем куба, если известна его диагональ?

Ответ: Да, можно. Если известна диагональ куба d, то можно найти длину стороны куба по формуле a=d/(3^(1/2)), а затем легко вычислить объем куба по формуле V=a^3.

Вопрос: Каким образом найти объем куба, если известна его высота и площадь основания?

Ответ: Если известна высота h и площадь основания S, то можно найти длину стороны куба по формуле a=(S/h)^(1/2), а затем легко вычислить объем куба по формуле V=a^3.

Вопрос: Какие формулы помогут найти объем и длину стороны куба?

Ответ: Формула для нахождения объема куба: V=a^3, где a — длина стороны куба. Формула для нахождения длины стороны куба по площади поверхности: a=(S/6)^(1/2). Формула для нахождения длины стороны куба по диагонали: a=d/(3^(1/2)). Формула для нахождения длины стороны куба по высоте и площади основания: a=(S/h)^(1/2).

Главная — Полезно — Легко вычисляем объем куба: гайд по поиску при известной площади поверхности.

Комментарии

MaxPayne

5.0 out of 5.0 stars5.0

Я долго искал информацию о том, как найти объем куба по его площади поверхности. Эта статья мне очень помогла. Я понял, что нужно просто возвести площадь в 3/2 степень и получить ответ. Конечно, было бы неплохо, если бы статья описывала более подробно процедуру вычисления, но в целом я доволен.

Петр Петров
5.0 out of 5.0 stars5.0

Хорошая статья, спасибо.

Анна Иванова
5.0 out of 5.0 stars5.0

Я уже давно ищу информацию о том, как найти объем куба. Мне понравилась эта статья, потому что я, наконец-то, поняла, что в этом вопросе самое главное – всегда уметь вспомнить о формулах. Я вообще слабовата в математике, но эта статья помогла мне понять материал. Было интересно, когда автор объяснял примеры, тогда я понимала, что наконец-то понимаю, о чем идет речь. Я могу сказать, что теперь быстро решу задачку про кубик. Уверена, что статья поможет многим, кто не уверен в своей способности решать математические задачи. Рекомендую!

Александр
5.0 out of 5.0 stars5.0

Меня всегда интересовала математика, и поэтому я часто ищу информацию в Интернете, чтобы узнать что-то новое. Когда я наткнулся на эту статью, я подумал, что это может быть полезно для меня, ведь я никогда не знаю, когда мне понадобятся знания о том, как найти объем куба. Сначала я подумал, что статья будет очень сложной и запутанной, но на самом деле все оказалось довольно просто. Однако, я полагаю, что автору стоило бы уделить немного больше внимания процедуре вычисления объема куба, потому что у меня остались некоторые вопросы. Тем не менее, статья очень полезна для тех, кто интересуется математикой и хочет обогатить свои знания. Я думаю, что в будущем мне понадобятся эти знания, и я уже знаю, где их искать. Спасибо автору за эту статью!

BlackWidow
5.0 out of 5.0 stars5.0

Анна
5.0 out of 5.0 stars5.0

Статья была короткой и понятной. Теперь я знаю, как найти объем куба, используя только его площадь поверхности.

Понятие о диметрической прямоугольной проекции

Расположение осей диметрической проекции и способ их построения приведены на рис. 3.19. Ось z проводят вертикально, ось х – под углом около 7° к горизонтали, а ось у образует с горизонталью угол приблизительно в 41° (рис. 3.19, а). Построить оси можно, пользуясь линейкой и циркулем. Для этого из точки О откладывают по горизонтали вправо и влево по восемь равных делений (рис. 3.19, б). Из крайних точек восставляют перпендикуляры. Высота их равна: для перпендикуляра к оси х – одному делению, для перпендикуляра к оси у – семи делениям. Крайние точки перпендикуляров соединяют с точкой О.

Рис. 3.19. Расположение осей диметрической проекции

При вычерчивании диметрической проекции, как и при построении фронтальной, размеры по оси у сокращают в 2 раза, а по осям х и z откладывают без сокращений.

На рис. 3.20 показана диметрическая проекция куба с вписанными в его грани окружностями. Как видно из этого рисунка, окружности в диметрической проекции изображаются эллипсами.

Рис. 3.20. Диметрические проекции окружностей, вписанных в грани куба

Важные моменты при поиске ребра куба по объему:

При решении задачи по поиску ребра куба по известному объему есть несколько важных моментов, которые следует учитывать.

Используйте формулу для нахождения объема куба: V = a^3, где V — объем, a — ребро куба

Перепроверьте правильность введенных данных.
Обратите внимание на единицы измерения объема и ребра куба. Убедитесь, что они согласованы и переведены в одну систему измерения.
При решении задачи используйте алгоритм для нахождения корня третьей степени

Воспользуйтесь калькулятором или программными инструментами для выполнения расчетов точно и быстро.
Если объем куба задан не в точных числах, а в виде десятичной дроби, округлите результат до необходимой точности в соответствии с условиями задачи.
Проверьте полученный результат и его правдоподобность. Если он кажется вами сомнительным, пересчитайте задачу еще раз либо обратитесь за помощью к учителю или профессионалам в данной области.

Куб, параллелепипед. Видео (1 час 53 минуты)

Это видео – один из вебинаров нашей Программы подготовки к профильному ЕГЭ по математике.  Вся программа – это: 

• 3 вебинара в неделю c Алексеем Шевчуком до самой даты экзамена;
• проверка домашних работ по каждому вебинару;
• майский марафон “Год за месяц”, где мы повторим все темы ЕГЭ, то есть “упакуем” ваши знания, чтобы получить максимум на ЕГЭ.

НЕ ПРОПУСТИ!

Автор этого учебника, Алексей Шевчук, проводит бесплатные вебинары по самым сложным задачам ЕГЭ по математике и информатике.

На вебинарах все будет еще понятнее. Шорткаты, лайфхаки, разбор “капканов” – все там.

Регистрируйся здесь и приходи!

Если слишком сложно, просто посмотри на картинку.

Какую фигуру из планиметрии (геометрии с «плоскими» фигурами) напоминает параллелепипед?

Немного похоже на параллелограмм, правда? Только «потолще» и слово подлиннее.

Смотри, запоминай и не путай!

Та грань, на которую опущена высота, называется основанием.

• Все грани параллелепипеда – параллелограммы.
• Противоположные грани параллелепипеда параллельны и равны.

Внимание: передняя и задняя грани параллелепипеда равны, верхняя и нижняя – тоже равны, но не равны (не обязаны быть равны) передняя и верхняя грани – потому что они не противоположные, асмежные

Точка пересечения диагоналей называется центром параллелепипеда.

НРАВИТСЯ УЧЕБНИК?

Его автор, Алексей Шевчук, ведет курсы подготовки к ЕГЭ по математике и информатике.

Приходи, научишься решать задачи любой сложности с самого нуля. Шаг за шагом.

До 3990 руб / месяц, 3 раза в неделю по 2 часа.

Вот так:

Это такая обувная коробка:

У прямоугольного параллелепипеда все грани – прямоугольники.

Давай-ка теперь выведем одну интересную формулу для диагонали прямоугольного параллелепипеда.

Видишь, как красиво? На теорему Пифагора похоже, правда? И формула эта как раз и получается из теоремы Пифагора.

Смотри:

( displaystyle Delta BAD) – прямоугольный, поэтому

( displaystyle B{{D}^{2}}=A{{B}^{2}}+A{{D}^{2}}={{b}^{2}}+{{c}^{2}})

( displaystyle Delta BD{{D}_{1}}) – тоже прямоугольный!

Поэтому

( displaystyle B{{D}_{1}}^{2}=B{{D}^{2}}+D{{D}_{1}}^{2}),

Подставим:

( displaystyle {{d}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}})

Вывели формулу.

Все ребра куба равны.

Кстати, заметь, что куб – частный вид прямоугольного параллелепипеда.

Поэтому для диагонали куба действует формула, которую мы получили для прямоугольного параллелепипеда.

( displaystyle {{d}^{2}}={{a}^{2}}+{{a}^{2}}+{{a}^{2}}),

То есть

( displaystyle d=asqrt{3})

Давай убедимся в пользе этой формулы.

Представь, что у тебя задача: «Диагональ куба равна ( displaystyle 5sqrt{3}). Найти полную поверхность».

Решим ее.

Пользуясь нашей формулой: ( displaystyle d=asqrt{3}), мы узнали, что ( displaystyle 5sqrt{3}=asqrt{3} ), то есть ( displaystyle a=5).

Значит полная поверхность – шесть площадей квадратов со стороной ( displaystyle a) -равна:

( displaystyle S=6cdot {{a}^{2}}=6cdot 25=150).

Видишь, как быстро? И ты применяй!

Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:

Элементы куба

Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

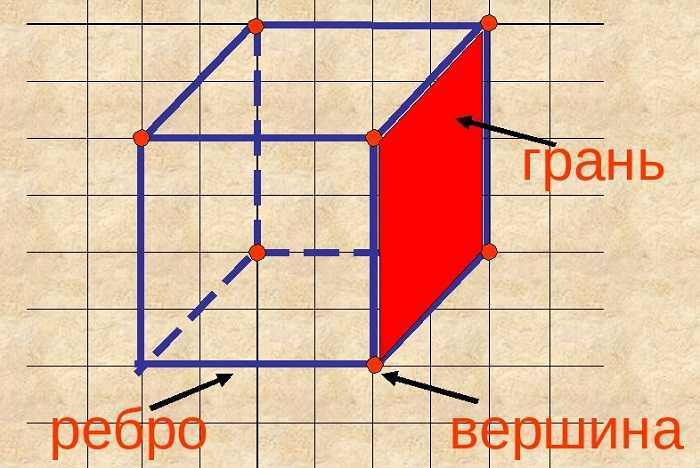
Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

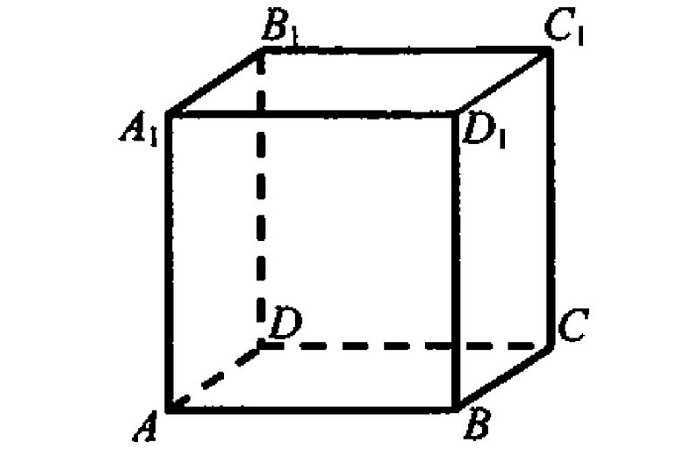
Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

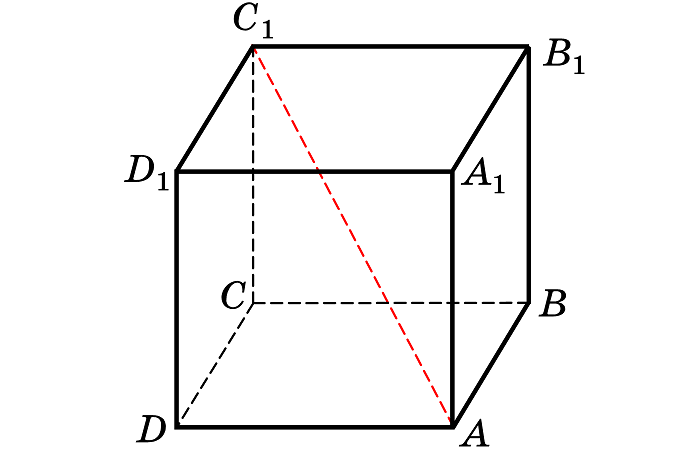
Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.

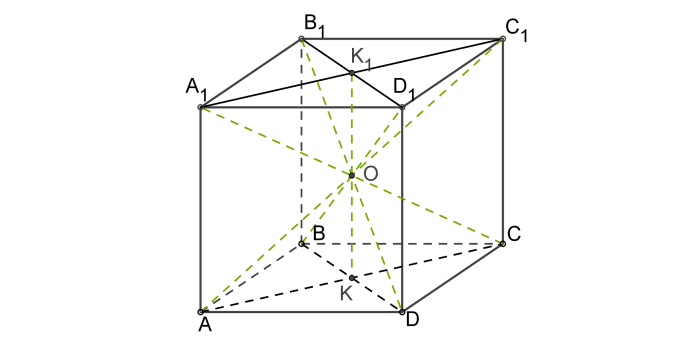
Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

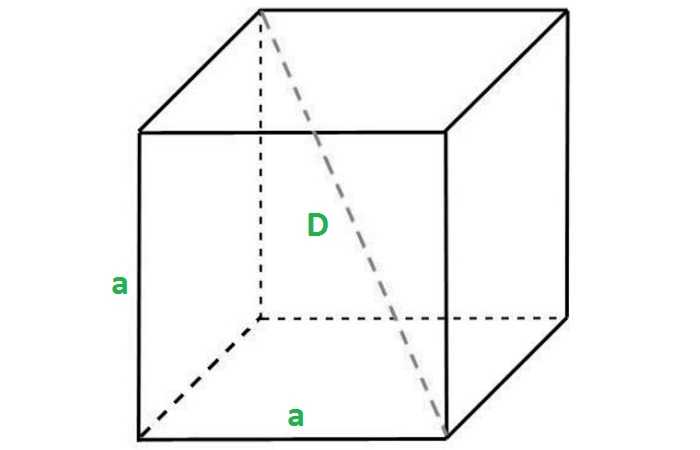
Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Диагональ куба — одна из осей симметрии.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Диагональ грани куба

Длина диагонали грани в √2 раз больше ребра, то есть:

Эта формула доказывается также с помощью теоремы Пифагора.

Видео:Как вычислить объем куба, площадь, периметрСкачать

Задачи по теме «Прямоугольный параллелепипед»

\(\blacktriangleright\) Прямоугольный параллелепипед – это параллелепипед, все грани которого являются прямоугольниками.Другими словами, это прямая призма, основания которой – прямоугольники.(эти определения эквивалентны).

1) противоположные грани равны между собой;

2) боковые ребра перпендикулярны основаниям, то есть являются высотами;

3) как следствие, формула для объема принимает вид: \(>\) , где \(a,\ b,\ c\) – три различных боковых ребра.

\(\blacktriangleright\) Диагональ прямоугольного параллелепипеда – это отрезок, соединяющий две противоположные (не лежащие в одной грани) вершины.

1) Все диагонали равны, пересекаются в одной точке и делятся ею пополам;

2) Диагональ \(d\) можно найти по формуле: \(=a^2+b^2+c^2>>\) .

Дан прямоугольный параллелепипед, стороны основания которого равны \(4\) и \(5\) , а боковое ребро равно \(3\) . Найдите наибольшую площадь его грани.

Заметим, что все варианты для площадей его граней – это всевозможные попарные произведения чисел \(3,4,5\) , то есть \(3\cdot 4\) , \(4\cdot 5\) или \(3\cdot 5\) . Среди этих произведений наибольшим является \(4\cdot 5=20\) .

Даны два прямоугольных параллелепипеда: ребра одного равны \(185\) , \(185\) и \(37\) ; а ребра другого равны \(185, 37\) и \(37\) . Во сколько раз объем первого параллелепипеда больше объема второго параллелепипеда?

Даны два прямоугольных параллелепипеда: ребра одного равны \(a, b\) и \(b\) , а ребра другого равны \(a, a\) и \(b\) . На сколько площадь полной поверхности первого параллелепипеда больше, чем площадь поверхности второго параллелепипеда, если \(a=1000, b=1001\) .

Площадь полной поверхности первого параллелепипеда \ Площадь полной поверхности второго параллелепипеда \ Следовательно, \

Дан прямоугольный параллелепипед \(ABCDA_1B_1C_1D_1\) . Во сколько раз объем пирамиды \(AA_1BD\) меньше объема этого параллелепипеда?

Пусть \(AB=x\) , \(AD=y\) , \(AA_1=z\) . Тогда объем параллелепипеда равен \ Так как \(S_=0,5S_\) (потому что по определению прямоугольного параллелепипеда в основании лежит прямоугольник), то объем пирамиды \ Следовательно, объем пирамиды в 6 раз меньше объема параллелепипеда.

В прямоугольном параллелепипеде диагональ грани \(AA_1D_1D\) равна \(5\) , а \(AB=2\sqrt6\) . Найдите диагональ параллелепипеда.

Так как параллелепипед прямоугольный, то все его грани – прямоугольники, а у прямоугольника обе диагонали равны. Следовательно, \(A_1D=AD_1\) . Рассмотрим диагональ \(A_1D\) и диагональ параллелепипеда \(B_1D\) . Треугольник \(A_1B_1D\) прямоугольный, так как ребро \(A_1B_1\) перпендикулярно грани \(AA_1D_1D\) (по определению прямоугольного параллелепипеда). Следовательно, гипотенуза \

Дан прямоугольный параллелепипед с ребрами \(2, \ 3\) и \(6\) . Найдите его диагональ.

Пусть \(AB=2, AD=3 , AA_1=6\) .

По теореме Пифагора из прямоугольного треугольника \(ABD\) ( \(\angle A=90^\circ\) ) имеем: \(BD^2=AB^2+AD^2\) .

Из прямоугольного треугольника \(BB_1D\) ( \(\angle B=90^\circ\) ) по теореме Пифагора \(B_1D^2=BD^2+BB_1^2\) .

Подставляя \(BD^2\) из первого равенства во второе, получим:

\

Найдите объём фигуры, получившейся после удаления маленького прямоугольного параллелепипеда из большого.

Объём оставшейся фигуры равен разности объёмов большого прямоугольного параллелепипеда (каким он был до удаления) и маленького (удалённого).

Таким образом, искомый объём равен \

Учащимся старших классов будет полезно научиться решать задачи ЕГЭ на нахождение объема и других неизвестных параметров прямоугольного параллелепипеда. Опыт предыдущих лет подтверждает тот факт, что подобные задания являются для многих выпускников достаточно сложными.

При этом понимать, как найти объем или площадь прямоугольного параллелепипеда, должны старшеклассники с любым уровнем подготовки. Только в этом случае они смогут рассчитывать на получение конкурентных баллов по итогам сдачи единого госэкзамена по математике.

Примеры задач

Задание 1 Найдите площадь поверхности куба, если длина его ребра составляет 12 см.

Решение: Используем первую формулу выше и получаем: S = 6 ⋅ (12 см) 2 = 864 см 2 .

Задание 2 Площадь поверхности куба равняется 294 см 2 . Вычислите длину его ребра.

Решение: Примем ребро куба за a. Из формулы расчета площади следует:

Задание 3 Вычислите площадь поверхности куба, если диагональ его грани равняется 5 см.

Решение: Воспользуемся формулой, в которой задействована длина диагонали: S = 6 ⋅ (5 см : √ 2 ) 2 = 75 см 2 .

Объем куба и прямоугольного параллелепипеда

Докажем важную вспомогательную теорему:

Действительно, пусть у двух параллелепипедов одинаковы основания. Тогда их можно совместить. Пусть общим основанием будет АВСD, а высотами параллелепипедов будут отрезки АР и АК, причем АР <АК. Объем меньшего параллелепипеда с высотой АР обозначим как V_Р, а большего – как V_K:

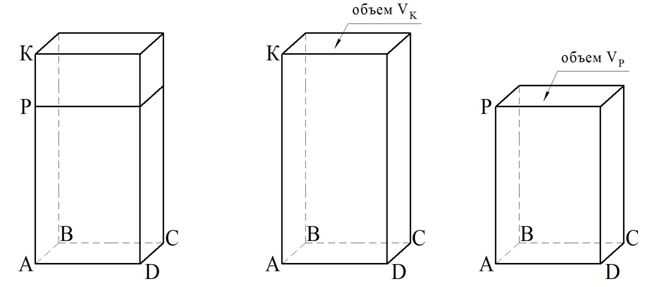
Нам надо доказать, что объемы фигур пропорциональны их высотам:

Для начала рассмотрим случай, когда отношение высот является рациональным числом. Это означает, что существует некоторая дробь m/n, такая, что

где m и n – натуральные числа. Тогда разобьем отрезок АК как раз на n равных отрезков. В этом случае отрезок АР будет состоять в точности из m таких отрезков. Далее через концы отрезков проведем плоскости, параллельные основанию:

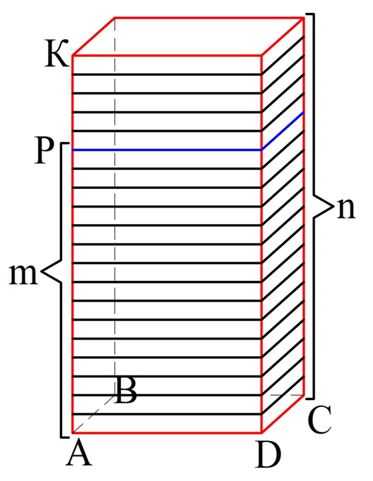
В результате мы получили n равных параллелепипедов («пластин»), которые все вместе образуют большой параллелепипед объемом V_K. Поэтому объем одной такой пластины равен величине V_K/n:

Итак, мы доказали теорему для случая, когда отношение высот является рациональным числом. Теперь перейдем к более сложному случаю, когда это отношение представляет собой иррациональное число. Здесь можно рассуждать от противного. Предположим, что теорема ошибочна, тогда для каких-нибудь двух параллелепипедов отношение их объемов будет равно не отношению их высот, а какому-то другому числу k:

Это значит, что k либо меньше, либо больше, чем отношение АР/АК. Рассмотрим случай, когда k< АР/АК (случай, когда k> АР/АК, рассматривается аналогичным образом). Тогда возьмем какое-нибудь рациональное число R, находящееся между числами k и АР/АК:

(Примечание. Здесь мы неявно используем утверждение, которое можно доказать в рамках алгебры – между любыми двумя различными действительными числами располагается хотя бы одно рациональное число).

Умножим это неравенство на длину АК:

Построим параллелепипеды с общим основанием АВСD и высотами АК и АР, а также с высотой АЕ = R•АК. Так как R•АК < АР, то точка Е будет лежать между А и Р:

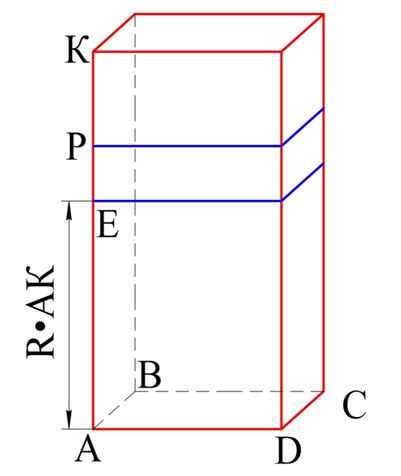
Объем параллелепипеда с высотой АЕ обозначим как V_Е. Ясно, что

ведь число k не может быть одновременно и больше, и меньше R. Полученное противоречие означает, что исходное предположение об ошибочности теоремы неверно, и на самом деле она справедлива, ч. т. д.

Теперь с помощью доказанной теоремы можно вывести известную ещё из младших классов формулу для расчета объема прямоугольного параллелепипеда.Пусть измерения прямоугольного параллелепипеда являются числами а, b и c. Построим:

• единичный куб;
• параллелепипед с габаритами а, 1, 1 с объемом V₁;
• параллелепипед с габаритами а, b, 1 с объемом V₂;
• параллелепипед с габаритами а, b, c с объемом V.

Тогда можно последовательно вычислить их объемы. Объем первого параллелепипеда будет в а раз больше объема единичного куба, то есть он будет равен а. Объем второго параллелепипеда будет больше ещё в bраз, а третьего – ещё в с раз:

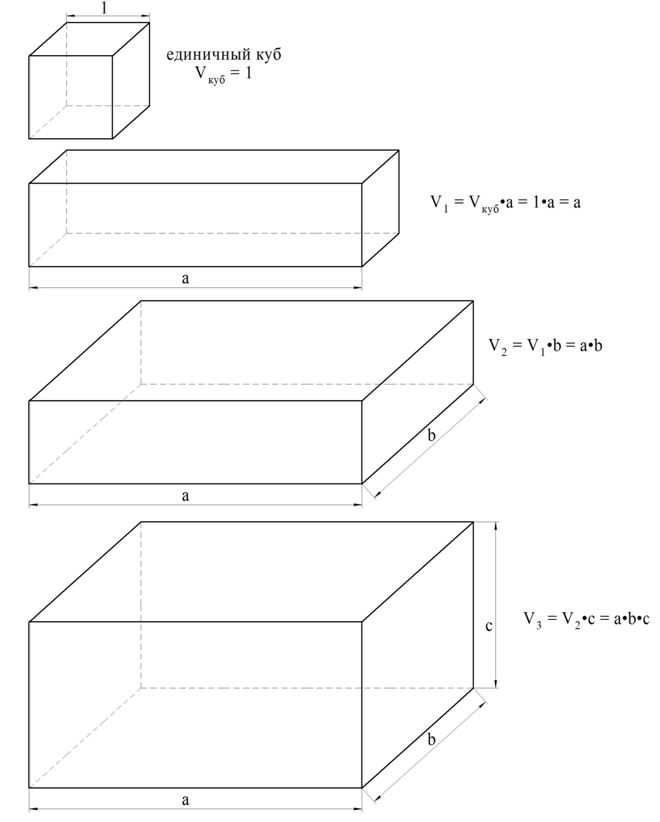
Соответственно, для расчета объема параллелепипеда используется формула

Иногда эту формулу формулируют несколько иначе: объем параллелепипеда – это произведение площади его основания на длину высоты, перпендикулярной этому основанию.

Задание. Три смежных ребра прямоугольного параллелепипеда имеют длины 9, 4 и 7 см. Каков объем параллелепипеда?

Решение. Здесь надо просто перемножить габариты параллелепипеда:

Ответ: 252 см3.

Куб можно рассматривать как прямоугольный параллелепипед с одинаковыми измерениями. Поэтому для вычисления его объема надо умножить ребро куба само на себя дважды, то есть возвести его в куб.

Задание. Вычислите объем куба с ребром 8 метров.

Решение. Просто возводим сторону ребро куба в третью степень:

Задание. Если ребро куба увеличить на 2 дм, то его объем вырастет на 98 дм3. Какова длина ребра этого куба?

Решение. Обозначим длину ребра буквой х. Тогда объем куба будет составлять х3 дм. Если ребро увеличить на 2 дм, то оно будет иметь длину х + 2 дм, и тогда объем куба будет равен уже (х + 2)3 дм. Условие задачи можно записать в виде уравнения:

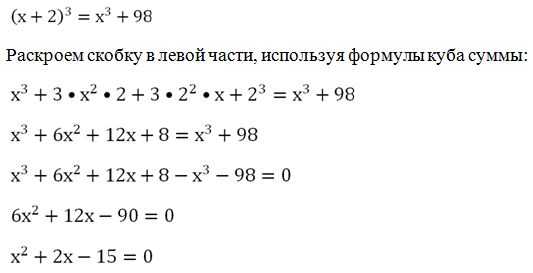
Это квадратное уравнение имеет два корня, 3 и (– 5), что можно проверить с помощью теоремы Виета. Корень х = – 5 не имеет геометрического смысла, поэтому остается ответ х = 3.

Ответ: 3 дм.

Далее рассмотрим перевод единиц измерения объема. Например, как перевести 1 м3 в кубические сантиметры? Рассмотрим куб с ребром 1 м. Ясно, что его объем будет равен 1 м3. С другой стороны, можно сказать, что длина ребра этого куба составляет 100 см:

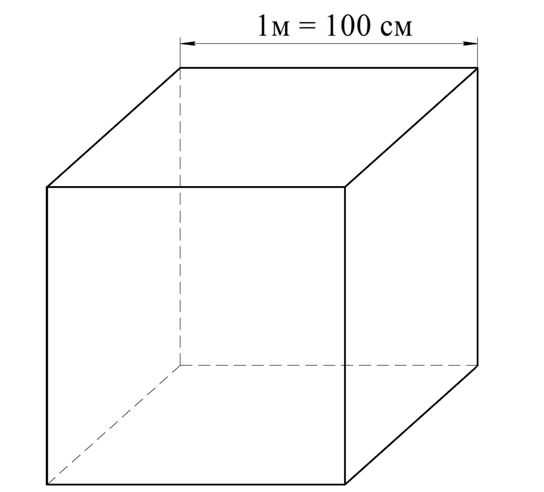
Тогда объем этого куба можно посчитать так:

Аналогично можно переводить и другие единицы измерения.

Рекомендации по использованию полученного результата

После вычисления объема куба и нахождения его ребра, вы можете использовать эту информацию в различных практических целях. Вот несколько рекомендаций, как применить полученные результаты:

1. Планирование пространства

Если вам необходимо спланировать пространство для размещения предметов или мебели, зная размеры куба, вы сможете определить, поместится ли он в выбранное вами место. Таким образом, вы сможете избежать проблем с нехваткой места или наоборот, избыточным пространством.

2. Расчет материалов

Если вы планируете строительство или ремонт, зная размеры ребра куба, вы можете легко рассчитать необходимое количество материалов, таких как плитка, ламинат или обои. Это поможет избежать излишеств или недостатка материалов, что может привести к дополнительным затратам времени и денег.

3. Создание упаковки

Если вам необходимо сделать упаковку для какого-либо товара или подарка, вычисленный размер куба поможет вам определить высоту, ширину и длину упаковки, чтобы она точно соответствовала размерам товара. Таким образом, вы сможете создать идеальную упаковку, которая обеспечит надежную защиту товара.

4. Определение вместимости

Если вам нужно знать вместимость какого-либо объекта или емкости, вы можете использовать ребро куба для определения объема. Например, если вам нужно узнать, сколько воды может вместить ведро или бассейн, вычислите объем куба и сможете точно определить вместимость объекта.

5. Архитектурное планирование

Архитекторы и дизайнеры могут использовать полученный результат для планирования архитектурных объектов, создания моделей или расчета пространства для размещения мебели. Зная размеры куба, вы сможете создать более точные и эффективные проекты, которые соответствуют требованиям заказчика.

Используя эти рекомендации, вы сможете максимально эффективно использовать полученный результат и применить его для решения различных практических задач.

Куб и его свойства

В настоящее время видеоуроки нельзя просматривать или распространять среди студентов.

Чтобы получить доступ к этому и другим видеоурокам из комплекта, добавьте его в свой личный кабинет через покупку в каталоге.

Конспект урока “Куб и его свойства”

На предыдущем уроке мы узнали о таких многогранниках, как Прямоугольный параллелограмм..

Решив задачу со спичками, мы получили геометрическую фигуру под названием пирамида.

Перед этим вас познакомят и с другими многогранниками. Теперь вернемся к параллелепипеду.

Таким образом, поверхность параллелепипеда состоит из шести прямоугольников. Эти прямоугольники называются лица параллелограмм.

Обратите внимание, что два соседних прямоугольника имеют общую сторону, которую мы называем край прямоугольного параллелепипеда. Концы ребер называются вершины прямоугольного параллелепипеда

Таким образом, прямоугольный параллелепипед имеет 6 граней, 12 ребер и 8 вершин.

Обратите внимание, что хотя многогранники различны, поверхность каждого многогранника состоит из правильных многоугольников, которые мы называем гранями многогранника. Два соседних правильных многоугольника имеют общую сторону – ребро многогранника

Концы ребер являются вершинами многогранника.

Этот многогранник называется октаэдр. Он имеет 8 ребер, которые являются треугольниками, 12 граней и 6 вершин.

Куб – это прямоугольный параллелограмм, у которого все ребра равны

Обратите внимание, что мы рисуем пунктирные линии для граней куба, которые не видны. Это дает полное представление о фигуре и ее положении относительно нас

Все грани куба – равные квадраты. Поверхность куба состоит из 6 равных квадратов. Убедитесь, что грани напротив друг друга не имеют общих ребер. Эти называются напротив.

лицакоторые имеют общее ребро, называются прилегающая территория.

Теперь давайте проведем небольшой эксперимент. Возьмите коробку, имеющую форму куба. Мы раскрываем его, затем разрезаем вдоль четырех вертикальных ребер, а затем разворачиваем.

Форма, которую мы имеем, называется Разворачивание куба.. Он состоит из 6 равных квадратов.

Фигуры ниже также являются взрывающимися кубами.

Используя каждую из разверток, вы можете сделать модель куба. Для этого выполните следующие действия. Нарисуйте чертеж куба на листе бумаги. Выключите его. Согните его вдоль секций, соответствующих граням куба, и склейте.

Теперь нарисуйте отрезок, который соединит самые удаленные вершины куба. Мы называем эти вершины противоположными вершинами.

Отрезок, соединяющий две противоположные вершины куба, называется диагональю куба.

Теперь давайте решим несколько задач.

Проблема первая. Определите, какой кубик мы получим из данной сборки.

Давайте представим, какие грани куба являются смежными, то есть имеют общее ребро, и сравним с предложенными вариантами, чтобы найти правильный. Для этого нам удобнее всего сравнивать лица, которые отличаются в зависимости от рисунка на них

Обратите внимание на лицо с желтым треугольником и лицо с зеленым треугольником. Конечно, при сборке куба эти грани будут примыкать друг к другу

Следовательно, при различных поворотах куба возможны четыре варианта взаимного расположения этих граней.

Давайте теперь сравним четыре предложенных варианта. Сразу видно, что первый вариант неверен. Второй вариант неверен. Конечно, третий вариант также неверен. Однако вариант четыре является правильным, поскольку грани, на которых изображены треугольники, правильные. В этом случае на верхней поверхности должен быть синий круг. Это правильно.

Таким образом, мы выяснили, что из данного расширения получится куб с числом 4.

Вы можете решить эту проблему другим способом. Вы можете нарисовать этот контур на бумаге. Удобнее это делать на листе бумаги с квадратами, тогда вам не придется пользоваться линейкой, чтобы соблюсти размеры куба. Вы просто посчитаете количество квадратов, которое вам необходимо.

Затем вам нужно будет раскрасить и вырезать нарисованный контур. Затем скатайте его в кубик и склейте. После этого вы можете легко сравнить полученный куб с любым из предложенных вариантов и выбрать подходящий.

Вторая задача. Модель куба с длиной ребра 4 см была окрашена серой краской и разрезана вдоль ребра на кубики с длиной ребра 1 см. Сколько кубиков получилось: а) окрашенных по трем граням; б) окрашенных по двум граням?

Третья проблема. На рисунке показан скелет куба. Затем нарисуйте видимые грани так, чтобы на куб можно было смотреть: a) сверху слева; b) снизу справа.

Проблема четвертая .. Фигура, показанная на рисунке, состоит из пяти кубиков. Какой формы фигура, если смотреть на нее: a) спереди; b) слева; c) сверху?