Геометрия

Инструкция:

• В первую очередь надо определиться, какая формула площади куба применима в конкретном случае . Для этого нужно посмотреть на заданные параметры фигуры. Какие данные известны: длина ребра, объем, диагональ, площадь грани. В зависимости от этого выбирается формула.
• Если по условиям задачи известна длина ребра куба, то достаточно применить простейшую формулу для нахождения площади. Известно практически каждому, что площадь квадрата находится умножением длин двух его сторон. Грани куба — квадраты, следовательно, площадь его поверхности равна сумме площадей этих квадратов. У куба шесть граней, поэтому формула площади куба будет выглядеть так: S=6*х 2. Где х — длина ребра куба.
• Допустим, что ребро куба не задано, но известен. Так как объем данной фигуры вычисляется возведением в третью степень длины его ребра, то последнюю можно получить достаточно легко. Для этого из числа, обозначающего объем, необходимо извлечь корень третей степени. Например, для числа 27 корнем третей степени будет число 3. Ну а что делать дальше, мы уже разбирали. Таким образом, формула площади куба при известном объеме также существует, где вместо х стоит корень третей степени из объема.
• Бывает, что известна только длина диагонали. Если вспомнить теорему Пифагора, то можно легко вычислить длину ребра. Здесь достаточно базовых знаний. Полученный результат подставляется в уже известную нам формулу площади поверхности куба: S=6*х 2.
• Подводя итог, стоит отметить, что для правильных вычислений нужно узнать длину ребра. Условия в задачах встречаются самые разные, поэтому следует научится выполнять сразу несколько действий. Если известны другие характеристики геометрической фигуры, то с помощью дополнительных формул и теорем можно вычислить ребро куба. И уже на основании полученного результата посчитать результат.

Под кубом подразумевается правильный многогранник, у которого все грани образованы правильными четырехугольниками — квадратами. Для того, чтобы найти площадь грани любого куба, не потребуется тяжелых расчетов.

Структура и форма куба

Куб — это геометрическое тело, являющееся одним из пяти правильных многогранников. Куб обладает следующими характеристиками:

• У куба 6 граней. Каждая грань куба является квадратом, который имеет одинаковую длину всех его сторон.
• Длина стороны куба определяет размеры всех его граней. Если сторона куба равна a, то площадь каждой его грани равна a2.
• Углы между гранями куба равны 90 градусам. Куб является прямоугольным параллелепипедом.
• Объем куба равен a3, где a — длина стороны куба.
• Диагональ куба — это отрезок, соединяющий противоположные вершины куба с длиной a√3.

Структура и форма куба делают его одним из наиболее изучаемых и распространенных геометрических тел. Кубы применяются в разных сферах жизни, например, в архитектуре, геометрии, игрушках и в науках, связанных с геометрией и пространством.

Как найти периметр грани куба?

Периметр грани куба — это сумма длин всех его ребер, которые лежат в одной плоскости. Каждая грань куба является квадратом, поэтому периметр грани куба можно найти, умножив длину одной стороны квадрата на 4.

Если у вас есть данные о длине одной ребер куба, то вы можете найти длину одной стороны квадрата грани, разделив длину ребра на √2. Затем умножьте длину одной стороны на 4 для нахождения периметра грани.

Таким образом, зная длину стороны квадрата грани куба, вы можете легко найти его периметр. Эту формулу можно использовать как для поиска периметра грани куба, так и для решения других задач, связанных с кубами.

Что такое сторона куба

Куб — это геометрическое тело, которое имеет форму прямоугольного параллелепипеда, все грани которого равны между собой. Таким образом, сторона куба — это отрезок прямой линии, который соединяет две противоположные вершины куба.

Важно отметить, что все стороны куба имеют одинаковую длину. Куб отличается от прямоугольного параллелепипеда тем, что у него все стороны равны, в то время как у прямоугольного параллелепипеда могут быть различные длины сторон

Длина стороны куба может быть измерена с помощью линейки или другого измерительного инструмента. Она обычно выражается в единицах измерения, таких как сантиметры, метры или дюймы.

Строить кубы и измерять их стороны является одной из основных задач в геометрии. Знание длины стороны куба позволяет решать множество задач, связанных с этим геометрическим телом.

Важность понимания стороны куба

Сторона куба является одним из основных понятий в геометрии и математике

Понимание стороны куба и его свойств имеет большую важность в различных областях знаний и практической деятельности

1. Геометрия:

• Сторона куба – это одна из шести равных граней куба, являющаяся прямоугольником
• Понимание стороны куба помогает в изучении геометрических форм и их взаимосвязей

2. Математика:

• Сторона куба используется для вычислений объема, площади поверхности и диагонали куба
• Определение стороны куба позволяет проводить геометрические преобразования и решать задачи на построение

3. Архитектура и строительство:

Знание сторон куба важно при проектировании и строительстве зданий и сооружений
Расчет размеров и объемов кубических элементов помогает в оптимизации использования пространства и рациональном планировании

4. Программирование и компьютерная графика:

• Сторона куба является основным параметром для создания трехмерных моделей и визуализации объектов
• Понимание размеров и пропорций сторон куба позволяет создавать реалистичные и точные визуализации

В итоге, понимание стороны куба и умение работать с ним являются важными навыками в различных областях науки и практики. Благодаря этому понятию, возможно решать сложные задачи в геометрии, математике, архитектуре, строительстве, программировании и компьютерной графике.

Классификация двумерных полиэдров

Наша задача состоит в том, чтобы связать символы Шлефли {n,m} с количеством вершин, ребер и граней. Для примера рассмотрим тетраэдр и попытаемся выяснить зависимость.

1. У тетраэдра 4 грани, в каждой из которых три угла. Т.о., если умножить 4 грани на 3 угла получим 12 чего-то там, что в два раза больше, чем количество его ребер (каждое из них посчитано дважды).

2. В каждой вершине сходятся m=3 граней. Если умножить 4 вершины на 3 грани получим 12 чего-то там, что в два раза больше количества ребер (их так же считали дважды

В качестве упражнения можно посчитать для куба. В каждой из 6 граней 4 угла, отсюда (6*4)/2 = 12 ребер. В каждой из 8 вершин сходятся 3 грани, что даёт (8*3)/2 = 12 ребер.

Получили три уравнения с тремя неизвестными, которые будем сейчас решать, чтобы получить в чистом виде зависимость от составляющих символа Шлефли:

Такую систему уравнений удобно решить, воспользовавшись параметризацией через некое t. Во второй строчке подставили данные в уравнение Эйлера и затем привели дроби к одному знаменателю

Из очевидных соображений, что t > 0 , мы должны потребовать положительности знаменателя. Остается в целых числах решить соответствующее неравенство:

Не только лишь все натуральные числа при умножении дают результат, меньший 4, поэтому у нас не так много работы:

А теперь вспомните рисунок с символами Шлефли для платоновых тел! Как видите, мы получили одно и то же с помощью решения обычной системы уравнений! Алгебраизация — один из самых мощных способов исследования окружающего нас мира.

Математика. 4 класс

Конспект урока

Математика, 4 класс

Перечень вопросов, рассматриваемых в теме:

Как распознавать и называть куб, его грани, ребра, вершины.?

Грани куба – это стороны куба, которые представляют собой квадрат.

Ребра куба – это стороны граней куба.

Вершина куба— это точка, где сходятся три грани или точка, в которой сходятся три ребра куба.

Площадь фигуры – это часть плоскости, ограниченная замкнутой ломаной или кривой линией.

Основная и дополнительная литература по теме урока:

Теоретический материал для самостоятельного изучения

Подумайте, на какие две группы можно разделить фигуры?

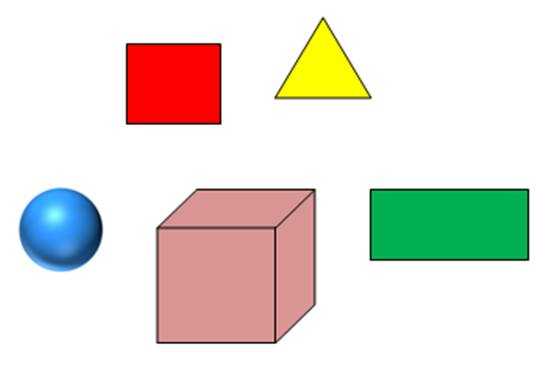
Верно, на плоские и объемные.

Назовите плоские геометрические фигуры.

Верно, квадрат, треугольник, прямоугольник.

Объемные фигуры называются – геометрическими телами.

Вы видите геометрическое тело «шар» и геометрическое тело «куб».

Внимательно посмотрите и скажите, из какой фигуры состоит поверхность куба?

Верно, поверхность куба состоит из квадратов, их называют гранями куба.

Посчитайте, сколько граней у куба.

Правильно, у куба 6 граней.

Стороны граней (квадратов) называют ребрами куба.

Посчитайте, сколько ребер у куба?

Верно, у куба 12 ребер.

Вершины граней – это вершины куба.

Посчитайте, сколько вершин у куба.

Правильно, у куба 8 (восемь) вершин.

Таким образом, у куба 6 граней, 12 ребер, 8 вершин.

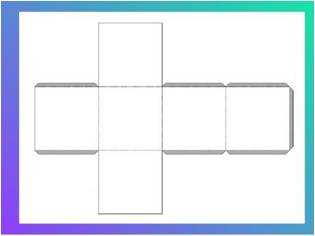
Для того чтобы изготовить модель куба необходимо построить развертку куба.

И какого бы куб ни был роста, сшить костюм для него очень просто. Для начала же, сделав разметку, изготовьте раскройку – развертку. Шесть квадратов! Нехитрое дело. Но расклеить их надо умело.

Куб в жизни человека.

Где можно встретить куб? Здания чаше всего имеют кубическую форму, так что можно просто выглянуть в окно, и вы сразу увидите куб.

Самая знаменитая игрушка-головоломка «кубик-рубик».

Кристаллы поваренной соли имеют форму куба.

Выполним несколько тренировочных заданий.

1. Найдите и напишите номер того куба, который сделан из данной развёртки.

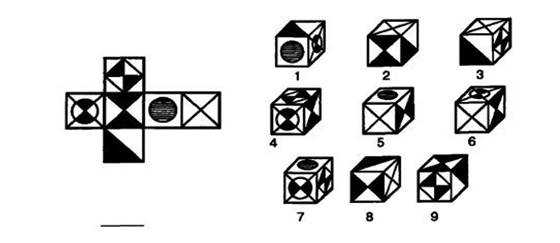
Правильный вариант/варианты (или правильные комбинации вариантов): 4

2. Выберите правильное утверждение.

а) площадь круга больше площади квадрата;

б) площадь круга меньше площади квадрата;

в) площади фигур равны.

Правильные варианты: б) площадь круга меньше площади квадрата.

Источник

Элементы композиции куба

Зная, что у куба 12 ребер, 8 вершин и 6 граней, см. следующее изображение.

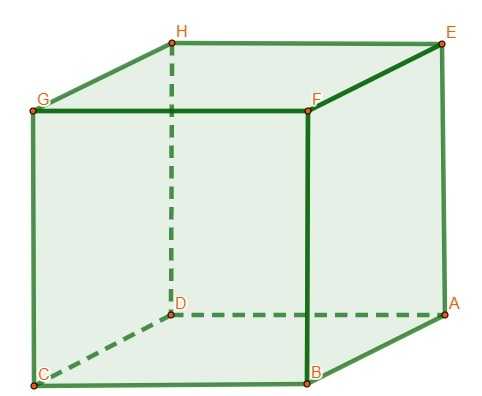
• A, B, C, D, E, F, G и H — вершины куба.

• \(\overline{AB},\ \overline{AD},\ \overline{AE},\ \overline{BC},\ \overline{BF},\ \overline{CD,\ }\overline{CG}, \ \overline{DH,\ }\overline{HG},\ \overline{EH}\overline{,\ EF},\ \overline{FG}\) являются ребрами куба.

• ABCD, ABFE, BCFG, EFGH, ADHE, CDHG — грани куба.

Куб состоит из 6 квадратных граней, поэтому все его ребра равны. Поскольку его ребра имеют одинаковую меру, куб классифицируется как многогранник Правильный или твердый Платон вместе с тетраэдром, октаэдром, икосаэдром и додекаэдром.

Не останавливайся сейчас… После рекламы есть еще

Геометрические фигуры. Куб.

Куб или правильный гексаэдр – это правильный многогранник, у которого все грани это квадраты.

Куб является частным случаем параллелепипеда и призмы. 4 сечения куба имеют вид правильных

шестиугольников — это сечения через центр куба перпендикулярно 4-м главным диагоналям.

В кубе насчитывается шесть квадратов. Все вершины куба являются вершинами 3-х квадратов. То есть,

сумма плоских углов у каждой вершины = 270º.

Число рёбер примыкающих к вершине – 3;

Предположим, что а – длина стороны куба, а d — диагональ, тогда:

Диагональ куба – это отрезок, который соединяет 2 вершины, которые симметричны относительно центра

Свойства куба.

4 сечения куба имеют вид правильных шестиугольников — они проходят сквозь центр куба

перпендикулярно четырём его главным диагоналям.

В куб вписывают тетраэдр 2-мя способами. В любом из них 4-ре вершины тетраэдра всегда

совмещены с 4-мя вершинами куба и каждое из шести ребер тетраэдра принадлежат граням куба. В 1-м

случае каждая вершина тетраэдра принадлежит граням трехгранного угла, вершиной совпадающего с одной

из вершин куба. Во 2-м случае ребра тетраэдра, которые попарно скрещиваются принадлежат попарно

противоположным граням куба. Такой тетраэдр будет правильным, а его объём будет составлять треть от

В куб вписывают октаэдр, при этом все 6 вершин октаэдра совмещаются с центрами 6-ти граней

Куб вписывают в октаэдр, при этом все 8 вершин куба располагаются в центрах 8-ми граней

В куб вписывают икосаэдр, притом 6 взаимно параллельных рёбер икосаэдра располагаются на

6-ти гранях куба, следующие 24 ребра располагаются внутри куба. Каждая из 12 вершин икосаэдра

располагается на 6-ти гранях куба.

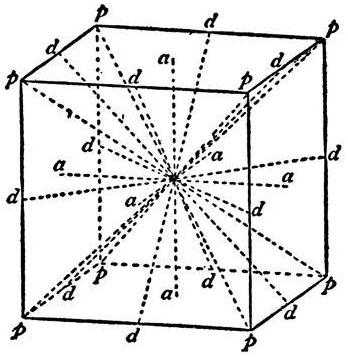
Элементы симметрии куба.

Ось симметрии куба может пролегать или сквозь середины ребер, которые

параллельны, не принадлежащих одной из граней, или сквозь точку

пересечения диагоналей противолежащих граней. Центром симметрии

куба будет точка пересечения диагоналей куба.

Сквозь центр симметрии куба проходят 9 осей симметрии.

Плоскостей симметрии у куба тоже 9, они пролегают или

через противолежащие ребра (таких плоскостей 6), или

через середины противолежащих ребер (таких 3).

Источник

Adblockdetector

Примечания[править | править код]

1. ↑ Древнегреческо-русский словарь Дворецкого «κύβος». Дата обращения: 7 октября 2018. Архивировано из оригинала 28 декабря 2014 года.
2. ↑ Справочник по элементарной математике / Выгодский М. Я.. — М.: АСТ, Астрель, 2006. — С. 383−384.
3. ↑ Англо-русский словарь математических терминов / под ред. П. С. Александрова. — 2-е, исправл. и дополн. изд.. — М.: Мир, 1994. — С. 129. — 416 с. — ISBN 5-03-002952-4.
4. ↑ Гексаэдр // Математическая энциклопедия / И. М. Виноградов. — 1977. — Т. 1.
5. ↑ Энциклопедия элементарной математики. Книга 4 (геометрия) / П. С. Александров, А. И. Маркушевич, А. Я. Хинчин. — ГИФМЛ, 1963. — С. 426.

Что такое грань куба?

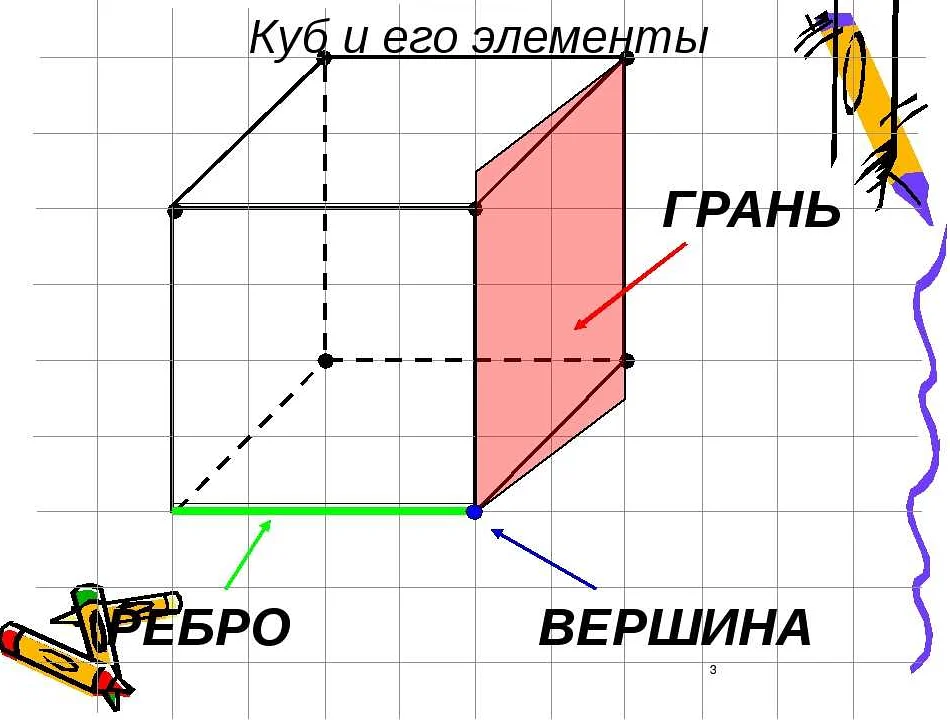
Грань куба — это плоская поверхность, которая образует его боковые стороны. Куб — это трехмерный геометрический объект, имеющий шесть граней, которые являются квадратами одинаковой площади.

Грани куба составляют прямые углы друг с другом и параллельны двум основным плоскостям. Каждая грань имеет три ребра и соединяется с другими гранями в вершинах куба.

Грани куба используются в различных математических задачах, например, для вычисления его объема, площади поверхности или длины его ребер. Также грани куба могут быть использованы для создания дизайна или архитектурных проектов.

Определение куба

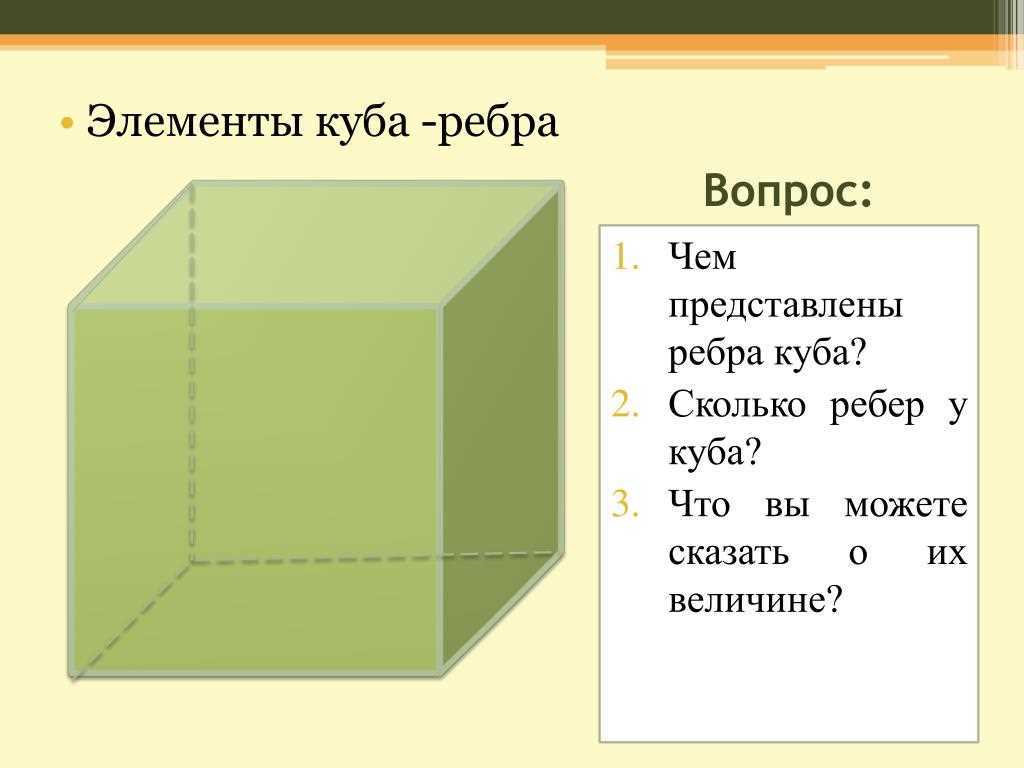
Куб — это геометрическое тело, которое имеет все стороны одинаковой длины и все грани являются квадратами. Куб является одним из пяти правильных многогранников, вместе с тетраэдром, октаэдром, додекаэдром и икосаэдром.

Основные характеристики куба:

• Количество граней: у куба 6 граней;
• Количество ребер: у куба 12 ребер;
• Количество вершин: у куба 8 вершин;
• Углы: все углы куба прямые;
• Диагонали: в кубе есть три основные диагонали, которые проходят через центры противоположных граней: пространственная диагональ, горизонтальная диагональ и вертикальная диагональ.

Куб является важной фигурой в геометрии и имеет множество применений в нашей повседневной жизни, включая строительство, дизайн, математику и другие области

Краткое описание куба

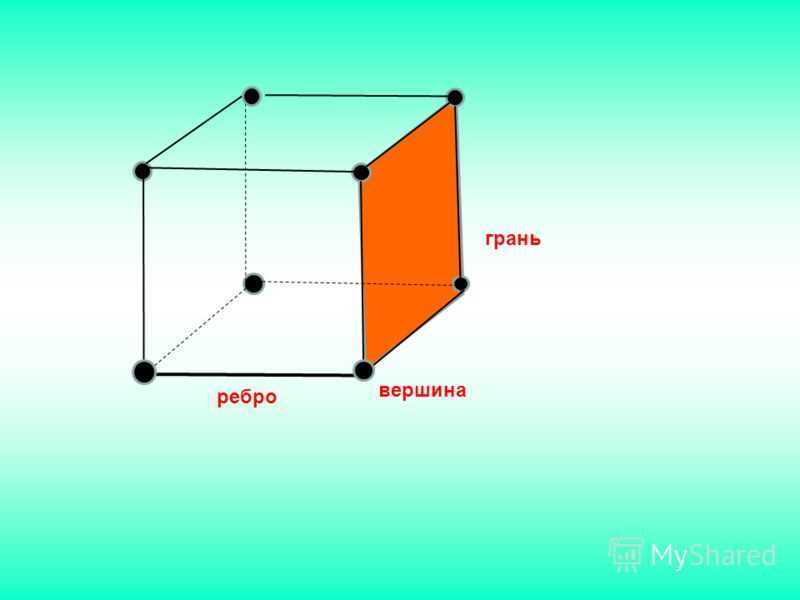
Куб является одним из самых известных геометрических тел. Это трехмерная фигура, которая обладает рядом особенностей.

Основные характеристики куба:

• У куба 6 граней, которые являются квадратами.
• Все грани куба равны по площади и форме.
• У куба 12 ребер, которые соединяют грани.
• У куба 8 вершин, где сходятся ребра.
• Все ребра и грани куба перпендикулярны друг другу.

Куб является простейшим из всех правильных многогранников. Он обладает симметрией и равномерностью. Благодаря своим особенностям и простой форме, куб находит широкое применение в различных сферах, включая геометрию, математику, архитектуру, игры и дизайн.

Свойства куба

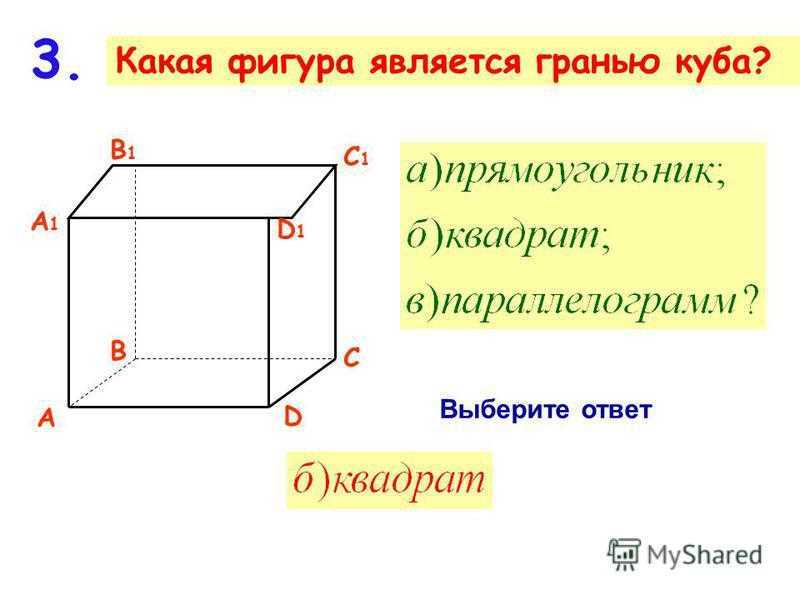
1. Количество граней: Куб имеет шесть граней.

2. Равные стороны: Все стороны куба равны между собой. Каждая сторона куба является квадратом.

3. Равные углы: Все углы куба равны между собой и равны 90 градусам.

4. Симметричность: Куб обладает симметрией, что означает, что его грани и углы можно перевернуть или повернуть без изменения его формы.

5. Диагонали: Диагонали куба соединяют противоположные вершины куба, образуя пересечения внутри куба.

6. Объем и площадь: Объем куба можно вычислить, возведя в квадрат длину любой стороны. Площадь поверхности куба равна шести разам квадрату длины любой из его сторон.

7. Куб в трехмерном пространстве: Куб является одним из основных геометрических тел в трехмерном пространстве и может служить моделью для различных строений и объектов.

8. Связь с другими геометрическими фигурами: Куб связан с другими геометрическими фигурами, такими как квадрат, прямоугольник, треугольник и параллелограмм. Куб также является частным случаем прямоугольного параллелепипеда.

Примеры кубов в реальной жизни

Кубы – это геометрические фигуры, которые имеют все стороны равными между собой и углы правильные. Вот несколько примеров, где мы можем встретить кубы в реальной жизни:

• Игральные кости – они имеют форму куба и обычно используются в настольных играх, где случайность играет важную роль.
• Кубики рубика – это головоломка, состоящая из множества маленьких кубиков, которые можно поворачивать таким образом, чтобы их грани совпали.
• Кубик для детской игры «Пирамидка» – это игрушка для развития мелкой моторики у детей, в которой нужно правильно собрать кубики один на другой.

Также кубы используются в архитектуре и строительстве. Возьмем в пример строительные блоки, которые могут быть кубической формы. Они используются для постройки стен, фундамента и других конструкций.

Таблицы и шкафы могут иметь форму куба, особенно если они имеют одинаковые стороны и грани.

В мире техники, кубы можно встретить в виде микрочипов или кристаллов. Они могут быть использованы, например, в компьютерах или сотовых телефонах, чтобы обеспечивать устойчивость и надежность работы электронных устройств.

В заключение, кубы находят применение во многих сферах человеческой деятельности, от игрушек и игр до архитектуры и техники. Их форма обладает определенными свойствами, которые делают их полезными и удобными для использования в различных областях.

Как найти длину ребра куба с известной площадью грани?

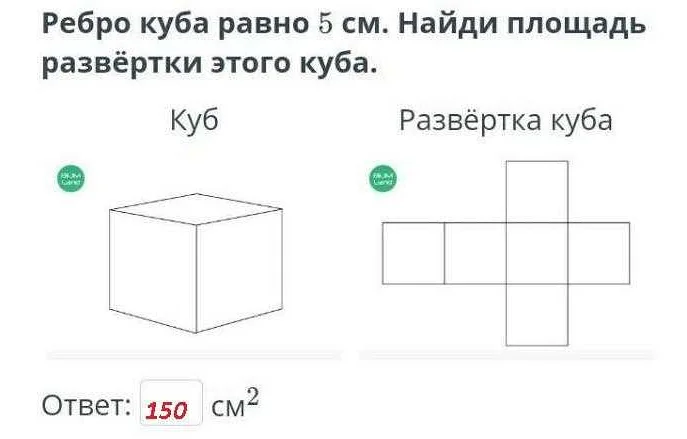
Для того чтобы найти длину ребра куба с известной площадью грани, необходимо воспользоваться формулой, которая связывает площадь грани и длину ее ребра. Формула звучит следующим образом:

Длина ребра куба равна квадратному корню из площади его грани:

а = √S

Где а — длина ребра куба, а S — площадь его грани.

Например, если известно, что площадь грани куба равна 25 квадратных сантиметров, то длина его ребра равна:

a = √25 = 5

Таким образом, длина ребра куба с известной площадью грани будет равна 5 сантиметров.

Эта формула очень проста и позволяет легко определить длину ребра куба по известной площади его грани. Она является основой для решения многих задач, связанных с кубами и их свойствами.

Формула вычисления площади куба

1. Через длину ребра

Площадь (S) поверхности куба равна произведению числа 6 на длину его ребра в квадрате.

S = 6 ⋅ a2

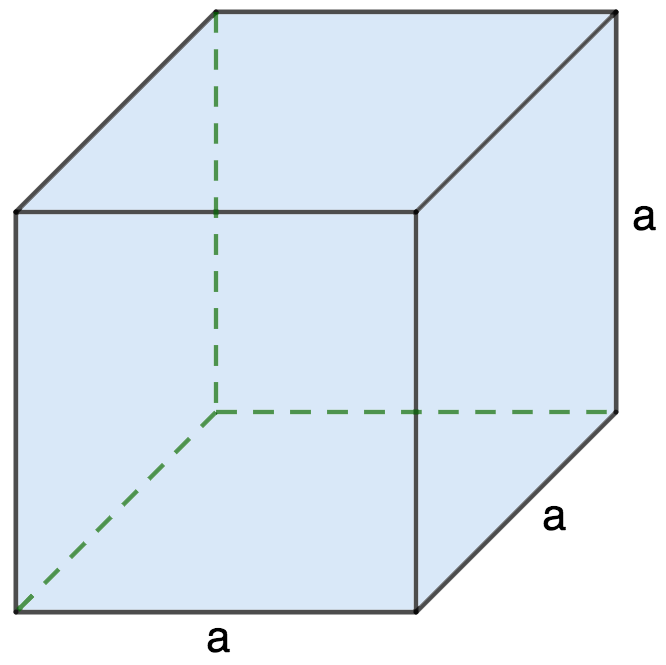
Данная формула получена следующим образом:

• Куб – это правильная геометрическая фигура, все грани которого являются равными квадратами с длиной стороны a (одновременно является ребром куба).
• Площадь каждой грани считается так: S = a ⋅ a = a2.
• Всего у куба 6 граней, а значит, площадь его поверхности равняется шести площадям одной грани: S = 6 ⋅ a2.

2. Через длину диагонали грани

Сторона любой грани куба (ребро) может быть рассчитана через длину ее диагонали по формуле: a=d/√2.

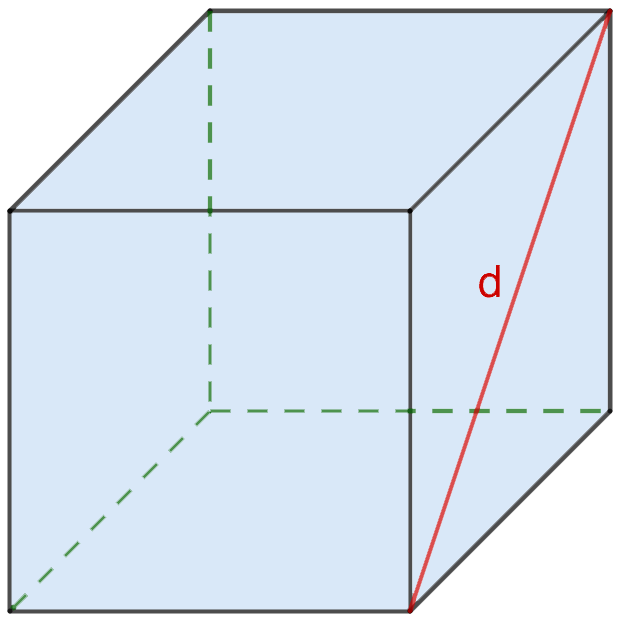
Это значит, что вычислить площадь поверхности фигуры можно так:

S = 6 ⋅ (d/√2)2

Примеры заданий из ЕГЭ

Они используются в части В, то есть там, где нужно выполнить развернутое решение задания. Просто выбрать ответ здесь не удастся. Поэтому придется знать формулы и уметь их применять в различных ситуациях.

Первая группа заданий. В ней известна длина диагонали куба. Требуется вычислить его объем или узнать площадь поверхности.

К примеру, известная величина может быть равна единице. Тогда, чтобы узнать объем и площадь, нужно воспользоваться формулами № 1 и 3. Но в них идет речь о ребре, а дана диагональ. Потребуется записать еще одну формулу.

Если посмотреть на чертеж куба и проведенную в нем диагональ, то можно увидеть, что образуется прямоугольный треугольник. Один его катет совпадает с ребром, второй — с диагональю грани, а гипотенузой оказывается диагональ куба.

Тогда можно записать теорему Пифагора: квадрат гипотенузы (d 2) равен квадрату перового катета (а 2), сложенному с квадратом второго (а√2) 2 . После выполнения преобразований получается, что ребро куба а так связано с диагональю, что равно d, деленному на корень квадратный из 3.

Теперь можно начала узнать ребро, а потом подсчитать объем и площадь. В конкретной задаче а=1/√3=(√3)/3. Тогда объем получается равным (√3)/9. Площадь же — два.

Вторая группа заданий. Обратная предыдущей, когда известны площадь или объем, а требуется вычислить значение диагонали куба.

Примером может служить задача, в которой известна площадь поверхности, и она равна 8. Необходимо будет воспользоваться формулой №3 и той зависимостью, которая выведена в предыдущей задаче.

Сначала потребуется узнать длину ребра. Она равна квадратному корню из частного S на 6. После подстановки известной величины а=√(8/6)=√(4/3). Теперь осталось вычислить диагональ куба, возведя это число в квадрат и умножив его на 3. Получится 2.