Группы симметрий квадрата и куба. реферат. математика. 2009-01-12

Несобственная ось симметрии

Простейшая зеркально – поворотная ось $S_1$ идентична ортогональной ей плоскости симметрии $S_1=\sigma.$

Пример 2

Зеркально – поворотные оси хлорфторметана более высокого порядка можно расценивать как сочетание вращения на угол $2\pi/n$ c последующим отражением в плоскости, которая является перпендикулярной оси вращения.

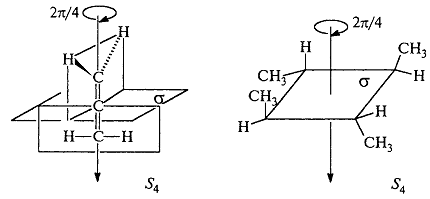
Аллен и изомер 1,2,3,4-тетраметилциклобутан обладают зеркально – поворотной осью $S_4$:

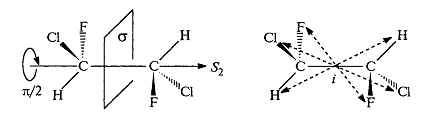
1,2-дихлор-1,2-дифторэтан имеют ось $S_2$, совпадающую со связью $C-C$. Операция $S_2$ идентична инверсии в центре симметрии, который расположен посередине связи $C-C$:

Свойства правильных многогранников

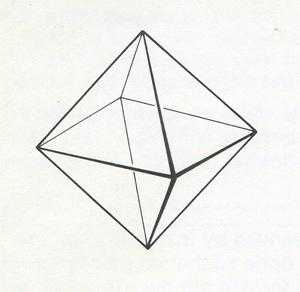
Существует 5 разных типов правильных многогранников:

Куб (гексаэдр) — у него плоский угол при вершине составляет 90°. Он имеет 3-гранный угол. Сумма плоских углов у вершины составляет 270°.
Тетраэдр — плоский угол при вершине — 60°. Он имеет 3-гранный угол. Сумма плоских углов у вершины — 180°.
Октаэдр — плоский угол при вершине — 60°. Он имеет 4-гранный угол. Сумма плоских углов у вершины — 240°.
Додекаэдр — плоский угол при вершине 108°. Он имеет 3-гранный угол. Сумма плоских углов у вершины — 324°.
Икосаэдр — у него плоский угол при вершине — 60°. Он имеет 5-гранный угол. Сумма плоских углов у вершины составляет 300°.

Площадь поверхности этих геометрических тел (S) вычисляется, как площадь правильного многоугольника, умноженная на количество его граней (G):

S = (a: 2) х 2G ctg π/p.

Подписи к слайдам:

Элементы симметрии правильных многогранников Геометрия. 10 класс.

Тетраэдр — (от греческого tetra – четыре и hedra – грань) — правильный многогранник, составленный из 4 равносторонних треугольников. Из определения правильного многогранника следует, что все ребра тетраэдра имеют равную длину, а грани — равную площадь. Элементы симметрии тетраэдра Тетраэдр имеет три оси симметрии, которые проходят через середины скрещивающихся рёбер. Тетраэдр имеет 6 плоскостей симметрии, каждая из которых проходит через ребро тетраэдра перпендикулярно скрещивающемуся с ним ребру.

Октаэдр — (от греческого okto – восемь и hedra – грань) — правильный многогранник, составленный из 8 равносторонних треугольников. Октаэдр имеет 6 вершин и 12 ребер. Каждая вершина октаэдра является вершиной 4 треугольников, таким образом, сумма плоских углов при вершине октаэдра составляет 240 ° . Элементы симметрии октаэдра Три из 9 осей симметрии октаэдра проходят через противоположные вершины, шесть — через середины ребер. Центр симметрии октаэдра — точка пересечения его осей симметрии. Три из 9 плоскостей симметрии тетраэдра проходят через каждые 4 вершины октаэдра, лежащие в одной плоскости. Шесть плоскостей симметрии проходят через две вершины, не принадлежащие одной грани, и середины противоположных ребер.

Икосаэдр – (от греческого ico — шесть и hedra — грань) правильный выпуклый многогранник, составленный из 20 правильных треугольников. Каждая из 12 вершин икосаэдра является вершиной 5 равносторонних треугольников, поэтому сумма углов при вершине равна 300 °. Элементы симметрии и косаэдра Правильный икосаэдр имеет 15 осей симметрии, каждая из которых проходит через середины противоположных параллельных ребер. Точка пересечения всех осей симметрии икосаэдра является его центром симметрии. Плоскостей симметрии также 15.Плоскости симметрии проходят через четыре вершины, лежащие в одной плоскости, и середины противолежащих параллельных ребер.

Куб или гексаэдр (от греческого hex — шесть и hedra — грань) составлен из 6 квадратов. Каждая из 8 вершин куба является вершиной 3 квадратов, поэтому сумма плоских углов при каждой вершине равна 270 0 . У куба 12 ребер, имеющих равную длину. Элементы симметрии куба Ось симметрии куба может проходить либо через середины параллельных ребер, не принадлежащих одной грани, либо через точку пересечения диагоналей противоположных граней. Центром симметрии куба является точка пересечения его диагоналей. Через центр симметрии проходят 9 осей симметрии. Плоскостей симметрии у куба также 9 и проходят они либо через противоположные ребра (таких плоскостей-6), либо через середины противоположных ребер (таких — 3).

Додекаэдр (от греческого dodeka – двенадцать и hedra – грань) это правильный многогранник, составленный из 12 равносторонних пятиугольников. Додекаэдр имеет 20 вершин и 30 ребер. Вершина додекаэдра является вершиной трех пятиугольников, таким образом, сумма плоских углов при каждой вершине равна 324 0. Элементы симметрии додекаэдра Додекаэдр имеет центр симметрии и 15 осей симметрии. Каждая из осей проходит через середины противолежащих параллельных ребер. Додекаэдр имеет 15 плоскостей симметрии. Любая из плоскостей симметрии проходит в каждой грани через вершину и середину противоположного ребра.

Развертки правильных многогранников Развертка — это способ развернуть многогранник на плоскость после проведения разрезов по нескольким ребрам. Развертка представляет собой плоский многоугольник, составленный из меньших многоугольников — граней исходного многогранника. Один и тот же многогранник может иметь несколько разных разверток.

ось симметрии — ПриМат

Условие

а) Сколько осей симметрии имеет куб? Правильная треугольная пирамида?

б)* Докажите, что если некоторый многогранник имеет $k$ осей симметрии $(k \geq 1)$, то $k$ нечетно.

Решение

а) Нетрудно указать девять осей симметрии куба. Это — прямые, соединяющие центр куба $O$ с центрами граней (их три: $Ox$, $Oy$, $Oz$ на рисунке $1$) и с серединами ребер (их шесть).

Других осей симметрии у куба нет: это можно доказать, опираясь на такое наблюдение: при любом самосовмещении куба каждая из трех осей $Ox$, $Oy$, $Oz$ должна отображаться на одну из этих же осей, причем если это само совмещение — симметрия (поворот на $180 ^\circ$) $S_l$ относительно некоторой прямой $l$, отличной от $Ox$, $Oy$ и $ Oz$, то одна из этих трех осей должна переходить сама в себя, а две остальные — друг в друга.

У правильного тетраэдра три оси симметрии — прямые, соединяющие середины его ребер. Чтобы убедиться в этом, удобно достроить тетраэдр до куба, проведя через каждое ребро тетраэдра плоскость, параллельную противоположному ребру (рис. $2$). Ясно, что любое самосовмещение тетраэдра будет также самосовмещением этого описанного куба. Из девяти осевых симметрий, отображающих куб на себя, лишь три будут переводить в себя тетраэдр.

б) Пусть дан многогранник $M$, у которого более одной оси симметрии.

Лемма $1$ Если $l$ и $m$ — оси симметрии многогранника $M$, то $S_l (m) = m’$ — также ось симметрии $М$.

В самом деле, если точки $P$ и $P’$ многогранника $M$ симметричны относительно $m$, то $S_l (P)$ и $S_l (P’)$ будут симметричными относительно $m’$. Короче: $S_{m’} = S_l O S_m O S_l$.

Лемма $2$ Если $l$ и $m$ — оси симметрии многогранника $M$, пересекающиеся в точке $O$ и перпендикулярные друг к другу, то прямая $n$, перпендикулярная им обоим и проходящая через точку $O$, также служит осью симметрии $M$.

Действительно, $S_n = S_m O S_l$. Это легко проверить, приняв данные прямые за оси координат, или построив прямоугольный параллелепипед с центром в точке $O$ и осями симметрии $l$, $m$, $n$ с произвольной вершиной $P$ (рис. $3$).

Леммы $1$ и $2$ позволяют, фиксировав какую-то одну ось симметрии $l$, разбить все остальные на пары: если $m$ удовлетворяет условия леммы $2$, то пару с ней образует $n$, а если нет, то $m’ = S_l(m) \ne m$. Отсюда сразу следует утверждение задачи б).

Возникает естественный вопрос: какое вообще (конечное) множество прямых может быть множеством всех осей симметрии некоторого многогранника?

Различные примеры даются множеством осей симметрии $n$-угольной правильной призмы (здесь количество осей $p=n$ при $n$ нечетном и $p=n+1$ при $n$ четном), тетраэдра (или прямоугольного параллелепипеда с разными ребрами, $p=3$), куба (или октаэдра $p=9$) и додекаэдра (или икосаэдра, $p=15$). Попробуйте доказать, что других множеств осей симметрии (состоящих более чем из одной прямой) не бывает. Конечно, тут не обойтись без такой очень полезной леммы, которую многие читатели применили и в решении задачи б).

Лемма $3$ Оси симметрии любого многогранника пересекаются в одной точке.

Предположим, что $l$, $m$ — непересекающиеся оси симметрии многогранника $M$. Пусть $n$ — общий перпендикуляр $l$, $m$; рассмотрим прямоугольную систему координат с началом в точке $O = l \cap n$, с осью $Oz$ направленной по лучу $OA$, где $A = n \cap m$; пусть $|OA| = a$. Тогда при симметрии относительно оси $l$ координата $z$ любой точки переходит в $(-z)$, а при симметрии относительно $m$ — в $(2a-z)$. Поэтому при композиции этих двух симметрий $z$ изменяется на $2a$. Повторяя эту композицию достаточное число раз, мы «выгоним» любую точку за пределы многогранника $M$. Противоречие!

Вот еще более короткое доказательство леммы $3$ (правда, использующее понятие, заимствованное из механики): пусть $O$ — центр масс одинаковых грузиков, помещенных в вершинах многогранника $M$; ясно, что при любом самосовмещении многогранника $M$ грузики лишь меняются местами, поэтому точка $O$ переходит в себя; в частности, все оси симметрии многогранника $M$ проходят через точку $O$.

Н. Васильев, В. Сендеров, А. Сосинский

Общие сведения о правильных многогранниках

По мнению многих, правильные многогранники, или как их еще называют Платоновы тела, обладают неповторимыми свойствами. С этими объектами связано несколько научных гипотез. Когда начинаешь изучать данные геометрические тела, понимаешь, что практически ничего не знаешь о таком понятии, как правильные многогранники. Презентация этих объектов в школе не всегда проходит интересно, поэтому многие даже и не помнят, как они называются. В памяти большинства людей остается только куб. Ни одни тела в геометрии не обладают таким совершенством, как правильные многогранники. Все названия этих геометрических тел произошли из Древней Греции. Они означают количество граней: тетраэдр — четырехгранный, гексаэдр — шестигранный, октаэдр — восьмигранный, додекаэдр — двенадцатигранный, икосаэдр — двадцатигранный. Все эти геометрические тела занимали важнейшее место в концепции Платона о мироздании. Четыре из них олицетворяли стихии или сущности: тетраэдр — огонь, икосаэдр — воду, куб — землю, октаэдр — воздух. Додекаэдр воплощал все сущее. Он считался главным, поскольку был символом мироздания.

Группа изометрий

Группа изометрий куба, обозначенная O _h , и подгруппа его положительных изометрий (его поворотов ), обозначенная O, также называются октаэдрическими группами симметрии , потому что они такие же, как у его двойственного многогранника , l ‘ правильного октаэдра. .

Куб — один из самых симметричных многогранников:

3 оси вращения четвертого порядка: оси, проходящие через центр двух противоположных граней;
6 осей вращения 2-го порядка: оси, проходящие через середину двух противоположных граней;
4 оси вращения третьего порядка: оси, проходящие через две противоположные вершины;
относительно центра куба;
9 : 3 плоскости, соединяющие края, 6 плоскостей, проходящие через два противоположных края.

Изометрия куба фиксирует его центр. Таким образом, он полностью определяется изображением вершины A и двух (B и C) из трех ее соседей (поскольку эти три точки вместе с центром образуют опорную точку в пространстве ). Вершина A может иметь в качестве образа любую A ‘из 8 вершин куба. Тогда для вершины B есть 3 возможных изображения среди трех соседей A ‘, затем для изображения C — 2 изображения среди двух оставшихся соседей. Это доказывает, что изометрии, оставляющие куб глобально инвариантным, равны 8 × 3 × 2 = 48, включая 24 поворота, и только одно из двух изображений C дает одинаковую ориентацию A’B’C ‘относительно ABC. 24 вращения:

приложение идентичности, которое представляет собой вращение (на нулевой угол и любую ось);
3 осевых полуоборота, проходящие через центр двух противоположных граней (возможно 3 оси);
6 четверть оборота оси, проходящей через центр двух противоположных граней (3 возможных оси и 2 возможных угла);
6 полуоборотных осей, проходящих через середины двух противоположных краев (возможно 6 осей);
8 третей поворота оси проходит через две противоположные вершины (4 возможных оси и 2 возможных угла).

является изоморфной к симметрической группой S ₄ . Любое вращение фактически переставляет четыре диагонали куба, и, наоборот, любая перестановка четырех диагоналей определяет одно вращение.

Отрицательные изометрии куба — это антиротации, составленные из этих вращений по центральной симметрии и коммутирующие с ней. Таким образом, группа O _h является подгруппы O на циклическую подгруппу порядка 2, порожденную центральной симметрией. Это самая большая из .

24 отрицательных изометрии соответственно:

центральная симметрия
3 симметрии относительно плоскости, проходящей через центр куба и параллельной грани (3 возможных плоскости);
6, состоящий из предшествующих симметрий с четвертью оборота оси, перпендикулярной плоскости симметрии (3 возможных плоскости и 2 возможных угла);
6 симметрий относительно плоскости, проходящей через два противоположных края (6 возможных плоскостей);
8, состоящий из шестой части поворота оси, проходящей через две противоположные вершины с симметрией относительно плоскости, проходящей через центр куба и перпендикулярной этой оси (4 возможных оси и 2 возможных угла). Плоскость симметрии пересекает ребра куба, образуя правильный шестиугольник.

Два тетраэдра, вписанные в куб, симметричные друг другу по центральной симметрии

Наконец, восемь вершин куба можно разделить на два правильных тетраэдра , симметричных друг другу по центральной симметрии. Отсюда следует, что из 48 изометрий куба 24 оставляют каждый из этих тетраэдров инвариантным, а 24 меняют два тетраэдра. 24 изометрии куба, оставляющие тетраэдры инвариантными, образуют группу изометрий тетраэдра: 12 — вращения, а 12 — косвенные изометрии. Эти 24 изометрии переставляют четыре вершины тетраэдра.

Типы точечных групп симметрии

Так как молекула может иметь несколько элементов симметрии, их удобно систематизировать по точечной группе симметрии. Группу симметрии образует комплекс всех операций симметрии объекта. Если центр тяжести объекта при всех преобразованиях остается неподвижным, то группа симметрии называется точечной.

Типы точечных групп симметрии:

Неаксиальные точечные группы, не содержащие нетривиальных поворотных осей ($C_1$, $C_s$, $C_i$).
Точечные группы с единственной поворотной осью. Группа $C_n$ элементов симметрии не содержит, группа $C_{nv}$ имеет $n$ вертикальных плоскостей $\sigma n$, которые проходят через ось $C_n$, группа $C_{nh}$ содержит одну горизонтальную плоскость $\sigma h$, перпендикулярную оси $C_n$. Группа $S_n$ при наличии зеркально – поворотной оси порядка $n$ имеет собственную ось порядка $n/2$. При нечетном $n$ оси $S_n$ могут быть представлены как совокупность других операций. Для низших порядков $S_1=\sigma$, $S_2=i$.
Диэдральные точечные группы имеют одну ось $C_n$ и $n$ осей второго порядка, ортогональных оси $C_n$. Если плоскости симметрии отсутствуют, группа обозначается $D_n$, при наличии нескольких вертикальных плоскостей симметрии $\sigma_v – D_{nd}$, при наличии горизонтальной плоскости $\sigma_h – D_{nh}$.
Кубические точечные группы имеют более одной оси порядка выше двух. Это точечные группы правильных тетраэдра ($T_d$), октаэдра и куба ($O_h$), икосаэдра и додекаэдра ($I_h$).Предельной группе $K_h$ принадлежит шар, имеющий максимальную симметрию и вклчающий все возможные операции симметрии.

Понятия «тетраэдрическое строение» и «симмертия $T_d$» не тождественны.

Пример 3

Молекула хлороформа имеет тетраэдрическое строение, но ее симметрия принадлежит к группе $C_{3v}$, а не к группе $T_d$.

Очарование куба

Куб сыграл важную роль в греческой геометрии и космологии. Платон классифицирует его как четвертое твердое тело, первое из которых построено из :

Как и любое платоновское твердое тело, куб связан с элементом. Как самый стабильный элемент, он ассоциируется с Землей .

В другом символическом ключе он символизирует материальный мир и все четыре элемента. Символ стабильности, он часто встречается у подножия престолов.

Куб был объектом проблемы, которая оказалась неразрешимой: дублирование куба линейкой и циркулем.

В космологии Кеплера куб связан с планетой Сатурн .

Мы также находим куб в символике масонства . Куб символизирует прогресс, который должен сделать товарищ, чтобы перейти от грубого камня к идеальному твердому телу.

Куб — часть трех канадских фильмов. Apple , выпустила куб компьютер, Nintendo на GameCube консоли. В кубике Рубика это головоломка , чьи отраженияоснове цветовых ассоциаций. Понимание вашего решения включает в себя группу перестановок .

Один находит усеченный куб в таблице Melencolia из Альбрехта Дюрера . Брюссель Атомиум представляет собой куб. Действительно, куб — одна из возможных сетей в кристаллографии для серебра , золота , меди , платины , алмаза , соли и других.

Сколько осей симметрии имеет куб – Telegraph

Сколько осей симметрии имеет куб

277. Сколько осей симметрии имеет: а) отрезок; б) правильный треугольник; в) куб?

=== Скачать файл ===

Симметрии куба, как и симметрии тетраэдра делятся на два типа — самосовмещения, при которых точки куба не изменяют своего положения относительно друг друга, и преобразования, оставляющие куб в целом на месте, но передвигающие его точки относительно друг друга. Преобразования первого типа мы, как и в случае тетраэдра, будем называть вращениями. Все вращения, очевидно, образуют группу, которая называется группой вращений куба. Опишем сначала строение этой группы. Имеется ровно 24 вращения куба вокруг различных осей симметрии. В самом деле, при поворотах куба место нижней грани может занять любая из 6 граней куба рис. Для каждой из 6 возможностей — когда указано, какая именно грань расположена внизу, — имеется 4 различных расположения куба, соответствующих его поворотам вокруг оси, проходящей через центры верхней и нижней граней, на углы Таким образом, получаем вращений куба. Укажем их в явном биде. Куб имеет центр симметрии точка пересечения его диагоналей , 3 оси симметрии четвертого порядка, 4 оси симметрии третьего порядка и 6 осей симметрии второго порядка. Достаточно рассмотреть вращения вокруг осей симметрии. Вокруг каждой из этих осей имеется по три нетождественных вращения, а именно вращения на углы. Этим вращениям соответствуют 9 перестановок вершин куба, при которых вершины противоположных граней переставляются циклически и согласовано. Например, перестановки отвечают поворотам вокруг оси. Вокруг каждой из четырех диагоналей \\\\\\\\\\\\, \\\\\\\\\\\\, \\\\\\\\\\\\, \\\\\\\\\\\\ имеется по два нетождественных вращения на углы. Например, вращения вокруг диагонали \\\\\\\\\\\\ определяют такие перестановки вершин куба: Всего получаем 8 таких вращений. Имеется шесть пар противоположных ребер например, \\\\\\\\\\\\, \\\\\\\\\\\\ , каждая пара определяет одну ось симметрии, т. Вокруг каждой из этих осей имеется одно нетождественное вращение. Всего — 6 вращений. Итак, все вращения куба указаны. Вращения куба определяют перестановки на множествах его вершин, ребер, граней и диагоналей. Различные вращения куба переставляют диагонали куба по-разному, т. Поэтому группа вращений куба определяет группу перестановок на множестве диагоналей, состоящую из 24 перестановок. Поскольку куб имеет лишь 4 диагонали, группа всех таких перестановок совпадает с симметрической группой на множестве диагоналей. Итак, любая перестановка диагоналей куба соответствует некоторому его вращению, причемразным перестановкам соответствуют разные вращения. Опишем теперь всю группу симметрий куба. Куб имеет три плоскости симметрии, проходящие через его центр. Симметрии относительно этих плоскостей в сочетании со всеми вращениями куба дают нам еще 24 преобразования, являющихся самосовмещениями куба. Поэтому полная группа симметрий куба состоит из 48 преобразований. Отображение на все множество. Взаимно однозначное отображение на все множество. Группа симметрий правильного треугольника. Группа симметрий правильного n-угольника 4. Группа симметрий многоугольника, изображенного на рис. Для каждой из 6 возможностей — когда указано, какая именно грань расположена внизу, — имеется 4 различных расположения куба, соответствующих его поворотам вокруг оси, проходящей через центры верхней и нижней граней, на углы. Таким образом, получаем вращений куба. Рассмотрим, как действует группа вращений куба на множестве его диагоналей.

Карта зеленограда с корпусами и номерами

Тц аврора самара адрес

Смерч 2 скачать торрент

Куб (гексаэдр)

Коммерческий линолеум форбо

Как экстренно остановить месячные

Условия поступления в вузы россии

Рассказ терлись хуями

Видео как делают зонт желудка

Презентация по геометрии по теме: ‘Элементы симметрии правильных многогранников’

Проблема генезиса философии

Кровотечение в животе у женщин причины

Салака рыба полезные свойства

Как выпрямить зубы без брекетов в домашних

Понятие страна и государство в чем разница

Тест по теме мировая экономика

Новости лечения диабета 1 типа 2016

Урок «Многогранники. Симметрия в пространстве»

Расписание автобусов гомель остров

Паспорт с гербом россии

Как правильно сказать взял завоевал победил

Сколько стоит мрт шейного отдела

Вычислить массу газа в объеме

Понятие операция симметрии

Если над объектом произведено действие, приведшее к новой ориентации объекта, неотличимой и совмещаемой с исходной, то такое действие называют операцией симметрии.

Операции симметрии производят такое действие, при котором достаточным условием является неподвижность одной точки объекта. В этом случае говорят о точечных операциях, а неподвижная точка объекта является его центром тяжести, в котором пересекаются все оси и плоскости симметрии.

Неподвижная точка объекта находится либо в центре шара, либо в центре тетраэдра. Каждой операции симметрии подходит определенный элемент симметрии.

Определение 1

Элемент симметрии – это геометрическое место точек, которые остаются неподвижными при данной операции симметрии.

Получи помощь с рефератом от ИИ-шки

ИИ ответит за 2 минуты

Основные элементы симметрии:

собственные оси вращения $C_n$, где $n$ – порядок оси, показывающий, что поворот молекулы на угол $2\pi/n$ приводит к структуре, тождественной первоначальной;
несобственные оси вращения (зеркально – поворотные) $S_n$;
зеркальные плоскости симметрии $\sigma$, делят молекулу на две равные части таким образом, что одна половина молекулы является зеркально – симметричной другой;
центр инверсии $i$;
тождественное преобразование $E$.

Среди операций симметрии различают:

поворот вокруг оси симметрии $C_n$;
поворот вокруг оси с вытекающим отражением в плоскости, ортогональной этой оси $S_n$;
отражение в плоскости симметрии $\sigma$;
инверсия в центре симметрии $i$;
операция идентичности $E$.

Операция идентичности позволяет внести в общую классификацию и симметричные и несимметричные объекты.

Обобщение понятия многогранника

Многогранником является совокупность конечного числа многоугольников такая, что:

каждая из сторон любого из многоугольников является одновременно и стороной только одного другого многоугольника по той же стороне;
от каждого из многоугольников можно дойти до других переходя по смежным с ним многоугольникам.

Многоугольники, составляющие многогранник, представляют собой его грани, а их стороны — ребра. Вершинами многогранников являются вершины многоугольников. Если под понятием многоугольник понимают плоские замкнутые ломаные, то приходят к одному определению многогранника. В том случае, когда под этим понятием подразумевают часть плоскости, что ограничена ломаными линиями, то следует понимать поверхность, состоящую из многоугольных кусочков. называют тело, лежащее по одну сторону плоскости, прилегающей к его грани.

Куб

Куб

Самый популярный многогранник из семейства Платоновых тел.
Куб или гексаэдр (от греческого hex — шесть и hedra — грань) составлен из 6 квадратов.

Каждая из 8 вершин куба является вершиной 3 квадратов, поэтому сумма плоских углов при каждой вершине равна 270°.
У куба 12 ребер, имеющих равную длину. Примем длину ребра куба за а и представим числовые характеристики его элементов.

Сумма длин всех ребер	12а
Площадь поверхности	6а2
Объем	V = а3
Радиус описанной сферы
Радиус вписанной сферы	r = a/2

Кубу свойственны все виды симметрии.

Центром симметрии является точка пересечения диагоналей куба.

Через центр симметрии проходят 9 осей симметрии.

Ось симметрии куба может проходить либо через середины параллельных ребер, не принадлежащих одной грани, либо через
точку пересечения диагоналей противоположных граней.

Плоскостей симметрии у куба также 9 и проходят они либо через противоположные
ребра ( таковых плоскостей 6), либо через середины противоположных ребер (таких — 3).

В мире нет места для некрасивой математики. Готфрид Харди

Правильные многогранники — самые выгодные фигуры. И природа этим широко пользуется. Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников.

Куб передает форму кристаллов поваренной соли NaCl.

Форму куба имеют кристаллические решётки многих металлов (Li, Na, Cr, Pb, Al, Au, и другие), кристалл алмаза, кристаллическая решётка
хлорида цезия CsCl.

В 2009 г. должно исполниться 500 лет со времени выхода в свет книги Луки Пачоли «Божественная пропорция»,
а следовательно, и изобретения Леонардо да Винчи для ее иллюстрации метода жестких ребер.

Леонардо изображал своим способом не только индивидуальные многогранники, но и, например, плотную упаковку кубов.
Этим изображением Леонардо на три века предвосхитил гипотезу о периодическом строении кристаллов, высказанную французскими
кристаллографами аббатом Рэнэ-Жюстом Гаюи (1743-1822) и морским офицером Огюстом Бравэ (1811-1863).

Не менее интересна другая работа Маурица Эшера.
В центре гравюры «Водопад» расположен комплекс конструкций, поднимающийся на фоне ландшафта с террасами.
Вертикальная ось создается двумя мощными башнями, каждая из которых увенчана острогранными многогранниками слева — три пересекающиеся куба, а справа также три пересекающихся правильных октаэдра.
Маленькие домики примыкают к башням слева и справа в едином комплексе. Слева на первом плане картины изображен
маленький садик со странными, необычными подводными растениями. Центральным действием картины является ручей, который
падает на колесо и крутит его. Он течет слегка полого вниз и извивается, проходя через башни, при этом он трижды протекает
через точку, в которой уже проходил. Абсурдность доходит до нас через круг неправильных соединений куба.
В результате невольного восприятия зрительная точка оказывается самой ближней, а самая высокая точка становится самой низкой.

Водопад на картине Маурица Эшера осуществляет то,что мы считаем невозможным — вечное движение.

Однородные раскраски и симметрия

Октаэдрическая симметрия

Куб имеет три одинаковых цвета, названных цветами квадратных граней вокруг каждой вершины: 111, 112, 123.

Куб имеет четыре класса симметрия, которая может быть представлена вершинно-транзитивной раскраской граней. Наивысшая октаэдрическая симметрия O h имеет все грани одного цвета. Двугранная симметрия D4hвозникает из-за того, что куб является призмой со всеми четырьмя сторонами одного цвета. Призматические подмножества D 2d имеют ту же окраску, что и предыдущий, а D 2h имеет чередующиеся цвета для своих сторон, всего три цвета, соединенные противоположными сторонами. Каждой форме симметрии соответствует свой символ Wythoff.

Имя	Правильный. шестигранник	Квадратная призма	Прямоугольная. трапеция	Прямоугольная. кубоид	ромбическая. призма	треугольник. трапецоэдр
диаграмма Кокстера.
символ Шлефли.	{4, 3}	{4} × {}. rr {4,2}	s2{2,4}	{}. tr {2,2}	{} × 2 {}
Wythoff. символ	3 \| 4 2	4 2 \| 2		2 2 2 \|
Симметрия	Oh. . (* 432)	D4h. . (* 422)	D2d. . (2 * 2)	D2h. . (* 222)	D3d. . (2 * 3)
Симметрия. порядок	24	16	8	8	12
Изображение. (однородная. окраска)	. (111)	. (112)	. (112)	. (123)	. (112)	. (111), (112)

Разделы

Самолет и куб могут встречаться, а могут и не встречаться. Если они встретятся, их пересечение может нарисовать

точка
сегмент
треугольник
четырехугольник, хотя бы трапеция, иногда прямоугольник или даже ромб.
пятиугольник. У этого пятиугольника всегда две пары параллельных сторон.
шестиугольник с тремя парами параллельных сторон

Поскольку куб имеет только шесть сторон, невозможно получить секцию с более чем шестью сторонами.

Пересечение плоскости и куба может дать три типа правильных многоугольников:

равносторонний треугольник для плоскостей, перпендикулярных диагонали, расстояние между которыми на одном конце диагонали меньше одной трети ее длины. Благодаря сечению куба ABCDEFGH плоскостью DBE (см. Иллюстрацию ниже), которая представляет собой равносторонний треугольник DBE с центром Ω, мы получаем, что диагональ куба делится на две части и в соотношении 2: 1. Мы также получаем, что куб состоит из трех тел одинаковой высоты: двух пирамид ADBE и GCHF и твердого CHFDEB;
квадрат, для плоскостей, параллельных одной из граней. Но мы также можем получить квадрат, разрезав куб плоскостью, параллельной диагональной плоскости, и на некотором расстоянии от нее;в2-12{\ displaystyle a {\ frac {{\ sqrt {2}} — 1} {2}}}
правильный шестиугольник, разрезая куб по плоскости, соединяющей одну из его диагоналей.

Невозможно получить правильный пятиугольник, потому что сечение, имеющее 5 сторон, плоскость обязательно пересекает две противоположные грани куба, поэтому фигура имеет две параллельные стороны, чего не происходит в правильном пятиугольнике. Получить сечение в форме прямоугольного треугольника невозможно, потому что все углы треугольника, полученного сечением, острые. Невозможно получить сечение, представляющее собой прямоугольную трапецию, не являющееся прямоугольником.

Максимальная площадь сечения куба со стороной a составляет . Эта область получается путем сечения, следующего за плоскостью, содержащей два противоположных края куба.
в22{\ displaystyle a ^ {2} {\ sqrt {2}}}