Химия. 10 класс

Методы измерения плотности газа

1. Метод гравиметрии: Этот метод основан на измерении массы газа, заполненного в конкретный объем. Газовый образец помещается в прибор с известным объемом, после чего определяется его масса с помощью весов. Затем, используя формулу плотности, рассчитывается значение плотности газа.
2. Метод давления: В этом методе используется закон Бойля-Мариотта, который устанавливает прямую зависимость между давлением и плотностью газа. Измеряется давление газа в известном объеме, а затем с помощью уравнения состояния газа рассчитывается его плотность.
3. Метод ультразвука: Этот метод основан на использовании ультразвуковых волн для измерения плотности газа. Ультразвуковая волна проходит через газовый образец и затем измеряется время, за которое волна проходит через определенное расстояние. С помощью физических законов и формул рассчитывается значение плотности газа.
4. Метод диффузии: В этом методе используется явление диффузии газов. Газовые смеси разных плотностей разностепенно проходят через тонкую перегородку, и время прохождения газов по перегородке измеряется. Из полученных данных рассчитывается плотность газа.

Выбор метода измерения плотности газа зависит от его свойств, доступного оборудования и точности, которую требуется достичь. Каждый из этих методов имеет свои преимущества и ограничения, и их выбор должен быть обоснован исходя из конкретных условий опыта или промышленного процесса.

Зависимость плотности от температуры

Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность ведёт себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого значения.

При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Вода, кремний, германий и некоторые другие вещества являются исключениями из данного правила, так как их плотность при переходе в твердую фазу уменьшается.

Примеры решения задач

Задание	Вычислите плотность по хлору смеси 55 л азота и 180 л кислорода.
Решение	Найдем объемные доли веществ в смеси:

φ (N₂) = 55 / (55 + 180) = 55 / 235 = 0,23.

φ (O₂) = 180 / (180 + 55) = 180 / 235 = 0,77.

Объемные доли газов будут совпадать с молярными, т.е. с долями количеств веществ, это следствие из закона Авогадро. Найдем условную молекулярную массу смеси:

M_r conditional (mixture) = 0,23 × 28 + 0,77 × 32 = 6,44 + 24,64 = 31,08.

Найдем относительную плотность смеси по водороду:

Относительную молекулярную массу воздуха принимают равной 29 (с учетом содержания в воздухе азота, кислорода и других газов). Следует отметить, что понятие «относительная молекулярная масса воздуха» употребляется условно, так как воздух – это смесь газов.

M_r(NOCl) = A_r(N) + Ar(O) + Ar(Cl) = 14 + 16 + 35,5 = 65,5.

Основные правила расчета плотности газа

Плотность газа определяет количество массы газа, занимающего единицу объема. Расчет плотности газа может быть полезен для решения различных задач в физике, химии и других науках.

Основными правилами для расчета плотности газа являются:

1. Найти молекулярную массу газа: это масса одной молекулы газа в атомных единицах массы (у). Она может быть найдена в химических таблицах или вычислена путем сложения масс атомов в молекуле газа.
2. Измерить количество газа: это обычно делается в единицах объема, таких как литры (л) или кубические метры (м³).
3. Найти количество вещества газа, выразив его в молях:

• В случае измерения объема газа в литрах, можно использовать следующую формулу: количество вещества = (объем газа) / (22,4 л/моль).
• В случае измерения объема газа в кубических метрах, можно использовать следующую формулу: количество вещества = (объем газа) / (24,05 м³/моль).

Рассчитать плотность газа, используя формулу: плотность = (молярная масса газа) / (количество вещества газа).

Пример расчета плотности газа:

1. Дано: масса кислорода (O2) равна 32 г.
2. Найти молекулярную массу кислорода: 16 г/моль (молярная масса кислорода).
3. Измерить объем кислорода: 22,4 л (объем одного моля газа при нормальных условиях).
4. Найти количество вещества кислорода в молях: (22,4 л) / (22,4 л/моль) = 1 моль.
5. Рассчитать плотность кислорода: 32 г / 1 моль = 32 г/моль (плотность кислорода).

Итак, плотность кислорода равна 32 г/моль.

Теплоемкость идеальных газов

Рисунок 4. Теплоемкость идеального газа. Автор24 — интернет-биржа студенческих работ

Экспериментально измеренные теплоемкости идеальных газов при обычных внешних условиях практически идеально согласуются с другими постулатами классической термодинамики. Однако, в целом классическая гипотеза теплоемкости данных веществ не может считаться вполне удовлетворительной и подходящей для всех систем. Существует много различных примеров весомых расхождений между экспериментом и теорией. Это обуславливается тем, что существующая теория не в состоянии в полной мере учесть энергию, непосредственно связанную с внутренними движениями в самой молекуле.

Гипотезу о равномерном и прямолинейном распределении тепловой энергии по степеням свободы возможно применить и к движению частиц в твердом теле. Атомы, которые входят в состав кристаллической решетки, совершают определенные колебания возле положений равновесия. Энергетический потенциал таких вибраций представляет собой внутреннюю силу физического вещества.

Замечание 2

Опыт доказывает, что практически все идеальные газы имеют молярную теплоемкость, возникающую при обычных температурах.

Но, при нулевой температуре сразу появляются значительные расхождения между движущимися элементами. Следует отметить, что «количество теплоты» и «теплоемкость» — достаточно неудачные термины. Они достались современной науке в наследство от устаревших принципов теории теплорода, которая господствовала в начале XVIII столетия.

Эта гипотеза рассматривала теплоту и энергию идеальных газов как универсальное невесомое вещество, содержащееся во всех физических телах. Считалось, что такие параметры не могут быть ни созданы, ни уничтожены. Нагревание материальных веществ объяснялось увеличением, а охлаждение – уменьшением содержащегося внутри них теплорода. Однако теория теплорода не совсем состоятельна. Она не может описать, почему одинаковые изменения внутренней энергии тела возможно получить, передавая ему абсолютно разное количество теплоты в зависимости от совершаемой системой работы. Поэтому лишено физического смысла и само утверждение, что «в физическом теле содержится определенный запас теплоты».

Слайд 21Опр. Соприкосновение тел, при котором возможна лишь передача тепла от одного

тела к другому, будем наз. тепловым контактом этих тел. Мы говорим, две системы имеют равные температуры, если при тепловом контакте их состояния не меняются.Впервые понятие температуры возникло из субъективных ощущений в области восприятия «степени нагретости» тела. Объективная возможность введения понятия температуры связана с важным постулатом термоди­намики: «Если две термодинамические системы находятся в тепловом равновесии с третьей, то они должны быть в равновесии и между собой». Указанное равновесие не зависит от объема, давления, плотности и других (помимо температуры) величин, определяющих состояние систем.

Плотность газа и другие его физические свойства

Одной из важнейших физических свойств газообразных веществ является значение их плотности.

Данную величину обычно обозначают греческой буквой r или латинскими D и d. Единицей измерения плотности в системе СИ принято считать кг/м 3 , а в СГС – г/см 3 . Плотность газа – справочная величина, её обычно измеряют при н. у.

Зачастую, применительно к газам используют понятие «относительная плотность». Данная величина представляет собой отношение массы данного газа к массе другого газа, взятого в том же объеме, при той же температуре и том же давлении, называется относительной плотностью первого газа по второму.

Например, при нормальных условиях масса диокисда углерода в объеме 1 л равна 1,98 г, а масса водорода в том же объеме и при тех же условиях – 0,09 г, откуда плотность диоксида углерода по водороду составит: 1,98 / 0,09 = 22.

Примеры расчета плотности газа

Расчет плотности газа может быть полезен при проведении различных физических и химических измерений. Ниже представлены несколько примеров расчета плотности газа.

Пример	Исходные данные	Расчет	Результат
Пример 1	Объем: 10 лМасса: 5 г	Плотность = Масса / Объем	Плотность = 5 г / 10 л = 0.5 г/л
Пример 2	Масса газа: 2.5 кгОбъем: 1000 л	Плотность = Масса / Объем	Плотность = 2.5 кг / 1000 л = 0.0025 кг/л
Пример 3	Молярная масса: 32 г/мольДавление: 2 атмТемпература: 273 К	Расчет плотности при помощи уравнения состояния идеального газа: Плотность = (Молярная масса * Давление) / (Универсальная газовая постоянная * Температура)	Плотность = (32 г/моль * 2 атм) / (0.0821 л*атм/(моль*К) * 273 К) ≈ 1.01 г/л

Это лишь несколько примеров расчета плотности газа. Зависимости от конкретной ситуации и входных данных, формулы и принципы расчета могут отличаться. Однако основные правила остаются прежними: плотность газа вычисляется как отношение массы газа к его объему. Расчеты плотности газа могут быть полезны для различных исследований и практических задач в различных областях науки и техники.

Формула для определения плотности газа

Плотность газа может быть определена по формуле, которая связывает массу и объем газовой смеси. Данная формула выражается следующим образом:

Плотность (ρ) = Масса (m) / Объем (V)

Плотность газа измеряется в килограммах на кубический метр (кг/м³) или в граммах на литр (г/л). Масса газа обычно измеряется в килограммах (кг), а объем – в кубических метрах (м³) или литрах (л).

Для расчета плотности газа, необходимо известным образом определить массу газовой смеси, а также ее объем. После этого достаточно разделить массу на объем с помощью указанной формулы, чтобы получить значение плотности.

Например, если известны масса газовой смеси (например, 2 кг) и объем (например, 1 м³), то плотность будет равна 2 кг / 1 м³ = 2 кг/м³.

Идеальный газ

В газах расстояния между молекулами обычно значительно больше их размеров. Силы взаимодействия между молекулами на таких больших расстояниях малы, и каждая молекула движется вдоль прямой линии до очередного столкновения с другой молекулой или со стенкой сосуда. Среднее расстояние между молекулами воздуха при нормальных условиях порядка 10-8 м, то есть в сотни раз превышает размер молекул. Слабое взаимодействие между молекулами объясняет способность газов расширяться и заполнять весь объем сосуда. В пределе, когда взаимодействие стремится к нулю, мы приходим к представлению об идеальном газе.

Идеальный газ — это газ, молекулы которого не взаимодействуют друг с другом, за исключением процессов упругого столкновения и считаются материальными точками.

В молекулярно-кинетической теории количество вещества принято считать пропорциональным числу частиц. Единица количества вещества называется молем (моль). Моль — это количество вещества, содержащее столько же частиц (молекул), сколько содержится атомов в 0,012 кг углерода 12C. Молекула углерода состоит из одного атома. Таким образом, в одном моле любого вещества содержится одно и то же число частиц (молекул). Это число называется постоянной Авогадро: NА = 6,022·1023 моль-1.

Постоянная Авогадро — одна из важнейших постоянных в молекулярно-кинетической теории. Количество вещества определяется как отношение числа N частиц (молекул) вещества к постоянной Авогадро NА, или как отношение массы к молярной массе:

Массу одного моля вещества принято называть молярной массой M. Молярная масса равна произведению массы m0 одной молекулы данного вещества на постоянную Авогадро (то есть на количество частиц в одном моле). Молярная масса выражается в килограммах на моль (кг/моль). Для веществ, молекулы которых состоят из одного атома, часто используется термин атомная масса. В таблице Менделеева молярная масса указана в граммах на моль. Таким образом имеем еще одну формулу:

где: M – молярная масса, NA – число Авогадро, m0 – масса одной частицы вещества, N – число частиц вещества содержащихся в массе вещества m. Кроме этого понадобится понятие концентрации (количество частиц в единице объема):

Напомним также, что плотность, объем и масса тела связаны следующей формулой:

Если в задаче идет речь о смеси веществ, то говорят о средней молярной массе и средней плотности вещества. Как и при вычислении средней скорости неравномерного движения, эти величины определяются полными массами смеси:

Не забывайте, что полное количество вещества всегда равно сумме количеств веществ, входящих в смесь, а с объемом надо быть аккуратными. Объем смеси газов не равен сумме объемов газов, входящих в смесь. Так, в 1 кубометре воздуха содержится 1 кубометр кислорода, 1 кубометр азота, 1 кубометр углекислого газа и т.д. Для твердых тел и жидкостей (если иное не указано в условии) можно считать, что объем смеси равен сумме объемов ее частей.

Относительная плотность газа

Обозначим относительную плотность газа m₁ / m₂ буквой D. Тогда

Следовательно, молярная масса газа равна его плотности по отношению у другому газа, умноженной на молярную массу второго газа.

Часто плотности различных газов определяют по отношению к водороду, как самому легкому из всех газов. Поскольку молярная масса водорода равна 2,0158 г/моль, то в этом случае уравнение для расчета молярных масс принимает вид:

или, если округлить молярную массу водорода до 2:

Вычисляя, например, по этому уравнению молярную массу диоксида углерода, плотность которого по водороду, как указано выше равна 22, находим:

Плотность газа в лабораторных условиях самостоятельно можно определить следующим образом: необходимо взять стеклянную колбу с краном и взвесить её на аналитических весах. Первоначальный вес – вес колбы, из которой откачали весь воздух, конечный – вес колбы, наполненной до конкретного давления исследуемым газом. Разность полученных масс следует разделить на объем колбы. Вычисленное значение и есть плотность газа в данных условиях.

Чтобы рассчитать плотность газа при н.у. нужно воспользоваться уравнением состояния идеального газа:

В таблице ниже приведены значения плотностей некоторых газов.

Таблица 1. Плотность газов при нормальных условиях.

Плотность идеального газа и другие его физические свойства

Представление об идеальном газе возникло при изучении свойств разреженных газов. В движении каждой частицы любого газа всегда можно различить две фазы: свободное движение и столкновение. Некоторое время частица движется настолько далеко от остальных, что её движение можно считать свободным. Среднее время τ такого движения называется временем свободного пробега. Путь l, который частица в среднем проходит за это время, называется длиной свободного пробега. По истечении времени порядка τ частица сближается с какой-то другой и начинает с ней взаимодействовать. Среднее время τ ’ взаимодействия двух частиц называется временем столкновения.

Данную величину обычно обозначают греческой буквой или латинскими D и d. Единицей измерения плотности в системе СИ принято считать кг/м 3 , а в СГС – г/см 3 .

Плотность идеального газа можно вычислить по формуле:

Выразив величину массы из уравнения Менделеева-Клапейрона получим новую формулу для вычисления плотности идеального газа:

Ссылки

Wikimedia Foundation . 2010 .

Смотреть что такое «Плотность (физика)» в других словарях:

ФИЗИКА. — ФИЗИКА. 1. Предмет и структура физики Ф. наука, изучающая простейшие и вместе с тем наиб. общие свойства и законы движения окружающих нас объектов материального мира. Вследствие этой общности не существует явлений природы, не имеющих физ. свойств … Физическая энциклопедия

Физика звёзд — Физика звезд одна из отраслей астрофизики, изучающая физическую сторону звезд (масса, плотность, …). Содержание 1 Размеры, массы, плотность, светимость звезд 1.1 Масса звёзд … Википедия

Плотность состояний — величина, определяющая количество энергетических уровней в интервале энергий на единицу объёма в трёхмерном случае (на единицу площади в двумерном случае). Является важным параметром в статистической физике и физике твёрдого тела. Термин может… … Википедия

ФИЗИКА — наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, св ва и строение материи и законы её движения. Понятия Ф. и её законы лежат в основе всего естествознания. Ф. относится к точным наукам и изучает количеств … Физическая энциклопедия

ФИЗИКА — ФИЗИКА, наука, изучающая совместно с химией общие законы превращения энергии и материи. В основе обеих наук лежат два основных закона естествознания закон сохранения массы (закон Ломоносова, Лавуазье) и закон сохранения энергии (Р. Майер, Джауль… … Большая медицинская энциклопедия

Физика взрыва — (a. explosion physics; н. Physik der Explosion; ф. physique de l explosion; и. fisica de explosion, fisica de estallido, fisica de detonacion) наука, изучающая явление взрыва и механизм его действия в среде. Hарушение механич.… … Геологическая энциклопедия

Физика моря — физика океана, раздел геофизики (См. Геофизика), посвященный изучению физических процессов в Мировом океане. Термин «физическая океанография» иногда используется как синоним Ф. м., но в узком смысле означает часть Ф. м., посвященной… … Большая советская энциклопедия

Физика — I. Предмет и структура физики Ф. – наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, свойства и строение материи и законы её движения. Поэтому понятия Ф. и сё законы лежат в основе всего… … Большая советская энциклопедия

Физика — 1) Ф. и ее задачи. 2) Методы Ф. 3) Гипотезы и теории. 4) Роль механики и математики в Ф. 5) Основные гипотезы Ф.; вещество и его строение. 6) Кинетическая теория вещества. 7) Действие на расстоянии. Эфир. 9) Энергия. 10) Механические картины,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Плотность — У этого термина существуют и другие значения, см. Плотность (значения). Плотность Размерность L−3M Единицы измерения СИ … Википедия

Основное уравнение мкт идеального газа:

Основное уравнение
МКТ позволяет вычислить давление газа,
если известны масса молекулы, среднее
значение квадрата скорости и концентрация
молекул.

Давление идеального
газа
заключается
в том, что молекулы при столкновениях
со стенками сосуда взаимодействуют с
ними по законам механики как упругие
тела. При столкновении молекулы со
стенкой сосуда проекция скорости v x
вектора
скорости на ось OX,
перпендикулярную стенке, изменяет свой
знак на противоположный, но остается
постоянной по модулю. Поэтому в результате
столкновений молекулы со стенкой
проекция ее импульса на ось OX
изменяется от mv 1x =-mv x
до mv 2x =mv x .
Изменение импульса молекулы при
столкновении со стенкой вызывает сила
F 1 ,
действующая на нее со стороны стенки.
Изменение импульса молекулы равно
импульсу этой силы:

Во
время столкновения, согласно третьему
закону Ньютона, молекула действует на
стенку с силой F 2 ,
равной по модулю силе F 1
и направленной противоположно.

Молекул
много, и каждая передает стенке при
столкновении такой же импульс. За секунду
они передают импульс
,
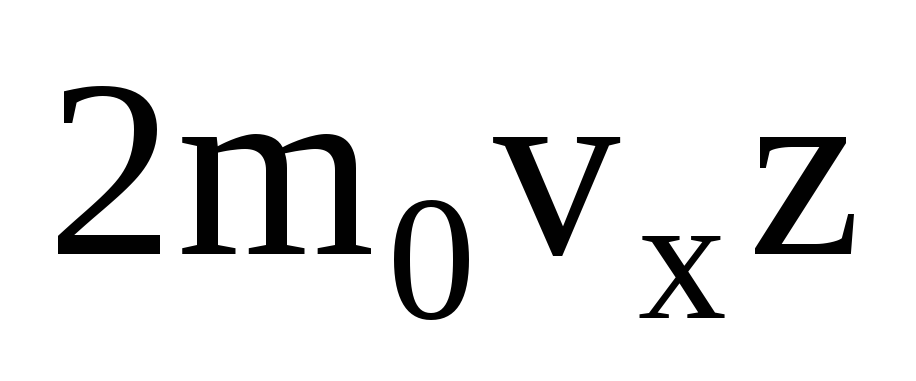гдеz
– число столкновений всех молекул со
стенкой, которое пропорционально
концентрации молекул в газе, скорости
молекул и площади поверхности стенки:
.
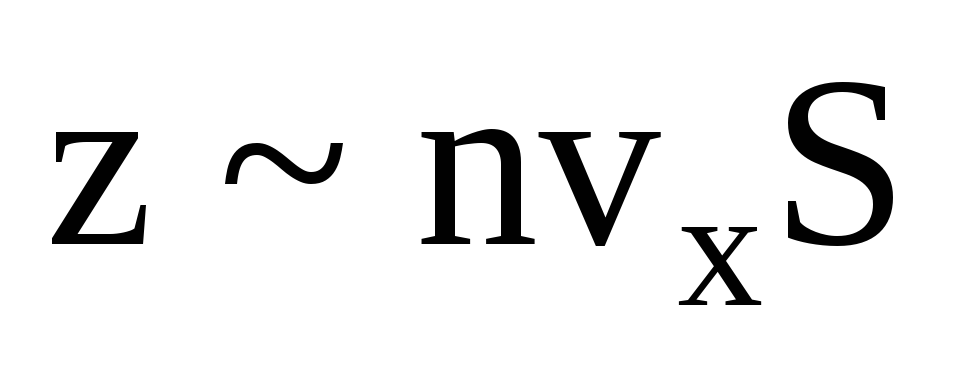К стенке движется только половина
молекул, остальные движутся в обратную
сторону:.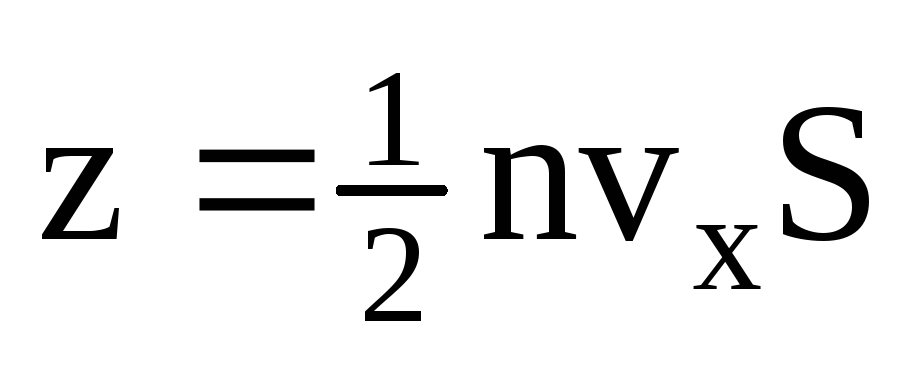
Тогда полный импульс, переданный стенке
за 1 секунду:.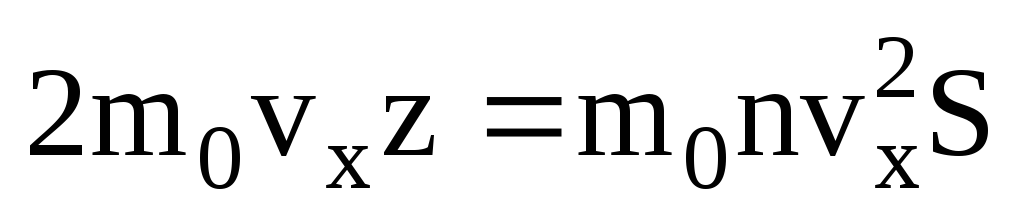
Согласно второму закону Ньютона изменение
импульса тела за единицу времени равно
действующей на него силе:

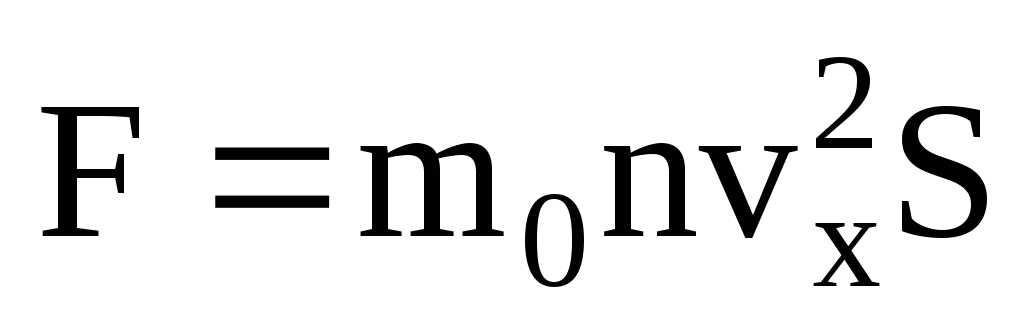
Учитывая,
что не все молекулы имеют одинаковую
скорость, сила, действующая на стенку
будет пропорциональна среднему квадрату
скорости. Так как молекулы движутся во
всех направлениях, средние значения
квадратов проекций скорости равны.
Следовательно, средний квадрат проекции
скорости:
;.
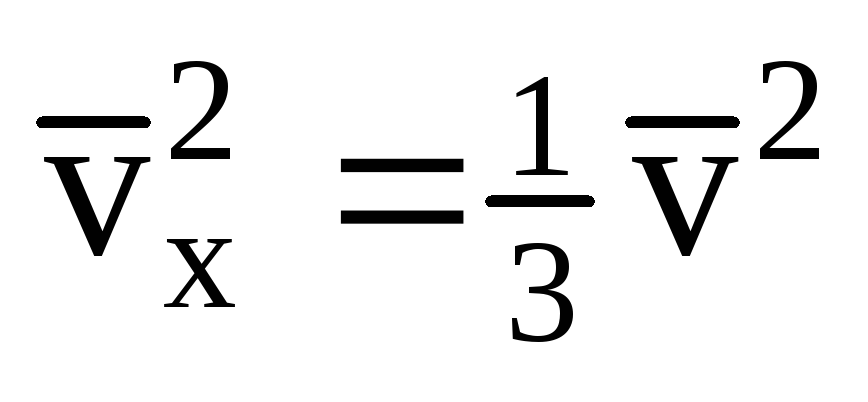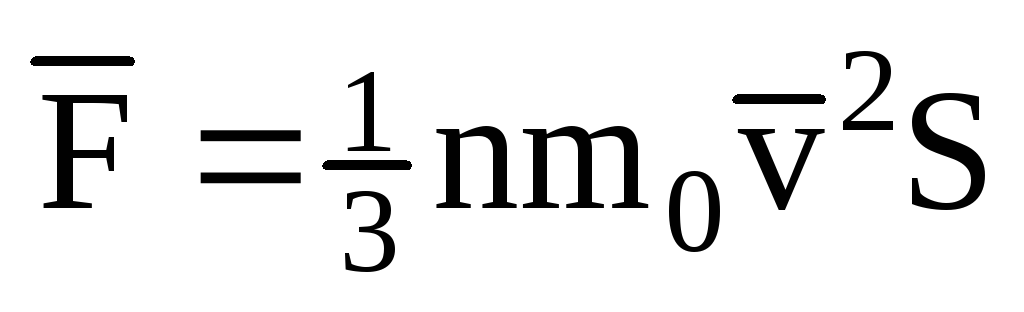Тогда давление газа на стенку сосуда
равно:

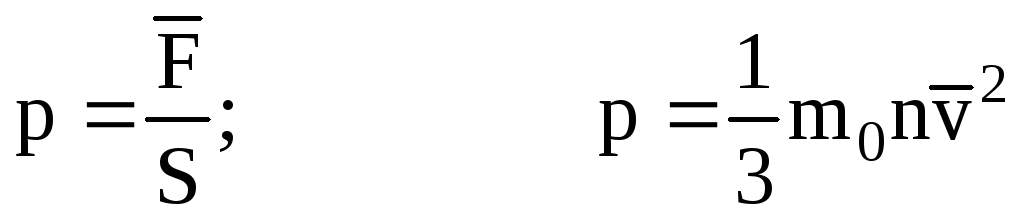— основное уравнение
МКТ.

Обозначив
среднее значение кинетической энергии
поступательного движения молекул
идеального газа:

,
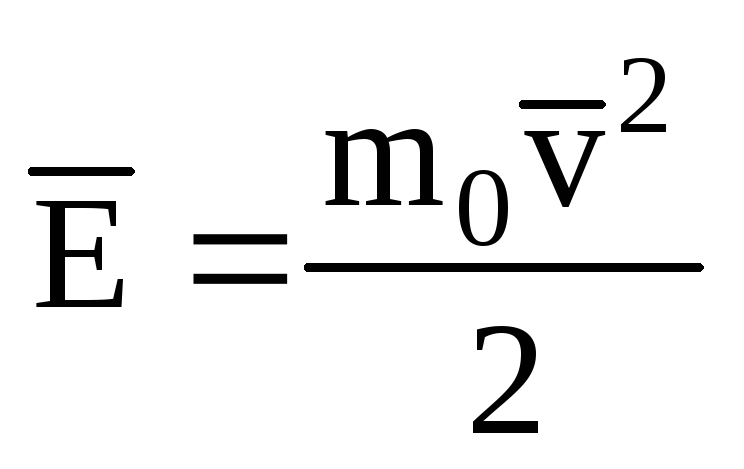получим

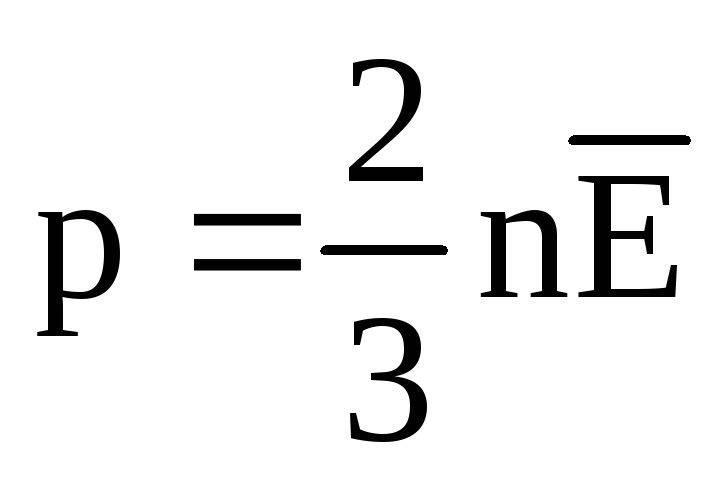
Физическая формула плотности газа

Для обозначения плотности обычно используется символ (ро). Пло́тность — скалярная физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму или площади (поверхностная плотность).

Более точное определение плотности требует уточнение формулировки:

• Средняя плотность тела — отношение массы тела к его объёму. Для однородного тела она также называется просто плотностью тела.
• Плотность вещества — это плотность тел, состоящих из этого вещества.
• Плотность тела в точке — это предел отношения массы малой части тела (), содержащей эту точку, к объёму этой малой части (), когда этот объём стремится к нулю , или, записывая кратко, . При таком предельном переходе необходимо помнить, что на атомарном уровне любое тело неоднородно, поэтому необходимо остановиться на объёме, соответствующем используемой физической модели.