Как найти площадь поверхности призмы?

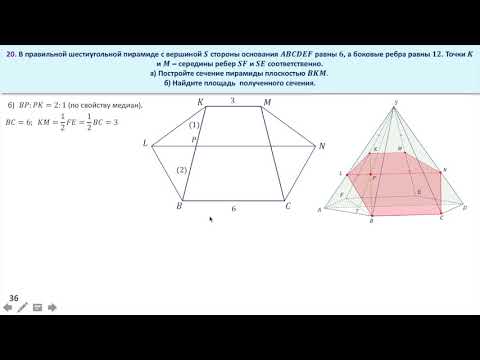
Диагонали куба

Первое, что хотелось бы отметить, это то, что диагонали куба равны между собой. Давайте представим, что у нас есть куб, и мы проводим диагонали от одной вершины к другой

Обратите внимание, что эти две диагонали имеют одинаковую длину. Это означает, что если одна диагональ равна d, то и вторая диагональ также будет равна d

Одно из интересных свойств диагоналей куба связано с их взаимосвязью с сторонами куба. Диагональ куба будет равна противоположной стороне куба, умноженной на корень квадратный из двух. Другими словами, если сторона куба равна a, то диагональ будет равна a√2. Это можно записать математическим выражением: d = a√2.

А что происходит с площадями граней куба? Когда мы взглянем на диагонали, мы увидим, что они делят грани куба на две равные части. Таким образом, площадь каждой грани будет равна половине площади соответствующей грани. Это означает, что площадь каждой грани куба равна половине площади одной диагонали, умноженной на корень квадратный из двух: S = (1/2) * a^2 * √2.

И наконец, что происходит с объемом куба? Объем куба можно вычислить, зная длину его стороны. Он равен стороне, возведенной в куб: V = a^3. Но мы также можем выразить объем куба через диагональ и площадь грани

Обратите внимание, что объем куба равен произведению длины любой из его диагоналей на площадь грани, деленное на корень квадратный из двух. Это дает нам формулу: V = (a * S) / √2

Вы обратили внимание на то, как все эти свойства диагоналей куба связаны друг с другом? Уже заинтересовался? Тогда давайте продолжим изучать математические аспекты куба и его диагоналей

• Диагонали куба равны между собой. Это значит, что диагональ, соединяющая противоположные вершины куба, имеет такую же длину, как и другая диагональ.
• Диагональ куба равна противоположной стороне, умноженной на корень квадратный из двух. Если сторона куба равна a, то диагональ будет равна a√2.
• Площадь каждой грани куба равна половине площади соответствующей диагонали. Это означает, что площадь каждой грани куба равна половине площади одной диагонали, умноженной на корень квадратный из двух: S = (1/2) * a^2 * √2.
• Объем куба можно выразить через длину стороны, диагональ и площадь грани. Объем куба равен произведению длины диагонали на площадь грани, деленное на корень квадратный из двух: V = (a * S) / √2.

Сфера и шар

10. Сфера — это множество всех точек пространства, равноудаленных от данной точки, называемой центром сферы. Радиусом сферы называется отрезок, соединяющий центр сферы с точкой на сфере, или длина этого отрезка. Хордой сферы называется отрезок, соединяющий две точки на сфере. Диаметр сферы — это хорда, которая проходит через центр сферы. Диаметр сферы равен двум радиусам сферы.

11. Площадь сферы находится по формуле: \(S_{сф}=4πR^2\).

12. Шаром называется часть пространства, ограниченная сферой, вместе с самой сферой и ее центром. Данная сфера называется поверхностью шара.
Сечение шара с радиусом \(R\) плоскостью, проходящей через центр шара, называется большим кругом шара. Радиус, хорда, диаметр шара те же, что и его сферы.

13. Объем шара находится по формуле \(V_{шара}=\frac{4}{3} πR^2\).

Задача высокого уровня

Решение примеров повышенного уровня сложности предполагает не только хорошее понимание изучаемого материала, но и знание предыдущих тем. Понадобится вспомнить формулы для нахождения площадей и объёмов плоских фигур и их свойства. Вот пример одной из таких задач.

Пусть имеется шестиугольная объёмная фигура, у которой баковая грань равняется 6, а площадь основания 12. Нужно найти объём геометрического тела с вершинами в точках A, B1, C1, D1, E1, F1.

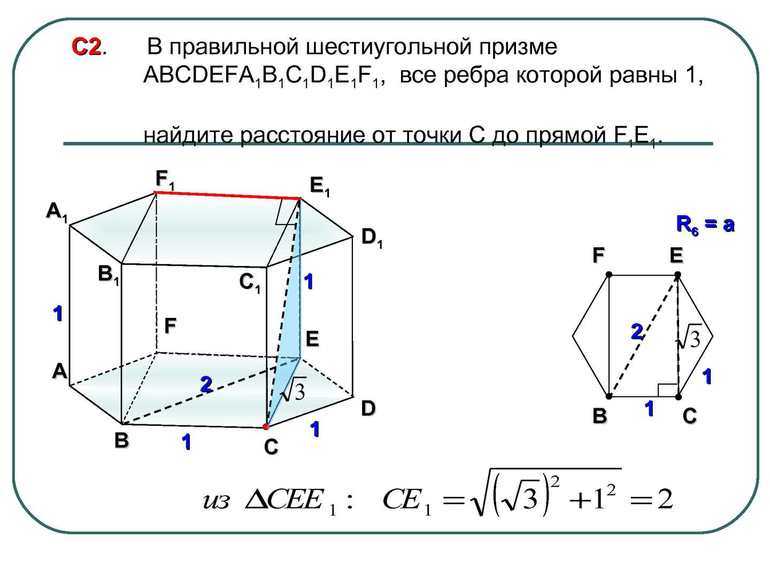
В таких задачах перед тем как непосредственно приступить к вычислениям, желательно использовать вспомогательный рисунок. На нём нужно изобразить фигуру в трёхмерной системе координат и подписать все её вершины.

Согласно условию, площадь основания Sabcde1f1 = 12, отрезок AA1 = 6. Так как фигура правильная, то все ребра у призмы буду равны. Чтобы найти, сколько будет составлять объём, понадобится обозначить многогранник. Для этого следует построить отрезки F1B, F1A, B1, E1A, D1A, C1A. Получившаяся фигура представляет собой пирамиду.

Таким образом, искомая площадь будет равняться шести поверхностям правильного треугольника. В свою очередь, его занимаемый размер можно определить как Sтр = (a * b) * sin / 2. Значит, площадь основания призмы равна: S = (6 * R * R * sin 60) / 2. Подставив заданное условием значение из формулы, можно выразить радиус: R 2 = (12 * 2) / 3 √ 3 = 8 /√3.

Площадь треугольника A1B1F1 находится как произведение сторон, умноженное на синус угла и разделённое на 2: S = (a * a * sin120) / 2 = a 2 * sin60 / 2 = (R 2 * √ 3/3) / 2. Подставив значение R, можно получить: S = (½) * (8 / √ 3) * (√3 / 2) = 2. Тогда площадь пятиугольника будет равняться разнице поверхностей шестиугольника и треугольника A1B1F1, то есть S = 12 — 2 = 10. Теперь можно будет подсчитать и объём пирамиды: Vab1c1d1e1f1 = (1 / 3) * 6 * 10 = 20. Задача решена.

Что такое куб: определение, свойства, формулы

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Что такое куб: определение, свойства, формулы

В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).

• Определение куба
• Свойства куба
  • Свойство 1
  • Свойство 2
  • Свойство 3
• Формулы для куба
  • Диагональ
  • Диагональ грани
  • Площадь полной поверхности
  • Периметр ребер
  • Объем
  • Радиус описанного вокруг шара
  • Радиус вписанного шара

Определение куба

Куб – это правильный многогранник, все грани которого являются квадратами.

• Вершины куба – это точки, являющиеся вершинами его граней.Всего их 8: A, B, C, D, A₁, B₁, C₁ и D₁.
• Ребра куба – это стороны его граней.Всего их 12: AB, BC, CD, AD, AA₁, BB₁ , CC₁, DD₁, A₁B₁, B₁C₁, C₁D₁ и A₁D₁.
• Грани куба – это квадраты, из которого состоит фигура.Всего их 6: ABCD, A₁B₁C₁D₁, AA₁B₁B, BB₁C₁C, CC₁D₁D и AA₁D₁D.

Примечание: куб является частным случаем параллелепипеда или призмы.

Свойства куба

Свойство 1

Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.

• ABCD || A₁B₁C₁D₁
• AA₁B₁B || CC₁D₁D
• BB₁C₁C || AA1D₁D

Свойство 2

Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.

• AC₁ = BD₁ = A₁C = B₁D (диагонали куба).
• О – точка пересечения диагоналей:AO = OC₁ = BO = OD₁ = A₁O = OC = B₁O = OD.

Свойство 3

Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.

Например, на рисунке выше угол между гранями ABCD и AA₁B₁B является прямым.

Формулы для куба

Примем следующие обозначения, которые будут использоваться далее:

• a – ребро куба;
• d – диагональ куба или его грани.

Площадь полной поверхности

Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Cube Formula — Что такое Cube Formula? Примеры

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Куб числа непосредственно отражает объем куба, имеющего длину ребра, равную данному числу.

Что такое формула куба?

Куб является одним из пяти платоновых тел и также известен как правильный шестигранник.

Формула куба

Объем куба

Объем куба можно рассчитать с использованием различных формул на основе заданных параметров. Его можно рассчитать, используя длину стороны, а также размер диагонали куба.

• Объем куба (на основе длины стороны) = a 3  кубических дюймов, где a – длина стороны куба
• Объем куба (по диагонали) = (√3×d 3 )/9кубических дюймов, где d — длина диагонали куба

Боковая площадь куба

Боковая площадь куба равна сумме площадей всех боковых граней куба.

LSA куба = 4a 2

, где a — длина стороны.

Общая площадь куба

Общая площадь поверхности куба будет равна сумме площади основания и площади вертикальных поверхностей куба. Поскольку все грани куба состоят из квадратов одинакового размера, то общая площадь поверхности куба будет равна площади поверхности одной грани, сложенной с самой собой в пять раз. Таким образом, формула для нахождения площади поверхности куба:

Общая площадь поверхности (TSA) куба = 6a 2

, где a — длина стороны.

Диагональ куба

Куб имеет диагонали двух разных длин, более короткие лежат на квадратных гранях, а более длинные проходят через центр. Главной диагональю куба называется та, которая проходит через центр, который можно найти, умножив длину одной стороны на квадратный корень из 3.

Диагональ куба = a√3

Давайте лучше разберемся с формулами куба на нескольких решенных примерах.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запись на бесплатный пробный урок

Примеры с использованием формулы куба

Пример 1: Найдите объем кубика Рубика длиной 4 дюйма. Решение:

Чтобы найти объем кубика Рубика: кубик Рубика0003

Длина стороны куба = 4 дюйма (дано)

Используя формулу куба, объем = с × с × с = с 3

Поместите значения,

объем = 4 × 4 × 4 = 4 3  = 64

Ответ: Объем кубика Рубика составляет 64 кубических дюйма.

Пример 2: Размеры куба – 64 дюйма. Найдите его диагональ по формуле куба. Решение: 

Чтобы найти диагональ куба:

Размеры куба: длина (l) = ширина (w) = высота (h) = 64 дюйма (данные)

Используя формулу куба,

диагональ = a√3 

Поместите значения,

Диагональ = 64√3 = 110,848 дюйма

Ответ: Диагональ куба равна 110,848 дюйма

Пример 3: Найдите общую площадь поверхности куба, если длина стороны куба равна 25 дюймам.

Решение:

Длина стороны куба, a = 25 дюймов 

Используя формулу площади куба, а именно: A = 6a 2

Поместите значения,

A = 6 × 25 × 25 = 3750 квадратных дюймов

Ответ: Площадь поверхности куб равен 3750 квадратных дюймов.

Часто задаваемые вопросы о формуле куба

Что такое формула куба?

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Это простые формулы, зависящие в основном от одного параметра — длины ребра или стороны куба.

Как рассчитать диагональ куба по формуле куба?

Главную диагональ куба , пересекающую центр, можно найти, умножив длину одной стороны на квадратный корень из 3. Таким образом, диагональ куба = a√3, где a – ребро куба. .

Что такое s в формуле куба?

В формуле куба s относится к ребру куба. Все формулы куба — объем, площадь поверхности и диагонали — зависят от ребра куба, представленного как s, так и a.

Как вывести формулу куба?

Чтобы вычислить объем по формуле куба,

• Шаг 1: Рассмотрим любой квадратный лист бумаги.
• Шаг 2: Теперь площадь, покрытая этим квадратным листом, будет равна площади его поверхности, т. е. его длине, умноженной на его ширину. Оба одинаковы в случае куба. Таким образом, площадь поверхности будет равна «s 2 ».
• Шаг 3: Куб получается путем складывания нескольких квадратных листов таким образом, чтобы высота стала равной длине и ширине, т. е. единицам «s». Таким образом, высота или толщина куба равна «s».

Таким образом, можно сделать вывод, что общее пространство, занимаемое кубом, то есть объем, равно площади основания, умноженной на высоту. Объем куба = s 2  × s = s 3

Чтобы вывести формулу поверхности куба,

• Шаг 1. Рассмотрим любой лист бумаги квадратной формы.
• Шаг 2: В случае квадрата, поскольку длина и ширина равны, площадь поверхности будет равна «s 2 » (длина, умноженная на ширину).
• Шаг 3: Поскольку у куба 6 граней, общая площадь поверхности куба равна площади одной грани, умноженной на 6 = 6s 2

Призма

Определения:

1. Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.
2. Основания – это две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях. На чертеже это: ABCDE и KLMNP.
3. Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. На чертеже это: ABLK, BCML, CDNM, DEPN и EAKP.
4. Боковая поверхность – объединение боковых граней.
5. Полная поверхность – объединение оснований и боковой поверхности.
6. Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.
7. Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.
8. Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.
9. Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания. Другое определение: диагональная плоскость – плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани.
10. Диагональное сечение – пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе, иногда, его частные случаи – ромб, прямоугольник, квадрат. На чертеже это, например, EBLP.
11. Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Свойства и формулы для призмы:

• Основания призмы являются равными многоугольниками.
• Боковые грани призмы являются параллелограммами.
• Боковые ребра призмы параллельны и равны.
• Объём призмы равен произведению её высоты на площадь основания:

где: S_осн – площадь основания (на чертеже это, например, ABCDE), h – высота (на чертеже это MN).

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания:

• Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы (на чертеже ниже перпендикулярное сечение это A₂B₂C₂D₂E₂).
• Углы перпендикулярного сечения – это линейные углы двугранных углов при соответствующих боковых рёбрах.
• Перпендикулярное (ортогональное) сечение перпендикулярно ко всем боковым граням.
• Объем наклонной призмы равен произведению площади перпендикулярного сечения на длину бокового ребра:

где: S_сеч – площадь перпендикулярного сечения, l – длина бокового ребра (на чертеже ниже это, например, AA₁или BB₁ и так далее).

Площадь боковой поверхности произвольной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра:

где: P_сеч – периметр перпендикулярного сечения, l – длина бокового ребра.

Виды призм в стереометрии:

• Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (изображены выше). Основания такой призмы, как обычно, расположены в параллельных плоскостях, боковые рёбра не перпендикулярны этим плоскостям, но параллельны между собой. Боковые грани – параллелограммы.
• Прямая призма – призма, у которой все боковые ребра перпендикулярны основанию. В прямой призме боковые ребра являются высотами. Боковые грани прямой призмы — прямоугольники. А площадь и периметр основания равны соответственно площади и периметру перпендикулярного сечения (у прямой призмы, вообще говоря, перпендикулярное сечение целиком является такой же фигурой, как и основания). Поэтому, площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы):

где: P_осн – периметр основания прямой призмы, l – длина бокового ребра, равная в прямой призме высоте (h). Объем прямой призмы находится по общей формуле: V = S_осн∙h = S_осн∙l.

Правильная призма – призма в основании которой лежит правильный многоугольник (т.е. такой, у которого все стороны и все углы равны между собой), а боковые ребра перпендикулярны плоскостям основания. Примеры правильных призм:

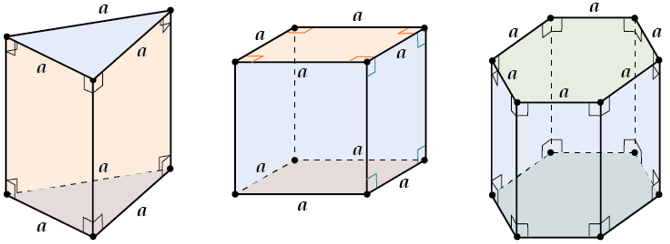
Свойства правильной призмы:

1. Основания правильной призмы являются правильными многоугольниками.
2. Боковые грани правильной призмы являются равными прямоугольниками.
3. Боковые ребра правильной призмы равны между собой.
4. Правильная призма является прямой.

Примеры использования куба в реальной жизни

1. Архитектура

Куб используется в архитектуре для создания кубических форм зданий. Например, многие современные небоскребы имеют квадратную или кубическую форму. Кубы также используются для создания стилей и украшения на зданиях.

2. Индустрия

Куб используется в индустрии для создания кубической формы некоторых изделий. Например, кубы могут использоваться для создания покрытий для защиты оборудования или для создания ящиков для хранения и перевозки товаров.

3. Головоломки

Кубы известны и как головоломки. Например, Rubik’s Cube – это головоломка, состоящая из множества маленьких кубиков, которые необходимо поворачивать и менять местами, чтобы получить одинаковые цвета на каждой грани.

4. Визуальное искусство

Визуальные художники могут использовать кубы в своих работах. Например, кубические формы могут использоваться для создания абстрактных композиций, скульптур и других произведений искусства.

5. Математика

Куб используется в математике при решении уравнений и задач. Например, кубическая формула используется для нахождения корней кубического уравнения. Также куб может использоваться для определения объема кубической фигуры.

Вопрос-ответ:

Что такое куб в математике?

Куб — это геометрическое тело, состоящее из шести квадратных граней, у которых все ребра равны между собой. В математике куб является особым случаем параллелепипеда.

Какие примеры использования куба в математике есть?

Куб используется для решения задач по геометрии, а также в различных областях математики, таких как алгебра, геометрия, теория чисел и т.д. Например, кубы используются в задачах по нахождению объема, площади поверхности, диагоналей и т.д.

Как проверить, является ли параллелепипед кубом?

Для того чтобы узнать, является ли параллелепипед кубом, нужно проверить, равны ли все его ребра. Если они равны, то это куб, если нет, то это параллелепипед, но не куб.

Можно ли разложить куб на две равные части?

Нет, нельзя разложить куб на две равные части, так как куб имеет нечетное количество ребер и нечетное количество диагоналей.

Зачем нужны кубические уравнения в математике?

Кубические уравнения используются в различных областях математики, таких как теория чисел, аналитическая геометрия и т.д. Также они находят свое применение в физике, химии и других науках. Например, кубические уравнения используются для поиска корней уравнения, а также для решения задач, связанных с геометрией и физикой.

Площадь поверхности куба, формула.

На следующей диаграмме показана прямоугольная призма. А right prism призма, основания которой перпендикулярны ее боковым поверхностям. В surface area призмы — это общая площадь всех ее внешних граней. To calculate the surface area of a rectangular prism Вычисляем площадь каждой из шести граней призмы.

Знание площади куба позволяет проводить точные расчеты и улучшать практическую реализацию задач, связанных с кубическими формами. Как найти площадь куба? Таким образом, чтобы найти площадь куба, необходимо возвести длину ребра в квадрат и умножить на шесть. Простое объяснение шагов для расчета площади куба Первым шагом является измерение длины одной из сторон куба. Обозначим ее за a. Учитывая, что у куба шесть граней, мы должны умножить площадь одной грани на шесть: Площадь куба.

Пример 2: Предположим, у нас есть куб с ребром длиной 8 м. Методы расчета площади куба позволяют решать разнообразные задачи, связанные с данным геометрическим телом.

Какие данные известны: длина ребра , объем , диагональ , площадь грани. В зависимости от этого выбирается формула. Если по условиям задачи известна длина ребра куба , то достаточно применить простейшую формулу для нахождения площади. Известно практически каждому, что площадь квадрата находится умножением длин двух его сторон. Грани куба — квадраты, следовательно, площадь его поверхности равна сумме площадей этих квадратов. Где х — длина ребра куба. Допустим, что ребро куба не задано, но известен. Так как объем данной фигуры вычисляется возведением в третью степень длины его ребра , то последнюю можно получить достаточно легко. Для этого из числа, обозначающего объем, необходимо извлечь корень третей степени. Например, для числа 27 корнем третей степени будет число 3. Ну а что делать дальше, мы уже разбирали. Таким образом, формула площади куба при известном объеме также существует, где вместо х стоит корень третей степени из объема. Бывает, что известна только длина диагонали. Если вспомнить теорему Пифагора , то можно легко вычислить длину ребра. Здесь достаточно базовых знаний. Подводя итог, стоит отметить, что для правильных вычислений нужно узнать длину ребра. Условия в задачах встречаются самые разные, поэтому следует научится выполнять сразу несколько действий. Если известны другие характеристики геометрической фигуры, то с помощью дополнительных формул и теорем можно вычислить ребро куба. И уже на основании полученного результата посчитать результат. Под кубом подразумевается правильный многогранник, у которого все грани образованы правильными четырехугольниками — квадратами. Для того, чтобы найти площадь грани любого куба, не потребуется тяжелых расчетов

Инструкция Для начала стоит заострить внимание на само определение куба. Из него видно, что любая из граней куба представляет собой квадрат

Можно взять именно любую из граней куба, так как длины всех его ребер равны между собой. Для того, чтобы найти площадь грани куба, требуется перемножить между собой пару любых из его сторон, ведь все они между собой равны. Ответ: площадь грани куба с ребром 11 см равна 121 см? Обратите внимание Любой куб имеет 8 вершин, 12 ребер, 6 граней и 3 грани при вершине. Помимо различных кубических единиц измерения объема, в нефтяной и газовой промышленности возможно применение иной единицы — баррель 1м? Как найти площадь у куба? Формула вычисления площади куба Через длину ребра Площадь S поверхности куба равна произведению числа 6 на длину его ребра в квадрате. Как найти площадь и объем куба? Запишите формулу для вычисления площади поверхности куба. Чтобы вычислить объем куба, нужно перемножить значения трех его ребер длину, ширину и высоту. У куба длина, ширина и высота равны, поэтому нужно найти значение одного любого ребра, чтобы вычислить объем куба.

Свойства шестигранника

Правильную шестиугольную призму принято обозначать большими латинскими буквами: ABCDEFA1B1C1D1E1F1. Длину основания подписывают маленьким символом a, а длину боковой стороны h. К характеристикам фигуры относят площади основания, боковые грани, полную поверхность, объём многогранника. Всего у геометрического тела 8 граней, 18 рёбер и 12 вершин.

Для успешного вычисления различных параметров фигуры понадобится знать следующие формулы:

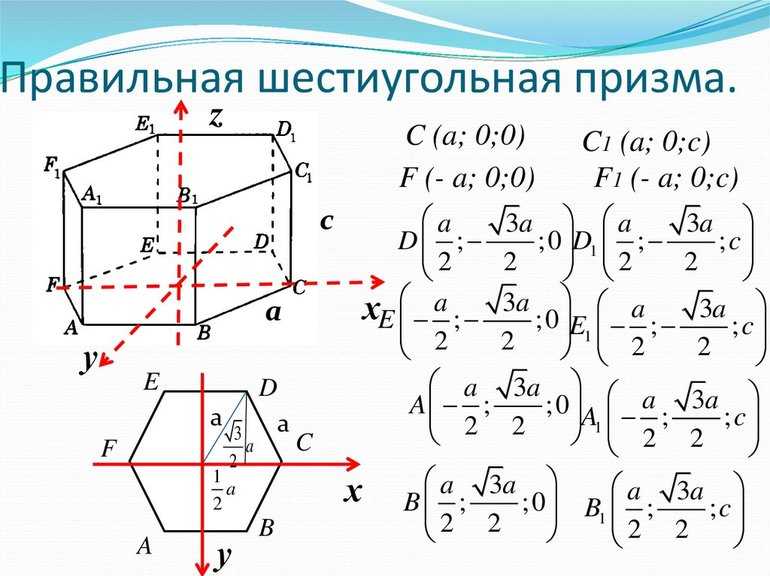
1. Площадь основания. Так как в основе тела лежат правильные шестиугольники, то, используя их свойства, можно получить формулу: S = (3 * a 2 * √ 3) / 2, где: а — сторона многоугольника.
2. Площадь полной поверхности. Определяется она из равенства: Sb = 6 * a * h + 2 * (3 * a 2 * √ 3) / 2. Из-за того, что площадь плоскости можно получить путём сложения сторон призмы и двух поверхностей её основания, а грань — прямоугольник (S прямоугольника = a * h), то указанная формула будет верной.
3. Объём. Он равняется произведению площади основания на высоту. Роль последней может играть ребро любой стороны, например, BB1. Учитывая сказанное, формулу можно записать так: V = S * BB 1 = ((3 √ 3) / 2) * (a 2 * h).

Если рассмотреть правильный шестиугольник, лежащий в основе призмы ABCDEF, и провести отрезки AB, CD, EF, у них будет общая точка пересечения. Для удобства обозначить её можно буквой O. Так как, в соответствии со свойствами, треугольники AOB, BOC, COD, DOE, EOF, FOA будут правильными, можно составить равенство: AO = OD = EO = OB = CO = OF = a .

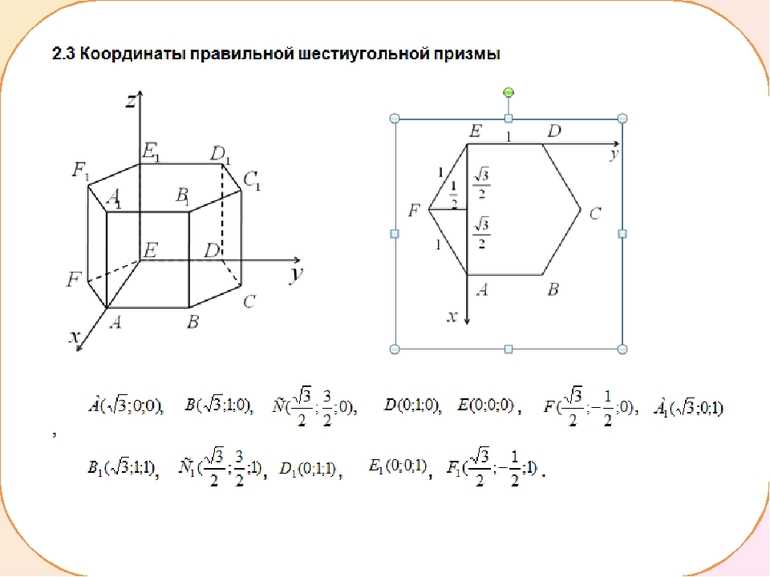
Через точку М можно провести прямую AC и CF. Образованный ранее треугольник AEO будет равнобедренным. В нём отрезок AO равняется по величине OE. Значит, угол EOA будет развёрнутым и равняться 120 градусам. Используя свойства равнобедренного треугольника, можно записать: AE = a * √2 * (1 — cos EOA). То есть: AE = AC = √3 * a.

По аналогии можно найти и стороны: EA1, FB1, AC1, BD1, CE1, DF1. Так как AA1 = h, а из свойств правильной призмы следует, что угол EAA1 — прямой, длины сторон будут равны между собой, и их можно найти, используя формулу: √(AA1 2 + AE 2 )= √(h 2 + 3 * a) = 2 * a. Грань EB1 = FC1 = AD1 = BE1 = CF1 = DA1 = √(BB1 2 + BE 2 ) = √(h 2 + 4 *a) = √5 *a. Сторона FE1 = √(FE 2 + EE 2 ) = √(h 2 + a 2 ) = √2 *a.

Видео:Построение сечения шестиугольной пирамиды и нахождение площади сеченияСкачать