Как сделать кубик из картона. интересно, а как сделать куб из бумаги? создание куба на скорую руку

Занимательные грани

Удивительно, но многие знания об окружающем мире становятся интересны не на школьной скамье, а лишь тогда, когда можно найти в них нечто увлекательное, способное дать что-то новое, необычное в привычной жизни. Не многие взрослые помнят, что те же многогранники делятся на огромное количество видов и подвидов. Например, есть так называемые платоновы тела — выпуклые многогранники, состоящие только лишь из Таких тел всего пять: тетраэдр, октаэдр, гексаэдр (куб), икосаэдр, додекаэдр. Они представляют собой выпуклые фигуры без впадин. Звездчатые многогранники состоят из этих основных фигур в различных конфигурациях. Поэтому-то
развертка многогранника простого позволяет нарисовать, вернее начерить, а затем и склеить из бумаги звездчатый многогранник.

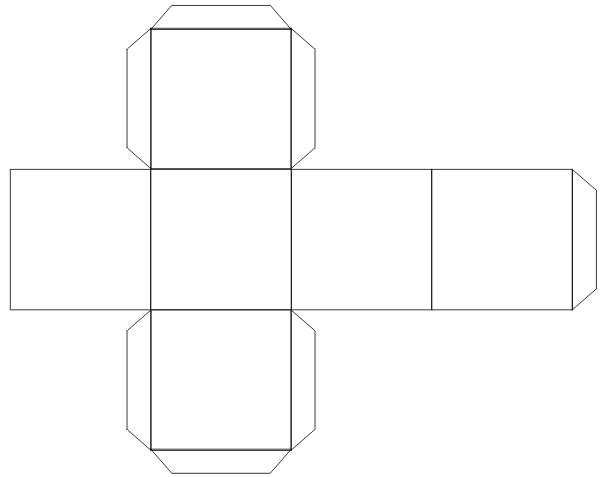
Как сделать куб из бумаги?

Куб – правильный многогранник, каждая грань которого представляет собой квадрат

Создание куба состоит из двух этапов: создание развертки и склеивание. фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.

Рисование развертки:

1. Выбираем размеры квадрата — одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон.
2. Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба. Рисуем их строго на одной линии, вплотную друг к другу.
3. Над и под любыми из квадратов рисуем по одному такому же квадрату.
4. Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской.
5. Куб готов!

После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!

Правильные и неправильные звездчатые многогранники

Складывая платоновые тела между собой в определенном порядке, вы можете построить немало звездчатых многоранников — красивых, сложных, многокомпонентных. Но они будут называться «неправильными звездчатыми многогранниками». Правильных звездчатых многогранников всего четыре: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Развертки многогранников для склеивания не будут простыми чертежами. Они, как и фигуры, будут состоять из нескольких компонентов. Так, например, малый звездчатый додекаэдр строится из 12 пятиугольных равнобочных пирамид, сложенных по типу правильного додекаэдра. То есть для начала придется начертить и склеить 12 одинаковых штук правильных пирамид, состоящих из 5 равных граней. И только затем из них можно сложить звездчатый многогранник. Развертка самого малого звездчатого додекаэра — сложное и практически невыполнимое задание. Чтобы ее простроить, нужно суметь на одной плоскости уместить соединенные друг с другом 13 разверток разных геометрических объемных тел.

Поделки из бумаги — увлечение на всю жизнь

Что-то делать руками всегда интересно и полезно, особенно если получается красиво. Ручная несложная работа помогает успокоить нервы после тяжелого трудового дня и развивает фантазию (особенно у детей). В Китае данный вид творчества известен как оригами, и давно с успехом помогает лечить душевнобольных людей и детишек, страдающими нервными заболеваниями. Такие занятия повсеместно применяются на уроках труда в школах или в старших группах в детских садах, что позволяет развить усидчивость, воображение и мелкую моторику, которая в свою очередь развивает умственную деятельность. Часто детские журналы предлагают схемы различных зверюшек, фигурок для совместной работы взрослых с детьми. Мы предлагаем схемы кубиков из бумаги или картона с различными вариантами картинок. Такие поделки будут интересны как малышам, так и школьникам, их можно преподнести в качестве подарка, сделанного своими руками. Взрослые так же могут использовать сделанные по нашим разверткам кубики, например кубик-календарь.

Пошаговая инструкция: как сделать куб из картона

1. Распечатайте необходимое количество шаблонов, например для кубика-календаря – необходимо оба варианта, а для кубиков с алфавитом – распечатайте столько, сколько нужно для складывания слов.
2. Аккуратно вырежьте схему куба. Вырезать удобнее ножницами, но можно воспользоваться и канцелярским ножом.
3. Согните вырезанный шаблон куба по линиям, чем аккуратнее вы согнёте схему куба, тем лучше будет смотреться ваше изделие.
4. Смажьте затемненные участки клеем и сторону за стороной соберите весь куб.

Разверткапростого куба(грань 5 см)	Развертка кубас арабскими цифрами1,2,3,4,5,6(грань — 5 см)	Развертка кубас арабскими цифрами7,8,9,0,1,2(грань — 5 см)
JPG	JPG	JPG

I, X, L, C, V, D (грань — 5 см)	Развертка куба с римскими цифрамиI, M, V, X, ↁ, ↂ (грань — 5 см)	Куб с формулами(грань — 5 см)
JPG	JPG	JPG

A, B, C, D, E, F(грань 6,5 см)	Схема куба с английским алфавитом G, H, I, J, K, L(грань 6,5 см)	Схема куба с английским алфавитом M, N, O, P, R, Q(грань 6,5 см)
JPG	JPG	JPG

Схема куба с английским алфавитом S, T, U, R, V, W (грань 6,5 см)	Схема куба с английским алфавитом X, Y, Z, A, B, C (грань 6,5 см)	Схема куба с русским алфавитомА, Б, В, Г, Д, Е (грань 6,5 см)
JPG	JPG	JPG

Схема куба с русским алфавитом Ж, З, И, Й, К, Л (грань 6,5 см)	Схема куба с русским алфавитом М, Н, О, П, Р, С (грань 6,5 см)	Схема куба с русским алфавитом У, Ф, Х, Ц, Ч, Т (грань 6,5 см)
JPG	JPG	JPG

Схема куба с русским алфавитом Ш, Э, Ъ, Ы, Ь, Щ (грань 6,5 см)	Схема куба с русским алфавитом Ю, Я, А, Б, В, Г (грань 6,5 см)	Схема куба с материками (грань 6,5 см)
JPG	JPG	JPG

И еще немного о кубиках из бумаги

Сейчас детские магазины переполнены всякими игрушками, в том числе и развивающими. Можно найти практически всё на любой возраст и кошелёк. Но иногда бывет трудно найти кубики, которые нам знакомы с детства. Кубики — это своего рода конструкторы, с которыми с удовольствием играют детишки.По рекомендациям педагогов, психологов и педиаторов малышам до 1 года уже можно давать игрушки-кубики. Они отлично развивают не только координацию, воображение, но при этом задействуют практически все мышцы рук, что прекрасно развивает мелкую моторику малыша. Из какого только материала не делают кубики — и из пластика, из дерева, из стекла, мы предлагаем вам сделать кубики из бумаги.Кубики с картинками с изображением цифр или букв будут прекрастным подспорьем для родителей и воспитателей в процессе подготовки ребёнка к школе. Более того, игра с кубиком даст малышу представление о геометрическх фигурах, в частности о кубе, о его свойствах. Если вы распечатаете и другие объемные геометрические фигуры (пирамиды, тетраэдр и т.д.), это значительно расширит кругозор ребёнка и поможет в процессе обучения в школе. Совместные занятия взрослых и детей очень сближают и укрепляют семью.

Сейчас практически в каждом доме есть компьютер и принтер, т.е. ваши затраты — это стоимость бумаги, формата А4. Приведённые на данной странице шаблоны куба можно редактировать, т.е. взяв чистую развёртку куба, вы можете смело вставлять свои картинки и распечатать новый вариант. В качестве картинок можно взять рисунки или фотографии зверей, животных, машин, а так же фотографии знаменитостей или своих родственников, полет фантазии безграничен. Успехов вам в творчестве и в воспитании!

Развертка и схема куба из бумаги

Разноцветный куб 1 (грань 6,5 см)	Разноцветный куб 2 (грань 6,5 см)	Игральный куб (грань 5 см)
		JPG

Григорий Андреев

Куб является, многогранной фигурой, стороны, которой представлены квадратом. Если вы или ваш малыш любит загадки, то прочитав статью, узнаете, как сделать кубик из бумаги. Также узнаете о разнообразных вариантах кубов и подробный процесс изготовления, каждого из видов.

Из развертки

Развертками называют схемы, позволяющие сделать объемную фигуру из бумаги или картона. Для начала научимся строить развертку. Для ее изготовления вам нужна бумага, карандаш, линейка и ножницы.

Все стороны куба представляют собой квадраты. Значит, для начала на листе бумаги нужно начертить квадрат. При этом не забывайте о правилах геометрии – у квадрата все стороны равны, а углы составляют 90°. Далее, вспоминаем, сколько граней у куба – шесть. То есть на схеме для склеивания их тоже должно быть шесть. Вокруг центрального квадрата начертите четыре квадрата. Куда же деть еще один? Просто начертить его сбоку от одного из квадратов. Грани на месте, не хватает припусков для склеивания. Их нужно начертить на трех боковых квадратиках. Составляют они 0,5-1 см.

Развертка готова! Вот что у вас должно получиться:

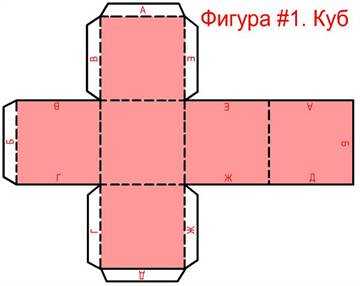
Теперь нужно вооружиться ножницами и клеем и собрать фигуру. Вырежьте развертку при помощи ножниц. Далее, нужно согнуть все грани куба, а также припуски. Смажьте грани клеем и соедините куб воедино. Объемный куб из бумаги готов!

Кубик техникой оригами

Существует огромное количество способов сборки фигур в технике оригами. Но для простоты следует изучить самый простой метод, для которого требуется осуществить следующие действия:

1Приготовить форму – стандартный квадрат из бумаги. Картон лучше не использовать, поскольку он плотный и собрать из него фигуру будет неудобно.

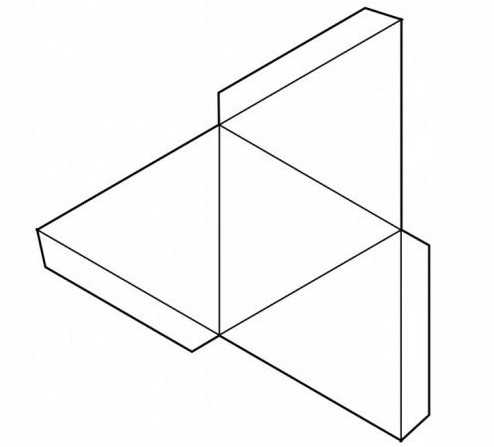
2Сложить квадрат пополам вдоль одной стороны и по диагонали в каждом направлении. Складывают лист по стороне и по диагоналям в противоположные направления: по стороне в одном направлении, по диагоналям в противоположные. Сделать треугольник, как представлено на картинке.

Схема сборки куба в технике оригами

3Одну часть треугольника отделить, приставить ее к середине и загнуть – получится, что угол поднимется к вершине треугольной основы. Аналогичным образом делают со второй стороной.

4Далее у уменьшенных треугольников углы, расположенные в разные стороны, направляют друг к другу – сгибают вершину треугольника пополам.

5Затем требуется согнуть свободную вершину треугольника в более меньший. Продолжить сгиб так, чтобы собранная вершина смогла разместиться между двумя прослойками предварительной треугольной заготовки.

6Расположить будущую фигуру на столе и загнуть оставшиеся треугольные верхушки вовнутрь. Получится, что загнуться две верхушки – их необходимо только загнуть и разогнуть обратно. Эти действия только формируют грани будущего куба. Аналогичным образом делают грани будущей фигуры, согнув вершины в противоположную сторону и также расправив их.

7Далее расправляют основу, отправив вовнутрь стороны с согнутыми треугольниками.

8В одной вершине треугольника сформировалось отверстие, в которое задувают, чтобы расправить заготовку для формирования куба. .

Получился стандартный куб с одинаковыми гранями и равными сторонами. Его можно использовать для декора и прочих действий. Написать на нем что-то будет сложно, но возможно. Поскольку изделие получается большим, их рекомендуется использовать для игр с маленькими детьми – с малышами и дошкольного возраста.

Как сделать цилиндр из бумаги?

Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

Рисование развертки:

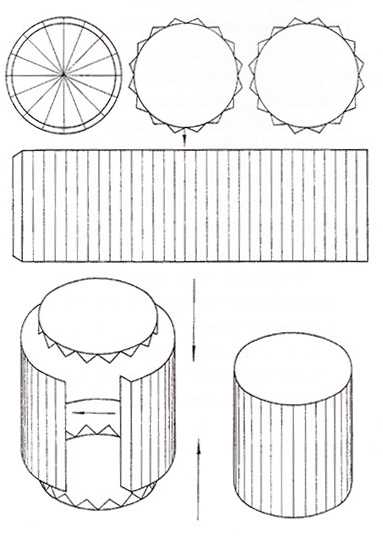
1. Рисуем прямоугольник на бумаги, в котором ширина — это высота цилиндра, а длина определит диаметр будущей фигуры. Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
2. Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
3. Вырезаем все детали будущего бумажного цилиндра.
4. Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.
5. Цилиндр готов!

Ссылки

Трёхмерные (Тетраэдр • Куб • Октаэдр • Додекаэдр • Икосаэдр) Четырёхмерные (6 правильных многогранников) Большей размерности (только 3 типа правильных многогранников: n-мерный симплекс, n-мерный октаэдр, n-мерный куб)

Звёздчатый многогранник (Звёздчатый октаэдр, Звёздчатый додекаэдр, Звёздчатый икосаэдр, Звёздчатый икосододекаэдр)

Wikimedia Foundation . 2010 .

Смотреть что такое «Куб (геометрия)» в других словарях:

ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера

МНОГОМЕРНАЯ ГЕОМЕТРИЯ — геометрия пространств размерности, большей трех; термин применяется к тем пространствам, геометрия к рых была первоначально развита для случая трех измерений и только потом обобщена на число измерений n>3, прежде всего евклидово пространство,… … Математическая энциклопедия

N-мерная евклидова геометрия — N мерная евклидова геометрия обобщение евклидовой геометрии на пространство большего числа измерений. Хотя физическое пространство является трёхмерным, и человеческие органы чувств рассчитаны на восприятие трёх измерений, N мерная… … Википедия

Пирамида (геометрия) — У этого термина существуют и другие значения, см. Пирамидацу (значения). Достоверность этого раздела статьи поставлена под сомнение. Необходимо проверить точность фактов, изложенных в этом разделе. На странице обcуждения могут быть пояснения … Википедия

Конструктивная блочная геометрия — (Constructive Solid Geometry, CSG) технология, используемая в моделировании твёрдых тел. Конструктивная блочная геометрия зачастую, но не всегда, является способом моделирования в трёхмерной графике и САПР. Она позволяет создать сложную сцену или … Википедия

Координационная геометрия — Содержание 1 Молекулы 2 Координационные комплексы неорганических соединений … Википедия

Конструктивная сплошная геометрия — Конструктивная блочная геометрия (Constructive Solid Geometry, CSG) технология, используемая в моделировании твёрдых тел. Конструктивная блочная геометрия зачастую, но не всегда, является способом моделирования в трёхмерной графике и САПР. Она… … Википедия

Призма (геометрия) — У этого термина существуют и другие значения, см. Призма … Википедия

Объём (геометрия) — У этого термина существуют и другие значения, см. Объём (значения). Объём это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого… … Википедия

Объем (геометрия) — Объём это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого определения в отношении трёхмерных тел трёхмерного евклидова пространства.… … Википедия

Простой бумажный кубик

Объемный шестигранный куб 3Д складывают из квадратного листка бумаги без клея. И даже ножницы здесь не потребуются. Разве что отрезать лишний «хвостик» от листа А4, чтобы получить заготовку-квадрат. Зато пригодится навык надувания воздушных шариков, ведь мы сейчас научим вас тому, как сделать надувной кубик. Заинтригованы? Тогда начнем:

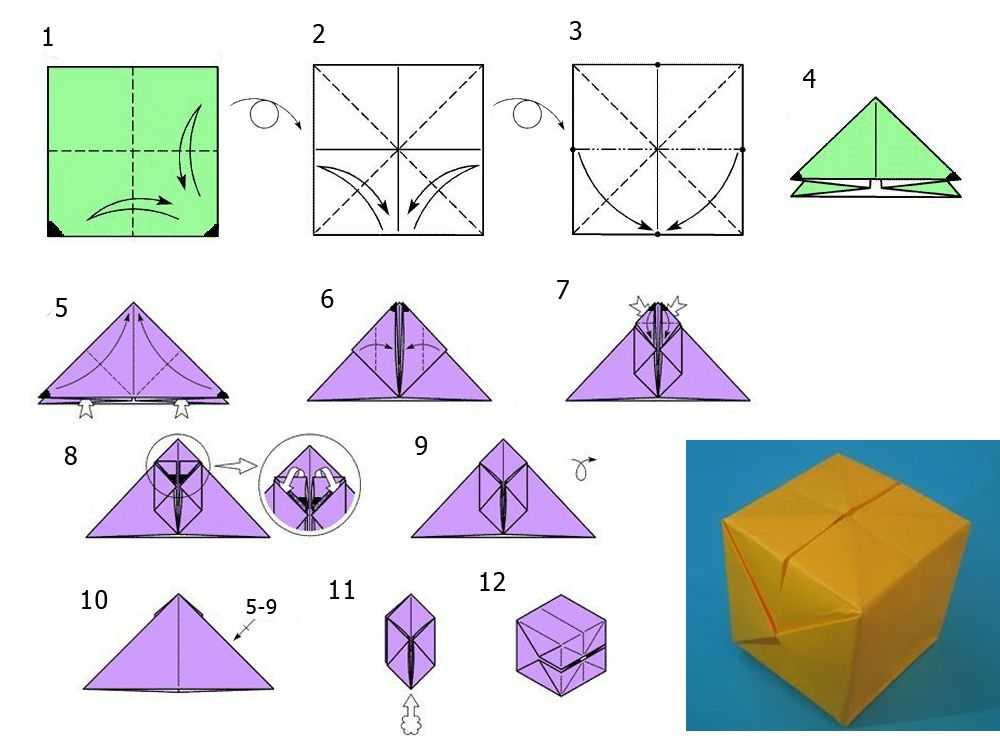
• Схема 1 — ваш наглядный ориентир. К нему следует прибегать каждый раз, когда алгоритм складывания кажется сложным. Возьмите бумажный квадрат и сложите его по диагоналям, затем пополам — все это просто разметка;
• Ориентируясь на диагонали-сгибы, сформируйте треугольник, подгибая внутрь боковые плоскости заготовки (см. схему). 4 гуляющих угла у основания треугольника нужно подогнуть к вершине по 2 с каждой стороны заготовки;
• Боковые противоположные уголки подогните к центру — у вас здесь есть вертикальная ось-ориентир. Повторите действие с другой стороны. Гуляющие уголки одного из конических выступов (на втором углы «закрыты») дважды подгибают, чтобы их можно было аккуратно заправить в срединные уголки-кармашки;
• Аналогично заправьте дважды сложенные уголки в кармашки с обратной стороны заготовки. Модель куба готова, осталось дать ей объем. Найдите открытый уголок и через него надуйте макет.

Как сделать из бумаги или картона куб-трансформер

Для того чтобы выполнить куб-трансформер, потребуются лист картона, линейка, карандаш, скотч или клей.

Первым делом, надо обозначить на листе картона восемь разверток кубиков со сторонами три сантиметра. Затем каждую развертку следует вырезать и сложить из них кубики. После того, как кубики будут готовы, их необходимо соединить, используя кусочки скотча. На фото, размещенном ниже, будет показано, где должны располагаться места соединения. Кубики склеивать между собой необходимо с двух сторон.

Кубик можно украсить, наклеив на каждую сторону кубика картинки одной тематики. Чаще всего такие кубики используют в качестве календаря, меню или памятного сувенира, например, для туристов, обклеив кубик изображениями достопримечательностей города.

Дополнительные материалы

Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Геометрия и куб

Куб — это фигура, которые мы встречаем не только на уроках геометрии и изобразительного искусства, но и в нашей повседневной жизни. Другое название куба — правильный гексаэдр. Кубом называется правильный многогранник, каждая грань которого является квадратом. Куб можно назвать объемный, трехмерным или даже 3D квадратом. Куб имеет 8 вершин, 6 граней, 12 ребер. Куб — это удивительная геометрическая фигура, в которую можно спрятать или вписать другие фигуры, например такие: октаэдр, тетраэдр, икосаэдр и другие.

Удивительная фигура «куб»

Куб или гексаэдр также называют кубом Неккера, назван он так в честь швейцарского кристаллографа Луиса Альберта Неккера. В 1832 году Неккер предложил иллюзию, вглядываясь в куб с гранями можно заметить, что маленькая черная точка появляется то на переднем, то на заднем плане, то в углу или в центре. Она перемещается из одного места в другое, как бы движется. Еще одна особенность куба Неккера в том что, его параллельные боковые ребра кажутся расходящимися. Можно перекрасить одну из граней в другой цвет, и посмотреть, как эта цветная грань фантастическим образом перемещается.

Еще один необычный куб — это куб художника Маурица Эшера. Это куб, который невозможен.

Еще одно интересное открытие, имеющие отношение к кубу, было сделано в 1966 году благодаря фотографу Чарльзу Ф. Кокрану. Он сделал фотографию, которую окрестили «сумасшедший ящик». Что же из себя представляет «сумасшедший язык»? Это вывернутый наизнанку каркас фигуры гексаэдра (куба). «Сумасшедший ящик» основывается на неправильных соединениях, которые допустили при рисовании фигуры.

Куб Неккера

«Сумасшедший ящик»

В список самых удивительных и странных фигур можно занести: интегральный куб, разрастающийся куб (также может называться бесконечным кубом), повторяющиеся кубы, кубическую снежинку, парящие кубы, двухэтажный куб и многие, многие другие. Все эти фигуры завораживают, от них не возможно оторвать глаз. Каждый, кто их видит, хочет понять, как они устроены.

Куб всегда таил в себе много загадок — удивительно сложная и в тоже время удивительно простая геометрическая фигура, помогающая заглянуть в глубины сознания. Еще в древности Платон называл ее священной фигурой и относил к знаку Земли, потому что это самая устойчивая фигура из всех других. Куб является фигурой сакральной геометрии. Еще в 16 веке немецкий математик и астроном Иоганн Кеплер составил модель солнечной системы, в которую вписал куб.

Где можно встретить куб? Здания чаше всего имеют кубическую форму, так что можно просто выглянуть в окно, и вы сразу увидите куб. Самая знаменитая игрушка-головоломка, которую хотя бы раз в жизни каждый ребенок держал в руках, а некоторым даже удалось ее собрать, это кубик Рубика. Название говорит само за себя. В 1975 году венгерский архитектор Эрне Рубик создал игрушку-головоломку, которая стала популярной во всем мире. Кубик-рубик представляет собой куб, сделанный из пластмассы, который в свою очередь состоит из 26 кубиков. И когда «Кубик-рубик» собран, каждая его грань окрашивается в один определенный цвет.

Различные вещества кристаллизуются в форме куба, например поваренная соль, минерал флюорит и другие.

Инструменты и материалы, чтобы сделать куб из бумаги

Чтобы комфортно и удобно работать с бумагой или картоном, в нашем случае вырезать и склеивать геометрические фигуры, вам понадобятся следующие инструменты:- ножницы (или канцелярский нож с железной линейкой и твердой поверхностью, которую не жалко испортить);- плотная бумага или картон (белый или цветной), формата А4;- клей.Так же вам необходим компьютер с принтером, лучше цветным, чтобы распечатать понравившуюся схему для дальнейшего склеивания фигуры.

Инструкция

1. Для начала выберите размер вашего будущего куба. Например, в его основании может быть квадрат размером 6х6 см или меньше. В этом случае для изготовления куба вам точно хватит обычного плотного листа формата А4.
2. Возьмите карандаш и линейку – с помощью этих инструментов вы сможете построить развёртку куба. Она должна состоять из шести квадратов, соединённых между собой в форме креста. Расположите лист вертикально и начните рисовать развёртку, немного отступив от верхнего края листа. Чтобы не запутаться, смотрите на рисунок.
3. Постройте первый квадрат выбранного размера. Затем строго под ним нарисуйте ещё один такой же квадрат так, чтобы одна грань у них была общей. На рисунке этот квадрат обозначен цифрой 3. Теперь справа, слева и снизу от этого квадрата нарисуйте ещё по одному. Наконец, последний квадрат (номер 6) нарисуйте под самым нижним из уже построенных.
4. У квадратов под номерами 1, 2 и 4 нарисуйте небольшие клапаны, которые в дальнейшем помогут склеить из развёртки готовую фигуру. Один клапан расположите над верхней гранью первого квадрата (именно для этого было оставлено место у края листа), а ещё шесть – возле всех свободных граней двух боковых квадратов.
5. Теперь возьмите ножницы и аккуратно вырежьте получившуюся развёртку по контуру.
6. При помощи линейки согните развёртку по линиям. Для начала отогните все клапаны вверх, а затем поднимите квадраты под номерами 1, 2, 4 и 5. Шестой квадрат должен оказаться на самом верху – это «крышка» куба.
7. Возьмите клей, промажьте им все клапаны и соедините их с соседними гранями с внутренней стороны. Ваш куб готов!

Занятие прикладными видами творчества — увлекательный процесс. Трёхмерные фигурки, выполненные из таких привычных материалов, как простая бумага или картон, завораживают. Увидев хоть раз работы мастеров оригами или йошимото, невозможно бороться с желанием постичь основы этого искусства и создать свой шедевр. Вспомним наше детство, но подойдём к основам мастерства серьёзно и узнаем, как сделать куб из бумаги или картона.

Если кто-то не помнит школьной геометрии, то речь идёт о шестиграннике с равными сторонами. Какого размера он будет, зависит от вашей фантазии и величины листа бумаги. Для фигуры понадобятся:

• бумага или картон;
• линейка;
• треугольник;
• карандаш;
• ножницы;
• клей.

Оригами кубик

Техника оригами очень древняя. Ее появление связано с изготовлением бумаги в Древнем Китае. Ее секрет переняли японцы, именно там и зародилось искусство оригами. Раньше фигурки, сложенные из бумаги, носили сакральный смысл. Ими украшали храмы, свадебные и траурные церемонии. Японцы верили, что подвешенные над головой больного шары, сложенные в технике оригами, помогут отогнать болезнь и злых духов. Позже это искусство стало носить не только религиозный, но и развлекательный характер.

Большинство схем для оригами происходит еще с древних времен, но и современные мастера внесли немалый вклад в развитие этого необычного вида творчества. Предлагаем вам попробовать сложить куб в технике оригами. Для этого нужно взять квадратный лист бумаги и сделать сгиб по центру, а потом согнуть края к середине. Такая начальная фигура называется дверь.

Сложите края к центру и заправьте верхние и нижние уголки в кармашки:

Переверните заготовку и согните по линиям, указанным на схеме:

Получился модуль. Для сбора кубика таких модулей нужно шесть. В каждой детали есть кармашки, именно в них вставляются соседние модули. Соедините детали по схеме:

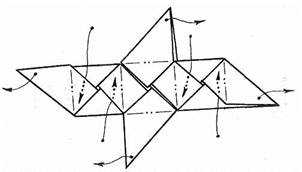
Оригами кубик готов. Для красоты можно сделать каждую грань из бумаги разных цветов.

Использование куба в инженерии

Однородность и прочность куба делают его популярной формой для создания структурных и механических компонентов. Симметричная конструкция куба обеспечивает равномерное распределение напряжения и нагрузки, что делает его идеальным для создания прочных и устойчивых оснований в механических системах. Например, кубы можно найти в:

• кубических шестернях, которые эффективно передают крутящий момент и имеют меньший износ.
• кубические соединительные блоки, используемые в электронике и электропроводке.
• Кубические топливные элементы, производящие электричество с использованием водородного топлива и кислорода.

Преимущества использования кубов в инженерии	Недостатки использования кубов в инженерии
Простота изготовления и сборки благодаря их одинаковой форме и размеру.	Ограничения в диапазоне форм, которые могут быть изготавливается из кубов, что ограничивает творческий потенциал дизайнеров и инженеров.
Равномерное распределение напряжения и нагрузки, обеспечивающее прочность, стабильность и долговечность конструкций и механических компонентов.	Кубы могут быть тяжелыми и громоздкими, что делает их непригодными для определенных применений, требующих легких материалов.
Кубы могут быть штабелируемыми и модульными, что позволяет создавать гибкие конфигурации и легко адаптироваться к изменениям. потребностей.	Чрезмерное использование кубов может привести к однообразию дизайна и упущению творческих альтернатив.

В целом, использование куба в архитектуре и инженерия является свидетельством его универсальности, силы и символизма. Его вездесущность в этих областях, вероятно, сохранится, поскольку архитекторы и инженеры будут стремиться создавать эффективные и эстетически привлекательные конструкции и системы.

Отличие куба от квадрата, разница между ними

Куб и квадрат часто путают, думая, что это тождественные геометрические фигуры. В действительности они отличаются друг от друга, ведь у каждого из этих объектов имеются только им присущие признаки. Какие, нетрудно понять, зная определение куба и квадрата.

Что такое квадрат и что такое куб

Фото: Квадрат

Квадрат – фигура, лежащая на плоскости, и она двухмерная. Её можно отобразить в виде прямоугольника с идентичными по длине сторонами. Квадрат можно вырезать из бумаги.

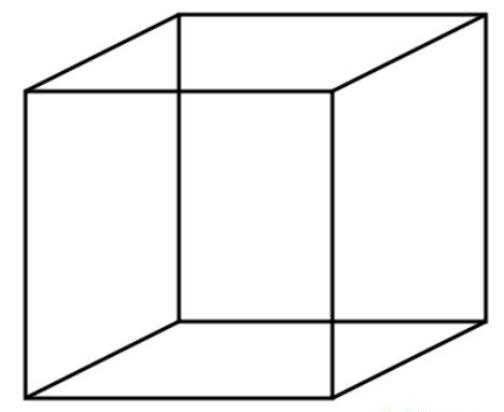
Фото: Куб

Куб же является трехмерным объектом, имеющим объём и 12 одинаковых граней. Таким образом, это правильный многогранник. Если разложить его на плоскости, то он будет состоять из 6 квадратов. Для наглядности куб можно склеить из плотной бумаги, а лучше слепить из гипса, пластилина.

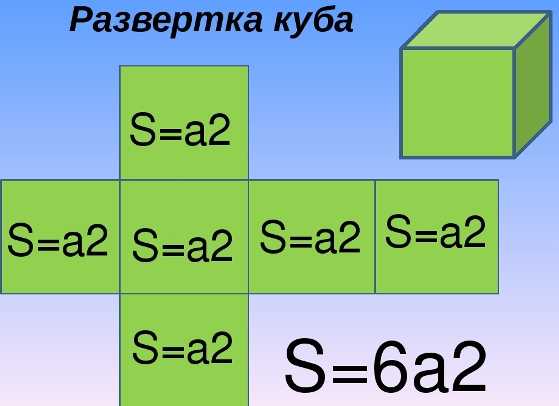
Фото: разложенный куб на плоскости

В чем разница между кубом и квадратом: сравнение двух фигур

По сравнению с квадратом, куб – более сложная геометрия. Квадрат является фигурой простой, в нём только 4 стороны и 4 угла, между которыми абсолютное равенство. Квадрат можно назвать подвидом прямоугольника, только у которого ширина и длина сторон одинаковы. При этом квадрат всегда плоский. Чтобы посчитать площадь квадрата, достаточно умножить одну его сторону на другую.

Конфигурация куба сложнее, поскольку в нём уже присутствует третья мера – объём. Эта характеристика отражает пространство, которое занимает объект, в нашем случае куб. У куба также есть и третье измерение (параметр) – высота. Между собой ширина, длина и высота у куба равны.

Нахождение объема и площади

Если необходимо посчитать объем фигуры, то для расчета берут длину любого ребра между гранями и возводят её в третью степень. Для нахождения площади трехмерной фигуры куба надо узнать сумму площади всех его сторон. Поскольку они идентичны, то просто площадь одной стороны умножаем на 6. А чтобы найти площадь одной из сторон, умножаем длину ребра на себя же. Допустим, длина ребра 4 см, чтобы найти площадь одной стороны куба, 4 умножаем на 4 – получаем 16. И эту цифру уже увеличиваем в 6 раз. Значит, объём куба будет равен 96 см²

Сложные свойства куба

По сравнению с квадратом куб обладает более сложными, дополнительными характеристиками. Например, геометрический объект имеет четыре сечения, которые представляют собой правильные шестиугольники. Все сечения куба проходят через его центр и располагаются перпендикулярно относительно четырех главных его диагоналей.

Поскольку куб имеет объём, то в него можно вписать различные многогранники – такие как тетраэдр (простейший многогранник с гранями в виде 4-х треугольников), октаэдр (у этого многогранника уже 8 граней), икосаэдр (20 граней многогранника).

Чтобы ещё легче было понять разницу между кубом и квадратом, имеет смысл оценить свойства каждой фигуры наглядно. К примеру, взять обычный детский кубик с наклеенными картинками на его стороны. Так вот, сам кубик – это фигура куб, а каждая наклеенная на его сторону картинка – квадрат.

Модульный кубик

Имея знания, как сделать кубик из бумаги в технике оригами и изготовив поделку несколько раз, можно попробовать сконструировать кубик из модулей. Потребуется шесть листов цветной бумаги, желательно, чтобы листов было по 2 одинакового цвета. Что касается цветного картона, то для этой поделки его лучше не использовать.

Также нужно понимать, что подобная работа требует много времени, но в итоге получится прекрасная поделка. При изготовлении нужно соблюдать точную последовательность.

Изготовление модульных поделок, заключается в соединение отдельных элементов в цельную конструкцию. Подобные действия мы проводили при

Процесс изготовления кубика из модулей:

Потратив некоторое время, вы узнали, как сделать модульный кубик из бумаги. И наверняка убедились, что итоговый результат изготовления обладает прекрасным внешним видом.

Если желаете, чтобы поделка не распадалась, то во время конструирования, лучше использовать клей. Он обеспечит надежность крепления деталей.

Оригами кубик

Техника оригами очень древняя. Ее появление связано с изготовлением бумаги в Древнем Китае. Ее секрет переняли японцы, именно там и зародилось искусство оригами. Раньше фигурки, сложенные из бумаги, носили сакральный смысл. Ими украшали храмы, свадебные и траурные церемонии. Японцы верили, что подвешенные над головой больного шары, сложенные в технике оригами, помогут отогнать болезнь и злых духов. Позже это искусство стало носить не только религиозный, но и развлекательный характер.

Большинство схем для оригами происходит еще с древних времен, но и современные мастера внесли немалый вклад в развитие этого необычного вида творчества. Предлагаем вам попробовать сложить куб в технике оригами. Для этого нужно взять квадратный лист бумаги и сделать сгиб по центру, а потом согнуть края к середине. Такая начальная фигура называется дверь.

Сложите края к центру и заправьте верхние и нижние уголки в кармашки:

Переверните заготовку и согните по линиям, указанным на схеме:

Получился модуль. Для сбора кубика таких модулей нужно шесть. В каждой детали есть кармашки, именно в них вставляются соседние модули. Соедините детали по схеме:

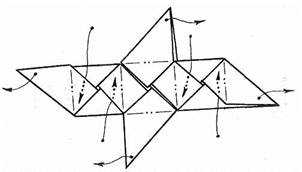
Оригами кубик готов. Для красоты можно сделать каждую грань из бумаги разных цветов.

Как сделать цилиндр из бумаги?

Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

Рисование развертки:

1. Рисуем прямоугольник на бумаги, в котором ширина — это высота цилиндра, а длина определит диаметр будущей фигуры. Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
2. Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
3. Вырезаем все детали будущего бумажного цилиндра.
4. Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.
5. Цилиндр готов!

Квадрат из бумаги: схема изготовления

Геометрические фигурки полюбят изготавливать дети и взрослые — процесс настолько увлекательный, что очень скоро у вас появится целая коллекция разнообразных кубиков. Перед началом работы необходимо запастись нужным количеством бумаги, которой хватит на все стороны, чтобы впоследствии не пришлось доклеивать к имеющемуся каркасу недостающие элементы. Развертка выполняется на ватмане или картоне. Материал должен быть в меру плотным, чтобы фигура не помялась при сборке, но слишком толстый лист бумаги также не подойдет. Особое условие — наличие дополнительных граней по бокам некоторых сторон, при помощи которых будет происходить склеивание куба. Объемный квадрат состоит из восьми одинаковых сторон. Чтобы не ошибиться с выбором ватмана, выполните все расчеты до нанесения чертежа на лист бумаги.

Правильные и неправильные звездчатые многогранники

Складывая платоновые тела между собой в определенном порядке, вы можете построить немало звездчатых многоранников — красивых, сложных, многокомпонентных. Но они будут называться «неправильными звездчатыми многогранниками». Правильных звездчатых многогранников всего четыре: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Развертки многогранников для склеивания не будут простыми чертежами. Они, как и фигуры, будут состоять из нескольких компонентов. Так, например, малый звездчатый додекаэдр строится из 12 пятиугольных равнобочных пирамид, сложенных по типу правильного додекаэдра. То есть для начала придется начертить и склеить 12 одинаковых штук правильных пирамид, состоящих из 5 равных граней. И только затем из них можно сложить звездчатый многогранник. Развертка самого малого звездчатого додекаэра — сложное и практически невыполнимое задание. Чтобы ее простроить, нужно суметь на одной плоскости уместить соединенные друг с другом 13 разверток разных геометрических объемных тел.