Существует ли корень 3 степени из минус 125

Зависимость числа 125 от других математических констант

1. Факториал: факториал числа 5 равен 5! = 5 * 4 * 3 * 2 * 1 = 120. Куб числа 5 (125) является числом, большим, чем факториал числа 5 (120).

2. Логарифмы: натуральный логарифм числа 125 (ln(125)) равен 4.828, а двоичный логарифм (log₂(125)) равен 6.97. Логарифмы показывают, какую степень нужно возвести основание (e или 2) для получения числа 125.

3. Корень: корень кубический из числа 125 равен 5. Корень показывает число, которое нужно возвести в степень, чтобы получить число 125.

4. Пи (π): число π не имеет непосредственной связи с числом 125, хотя оно может быть использовано в выражениях, которые включают 125. Например, радиус сферы, объем которой равен 125, равен ∛(125/(4/3π)).

Таким образом, число 125 может быть связано с различными математическими константами, такими как факториал, логарифмы, корень и пи. Эти связи могут быть полезными при решении математических задач и в научных исследованиях.

Каковы шаги для упрощения квадратных корней?

• Шаг 1: Определите корневое выражение и оцените, есть ли у вас один или несколько радикалов.
• Шаг 2: Если у вас есть более одного радикала, вы можете сгруппировать их, которые перемножаются друг с другом, используя Правило 1. Вы можете сгруппировать их под одним радикалом.
• Шаг 3: Если есть разделение радикалов, можно использовать Правило 3, чтобы сгруппировать их под одним радикалом.
• Шаг 4: После того, как вы воспользовались Правилом 1 или 3, чтобы максимально сгруппировать радикалы, вы используете Правило 2, поэтому посмотрите, какую часть выражения можно убрать из радикала.

В конечном счете игра групповая и потенциальная «отмена» подкоренной части выражения (если не всей) числителя на знаменатель дроби).

Как вычислить корень кубический из числа 125?

Корень кубический из числа 125 можно вычислить следующим образом:

1. Для начала, мы должны найти такое число, которое при возведении в куб даст нам 125. Изучив целые числа от 1 до 5, мы обнаружим, что число 5 удовлетворяет этому условию.

2. Затем мы можем записать это как уравнение: 5^3 = 125. Здесь символ ^ означает возведение в степень.

3. Теперь, чтобы найти корень кубический из числа 125, мы должны найти число, которое возводится в куб и дает нам 125. Обратная операция возведению в степень — это извлечение корня. Поэтому мы можем записать это как ∛125 = 5.

Таким образом, корень кубический из числа 125 равен 5.

Теперь извлечем кубический корень из числа 636 056

Шаг второй

Зачеркиваем три последние цифры и смотрим на оставшиеся три. 636 056 -> 636. Ближайший к этому числу куб, не превосходящий его — 512. Следующий куб —729, он уже больше 636.

512=8³, поэтому второе число, которое мы должны запомнить — 8. Объединяем оба числа и получаем 86. И в самом деле 86³=636056 .

Где это пригодится?

Например, чтобы провести математический фокус. Попросите друга загадать какое-то двухзначное число про себя и никому его не говорить. Теперь пусть он возведет его в куб и скажет вам результат. А вы спустя пару секунд назовете ему загаданное им число. Уверен, что у вас это получится сделать в уме гораздо быстрее, чем он будет дважды умножать число само на себя столбиком на листочке.

Ещё это может пригодиться, чтобы удивить учительницу. Ну или для того, чтобы сэкономить время на ЕГЭ. Хотя последнее очень сомнительно. В школе не учат извлекать кубические корни в уме, поэтому и заданий там таких нет.

Разложение подкоренного числа на простые множители

Двигаясь от наиболее удобного и быстрого способа к более сложному, давайте разберемся во втором из них — разложение подкоренного числа на простые множители.

Этот метод состоит в том, чтобы представить какое-либо число в виде степени с нужным нам показателем, из чего мы можем получить значение этого корня.

Пример 1:

Возьмём число 196. Для извлечения его квадратного корня, разложим это число на простые множители: √196=2×2×7×7=2²×7²

Теперь делаем следующие действия: 2×7=14.

Ответ: √196=14.

Объяснение:

Множители находятся так: 196 делим на 2, а полученное число 98 мы тоже делим на 2. Делим до тех пор, пока деление станет невозможным. Так, число 49 нельзя поделить пополам, поэтому мы действуем методом подбора. Находим такое число, которое делится. В данном случае — это 7. Два числа, что у нас получились (2 и 7), мы умножаем друг на друга, но уже без степени и получаем число 14, что есть извлечённый корень из числа 196.

Пример 2:

Для того, чтобы лучше понять, как раскладывать на множители, приведем ещё одно число и перейдем к действиям. Деление 441 на 2 невозможно, поэтому подбираем число. Оно делится на 3 два раза. Опять выходит число 49, которое мы делим 2 раза на 7. Из этого следует: √441=3×3×7×7=3²×7²

3×7=21. Значит, ответ: √441=21.

Объяснение:

3 мы умножили на 7, так как это два числа, имеющих 2 степень. Будь у одного из них 4 степень, например: 3⁴×7² — нужно было бы сделать так: 3×3×7. Проще сказать, что мы сокращаем степени ⁴ и ².

Интересно

Подкоренные числа, разложенные на простые множители, могут иметь лишь чётную степень.

Корень третьей степени из 125 в различных системах счисления

Корень третьей степени из 125 равен 5. Так как число 125 можно представить в виде 5 * 5 * 5, то корнем третьей степени будет являться число 5. В различных системах счисления, таких как десятичная, двоичная и восьмеричная, корень третьей степени из 125 будет равен 5.

В десятичной системе счисления число 125 записывается так: 125. Корень третьей степени из 125 также будет равен 5.

В двоичной системе счисления число 125 записывается так: 1111101. Для нахождения корня третьей степени из 125 в двоичной системе счисления необходимо разделить количество цифр на 3 и найти целую часть полученного значения. В данном случае, корень третьей степени из 125 равен 5.

В восьмеричной системе счисления число 125 записывается так: 175. Корень третьей степени из 125 в восьмеричной системе счисления также будет равен 5.

Примечание: В шестнадцатеричной системе счисления число 125 записывается как 7D. Однако, корень третьей степени из 125 не является целым числом в шестнадцатеричной системе счисления.

Приложения корня третьей степени из 125 в математике и физике

Корень третьей степени из 125 равен 5. Это простое математическое выражение, которое имеет несколько приложений и используется в различных областях.

В математике корень третьей степени из 125 широко используется при решении уравнений и вычислении различных значений. Он позволяет находить значения не только для числа 125, но и для других чисел, которые можно представить в виде куба. Также этот корень используется в алгебре, геометрии и других областях математики.

В физике корень третьей степени из 125 может быть использован для нахождения объема кубического объекта, если известен один из его параметров, например длина ребра. Это позволяет быстро и удобно вычислить объем, что может быть полезно при исследовании твердых тел и расчете их характеристик.

Корень третьей степени из 125 также может быть использован при решении некоторых задач, связанных с вероятностью и статистикой. Это может быть полезно, когда необходимо вычислить вероятность или ожидаемую величину в определенной ситуации.

В общем, корень третьей степени из 125 является важной математической операцией, которая имеет множество приложений и может быть использована в различных областях знания

Отличная возможность изучить простую математику и посчитать корень

Если вы хотите знать, как вычислить корень из 125 в кубе, у вас отличная возможность познакомиться с простой математикой и научиться справляться с такими задачами. В следующем разделе мы расскажем вам о простой формуле и алгоритме, при помощи которых вы сможете легко вычислить данный корень.

Для начала, вам потребуется знать некоторые основные понятия математики. Корень из числа можно представить в виде числа, возведенного в степень. В данном случае мы ищем корень из 125 в кубе, что означает, что нам нужно найти число, при возведении которого в куб, получим 125.

Для этого можно использовать простую формулу: корень из числа в кубе равен число, возведенное в степень, обратную третей степени. То есть, чтобы найти корень из 125 в кубе, нужно возвести 125 в степень 1/3.

Теперь перейдем к вычислениям. Возведение числа в степень 1/3 означает, что нужно найти число, умноженное на себя два раза. В нашем случае это 125, поэтому получается:

125 * 125 * 125 = 125,^3 = 125 * 625 = 78125

Таким образом, корень из 125 в кубе равен 78125.

Теперь у вас есть простая формула и алгоритм, с помощью которых вы можете вычислить корень из числа в кубе. Используйте их для изучения математики и решения подобных задач! Не бойтесь экспериментировать с разными числами и степенями, чтобы углубить свои знания и навыки в математике.

Арифметический корень

Давайте предположим на минутку, что под знаком корня могут находиться лишь положительные числа или в крайнем случае ноль. Забьём на чётные/нечётные показатели, забьём на все определения, приведённые выше — будем работать только с неотрицательными числами. Что тогда?

А тогда мы получим арифметический корень — он частично пересекается с нашими «стандартными» определениями, но всё же отличается от них.

Как видим, нас больше не интересует чётность. Взамен неё появилось новое ограничение: подкоренное выражение теперь всегда неотрицательно, да и сам корень тоже неотрицателен.

Чтобы лучше понять, чем арифметический корень отличается от обычного, взгляните на уже знакомые нам графики квадратной и кубической параболы:

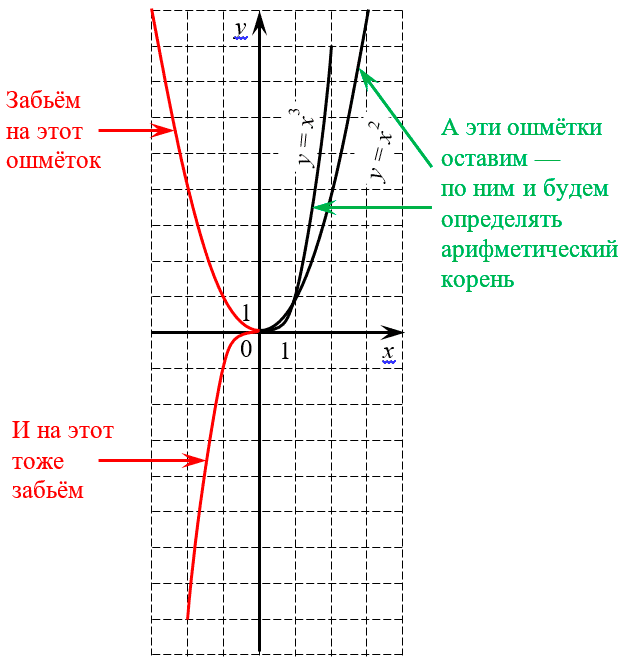Область поиска арифметического корня — неотрицательные числа

Как видите, отныне нас интересуют лишь те куски графиков, которые расположены в первой координатной четверти — там, где координаты $x$ и $y$ положительны (или хотя бы ноль). Больше не нужно смотреть на показатель, чтобы понять: имеем мы право ставить под корень отрицательное число или нет. Потому что отрицательные числа больше в принципе не рассматриваются.

Возможно, вы спросите: «Ну и зачем нам такое кастрированное определение?» Или: «Почему нельзя обойтись стандартным определением, данным выше?»

Что ж, приведу всего одно свойство, из-за которого новое определение становится целесообразным. Например, правило возведения в степень:

\{a}=\sqrt{{{a}^{k}}}\]

Обратите внимание: мы можем возвести подкоренное выражение в любую степень и одновременно умножить на эту же степень показатель корня — и в результате получится то же самое число! Вот примеры:

\{5}=\sqrt{{{5}^{2}}}=\sqrt{25} \\ & \sqrt{2}=\sqrt{{{2}^{4}}}=\sqrt{16} \\ \end{align}\]

Ну и что в этом такого? Почему мы не могли сделать это раньше? А вот почему. Рассмотрим простое выражение: $\sqrt{-2}$ — это число вполне нормальное в нашем классическом понимании, но абсолютно недопустимо с точки зрения арифметического корня. Попробуем преобразовать его:

$\begin{align} & \sqrt{-2}=-\sqrt{2}=-\sqrt{{{2}^{2}}}=-\sqrt{4} \lt 0; \\ & \sqrt{-2}=\sqrt{{{\left( -2 \right)}^{2}}}=\sqrt{4} \gt 0. \\ \end{align}$

Как видите, в первом случае мы вынесли минус из-под радикала (имеем полное право, т.к. показатель нечётный), а во втором — воспользовались указанной выше формулой. Т.е. с точки зрения математики всё сделано по правилам.

WTF?! Как одно и то же число может быть и положительным, и отрицательным? Никак. Просто формула возведения в степень, которая прекрасно работает для положительных чисел и нуля, начинает выдавать полную ересь в случае с отрицательными числами.

Вот для того, чтобы избавиться от подобной неоднозначности, и придумали арифметические корни. Им посвящён отдельный большой урок, где мы подробно рассматриваем все их свойства. Так что сейчас не будем на них останавливаться — урок и так получился слишком затянутым.

Шаги поиска числа

• Известно, что куб числа 5 равен 125.
• Чтобы найти число, куб которого равен 125, нужно найти корень третьей степени из этого числа.
• Для этого можно воспользоваться калькулятором или математической программой.
• Корень третьей степени из 125 равен 5.
• Таким образом, число, куб которого равен 125, равно 5.

Определение границ поиска

Для того чтобы найти число, куб которого равен 125, необходимо определить границы для поиска. Как мы знаем, для нахождения куба числа нужно число возвести в третью степень.

Таким образом, нам нужно найти число, у которого куб равен 125. Мы можем начать поиск, используя числа от 1 и последовательно увеличивая их значение, пока не найдем число, куб которого равен 125.

Определим границы поиска более точно:

• Минимальное значение: 1
• Максимальное значение: неограничено

Таким образом, мы можем начать поиск с числа 1 и продолжать его до тех пор, пока не найдем число, куб которого равен 125.

Примечание: в данном случае уже известно, что число, куб которого равен 125, равно 5, так как 5^3 = 125. Однако, в целях обучения, мы рассмотрим общий метод поиска числа с заданным кубом.

Запуск выбранного метода поиска

Если нам необходимо найти число, куб которого равен 125, мы можем воспользоваться несколькими различными методами. Рассмотрим два из них:

• Метод итераций
• Метод взятия корня

Метод итераций

Этот метод основан на последовательном переборе чисел. Мы начинаем с некоторого начального приближения и последовательно увеличиваем его, пока не найдем число, куб которого будет близким к 125.

Метод взятия корня

Этот метод основан на свойстве корня – если число возведено в степень, равную 1/3 (квадратный корень), то результат будет равен числу, куб которого мы ищем. Применение данного метода позволяет найти искомое число без необходимости перебирать все числа.

Оба метода могут быть использованы для нахождения числа, куб которого равен 125. Выбор метода зависит от поставленной задачи и доступных алгоритмов.

Проверка результата

Куб — это число, полученное при умножении числа на себя два раза.

Мы ищем число, куб которого равен 125.

Значит, нам нужно найти такое число, которое, возвести в степень 3 (получить его куб), даст нам результат 125.

Попробуем найти это число:

1. Пусть искомое число равно x.
2. Тогда уравнение будет иметь вид: x^3 = 125.
3. Чтобы найти значение x, возьмем кубический корень от обоих частей уравнения:

∛(x^3) = ∛125

x = 5

Проверим результат:

1. Возведем число 5 в куб:

5^3 = 5 * 5 * 5 = 125

Получили значение, которое равно 125.

Таким образом, число 5 является решением уравнения и его куб равен 125.

Зачем вообще нужны корни?

Прочитав определение, многие ученики спросят: «Что курили математики, когда это придумывали?» И вправду: зачем вообще нужны все эти корни?

Чтобы ответить на этот вопрос, вернёмся на минутку в начальные классы. Вспомните: в те далёкие времена, когда деревья были зеленее, а пельмени вкуснее, основная наша забота была в том, чтобы правильно умножать числа. Ну, что-нибудь в духе «пять на пять — двадцать пять», вот это вот всё. Но ведь можно умножать числа не парами, а тройками, четвёрками и вообще целыми комплектами:

\

Ну и так далее. Ладно, ладно: последние две строчки я считал на калькуляторе.:)

Однако суть не в этом. Фишка в другом: математики — людишки ленивые, поэтому им было в лом записывать умножение десяти пятёрок вот так:

\

Поэтому они придумали степени. Почему бы вместо длинной строки не записать количество множителей в виде верхнего индекса? Типа вот такого:

\

Это же очень удобно! Все вычисления сокращаются в разы, и можно не тратить кучу листов пергамента блокнотиков на запись какого-нибудь 5183. Такую запись назвали степенью числа, у неё нашли кучу свойств, но счастье оказалось недолгим.

После грандиозной пьянки, которую организовали как раз по поводу «открытия» степеней, какой-то особо упоротый математик вдруг спросил: «А что, если нам известна степень числа, но неизвестно само число?» Вот, действительно, если нам известно, что некое число $b$, допустим, в 5-й степени даёт 243, то как нам догадаться, чему равно само число $b$?

Проблема эта оказалась гораздо более глобальной, чем может показаться на первый взгляд. Потому что выяснилось, что для большинства «готовых» степеней таких «исходных» чисел нет. Судите сами:

\

А, что если ${{b}^{3}}=50$? Получается, что нужно найти некое число, которое будучи трижды умноженное само на себя даст нам 50. Но что это за число? Оно явно больше 3, поскольку 33 = 27 < 50. С тем же успехом оно меньше 4, поскольку 43 = 64 > 50. Т.е. это число лежит где-то между тройкой и четвёркой, но чему оно равно — фиг поймёшь.

Именно для этого математики и придумали корни $n$-й степени. Именно для этого ввели значок радикала $\sqrt{*}$. Чтобы обозначить то самое число $b$, которое в указанной степени даст нам заранее известную величину

\{a}=b\Rightarrow {{b}^{n}}=a\]

Не спорю: зачастую эти корни легко считаются — мы видели несколько таких примеров выше. Но всё-таки в большинстве случаев, если вы загадаете произвольное число, а затем попробуете извлечь из него корень произвольной степени, вас ждёт жестокий облом.

Да что там! Даже самый простой и всем знакомый $\sqrt{2}$ нельзя представить в привычном нам виде — как целое число или дробушка. А если вы вобьёте это число в калькулятор, то увидите вот это:

\

Как видите, после запятой идёт бесконечная последовательность цифр, которые не подчиняются никакой логике. Можно, конечно, округлить это число, чтобы быстро сравнить с другими числами. Например:

\

Или вот ещё пример:

\

Но все эти округления, во-первых, довольно грубые; а во-вторых, работать с примерными значениями тоже надо уметь, иначе можно словить кучу неочевидных ошибок (кстати, навык сравнения и округления в обязательном порядке проверяют на профильном ЕГЭ).

Поэтому в серьёзной математике без корней не обойтись — они являются такими же равноправными представителями множества всех действительных чисел $\mathbb{R}$, как и давно знакомые нам дроби и целые числа.

Рассмотрим несколько примеров, где после всех вычислений иррациональные числа всё же останутся в ответе.

Естественно, по внешнему виду корня практически невозможно догадаться о том, какие числа будут идти после запятой. Впрочем, можно, посчитать на калькуляторе, но даже самый совершенный калькулятор дат нам лишь несколько первых цифр иррационального числа. Поэтому гораздо правильнее записать ответы в виде $\sqrt{5}$ и $\sqrt{-2}$.

Именно для этого их и придумали. Чтобы удобно записывать ответы.

Перевод десятичной дроби в градусах в градусы, минуты, секунды

Для этой цели применяем кнопку $stackrel< o D.MS D><fbox>$. Эта функция не зависит от режимов deg, rad и grad.

Чтобы перевести десятичную дробь $A$ (быть может, отрицательную) в градусы, минуты, секунды (Degrees, Minutes, Seconds), вводим $$ A > stackrel. $$ При этом цифры до точки будут обозначать градусы, первая пара цифр после точки — минуты, вторая пара цифр после точки — секунды, третья пара цифр — сотые доли секунды

Обратите внимание на символ $$ o D.MS. $$

Для перевода меры угла, выраженной в градусах, минутах, секундах в десятичную дробь используем $$ A stackrel< o D.MS D><fbox>, $$ где во введённом числе $A$ цифры перед точки интерпретируются как градусы, вторая пара цифр после точки — минуты, третья пара цифр после точки — секунды, остальные цифры — десятые, сотые, тысячные и т.д. доли секунды.

В нашем случае разделителем целой и дробной частей числа является точка, а не запятая.

Если результат вычисления не умещается в десяти разрядах, то он выводится в экспоненциальной форме.

Выведенный результат можно преобразовать в экспоненциальную форму и обратно, нажимая $$ stackrel < <
m TAB>> < fbox< F $leftrightarrow$ E>>. $$

Чтобы ввести число в экспоненциальной форме, вводим сначала мантиссу, затем нажимаем $stackrel< pi A>< fbox< EXP >>$, и, наконец, вводим порядок.

Для работы с комплексными числами нам потребуется переключить калькулятор в режим cplx> (complex numbers): $$ <fbox<2ndF>> stackrel<<
m CPLX>><fbox< $lacktriangleright$ >>. $$ В режиме cplx доступны четыре арифметические операции $fbox<+>$, $fbox<—>$, $fbox<$ imes$>$, $fbox<$div$>$, а также вычисление полярного представления комплексного числа, и обратное действие — вычисление действительной и мнимой частей комплексного числа по радиусу и полярному углу.

Чтобы ввести комплексное число $A+Bi$, вводим действительную часть $A$, жмём $stackrel< o r heta><fbox>$, затем мнимую часть $B$, и жмём $stackrel< o xy><fbox>$.

Пусть мы знаем модуль (длину радиус-вектора) $r$ и аргумент (величину полярного угла) $ heta$ некоторого комплексного числа, и хотим найти действительную и мнимую составляющие этого числа. Поступаем следующим образом. Вводим длину радиус-вектора $r$, жмём $stackrel< o r heta><fbox>$, затем величину полярного угла $B$, жмём $stackrel< o xy><fbox>$, и, наконец, $$ <fbox<2ndF>> stackrel< o xy><fbox>. $$ Здесь так же единицы измерения угла зависят от режимов deg, rad и grad.

Кстати, функция кнопки $ stackrel<<
m CPLX>><fbox< $lacktriangleright$ >> $ — удаление последней введённой цифры.

Чтобы работать со статистическими функциями, нужно включить режим stat: $$ <fbox<2ndF>> stackrel<<
m STAT>><fbox>. $$ На дисплее появится соответствующий знак. Все дальнейшие действия выполнимы лишь в режиме stat.

При работе в режиме stat используются три регистра. Мы обозначим эти регистры через $n$, $Sigma x$ и $Sigma x^2$.

После включения режима stat в каждом из регистров $n$, $Sigma x$ и $Sigma x^2$ хранится нулевое значение.

Если теперь набрать какое-либо число и нажать клавишу $stackrel<<
m DATA CD>><fbox>$, то произойдёт следующее:

• Значение в регистре $n$ будет увеличено на $1$;
• Значение в регистре $Sigma x$ будет увеличено на число, отображаемое на дисплее;
• Значение в регистре $Sigma x^2$ будет увеличено на квадрат числа, отображаемого на дисплее;
• Значение в регистре $n$ будет выведено на дисплей.

Таким образом происходит накопление статистических данных.

Чтобы увидеть содержимое регистра $n$, нажмите $$ stackrel<fbox<)>>. $$

Чтобы увидеть содержимое регистра $Sigma x$, нажмите $$ <fbox<2ndF>> stackrel<fbox<)>>. $$

Если набрать какое-либо число и набрать последовательность $<fbox<2ndF>> stackrel<<
m DATA CD>><fbox>$, то произойдёт следующее:

• Значение в регистре $n$ будет уменьшено на $1$;
• Значение в регистре $Sigma x$ будет уменьшено на число, отображаемое на дисплее;
• Значение в регистре $Sigma x^2$ будет уменьшено на квадрат числа, отображаемого на дисплее;
• Значение в регистре $n$ будет выведено на дисплей.

Так можно откорректировать введённые данные.

Предположим, что мы ввели $n$ (не путать с нашим условным названием регистра) чисел $x_1, . x_n$. Тогда у нас есть следующие исходные данные:

• Количество введённых чисел $n$ (в регистре $n$);
• Значение $$ sum_^ x_i $$ в регистре $Sigma x$;
• Значение $$ sum_^ x_i^2 $$ в регистре $Sigma x^2$.

Именно эти три величины используются статистическими функциями калькулятора.

Далее мы будем использовать символы $n$, $Sigma x$ и $Sigma x^2$ для обозначения значений в соответсвующих регистрах.

Свойство корня как функции

На [0; +∞) можно поставить каждому числу х в соответствие единственное число корень n-степени из x при любом значении n.

То есть это означает, что на множестве [0; +∞) можно говорить о функции корня:

Теперь определим свойства функции корня и построим ее график.

Основные свойства корня как функции:

Промежуток [0; +∞) – является областью определения.

Так как неотрицательное число является корнем n-степени из неотрицательного числа, значит промежуток [0; +∞) будет областью значения функции.

Поскольку симметричным множеством не является область определения функции, поэтому данная функция не является ни нечетной, ни четной.

Операция по извлечению корня вводилась как обратная операция возведения в соответствующую степень.

Значит можно утверждать, что:

Теперь можно построить график функции корня.

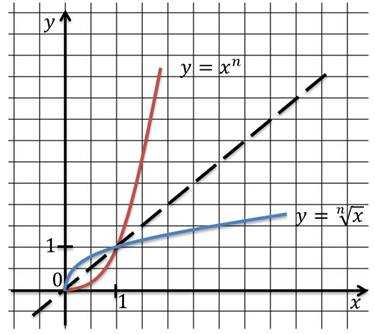
Пользуясь графиком, можно записать оставшиеся свойства функции.

На промежутке [0; +∞) функция возрастает.

Сверху функция не ограничена, но она ограничена снизу, например, прямой у, которая = -0,5.

На всей области определения функция выпукла вверх.

У функции наименьшим значением будет являться 0, а наибольшего значения она не имеет.

Если в каждой из точек некоторого промежутка функция дифференцируема, то это значит, что на данном промежутке она непрерывна.

Тогда:

В любой точке промежутка [0; +∞) существует эта производная, исключением является только точка 0.

Поскольку в любой точке промежутка (0; +∞) функция имеет производную, значит на промежутке (0; +∞) функция дифференцируема.

Кубический корень из числа

Определение кубического корня
из числа a
дается аналогично определению квадратного корня. Только оно базируется на понятии куба числа, а не квадрата.

Определение

Кубическим корнем из числа a

называется число, куб которого равен a
.

Приведем примеры кубических корней
. Для этого возьмем несколько чисел, например, 7
, 0
, −2/3
, и возведем их в куб: 7 3 =7·7·7=343
, 0 3 =0·0·0=0
, . Тогда, основываясь на определении кубического корня, можно утверждать, что число 7
– это кубический корень из 343
, 0
есть кубический корень из нуля, а −2/3
является кубическим корнем из −8/27
.

Можно показать, что кубический корень из числа a
, в отличие от квадратного корня, всегда существует, причем не только для неотрицательных a
, но и для любого действительного числа a
. Для этого можно использовать тот же способ, о котором мы упоминали при изучении квадратного корня.

Более того, существует только единственный кубический корень из данного числа a
. Докажем последнее утверждение. Для этого отдельно рассмотрим три случая: a
– положительное число, a=0
и a
– отрицательное число.

Легко показать, что при положительном a
кубический корень из a
не может быть ни отрицательным числом, ни нулем. Действительно, пусть b
является кубическим корнем из a
, тогда по определению мы можем записать равенство b 3 =a
. Понятно, что это равенство не может быть верным при отрицательных b
и при b=0
, так как в этих случаях b 3 =b·b·b
будет отрицательным числом либо нулем соответственно. Итак, кубический корень из положительного числа a
является положительным числом.

Теперь предположим, что помимо числа b
существует еще один кубический корень из числа a
, обозначим его c
. Тогда c 3 =a
. Следовательно, b 3 −c 3 =a−a=0
, но b 3 −c 3 =(b−c)·(b 2 +b·c+c 2)
(это формула сокращенного умножения разность кубов
), откуда (b−c)·(b 2 +b·c+c 2)=0
. Полученное равенство возможно только когда b−c=0
или b 2 +b·c+c 2 =0
. Из первого равенства имеем b=c
, а второе равенство не имеет решений, так как левая его часть является положительным числом для любых положительных чисел b
и c
как сумма трех положительных слагаемых b 2
, b·c
и c 2
. Этим доказана единственность кубического корня из положительного числа a
.

При a=0
кубическим корнем из числа a
является только число нуль. Действительно, если предположить, что существует число b
, которое является отличным от нуля кубическим корнем из нуля, то должно выполняться равенство b 3 =0
, которое возможно лишь при b=0
.

Для отрицательных a
можно привести рассуждения, аналогичные случаю для положительных a
. Во-первых, показываем, что кубический корень из отрицательного числа не может быть равен ни положительному числу, ни нулю. Во-вторых, предполагаем, что существует второй кубический корень из отрицательного числа и показываем, что он обязательно будет совпадать с первым.

Итак, всегда существует кубический корень из любого данного действительного числа a
, причем единственный.

Дадим определение арифметического кубического корня
.

Определение

Арифметическим кубическим корнем из неотрицательного числа a

называется неотрицательное число, куб которого равен a
.

Арифметический кубический корень из неотрицательного числа a
обозначается как , знак называется знаком арифметического кубического корня, число 3
в этой записи называется показателем корня
. Число под знаком корня – это подкоренное число
, выражение под знаком корня – это подкоренное выражение
.

Хотя арифметический кубический корень определяется лишь для неотрицательных чисел a
, но удобно также использовать записи, в которых под знаком арифметического кубического корня находятся отрицательные числа. Понимать их будем так: , где a
– положительное число. Например, .

О свойствах кубических корней мы поговорим в общей статье свойства корней .

Вычисление значения кубического корня называется извлечением кубического корня, это действие разобрано в статье извлечение корней: способы, примеры, решения .

В заключение этого пункта скажем, что кубический корень из числа a
является решением вида x 3 =a
.

Умножение корней

Существует несколько вариантов умножения корней, это умножение с множителем, без множителя и с разными показателями.

Умножение без множителей

Первым делом рассмотри, как умножаются корни без множителя.

Убедившись, что корни, с которыми необходимо произвести действие имеют одинаковые степени. Например квадратный корень из числа а, можно умножать на квадратный корень из d.

Рассмотрим правило на двух примерах произведения двух квадратных и двух кубических корней.

Примеры:

\ первый пример умножение квадратных корней.

\{3} * \sqrt{18}=\] второй пример умножение кубических корне.

Решение:

Для того чтобы решить данные примеры необходимо произвести умножение под корнем.

\

\{18} * \sqrt{3}=\sqrt{18 * 3}=\sqrt{54}\]

Следующим шагом полученное выражение стоит упростить. Для этого полученное число под корнем необходимо представить в виде множителей, где в зависимости от корня одно из чисел чисел это полный квадрат или куб.

\, в данном примере число 12 можно разложить на произведение чисел 4 и 3, где 4 равно двум в квадрате.  Поэтому 2 выносим за приделы корня и упрощаем выражение.

\{54}=\sqrt{27 * 2}=\sqrt{(3 * 3 * 3) * 2}=3 \sqrt{2}\] в данном случае получившееся подкоренное число 54 можно разложить на произведение двух чисел 27 и 2 , где 27 = 33, тройку выносим за корень кубический, тем самым мы упростили выражение.

Точно также производится умножение корней других степеней, при этом не важно количество умножаемых корней, правило не изменится

Умножение корней с множителями

В данном случае мы так же рассматриваем примеры умножения корней с одинаковыми степенями. Множителем является число, стоящее перед корнем. Если при написании множитель отсутствует, то он равен единице. Умножить корень на число значит умножить число на множитель перед корнем. Для того чтобы произвести умножение с такими корнями, необходимо перемножить множители.

Пример умножения корней:

\ в данном примере мы сначала произвели умножение множителей 1 и 2 , затем воспользовавшись первым правилом умножения корней, произвели умножение под знаком корня чисел 6 и 6.

Следующим шагом упрощаем выражение, корень из 36, равен целому числу 6. последним действием умножаем его на полученный множитель 2. и получаем ответ 12.

Пример 2.

\

В приведённом примере, мы также в начале производим умножение множителей 2 и 3, затем производим умножение подкоренных чисел 6 и 3, в результате получаем 6 корней из 18.

 После производим упрощение выражения под знаком корня, для этого разложили его на множители, таким образом чтобы одно из чисел можно было вынести за пределы знака корень такими числами стали 9 и 2, в результате получилось, что вынесенное число равно трём, так как 9 = \ .

Теперь умножим получившийся ранее множитель 6 на вынесенное из под корня число 3, и получим ответ 18 корней из двух.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Умножение корней с разными показателями

Теперь разберём, как умножить корни если их показатели степени разные. Для этого необходимо найти наименьшее общее кратное число для этих показателей.  Таким числом является наименьшее число, которое можно разделить на оба эти показателя. Для того чтобы разобраться лучше в данном методе, приведём пример.

Пример:

\{2} * \sqrt{5}=\]

Сначала необходимо найти наименьшее общее кратное, наименьшим в данном случае является произведение 2*3 = 6. Значит для того чтобы произвести умножение корней необходимо привести их к показателю шестой степени.

Записываем новое полученное выражение \{2} * \sqrt{5}=\]

Теперь находим числа на которые нужно умножить показатели, чтобы найти наименьшее общее кратное

Для первого корня это деление 6\2 = 3, для второго 6\3 =2

Следующим шагом нужно возвести подкоренное число в степень, которая ровна числам найденным ранее, при нахождении НОК, то есть \{2^{3}} * \sqrt{5^{2}}=\]

Далее имея одинаковые показатели производим действия по умножению корней, так как делали это в предыдущих правилах. Производим действия под корнем.

\{2^{3}} * \sqrt{5^{2}}=\sqrt{2^{3} * 5^{2}}=\sqrt{8 * 25}=\sqrt{200}\]

Если полученное выражение можно упростить, то упрощаем его. В данном случае это невозможно.

Как мы видим произвести умножение корней не так и сложно, главное запомнить основные правила и формулы умножения корней и пользоваться ними.

Вводные данные и задача

Поднимаем воздух над пухлыми шоколадными облаками, вы увлекаете, когда замечаете столбики сахара, выложенные перед вами. Вы подошли поближе, чтобы рассмотреть их. Как оказалось, сахар был выложен в форме куба со стороной 5 единиц. Вы радуетесь и мечтаете передвинуть один из кубиков, чтобы раскрыть его секрет. Но какой кубик вы должны передвинуть и сколько раз должны его вращать, чтобы распутать эту загадку?

Параметр	Значение
Размер кубика сахара (сторона)	5 единиц
Количество кубиков сахара	125

Вам необходимо найти кубик сахара внутри этой кубической структуры и определить, сколько раз и как его можно передвинуть, чтобы его разместить в другую часть структуры. Для достижения результата вы можете использовать вращение одного из кубиков на месте в любом направлении. Ваша задача — найти оптимальное решение, чтобы раскрыть тайну сахара.

Зачем нужно считать корень третьей степени из 125?

Расчет корня третьей степени из 125 имеет ряд практических применений и может быть полезен в различных сферах. Вот некоторые причины, почему может быть необходимо считать этот корень:

1. Математика и научные исследования: Корень третьей степени из 125 является простым математическим выражением, которое может использоваться в различных математических и научных задачах. Например, для нахождения кубического корня из числа при решении уравнений или в формулах для рассчетов физических величин.

2. Инженерия и техника: В сфере инженерии и техники корень третьей степени из 125 может использоваться для решения различных задач, связанных с объемом, площадью или длиной. Например, при проектировании конструкций или расчетах в области электротехники.

3. Финансы и экономика: В финансовой и экономической сферах корень третьей степени из 125 может быть полезен при рассчете процентных ставок или при измерении изменений величин. Например, для определения процентного прироста или убыли в инвестициях или стоимости товаров.

4. Образование и учеба: Расчет корня третьей степени из 125 может быть использован в учебных целях для развития математических навыков и понимания основных математических операций. Это также может помочь учащимся в построении логических связей и развитии аналитического мышления.

Исходя из вышесказанного, можно заключить, что расчет корня третьей степени из 125 имеет практическую значимость и может применяться в различных областях знаний и деятельности.