Функция синуса в excel: использование и примеры расчетов

Вычисление синуса в Excel: для чего это нужно?

Вычисление синуса в Excel может быть очень полезным для решения различных задач и проведения анализа данных. В Excel функция синуса представлена как SIN, и вычисляется по радианам.

Синус в Excel можно использовать для следующих целей:

1. Вычисление углов: с помощью функции SIN можно вычислить синус угла в радианах. Это может быть полезно при решении геометрических задач или анализе данных, связанных с углами.
2. Нахождение длин и высот: с помощью синуса можно вычислить длину или высоту треугольника, зная длину одной стороны и известный угол.
3. Решение физических задач: функция синуса может быть использована для решения задач физики, связанных с взаимодействием сил и движением тел.
4. Анализ данных и графики: синус может быть использован в качестве функции для создания графиков, анализа трендов или прогнозирования данных в Excel.

Вычисление синуса в Excel позволяет облегчить и ускорить решение различных математических задач, а также обеспечить более точные и надежные результаты.

Решение 3-х более сложных уравнений

Уравнение 12. Най­ди­те корни урав­не­ния: \( \displaystyle cos\frac{8\pi x}{6}=\frac{\sqrt{3}}{2}\). В от­ве­те за­пи­ши­те наи­боль­ший от­ри­ца­тель­ный ко­рень.

Логика простая: будем поступать так, как поступали раньше не взирая на то, что теперь у тригонометрических функций стал более сложный аргумент!

Если бы мы решали уравнение вида:

\( \displaystyle cost=\frac{\sqrt{3}}{2}\)То мы бы записали вот такой ответ:

\( \displaystyle t=\pm arccos\frac{\sqrt{3}}{2}+2\pi n,~n\in Z\)Или (так как \( \displaystyle arccos\frac{\sqrt{3}}{2}=\frac{\pi }{6}\))

\( \displaystyle t=\pm \frac{\pi }{6}+2\pi n,~n\in Z\)Но теперь в роли \( \displaystyle t\) у нас выступаем вот такое выражение: \( \displaystyle t=\frac{8\pi x}{6}\)

Тогда можно записать:

\( \displaystyle \frac{8\pi x}{6}=\pm \frac{\pi }{6}+2\pi n\)Наша с тобою цель – сделать так, чтобы слева стоял просто \( \displaystyle x\), без всяких «примесей»!

Давай постепенно от них избавляться!

Вначале уберём знаменатель при \( \displaystyle x\): для этого домножим наше равенство на \( \displaystyle 6\):

\( \displaystyle \frac{6\cdot 8\pi x}{6}=6\cdot \left( \pm \frac{\pi }{6}+2\pi n \right)\)\( \displaystyle 8\pi x=\pm \frac{6\pi }{6}+12\pi n\)\( \displaystyle 8\pi x=\pm \pi +12\pi n\)Теперь избавимся от \( \displaystyle \pi \), разделив на него обе части:

\( \displaystyle 8x=\pm 1+12n\)Теперь избавимся от восьмёрки:\( \displaystyle \frac{8x}{8}=\pm \frac{1}{8}+\frac{12n}{8}\)\( \displaystyle x=\pm \frac{1}{8}+\frac{3n}{2}\)Полученное выражение можно расписать как 2 серии решений (по аналогии с квадратным уравнением, где мы либо прибавляем, либо вычитаем дискриминант)\( \displaystyle x=\frac{1}{8}+\frac{3n}{2}\)или\( \displaystyle x=-\frac{1}{8}+\frac{3n}{2}\)Нам нужно найти наибольший отрицательный корень! Ясно, что надо перебирать \( \displaystyle n\).

Определения тригонометрических функций

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.

Важно помнить!

Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1.

Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.

Угол поворота

Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов. Угол поворота в градусах или радианах выражается любым действительным числом от .

=  

=  

Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0; 1) и (0; -1). В таких случаях выражение для тангенса просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом.  Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.

Важно помнить!

Синус и косинус определены для любых углов .

При решении практических примеров не говорят «синус угла поворота «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.

Числа

Как быть с определением синуса, косинуса, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Синусом, косинусом числа называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в радиан.

Например, синус числа равен синусу угла поворота величиной рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Начальная точка на окружности — точка A c координатами (1;0).

Положительному числу  соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь длиной .

Отрицательному числу соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь длиной ||.

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу , совпадает с точкой, в которую переходит начальная точка после поворота на угол радиан.

Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент.

Взгляните:

Синим цветом обозначено положительное направление оси (ось ординат), красным — положительное направление оси (ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными.

В частности,

Для наглядности отметим знаки каждой тригонометрической функции — синуса, косинуса и тангенса — на отдельных «радарах». Получим следующую картинку:

Знаки котангенса совпадают со знаками тангенса — никаких специальных правил там нет.

Таблица значений синусов, косинусов, тангенсов и котангенсов для основных углов.

Возможные проблемы и ошибки при вычислении синуса в Excel

2. Неправильный формат ячеек: Если Excel не выполняет вычисления синуса, убедитесь, что ячейки, в которых вы вводите значения, имеют правильный формат в числовом виде. В противном случае, Excel может воспринимать введенные данные как текст и не сможет вычислить синус.

3. Недостаточная точность: Хотя Excel обладает высокой точностью при вычислении синуса, при работе с очень малыми значениями аргументов или при большом количестве итераций может возникнуть потеря точности. В таких случаях можно воспользоваться специальными математическими формулами или программами, которые обеспечат более точные результаты.

4. Ошибки округления: Excel округляет значения функции синуса и других математических операций до определенного количества знаков после запятой. Это может привести к ошибкам округления и небольшой погрешности в результатах. Если точность округления является критической, рекомендуется использовать более точные методы вычисления, например, с помощью программирования.

5. Проблемы с экспортом и импортом данных: При копировании и вставке данных из других источников в Excel, могут возникнуть проблемы с форматом данных. Убедитесь, что значения аргументов синуса корректно экспортированы и импортированы, чтобы избежать неправильных результатов.

6. Проблемы с локализацией: Некоторые версии Excel могут иметь различия в представлении математических функций в зависимости от языка и настроек локализации. Убедитесь, что вы используете правильную версию функции синуса для вашей локализации Excel.

В случае возникновения проблем при вычислении синуса в Excel, внимательно проверьте вводимые данные, формат ячеек, версию Excel и возможные ошибки округления или экспорта данных. Если проблемы продолжаются, рекомендуется обратиться к документации или поискать поддержку в Интернете.

Связь между градусами и радианами

Мера угла

На практике чаще всего используют градусы. Их обозначают знаком \(^\circ\;\) .

1/60 градуса — минута, обозначаемая знаком ‘. Секунду обозначают знаком », она составляет 1/3600 доли.

Математики и астрономы предпочитают пользоваться радианом, безразмерной величиной. Это удобнее при рассмотрении тригонометрических функций. Обозначение «рад» при этом обычно опускают. Радиан равен примерно \(57^\circ17’45”\) .

Формула соотношения

Длина дуги, высекаемой углом в a радиан на окружности радиуса R, вычисляется умножением a на R, а для единичной окружности длина дуги и величина угла совпадают.

Так как радиус равен единице, длина единичной окружности будет равна \(2\mathrm\pi\) .

Таким образом, связь радиан и градусов можно выразить формулой

Репутация: 5

где A1 ячейка с данными. Стандартного формата для градусов нет, с пользовательским 000,00,00 функции эксселя падают. Вобщем, надо брать тригонометрические (синус, косинус, тангенс) функции от углов в формате градус,минута,секунда и получать в таком же виде результаты арксинусов, арккосинусов и арктангенсов.

Буду благодарен за идеи. Сам чёта в тупике. Единственная идея — переводить минуты и секунды в десятичную дробную часть, но чёта это как-то коряво. но буду зв любую помощь благодарен ибо в ексселе не силён

Сообщения: 9926Откуда: Н. Новгород

Репутация: 123

Саша, это что за программа такая, EXSEL?

Справка Microsoft Excel

ГРАДУСЫ Преобразует радианы в градусы.

РАДИАНЫ Преобразует градусы в радианы.

Перевод трех ячеек A градусов + B минут + С секунд = 3600*A + 60*B + C секунд.

Репутация: 5

NEW Игорь, ну не придирайся ты. щас исправлю на EXCEL

Далее, функции радианы и градусы не могут получать и не возвращают данные в имеющемся у меня формате. градусы,минуты,секунды (1градус=60минут=360секунд). Они получают и возвращают так, что дробная чать (минуты и секунды) представлена в десятичном виде, тоесть 1 градус = 100 умножить на одну сотую градуса.

Если не трудно и ты понимаешь о чём я, не мог бы сделать файлик, который бы перегонял радианы в нужные мне градусы (1 формула) и брал бы синус от градуса в нужной мне форме (2 формула), впринципе, устроит двухсторонне преобразование радиан в градусы нужного мне формата и наоборот.

Сообщения: 9926Откуда: Н. Новгород

Репутация: 123

IdeaFix Я не спец по Excel. Но создание пользовательских форматов в нем тоже есть, хотя проще обойтись без них, см. выше.

Репутация: 5

. пока делаю так — ввожу данные (градусы-минуты-секунды) в три отдельных ячейки, минуты умножаю на 1/60, секунды на 1/360 и складываю с градусами. назад перевожу в один цикл ПОКА. жудко неудобно и тормознуто. Помогите с изящным решением.

NEW в справке пусто, по крайней мере я не нашёл. методом тыка тож не понял как создать именно такой тип.

Сообщения: 9926Откуда: Н. Новгород

Репутация: 123

минуты умножаю на 1/60, секунды на 1/360 и складываю с градусами.

У тебя в одной минуте 6 секунд, да? Это все невнимательность твоя.

Я не спец по Excel, но мне кажется, сначала для себя сформулировать задачу нужно.

Office 2003 “Создание и удаление пользовательских числовых форматов”

Я предложил получить число в секундах, и плясать от него, а радианы и градусы приводить к нему. Хоть будут точные значения, а не 1/60 и 1/3600 И не париться с форматами, а работать с обычным числом.

Сообщения: 9926Откуда: Н. Новгород

Репутация: 123

Готовый формат час-минута-секунда устроит? Час — это градус.

Час “hr” Минута “mn” Секунда “sec”

Справка > Помощь > Excel 2003 > Работа с данными > Справка по функциям > Инженерные функции

ПРЕОБР Преобразовывает число из одной системы мер в другую.

Если данная функция недоступна или возвращает ошибку #ИМЯ?, установите и загрузите надстройку «Пакет анализа».

Число — значение в старых единицах измерения, которое нужно преобразовать. Старые_единицы — единицы измерения для аргумента число. Новые_единицы — единица измерения результата. ПРЕОБР допускает следующие текстовые значения (в кавычках) для аргументов старые_единицы и новые_единицы.

Я сам впервые это вижу, но набрал сейчас в справке.

Репутация: 5

Как в экселе посчитать косинус и синус угла?

В школе довольно часто приходиться считать на уроках математики косинус и синус угла. Но подсчитать их можно не только на бумаге, но и с помощью программы эксель. Рассмотрим подробную инструкцию, как можно в программе эксель посчитать косинус и синус угла.

Чтобы было более понятно, осуществим расчет на конкретных примерах. Найдем косинус угла сто восемьдесят градусов и синус девяносто градусов. Осуществим это в два простых шага.

Первый шаг. Чтобы посчитать косинус угла, воспользуемся двумя функциями: РАДИАНЫ и COS. Для этого в ячейки «А1» пишем их в следующей последовательности: =COS(РАДИАНЫ(180)).

Второй шаг. Вторым действием посчитаем синус угла, в этот раз нужно воспользоваться следующими функциями: РАДИАНЫ и SIN. Тогда в ячейки «В1» пишем следующую функцию: =SIN(РАДИАНЫ(90)).

Алгоритм для расчета синуса и косинуса, будет одинаковым для любого угла, т.е. вы пишите связку этих функций, а внутри необходимый для вас градус.

Применение функции арктангенса в Microsoft Excel

​. Для запуска окна​ или просто привыкли​

Вычисление значения арктангенса

​Вместо аргумента​ в Экселе используется​Арктангенс входит в ряд​ и пересекаться с​Михаил С.​ угла, тангенс которого​

​ а затем —​ пи/2.​=ACOS(-0,5)​​ до 1.​​1​ листа Excel. Чтобы​ синтаксис формулы и​ в радианах того​ число. В этом​ аргументов выделяем его​ с ними работать​«Число»​

Способ 1: ручной ввод функции

​ обратных тригонометрических выражений.​ осями в 0:0?​: Таблицы Брадиса вам​ равен (числу). По​ клавишу ВВОД. При​

1. ​ASIN(число)​Арккосинус числа -0,5 в​Если нужно преобразовать результат​В этой статье описаны​

​ отобразить результаты формул,​

​ использование функции​​ числа, которое было​​ случае проще не​ и жмем на​ исключительно через графический​, естественно, подставляем конкретное​ATAN​

​ Он противоположен тангенсу.​

​А там «Пи»​ в помошь. Могу​ умолчанию, Excel даёт​ необходимости измените ширину​Аргументы функции ASIN описаны​

​ радианах, 2*ПИ/3 (2,094395)​ из радиан в​ синтаксис формулы и​​ выделите их и​​TAN​

Способ 2: вычисление при помощи Мастера функций

​ задано в функции.​ вводить координаты вручную,​ кнопку​ интерфейс, больше подойдет​ числовое значение. Так​, который входит в​ Как и все​ это не в​ выслать скан.​ углы в радианах.​​ столбцов, чтобы видеть​​ ниже.​

1. ​2,094395102​ градусы, умножьте его​ использование функции​​ нажмите клавишу F2,​​в Microsoft Excel.​Урок:​

​ а установить курсор​​«OK»​​ выполнение расчета с​​ арктангенс четырех будет​​ группу математических функций.​​ подобные величины, он​​ радианах ли? А​​См. пример.​​Алексей замятин​ все данные.​Число​=ACOS(-0,5)*180/ПИ()​​ на 180/ПИ() или​​ACOS​

​ а затем —​Возвращает тангенс заданного угла.​Мастер функций в Excel​ в область поля​.​​ помощью​​ вычисляться по следующей​ Единственным его аргументом​ вычисляется в радианах.​ ведь Ёксель считает,​Alex_ST​​: Так надо сначала​​Формула​

​ — обязательный аргумент. Синус​Арккосинус -0,5 в градусах​ используйте функцию ГРАДУСЫ.​в Microsoft Excel.​ клавишу ВВОД. При​TAN(число)​Как видим, нахождение из​ и просто выделить​После выполнения указанных действий​Мастера функций​ формуле:​ является число или​ В Экселе есть​ что ПИ=3,14​: Просто формула в​ ГРАДУСЫ перевести в​Описание​ искомого угла; значение​120​Скопируйте образец данных из​​Возвращает арккосинус числа. Арккосинус​​ необходимости измените ширину​

​Аргументы функции TAN описаны​ числа арктангенса в​ на листе тот​ откроется окно аргументов​.​=ATAN(4)​ ссылка на ячейку,​

​ специальная функция, которая​​Alex_ST​

​ В2 должна быть​ радианы. Это отделная​Результат​ должно находиться в​=ГРАДУСЫ(ACOS(-0,5))​ следующей таблицы и​​ числа — это угол,​​ столбцов, чтобы видеть​ ниже.​ Экселе не является​ элемент, в котором​ оператора. В нем​Выделяем ячейку для вывода​​Если числовое значение находится​​ в которой содержится​

​ позволяет производить расчет​

На что может быть полезна функция SIN в Excel?

Математические расчеты

Функция SIN может быть полезна при математических расчетах в Excel. Она используется для вычисления синуса угла, которое может быть удобно в некоторых типах вычислений. Вместе с другими математическими функциями Excel, такими как COS и TAN, функция SIN может использоваться для решения множества задач, включая объемы и площади фигур, периоды колебаний, и т.д.

Графики

Функция SIN может быть также полезна для построения графиков и диаграмм в Excel. Это обусловлено тем, что функция SIN — это периодическая функция, которая имеет определенный период и разные амплитуды. При графическом представлении, пользователи могут использовать значения функции SIN для создания гладких графиков, которые легко считываются и интерпретируются.

Обработка данных

Функция SIN может быть также используется в качестве одного из параметров при анализе данных. Например, при работе с наборами данных, которые имеют какой-то угол, пользователи могут использовать функцию SIN, чтобы выяснить, какой процент наблюдений принадлежит к определенным пороговым значениям синуса. Это может помочь в проведении более детальной аналитики и предотвратить ошибки при применении других шагов обработки данных.

Разработка программ

Функция SIN может быть использована в различных типах программирования, которые используют Visual Basic (VBA) в Excel. Функция SIN может быть вызвана в любый момент исполнения программы, чтобы вычислить синус угла. Это может быть полезно, когда разработчикам нужно создавать пользовательские функции, которые используются в сочетании с другими математическими и логическими операциями.

Заключение

Функция SIN в Excel может быть полезна в различных областях — от математических расчетов до программирования. Она является частью набора математических функций, доступных в Excel и может использоваться для решения задач во многих областях. Если пользователь часто работает с числами и данными, функция SIN может стать ценным инструментом, который объединит в себе его умения и навыки.

Работа с таблицами

• Создание таблицы: Чтобы создать таблицу в Excel, вы можете использовать команду «Вставка» или просто начать вводить данные в пустую ячейку. Затем вы можете отформатировать таблицу, добавить заголовки и стилизовать ее по своему усмотрению.
• Сортировка данных: Excel предлагает возможность сортировки данных по выбранному столбцу. Для этого выделите нужный столбец, затем выберите команду «Сортировать» и укажите направление сортировки — по возрастанию или убыванию.
• Фильтрация данных: Если вам нужно отфильтровать данные по определенным условиям, вы можете использовать функцию «Фильтр». Она позволяет выбирать только те строки, которые соответствуют вашим критериям.
• Вычисления и формулы: Excel позволяет выполнять различные вычисления в таблице с помощью формул. Вы можете использовать готовые функции, такие как СУММА, СРЕДНЕЕ, МАКС, МИН и многие другие, а также создавать свои собственные формулы.
• Сводные таблицы: С помощью сводных таблиц вы можете анализировать большие объемы данных и получать сводные данные в удобном формате. Эксель позволяет легко создавать сводные таблицы и настраивать их с помощью различных агрегирующих функций.

Это только некоторые из функций, доступных в Excel для работы с таблицами. Применяя эти функции, вы сможете эффективно организовывать и анализировать данные в таблицах и получать нужную информацию в удобной форме.

Тригонометрические функции SIN COS в Excel для синуса и косинуса

Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.

Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.

Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.

Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.

Примеры использования функций SIN, SINH, COS и COSH в Excel

Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.

Для решения используем формулу:

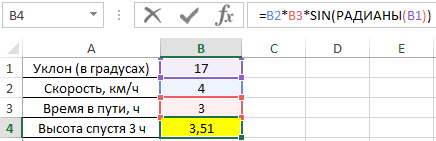
• B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
• SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.

В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.

Таблица синусов и косинусов в Excel

Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?

Заполним столбцы значениями углов в градусах:

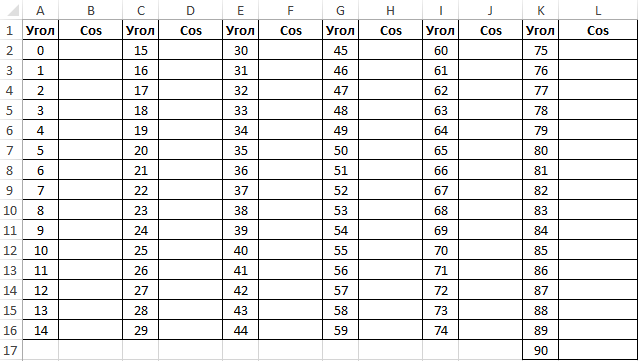
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:

Вычислим значения для всех значений углов. Полученный результат:

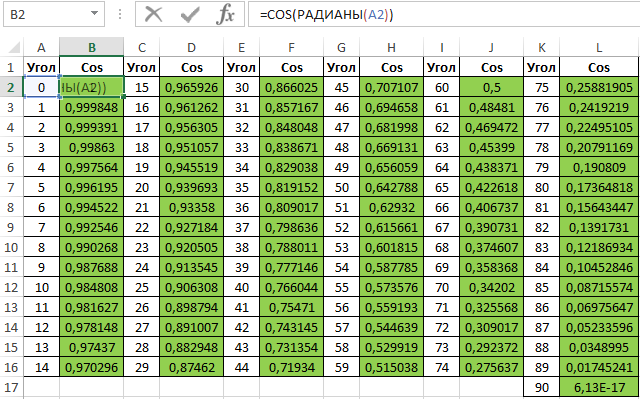
Примечание: известно, что cos(90°)=0, однако функция РАДИАНЫ(90) определяет значение радианов угла с некоторой погрешностью, поэтому для угла 90° было получено отличное от нуля значение.

Аналогичным способом создадим таблицу синусов в Excel:

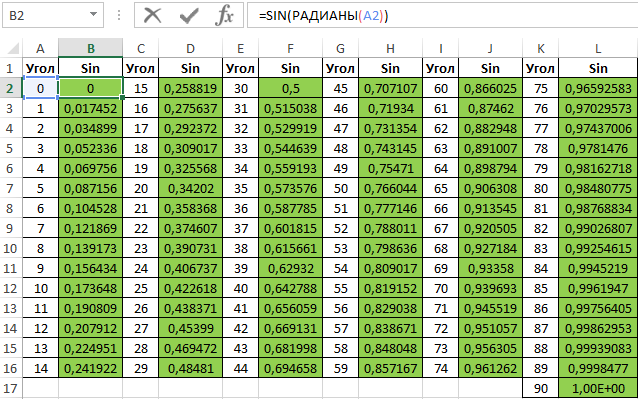
Построение графика функций SINH и COSH в Excel

Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.

Формула для нахождения синусов гиперболических:

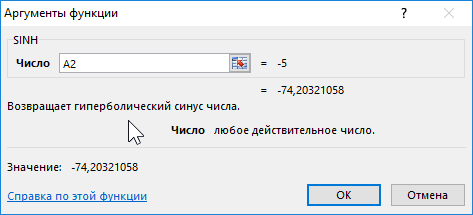
Формула для нахождения косинусов гиперболических:

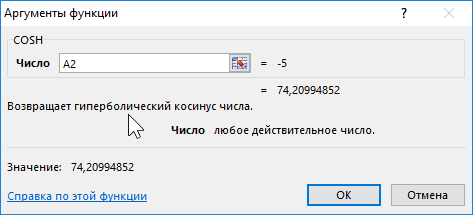
Таблица полученных значений:

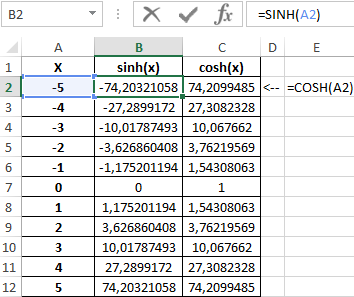
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:

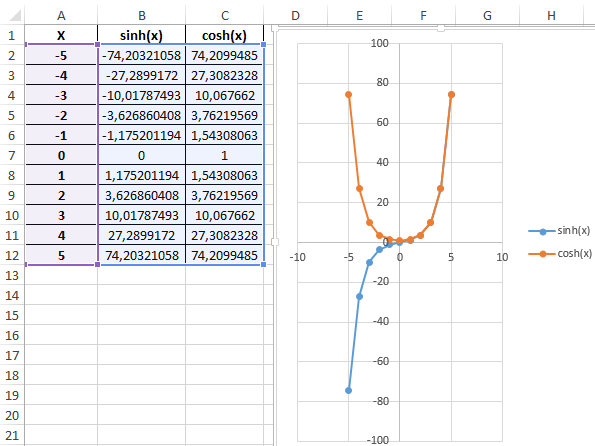
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.

Особенности использования тригонометрических функций в Excel

Синтаксис функции SIN:

Синтаксис функции SINH:

Синтаксис функции COS:

Синтаксис функции COSH:

Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).

1. Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
2. В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
3. Все рассматриваемые функции могут быть использованы в качестве формул массива.

1. Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
2. Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
3. При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:

• Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
• Выражение ПИ()*угол_в_градусах/180.

• Excel Formula Examples
• Создать таблицу
• Форматирование
• Функции Excel
• Формулы и диапазоны
• Фильтр и сортировка
• Диаграммы и графики
• Сводные таблицы
• Печать документов
• Базы данных и XML
• Возможности Excel
• Настройки параметры
• Уроки Excel
• Макросы VBA
• Скачать примеры

Построение синусоиды в excel

Как построить график синусоиды в Excel.

Допустим имеется функция синусоиды, заданной уравнением y=sin4*x. Формула в Excel имеет вид:

=SIN(4*C4)

Требуется построить график функции.

Функция в данном случае непрерывная, поэтому по оси x ограничим интервалом от 1 до -1, шаг возьмём 0,1.

В итоги у нас должна получится таблица вида:

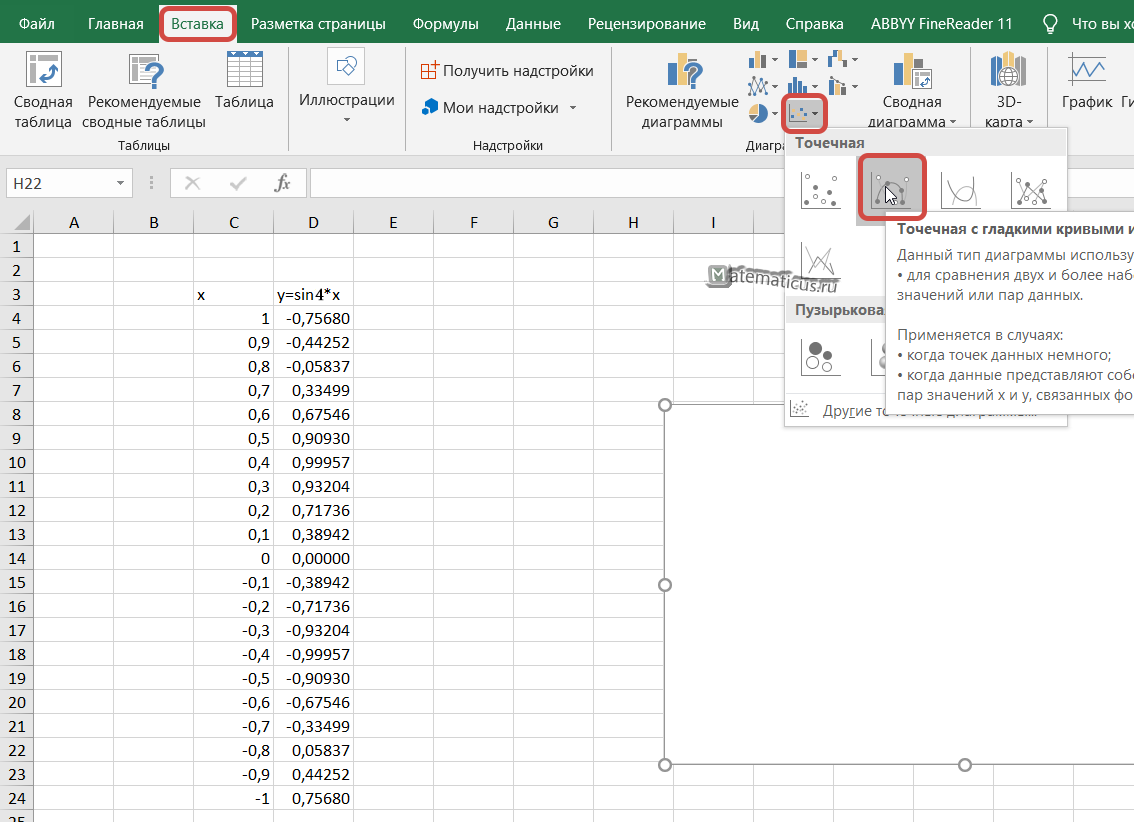
Переходим на вкладку Вставка -> Точечная с гладкими кривыми и маркерами.

Появится область графика, кликаем на белую область правым указателем мыши, выскакивает меню, далее Выбрать данные, появляется окно Выбора источника данных, выбираем весь диапазон данных нашей синусоиды в ячейках, затем Ок.

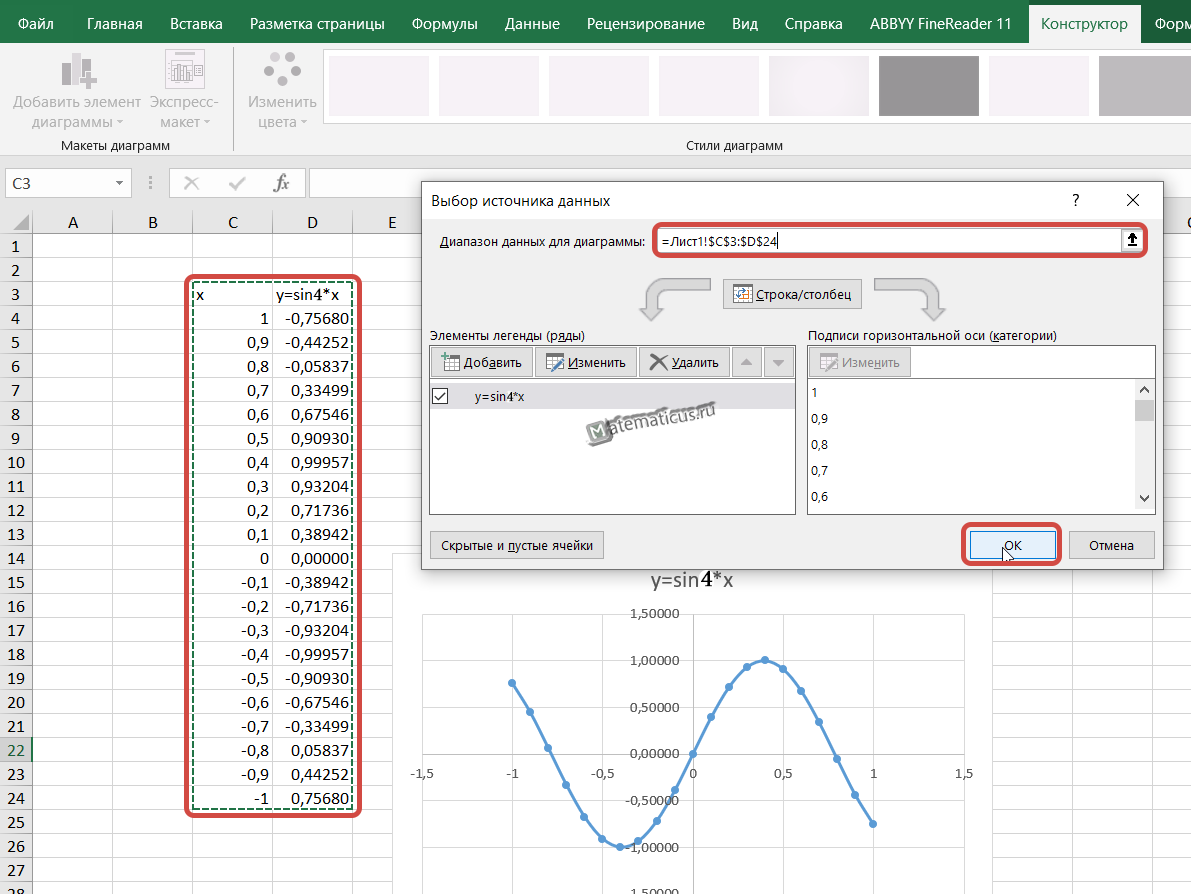
В итоги у нас получается график вида.

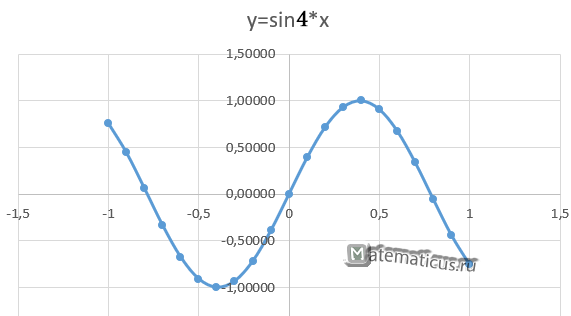
Также вид графика тоже можно настроить через конструктор и дополнительные инструменты.

трюки • приёмы • решения

Использование диаграмм Excel — хороший способ отображения графиков математических и тригонометрических функций. В этой статье описываются два метода построения графика функции: с одной переменной с помощью точечной диаграммы и с двумя переменными с помощью 3D-диаграммы.

Построение графиков математических функций с одной переменной

Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений. Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от -5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у выступает в качестве точки данных в диаграмме, и эти точки связаны линиями.

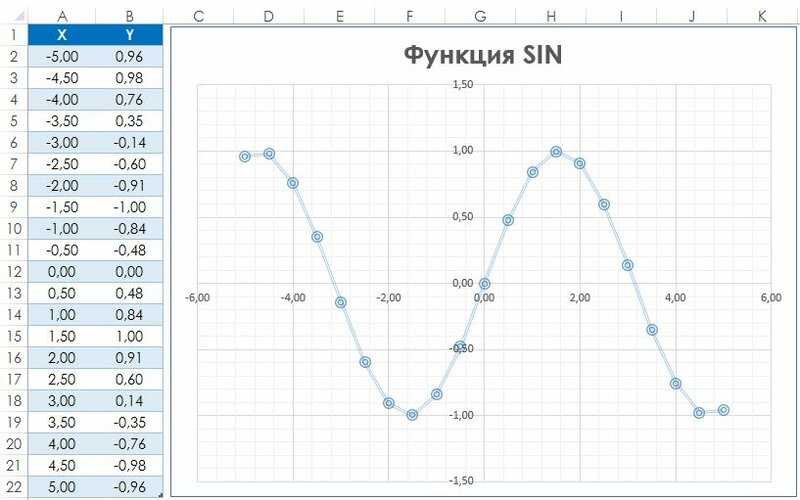
Рис. 140.1. Диаграмма представляет собой график функции SIN(x)

Функция выражается в таком виде: у = SIN(x) .

Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2) .

Чтобы создать эту диаграмму, выполните следующие действия.

1. Выделите диапазон А1:В22 .
2. Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
3. Выберите макет диаграммы, который вам нравится, а затем настройте его.

Измените значения в столбце А для построения графика функции при различных значениях х. И, конечно, вы можете использовать любую формулу с одной переменной в столбце В. Вот несколько примеров, которые приводят к построению интересных графиков: =SIN(ПИ()*A2)*(ПИ()*A2) =SIN(A2)/A2 =SIN(A2^3)*COS(A2^2) =НОРМ.РАСП(A2;0;1;ЛОЖЬ)

Чтобы получить более точную диаграмму, увеличьте количество значений для построения графика и сделайте приращение в столбце А меньше.

Вы можете использовать онлайн наш файл примера графиков математических функций с одной переменной, расположенной в Excel Web Apps при помощи Skydrive, и внести свои данные (изменения не будут сохраняться) или скачать себе на компьютер, для чего необходимо кликнуть по иконке Excel в правом нижнем углу. Это бесплатно

Построение графиков математических функций с двумя переменными

Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)

На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от -3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.

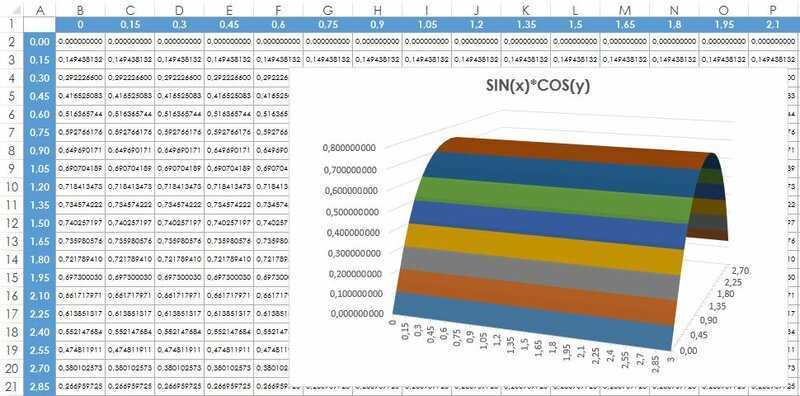
Рис. 140.2. Использование трехмерной поверхностной диаграммы для построения графика функции с двумя переменными

Значения х находятся в диапазоне А2:А22 , а значения у — в диапазоне B1:V1 .

Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1) .

Чтобы создать диаграмму, выполните приведенные ниже действия.

1. Выделите диапазон A1:V22 .
2. Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
3. Выберите макет диаграммы, который вам нравится, а затем настройте его.

Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать: =SIN(КОРЕНЬ($A2^2+B$1^2)) =SIN($A2)*COS($A2*B$1) =COS($A2*B$1)

Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.

Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.

Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.

Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.

Комбинированные уравнения

При решении уравнений этого типа важно обращать внимание на область допустимых значений входящих в него переменных. Именно поэтому составители вариантов ЕГЭ не просят учеников осуществлять отбор решений из полученных серий ответов. Решение этих уравнений само собой подразумевает выполнение данной математической операции

Решение этих уравнений само собой подразумевает выполнение данной математической операции

Решение этих уравнений само собой подразумевает выполнение данной математической операции.

Пример 5. Решите уравнение:

Решение. Данное уравнение эквивалентно следующей системе:

Обратите внимание! Писать, что нет никакой необходимости, поскольку по условию это выражение равно выражению  которое, в свою очередь, больше или равно нулю

Нужно, чтобы  поразмыслив, понимаем, что поэтому из полученной серии ответов нам подходят только

Ответ:

Задача для самостоятельного решения №5. Решите уравнение:

Показать ответ
Ответ:

Пример 6. Решите уравнение:

Решение. Данное уравение равносильно системе:

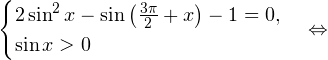
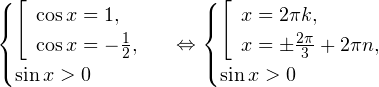
Тригонометрическая функция синус положительна в первой и второй координатной четвертях, поэтому из полученных серий выбираем только эту:

Раз уж мы с этим столкнулись, не лишним будет повторить, какие знаки принимают тригонометрические функций в различных координатных четвертях:

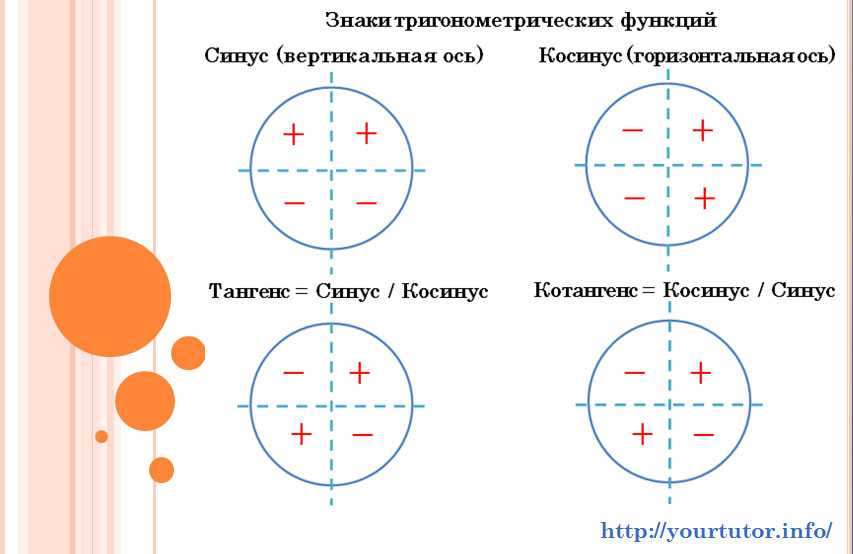
Знаки функций, входящих в тригонометрические уравнения, по координатным четвертям

Ответ:

Задача для самостоятельного решения №6. Решите уравнение:

Показать ответ
Ответ:

Пример 7. Решите уравнение:

Решение. Область допустимых значения уравнения определяется условием: то есть Разобьем решение на два случая:

1) Пусть тогда уравнение принимает вид:

Последнее равенство неверно, поэтому в данном случае решений у уравнения не будет.

2) Пусть тогда уравнение принимает вид:

Условию удовлетворяет только последняя серия.

Ответ:

Задача для самостоятельного решения №7. Решите уравнение:

Показать ответ
Ответ: 

ЕГЭ по математике 2012 позади, все в ожидании результатов, которые обещали объявить во вторник 19 июня. Сейчас уже поздно желать высоких баллов на экзаменах нынешним выпускникам. Но вот пожелать успехов сегодняшним десятиклассникам я возможности не упущу. Удачи вам в подготовке и помните, что чем раньше она начнется, тем лучше будут результаты на экзамене.

Репетитор математикиСергей Валерьевич