Как посчитать обратную матрицу в excel

Варианты решений

Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.

Способ 1: матричный метод

Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:

1. Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.

Аргумент «Массив» — это, собственно, адрес исходной таблицы.

Способ 2: подбор параметров

Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение

1. Принимаем значение x за равное . Высчитываем соответствующее для него значение f(x), применив следующую формулу:

Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.

Способ 3: метод Крамера

Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:

1. Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».

Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.

Способ 4: метод Гаусса

Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:

1. Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.

Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.

Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.

Мы рады, что смогли помочь Вам в решении проблемы.

Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

3.4. Пример пользовательской функции

Наконец, есть еще одно, самое изящное решение проблемы с
интегральной показательной функцией – написать на VBA собственную
функцию листа.  

Рис.45 Функция IntExp

На Рис. 45 приведен
и пример обращения к
ней.  

Мы не будем рассказывать о программировании на VBA, т.к.
это очень большой и сложный вопрос. Самостоятельно его можно изучить по
имеющимся в сети многочисленным пособиям, например,
здесь.

VBA – это довольно медленный язык и он плохо подходит
для больших вычислений. Например, не стоит писать на этом языке
процедуру для PCA декомпозиции – на больших массивах она будет считать
очень долго. Правильнее рассматривать Excel и VBA как интерфейс (front
end) для ввода и вывода данных, которые затем передаются в динамическую
библиотеку (DLL), написанную на быстром языке, таком как C++ (back end).
Именно эта концепция и была реализована в надстройках
Fitter и
Chemometrics.

Подробнее об использовании пользовательских функций для
расширения возможностей надстройки Chemometrics можно прочитать
.  

Этап 1. Вычисляем определитель

В программе данное действие выполняется с помощью функции МОПРЕД.

1. Переходим в свободную ячейку, в которой планируем производить расчеты, после чего кликаем по кнопке “Вставить функцию” (fx) слева от строки формул.
2. В открывшемся окне вставки функций выбираем категорию “Математические”, в которой кликаем по оператору “МОПРЕД”, затем – по кнопке OK.
3. В следующем окне нужно заполнить единственный аргумент функции – “Массив”, в значении которого указываем координаты нашей матрицы. Сделать это можно вручную, прописав адреса ячеек, используя клавиши клавиатуры. Либо можно сначала кликнуть внутри области ввода информации, затем зажав левую кнопку мыши выделить диапазон ячеек непосредственно в самой таблице. Когда все готово, нажимаем кнопку OK.
4. В выбранной ячейке отобразился результат, а именно, определитель матрицы. С учетом наших данных получилось число 157894, что значит, что у нашей матрицы обратная матрица существует, так как определитель не равен нулю.

Функции для работы с матрицами в Excel

В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.

Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.

Формулы массива

Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).

Порядок применения формулы массива:

1. Выделить диапазон, где должен появиться результат действия формулы.
2. Ввести формулу (как и положено, со знака «=»).
3. Нажать сочетание кнопок Ctrl + Shift + Ввод.

В строке формул отобразится формула массива в фигурных скобках.

Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.

Решение матриц в Excel

С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.

Транспонирование

Транспонировать матрицу – поменять строки и столбцы местами.

Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.

• 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
• 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.

Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.

Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.

Сложение

Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.

В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.

Умножение матриц в Excel

Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).

Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.

В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.

Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.

Обратная матрица в Excel

Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).

Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.

Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:

Нахождение определителя матрицы

Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.

Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).

Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.

Решение матриц в Excel

С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число/матрицу; найти обратную матрицу и ее определитель.

Транспонирование

Транспонировать матрицу — поменять местами строки и столбцы.

Сначала отмечаем пустую область, куда будем транспонировать матрицу. В исходном массиве 4 строки — в области транспонирования должно быть 4 столбца. 5 столбцов — это пять строк в пустой области.

• 1 способ. Выберите исходную матрицу. Нажмите «копировать». Выберите пустую область. Клавиша «Развернуть» «Вставить». Откройте специальное меню «Вставить». Выберите операцию «Транспонирование». Закройте диалоговое окно, нажав кнопку OK.
• 2 пути. Выберите ячейку в верхнем левом углу пустой области. Вызов мастера функций. Функция ТРАНСПОЗЕР. Аргумент представляет собой диапазон исходной матрицы.

Нажимаем ОК. Пока функция выдает ошибку. Выберите всю область, в которую вы хотите транспонировать матрицу. Нажмите кнопку F2 (переход в режим редактирования формулы). Нажмите комбинацию клавиш Ctrl+Shift+Enter.

Преимущество второго метода заключается в том, что при изменении исходной матрицы транспонированная матрица изменяется автоматически.

Сложение

Вы можете добавлять массивы с одинаковым количеством элементов. Количество строк и столбцов в первой области должно быть равно количеству строк и столбцов во второй области.

В первую ячейку полученного массива введите формулу вида: = первый элемент первого массива + первый элемент второго: (=B2+H2). Нажмите Enter и разверните формулу на весь диапазон.

Умножение матриц в Excel

Задание:

Чтобы умножить массив на число, необходимо умножить каждый его элемент на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).

Умножьте матрицу на матрицу для разных областей. Произведение матриц можно найти только в том случае, если количество столбцов в первой матрице равно количеству строк во второй.

В полученной матрице количество строк равно количеству строк в первой матрице, а количество столбцов равно количеству столбцов во второй.

Для удобства выделим область, где будут размещены результаты умножения. Делаем первую ячейку получившегося поля активной. Вводим формулу: = МНОЖЕСТВО (А9:С13; Е9:Н11). Введите как формулу массива.

Обратная матрица в Excel

Его имеет смысл найти, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).

Размер обратной матрицы равен размеру исходной. Функция Excel — МОБР.

Выберите первую ячейку в пустой области для обратной матрицы. Введите формулу «=MOBR(A1:D4)» в качестве функции массива. Единственным аргументом является диапазон исходного массива. Получили обратную матрицу в Excel:

Нахождение определителя матрицы

Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.

Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).

Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.

Вычислить значения корней сформированной системы уравнений двумя методами: обратной матрицы и методом Крамера.

Введем данные значения в ячейки А2:С4 – матрица А и ячейки D2:D4 – матрица В.

Решение системы уравнений методом обратной матрицы

Найдем матрицу, обратную матрице А. Для этого в ячейку А9 введем формулу =МОБР(A2:C4). После этого выделим диапазон А9:С11, начиная с ячейки, содержащей формулу. Нажмем клавишу F2, а затем нажмем клавиши CTRL+SHIFT+ENTER. Формула вставится как формула массива. =МОБР(A2:C4). Найдем произведение матриц A-1 * b. В ячейки F9:F11 введем формулу: =МУМНОЖ(A9:C11;D2:D4) как формулу массива. Получим в ячейках F9:F11

корни уравнения:

Решение системы уравнений методом Крамера

Решим систему методом Крамера, для этого найдем определитель матрицы. Найдем определители матриц, полученных заменой одного столбца на столбец b.

В ячейку В16 введем формулу =МОПРЕД(D15:F17),

В ячейку В17 введем формулу =МОПРЕД(D19:F21).

В ячейку В18 введем формулу =МОПРЕД(D23:F25).

Найдем корни уравнения, для этого в ячейку В21 введем: =B16/$B$15, в ячейку В22 введем: = =B17/$B$15, в ячейку В23 введем: ==B18/$B$15.

Получим корни уравнения:

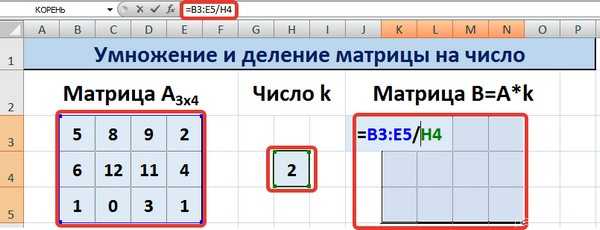
Способ 1

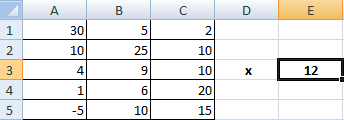
Рассмотрим матрицу А
размерностью 3х4
. Умножим эту матрицу на число k
. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А
умножается на число k
.

Введем элементы матрицы в диапазон В3:Е5
, а число k
— в ячейку Н4
. В диапазоне К3:
N
5
вычислим матрицу В
, полученную при умножении матрицы А
на число k
: В=А*
k
. Для этого введем формулу =B3*$H$4
в ячейку K
3
, где В3
— элемент а 11
матрицы А
.

Примечание:

адрес ячейки H
4
вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.

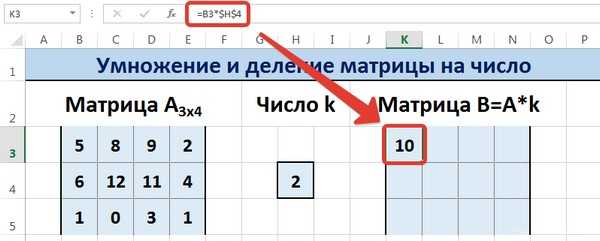
С помощью маркера автозаполнения копируем формулу ячейки К3
В
.

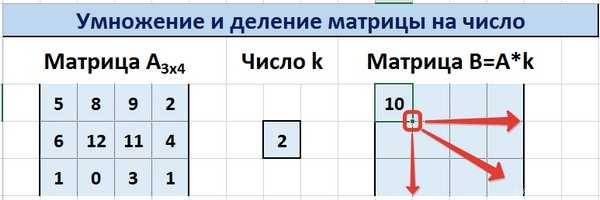
Таким образом, мы умножили матрицу А
в Excel и получим матрицу В
.

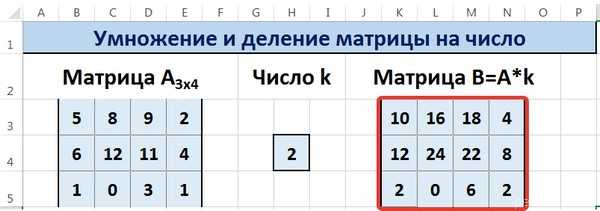
Для деления матрицы А
на число k в ячейку K
3
введем формулу =B3/$H$4
В
.

Способ 2

Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.

Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k
Ctrl+
Shift+
Enter

Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».

1.4. Область

Матрица занимает на листе область. Пример показан на Рис. 6, где расположена
матрица, которая имеет 9 строк (с 2 по 10) и 3 столбца (с B по D).  

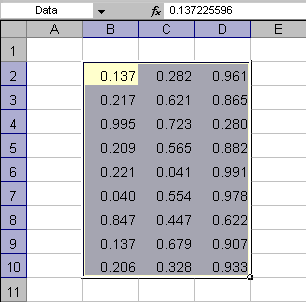
Рис.6 Область на листе

Для ссылки на область используется выражение, в котором адреса
верхней левой и правой нижней ячеек области соединяются двоеточием.
Например, B2:D10 или
$B$2:$D$10.

При работе с матрицами бывает удобно присвоить ее области имя. Для
этого есть два способа. Самый простой – это выделить нужную область на
листе, а затем кликнуть в окно Name Box (см.
), стереть там адрес и вписать имя – например
Data (Рис. 6). Другой способ – это
действовать через меню: Insert-Name-Define.

Имя области может быть глобальным – доступным для любых листов книги,
или локальным – определенным только для одного листа. В последнем
случае, имя следует определять в форме:
ListName!RangeName

Подробности смотри

здесь.

1.6. Функции

Функции – это стандартные формулы, проводящие вычисления по заданным
величинам, называемым аргументами. Некоторые примеры функций показаны на
Рис. 8.

Рис.8
Простейшие функции

Функция состоит из имени, за которым следует круглая
скобка, затем идет список аргументов, разделенных запятой и, наконец,
закрывающая скобка.

Например,
функция, показанная на Рис. 9 вычисляет
значение кумулятивного (cumulative=TRUE),
стандартного (mean=0,
standard_dev =1)
для величины, находящейся в ячейке
A1 .

Рис.9
Ввод функции через Formula Bar

Задать функцию можно по-разному. Проще всего ввести ее в окно
Formula Bar 
(см. ). Только предварительно нужно открыть
это окно через меню View-Formula Bar. Такой
способ удобен, когда вы хорошо помните синтаксис функции. Формулу можно
задать быстро, т.к. аргументы вводятся простым кликаньем по ячейкам, в
которых находятся аргументы.

Другой способ спасает тогда, когда мы плохо помним вид
функции, которая нам нужна. Тогда удобно воспользоваться кнопкой
Insert Function
(). После этого появится диалоговое окно (Рис. 10), из которого
можно выбрать нужную функцию .

 

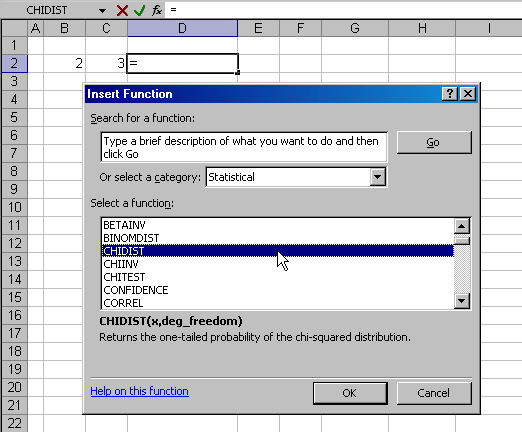
Рис.1
Ввод функции через Insert Function

Как только функция выбрана, появляется  второе окно, специфическое для выбранной функции,
в котором устанавливаются ссылки на аргументы функции

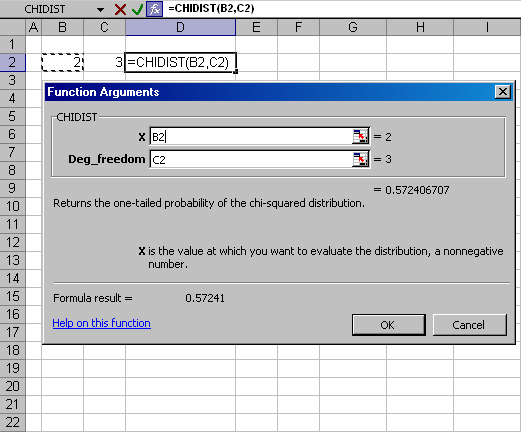
Рис.11
Задание значений аргументов

Подробнее изучить эту тему можно
здесь.

Функция МОБР

Синтаксис и описание функции МОБР в Excel:

Рассмотрим расчет обратной матрицы посредством функции МОБР на конкретном примере.
Предположим у нас имеется следующая квадратная матрица 3-го порядка:

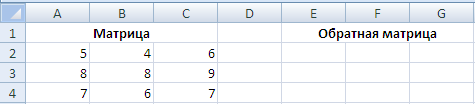
Выделяем диапазон пустых ячеек E2:G4, куда мы в дальнейшем поместим обратную матрицу.
Не снимая выделения ячеек вводим формулу =МОБР(A2:C4) и нажимаем комбинацию клавиш Ctrl + Shift + Ввод для расчета формулы массива по данному диапазону:

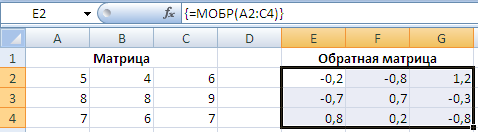
При работе с функцией МОБР могут возникнуть следующие ошибки:

• В том случае, когда исходная матрица является вырожденной (определитель равен нулю), то функция вернет ошибку #ЧИСЛО!;
• Если число строк и столбцов в матрице не совпадает, то функция возвратит ошибку #ЗНАЧ!;
• Функция также вернет ошибку #ЗНАЧ!, если хотя бы один из элементов матрицы является пустым или записан в текстовом виде.

Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР() или англ. MINVERSE .

Понятие обратной матрицы определено только для квадратных матриц, определитель которых отличен от нуля.

СОВЕТ: О нахождении определителя матрицы читайте статью Вычисление определителя матрицы в MS EXCEL

Матрица А -1 называется обратной для исходной матрицы А порядка n, если справедливы равенства А -1 *А=Е и А*А -1 =Е, где Е единичная матрица порядка n.

Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР() .

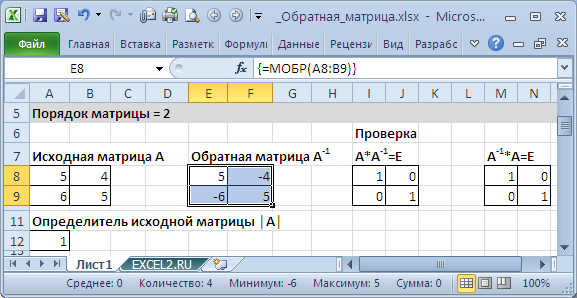
Если элементы исходной матрицы 2 х 2 расположены в диапазоне А8:В9, то для получения транспонированной матрицы нужно (см. файл примера ):

• выделить диапазон 2 х 2, который не пересекается с исходным диапазономА8:В9, например, Е8:F9
• в Cтроке формул ввести формулу = МОБР (A8:B9) и нажать комбинацию клавиш CTRL+SHIFT+ENTER, т.е. нужно ввести ее как формулу массива (формулу можно ввести прямо в ячейку, предварительно нажав клавишу F2)

Если матрица большей размерности, то перед вводом формулы нужно выделить соответственно больший диапазон ячеек.

Массив может быть задан не только как интервал ячеек, например A8:B9, но и как массив констант, например =МОБР() . Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией. Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.

Ссылка на массив также может быть указана как ссылка на именованный диапазон.

Некоторые квадратные матрицы не могут быть обращены: в таких случаях функция МОБР() возвращает значение ошибки #ЧИСЛО!. Матрицы не могут быть обращены, у которых определитель равен 0.

Если функция МОБР() вернула значение ошибки #ЗНАЧ!, то либо число строк в массиве не равно числу столбцов, либо какая-либо из ячеек в массиве пуста или содержит текст. Т.е. функция МОБР() пустую ячейку воспринимает не как содержащую 0 (как например, это делает СУММ() ), а как ошибочное значение.

Выполнение расчетов

Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.

Расчет определителя

Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.

1. Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
2. Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
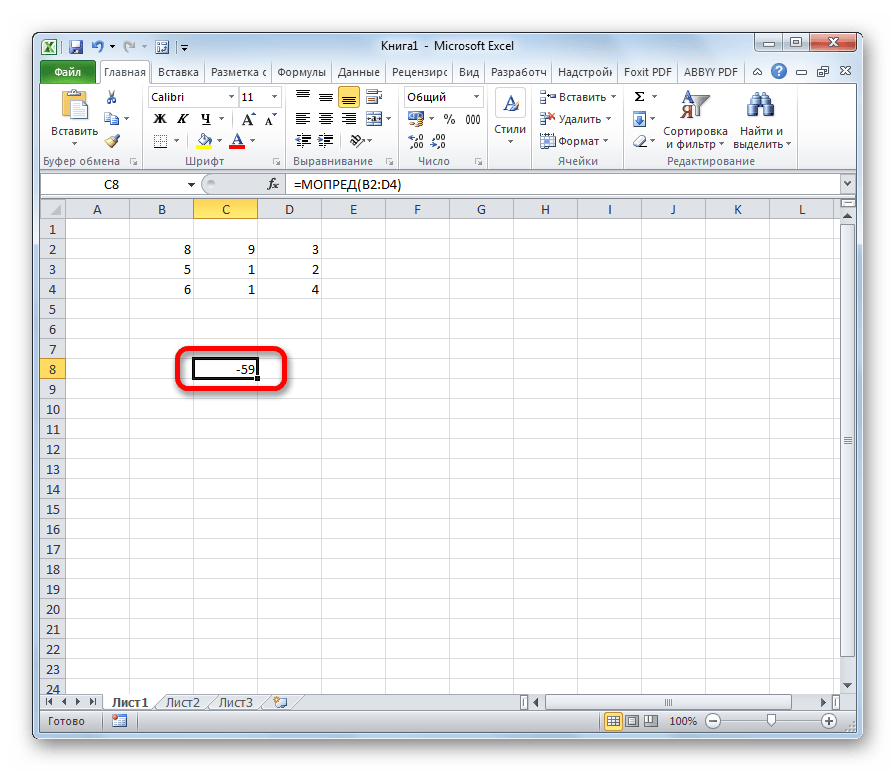
3. Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
4. Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.

Расчет обратной матрицы

Теперь можно преступить к непосредственному расчету обратной матрицы.

1. Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
2. В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
3. В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».
4. Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
5. Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.

На этом расчет можно считать завершенным.

Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Нахождение обратной матрицы всегда вызывало большие затруднения у учащихся, так как это был очень трудоемкий процесс. И вот такое задание вполне по силам EXCEL.  

Прежде всего, уясним одно правило:  Матрица имеет обратную только тогда, когда ее определитель не равен нулю.  А вот и задание: найдите матрицу, обратную к матрице А, где

Вычислять определитель этой матрицы мы умеем. Я его уже вычислил.

Он оказался равен -4, а  это значит, что у нашей матрицы есть обратная (если бы определитель оказался равен нулю, то мы сказали бы что матрица не имеет обратную и немедленно прекратили все вычисления). Теперь отметим ячейку, с которой начнем записывать ответ. Я отметил ячейку E1.  Нажимаем Формулы, затем Математические и в появившемся окне находим  МОБР

После нажатия появляется вот такое окно, в котором надо вписать адреса ячеек, в которых находятся элементы матрицы  в Массив

У нас элементы записаны в ячейки начиная с А1 и заканчивая в С3 , поэтому так и записываем (смотрите картинку)

Если все сделали правильно, то автоматически заполнится место, обведенное красным и запишется ответ, который обведен черным. В таком виде ответ трудно переваривать и поэтому нажимаем ОК.  В ячейке, которую мы застолбили под ответ, появилось число 3,  Это только первый элемент полученной обратной матрицы.

Чтобы виден был весь ответ, выполняем следующие действия: Начиная с  ячейки Е1 выделяем три строчки и три столбца (именно столько было у исходной матрицы и столько же будет у обратной)

нажимаем клавишу F2,  а затем на одновременно на три клавиши  Ctrl+Shift+Enter.

В выделенном месте появляются, теперь уже все, элементы обратной матрицы. Если Вы сохраните этот документ, то в следующий раз можете воспользоваться плодами своего труда. Так, меняя элементы исходной матрицы, Вы автоматически получаете для нее же обратную матрицу.

На этом все. Крепких вам знаний.

Рубрика: EXCEL в помощь, Статьи. Метки: EXCEL, ИКТ, матрица, обратная матрица

Этап 2. Находим обратную матрицу

Итак, после того, как мы вычислили, что определитель матрицы не равен нулю, можно приступить к нахождению обратной.

1. Встаем в ячейку, которая станет самым верхним левым элементом новой обратной матрицы. Заходим в окно Вставки функции, нажав на соответствующую кнопку.
2. В категории “Математические” выбираем функцию “МОБР”, после чего щелкаем по кнопке OK.
3. Аналогично заполнению значения аргумента “Массив” для функции МОПРЕД, рассмотренной в первом разделе, указываем координаты первичной матрицы, после чего нажимаем OK.
4. Получаем требуемый результат в выбранной ячейке.
5. Чтобы скопировать функцию в другие ячейки, выделяем область, которая совпадает по количеству столбцов и строк с начальной матрицей. Затем нажимаем клавишу F2 на клавиатуре, после чего жмем комбинацию Ctrl+Shift+Enter.
6. Все готово. В результате выполненных действий нам удалось найти обратную матрицу.