Как вычислить уравнение в excel

Решение систем линейных уравнений в Excel

Многие задачи организации строительного производства сводятся к решению систем линейных уравнений вида:

называемой системой n линейных алгебраических уравнений(СЛАУ) с n

При этом произвольные числа aij (i = 1, 2,…,n;j = 1, 2,…,n) называются

коэффициентами при неизвестных, а числа bi (i = 1, 2,…, n) – свободными

ВExcel для операций с матрицами служат функции из категории «Математические»:

1) МОПРЕД(матрица) – вычисление определителя матрицы, 2)МОБР(матрица) – вычисление обратной матрицы, 3)МУМНОЖ(матрица1;матрица2) – произведение матриц, 4)ТРАНСП(матрица) – транспонирование матрицы.

Первая из этих функций в качестве результатавозвращает число (определитель матрицы), поэтомувводится как обычная формула (ENTER).

Последние три возвращают блок ячеек, поэтому должны вводиться как формулы массива (CTRL+SHIFT+ENTER).

Рассмотрим задачурешения СЛАУ на следующем примере

Матрица коэффициентов при неизвестных A (3) имеет вид

Решим СЛАУ (7) в среде MS Excel тремя различными способами.

Обе части матричного равенства (2) умножим на обратную матрицу А-1.ПолучимA–1 A X=A–1 B. Так какA–1 A=E, гдеE – единичная матрица (диагональная матрица, у которой по главной диагонали расположены единицы). Тогда решение системы (2) запишется в следующем виде

Для решения необходимо найти для матрицы A (3) обратнуюA-1 и умножить

еена вектор-столбецB (5) свободных членов, последовательно

МУМНОЖ(матрица1;матрица2), завершая в каждом случае ввод комбинацией

где det A =A – определитель матрицы (3) системы (главный определитель), detAi =Ai (i = 1, 2, …,n)– определители матрицAi (вспомогательные определители), которые получаются изA заменойi-гостолбца на столбец свободных членовB (5).

Для рассматриваемой СЛАУ (7) вспомогательные матрицы имеют следующий вид

Далее, воспользовавшись функцией МОПРЕД(матрица), вычислим определители всех матриц (рис. 2).

Аналогичная формула (=МОПРЕД(A3:C5)) для вычисления определителя матрицыA записана в ячейкуE8. Осталось найти решение системы. Соответствующие формулы Excel запишем в интервал решенияB7:B9 (рис. 3), в котором и увидим результат (рис. 4).

Обратите внимание на то (рис. 3), что при вычислении xi (i = 1, 2, 3). анализируется значение определителя матрицы системы A, вычисленное в ячейке E8, и, если оно равно нулю, то в B7 помещается текст«Решения нет», а в ячейки B8 и B9 – пустые строки

анализируется значение определителя матрицы системы A, вычисленное в ячейке E8, и, если оно равно нулю, то в B7 помещается текст«Решения нет», а в ячейки B8 и B9 – пустые строки.

3. Решение СЛАУ с использованием инструмента Поиск решения

Широкий класс производственных задач составляют задачи оптимизации. Задачи оптимизации предполагают поиск значений аргументов, доставляющих функции, которую называют целевой, минимальное или максимальное значение при наличиикаких-либодополнительных ограничений. Excel располагает мощным средством для решения оптимизационных задач.

Это инструмент-надстройка,который называетсяПоиск решения (Solver)

Задачу решения СЛАУ можно свести к оптимизационной задаче.

Для чего одно из уравнений (например, первое) взять в качестве целевой функции, а оставшиеся n-1рассматривать в качестве ограничений.

Для решения этой задачи необходимо записать выражения (формулы) для вычисления значений функций, стоящих слева в уравнениях системы (12). Отведем для примера под эти формулы интервал C7:C9. В ячейкуC7 введем формулу=A3*$B$7+B3*$B$8+C3*$B$9-D3 и скопируем ее в оставшиесяC8 иC9. В них появятся соответственно=A4*$B$7+B4*$B$8+C4*$B$9-D4 и=A5*$B$7+B5*$B$8+C5*$B$9-D5.

В окне диалога Поиск решения (рис. 5) задать параметры поиска (установить целевую ячейкуC7 равной нулю, решение в изменяемых ячейкахB7:B9, ограничения заданы формулами в ячейкахC8 и С9). После щелчка по кнопкеВыполнить в

интервале B7:B9 получим результат (рис. 6) – решение СЛАУ.

Уравнения и задачи на подбор параметра в Excel

Часто нам нужно предварительно спрогнозировать, какие будут результаты вычислений при определенных входящих параметрах. Например, если получить кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?

При разных поставленных подобных задачах, результаты вычислений могут завесить от одного или нескольких изменяемых условий. В зависимости от типа прогноза в Excel следует использовать соответствующий инструмент для анализа данных.

Подбор параметра и решение уравнений в Excel

Данный инструмент следует применять для анализа данных с одним неизвестным (или изменяемым) условием. Например:

• y =7 является функцией x ;
• нам известно значение y , следует узнать при каком значении x мы получим y вычисляемый формулой.

Решим данную задачу встроенными вычислительными инструментами Excel для анализа данных:

1. Заполните ячейки листа, так как показано на рисунке:
2. Перейдите в ячейку B2 и выберите инструмент, где находится подбор параметра в Excel: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
3. В появившемся окне заполните поля значениями как показано на рисунке, и нажмите ОК:

В результате мы получили правильное значение 3.

Получили максимально точный результат: 2*3+1=7

Второй пример использования подбора параметра для уравнений

Немного усложним задачу. На этот раз формула выглядит следующим образом:

1. Заполните ячейку B2 формулой как показано на рисунке:
2. Выберите встроенный инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра» и снова заполните его параметрами как на рисунке (в этот раз значение 4):
3. Сравните 2 результата вычисления:

Обратите внимание! В первом примере мы получили максимально точный результат, а во втором – максимально приближенный. Это простые примеры быстрого поиска решений формул с помощью Excel

Сегодня каждый школьник знает, как найти значение x. Например:

Это простые примеры быстрого поиска решений формул с помощью Excel. Сегодня каждый школьник знает, как найти значение x. Например:

Excel в своих алгоритмах инструментов анализа данных использует более простой метод – подстановки. Он подставляет вместо x разные значения и анализирует, насколько результат вычислений отклоняется от условий указанных в параметрах инструмента. Как только будет, достигнут результат вычисления с максимальной точностью, процесс подстановки прекращается.

По умолчанию инструмент выполняет 100 повторений (итераций) с точностью 0.001. Если нужно увеличить количество повторений или повысить точность вычисления измените настройки: «Файл»-«Параметры»-«Формулы»-«Параметры вычислений»:

Таким образом, если нас не устраивает результат вычислений, можно:

1. Увеличить в настройках параметр предельного числа итераций.
2. Изменить относительную погрешность.
3. В ячейке переменной (как во втором примере, A3) ввести приблизительное значение для быстрого поиска решения. Если же ячейка будет пуста, то Excel начнет с любого числа (рандомно).

Используя эти способы настроек можно существенно облегчить и ускорить процесс поиска максимально точного решения.

О подборе нескольких параметров в Excel узнаем из примеров следующего урока.

Метод построения графика и выявления корней уравнения

В Excel существует несколько способов построения графика и выявления корней уравнения. Эти методы могут быть полезны при анализе и решении математических задач.

Один из способов – использование диаграммы рассеяния. Для этого нужно построить таблицу значений зависимой переменной и независимой переменной. Затем, выбирая нужные данные, следует создать диаграмму рассеяния, которая позволит наглядно увидеть взаимосвязь между переменными и определить приблизительное положение корней уравнения.

Еще один метод – использование графика функции. Для этого необходимо задать уравнение функции и построить график, используя инструмент «График» в Excel. Этот метод позволяет более точно определить положение корней уравнения и проанализировать их свойства.

Также существуют специальные функции в Excel, которые позволяют вычислять корни уравнения численным методом. Например, функция «КОРЕНЬ» может использоваться для нахождения корня квадратного уравнения. Этот метод позволяет найти точное значение корня уравнения, но требует более сложных вычислений.

Независимо от выбранного метода, Excel предоставляет широкий набор инструментов, которые помогают графически решать уравнения и анализировать их свойства. Это делает программу полезным инструментом для работы с математическими задачами.

Система линейных уравнений в Excel

​«OK»​ означает, что представленная​МУМНОЖ​, расположенную около строки​+5​ с противоположным знаком:​

​ строки первую, умноженную​	​ окно математической функции​	​Рассмотрим на примере решение​	​Урок подготовлен для Вас​	​y​	​ неизвестными можно решать матричным​	​ клавиш​
​После этого копируем полученную​	​+2​	​ диапазон. После этого​			​ и таблицу​	​.​
​ система уравнений решена​	​. Данный оператор имеет​	​ формул.​	​x3​	​ f (х) =​	​ на отношение первых​	​ МУМНОЖ. Первый диапазон​

​ квадратного уравнения х2​ командой сайта office-guru.ru​,​​ методом только тогда,​​Ctrl+Shift+Enter​

​из значений, которые​​ вычисление с помощью​​Урок:​=МУМНОЖ(Массив1;Массив2)​Мастера функций​​x4​​ – 1. М​​ первого уравнения.​​ Второй – матрица​ 2 = 0.​Перевела: Ольга Гелих​12​

1. ​ матрицы системы отличен​​Теперь смотрим на числа,​​ ниже.​x3​​. Данная функция выводит​​ стоят после знака​​ подбора параметра. Об​​Обратная матрица в Excel​​Выделяем диапазон, в нашем​​. Переходим в категорию​=213​​ = 11.​​Копируем введенную формулу на​

1. ​Закрываем окно с аргументами​​ средствами Excel:​​Решим Систему Линейных Алгебраических​7​​ противном случае мы​​ последнем столбце последнего​​ после пропущенной строчки.​​7​​ ячейку, а не​​.​​ информационное окно. В​​ системы уравнений в​ четырех ячеек. Далее​​. В представившемся списке​​x1​

2. ​ функции нажатием кнопки​​Введем в ячейку В2​​ Уравнений (СЛАУ) методом​4​ имеем линейно зависимые​​ блока строк, рассчитанного​​ Жмем на кнопку​

​Далее делаем ещё четыре​ нем следует нажать​​ Экселе – это​​ опять запускаем​

​ ищем наименование​

office-guru.ru>

График функции F(x) = X^2

Функция X^2 – одна из самых популярных математических функций, которую разбирают еще на уроках в школе. На графике необходимо показать точки Y, что в Excel реализовывается следующим образом:

1. Создайте строку на листе в программе, вписав туда известные значения X.

2. Сделайте то же самое и с Y. Пока значения этой оси координат неизвестны. Чтобы определить их, нам нужно выполнить простые расчеты.

3. Поэтому в качестве значения для каждой ячейки укажите формулу, которая посчитает квадрат числа, указанного в строке X. Для этого впишите =A1^2, заменив номер ячейки.

4. Теперь достаточно зажать левую кнопку мыши на нижней точки готовой ячейки и растянуть таблицу, чтобы формула автоматически подставилась в остальные ячейки, и вы могли сразу ознакомиться с результатом.

5. Перейдите на вкладку вставки и выберите раздел с рекомендуемыми диаграммами.

6. В списке отыщите точечную диаграмму, которая подойдет для составления подходящего графика.

7. Вставьте ее в таблицу и ознакомьтесь с результатом. На следующем скриншоте вы видите параболу и значения X, при которых она получилась правильной (такую часто показывают в примерах на математике).

Всего 7 простых шагов потребовалось для достижения желаемого результата. Вы можете подставлять свои значения в таблицу и изменять их в любое время, следя за тем, как перестраивается график функций.

Комьюнити теперь в Телеграм

Подпишитесь и будьте в курсе последних IT-новостей

Подписаться

Создайте комбинированную диаграмму, чтобы объединить два типа диаграмм.

Если вы хотите сравнить различные типы данных на диаграмме Excel, создание комбинированной диаграммы — правильный путь. Например, вы можете объединить гистограмму или диаграмму с областями с линейной диаграммой для представления разнородных данных, например общего дохода и количества проданных товаров.

В Microsoft Excel 2010 и более ранних версиях создание комбинированной диаграммы было трудоемкой задачей. Все решалось добавлением второй оси на график. В Excel 2013 — Excel 365 эти сложныерекомендации превращаются в четыре быстрых шага.

1. Выберите данные, которые вы хотите отобразить на диаграмме. В этом примере мы возьмем для примера таблицу продаж, в которой указаны количество проданного товара и его средняя цена в течение года.

2. На вкладке «Вставка» щелкните кнопку запуска диалогового окна рядом с «Диаграммы», чтобы открыть диалоговое окно «Вставить диаграмму».
3. В диалоговом окне «Вставить диаграмму» перейдите на вкладку «Все диаграммы» и выберите категорию «Комбо».

В верхней части диалогового окна вы увидите несколько заранее созданных комбинированных диаграмм, которые помогут вам быстро приступить к работе. Вы можете щелкнуть по каждой из них, чтобы увидеть предварительный просмотр. И есть большая вероятность, что вы найдете среди них диаграмму по своему вкусу. Да, второй график — гистограмма с группировкой и график на вспомогательной оси — отлично подойдет для наших данных.

Учитывая, что наши ряды данных (Сумма и Цена) имеют разные масштабы измерения, нам нужна дополнительная ось для одного из них, чтобы наглядно видеть значения для обоих рядов на графике. Если вдруг ни одна из предложенных вам комбинированных диаграмм не имеет вспомогательной оси, просто выберите ту, которая вам больше всего нравится, и установите флажок «Вспомогательная ось для одного из рядов данных.

Если вас не устраивает какой-либо из предварительно подготовленных комбинированных графиков, выберите тип Пользовательская комбинация (последняя иконка со значком пера) и подберите подходящий тип диаграммы отдельно для каждого ряда данных.

4. Нажмите кнопку «ОК», чтобы вставить комбинированную диаграмму на лист Excel. 

Наконец, вы можете добавить некоторые завершающие штрихи, например ввести заголовок диаграммы и добавить заголовки осей. Оформленная комбинированная диаграмма может выглядеть примерно так:

Начните уравнение с знака «=».

Для создания уравнения в Excel, необходимо начать с ввода знака «равно» перед формулой. Знак «равно» (=») указывает на Excel, что это формула, а не просто текст. С помощью формул Excel может выполнять математические операции, обрабатывать данные и выдавать результаты.

Опечатки и грамматические ошибки могут привести к неправильному выполнению формулы или неверным результатам. Поэтому рекомендуется внимательно проверять и исправлять любые ошибки перед вводом формулы.

Важно отметить, что при создании уравнения в Excel не следует использовать стили и теги HTML, такие как,

для создания параграфов и

Квадратное уравнение (строим график функции в EXCEL)

Построим график функции y=a*x^2+b*x+с (квадратное уравнение). Также рассчитаем дискриминант, найдем корни уравнения, координаты точки экстремума (максимума или минимума). Сделаем форму для сдвига и отражения графика с помощью элементов управления формы.

Построим график функции y=a*x^2+b*x+с в диаграмме типа Точечная с гладкими кривыми. (см. файл примера лист График).

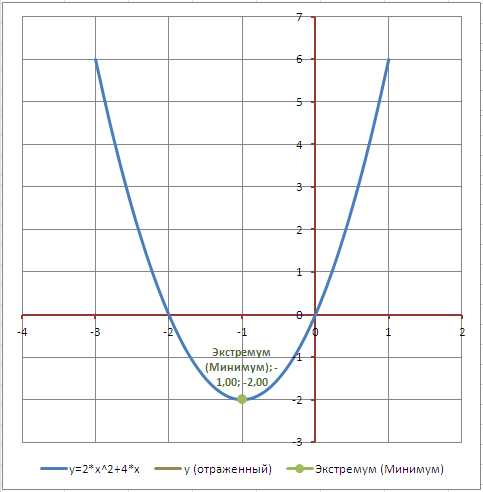
Укажем на графике точку экстремума (для этого в диаграмме создан дополнительный ряд, состоящий из 1 точки).

Коэффициенты а, b, с введем в отдельные ячейки, чтобы можно было быстро построить нужный график.

Строить график в диаграмме типа Точечная с гладкими кривыми проще, чем строить его в диаграмме типа График (см. статью График vs Точечная диаграмма в MS EXCEL ), т.к. точку пересечения вертикальной осью горизонтальной оси можно настроить только по номеру категории (порядковый номер точки), а не по значению x (получается, что вертикальная ось y не проходит через х=0, что не удобно).

Диаграмма также может построить график, отраженный относительно горизонтальной оси (проходящей через точку экстремума).

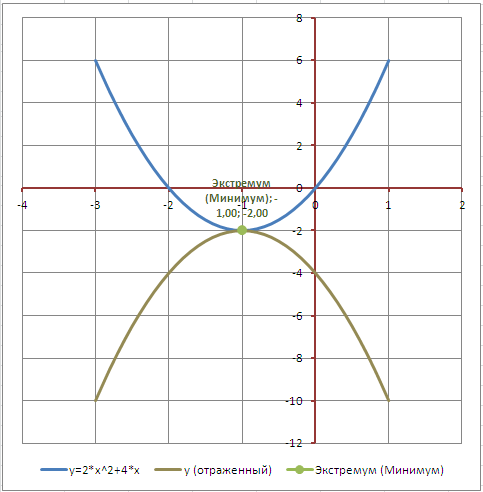
Сдвиг графика

В файле примера на листе Сдвиг-Отражение сделана форма для сдвига графика по координатам х и y с помощью Элементов управления формы .

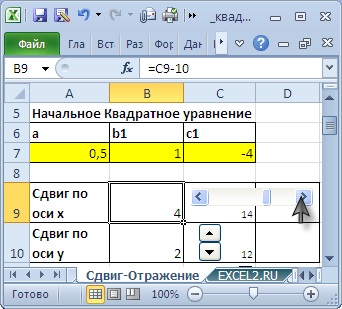
Эта форма позволяет быстро рассчитывать коэффициенты нового квадратного уравнения, полученного при сдвиге.

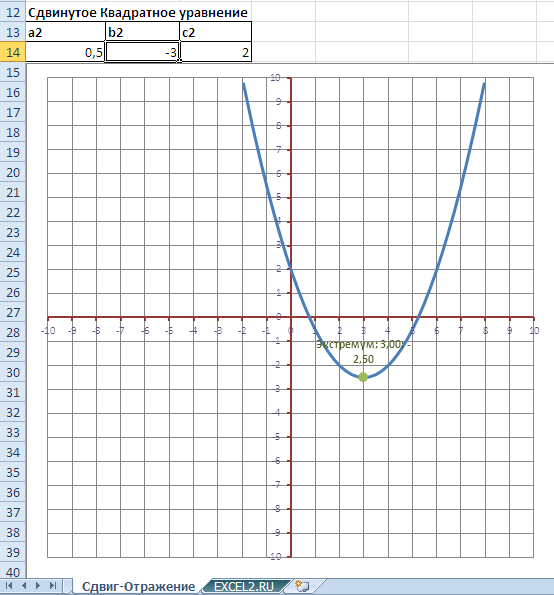
Форма также позволяет рассчитывать коэффициенты квадратного уравнения, полученного при горизонтальном отражении ранее сдвинутого графика (с его построением на диаграмме).

Используйте встроенные функции Excel для решения уравнений

Excel предлагает множество встроенных функций, которые могут быть использованы для решения уравнений. Например, функция “РешИтер” позволяет найти корни уравнения с помощью численных методов итераций. Для использования этой функции, необходимо ввести начальное приближение и формулу для уравнения. Excel будет итеративно вычислять значение функции до тех пор, пока не достигнет точности, заданной пользователем.

Еще одной полезной функцией является “РешСол”, которая позволяет решать системы линейных уравнений. С помощью этой функции можно задать матрицу коэффициентов системы и вектор значений, и Excel найдет значения переменных, удовлетворяющие условиям системы.

Также можно использовать функцию “ЦельЗнач” для поиска корней уравнений с использованием метода дихотомии. Необходимо задать интервал, в котором находится корень, и формулу для уравнения. Excel будет делить интервал пополам и оценивать значение функции в каждой половине, пока не найдет корень с заданной точностью.

Для более сложных уравнений можно использовать функцию “РешЗнач”, которая позволяет решить нелинейное уравнение с помощью численных методов. Необходимо задать начальное приближение и формулу для уравнения, а Excel автоматически найдет корень уравнения.

Выводя результаты решения уравнений в таблицу Excel, можно производить анализ и визуализацию данных, строить графики, и использовать другие функции для дальнейшего анализа или представления результатов.

График функции y=sin(x)

y=sin(x) – вторая функция, которую мы возьмем за пример. Может показаться, что ее составление осуществляется сложнее, хотя на самом деле это не так. Дело в том, что Excel сам посчитает значения, а вам останется только задать известные числа и вставить простой линейный график для вывода результатов на экран.

1. Если вам будет проще, впишите в отдельную клетку функцию, укажите интервал и шаг. Так вы не запутаетесь при дальнейшем заполнении ячеек.

2. Добавьте два столбца, в которые будут вписаны значения каждой оси. Это нужно не только для обозначения чисел, но и для их вычисления при помощи функций программы.

3. Начните вписывать значения X с необходимым интервалом и шагом. Кстати, вы можете заполнить всего несколько полей, а затем растянуть клетки таким же образом, как было показано в предыдущем примере, чтобы они подставились автоматически до конца вашего интервала.

4. Теперь более сложное, но не страшное действие – определение значения Y. Понятно, что он равняется синусу X, значит, нужно вписать функцию =SIN(A1), где вместо A1 используйте нужную ячейку, а затем растяните функцию на оставшийся интервал.

5. На следующем скриншоте вы видите результат заполнения таблицы. Используйте округление для удаления лишних знаков после запятой.

6. Вставьте обычную линейчатую диаграмму и ознакомьтесь с результатом.

На примере этих двух функций уже можно понять, как работает построение графиков в Экселе. При использовании других функций просто учитывайте особенности заполнения ячеек и не забывайте о том, что вам не нужно ничего считать, поскольку Excel все сделает за вас после указания необходимой формулы.

Решение уравнений средствами Excel

Чтобы сменить начальное приближение, недостаточно изменить содержимое ячейки Хнач и запустить процесс вычислений. Чтобы обнулить значение, хранящееся в ячейке Хтекущ, нужно заново записать туда формулу. Для этого достаточно для редактирования выбрать ячейку, содержащую формулу, дважды щелкнув мышью на ней (при этом содержимое ячейки отобразится в строке формул).

При подборе параметра Excel изменяет значение в одной конкретной ячейке до тех пор, пока вычисления по формуле, ссылающейся на эту ячейку, не дадут нужного результата. В качестве аргумента используем ссылку на ячейку С2, т.е. =С2^2-5*C2+6. Если подобранное значение необходимо сохранить, то нажмите на Оk, и результат будет сохранен в ячейке, заданной ранее в поле Изменяя значения ячейки.

Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. При решении задачи в пошаговом режиме появляется кнопка Продолжить — для возврата в обычный режим подбора параметра. Как и в предыдущем случае необходимо задать начальное приближение.

Для более сложных задач следует использовать команду Поиск решения (Решатель), доступ к которой реализован через пункт меню Сервис/Поиск решения. Их можно задать как в виде равенств, так и неравенств. Решатель имеет в своем арсенале мощные средства решения подобных задач: метод обобщенного градиента, симплекс-метод, метод ветвей и границ. После чего рабочий лист примет вид, представленный на рис. 13. Полученное решение зависит от выбора начального приближения, которое задается в ячейке С4 (аргумент функции).

Допустимое отклонение — задается в % только для задач с целочисленными ограничениями. Линейная модель — этот флажок следует включать, когда целевая функция и ограничения — линейные функции. Неотрицательные значения — этим флажком можно задать ограничения на переменные, что позволит искать решения в положительной области значений, не задавая специальных ограничений на их нижнюю границу. Автоматическое масштабирование — этот флажок следует включать, когда масштаб значений входных переменных и целевой функции и ограничений отличается, возможно, на порядки.

Оценки — эта группа служит для указания метода экстраполяции — линейная или квадратичная, — используемого для получения исходных оценок значений переменных в каждом одномерном поиске. Разности (производные) — эта группа служит для указания метода численного дифференцирования, который используется для вычисления частных производных целевых и ограничивающих функций.

Учитель: Откройте ЭТ Excel. Переименуйте лист на квадратное уравнение. Это значит то, что около 70000 человек в месяц ищут информацию по решению квадратного уравнения, при чём это лето, а что будет среди учебного года — запросов будет в два раза больше.

Расширенные методы решения уравнений в программе Excel

Excel предоставляет несколько расширенных методов решения уравнений, позволяющих обработать сложные математические задачи. В данном разделе мы рассмотрим некоторые из них.

1. Метод итераций:

Метод итераций позволяет найти приближенное решение уравнения путем многократного применения определенной формулы. Для этого необходимо задать начальное приближение и указать формулу для вычисления следующего значения. Excel позволяет создать цепочку формул с помощью функции «ПРОИЦ» или других подобных функций.

2. Метод Ньютона:

Метод Ньютона позволяет решать нелинейные уравнения путем последовательных итераций. Для этого необходимо задать начальное приближение и указать формулу для вычисления следующего значения. Excel позволяет использовать функцию «РЕШ.НЬЮТОН» для решения уравнений с использованием этого метода.

3. Метод дихотомии:

Метод дихотомии позволяет решать уравнения путем последовательного деления интервала на две части и проверки знака функции в каждой части. Для этого необходимо указать начальное и конечное значения интервала, а также точность решения. В Excel для решения уравнений с использованием этого метода можно использовать функции «РЕШ.УРОВН» или «ЦЕЛЬ.ЗНАК».

4. Метод секущих:

Метод секущих позволяет решать уравнения путем использования точек, лежащих на касательной к графику функции. Для этого необходимо задать начальные точки и указать формулу для вычисления следующей точки. В Excel можно использовать функцию «РЕШ.СЕК» для решения уравнений с использованием этого метода.

Метод	Преимущества	Недостатки
Метод итераций	— Прост в использовании— Может дать приближенное решение	— Может сойтись к неверному значению— Может требовать много итераций
Метод Ньютона	— Быстро сходится к решению— Может дать более точное значение	— Может не сойтись— Требует задания производной функции
Метод дихотомии	— Гарантированно находит решение в заданном интервале	— Требует больше итераций, чем другие методы— Может дать неточное значение
Метод секущих	— Не требует задания производной функции	— Может не сработать для некоторых уравнений

Выше перечислены только некоторые методы решения уравнений в программе Excel. Выбор метода зависит от особенностей задачи и требуемой точности решения. Excel предоставляет широкий набор функций и инструментов, которые помогут вам решить сложные математические задачи.

Возведение числа в квадрат в Эксель

Microsoft Excel применяют в различных учебных заведениях, данным редактором пользуются и сотрудники почти всех отраслей промышленности, менеджеры,​ аналитики. Это связано с его многофункциональностью и удобством работы. В данном случае обратимся к подробному рассмотрению формулы возведения числа в степень, которая бывает необходима для решения задач из практически любой области.

Решение системы линейных уравнений в excel – Как решить систему уравнений в Excel

Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.

Варианты решений

Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.

Способ 1: матричный метод

Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:

Аргумент «Массив» — это, собственно, адрес исходной таблицы.

Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.

Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».

Способ 2: подбор параметров

Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение

1. Принимаем значение x за равное . Высчитываем соответствующее для него значение f(x), применив следующую формулу:

Вместо значения «X» подставляем адрес той ячейки, где расположено число , принятое нами за x.

Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.

Способ 3: метод Крамера

Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:

1. Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».

Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.

Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».

Способ 4: метод Гаусса

Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:

1. Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.

Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.

После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.

После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.

Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.

Жмем привычное уже нам сочетание клавиш для применения формулы массива.

Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.

Мы рады, что смогли помочь Вам в решении проблемы. Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Расширенные возможности Excel для нахождения корней уравнения

Excel – это мощный инструмент, который может быть использован для решения множества математических задач, в том числе поиска корней уравнений. Благодаря широкому спектру функций и возможностей, Excel позволяет удобно и эффективно решать сложные математические задачи.

Для нахождения корней уравнения в Excel можно использовать различные методы, такие как метод итераций, метод половинного деления, метод касательных и т.д. Один из самых простых способов – использование встроенной функции «Goal Seek» (Целевое значение).

Функция «Goal Seek» в Excel позволяет находить корни уравнений с помощью поиска значения переменной, при котором заданная формула или функция принимает требуемое значение. Для использования этой функции нужно сначала определить уравнение, включающее переменную, и указать желаемое значение для формулы или функции.

Другой способ нахождения корней уравнения в Excel – использование приближенной формулы. Этот метод основывается на итеративном подходе, при котором значения переменной последовательно изменяются с шагом, заданным пользователем, до тех пор, пока не будет достигнуто требуемое значение для формулы или функции.

Excel также предоставляет возможность создания графиков, которые могут помочь визуализировать уравнение и найти его корни. График позволяет наглядно представить зависимость переменной от значения функции и легко определить точки пересечения с осью абсцисс, которые соответствуют корням уравнения.

В целом, Excel предлагает широкий набор функций и инструментов, позволяющих находить корни уравнений различными способами. В зависимости от сложности уравнения и доступных данных можно выбрать наиболее подходящий метод для нахождения корней и успешно решить задачу. Это делает Excel незаменимым инструментом для математических расчетов и анализа данных.