Как построить график синуса и косинуса в excel

Определение

Один радиан определяется как угол, проходящий из центра круга, который пересекает дугу, равную по длине радиусу круга. В более общем смысле величина в радианах суженного угла равна отношению длины дуги к радиусу круга; то есть θ = s / r , где θ — угол наклона в радианах, s — длина дуги, а r — радиус. И наоборот, длина перехваченной дуги равна радиусу, умноженному на величину угла в радианах; то есть s = rθ .

Как отношение двух длин радиан — это чистое число . В SI радиан определяется как имеющий значение . Как следствие, в математической письменной форме символ «рад» почти всегда опускается. При количественном определении угла в отсутствие какого-либо символа используются радианы, а когда подразумеваются градусы, используется знак градуса ° .

Полный оборот составляет 2 π радиан (здесь показан круг с радиусом один и, следовательно, окружностью 2 π ).

Отсюда следует, что величина в радианах одного полного оборота (360 градусов) равна длине всей окружности, деленной на радиус, или 2 π r / r , или 2 π . Таким образом, 2 π радиана равны 360 градусам, что означает, что один радиан равен 180 / π ≈ 57,29577 95130 82320 876 градусам.

Соотношение 2 π рад = 360 ° может быть получено с использованием формулы для длины дуги . Взяв формулу для длины дуги, или . Предполагая единичный круг; радиус поэтому 1. Так как радиан является мерой угла , который стягивает дугу длиной , равной радиусу окружности, . Это можно еще упростить до . Умножение обеих сторон на 360 ° дает 360 ° = 2 π рад .
ℓдугазнак равно2πр(θ360∘){\ displaystyle \ ell _ {\ text {arc}} = 2 \ pi r \ left ({\ tfrac {\ theta} {360 ^ {\ circ}}} \ right)}1знак равно2π(1 рад360∘){\ displaystyle 1 = 2 \ pi \ left ({\ tfrac {1 {\ text {rad}}} {360 ^ {\ circ}}} \ right)}1знак равно2π рад360∘{\ displaystyle 1 = {\ tfrac {2 \ pi {\ text {rad}}} {360 ^ {\ circ}}}}

Как создать синусоиду в Excel

1. Откройте программу Excel и создайте новую таблицу. Введите значения в столбцы A и B: в столбец A введите числовую последовательность, представляющую временные отметки, а в столбец B введите функцию SIN(A), которая вычисляет синус для соответствующего значения времени.

2. Выделите столбец B, щелкнув на заголовке столбца (буква B) или перетащив курсором мыши через все ячейки столбца. Затем нажмите правую кнопку мыши и выберите «Формат ячеек» из контекстного меню.

3. В диалоговом окне «Формат ячейки» выберите вкладку «Число» и задайте нужное количество знаков после запятой для отображения значений синусоиды. Например, если вы хотите, чтобы значения округлялись до двух знаков после запятой, установите значение «2» в поле «Десятичные знаки».

4. Нажмите кнопку «ОК», чтобы применить настройки формата ячеек. Теперь значения в столбце B будут отображаться с заданным количеством знаков после запятой.

5. Для удобства визуализации данных, создадим график синусоиды. Выделите столбцы A и B, затем щелкните правой кнопкой мыши на выделенной области и выберите «Вставить» из контекстного меню. В появившемся подменю выберите тип графика, который вы предпочитаете, например, «Диаграмма рассеяния».

6. Последний шаг — настройка осей графика. Щелкните правой кнопкой мыши на горизонтальной оси и выберите «Формат оси» из контекстного меню. В разделе «Общие» измените значения начала и конца оси так, чтобы она охватывала все значения времени в столбце A.

7. Повторите предыдущий шаг для вертикальной оси, выбрав «Формат оси» из контекстного меню. Измените значения начала и конца оси так, чтобы она охватывала все значения синусоиды в столбце B.

Теперь у вас есть созданная синусоида в Excel! Вы можете изменить параметры синусоиды, изменяя значения в столбцах A и B, а также настроить внешний вид графика с помощью доступных инструментов Excel.

Excel — мощный инструмент для работы с данными и визуализации результатов. Создание синусоиды в Excel поможет вам в анализе периодических данных и позволит визуально представить их изменения.

Особенности использования тригонометрических функций в Excel

Синтаксис функции SIN:

Синтаксис функции SINH:

Синтаксис функции COS:

Синтаксис функции COSH:

Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).

1. Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
2. В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
3. Все рассматриваемые функции могут быть использованы в качестве формул массива.

1. Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
2. Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
3. При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:

• Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
• Выражение ПИ()*угол_в_градусах/180.

7 Графики синуса и косинуса

Построим график функции . При этом нам опять пригодятся
часы из разд. 2.1.

Если , то, очевидно, . Когда возрастает от 0 до
, число возрастает от 0 до 1 (представьте себе,
как меняется ордината конца стрелки на наших фирменных часах).
Участок графика для от 0 до изображен на
рис. .
При

Чем ближе к , тем более полого идет наша кривая. Это
происходит потому, что проекция конца стрелки на ось
ординат, колеблясь по отрезку , быстрее всего
движется в середине отрезка и замедляется у его краев: мы
это уже обсуждали в разд. 2.1.

симметричны относительно прямой

Задача 7.1  
Запишите уравнение прямой, касающейся графика функции
в точке с координатами .

Кривая на рис бцентрально симметрична относительно точки
с координатами ; это следует из другой формулы
приведения:
(рис. б).

После того, как у нас есть участок графика функции для

, весь график строится уже просто. В самом деле,
когда конец стрелки прошел путь , стрелка вернулась
в исходное положение; при дальнейшем движении все будет
повторяться. Значит, график будет состоять из таких же кусков,
как на рис б. Окончательно график функции
выглядит так, как на рис. .

Теперь построим график функции . Можно было бы строить его так же, как
мы строили график синуса. Мы, однако, изберем другой путь,
который позволит использовать уже имеющуюся у нас информацию.

Именно, воспользуемся формулой приведения
. Эту формулу можно понимать так: функция
принимает те же значения, что и функция , но на
раньше. Например, функция принимает значение 1 при
, а функция
принимает это же
значение уже при . На графике это означает следующее: для
каждой точки графика есть точка графика ,
у которой ордината та же, а абсцисса на меньше
(рис. ).

сдвинуть график

Итак, мы выяснили, что график косинуса получается преобразованием
(сдвигом) из графика синуса. Случаи, когда график одной функции
можно получить преобразованием из графика другой функции,
интересны и сами по себе, поэтому скажем о них несколько слов.

Как, например, будет выглядеть график функции ? Ясно,
что ординаты точек этого графика получаются из ординат
соответствующих точек графика умножением на 2, так что
наш график изобразится сплошной кривой на рис. . Можно
сказать, что график получается из графика растяжением в два раза вдоль оси
ординат.

сжатием в 2 раза к оси ординат.

Попробуем еще построить график функции 
.
Понятно, что он должен получаться каким-то преобразованием из
графика . На первый взгляд может показаться, что это
преобразование — сдвиг влево на вдоль оси абсцисс, по
аналогии с тем, что изображено на рис. . Однако, если
бы это было так, то вышло бы, например, что функция

принимает значение 1 при

, что не соответствует действительности
(проверьте!). Правильно рассуждать так:
, так что функция
принимает те
же значения, что и функция , но на раньше. Так
что сдвиг влево — не на
, а на (рис. ).

Кривые, являющиеся графиками функций
, где ,
, называются синусоидами. Заметим, что кривой
«косинусоида» вводить не надо: как мы видели, график косинуса
— это та же кривая, что и график
синуса, только иначе
расположенная относительно осей координат.

Задача 7.2  
Каковы координаты точек, помеченных на
рис.  вопросительными знаками?

Задача 7.3  
Возьмите свечу, тонкий лист бумаги и острый нож. Намотайте лист
бумаги на свечу в несколько слоев и аккуратно разрежьте эту свечу
вместе с бумагой наискосок ножом. Теперь разверните бумагу. Вы
увидите, что она оказалась разрезанной по волнистой линии.
Докажите, что эта волнистая линия является синусоидой.

Задача 7.4  
Постройте графики функций:

Замечание. Если вы строите графики
тригонометрических функций на клетчатой бумаге, удобно выбрать
немного разные масштабы по осям, с тем чтобы на оси абсцисс
числу  соответствовало целое число клеточек. Например, часто
выбирают такой масштаб: по оси ординат отрезок длины 1 занимает
две клеточки, по оси абсцисс отрезок длины занимает 6
клеточек.

Задача 7.5  
Постройте графики функций:
а)
;
б)
.

Посмотрим, как выглядят на графиках уже известные нам решения
уравнений и . Эти решения являются
абсциссами точек пересечения горизонтальной прямой
с графиком функций (соответственно ). На
рис. , хорошо видны две серии решений,
получающихся при .

По графикам синуса и косинуса видно, на каких промежутках эти
функции возрастают, а на каких убывают. Ясно, например, что
функция возрастает на отрезках
,

,
,…- одним словом, на
всех отрезках
, где
,
и убывает на всех отрезках
, где

Задача 7.6  
На каких отрезках возрастает и на каких убывает
функция ?

Задача 7.7  
Сравните числа:

Задача 7.8  
Расположите в порядке возрастания:
, , , , , .

        Написать комментарий

Подготовка данных

Перед тем, как начать построение графика косинуса в Excel, необходимо подготовить данные, которые будут использоваться для построения графика. Для этого нам понадобится задать значения для оси X и рассчитать значения для оси Y.

Ось X будет представлять собой последовательность значений угла, на которых будет рассчитываться значение косинуса. Для этого можно воспользоваться функцией генерации последовательности чисел в Excel. Например, можно задать значения от -180 градусов до 180 градусов с шагом 5 градусов.

Ось Y будет представлять собой значения косинуса для каждого значения оси X. Для рассчета косинуса можно воспользоваться функцией COS в Excel. Необходимо применить эту функцию к каждому значению оси X, чтобы рассчитать соответствующее значение косинуса.

Получив значения оси X и оси Y, можно приступить к построению графика косинуса в Excel. Для этого необходимо выделить оба столбца с данными и воспользоваться функцией построения графика в Excel.

Как использовать графики для визуализации косинуса в Excel

Excel — это мощный инструмент для работы с числами и данными, который также позволяет строить разнообразные графики для визуализации информации. Одним из способов использования графиков в Excel является визуализация функции косинуса.

Для начала, вам понадобится создать таблицу с значениями углов и соответствующими им значениями косинуса. Для этого:

1. В первом столбце таблицы введите значения углов.
2. Во втором столбце таблицы используйте функцию COS() для вычисления косинуса каждого угла.

Например, если вы хотите построить график функции косинуса для углов от 0 до 360 градусов с шагом в 10 градусов, ваша таблица может выглядеть следующим образом:

Угол (градусы)	Косинус
=COS(RADIANS(A2))
10	=COS(RADIANS(A3))
20	=COS(RADIANS(A4))
…	…
350	=COS(RADIANS(A37))
360	=COS(RADIANS(A38))

После того, как вы создали таблицу с данными, вы можете построить график, используя эти данные. Для этого:

1. Выделите область данных (все значения углов и косинусов).
2. На главной вкладке Excel выберите тип графика, который вы хотите использовать (например, линейный график).
3. Excel автоматически построит график на основе вашей выделенной области данных.

Теперь у вас есть график, который визуализирует функцию косинуса. Вы можете настроить внешний вид графика, добавить заголовок, подписи осей и другие детали для лучшей визуализации данных.

График функции косинуса в Excel может быть полезным для иллюстрации математических концепций, а также для анализа данных, в которых значения меняются в соответствии с косинусной функцией.

Использование графиков для визуализации косинуса в Excel помогает лучше понять, как меняются значения косинуса в зависимости от угла и позволяет наглядно представить эту информацию.

Элементарный график изменения

График необходим, если от человека требуется продемонстрировать, насколько определенный показатель изменился за конкретный период времени. И обычного графика для выполнения этой задачи вполне достаточно, а вот различные вычурные диаграммы на деле могут только сделать информацию менее читаемой.

Предположим, у нас есть таблица, которая предоставляет информацию о чистой прибыли компании за последние пять лет.

1

Затем отправьтесь к вкладке «Вставка», где у вас есть возможность осуществить выбор типа графика, который будет подходящим в конкретной ситуации.

2

Нас интересует тип «График». После нажатия на соответствующую кнопку, появится окошко с настройками внешнего вида будущего графика. Чтобы понять, какой вариант подходит в конкретном случае, вы можете навести указатель мыши на определенный тип, и появится соответствующее приглашение.

3

После выбора нужного вида диаграммы вам необходимо скопировать таблицу данных связать ее с графиком. Результат будет следующим.

4

В нашем случае на диаграмме представлено две линии. Первая имеет красный цвет. Вторая — синий. Последняя нам не нужна, поэтому мы можем удалить ее, выбрав ее и нажав кнопку «Удалить». Поскольку мы имеем лишь одну линию, легенда (блок с названиями отдельных линий графика) также может быть удалена. Но маркеры  лучше назвать. Найдите панель «Работа с диаграммами» и блок «Подписи данных» на вкладке «Макет». Здесь вы должны определить положение чисел.

5

Оси рекомендуется называть, чтобы обеспечить большую удобочитаемости графика. На вкладке «Макет» найдите меню «Названия осей» и задайте имя для вертикальной или горизонтальной осей соответственно.

6

Но вы можете смело обходиться без заголовка. Чтобы удалить его, вам нужно переместить его в область графика, которая невидима для постороннего глаза (над ним). Если вам все еще нужно название диаграммы, вы можете получить доступ ко всем необходимым настройкам через меню «Название диаграммы» на той же вкладке. Вы также можете найти его на вкладке «Макет».

7

Вместо порядкового номера отчетного года достаточно оставить только сам год. Выберите требуемые значения и щелкните по ним правой кнопкой мышки. Затем кликните по пункту «Выбор данных» — «Изменить подпись горизонтальной оси». Далее вам следует задать диапазон. В случае с нами, это первая колонка таблицы, являющейся источником информации. Результат такой.

8

Но вообще, можно все оставить, этот график вполне рабочий. Но если есть необходимость сделать привлекательный дизайн графика, то к вашим услугам — Вкладка «Конструктор», которая позволяет указать фоновый цвет графика, его шрифт, а также разместить его на другом листе.

Построение синусоиды в excel

Как построить график синусоиды в Excel.

Допустим имеется функция синусоиды, заданной уравнением y=sin4*x. Формула в Excel имеет вид:

=SIN(4*C4)

Требуется построить график функции.

Функция в данном случае непрерывная, поэтому по оси x ограничим интервалом от 1 до -1, шаг возьмём 0,1.

В итоги у нас должна получится таблица вида:

Переходим на вкладку Вставка -> Точечная с гладкими кривыми и маркерами.

Появится область графика, кликаем на белую область правым указателем мыши, выскакивает меню, далее Выбрать данные, появляется окно Выбора источника данных, выбираем весь диапазон данных нашей синусоиды в ячейках, затем Ок.

В итоги у нас получается график вида.

Также вид графика тоже можно настроить через конструктор и дополнительные инструменты.

трюки • приёмы • решения

Использование диаграмм Excel — хороший способ отображения графиков математических и тригонометрических функций. В этой статье описываются два метода построения графика функции: с одной переменной с помощью точечной диаграммы и с двумя переменными с помощью 3D-диаграммы.

Построение графиков математических функций с одной переменной

Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений. Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от -5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у выступает в качестве точки данных в диаграмме, и эти точки связаны линиями.

Рис. 140.1. Диаграмма представляет собой график функции SIN(x)

Функция выражается в таком виде: у = SIN(x) .

Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2) .

Чтобы создать эту диаграмму, выполните следующие действия.

1. Выделите диапазон А1:В22 .
2. Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
3. Выберите макет диаграммы, который вам нравится, а затем настройте его.

Измените значения в столбце А для построения графика функции при различных значениях х. И, конечно, вы можете использовать любую формулу с одной переменной в столбце В. Вот несколько примеров, которые приводят к построению интересных графиков: =SIN(ПИ()*A2)*(ПИ()*A2) =SIN(A2)/A2 =SIN(A2^3)*COS(A2^2) =НОРМ.РАСП(A2;0;1;ЛОЖЬ)

Чтобы получить более точную диаграмму, увеличьте количество значений для построения графика и сделайте приращение в столбце А меньше.

Вы можете использовать онлайн наш файл примера графиков математических функций с одной переменной, расположенной в Excel Web Apps при помощи Skydrive, и внести свои данные (изменения не будут сохраняться) или скачать себе на компьютер, для чего необходимо кликнуть по иконке Excel в правом нижнем углу. Это бесплатно

Построение графиков математических функций с двумя переменными

Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)

На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от -3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.

Рис. 140.2. Использование трехмерной поверхностной диаграммы для построения графика функции с двумя переменными

Значения х находятся в диапазоне А2:А22 , а значения у — в диапазоне B1:V1 .

Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1) .

Чтобы создать диаграмму, выполните приведенные ниже действия.

1. Выделите диапазон A1:V22 .
2. Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
3. Выберите макет диаграммы, который вам нравится, а затем настройте его.

Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать: =SIN(КОРЕНЬ($A2^2+B$1^2)) =SIN($A2)*COS($A2*B$1) =COS($A2*B$1)

Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.

Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.

Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.

Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.

Свойства и доказательства

К главным свойствам синусоиды относятся область значений (включая нуль) и определений, чётность/нечётность, периодичность, точки пересечения с осью координат, промежуточности постоянства, убывания и возрастания, минимум и максимум. При пересечении графика функции (ГФ) с осью Ох результат равняется нулю. Под значением синуса подразумевается ордината соответствующей точки единичной окружности.

Значения ординаты единичной окружности (ЕД) расположены на отрезке . Они принимают значения от -1 до 1. Через любую точку указанного промежутка оси ординат, равного диаметром ЕД, проводится прямая, перпендикулярная оси ординат. Таким способом получается точка с рассматриваемой ординатой.

Из свойства вытекает следующее: функция y= sin x имеет область значений (-1; 1). Утверждение записывается так: E (sin x)=(-1; 1). Максимальное значение функции равняется единице. Подобное возможно, если соответствующей точкой ЕД является точка А. Минимальное число y равно -1 в случае, когда точкой ЕД является В (х=пи/2 +2пиk, где k принадлежит области Z.

Нечётность и постоянство

Функция считается нечётной, если sin (-x)=- sin x. Её график симметричен по отношению к началу координат. Сам синус является периодической величиной, у которой наименьший положительный период. Через отрезок 2пи вид кривой повторяется. Это свойство учитывается при построении графика.

Предварительно чертится кривая на любом отрезке соответствующей длины. При переносе линии влево и вправо соблюдается шаг в kT=2 πk, где k — любая натуральная цифра. Для вычисления точек пересечения линии с осями координат используется равенство х=0. Если значение подставить в функцию, получится следующее: y=sin 0=0. В таком случае график проходит через начало координат.

Так как y равен нулю, поэтому можно рассчитать х, воспользовавшись формулой y= sin x. Координата подходящей точки ЕД равняется нулю. Такое явление будет наблюдаться только в случае, если на ЕД будут выбраны точки D либо C, при x=πk, k принадлежит Z.

Функция имеет положительное значение в первой и во второй четвертях. На этих промежутках sin x больше нуля, а любое значение х находится в пределах 0-π. При решении задач учитывается период при всех x, принадлежащих отрезку (2πk; π+2πk), где k принадлежит Z. Функция считается отрицательной в третьем и четвёртом квадрате. При этом sin меньше нуля, а иск находится в пределах (пи+2пиk; 2пи+2пиk), k принадлежит области Z.

Больше и меньше

С учётом периодичности y с периодом T=2π исследуется функция на возрастание и убывание на любом отрезке длиной в 2пи. Если T= (-π/2;3π/2), а х принадлежит данному промежутку, тогда при увеличении аргумента изменится в большую сторону и ордината. Следовательно, на указанном отрезке синусоида возрастает.

Если учитывать её периодичность, можно прийти к выводу, что она возрастает на каждом интервале (-π/2+2πk; π/2+2πk), k принадлежит Z. Если х находится на отрезке (-π/2;3π/2), тогда при увеличении аргумента ордината ЕД уменьшается, а функция убывает. С учётом периодичности синусоиды можно сделать вывод, что она бывает на каждом отрезке (π/2+2πk;3π/2+2πk), k находится в области Z.

Основываясь на проведённом исследовании, строится график y=sin x. С учётом периодичности 2π предварительно строится график на любом отрезке соответствующей длины. Чтобы точно построить точки, рекомендуется придерживаться значения синуса (ордината ЕД). На основе нечётности проводится кривая, симметричная началу координат. При этом необходимо придерживаться интервала (-π;0). Так как линия строится на отрезке длиной 2π, поэтому учитывается периодичность величины.

Вид графика повторяется на каждом отрезке с аналогичной длиной. Таким способом получается синусоида. Рассматриваемая тригонометрическая функция получила широкое применение в технике, физике и математике. Большинство процессов, включая колебания струн, напряжения в цепи, описываются с помощью функции, задаваемой формулой y= A sin (wx + f). Подобные явления считаются гармоническими колебаниями.

Кривая получается из синусоиды за счёт разных колебаний и путём параллельного переноса вдоль оси Ох. Чаще изменения результата связаны с функцией времени t. В таком случае используется формула y= A sin (wx + f), где через А обозначается амплитуда колебания, через w — частота, f — начальная фаза, 2пи/f — период колебания.

Источник

Как объединить графики в экселе?

В программе эксель часто приходиться объединять несколько графиков. Классическим примером является отображение на одном графике показателей «Выручки» и «Чистой прибыли».

Сложность отображения данных графиков заключается в том, что числа могут еще отличаться на порядок. Давайте рассмотрим на примере данного примера, как можно объединить в программе эксель графики.

Первый шаг. Перед нами таблица, в которой представлены показатели «Выручки» и «Чистой прибыли». Выделим первые две строки (ячейки с «В1» по «D3»), после перейдем на верхнюю панель настройки, где войдем во вкладку «Вставить», где в блоке «Диаграммы» нажмем на иконку с надписью «График» и выберем первый тип графика.

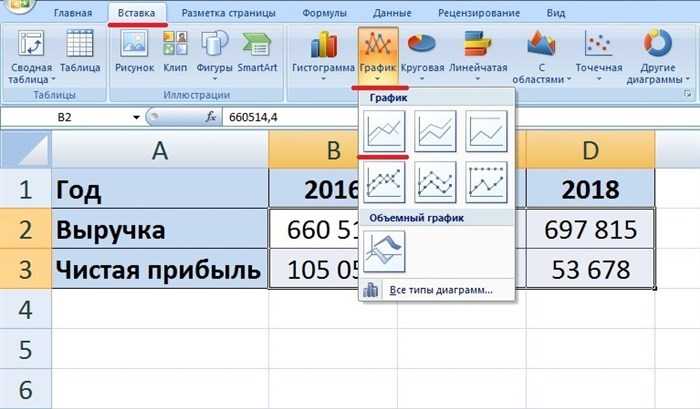
Второй шаг. Построили первый график. Теперь добавим дополнительную ось, чтобы график выглядел более презентабельно. Для этого выделим коричневую линию, после нажмем на правую кнопку мыши, в появившемся меню выбираем «Формат ряда данных».

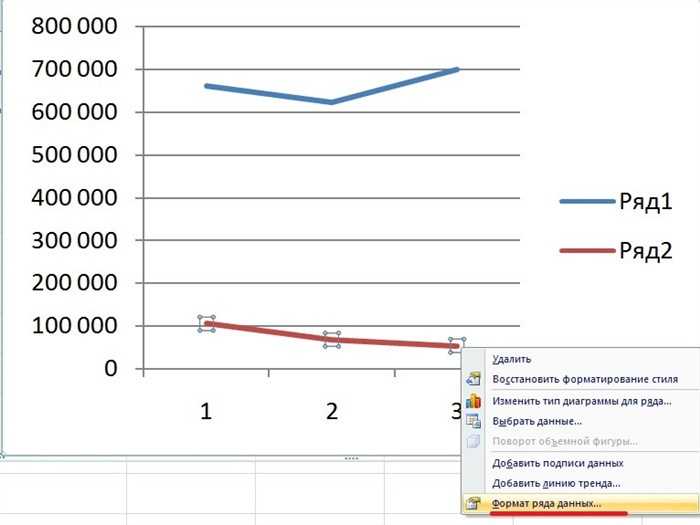
Третий шаг. На экране появится меню «Формат ряда данных», в закладке «Параметры ряда» ставим точку напротив строки «По вспомогательной оси». После можно закрыть данное меню.

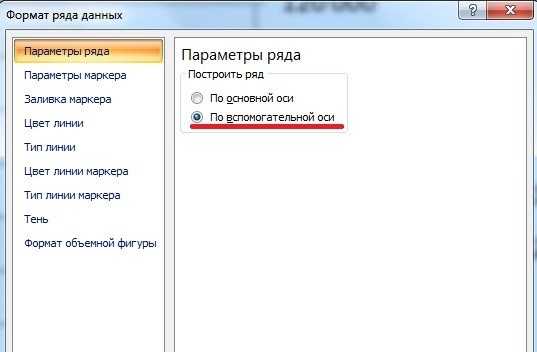
Четвертый шаг. Теперь изменим тип графика синий линии, для этого её выделим и нажмем правую кнопку мыши. В появившемся меню выберем «Изменить тип диаграммы для ряда».

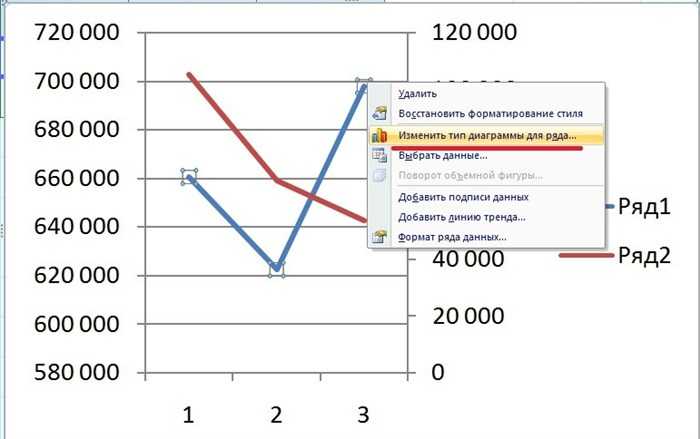
Пятый шаг. В открывшемся меню, выберем закладку «Гистограмма», где выберем первый вид графика, после нажмем на кнопку «ОК». Вы, конечно, можете выбрать любой нужный вам график.

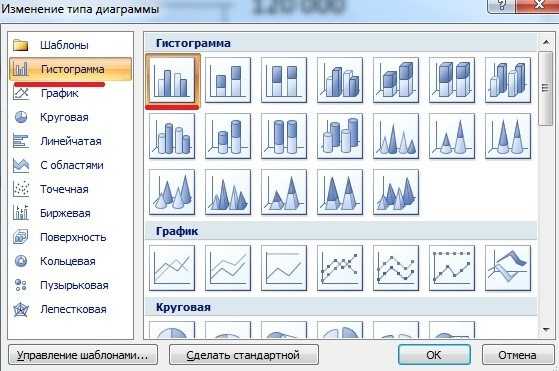
Шестой шаг. Теперь следует поменять данные на оси «Х», так как там стоят цифры 1, 2, 3, а надо, чтобы были года. Для этого выделим график, нажмем на правую кнопку мыши, чтобы появилось меню, в котором выберем «Выбрать данные».

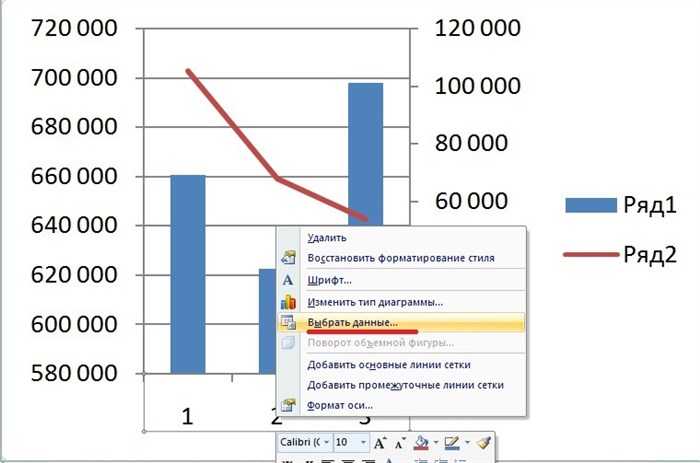
Седьмой шаг. На экране отобразится меню «Выбор источника данных», в левой его части есть блок «Подписи горизонтальной оси», нажмите на кнопку «Изменить».

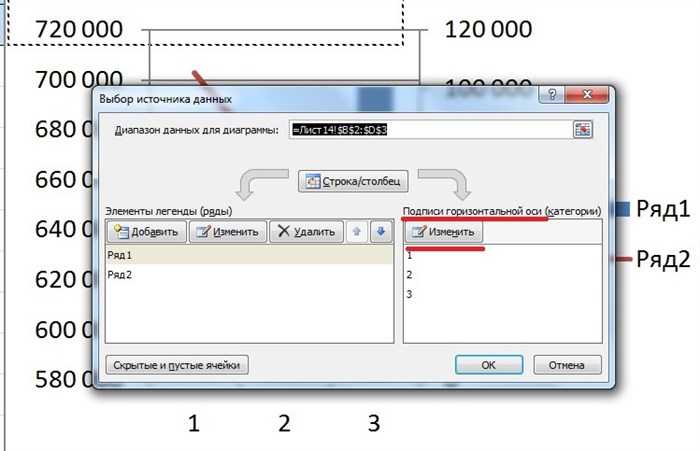
Восьмой шаг. Появится небольшое меню, в котором нажмите на иконку в виде сеточки и выделите диапазон ячеек «В1» по «D1». После закрываем все меню.

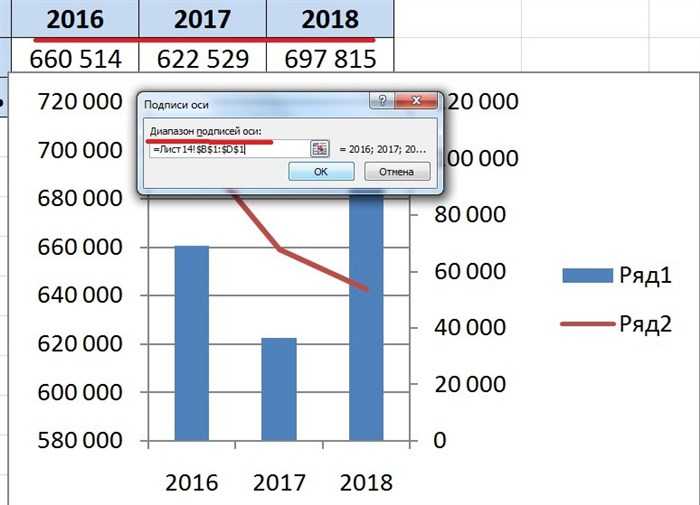
Девятый шаг. Поменяем название легенд, вместо «Ряд1» и «Ряд2» напишем «Чистая прибыль» и «Выручка». Для этого снова выполняем седьмой шаг и попадаем в меню «Выбор источника данных». Но теперь смотрим на правую часть меню «Элементы легенд», сначала выделим строку «Ряд1» и нажмем на кнопку «Изменить», в появившемся меню пишем «Выручка», затем выделяем «Ряд2» и меняем название на «Чистая прибыль».

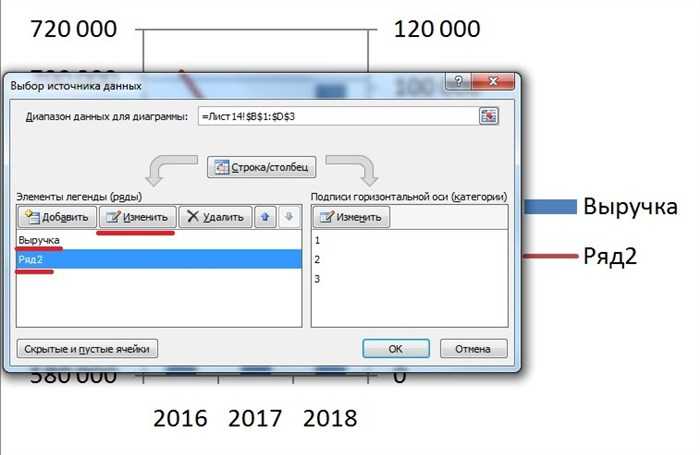
Десятый шаг. Сделаем подписи оси графиков, для этого нужно вставить блок для надписи. На верхней панели настроек заходим во вкладку «Вставка», там нажимаем иконку «Надпись» и подписываем оси: «руб.» и «года».

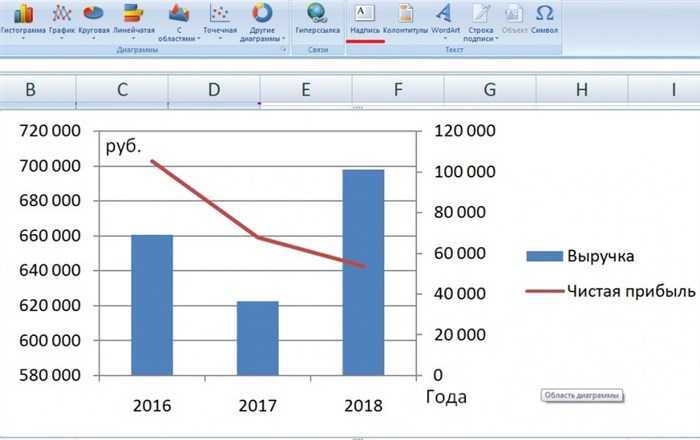
Таким образом, мы объединили в программе эксель два графика, одному из них сделали дополнительную ось, плюс сделали их разными типами.

Как наложить график на график в excel — все про Ексель
В Экселе можно результаты расчетов отобразить в виде диаграммы или графика, придавая им большую наглядность, а для сравнения иногда нужно построить два графика рядом. Как построить два графика в Excel на одном поле мы далее и рассмотрим.

Построение графика в программе Excel шаг за шагом для новичков

Сегодня рассмотрим на пошаговом примере, как построить график в Excel. Для этого мы будем использовать последнюю версию программы, актуальную на сентябрь 2016 года.

У многих новичков, которые только начинают осваивать программу Excel, часто возникает много вопросов. На самом деле, работать с этой программой не сложно, в чем вы сейчас сами убедитесь. Итак, начнем.

1. Шаг первый.

Дальше нужно создать файл Excel. Я это сделаю на рабочем столе моего компьютера. Для этого наведу курсор мыши на свободное место, нажму левую кнопку мыши и из выпадающего списка выберу «Создать». Затем в выпадающем меню выберу создать «Лист Microsoft Excel».

2. Шаг второй. Открываем созданный файл.

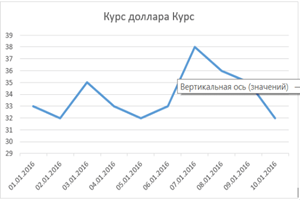
3. Шаг третий. Добавим в лист данные, которые будут отображаться в будущем графике. Для примера я взял произвольный курс доллара по отдельным дням.

4. Шаг четвертый. Выделим наши данные при помощи курсора мыши.

5. Шаг пятый. Теперь в верхней панели редактирования документа выбираем вкладку «Вставка». Откроется панель где будут предложены различные типы графиков и диаграмм. Выберем понравившийся или тот, который отвечает всем вашим требованиям и жмем на него.

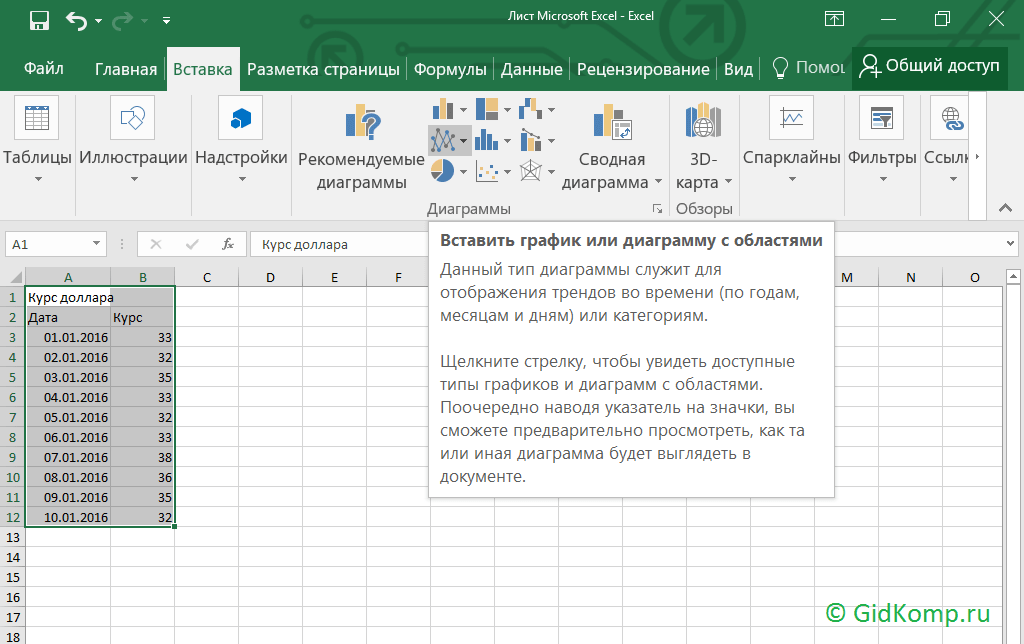
6. Шаг шестой. При нажатии на тип графика, программа предложит выбрать разновидности графиков в экселе, при этом предварительно можно видеть, как график будет отображен. Кликаем по нужному варианту.

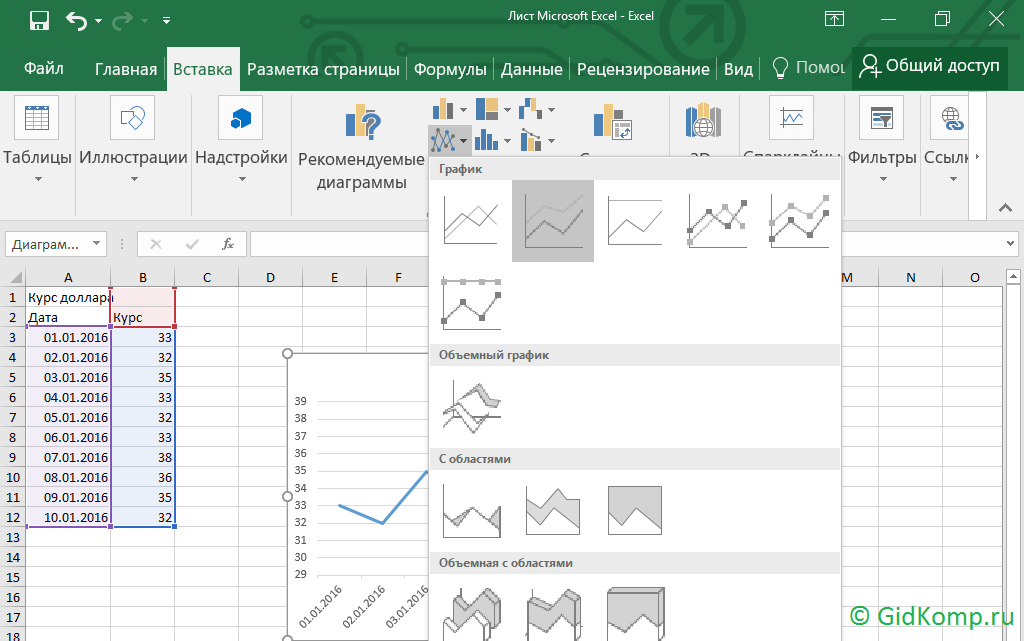
7. Шаг седьмой. График построен. Теперь его можно скопировать, например, для того, чтобы вставить в текстовый документ. В следующем шаге показано, как это сделать.

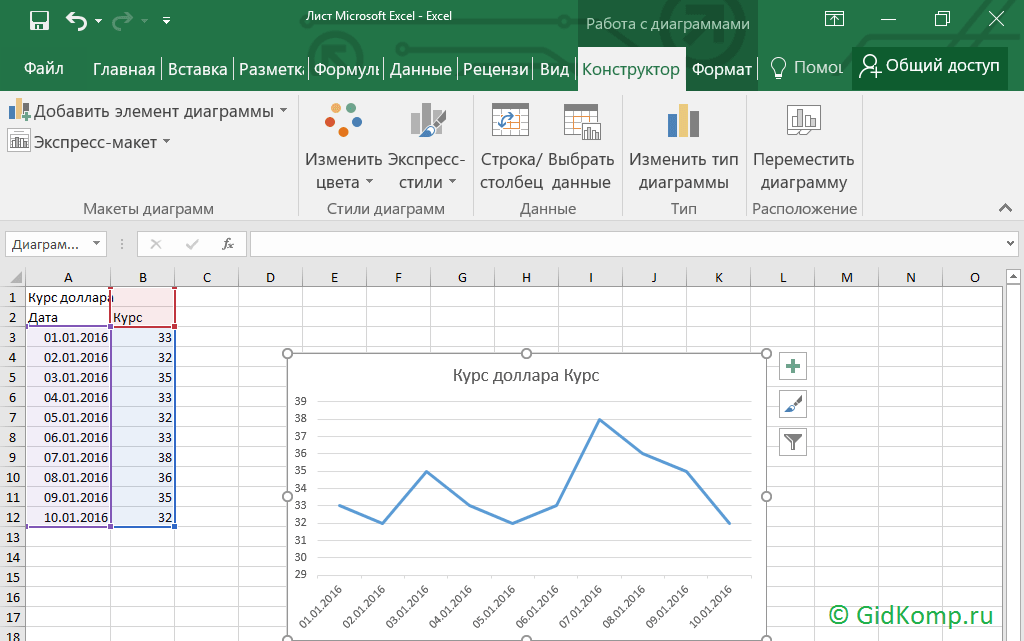
8. Шаг восьмой. Кликнем по графику левой кнопкой мыши и в появившемся окне выбираем «Копировать».

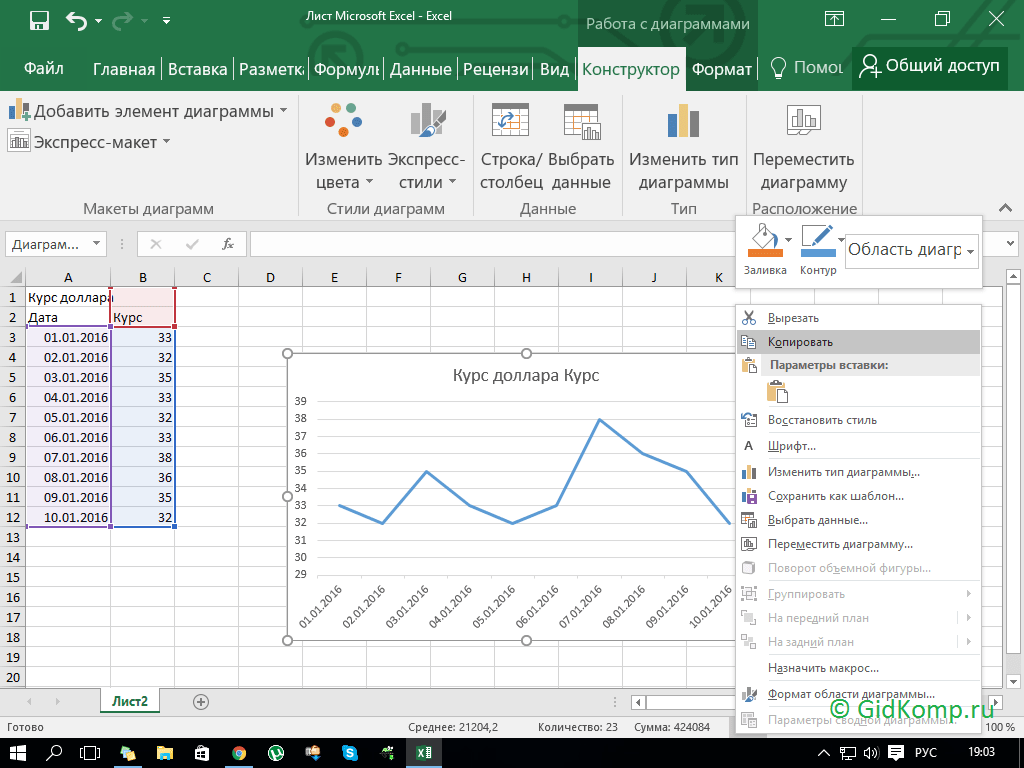
9. Шаг девятый. Отрываем документ Office Word и вставляем в туда наш график.

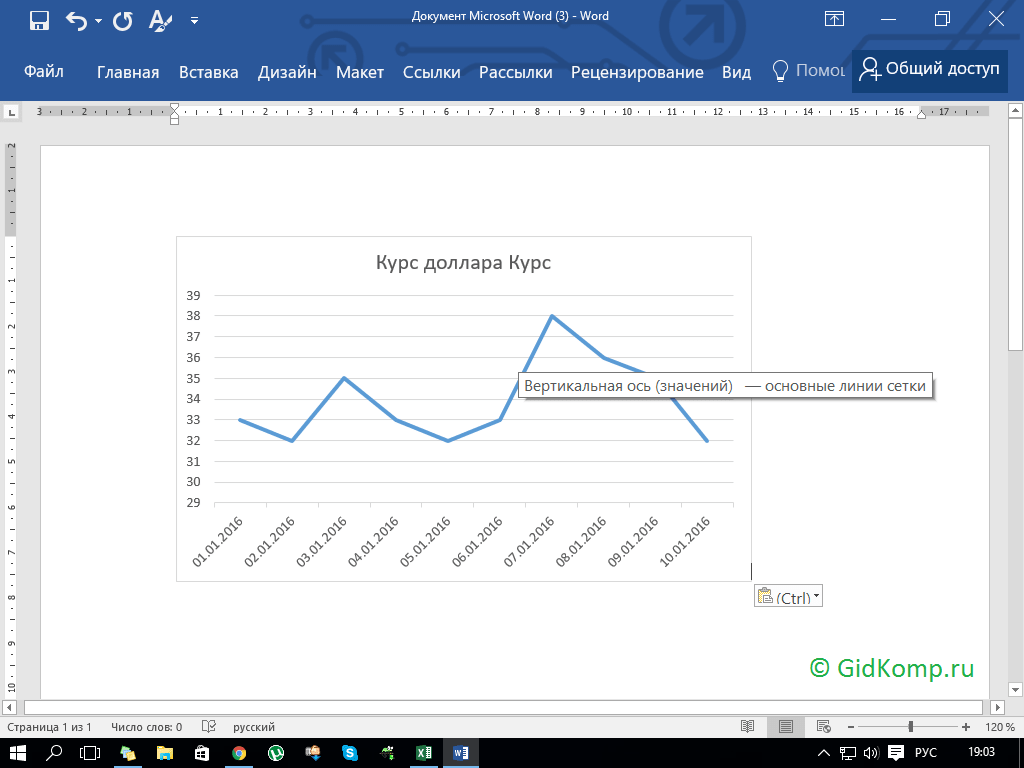
Как видно из этой пошаговой инструкции, не сложно работать в программе Эксель и построить график.

Более детальное построение диаграмм можно увидеть в видео.