Как построить график функции в excel

График функции F(x) = X^2

Функция X^2 – одна из самых популярных математических функций, которую разбирают еще на уроках в школе. На графике необходимо показать точки Y, что в Excel реализовывается следующим образом:

1. Создайте строку на листе в программе, вписав туда известные значения X.

2. Сделайте то же самое и с Y. Пока значения этой оси координат неизвестны. Чтобы определить их, нам нужно выполнить простые расчеты.

3. Поэтому в качестве значения для каждой ячейки укажите формулу, которая посчитает квадрат числа, указанного в строке X. Для этого впишите =A1^2, заменив номер ячейки.

4. Теперь достаточно зажать левую кнопку мыши на нижней точки готовой ячейки и растянуть таблицу, чтобы формула автоматически подставилась в остальные ячейки, и вы могли сразу ознакомиться с результатом.

5. Перейдите на вкладку вставки и выберите раздел с рекомендуемыми диаграммами.

6. В списке отыщите точечную диаграмму, которая подойдет для составления подходящего графика.

7. Вставьте ее в таблицу и ознакомьтесь с результатом. На следующем скриншоте вы видите параболу и значения X, при которых она получилась правильной (такую часто показывают в примерах на математике).

Всего 7 простых шагов потребовалось для достижения желаемого результата. Вы можете подставлять свои значения в таблицу и изменять их в любое время, следя за тем, как перестраивается график функций.

Комьюнити теперь в Телеграм

Подпишитесь и будьте в курсе последних IT-новостей

Подписаться

С помощью функции КОРЕНЬ

Модуль числа или массива чисел в Экселе может быть вычислен с помощью функции «Корень». В данной программе реализован расчет арифметического корня – вычисляются корни с четными степенями, имеющими знак + в любом случае. То есть, если извлечь квадратный корень от значения, полученного при возведении числа в квадрат, результатом будет являться абсолютная величина. Определить значение по модулю таким методом в excel возможно по следующим шагам:

• Возвращаемся все к той же таблице с произвольными значениями. Выделяем ячейку, кликаем на кнопку Мастера функций. Все три функции относятся к Математическому разделу. Выбираем Корень через поиск или выбранный раздел. Нажимаем на кнопку ОК.
• В качестве аргумента указываем интересующую нас ячейку – обозначается в соответствующем поле.
• Помним, что модуль числа через функцию корень в Excel вычисляется верно, если корень берется от возведенного во вторую степень исследуемого числа. Дополняется формула модуля до вида: =КОРЕНЬ(А2*А2). Если же сделать вычисление корня от отрицательного значения, программа выдаст ошибку – это неверное математическое действие.

Итоговый результат равен решению с помощью ЗНАК. Заполнение оставшихся ячеек для вычислений модуля в массиве производим уже известным способом.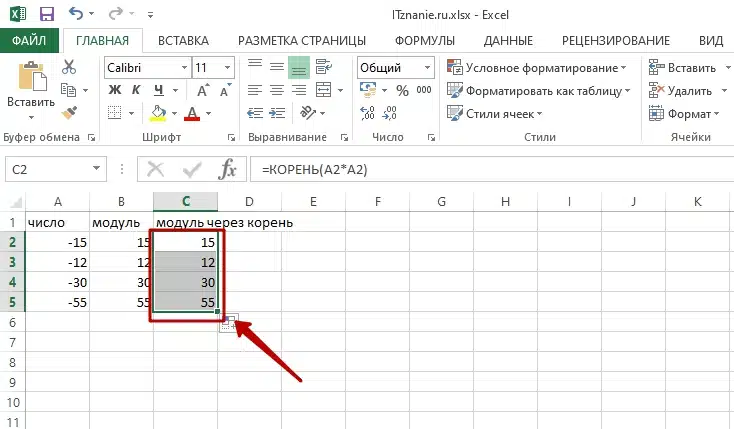

Любая методика вычисления модуля числа в Excel реализуется в несколько кликов. Несколько функций можно превратить в более сложную формулу, что позволяет производить в программе серьезные вычислительные процессы. В частности, в ексель применим простейший язык программирования vba, на котором возможно создавать макросы.

Мне нравитсяНе нравится

График функции F(x) = X^2

Функция X^2 – одна из самых популярных математических функций, которую разбирают еще на уроках в школе. На графике необходимо показать точки Y, что в Excel реализовывается следующим образом:

1. Создайте строку на листе в программе, вписав туда известные значения X.

2. Сделайте то же самое и с Y. Пока значения этой оси координат неизвестны. Чтобы определить их, нам нужно выполнить простые расчеты.

3. Поэтому в качестве значения для каждой ячейки укажите формулу, которая посчитает квадрат числа, указанного в строке X. Для этого впишите =A1^2, заменив номер ячейки.

4. Теперь достаточно зажать левую кнопку мыши на нижней точки готовой ячейки и растянуть таблицу, чтобы формула автоматически подставилась в остальные ячейки, и вы могли сразу ознакомиться с результатом.

5. Перейдите на вкладку вставки и выберите раздел с рекомендуемыми диаграммами.

6. В списке отыщите точечную диаграмму, которая подойдет для составления подходящего графика.

7. Вставьте ее в таблицу и ознакомьтесь с результатом. На следующем скриншоте вы видите параболу и значения X, при которых она получилась правильной (такую часто показывают в примерах на математике).

Всего 7 простых шагов потребовалось для достижения желаемого результата. Вы можете подставлять свои значения в таблицу и изменять их в любое время, следя за тем, как перестраивается график функций.

Комьюнити теперь в Телеграм

Подпишитесь и будьте в курсе последних IT-новостей

Подписаться

Работа с таблицами

• Создание таблицы: Чтобы создать таблицу в Excel, вы можете использовать команду «Вставка» или просто начать вводить данные в пустую ячейку. Затем вы можете отформатировать таблицу, добавить заголовки и стилизовать ее по своему усмотрению.
• Сортировка данных: Excel предлагает возможность сортировки данных по выбранному столбцу. Для этого выделите нужный столбец, затем выберите команду «Сортировать» и укажите направление сортировки — по возрастанию или убыванию.
• Фильтрация данных: Если вам нужно отфильтровать данные по определенным условиям, вы можете использовать функцию «Фильтр». Она позволяет выбирать только те строки, которые соответствуют вашим критериям.
• Вычисления и формулы: Excel позволяет выполнять различные вычисления в таблице с помощью формул. Вы можете использовать готовые функции, такие как СУММА, СРЕДНЕЕ, МАКС, МИН и многие другие, а также создавать свои собственные формулы.
• Сводные таблицы: С помощью сводных таблиц вы можете анализировать большие объемы данных и получать сводные данные в удобном формате. Эксель позволяет легко создавать сводные таблицы и настраивать их с помощью различных агрегирующих функций.

Это только некоторые из функций, доступных в Excel для работы с таблицами. Применяя эти функции, вы сможете эффективно организовывать и анализировать данные в таблицах и получать нужную информацию в удобной форме.

Построение графика функций SINH и COSH в Excel

Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.

Формула для нахождения синусов гиперболических:

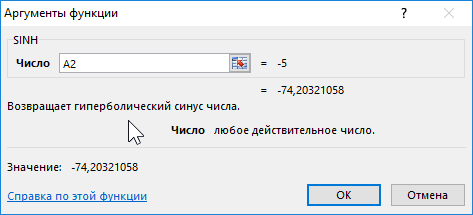
Формула для нахождения косинусов гиперболических:

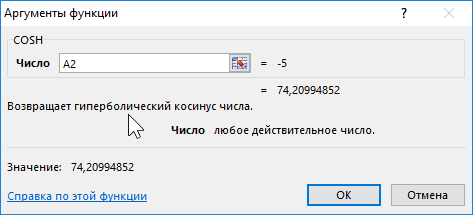
Таблица полученных значений:

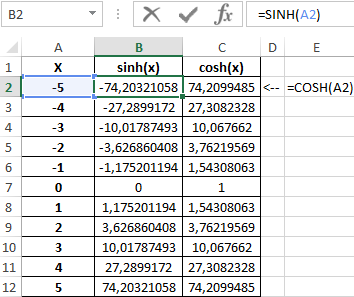
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:

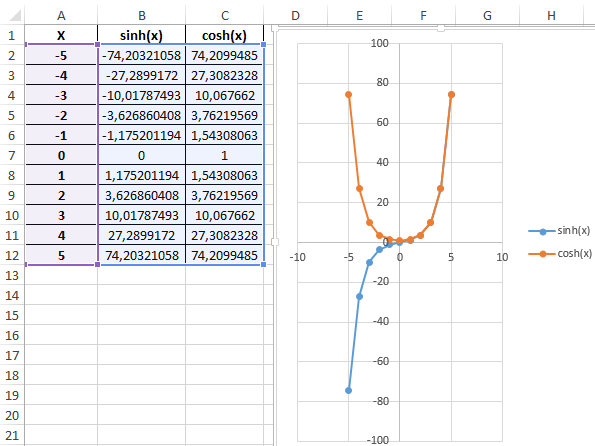
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.

Использование математических функций в программе

В категорию математических функций входит более 60 различных операторов, которые позволяют выполнять различные вычисления.

Вставить функцию в свободную ячейку таблицы можно по-разному:

1. Жмем кнопку “Вставить функцию” (fx) слева от строки формул. Выполнить данное действие можно, находясь в любой вкладке.
2. Переключаемся во вкладку “Формулы”. Здесь также представлена кнопка “Вставить функцию” – в левом углу ленты инструментов.
3. Нажимаем комбинацию клавиш Shift+F3, чтобы вызвать Мастер функций.

Результатом любого из вышеописанных способов будет открытие окна вставки функции. Здесь мы выбираем категорию “Математические”.

Теперь, когда категория выбрана, в поле ниже отмечаем требуемую функцию и щелкаем OK. 

После этого откроется окно с аргументами для заполнения.

Примечание: Если мы, находясь во вкладке “Формулы”, в группе инструментов “Библиотека функций” нажмем по значку математических функций, сразу откроется список операторов, которые мы можем выбрать, минуя окно вставки функции.

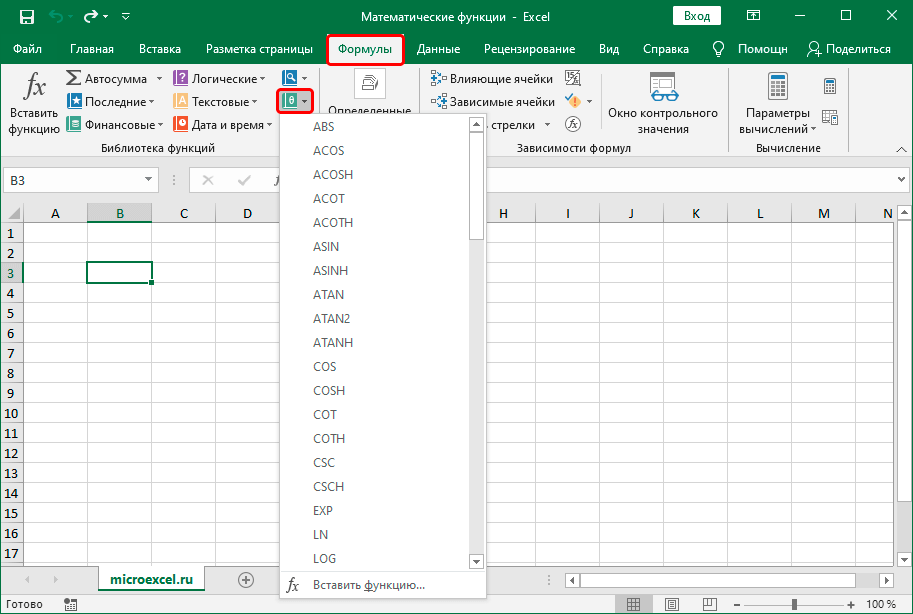
Стоит учитывать, что в предлагаемом перечне присутствуют не все операторы, но самые необходимые здесь все же есть, и в большинстве случаев их достаточно.

Теперь перейдем к детальному рассмотрению самых популярных функций.

СУММ

Пожалуй, это самая популярная функция, которая используется в Эксель. С помощью нее выполняется суммирование числовых данных. Формула функции:

В аргументах можно указать как конкретные числа, так и ссылки на ячейки, содержащие числовые значения. Причем указать координаты можно вручную (с помощью клавиш клавиатуры) или методом клика/выделения непосредственно в самой таблице.

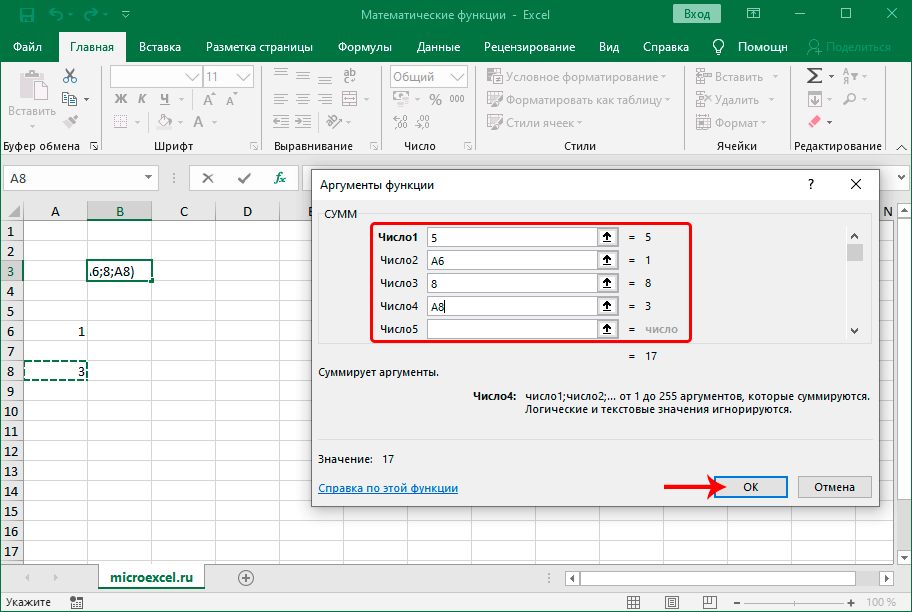
Для перехода к заполнению следующего аргумента достаточно кликнуть по полю напротив него или нажать клавишу Tab.

СУММЕСЛИ

Данная функция позволяет считать сумму чисел с заданным условиями, с помощью которых будет выполняться отбор значений, учитывающихся в суммировании. Формула выглядит следующим образом:

В аргументах функции указывается диапазон ячеек (вручную или путем выделения в таблице), значения которых нужно просуммировать. В качестве критерия можно задать следующие условия (в кавычках):

• больше (“>”)
• меньше (“<“)
• не равно (“<>”)

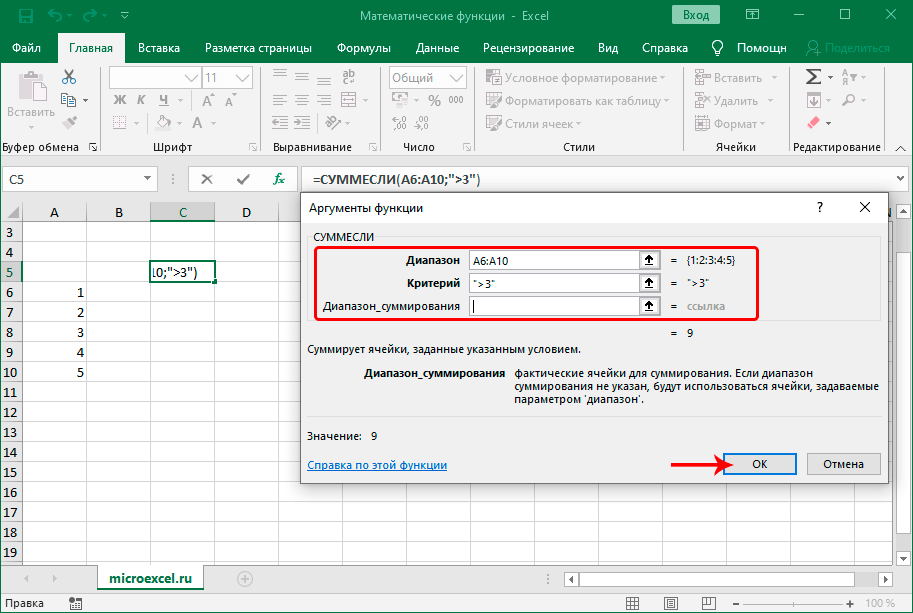
Аргумент “Диапазон_сумирования” заполнять не обязательно.

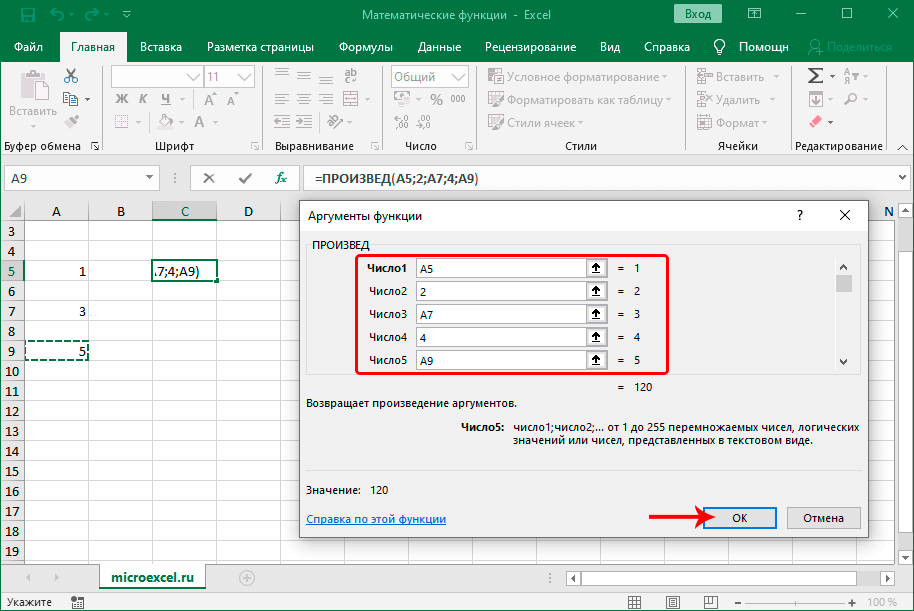
ПРОИЗВЕД

С помощью данного оператора выполняется умножение чисел. Синтаксис выглядит следующим образом:

В аргументах функции, как и в СУММ, можно указывать как конкретные числа, так и адреса ячеек (диапазоны ячеек), которые содержат числовые значения.

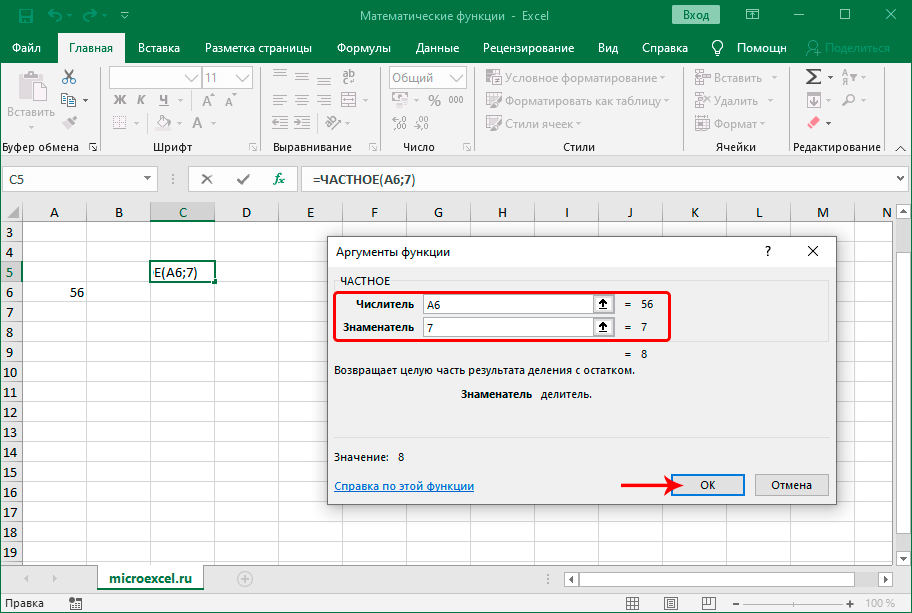
ЧАСТНОЕ

Чаще всего для деления используется формула со знаком “/” между делимым и делителем: .

Однако в программе также есть отдельная функция для выполнения деления, синтаксис которой представлен ниже:

Заполнить нужно два аргумента: Числитель (Делимое) и Знаменатель (Делитель).

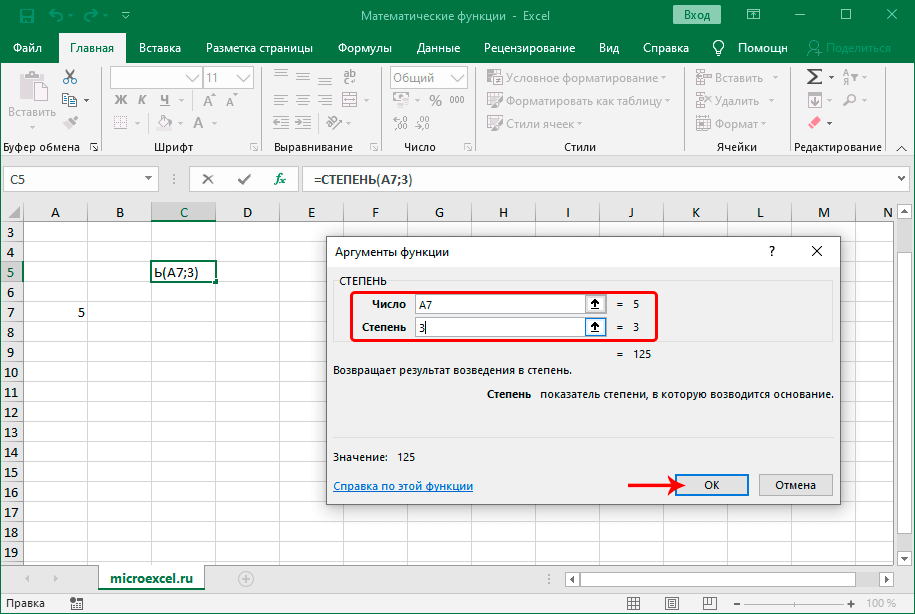
СТЕПЕНЬ

Оператор позволяет возвести число в указанную степень. Формула выглядит так:

В аргументах функции указывается само число, а также, степень, в которую нужно его возвести.

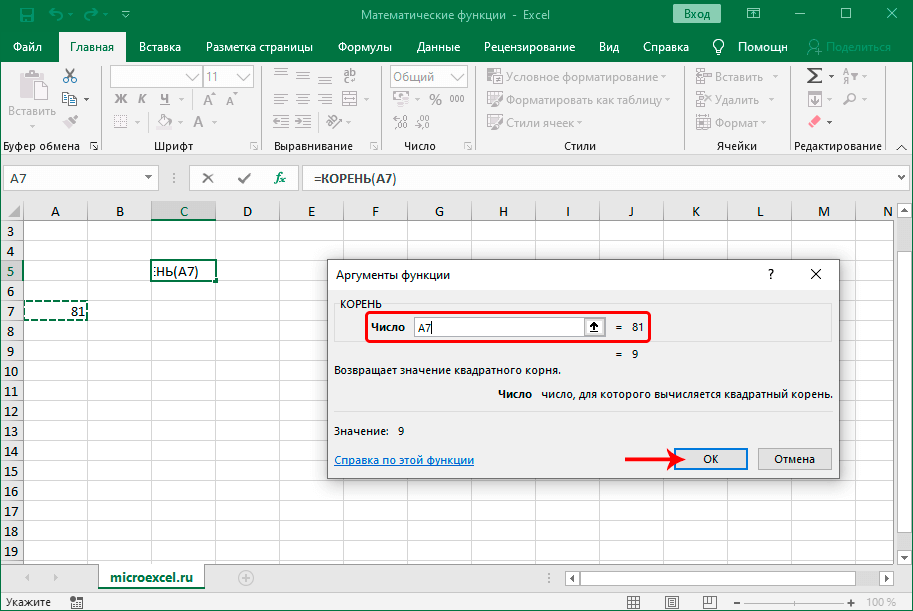
КОРЕНЬ

С помощью данного оператора можно извлечь квадратный корень из числа. Синтаксис выглядит следующим образом:

Заполнить требуется только один аргумент – “Число”.

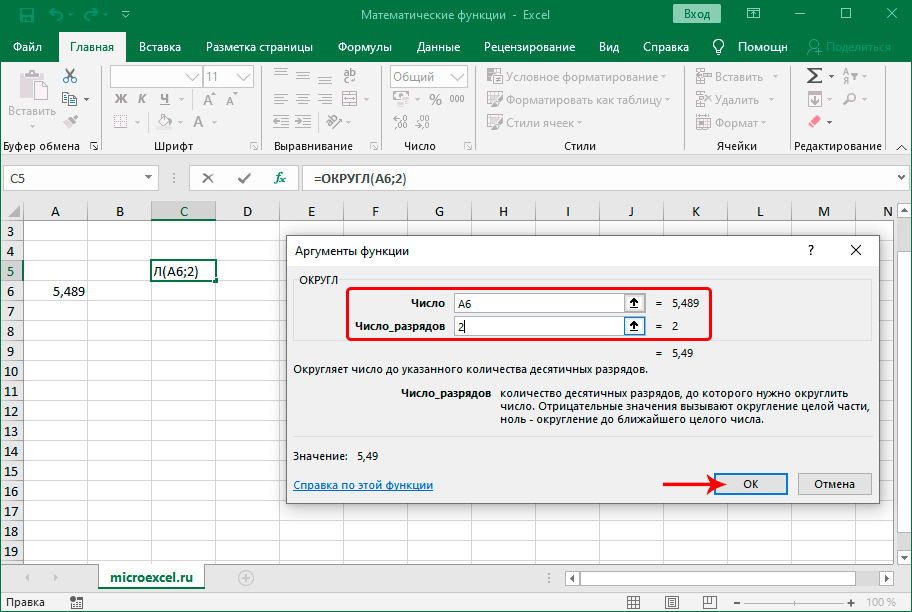
ОКРУГЛ

Функция применяется для выполнения еще одного распространенного математического действия – округления чисел (по общематематическим правилам, т.е., к ближайшему по модулю значению). Синтаксис функции представлен ниже:

В аргументе “Число” указывается значение, которое требуется округлить. В числе разрядов, соответственно, пишем количество цифр, которые хотим оставить после запятой.

Также, в Excel доступны операторы ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые, как следует из их названий, используются для округления до ближайшего верхнего и нижнего числа, соответственно (по модулю).

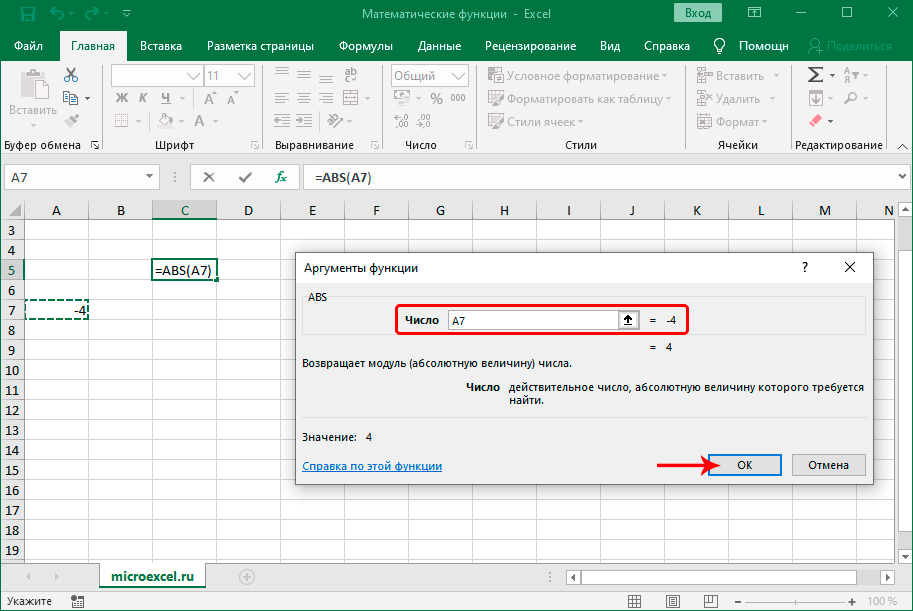
ABS

Позволяет получить модуль числа. Формула функции представлена ниже:

Заполнить нужно всего один аргумент – “Число”, модуль которого требуется найти.

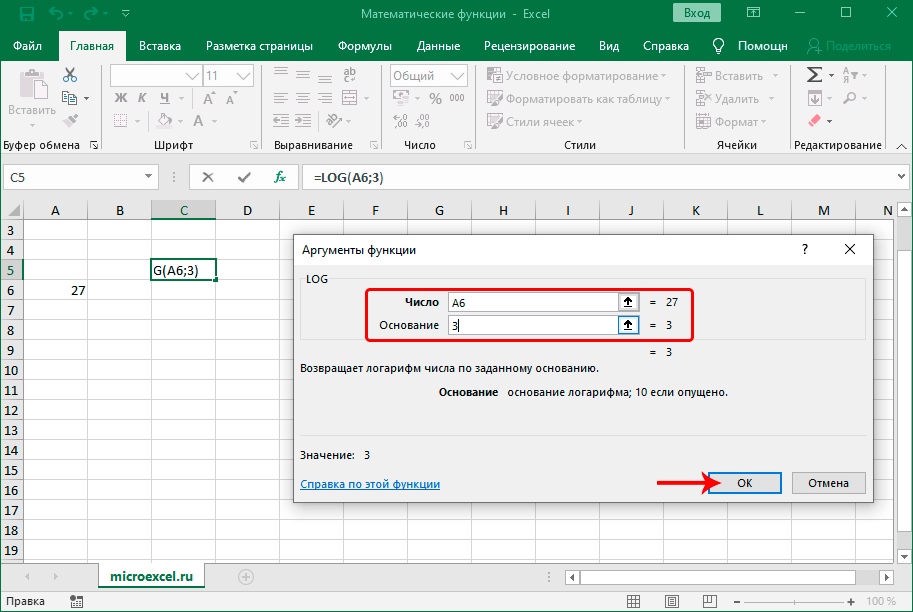
LOG

С помощью этого оператора определяется логарифм числа по заданному основанию. Синтаксис функции представлен в виде:

Необходимо заполнить два аргумента: Число и Основание логарифма (если его не указать, программа примет значение по умолчанию, равное 10).

Также для десятичного логарифма предусмотрена отдельная функция – LOG10.

ОСТАТОК

Применяется для получения остатка от деления чисел. Формула оператора выглядит следующим образом:

Для того, чтобы получить результат, требуется заполнить значения двух аргументов: Число и Делитель.

Функция COS

В этой статье описаны синтаксис формулы и использование функции COS в Microsoft Excel.

Синтаксис

Аргументы функции COS описаны ниже.

Число — обязательный аргумент. Угол в радианах, для которого определяется косинус.

Замечания

Если угол задан в градусах, умножьте его на ПИ()/180 или воспользуйтесь функцией РАДИАНЫ, чтобы преобразовать его в радианы.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Как использовать функцию синуса в программе Excel: полезные советы и инструкция

Для того чтобы использовать функцию синуса в программе Excel, вам необходимо следовать этим шагам:

1. Откройте программу Excel и создайте новую таблицу или откройте существующую таблицу, в которой вы хотите использовать функцию синуса.
2. Выберите ячейку, в которую вы хотите поместить результат вычисления синуса.
3. Введите формулу синуса в выбранную ячейку, начиная с знака «равно». Например, если вы хотите вычислить синус числа 45 градусов, формула будет выглядеть следующим образом: . В этой формуле мы умножаем число 45 на PI() (числовую константу, представляющую число Пи), а затем делим на 180 для перевода градусов в радианы.
4. Нажмите клавишу «Enter», чтобы завершить ввод формулы. Результат вычисления синуса будет показан в выбранной ячейке.

Полезные советы:

• Если вы хотите вычислить синус значения в градусах, убедитесь, что вы перевели градусы в радианы, как показано в инструкции выше.
• Если вы работаете с углами в градусах, используйте функцию DEGREES для преобразования радиан в градусы. Например, вычислит синус 1 радиана и преобразует результат в градусы.
• Если вам нужно вычислить синус для нескольких значений, вы можете использовать функцию СИНУС в комбинации с другими функциями Excel, такими как ФУНКЦИИ АВТОМАТИЧЕСКОГО ЗАПОЛНЕНИЯ или ФУНКЦИИ МАССИВА, чтобы автоматически заполнить результаты в нескольких ячейках.

Пример использования функции синуса в программе Excel:

Допустим, у вас есть список углов в градусах, и вы хотите вычислить синус для каждого из них. Вы можете использовать функцию синуса в комбинации с ФУНКЦИЕЙ АВТОМАТИЧЕСКОГО ЗАПОЛНЕНИЯ, чтобы автоматически заполнить результаты для всех углов.

Угол (градусы)	Синус
30	=SIN(A2*PI()/180)
45	=SIN(A3*PI()/180)
60	=SIN(A4*PI()/180)

В этом примере мы использовали ФУНКЦИЮ АВТОМАТИЧЕСКОГО ЗАПОЛНЕНИЯ, чтобы автоматически заполнить результаты для углов 30, 45 и 60 градусов. Формула синуса используется для вычисления синуса для каждого угла. Результаты вычислений будут автоматически отображены в соответствующих ячейках.

Теперь вы знаете, как использовать функцию синуса в программе Excel и можете применить эту функцию для вычисления синуса различных значений в радианах или градусах.

Как сделать синус в квадрате в excel?

Формулы тригонометрии – редкая и сложная задача для работы в Майкрософт Эксель. Тем не менее, здесь есть ряд встроенных функций, помогающих в геометрических расчетах. В этом посте мы рассмотрим основные из них, которые, в компании с учебниками и справочниками, могут решить многие математические задачи. Они участвуют в расчете площади, объема, угла наклона и т.д. Если Вы школьник, студент, или работаете, например, в сфере строительства, эта статья будет Вам очень полезна.

Для корректного расчета геометрических величин, Вам понадобятся познания в элементарных расчетах и некоторые из функций Excel. Так, функция КОРЕНЬ извлечет квадратный корень из заданного числа. Например, запишем: =КОРЕНЬ(121), и получим результат «11». Хотя правильным решением будет «11» и «-11», программа возвращает только положительный результат в таких случаях.

Еще одна функция – ПИ(), не нуждается в аргументах и является зарезервированной константой. Ее результатом будет известное число 3,1415, описывающее соотношение длины окружности к ее диаметру. Эту функцию-константу можно активно применять в расчетах.

Тригонометрические функции Excel, до которых мы еще доберемся, используют запись угла в радианах. Эта общепринятая практика часто бывает ненаглядной, ведь нам привычнее выражать угол в градусах. Чтобы устранить эту проблему, есть две функции преобразования величин:

• ГРУДУСЫ(Угол в радианах) – преобразует радиальные величины в градусы
• РАДИАНЫ(Угол вградусах) – наоборот, преобразует градусы в радианы.

Пользуясь этими функциями, Вы обеспечиваете совместимость и наглядность вычислений.

Конечно, Вы знаете эти функции:

• COS(Угол в радианах) – косинус угла, соотношение между прилежащим катетом и гипотенузой прямоугольного треугольника
• SIN(Угол в радианах) – синус угла, отношение противолежащего катета к гипотенузе

Для удобства чтения формул, можно использовать вложенную функцию РАДИАНЫ и задать угол в градусах. Например, формула =COS(РАДИАНЫ(180)) вернет результат «-1».

Еще две функции Вам так же знакомы – это тангенс и котангенс:

• TAN(Угол в радианах) – отношение длины противолежащего катета к прилежащему
• COT(Угол в радианах) – обратная величина – соотношение прилежащего угла к противолежащему.

Здесь так же рекомендую использовать функции преобразования величин РАДИАНЫ и ГРАДУСЫ.

Среди прочих тригонометрических функций можно выделить секанс и косеканс:

• SEC(Угол в радианах) – отношение гипотенузы к прилежащему катету
• CSC(Угол в радианах) – отношение гипотенузы к противолежащему катету

Легко заметить, что секанс – обратно-пропорциональная величина к косинусу, косеканс – к синусу.

Такие функции выполняют обратный расчет по отношению к перечисленным выше:

• Арккосинус – это угол, который образуют прилежащий катет и гипотенуза с определенным косинусом. Чтобы посчитать эту величину, используйте функцию ACOS(Значение косинуса).
• Арксинус – угол между противолежащим катетом и гипотенузой с определенным синусом, вычисляется так: ASIN(Значение синуса).
• Арктангенс – угол между противолежащим и прилежащим катетами для заданного тангенса: ATAN(Значение тангенса).
• Арккотангенс – угол, для которого справедливо заданное значение котангенса: ACOT(Значение котангенса).

Все перечисленные функции вернут угол в радианах. Естественно, для перевода его в градусы, используем функцию ГРАДУСЫ.

Знание и умелое применение перечисленных функций, конечно, не сделает Вас богом в тригонометрии, но все же позволит выполнить сложные расчеты, «стоимость» которых часто довольно высока. Научитесь комбинировать их с другими функциями, построением графиков, чтобы получить максимальный эффект от полученных знаний.

Это все о тригонометрических функциях, спасибо, что читаете мой блог и развиваетесь в своих знаниях. Следующую статью я напишу об округлении чисел и очень Вам рекомендую ее не пропустить!

Поделиться, добавить в закладки или статью

x,y принадлежит дельта x,y = 0.3 Построить поверхность, соответствующую заданной функции двух переменных На поверхности определить координаты экстремумов(максимум и минимум) и выделить их в таблице красным цветом

До этих заданий считал что нормально владею экселем(

Нажмите, чтобы раскрыть…

Удалите топик модеры если не трудно)

Пользователи просматривающие тему

10 Окт 2018 08:32:03

29 Янв 2017 17:28:40

28 Июн 2018 15:25:11

21 Сен 2018 06:21:34

9 Окт 2018 19:58:10

9 Окт 2018 15:21:02

10 Окт 2018 06:06:37

1 Окт 2018 11:22:35

Сейчас на форуме (гостей: 577, пользователей: 11) , , , , , , , , , ,

Сегодня отмечают день рождения (29), (21), (31), (25), (29), (18)

Всего зарегистрированных пользователей: 83110

Источник

Шаг 2: Вычислите sin 2

Чтобы вычислить квадрат синуса (sin 2) в Excel, можно воспользоваться функцией POWER, которая возводит число в заданную степень. Для этого выполните следующие действия:

1. Введите значение синуса в ячейку.

Пример: sin(α) = 0,5

2. Введите формулу для вычисления sin 2 в другую ячейку, используя функцию POWER.

Пример: sin^2(α) = POWER(0,5, 2)

Функция POWER принимает два аргумента. Первый аргумент — это значение синуса, которое вы хотите возвести в степень. Второй аргумент — это значение степени, в которую нужно возвести синус.

3. Нажмите Enter, чтобы получить результат.

Пример: sin^2(α) = 0,25

Теперь вы знаете, как вычислить квадрат синуса (sin 2) в Excel, используя функцию POWER. Это может быть полезно при решении различных задач, связанных с тригонометрией.

Добавление второй оси

Иногда информация может быть представлена в таблице так, что поместить ее на одной общей диаграмме, на первый взгляд, невозможно. Если представить, что накладные расходы указаны не в рублях, а в долларах, график получится некорректным.

Можно построить две разных диаграммы для каждого ряда данных. Или перед тем, как сделать график в Экселе, пересчитать сумму по действующем курсу — но это будет не слишком правильно, если затраты определялись именно в валюте. Решение проблемы — добавить вторую ось со своими единицами измерения. 

Для этого можно выполнить такие действия: 

1. Построить основу — график, единицы измерения у которого одинаковые для каждого ряда. 
2. Выделить диаграмму и на вкладке «Конструктор» перейти к изменению ее типа. 
3. Выбрать вариант «Комбинированная» и второй вариант в списке — гистограмму с группировкой и график на вспомогательной оси. 
4. Настроить отображение — указать, для какого ряда будет построена вспомогательная ось, изменить виды диаграмм. 
5. Нажать «ОК» для перехода к дальнейшим настройкам. 

Теперь на графике будет две отличающихся друг от друга диаграммы, каждая из которых имеет свою шкалу с отдельными единицами измерения. Можно сделать так, чтобы на экране были, например, две похожих линии, выбрав соответствующие варианты на этапе изменения типа. Хотя это будет не так удобно даже при наличии легенды. 

Преимущества использования Excel для вычисления синуса квадрата x

1. Удобство и простота в использовании	Excel обладает понятным и простым интерфейсом, что позволяет легко создавать и редактировать формулы для вычисления синуса квадрата x. Для этого достаточно знать основные математические операции и функции Excel.
2. Гибкость и настраиваемость	Excel позволяет настраивать вычисления синуса квадрата x в зависимости от требований пользователя. Возможности настройки формул и функций позволяют получить нужный результат с учетом конкретных условий.
3. Возможность использования других функций и операций	Excel предоставляет широкий набор функций и операций, которые могут быть полезны при вычислении синуса квадрата x. Это позволяет выполнять дополнительные вычисления или реализовывать формулы, основанные на других математических функциях.
4. Возможность автоматического обновления результатов	Благодаря своей автоматизации, Excel позволяет автоматически обновлять результаты вычислений синуса квадрата x при изменении значения переменной x. Это позволяет экономить время и упрощает процесс работы.
5. Возможность визуализации и анализа данных	Excel предоставляет возможность визуализировать результаты вычислений синуса квадрата x с помощью графиков и диаграмм. Это позволяет лучше понять и проанализировать полученные данные.

В целом, использование Excel для вычисления синуса квадрата x позволяет получить точный результат, сохранить гибкость в настройках и сэкономить время при выполнении математических операций.