Четырёхмерный куб презентация

Единый тип данных для точек и векторов

Давайте представим, что нам поставили задачу: создать единый тип данных, способный хранить как трёхмерную точку, так и трёхмерный вектор. Этот тип данных должен поддерживать операции вращения, перемещения и масштабирования, причём по-разному для векторов и точек: например, перемещение вектора никак не меняет его, а перемещение точки изменяет эту точку.

Если использовать процедурную парадигму программирования, получится нечто такое:

Объектно-ориентированный подход предлагает такой вариант:

Оба подхода одинаково плохи: во-первых, мы в любом случае дублируем код. Во-вторых, на видеокартах с современной архитектурой любое ветвление или условное выполнение оборачивается огромным падением производительности, и желательно его избегать; в данных двух реализациях мы не сможем избежать ветвлений при выполнении трансформаций точек и векторов прямо на видеокарте.

Проблема решается с помощью математического приёма — однородного представления точек и векторов.

Класс CAnimatedCube

Давайте запомним несколько простых правил. Некоторые из них даже будут доказаны чуть ниже.

• умножение матрицы преобразования на вектор или точку в однородном представлении даёт преобразованный вектор или точку
• можно легко составить базовую матрицу, представляющих одно элементарное аффинное преобразование
• умножение матрицы A на матрицу B даёт новую матрицу, которая описывает новую трансформацию, созданную путём применения трансформации B, а затем A (именно в таком порядке)
• умножение матриц не коммутативно: вы не можете заменить на
• инвертирование матрицы (например, с помощью детерминанта матрицы) даёт матрицу обратной трансформации, которая вернёт точку или вектор в исходное состояние — в идеальном мире. В дискретном мире компьютеров обратное преобразование может быть чуть-чуть неточным из-за особенностей представления типов float и double.

Для демонстрации этих правил расширим класс CIdentityCube из предыдущего урока. Новый класс будет называться CAnimatedCube, и он будет демонстрировать работу трёх базовых аффинных трансформаций. Смена и продвижение анимации будет выполняться в методе Update, вызываемом периодически снаружи.

С учётом перечисленных выше правил, мы можем написать метод Draw для анимированного куба. При этом вместо glLoadMatixf следует применить glMultMatrixf, чтобы вместо замены уже существующей трансформации всего лишь модифицировать её. Если мы заменим матрицу GL_MODELVIEW, камера будет работать некорректно.

Функции для работы с аффинными трансформациями (и не только!) можно найти в GML:

Применение трехмерной геометрии в практике

Трехмерная геометрия имеет широкое применение в различных практических областях. В этом разделе мы рассмотрим некоторые из них:

1. Архитектура и дизайн: Трехмерная геометрия используется в архитектуре и дизайне для создания и моделирования трехмерных структур и объектов. Она позволяет архитекторам и дизайнерам визуализировать и представить свои идеи, а также анализировать пространственные отношения и пропорции.
2. Инженерия и машиностроение: В трехмерной геометрии используются при разработке и проектировании машин, автомобилей, самолетов и других инженерных конструкций. Она позволяет моделировать и анализировать компоненты и системы в трехмерном пространстве, учитывая их геометрические свойства и взаимодействия.
3. Компьютерная графика и визуализация: Трехмерная геометрия играет ключевую роль в создании компьютерной графики и визуализации. Она позволяет создавать реалистичные трехмерные модели объектов, анимацию, эффекты и симуляции. Это применяется в фильмах, видеоиграх, виртуальной реальности и других сферах развлечений и индустрии.
4. Геодезия и картография: Трехмерная геометрия используется для измерения и представления поверхности Земли и других географических объектов. Она помогает в создании точных карт, моделей местности, планировании маршрутов и решении геодезических задач.
5. Медицина и биология: В трехмерной геометрии применяются в медицине и биологии для моделирования органов и тканей, планирования хирургических операций, анализа медицинских изображений и создания протезов. Она также используется в изучении структуры молекул и белков.

Трехмерная геометрия имеет множество других применений в различных областях, таких как геоинформационные системы, робототехника, физика, геология и многое другое. Она позволяет нам лучше понять и взаимодействовать с трехмерным миром и применять это знание для решения практических задач.

Трёхмерная система координат

В OpenGL используется правосторонняя система координат, в которых пользователь может задавать вершины примитивов, из которых состоят трехмерные объекты. Правосторонней система координат называется потому, что ее можно образовать при помощи большого, указательного и среднего пальцев правой руки, задающих направления координатных осей X, Y и Z соответственно.

Система координат задаётся точкой отсчёта и координатными осями, которые, в свою очередь, задают направления и длины трёх единичных векторов (1, 0, 0), (0, 1, 0) и (0, 0, 1). Как точка отсчёта, так и координатные оси могут меняться при переходе из одной системы координат в другую.

Например, представьте себе систему координат комнаты, где в качестве центра взята точка в геометрическом центре пола, а ось z указывает вверх, и расстояния измеряются в метрах. Тогда точки головы человека в комнате всегда будут иметь координату z, большую нуля, обычно в диапазоне . Если же перейти в другую систему отсчёта, где центром служит точка в геометрическом центре потолка, то голова человека в комнате будет иметь отрицательную координату z.

В любой трёхмерной сцене есть система координат, которую можно считать мировой системой коодинат. Это очень удобно: любая точка или вектор в мировой системе координат представляется однозначно. Благодаря этому, если у нас есть несколько локальных систем координат (например: комната, салон автомобиля, камера), и мы знаем способ преобразования из любой системы в мировые координаты, то мы можем спокойно перейти, например, от системы координат комнаты к системе координат камеры:

О локальных системах координат можно сказать следующее:

• для перехода к мировой системе координат всегда есть аффинное преобразование, состоящее из некоторого числа перемещений, вращений и масштабирований
• если точка отсчёта в разных координатах разная, это можно представить перемещением (англ. translate)
• если координатные оси направлены в другие стороны, это можно представить вращением (англ. rotate)
• если единицы измерения разные, например, метры в одной системе и километры в другой, это можно представить масштабированием (англ. scale)

Самый удивительный факт: любое элементарное трёхмерное преобразование, а также их комбинацию можно представить в виде матрицы 4×4! Чтобы понять, как это происходит, разберёмся с однородным представлением точек и векторов.

Развёртки

Итак, житель четырёхмерного пространства может увидеть
трёхмерный объект одновременно со всех сторон.
Можем ли мы одновременно со всех сторон увидеть трёхмерный
куб? Глазом — нет. Но люди придумали способ, как
изобразить на плоском рисунке все грани трёхмерного куба одновременно.
Такое изображение называется развёрткой.

Развёртка трёхмерного куба

Как образуется развёртка трёхмерного куба все наверно знают.
Этот процесс показан на анимации.

Для наглядности края граней куба сделаны полупрозрачными.

Следует отметить, что мы способны воспринять эту двумерную картинку
только благодаря воображению. Если рассмотреть фазы разворачивания
с чисто двумерной точки зрения, то процесс будет казаться странным
и совсем не наглядным.

Он выглядит, как постепенное появление сперва очертаний
искажённых квадратов, а потом их расползание на свои места
с одновременным принятием необходимой формы.

Если смотреть на разворачивающийся куб в направлении
одной из его граней (с этой точки зрения куб выглядит как
квадрат), то процесс образования развёртки ещё менее нагляден.
Всё выглядит как выползание квадратов из начального квадрата
(не развёрнутого куба).

Но не наглядна развёртка только для глаз. Как раз
благодаря воображению из неё можно почерпнуть много информации.

Развёртка четырёхмерного куба

Сделать анимированный процесс разворачивания гиперкуба
хоть сколько нибудь наглядным просто невозможно. Но этот
процесс можно представить. (Для этого надо посмотреть на него
глазами четырёхмерного существа.)

Развёртка выглядит так.

Здесь видны все восемь кубов, ограничивающих гиперкуб.

Одинаковыми цветами покрашены грани, которые должны совместиться
при сворачивании. Серыми оставлены грани для которых парных не видно.
После свёртки самая верхняя грань верхнего куба должна совместиться
с нижней гранью нижнего куба. (Аналогично сворачивается развёртка
трёхмерного куба.)

Обратите внимание, что после свёртки все грани восьми кубиков
придут в соприкосновение, замкнув гиперкуб. И наконец, представляя
процесс свёртывания, не забывайте, что при свёртывании происходит не наложение
кубов, а оборачивание ими некой (гиперкубической) четырёхмерной области

Сальвадор Дали (1904-1989) много раз изображал распятие, а кресты
фигурируют в очень многих его картинах. На картине
«Распятие» (1954)
используется развёртка гиперкуба.

Тест буфера глубины

Буфер глубины OpenGL — это двумерная матрица дополнительных данных, где каждому пикселю соответствует одно значение float: глубина фрагмента примитива, оказавшегося ближе к пикселю, чем остальные фрагменты примитивов, проецируемые на тот же пиксель. Это позволяет реализовать попиксельный алгоритм художника: после приведения в нормализованное пространство каждая примитивная фигура будет разбита на фрагменты, для которых будет проведён тест глубины.

Фрагмент — это атомарная, то есть неделимая, часть фигуры. Если видеокарта не совершает сглаживание, то один фрагмент станет одним пикселем фигуры.

Тест глубины устроен следующим образом: если фрагмент в нормализованном пространтсве стал ближе, чем последнее значение буфера глубины, то мы выбираем его и обновляем значение в буфере глубины, иначе мы отбрасываем фрагмент. В псевдокоде способ выглядит так:

Как и любой другой буфер OpenGL, буфер глубины следует очищать. Для этого вызов должен получать ещё один флаг :

Также нужно после создания контекста включить режим теста глубины командой glEnable:

Трехмерный вектор

Если мы уже разобрались, что такое вектор на плоскости — давайте перейдем к вектору в трехмерном пространстве — в объемном мире.

Достаточно просто представить себе стрелку в объеме — достаточно вспомнить, как Вы что-то измеряли рулеткой. Прислонили конец к шкафу, другой к полу, и померили его диагональ. Ну или не шкаф… каждому свое. Но точно можно сказать, что такое трехмерный вектор.

Но давайте немного формулизируем то, что мы поняли. Представим трехмерные координаты и в них наш радиус-вектор AB.

Трехмерный вектор AB

Понятно, что нам теперь совсем не хватит двух координат для описания вектора AB. Так что давайте добавим третью координату, просто дописав ее в конце.

Хммм… интересно, а по какому признаку мы можем вот так просто приписывать координаты? Может, можно просто так добить вектор до семимерного? Ну в принципе, нас никто остановить не может, и мы именно так и поступим, но сначала немного окунемся в линейную алгебру.

Векторные операции в трехмерном пространстве

В трехмерной геометрии векторы играют важную роль и используются для описания и анализа различных объектов и физических величин. В этом разделе мы рассмотрим основные векторные операции в трехмерном пространстве:

1. Сложение векторов: Сложение векторов выполняется путем суммирования соответствующих компонентов векторов. Для векторов A = (A₁, A₂, A₃) и B = (B₁, B₂, B₃) их сумма A + B равна (A₁ + B₁, A₂ + B₂, A₃ + B₃). Геометрически это соответствует перемещению точки из начала координат вдоль двух векторов.
2. Вычитание векторов: Вычитание векторов выполняется путем вычитания соответствующих компонентов векторов. Для векторов A и B их разность A — B равна (A₁ — B₁, A₂ — B₂, A₃ — B₃). Геометрически это соответствует перемещению точки из начала координат вдоль первого вектора и обратно вдоль второго вектора.
3. Умножение вектора на скаляр: Умножение вектора на скаляр выполняется путем умножения каждой компоненты вектора на заданное число. Для вектора A и скаляра k, результатом будет вектор kA = (kA₁, kA₂, kA₃). Геометрически это приводит к изменению длины вектора без изменения его направления.
4. Скалярное произведение векторов: Скалярное произведение двух векторов A и B определяется как A · B = A₁B₁ + A₂B₂ + A₃B₃. Результат скалярного произведения является числом, которое характеризует угол их между векторами и их проекцию.
5. Векторное произведение векторов: Векторное произведение двух векторов A и B определяется как A × B = (A₂B₃ — A₃B₂, A₃B₁ — A₁B₃, A₁B₂ — A₂B₁). Результат векторного произведения является вектором, перпендикулярным плоскости, образованной A и B, с направлением, определяемым правилом буравчика.

Векторные операции в трехмерном пространстве позволяют нам моделировать и анализировать различные физические явления, такие как силы, скорости, моменты и многое другое. Они являются важным инструментом в механике, физике и инженерии.

Слайд 9С определением плоскости в четырёхмерном пространстве дело обстоит не так просто.

Дело в том, что здесь бывают как обычные двумерные плоскости, так и трёхмерные плоскости, называемые гиперплоскостями. С точки зрения задания плоскостей уравнениями, именно гиперплоскость является точным аналогом обычной плоскости в трёхмерном пространстве. В уравнении Ax+By +Cz+D=0 обычной плоскости двум из трёх переменных x, y, z, можно придавать произвольные значения, и тогда значение третьей переменной будет определяться из уравнения однозначно. Таким образом, множество всех решений этого уравнения описывается двумя произвольными параметрами, то есть оно двумерно. По той же причине множество всех решений одного линейного уравнения в четырёхмерном пространстве Ax+By+Cz+Dt+E=0 само по себе трехмерно. Аналогично трехмерному случаю, вектор с координатами (A;B;C;D) перпендикулярен данной гиперплоскости и называется ее нормальным вектором.

Слайд 1Четырёхмерный кубТЕМА: ”Четырёхмерный куб и его свойства”

Выполняли работу Воробьёв Иван и Лобок Дмитрий,11 класс, школа № 364 Руководитель Михайлова Е.А., учитель математики.I.Объект исследования:Четырёхмерный кубII.Цель исследования:Определить, что такое четырёхмерный куб, описать его геометрически.III.Исследования:1.Как увидеть четырёхмерный куб.Чтобы представить себе четырёхмерный куб, сначала необходимо посмотреть на обычный – трехмерный — куб, а также на “двумерный куб” (квадрат) и “одномерный куб” (отрезок) в динамике, применяя параллельный перенос. 2.Развёртка четырёхмерного куба.Аналогично тому, как обычный куб имеет плоскую развёртку, гиперкуб может быть “развёрнут” в трёхмерном пространстве. Эта развёртка будет состоять из 8 трёхмерных граней – обычных кубов.Развёртка похожа на макет своеобразного восьмикомнатного дома. Такой дом был описан американским писателем- фантастом Р. Хайнлайном в рассказе “Дом, который построил Тил”3.Как спроектировать четырёх мерный куб.Есть ещё один способ изображения четырёхмерного куба. Восемь трёхмерных граней изображены здесь внутренним (малым кубом), внешним (большим) кубом и шестью усечёнными пирамидами, соединяющими соответственные грани малого и большого кубов. По этому изображению удобнее всего сосчитать количество разного рода составляющих элементов четырёхмерного куба.4.Как строго определить четырёхмерный куб.Четырёхмерный куб – это множество всех четвёрок действительных чисел (x; y; z; t), для которыхIV.Результаты исследования:Выполняя эту работу, мы узнали много нового. Нас уже не пугает понятие “ четырёхмерное пространство” , “ четырёхмерное измерение” . Мы узнали, что четырёхмерный куб легко описать геометрически как фигуру, аналогичную квадрату на плоскости или кубу в трехмерном пространстве.

Коническая поверхность

Каноническое уравнение  в декартовых координатах задаёт коническую поверхность 2-го порядка или, если короче, конус. Но это опять же не совсем тот конический колпак, который всем знаком со времён далёкого детства.

Форму многих поверхностей удобно исследовать методом сечений, который я потихоньку начал использовать ещё в предыдущих параграфах. Суть метода состоит в том, что мы «рассекаем пациентов» плоскостями  (прежде всего, координатными), и получившиеся сечения позволяют нам хорошо понять, как выглядит та или иная поверхность.

Перепишем уравнение в виде  и исследуем сечения конуса плоскостями , параллельными плоскости . Подставим  в уравнение конической поверхности:

Очевидно, что случаю  соответствует уравнение , задающее пару мнимых пересекающихся прямых с единственной действительной точкой пересечения в начале координат. Данная точка называется вершиной конуса.

Если же , то уравнение  задаёт эллипсы различных размеров, причём из последнего уравнения хорошо видно, что с увеличением абсолютных значений «цэ большого» полуоси эллипсов неограниченно возрастают. Таким образом, коническая поверхность бесконечна:
Если коническую поверхность «разрезать» произвольной плоскостью (которая проходит через ось ), то в сечении получатся две пересекающиеся в начале координат прямые. Множество таких сечений, собственно, и образует коническую поверхность. И логично, что каждая из этих прямых называется образующей конуса. 

На практике почти всегда приходится иметь дело с конусом вращения, в котором сечения плоскостями  представляют собой окружности. И во многих практических задачах типичен следующий «опознавательный» вид уравнения: – с «зет» в левой части и равными коэффициентами при  и .

Как многие догадались,  функция  задаёт верхнюю часть конуса, а функция  – его нижнюю часть.

Распространённая вариация по теме:

Пример 16

Построить поверхность

Решение: уравнение имеет вид  и определяет половину конуса, располагающуюся в верхнем полупространстве. Вершина конической поверхности, понятно, расположена в начале координат, но как построить всё остальное?

Возведём обе части исходного уравнения в квадрат:

Далее выберем небольшое положительное значение «зет», например , и найдём линию пересечения этой плоскости с нашей поверхностью: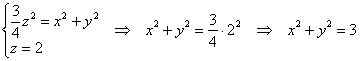 – окружность радиуса .

Пояснение на всякий случай:  подставили в 1-е уравнение

Теперь на высоте  изобразим окружность  и аккуратно проведём 4 образующие конуса:
Образующие, в принципе, можно было продолжить и выше плоскости .

Не забываем, что уравнение  задаёт только верхнюю часть поверхности и поэтому никаких «хвостиков» в нижнем полупространстве быть не должно.

Пожалуй, простейшая коническая поверхность:

Пример 17

Построить коническую поверхность .  Записать неравенства, определяющие внутреннюю и внешнюю часть конуса.

В образце решения изображён фрагмент конуса, расположенный между плоскостями . Ну, а с неравенствами, думаю, сообразите самостоятельно. В случае мучительных сомнений всегда можно взять точку (внутри или снаружи конуса) и проверить, удовлетворяют ли её координаты неравенству.

В заключение статьи подробно рассмотрим ещё одну мегапопулярную поверхность:

Понятие радиус-вектора

Как мы уже увидели, в векторе нам важны только две вещи: длина и направление, так зачем его рисовать где-то в середине нашей координатной плоскости. Давайте сместим наш вектор к началу оси координат. Тогда нам надо будет хранить только координаты конца вектора — а координаты начала вектора у нас будут нулевыми.

Смещенная ось координат

Так теперь надо будет меньше мучаться — храним в векторе просто координаты его конца.

Такие вектора называются в школе радиус-векторами, но в дальнейшем мы будем все вектора брать радиус-векторами, ведь, как мы помним, все вектора имеющие одно направление и одну длину — одинаковые, один и тот же вектор, так почему бы нам не взять тот, который удобнее всего записывается.

Можно ли представить четырёхмерное пространство и гиперкуб?

Этот вопрос сродни вопросу: «можно ли представить Тайную
Вечерю, посмотрев на
одноимённую картину
(1495-1498)
Леонардо да Винчи (1452-1519)?»

С одной стороны, вы конечно не представите то, что видел Иисус (он сидит
лицом к зрителю), тем более вы не почувствуете запаха сада за окном
и вкуса еды на столе, не услышите пения птиц…
Вы не получите полного представления о
происходившем в тот вечер, но нельзя сказать, что вы
не узнаете ничего нового и что картина не представляет никакого
интереса.

Аналогичная ситуация и с вопросом о гиперкубе.
Полностью представить его нельзя, но можно приблизиться к
пониманию, каков он.

7ми мерное пространство и почему только 7ми?

Как нам представить 5ти мерное пространство? Но мы же уже сказали, что на самом деле пространство — это то, что его задает — базис. То есть давайте теперь мыслить о пространстве, как о наборе параметров каждой его точки. Например для трехмерного объекта мы помним 3 координаты в пространстве — по x, y, z. И у нас это не вызывает диссонанса.

Давайте к координатам припишем еще и время, в которое у нас наблюдалась данное расположение тел. Например, у нас катится шар и мы следим за положением его центра. В момент времени 0 шар покоился. В 0,0…01 он уже сместился. В момент времени 9…9,0 он уже находится в совершенно другом месте. Но зачем нам так думать? Пусть эта точка шара существует одновременно везде, где проехался шар, только мы будем помнить, что в каждой точке мы еще приписываем время, когда шар был именно в данной позиции. Вот Вам и 4х мерное пространство — не сложно.

Казалось, так можно навесить еще какие-то параметры, такие как скорость ветра, влажность воздуха, сила трения и так далее, но давайте не будем извращаться и перейдем к более жизненному понятию.

Допустим у нас есть разные гаечки (прошу прощения, если я ошибусь в параметрах или названиях, я совсем не инженер). Для удобной фасовки и продажи гаек надо распределить их на группы одинаковых. Но как мы будем их отличать? Давайте запишем какой-то набор параметров (не претендующий на правильность):

1. Сплав метала гайки

2. Внутреннее сечение гайки

3. Внешняя форма гайки

4. Направление резьбы гайки

5. Максимальная нагрузка на гайку

6. Самозажимающаяся ли гайка?

7. Максимальная температура, при которой гайка выдерживает достаточную нагрузку

8. …

Понятно, что таких параметров может быть сколь угодно много. Но мы остановимся на 7ми — именно столько заявлено в заголовке статьи

Важно помнить! каждый параметр обязан быть независим от любого предыдущего. В нашем случае это условие выполняется: направление резьбы никак не зависит от сплава метала или от внутреннего сечения гайки..

И так с каждым из параметров.

То есть только что мы создали свой, очень странный базис, где элементами нашего пространства выступают гайки, и мы их можем удобно расфасовать. Это и есть элементарное представление нашего 7ми и не только 7ми, но и большего, пространства.

Вычисление нормальных векторов для плоскостей

Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.

Другими словами, нормаль — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.

Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).

Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:

Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A₁, B и C₁, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;

Аналогично, для точек B = (1; 0; 0) и C₁ = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;

Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.

Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).

В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A₁ и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;

Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;

Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).

Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.

Система координат[править]

Поскольку достаточно трудно работать с многомерными объектами, используя интуитивные представления трёхмерного мира, в N-мерной геометрии широко применяются аналитические методы. В качестве системы координат чаще всего используется прямоугольная декартова система с числом осей более трёх. Таким образом, некоторая точка А представляется в N-мерной геометрии как набор из N действительных чисел

A=(x1A,x2A,x3A, … xNA).{\displaystyle A=\left(x_{1A},x_{2A},x_{3A},~…~x_{NA}\right).}

Несмотря на то, что интуитивно трудно представить себе четыре взаимно перпендикулярные оси, понятие перпендикулярности естественным образом обобщается из трёхмерного пространства на случай четырёх и более измерений. Так, скалярное произведение взаимно перпендикулярных векторов в случае N измерений также равно нулю.

Проекции

На двумерное пространство

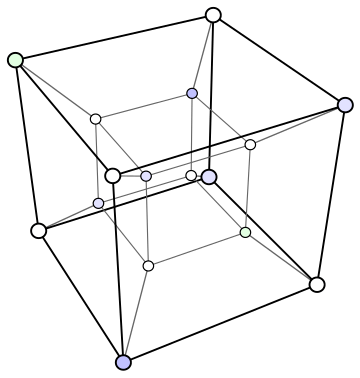
Данная структура сложна для воображения, но возможно спроектировать тессеракт в двумерные или трёхмерные пространства . Кроме того, проектирование на плоскость позволяет легко понять расположение вершин гиперкуба. Таким образом, можно получить изображения, которые больше не отражают пространственные отношения в пределах тессеракта, но которые иллюстрируют структуру связи вершин, как в следующих примерах:

Третья картинка демонстрирует тессеракт в изометрии , относительно точки построения. Это представление представляет интерес при использовании тессеракта как основания для топологической сети, чтобы связать многократные процессоры в параллельных вычислениях.

На трёхмерное пространство

Одна из проекций тессеракта на трёхмерное пространство представляет собой два вложенных трёхмерных куба, соответствующие вершины которых соединены между собой отрезками. Внутренний и внешний кубы имеют разные размеры в трёхмерном пространстве, но в четырёхмерном пространстве это равные кубы. Для понимания равности всех кубов тессеракта была создана вращающаяся модель тессеракта.

Шесть усечённых пирамид по краям тессеракта — это изображения равных шести кубов. Однако эти кубы для тессеракта — как квадраты (грани) для куба. Но на самом деле тессеракт можно разделить на бесконечное количество кубов, как куб — на бесконечное количество квадратов, или квадрат — на бесконечное число отрезков.

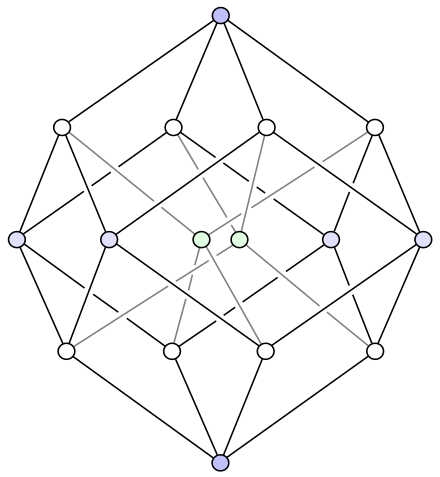
Ещё одна интересная проекция тессеракта на трёхмерное пространство представляет собой ромбододекаэдр с проведёнными четырьмя его диагоналями, соединяющими пары противоположных вершин при больших углах ромбов. При этом 14 из 16 вершин тессеракта проецируются в 14 вершин ромбододекаэдра , а проекции 2 оставшихся совпадают в его центре. В такой проекции на трёхмерное пространство сохраняются равенство и параллельность всех одномерных, двухмерных и трёхмерных сторон.

Стереопара

Стереопара тессеракта изображается как две проекции на трёхмерное пространство. Такое изображение тессеракта разрабатывалось с целью представить глубину, как четвёртое измерение. Стереопара рассматривается так, чтобы каждый глаз видел только одно из этих изображений, возникает стереоскопическая картина, воспроизводящая глубину тессеракта.

Развёртка тессеракта

Поверхность тессеракта может быть развёрнута в восемь кубов (аналогично тому, как поверхность куба может быть развёрнута в шесть квадратов). Существует 261 различная развёртка тессеракта . Развёртки тессеракта могут быть подсчитаны нанесением на граф соединённых углов.