Презентация урока математики в 6 классе по теме координатная плоскость итоговый урок доклад, проект

Разложение вектора

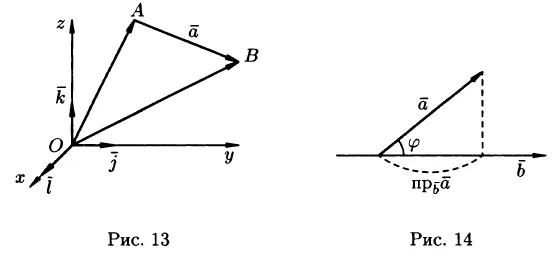
с векторами координатi → и j →в плоскостиМы выводим любой вектор a → из начала координат. Согласно геометрическому определению операций над векторами, вектор a → можно представить в виде a → = a x — i → + a y — j →, где коэффициентами являютсяКоэффициенты a x и a yназываются координатами вектора в соответствующей системе координат на плоскости.

Принято записывать координаты вектора в этой системе координат в скобках через запятую, при этом указанные координаты отделяются от векторного обозначения знаком равенства

Например, обозначение a → = ( 2 ; — 3 ) означает, что вектор a → в данной системе координат имеет координаты ( 2 ; — 3 ) и может быть представлен как продолжение координатных векторов i → и j → в виде a → = 2 — i → — 3 — j →.Обратите внимание, что порядок записи координат важен. Для прямоугольной системы координат в трехмерном пространстве все точки, упомянутые выше, могут быть определены аналогичным образом

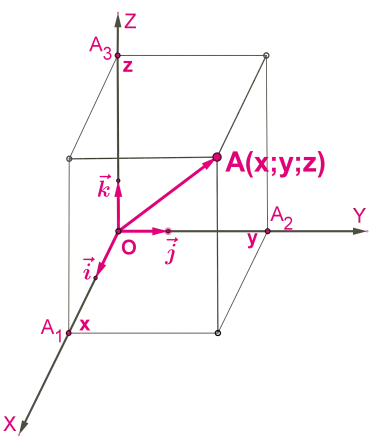
В этой системе координат есть три координатных вектора i →, j →, k →, и любой вектор a → расширяется не по двум, а по трем координатам и имеет вид a → = a x — i → + a y — j → + a z — k →, а коэффициенты этого расширения ( a x ; a y ; a z ) называются

Для прямоугольной системы координат в трехмерном пространстве все точки, упомянутые выше, могут быть определены аналогичным образом. В этой системе координат есть три координатных вектора i →, j →, k →, и любой вектор a → расширяется не по двум, а по трем координатам и имеет вид a → = a x — i → + a y — j → + a z — k →, а коэффициенты этого расширения ( a x ; a y ; a z ) называются

координаты вектора в заданной (трехмерной) системе координат.

Поэтому векторы координат в трехмерном пространстве также принимают значение 1 и имеют координаты i → = ( 1 ; 0 ; 0 ; 0 ), j → = ( 0 ; 1 ; 0 ), k → = ( 0 ; 0 ; 1 ), координаты нулевого вектора также нулевые 0 → = ( 0 ; 0 ; 1 ), координаты нулевого вектора также нулевые 0 → = ( 0 ; 0, 0, 0 ), и в этом случае два вектора считаются равными, если все три соответствующие координаты вектора между ними равны a → = b → ⇔ a x = b x, a y = b y, a z = b z, а координаты противоположного вектора a → противоположны соответствующим координатам вектора a →, т.е. т.е. — a → = ( — a x ; — a y ; — a z ) .

Из уроков алгебры мы знаем прямоугольную систему координат. Она имеет оси O и O, и каждая точка, отмеченная на плоскости, имеет свои координаты:

Признак коллинеарности векторов

Напомним, что если два вектора (назовем их a и b) коллинеарны, то обязательно существует число k такое, что

Из равенства (1) и правила умножения вектора на число, описанного выше, вытекают два соотношения между этими координатами:

Если числа x₂и y₂не равны нулю, то из каждого уравнения можно выразить число k, тогда выражения можно приравнять:

Получаем соотношение, которое можно считать свойством коллинеарных векторов. Это правило работает и в обратном направлении — если координаты векторов удовлетворяют производной, то можно смело утверждать, что векторы слиплись.

Примечание. Фраза «тогда и только тогда» означает, что правило работает в обе стороны — из пропорциональности координат следует конгруэнтность векторов, а из конгруэнтности векторов следует пропорциональность координат.

Мы покажем, как использовать этот символ для коллинеарности векторов. Предположим, что вектор a имеет координаты, а вектор b имеет координаты. Нам нужно определить, являются ли они коллинеарными. Для этого мы делим координаты x друг на друга:

Получаем число 3. Затем также делим координату y:

Снова получаем 3. Тот факт, что в обоих случаях мы получаем одно и то же число, говорит о том, что векторы коллинеарны. Кроме того, мы можем написать, что вектор b в три раза больше a:

В данном примере мы разделили координаты второго вектора b на координаты первого вектора a. Но можно разделить координаты a на координаты b и наоборот:

Конечно, мы все равно получим то же число.

Особый случай — когда одна из координат вектора равна нулю. Например, предположим, что вектор имеет координаты 1>и y₁≠ 0. Любой вектор, прилипший к нему, может быть определен умножением вектора на число k. В этом случае координаты 2; у₂>являются:

Оказывается, что координата x коллинеарного вектора также обязательно равна нулю. Координаты y, в свою очередь₂и y₁может быть произвольным, так как мы всегда можем найти число k, для которого выполняется условие

Например, если у нас есть вектор с, то можно сказать, что он коллинеарен с любым вектором, первая координата которого также равна нулю,

Но любой вектор, чья x-координата НЕ равна нулю, НЕ коллинеарен с. В частности, он не является коллинеарным с вектором:

Та же логика применима, если не x-координата, а y-координата равна нулю.

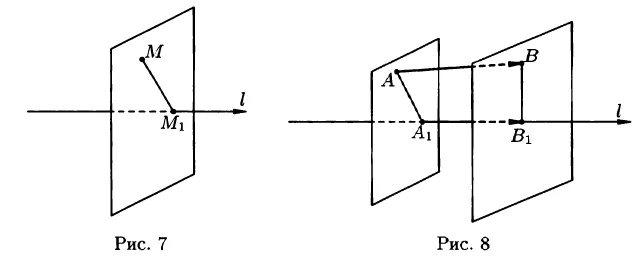
Если обе координаты вектора равны нулю, то это нулевой вектор, т.е. точка. Следует помнить, что такой вектор коллинеарен с любым другим вектором.

Задание. Определите, являются ли два вектора коллинеарными, если их координаты равны:

Уравнения прямой и плоскости

Вспомните, как вас знакомили с системой координат и объясняли, что положение каждой точки в системе координат можно определять координатами х и у. Это точки M(x_m; y_m) и N(x_n; y_n)

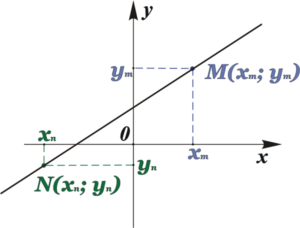Как известно, прямую можно провести через две точки, и при том, только одну. Задача по определению уравнения прямой на плоскости, проходящей через две точки, координаты которых известны, решалась очень просто. В этом случае в уравнение прямой y=kx+b подставляли сначала координаты точки М, затем – точки N.

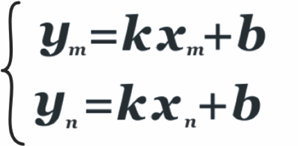
Получали систему двух линейных уравнений относительно неизвестных коэффициентов k и b, которые находили при решении этой системы.

Но уравнение прямой на плоскости можно задать и по-другому:

Ax + By + C = 0, (A² + B² ≠ 0)

И суть от этого не изменится, изменятся только коэффициенты. Условие в скобках означает, что А и В не могут быть равны нулю одновременно.

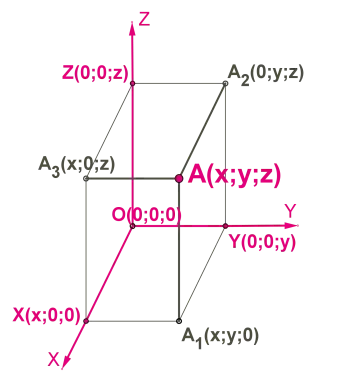
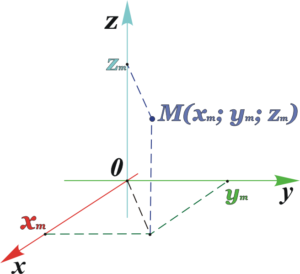Стереометрия рассматривает фигуры в пространстве, где каждая точка описывается уже тремя координатами – (x, y, z).

Уравнение прямой в пространстве задается через направляющий вектор. Но это уже не входит в рамки программы средней школы, поэтому просто принимаем к сведению.

Если известны две точки пространства M( x_m ; y_m ; z_m ) и N( x_n ; y_n ; z_n ) , то уравнения прямой, проходящей через данные точки, выражаются формулами:

Но вот что мы с вами можем, так это воспользоваться вектором этой прямой, который будет определяться расстоянием между точками в пространстве. И об этом подробно поговорим в следующем разделе —

Привязка фигур к системе координат позволяет не только определять координаты точек, но и записать уравнение плоскости. Как известно, на трех точках можно построить плоскость, притом, только одну. Соответственно, можно и записать плоскость уравнением. Выглядит это уравнение следующим образом:

Ax + By + Cz + D = 0

Очень похоже на вторую запись уравнения прямой на плоскости. Значит, и коэффициенты А, В, С и D мы будем находить также, как и коэффициенты для прямой на плоскости, по точкам.

Это действие сродни тому, что вы производили, определяя уравнение прямой, проходящей через две точки, заданные координатами.

Прямую можно провести через две точки, и мы составляли два уравнения для двух точек.

Плоскость можно провести через три точки, значит, и уравнений будет три!

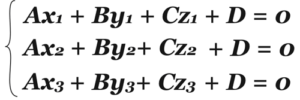
Но уравнений три, а неизвестных – четыре! Ну, и что! Мы же можем разделить все уравнения на D, при этом они не изменятся, будут равнозначны первоначальным! Так и будем поступать! Тогда вместо D будет единица, а все остальные коэффициенты будут делиться на D, назовем их также, А, В, С. И это уже вполне решаемая система!

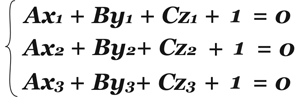
Здесь значения всех x, y и z известны, это координаты точек, принадлежащих данной плоскости.

Итак, точку описать можем, прямую описать можем, плоскость – можем. Осталось вспомнить сами векторы и их координаты, они нам тоже пригодятся при решении задач.

Полиморфизм

Кварцкристаллическихкремнеземаα-кварцβ-кварцтридимиткристобалиткоэсит и стишовит

Полиморфизм — это наличие нескольких кристаллических форм материала. Он во многих кристаллических материалах, включая полимеры, минералы и металлы. Согласно правилам фазового равновесия Гиббса, эти уникальные кристаллические характеристики зависят от интенсивных чисел, как давление и температура. Полиморфизм связан с аллотропией, которая относится к элементарным твердым веществам. Полная морфология материала описывается полиморфизмом и другими переменными, такими как габитус кристалла, аморфная фракция или кристаллографические дефекты. Полиморфы обладают разной стабильностью и могут спонтанно и необратимо преобразовываться из метастабильной формы (или термодинамически нестабильной формы) в стабильную форму при определенной температуре. Они также демонстрируют различные точки плавления, растворимости и картины дифракции рентгеновских лучей.

Одним из хороших примеров этого является кварцевая форма диоксида кремния или SiO 2. В подавляющем большинстве силикатов атом Si имеет тетраэдрическую координацию с помощью 4 атомов кислорода. Все кристаллические формы, кроме одной, включают тетраэдрические звенья {SiO 4 }, связанные вместе общими вершинами в различных положениях. В разных минералах тетраэдры демонстрируют разную степень сетки и полимеризации. Например, они встречаются поодиночке, соединены вместе парами, в более крупные конечные кластеры, включая кольца, цепочки, двойные цепи, листы и трехмерные каркасы. Минералы классифицируются на группы на основе этих структур. В каждой из 7 термодинамически стабильных кристаллических форм или полиморфов кристаллического кварца только 2 из 4 ребер тетраэдров {SiO 4 } являются общими с другими, что дает чистую химическую формулу кремнезема: SiO 2.

Другим примером является элементарное олово (Sn), которое является пластичным при температурах окружающей среды, но хрупким при охлаждении. Это изменение механических свойств связано с существованием двух основных аллотропов, α- и β-олова. Два аллотропа, которые встречаются при нормальном давлении и температуре, α-олово и β-олово, более широко известны как серое олово и белое олово соответственно. Еще два аллотропа, γ и σ, существуют при температурах выше 161 ° C и давлениях выше нескольких ГПа. Белое олово является металлическим и представляет собой стабильную кристаллическую форму при комнатной температуре или выше. Ниже 13,2 ° C олово существует в серой форме, которая имеет кристаллическую структуру кубической алмаза, аналогичную алмазу, кремнию или германию . Серое олово вообще не имеет металлических свойств, представляет собой тускло-серый порошкообразный материал и имеет несколько применений, кроме нескольких специализированных полупроводников. Хотя температура α – β превращения олова номинально составляет 13,2 ° C, примеси (например, Al, Zn и т. Д.) Понижают температуру перехода значительно ниже 0 ° C, и при добавлении Sb или Bi превращение может не происходить вообще..

Физические свойства

Двадцать из 32 классов кристаллов являются пьезоэлектрическими, и кристаллы, принадлежащие к одному из этих классов (точечные группы), демонстрируют пьезоэлектричество. Все классы пьезоэлектрических элементов не имеют инверсионной симметрии. Любой материал развивает диэлектрическую поляризацию при использовании электрического поля, но вещество, которое такое естественное разделение зарядов даже в отсутствие поля, называется полярным материалом. Полярность материала исключительно его кристаллической структурой. Только 10 из 32 групп точек являются полярными. Все полярные кристаллы являются пироэлектрическими, поэтому 10 классов полярных кристаллов иногда называют пироэлектрическими классами.

Есть несколько кристаллических структур, особенно структура перовскита, которые демонстрируют поведение сегнетоэлектрического. Это аналогично ферромагнетизму в том, что в отсутствие электрического поля во время производства сегнетоэлектрический кристалл не проявляет поляризации. При приложении электрического поля достаточной величины кристалл становится постоянно поляризованным. Эта поляризация может быть обращена достаточно большим противодействием, так же, как ферромагнетик может быть обращен. Однако, хотя они и называются сегнетоэлектриками, эффект обусловлен кристаллической структурой (а не наличием черного металла).

Согласование параметров решётки

Параметры решётки важны при эпитаксиальном выращивании тонких монокристаллических слоёв другого материала на поверхности иного монокристалла — подложки. При значительной разнице параметров решётки материалов трудно получить монокристалличность и бездислокационность наращиваемого слоя. Например, в полупроводниковой технологии для выращивания эпитаксиальных слоёв монокристаллического кремния в качестве гетероподложки обычно используют сапфир (монокристалл оксида алюминия), так как оба имеют практически равные постоянные решётки, но с разным типом сингонии, у кремния — кубическая типа алмаза , у сапфира — тригональная .

Обыкновенно параметры решётки подложки и наращиваемого слоя выбирают так, чтобы обеспечить минимум напряжений в слое плёнки.

Другим способом согласования параметров решёток является метод формирования переходного слоя между плёнкой и подложкой, в котором параметр решётки изменяется плавно (например, через слой твёрдого раствора с постепенным замещением атомов вещества подложки атомами выращиваемой плёнки, так чтобы параметр решётки слоя твёрдого раствора у самой плёнки совпадал с этим параметром плёнки).

Например, слой фосфида индия-галлия с шириной запрещённой зоны 1,9 эВ
может быть выращен на пластине арсенида галлия с помощью метода промежуточного слоя.

Объём элементарной ячейки

Объём элементарной ячейки можно вычислить, зная её параметры (длины и углы параллелепипеда). Если три смежных рёбра ячейки представить в виде векторов, то объём ячейки V

равен (с точностью до знака) тройному скалярному произведению этих векторов (т.е. скалярному произведению одного из векторов на векторное произведение двух других). В общем случае

V
=
a
b
c
1
+
2
cos
⁡
α
cos
⁡
β
cos
⁡
γ
−
cos
2
⁡
α
−
cos
2
⁡
β
−
cos
2
⁡
γ
.
{\displaystyle V=abc{\sqrt {1+2\cos \alpha \cos \beta \cos \gamma -\cos ^{2}\alpha -\cos ^{2}\beta -\cos ^{2}\gamma }}.}

Для моноклинных решёток α = γ = 90°
, и формула упрощается до

V
=
a
b
c
sin
⁡
β
.
{\displaystyle V=abc\sin \beta .}

Для орторомбических, тетрагональных и кубических решёток угол β
также равен 90°, поэтому

V
=
a
b
c
.
{\displaystyle V=abc.}

Общее понятие о металлах

«Химия. 9 класс» — это учебник, по которому проходят обучение школьники. Именно в нем подробно изучаются металлы. Рассмотрению их физических и химических свойств отведена большая глава, ведь разнообразие их чрезвычайно велико.

Именно с этого возраста рекомендуют давать детям представление о данных атомах и их свойствах, ведь подростки уже вполне могут оценить значение подобных знаний. Они прекрасно видят, что окружающее их разнообразие предметов, машин и прочих вещей имеет в своей основе как раз металлическую природу.

Что же такое металл? С точки зрения химии, к данным атомам принято относить те, что имеют:

малое на внешнем уровне;
проявляют сильные восстановительные свойства;
имеют большой атомный радиус;
как простые вещества обладают рядом специфических физических свойств.

Основу знаний об этих веществах можно получить, если рассмотреть атомно-кристаллическое строение металлов. Именно оно объясняет все особенности и свойства данных соединений.

В периодической системе для металлов отводится большая часть всей таблицы, ведь они образуют все побочные подгруппы и главные с первой по третью группу. Поэтому их численное превосходство очевидно. Самыми распространенными являются:

кальций;
натрий;
титан;
железо;
магний;
алюминий;
калий.

Все металлы имеют ряд свойств, которые позволяют объединять их в одну большую группу веществ. В свою очередь, эти свойства объясняет именно кристаллическое строение металлов.

Дефекты и

Настоящие кристаллы особенности дефекты или неровности в идеальных конструкциях, описанных выше, и именно эти дефекты критически определяют электрические и механические свойства реальных материалов. Когда один атом заменяет один из основных атомных компонентов в кристаллической структуре, могут произойти изменения электрические и тепловые свойства материала. Примеси также могут проявляться как примеси со спином электронов в некоторых материалах. Исследования магнитных примесей показывают, что может влиять небольшое количество примеси, например, примеси в полупроводниковых ферромагнитных сплавах могут приводить к другим свойствам. как впервые было предсказано в конце 1960-х. Дислокации в кристаллической решетке допускают сдвиг при меньшем напряжении, чем это необходимо для идеальной кристаллической структуры.

Координация элементов

Настоящее расположение относительно друг друга, их координационные числа (или количество ближайших соседей), межатомные расстояния, типы связей и т. Д., Можно определить образуют общий вид и альтернативные способы их визуализации.

Плотная упаковка

Используемые принципы можно понять, рассмотрев наиболее эффективный способ упаковки сфер одинакового размера и укладки плотно упакованных атомных плоскостей в трех измеренийх. Например, если плоскость лежит ниже плоскости B, есть два способа размещения другого слоя B. Если дополнительный слой был помещен непосредственно над плоскостью A, это привело к следующей серии:

… ABABABAB …

известно такое расположение элементов в однако кристаллической структуре как гексагональная плотная упаковка (ГПУ) .

Если, все три плоскости смещены относительно друг друга, и только после того, как четвертый слой будет расположен непосредственно над плоскостью A, последовательность будет повторяться, возникает следующая последовательность:

… ABCABCABC …

Этот тип структурной организации известна как кубическая плотная упаковка (ccp) .

Элементарная ячейка ccp-элементов — это гранецентрированная кубическая (ГЦК) элементарная ячейка. Это не сразу, поскольку плотно упакованные слои параллельны плоскостям {111} элементарной ГЦК-ячейки. Есть четыре разных ориентации плотноупакованных слоев.

Эффективность упаковки может быть вычислена путем вычисления сфер и деления на объемах следующим образом:

4 × 4 3 π r 3 16 2 р 3 = π 3 2 = 0, 7405… {\ displaystyle {\ frac {4 \ times {\ frac {4} {3}} \ pi r ^ {3}} {16 {\ sqrt {2}} r ^ {3}}} = {\ frac {\ pi} {3 {\ sqrt {2}}}} = 0,7405…}

Эффективность упаковки 74% — это максимальная плотность, возможная в элементарных ячейках, построенных из сфер только один размер. Большинство кристаллических форм металлических элементов — это ГПУ, ГЦК или ОЦК (объемно-центрированная кубическая). Координационное число элементов в ГПУ- и ГЦК-структурах равно 12, а его фактор упаковки элементов (APF) — это число, указанное выше, 0,74. Это можно сравнить с НПФ ОЦК-структуры, которое составляет 0,68.

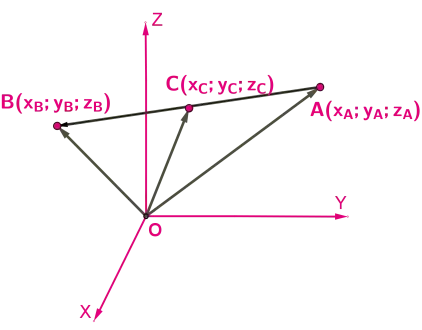
Сложение и вычитание векторов

Предположим, что у нас есть векторы a 1; у₁>Предположим, у нас есть векторы a и b 2; у₂>. Зная только их координаты, можете ли вы определить их сумму и разность? Оказывается, можно. Согласно определению координат вектора (мы помним, что это коэффициенты разложения вектора по оригиналам), мы действительно можем написать:

Это обозначение означает, что c имеет координаты 1+ х₂; у₁+ у₂>. В результате мы можем сформулировать правило сложения векторов:

Поясним это правило на примере. Добавим векторы a и b. Понятно, что в результате получается новый вектор, который мы обозначим через c. Чтобы найти его первую координату, мы складываем первые координаты векторов a и b :

Чтобы найти его вторую координату, мы складываем вторые координаты соответствующих векторов:

В результате получается вектор с .

Задача. Добавьте векторы, имеющие координаты:

Решение. Сначала просто сложите простые числа в скобках (и получите координату x ), затем сложите вторые числа (и получите координату y ):

Теперь давайте попробуем понять, как вычисляется разница между двумя векторами. Предположим, что у нас есть векторы с заданными координатами a 1; у₁>Предположим, у нас есть векторы a и b 2; у₂>. Давайте снова запишем их эволюцию в единичных векторах:

Теперь мы можем сформулировать правило для вычитания векторов:

Например, вычтем вектор b из вектора a. Искомая разность — это вектор, координата x которого равна разности простых координат векторов a и b:

Аналогично вычисляем координату y:

В результате мы имеем вектор с координатами .

Задача. Вычтите вектор b из вектора a, если их координаты известны:

Решение. Во всех случаях сначала вычтите первую координату вектора a из первой координаты вектора b, чтобы получить координату x искомого вектора. Затем повторите операцию со второй координатой (т.е. y):

Теперь рассмотрим такую операцию, как умножение вектора на число. Опять же, вектор a с координатами x₁и y₁можно разложить на коэффициенты следующим образом:

Прогнозирование структуры

Трудность предсказания стабильных кристаллических структур на основе химического состава долгое время. Теперь, благодаря более мощным алгоритмам и высокопроизводительным вычислениям, структуры средней сложности могут быть использованы с использованием таких подходов, как эволюционные алгоритмы, случайная выборка или метадинамика.

Кристаллические структуры простых ионных твердых веществ (например, NaCl или поваренная соль) уже давно рационализированы в терминах правил Полинга, впервые изложенных в 1929 году Линусом Полингом, которого многие многие с тех пор называют «отцом химической связи». Полинг также рассмотрел природу межатомных сил в металлах и пришел к выводу, что примерно половина из пяти d-орбиталей в переходных металлах участвует в связывании, оставшиеся несвязывающие d-орбитали ответственны за магнитные свойства. Таким образом, он смог соотнести количество d-орбиталей в образовании связи с длиной связи, а также многими физическими свойствами вещества. Впечатляющий резонанс валентных связей между различными электронными структурами. Впечатляющий резонанс валентных связей между различными электронными структурами.

В теории резонансных валентных связей факторы определяющие выбор альтернативных кристаллических структур металла или интерметаллического соединения вращаются вокруг энергии резонанса связей между межатомными положениями. Ясно, что некоторые режимы резонанса будут давать больший вклад (будут более механически устойчивыми, чем другие), и что, в частности, простое соотношение количества связей к количеству позиций будет исключительным. Результирующий принцип заключается в том, что особая стабильность связана с простейшими отношениями или «числами облигаций»: ⁄ 2, ⁄ 3, ⁄ 3, ⁄ 4, ⁄ 4 и т. Д. Таким образом, выбор структуры и значения отношения осей (определяет относительную длину скрепления) результат попытки атома использовать свою валентность для образования стабильных связей с простыми дробными числами связей.

Постулировав прямую корреляцию между концентрацией электронов и кристаллической структурой в сплаве с бета-фазой, Хьюм -Ротери проанализировал тенденции в температурех плавления, сжимаемости и длине связей в зависимости от номера группы в периодической таблице, чтобы установить систему валентностей переходных элементов в металлическом состоянии. Таким образом, эта обработка подчеркивания прочности сцепления в зависимости от номера группы. Действие подчеркивается в одной статье о связи между гибридами связей и металлическими структурами. Результирующая корреляция между электронной и кристаллической структурой резюмируется одним параметром, весом d-электронов на гибридизованную металлическую орбиталь. «D-вес» составляет 0,5, 0,7 и 0,9 для структур ГЦК, ГПУ и ОЦК соответственно. Таким образом, становится очевидной взаимосвязь между d-электронами и кристаллической структурой.

При прогнозировании / моделировании кристаллической структуры обычно используется периодичность, благодаря системе неограниченно большой во всех направлениях. Предложите дополнительные свойства симметрии, применительно к элементарной ячейке и недавно разработанное динамическое уравнение для векторов периодов системы (параметры решетки, включая углы). нагрузкам.

Источники

Большая советская энциклопедия
Физическая энциклопедия под. ред. А. М. Прохорова. Москва. Научное издательство «Большая российская энциклопедия», 1992 г. Т.3, стр.637.

Wikimedia Foundation . 2010 .

Смотреть что такое «Плотность» в других словарях:

ПЛОТНОСТЬ — ПЛОТНОСТЬ, плотности, жен. 1. только ед. отвлеч. сущ. к плотный. Плотность населения. Плотность ткани. Плотность воздуха. Плотность огня (воен.). 2. Масса какого нибудь тела, заключенная в единице его объема (физ.). За единицу плотности… … Толковый словарь Ушакова

ПЛОТНОСТЬ — (r), масса единицы объема вещества. В СИ единица плотности 1 кг/м3. Отношение плотностей двух веществ называется относительной плотностью (обычно плотность веществ определяют относительно плотности дистиллированной воды). Малой плотностью… … Современная энциклопедия

ПЛОТНОСТЬ — (обозначение r) отношение массы к объему для данного вещества, обычно выражаемое в единицах СИ как килограммы на кубический метр (кг/м 1). Эта величина является показателем концентрации частиц в материале. Плотность твердого или жидкого вещества… … Научно-технический энциклопедический словарь

плотность — густота, концентрация; массивность, тесность, коренастость, тучность, насыщенность, кряжистость, компактность, уплотненность, кучность Словарь русских синонимов. плотность компактность Словарь синонимов русского языка. Практический справочник. М … Словарь синонимов

плотность — (density) – это отношение массы тела к его объему. Выражается в кг/дм3 или в кг/м3. Объем зависит от температуры (в большой степени) и давления (в небольшой степени), следовательно, вязкость тоже зависит от этих параметров. С ростом температуры и … Автомобильный словарь

Плотность — (r), масса единицы объема вещества. В СИ единица плотности 1 кг/м3. Отношение плотностей двух веществ называется относительной плотностью (обычно плотность веществ определяют относительно плотности дистиллированной воды). Малой плотностью… … Иллюстрированный энциклопедический словарь

Плотность — – характеристика вещества, определяемая отношением массы вещества, заключенной в некотором объеме, к величине этого объема. Плотность – масса единичного объема … Энциклопедия терминов, определений и пояснений строительных материалов

ПЛОТНОСТЬ — (1) вещества (объёмная) одна из основных физ. характеристик вещества, в нормальных условиях численно равная отношению массы т однородного тела к его объёму V, обозначается р. В СИ выражается в кг/м3. П. вещества растёт с увеличением давления и,… … Большая политехническая энциклопедия

ПЛОТНОСТЬ — (?) масса единичного объема вещества. Величина, обратная удельному объему. Отношение плотности двух веществ называют относительной плотностью (обычно плотность веществ определяют относительно плотности дистиллированной воды) … Большой Энциклопедический словарь

ПЛОТНОСТЬ — (r), величина, определяемая для однородного в ва его массой в единице объёма. П. неоднородного в ва в определённой точке предел отношения массы т тела к его объёму V, когда объём стягивается к этой точке. Средняя П. неоднородного тела также есть… … Физическая энциклопедия

ПЛОТНОСТЬ — (Density) масса данного тела, заключенная в единице объема. За единицу плотности принимается плотность воды при 4° Цельсия. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 … Морской словарь