Состав и свойства природных газов

Физика 7 класс. Давление газа и жидкости. Закон Паскаля.

Физика 7 класс. Конспект. Давление газаДавление газа. Передача давления жидкостями и газами. Закон Паскаля. Расчет давления жидкости.

Задачи на тему Давление

Газы, в отличие от твердых тел и жидкостей, заполняют весь сосуд, в котором находятся.

Газ, находясь в каком-либо сосуде, оказывает давление на стенки, дно и крышку тела, в котором находится. Молекулы газа беспорядочно движутся, сталкиваясь друг с другом и со стенками сосуда, внутри которого находятся. Давление газа на стенки сосуда (и на помещенное в газ тело) вызывается ударами молекул газа.

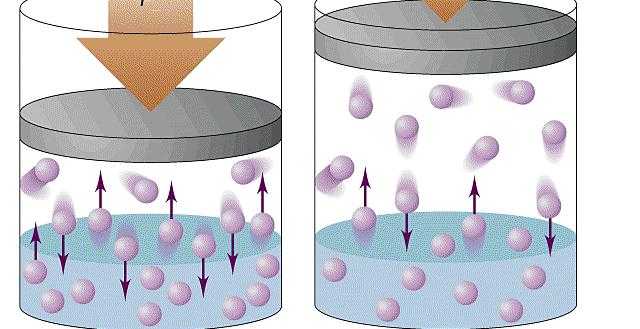
При уменьшении объема газа его давление увеличивается, а при увеличении объема давление уменьшается при условии, что масса и температура газа остаются неизменными.

Давление газа в закрытом сосуде тем больше, чем выше температура газа, при условии, что масса газа и объем не изменяются.

Из опытов получен общий вывод, что давление газа тем больше, чем чаще и сильнее молекулы ударяют о стенки сосуда.

Закон Паскаля:

Давление, производимое на жидкость или газ, передается в любую точку без изменений во всех направлениях.

Опыт иллюстрирует закон Паскаля

Свойство газов передавать давление используют в технике при устройстве различных пневматических машин и инструментов.

На жидкости, как и на все тела на Земле, действует сила тяжести. Поэтому каждый слой жидкости, налитой в сосуд, своим весом создает давление на другие слои, которое по закону Паскаля передается по всем направлениям. Следовательно, внутри жидкости существует давление.

Опыты подтверждают, что внутри жидкости существует давление и на одном и том же уровне оно одинаково по всем направлениям. С глубиной давление увеличивается.

Давление жидкости на дно и стенки сосуда зависит только от плотности и высоты столба жидкости.

Расчет давления жидкости на дно и стенки сосуда:

где p – давление (Па), ρ – плотность жидкости (кг/м3), h– высота столб жидкости (м), g– ускорение свободного падения (Н/кг).

Сосуды, соединенные между собой (например, чайник, лейка и т.п.), называют сообщающимися.

В сообщающихся сосудах любой формы и сечения поверхности однородной жидкости устанавливаются на одном уровне (при условии, что давление воздуха над жидкостью одинаково).

При равенстве давлений высота столба жидкости с большей плотностью будет меньше высоты столба с меньшей плотностью.

Конспект составлен на основании теоретического материала учебника «Физика 7 класс» А.В. Перышкин

Задачи

Атмосферное давление

Скачать конспект:

teoriya_7_davleniegaza

Для выпуска расплавленного металла из литейного ковша делают на дне ковша отверстие, закрываемое спе…

Почему футбольные и баскетбольные мячи помещают в прочные кожаные чехлы?

Поршневой насос может произвести давление 5·10 5 Па. На какую высоту можно поднять воду этим насосом…

При сжатии поршнем кислорода в закрытом сосуде изменяется ли: а) Масса кислорода; б) объем кислорода…

Формула давления газа идеального из молекулярно-кинетической теории

При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.

Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.

Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:

Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.

Давление газа — что это за параметр

Определение

Давление в физике представляет собой один из трех ключевых термодинамических макроскопических характеристик для измерения любой газовой системы.

Определение

Газ — это одно из четырех, включая плазму, агрегатных состояний материи, характеризующееся очень слабыми связями между составляющими его частицами, а также их большой подвижностью.

В газообразной среде частицы в определенной концентрации расположены не упорядоченно и перемещаются в хаотичном порядке в разных направлениях с одинаковой вероятностью. Подобное строение не позволяет газам сохранять стабильность объема и формы даже при малом внешнем силовом воздействии. Для любого газа, включая одноатомный, значение средней кинетической энергии его частиц в виде атомов и молекул будет превышать энергию межмолекулярного взаимодействия между ними.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Кроме того, расстояние, на которое удалены частицы, значительно превышает их собственные размеры. В том случае, когда молекулярными взаимодействиями и габаритами частиц допускается пренебрегать, газ считают идеальным. Для такой формы материи характерен только один тип внутреннего взаимодействия в виде упругих столкновений. Так как размер частиц пренебрежимо мал по сравнению с расстоянием, на которое они удалены, вероятность столкновений частиц между собой будет низкой.

Примечание

По этой причине в идеальной газовой среде можно наблюдать лишь столкновения частиц со стенками сосуда. Какой-либо реальный газ с хорошей точностью можно отнести к идеальному, когда их температура выше, чем комнатная, а давление несущественно больше, чем атмосферное.

Идеальные газы

Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.

В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.

В идеальном газе существует лишь единственный вид взаимодействия — упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.

Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.

Давление и работа

Пусть сосуд имеет форму цилиндра, в основании которого находится поршень площади $S$.
Молекулы постоянно налетают на поршень, «толкая его».
Поэтому для удержания поршня в неподвижном состоянии к нему необходимо прикладывать
некоторую силу $-F$, которая компенсирует такую же силу $F$ (с противоположным направлением) со стороны газа
(третий закон Ньютона).
На рисунке справа источником внешней силы $-F$ является сжатая пружина.
Когда система приходит в равновесие, давление со стороны газа уравновешивается силой со стороны пружины.
По определению, давление равно отношению силы $F$ со стороны газа,
приложенной к поршню площади $S$:
$$
~~~~~~~~~~~~P = \frac{F}{S}.
$$

Давление газа является его важной характеристикой,
описывающей (наравне с объёмом $V$) равновесное состояние газа. Давление — это положительная, скалярная величина.
Компенсирующая его нормальная (перпендикулярная поверхности) сила одинакова при любых ориентациях поверхности
и в любых точках объёма (см

второй рисунок).

Подчернём, что работа совершается газом только, если молекулы отражаются от поршня неупруго,
теряя при столкновении часть своего импульса.
Когда поршень резко выдвигают, молекулы не теряют своей энергии
и газ работу не совершает.
В качестве примера произведенной работы, рассмотрим цилиндрический сосуд,
в верхнем основании которого находится подвижный тяжёлый поршень массы $M$ и площади $S$.
В равновесии сила давления газа $P\,S$ уравновешивается весом поршня $M\,g$ (на поршень сверху ничего не давит).
Газ можно начать нагревать, в результате чего поршень начнёт подниматься.
Вторая возможность — медленно уменьшать массу поршня, что также приведёт к его поднятию.
В обоих этих случаях газ совершает работу.

При изменении объёма газа может меняться его давление.
Подобная зависимость $P=P(V)$ изображается на декартовой
плоскости $(P,V)$ с координатными осями на которых отложено давление
и объём. Работа, совершаемая газом, равна площади под кривой $P(V)$:
$$
~~~~~~~~A = \int\limits^2_1 P\,dV.
$$
Эта площадь положительна при расширении и отрицательна при сжатии.
В последнем случае стрелка на контуре будет направлена в обратную сторону (интегрирование от $2$ к $1$).

Влажность

Влажность — показатель содержания воды в телах и средах.Абсолютная влажность — физическая величина, показывающая массу водяных паров, содержащихся в 1 м³ воздуха или плотность водяного пара в воздухеОтносительная влажность () — отношение парциального давления паров воды () в газе к давлению насыщенного пара () при данной температуре.

Насыщенный пар — пар находящийся в термодинамическом равновесии с жидкостью или твердым телом (льдом). Другими словами можно сказать что это такое состояние пара, когда количество испарившейся жидкости будет равно количеству конденсированного пара. Если говорить о влажности в таком состоянии она будет равна 100%.

Закон Дальтона Давление смеси газов, химически не взаимодействующих между собой, равно сумме парциальных давлений каждого из компонентов смеси.

Газовые законы

Универсальная газовая постоянная (Дж/(моль К)) — произведение постоянной Больцмана на число Авогадро.Уравнение состояния идеального газа:

Уравнение Менделеева-Клапейрона:

Уравнение Клапейрона:

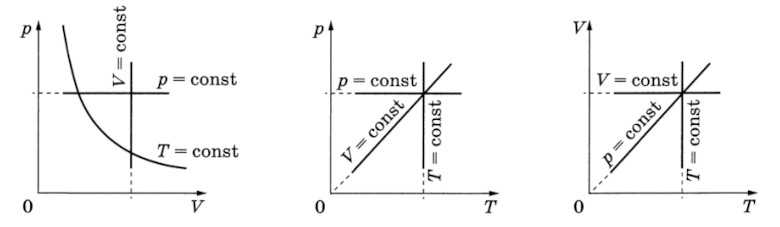
Изотермический процесс — термодинамический процесс, происходящий в физической системе при постоянной температуре.Закон Бойля-Мариотта

Изобарный процесс — термодинамический процесс, происходящий в физической системе при постоянном давлении.Закон Шарля

Изохорный процесс — термодинамический процесс, происходящий в физической системе при постоянном объеме.Закон Гей-Люссака

Причина возникновения давления в газах

Давление газа нельзя объяснить теми же причинами, что и давление твердого тела на опору. Расстояние, на которое удалены молекулы газообразной среды, существенно больше. В результате хаотичного движения они сталкиваются между собой и со стенками сосуда, который они занимают. Давление газа на стенки сосуда и вызвано ударами его молекул.

Данный параметр увеличивается по мере того, как нарастает сила ударов молекул о стенки. Газ характеризуется одинаковым давлением во всех направлениях, которое является следствием хаотичного движения огромного числа молекул.

Примечание

Важно отметить, что газ оказывает давление на дно и стенки сосуда, объем которого он занимает, во всех направления равномерно. В связи с этим, воздушный шарик сохраняет форму, несмотря на то, что его оболочка достаточно эластична

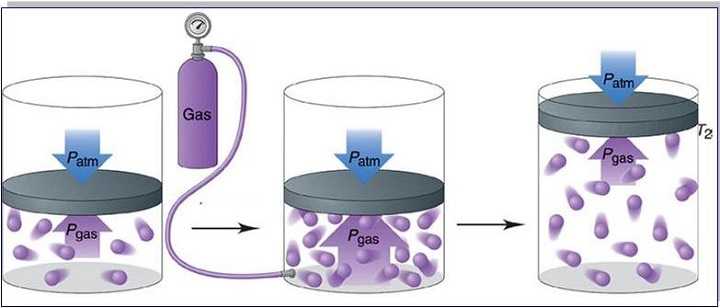
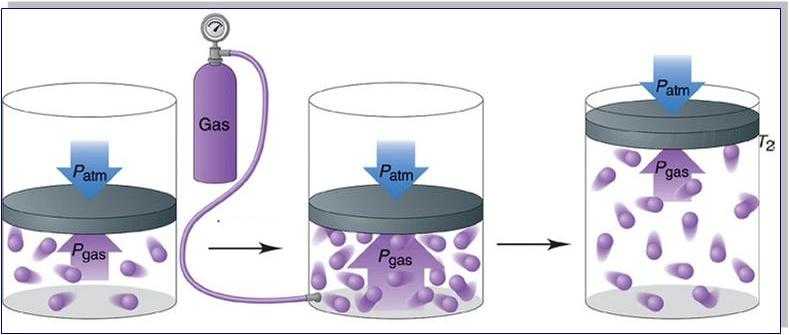
Перед тем как транспортировать или отправить на хранение газообразные вещества, их сильно сжимают. В этом случае давление газа увеличивается. Его помещают в специальные баллоны из стали высокой прочности. Такие емкости необходимы для хранения сжатого воздуха на подводных лодках и кислорода, предназначенного для сварки металлов.

Свойства давления газа:

1. Если объем уменьшается, то давление газа возрастает, а во время увеличения объема, давление будет снижаться при постоянных величинах массы и температуры вещества.
2. Газ, находящийся в закрытом сосуде, характеризуется давлением, которое возрастает по мере увеличения температуры вещества при условии постоянства его массы и объема.
3. В том случае, когда масса газа увеличивается, его давление также будет возрастать и наоборот.

Запись формул для определения давления газа начинают с выяснения причин, по которым оно возникает в рассматриваемой системе. Исходя из физического смысла, давление представляет собой величину, равную отношению силы, перпендикулярно воздействующей на некоторое основание, к площади этого основания:

\(P=\frac{F}{S}\)

Как было отмечено ранее, для идеальной газовой системы характерен лишь один тип взаимодействия — это абсолютно упругие столкновения. В процессе частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. В данном случае применим второй закон Ньютона:

\(F*Δt = Δp\)

Таким образом, конкретно сила F является причиной формирования давления на стенки сосуда. Данная величина F, производимая одной частицей, незначительна. Однако, когда количество частиц огромно, они в совокупности создают ощутимый эффект, проявляемый в виде наличия давления в сосуде.

Причина возникновения давления в газах

Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.

Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:

Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:

Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 1023), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.

Давление в газовой смеси

Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.

Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:

• Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
• Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.

Давление газа

Как уже неоднократно отмечалось, давление газа возникает в результате ударов молекул о стенки сосуда. Если мы считаем, что молекулы взаимодействуют со стенкой по законам абсолютно упругого удара, то частица передает стенке импульс, равный изменению импульса самой молекулы. Направим ось Х перпендикулярно стенке (рис.1), в этом случае изменение импульса стенки при ударе одной молекулой:

Получи помощь с рефератом от ИИ-шки

ИИ ответит за 2 минуты

где $m_0$- масса молекулы.

Рис. 1

Поток импульса, который передается стенке за счет ударов молекулами, которые движутся со скоростями близкими к v, направлен к стенке, равен $nf(v)m_0{v_x\ }^2dv$, отсюда:

где

В результате непосредственного интегрирования получаем:

Так как мы уже отмечали, что рассматриваем единичную площадку стены в течение времени. равном 1с, то можно записать, что давление будет равно:

Давление газа изотропно, это величина скалярная.

При постоянном объеме давление газа массы m подчиняется закону Шарля:

где $p_0$- давление газа при температуре $T_0=273\ К$.

Давление смеси идеальных газов равно сумме их парциальных давлений:

\

Уравнение (7) имеет название — это закон Дальтона.

Парциальным давлением называют давление компоненты смеси газа, каким оно бы было, если бы других газов в смеси не было.

Ряд важных уравнений молекулярной физики, в которые входит давление:

1. Уравнение состояния идеального газа(1):

   $p=nkT$(8).

2. Уравнение состояния идеального газа(2) в виде уравнения Менделеева — Клайперона:

   $pV=\nu RT$(9).

3. Основное уравнение МКТ:

   \

4. Работа газа:

   \

Пример 1

Задание: В процессе сжатия 1-2 с линейной зависимостью р(V). Давление идеального газа возросло в 3 раза. Затем газ сжали в изобарном процессе 2-3 до первоначального объема. Найти отношение работ, совершенных газом в процессах расширения и сжатия. Температуры в состояниях 1 и 2 считать одинаковыми.

Рис. 2

Решение:

Работу газа (или над газом) можно рассчитать по формуле:

\

Если мы рассматриваем процесс (как в условиях нашей задачи) в осях p(V), то исходя из геометрического смысла интеграла работа A будет равна площади криволинейной трапеции (в общем случае), а в нашем площади прямоугольника, когда газ расширяется и площади трапеции, когда газ сжимают. Найдем эти площади.

Площадь прямоугольника:

\

Площадь трапеции:

\

Из условий задачи имеем:

\

Найдем отношение $\frac{A_{2\to 3}}{A_{1\to 2}}$:

\

Ответ: Работа, которую совершает газ в процессе 2-3 в 1,5 больше, чем работа по сжатию газа при заданных условиях.

Пример 2

Задание: Определите, как изменяется давление постоянной массы идеального газа, если в процессе объем увеличивают, температура уменьшается?

Решение:

За основу решения возьмем уравнение Менделеева — Клайперона:

\

Выразим из него давление:

\

Ответ: В данном процессе давление уменьшается.

Пример 3

Задание: В процессе, график которого приведен на рисунке (рис.3) давление $p\sim T^n.\ $Найти значение n, если масса газа постоянна.

Рис. 3

Решение:

Из рисунка имеем зависимость p(V):

\

Из уравнения Менделеева — Клайперона:

\

Используем (3.1) заменив объем, получим:

\

Ответ: Получили $p\sim T^{\frac{1}{2}}$, следовательно, $n=\frac{1}{2}.$

Примеры применения формулы

Ниже представлены несколько примеров, иллюстрирующих использование простой и эффективной формулы расчёта давления по плотности газа:

Пример 1:

Пусть у нас есть баллон с гелием объёмом 10 литров. Мы знаем, что плотность гелия составляет 0,179 г/л. Используя формулу давления по плотности газа, мы можем вычислить давление внутри баллона:

P = ρRT

P = (0,179 г/л) * (8,31 Дж/(моль·К)) * T

P = 1,4889 Т * T

Если предположить, что температура газа равна 300 К, получим:

P = 1,4889 * 300

P ≈ 446,67 Дж/моль

Пример 2:

P = ρgh

P = (1,25 кг/м³) * (9,8 м/с²) * 2 м

P = 24,5 Па

Пример 3:

Рассмотрим закрытый сосуд объёмом 1 литр, в котором находится воздух. Плотность воздуха составляет примерно 1,225 кг/м³. Используя формулу давления по плотности газа, мы можем вычислить давление внутри сосуда:

P = ρRT

P = (1,225 кг/м³) * (8,31 Дж/(моль·К)) * T

P = 10147,575 T

Если предположить, что температура воздуха равна 293 К, получим:

P = 10147,575 * 293

P ≈ 2973767,675 Па

Как видно из приведённых примеров, формула давления по плотности газа позволяет легко и эффективно вычислять давление в различных системах и состояниях газа.

Гидростатическое давление

Гидростатическое давление – давление внутри столба жидкости или газа, находится по формуле:

$$p=p_{0}+\rho g h(4)$$

где $\rho$ – плотность вещества, g=9,8 м/с2 – ускорение свободного падения, h- высота столба вещества. p0 – внешнее давление на газ или жидкость.

Искривление поверхностного слоя жидкости ведет к возникновению дополнительного давления на жидкость, тогда давление под искривленной жидкостью определяется как:

$$p=p_{0}^{*}+2 \sigma H(5)$$

где $\mathrm{P}_{0}^{*}$ –поверхностное натяжение жидкости,p0* – давление под не искривлённым слоем жидкости, H — средняя кривизна поверхности жидкости, вычисляемая по закону Лапласа:

$$H=\frac{1}{2}\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right)$$

R1, R2 – главные радиусы кривизны.

Физические свойства компонентов, входящих в состав природных газов

Параметр	Метан СН4	Этан С2Н6	Пропан С3Н8	Н-Бутан С4Н10	И-Бутан С4Н10	н-Пентан С5Н12
Молярная масса, кг/кмоль	16.04	30.07	44.09	58.12	58.12	72.15
Плотность, кг/м3:   при  0С и 0,1013 МПа   при 20С и 0,01013 МПа	0.717 0.669	1.356 1.264	2.010 1.872	2.307 2.519	2.673 2.491	3.457 3.228
Вязкость: Динамическая  m ×10-7, Па×с   при  0С и 0,1013 МПа   при 20С и 0,01013 МПа Кинематическая  n ×106, м2/с  при  0С и 0,1013 МПа   при 20С и 0,01013 МПа	1.020 1.102 14.24 16.18	0.880 0.940 6.35 7.28	0.770 0.820 3.70 4.26	0.690 0.760 2.45 2.95
Критические параметры газа:   темпаратура, К   давление, МПа	190.68 4.52	305.75 4.88	370.00 4.34	425.17 3.75		460.90 3.29
Газовая постоянная, Дж/(кг×К)	518.57	276.64	188.68	143.08		115.23
Теплота сгорания, кДж/м3 (при 0С и 0,1013 МПа):   высшая   низшая	39830 35880	70370 64430	100920 92930	133890 123680	131800 121750	158360 146230
Теплоемкость  ср, кДж/(кг×К) при 0С	2.167	1.650	1.430	1.590	1.590

         Продолжение
табл. 1.3

	Азот N2	Водо-род Н2	Окись углеро-да СО	Двуо-кись уг-лерода СО2	Воздух (без СО2)	Серо-водород Н2S
Молярная масса, кг/кмоль	28.02	2.016	44.01	64.07	28.96	34.02
Плотность, кг/м3:   при  0С и 0,1013 МПа   при 20С и 0,01013 МПа	1.2505 1.1651	0.0899 0.0837	1.2500 1.1651	1.9768 1.8423	1.2928 1.2050	1.5392 1.4338
Вязкость: Динамическая  m ×10-7, Па×с   при  0С и 0,1013 МПа   при 20С и 0,01013 МПа Кинематическая  n ×106, м2/с  при  0С и 0,1013 МПа   при 20С и 0,01013 МПа	1.71 1.84 — —	— — — —	— — — —	1.40 1.65 — —	1.745 1.822 — —	1.23 — — —
Критические параметры газа:   темпаратура, К   давление, МПа	126.26 3.45	33.30 1.32	133.00 3.44	304.26 7.28	132.65 3.777	373.60 8.89
Газовая постоянная, Дж/(кг×К)	296.75	4124.7	296.94	188.97	292.70	115.23
Теплота сгорания, кДж/м3 (при 0С и 0,1013 МПа):   высшая   низшая	— —	12762 10798	12636 10649	— —	— —	25708 23698
Теплоемкость  ср, кДж/(кг×К) при 0С	1.058	—	—	0.816	1.005	0.993

В
соответствии с нормами технологического проектирования псевдокритические параметры природного газа могут быть определены по
известной плотности  r_ст
газовой смеси

Температура

Температура в житейском понимании этого слова можно сказать что это мера нагретости тела.Абсолютная температура — количественная мера средней кинетической энергии хаотического поступательного движения молекул. Измеряется в градусах по шкале Кельвина. За начало отсчета принят абсолютный ноль температуры — состояние когда при неизменном объеме газ оказывает нулевое давление на стенки сосуда в котором он находится.
Связь абсолютной температуры со средней кинетической энергией поступательного движения молекул.

Из уравнения видно что при абсолютном нуле температуры средняя кинетическая энергия молекул обращается в ноль, а значит молекулы перестают двигаться.Постоянная Больцмана ( Дж/К.) — коэффициент пропорциональности связывающий кинетическую энергию молекул с абсолютной температурой.

Шкала Цельсия — относительная температурная шкала связная с фазовыми переходами воды. За ноль в шкале Цельсия принимается температура плавления льда, а за 100 градусов температура кипения воды.

Связь абсолютной температуры по шкале Кельвина с относительной температурой по шкале Цельсия.

Средняя квадратичная скорость

Связь с другими законами состояния идеального газа

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса и один трех макропараметров (давление, температура или объем) — остаются неизменными.

Количественные зависимости между двумя параметрами газа при фиксированном третьем параметре называют газовыми законами, которые связывают эти параметры.

В зависимости от того, какой параметр остается неизменным различают разные процессы, которые выражаются законами, являющимися следствием уравнения состояния газа:

• изотермический процесс (T=const);
• изохорный процесс (V=const);
• изобарный процесс (p=const).

Изотермический процесс (T=const)

Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплотой с большой системой — термостатом. Им может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.

Согласно уравнению Клапейрона-Менделеева, в любом состоянии с неизменной температурой произведение давления газа на объем одно и то же, то есть постоянно:

Этот закон был открыт экспериментально английским ученым Бойлем и несколько позднее французским ученым Мариоттом. Именно поэтому он называется закон Бойля-Мариотта.

Закон Бойля-Мариотта справедлив для любых газов, а также для смеси газов (например, для воздуха).

Зависимость давления газа от объема при постоянной температуре изображается графической кривой — изотермой. Изотерма для различных температур представлена в координатах pV на рис.1. и представляет собой гиперболу.

Рис.1. Изотерма в pV — координатах.

Изохорный процесс (V=const)

Из уравнения состояния следует, что отношение давлений газа данной массы при постоянно объеме равно отношению его абсолютных температур:

Газовый закон был установлен экспериментально в 1787 г. французским физиком Ж. Шарлем и носит название закона Шарля: давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре.

Зависимость давления газа от температуры при постоянном объеме изображается графически прямой, которая называется изохорой (Рис.2).

Рис.2 Изображение изохоры в pT-координатах.

Изобарный процесс (p=const)

Из уравнения Клапейрона-Менделеева вытекает, что отношение объемов газа данной массы при постоянном давлении равно отношению его абсолютных температур.

Если в качестве второго состояния газа выбрать состояние при нормальных условиях (нормальном атмосферном давлении, температуре таяния льда) следует:

Этот газовый закон был установлен экспериментально в 1802 г французским ученым Гей-Люссаком.

Зависимость объема газа от температуры при постоянном давлении изображается графической прямой, которая называется изобарой (Рис.3).

Рис. 3. Изобара в VT-координатах.