Основные сведения о магнитных взаимодействиях в физике

Содержание / Contents

• 1 Что плохого в этом подмагничивании?
• 2 Теперь по поводу тороидальных трансформаторов
• 3 Выводы:

Общение на радиолюбительских форумах показало, что все сводится (я немного упрощаю) к двум позициям: 1. Постоянка присутствует исключительно в схеме выпрямителя со средней точкой:

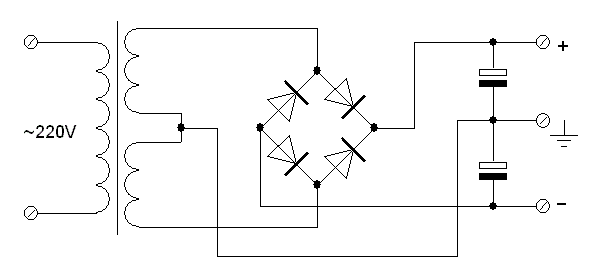
Если же у трансформатора две вторички, каждая из которых имеет свой выпрямитель:

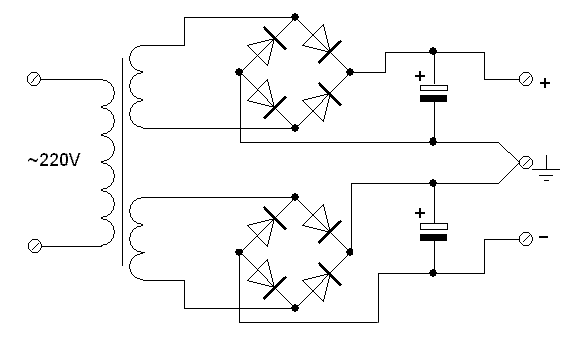
то никакого подмагничивания не случится.

2. Применять тороидальные трансформаторы опасно, т.к. из-за отсутствия зазора в сердечнике подмагничивание сказывается на них очень сильно. Поэтому мощность трансформатора надо выбирать раза в два больше, чем нужно.

Я проанализировал работу трансформатора в таком режиме (теоретически и экспериментально), но несколько сомневался в своих результатах. Поэтому я связался по электронной почте с автором статьи Константином Никитиным, доктором технических наук, профессором, заведующим кафедрой Силовой электроники в Санкт-Петербургском государственном университете телекоммуникаций им. Бонч-Бруевича.

И получил полное одобрение следующих «пяти положений о подмагничивании»:

1. При усилении синусоидального сигнала частотой 25 Гц возникает подмагничивание сердечника трансформатора постоянным током, вызывающим насыщение сердечника. Физическая причина подмагничивания при работе выпрямительно-трансформаторной схемы на усилитель проста: усилитель потребляет не постоянный ток, а сигнал с частотой, равной удвоенной частоте усиления. Следовательно, вполне возможны ситуации, когда условия работы трансформатора от периода к периоду сетевой частоты будут существенно разниться. Так как в штатной ситуации трансформатор подводится к насыщению исключительно током холостого хода (рабочие токи обмоток создают равные и противоположные потоки), то достаточно минимального, соизмеримого с током холостого хода (в пересчете на первичную обмотку), тока подмагничивания – и авария обеспечена.

2. Такое подмагничивание характерно для усилителей, выходной каскад которых работает в классе В или АВ и отсутствует у усилителей, выходной каскад которых работает в классе А.

3. На практике частота сигнала не обязательно должна быть именно 25 Гц – трансформатору для насыщения хватает и не нулевой (но достаточно малой) частоты подмагничивания.

4. Подмагничивание происходит как в схеме выпрямителя со средней точкой и одним общим диодным мостом, так и в схеме с отдельными обмотками трансформатора и отдельными мостами в каждом плече. С точки зрения подмагничивания схемы не эквивалентны, но оно есть везде.

5. В силу того, что в реальном звуковом сигнале составляющие «критических» частот имеют малую амплитуду и продолжительность, указанная опасность невелика, но вот на спецсигналах может быть спровоцирована ситуация, когда всё будет плохо.

3.23. Анализ массово-зарядового состояния (q/m) элементарных частиц

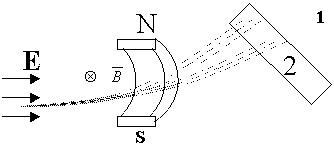
С поверхности вещества испаряют часть атомов или молекул. Как правило, при этом такие атомы обладают зарядовыми свойствами. Далее эти атомы ускоряются в электрическом поле E, и движущийся поток атомов пропускают через магнитное поле B. По закону Лоренца эти заряды в магнитном поле отклоняются. Тогда на экране за магнитным полем в разных местах оседают атомы разных зарядов. По степени отклонения атомов от прямолинейного распространения можно судить о заряде атома.

Частицы в магнитном поле отклоняются. Тогда на экране за магнитным полем в разных местах, например:

Заряд q= 1e – в точке 2 на экране.

Заряд q=2e – в точке 1 на экране.

Процесс разделения частиц по зарядам называется сепарированием, а прибор, анализирующий состав этих пучков — масспектрограф.

Описание процесса

Намагничивание трансформатора изза включения его под напряжение считается самым неблагоприятным случаем, вызывающим БНТ наибольшей амплитуды. Когда производится отключение трансформатора, напряжение намагничивания оказывается равным нулю, ток намагничивания снижается до нуля, в то время как магнитная индукция изменяется согласно характеристике намагничивания сердечника. Указанное обуславливает наличие остаточной индукции в сердечнике. Когда, по истечении некоторого времени, производится повторное включение трансформатора под напряжение, изменяющееся по синусоидальному закону, магнитная индукция начинает изменяться по тому же закону, однако со смещением на значение остаточной индукции. Остаточная индукция может составлять 80–90% номинальной индукции, и, таким образом, точка может переместиться за излом характеристики намагничивания, что, в свою очередь, обуславливает большую амплитуду и искажение формы кривой тока.

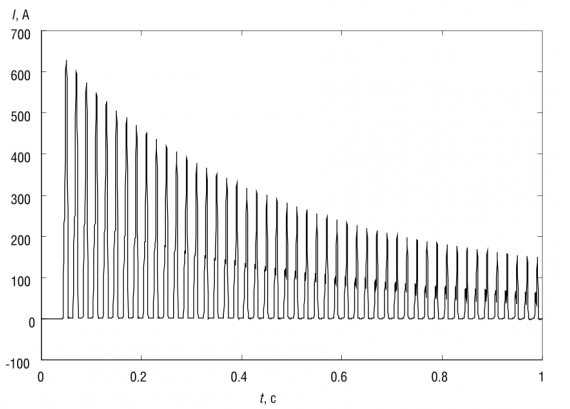
На рисунке представлена характерная форма БНТ. Данная осциллограмма отображает наличие длительно затухающей апериодической составляющей, может быть охарактеризована содержанием различных гармоник и большой амплитудой тока в начальный момент времени (до 30 раз превышающей значение номинального тока трансформатора). Кривая значительным образом затухает через десятые секунды, однако полное затухание характерно через несколько секунд. При определенных обстоятельствах БНТ затухает лишь спустя минуты после включения трансформатора под напряжение.

Определение

Поле намагничивания или М- поле можно определить в соответствии со следующим уравнением:

Mзнак равноdмdV{\ displaystyle \ mathbf {M} = {\ frac {\ mathrm {d} \ mathbf {m}} {\ mathrm {d} V}}}

Где — элементарный магнитный момент, а — элемент объема ; другими словами, М- поле — это распределение магнитных моментов в рассматриваемой области или многообразии. Лучше всего это проиллюстрировать следующим соотношением: dм{\ displaystyle \ mathrm {d} \ mathbf {m}}dV{\ displaystyle \ mathrm {d} V}

мзнак равно∭MdV{\ Displaystyle \ mathbf {m} = \ iiint \ mathbf {M} \, \ mathrm {d} V}

где m — обычный магнитный момент, а тройной интеграл означает интегрирование по объему. Это делает M- поле полностью аналогичным полю электрической поляризации или P- полю, используемому для определения электрического дипольного момента p, генерируемого подобной областью или многообразием с такой поляризацией:

пзнак равноdпdV,пзнак равно∭пdV{\ Displaystyle \ mathbf {P} = {\ mathrm {d} \ mathbf {p} \ over \ mathrm {d} V}, \ quad \ mathbf {p} = \ iiint \ mathbf {P} \, \ mathrm { d} V}

Где элементарный электрический дипольный момент. dп{\ Displaystyle \ mathrm {d} \ mathbf {p}}

Эти определения P и M как «моментов на единицу объема» широко используются, хотя в некоторых случаях они могут приводить к двусмысленностям и парадоксам.

Поле M измеряется в амперах на метр (А / м) в единицах СИ.

Связь намагниченности с молекулярными токами

Рассмотрим бесконечно маленький замкнутый контур L, который ограничивает элемент площади $triangle S$ (рис.1). Вычислим циркуляцию намагниченности ($overrightarrow{J}$) по контуру:

Рис. 1

где $J_{tau }$- тангенциальная составляющая вектора намагниченности вдоль контура L. Эта составляющая возникает за счет токов, которые текут по замкнутым контурам вокруг линии, вдоль которой проводится интегрирование. Умножим и разделим правую часть выражения (6) на величину $delta S$ (площадь которую обтекает ток в плоскости, которая перпендикулярная линии интегрирования), проведем преобразования в том числе используя выражение (5):

В соответствии с определением магнитного момента ($p_m=ISto {dp}_m=delta Idelta S, $)$ где delta I сила тока, который обтекает площадку delta S,$ причем$ delta I$ пересекает $triangle S$ по нармали. Получаем из (7):

где $triangle I_n$- нормальная составляющая силы тока, которая пересекает площадку $triangle S.$ В результате мы получили:

Из выражения (9) легко получить:

Формула (10) — выражение для объемной плотности молекулярных токов, которые являются причиной намагниченности $overrightarrow{J}$.

Молекулярные токи могут течь и по поверхности раздела меду магнетиками или между магнетиком и вакуумом. Тогда поверхностная плотность молекулярного тока ($i_{m.p}=frac{triangle I_{m.pov}}{l}$) равна:

Вектор магнитной поляризации

Эффект магнитной поляризации можно описать, связав микроскопические токи намагничивания с макроскопической векторной величиной, которая описывает глобальное поведение материала в зависимости от наличия магнитного поля. Вектор интенсивности намагниченности , также называемый вектором магнитной поляризации и обозначаемый значком , представляет собой магнитный дипольный момент на единицу объема, которым обладает материал. Определяемый как среднее значение магнитного момента частиц , содержащихся в бесконечно малом объеме , выражается соотношением:

В Международной системе единиц вектор магнитной поляризации измеряется в Амперах на метр (А/м), а в определении предел действителен для объема, содержащего значительное количество атомов, например, чтобы можно было вычислить среднее имущество.

Намагничивающие токи

Если атомная поляризация внутри материала однородна, токи Ампера, связанные с двумя соседними атомами, компенсируют друг друга, и единственными токами, вызывающими макроскопические эффекты, являются токи атомов, граничащих с разделяющей поверхностью между двумя областями с разным значением смещения. Эти токи описываются током поверхностного намагничивания , определяемым выражением:

то есть ток намагничивания равен интегралу потока вектора поверхностной плотности тока намагничивания по поверхности .

Если поляризация атомов внутри материала неоднородна, вместо этого вводится объемный ток намагничивания , определяемый формулой:

то есть объемный ток намагничивания равен потоку вектора плотности объемного тока намагничивания через поверхность .

Чтобы связать вектор намагниченности и плотность микроскопических амперных токов, рассмотрим магнитный потенциал , создаваемый в точке объемом материала, помещенным в точку :

где – магнитный момент, которым обладает бесконечно малый объем материала, и разность векторов между положением элементарного объема и точкой , в которой вычисляется потенциал.

С:

где верхний индекс на символе набла указывает, что переменная дифференцирования равна , отсюда следует, что:

а так как выполняется векторное соотношение:

отождествляя с и с мы получаем:

что можно записать как:

Приравнивается к общему выражению магнитного потенциала, создаваемого плотностью поверхностного и объемного токов:

позволяет идентифицировать выражения плотностей тока намагничивания:

где в первом уравнении — единичный вектор, определяющий направление нормали к поверхности материала.

Таким образом, мы имеем, что магнитный потенциал, создаваемый намагничиванием материала, равен:

который, добавленный к потенциалу, создаваемому любыми свободными токами, присутствующими в среде, обеспечивает общий потенциал и, следовательно, полное магнитное поле в среде.

3.14. Явление электромагнитной индукции (взаимоиндукции)

В 1831 году Фарадей установил, что если изменять магнитный поток, проходящий через контур, то в этом контуре возникает ЭДС, препятствующая изменению внешнего магнитного поля. Пусть есть контур I, к которому подключен гальванометр, и контур II, к которому подключен резистор, и источник ЭДС.

1. силовые линии II проводника пересекают первый контур. Если менять величину тока во II контуре, то меняется B2 , то есть магнитный поток, создаваемый вторым контуром также меняется. И по закону Фарадея в первом контуре возникает ЭДС.
2. Удаление или приближение второго контура также вызывает ЭДС в первом.
3. Можно поворачивать контура относительно друг друга, чтобы вызвать ЭДС в I контуре.
4. Вызвать ЭДС можно также изменением магнитной среды, которая находится между контурами.

Приложение:

1. Контуры с током, близко расположенные друг с другом называют связанными.
2. Влияние одного контура на другой возможно только, если ток в контурах переменный (принцип трансформатора). Для усиления взаимодействия используют последовательно соединенные контура – соленоиды.

Пусть:

Соленоид 1 содержит N витков, а соленоид, II: N₂ витков. S — поперечное сечение соленоида.

Если в соленоиде I изменить величину тока, то в соленоиде II возникает ЭДС, равная:

Если в каждом из контуров соленоида возникает ЭДС, то результирующая ЭДС соленоида будет равна произведению числа витков соленоида на ЭДС одного витка: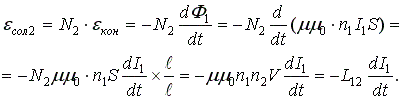

то есть: , где L₁₂ — коэффициент взаимной индукции первого соленоида относительно второго.

Если источник неэлектрических сил подключить ко второму соленоиду, а гальванометр к первому, то ЭДС, возникающую в первом соленоиде можно будет рассчитать аналогично:

, где — коэффициент взаимоиндукции II-ого соленоида относительно первого. Таким образом L₂₁=L₁₂

Понятие намагничивающего тока

Внезапное возрастание, то есть бросок тока намагничивания (БТН), объясняется насыщением сердечника магнитной индукцией. Трансформаторы динамически устойчивы к броскам благодаря изготовлению обмоток с учетом больших по кратности токов, как правило, возникающих при замыканиях накоротко. В среднем намагничивающий ток превышает номинальное значение прибора в 6-8 раз.

Рис. 1. Условия появления БТН

В режиме короткого замыкания напряжение силового агрегата характеризуется предельным понижением до нуля, а после отключения зоны повреждения устанавливается на зажимах устройства скачкообразно.

Восстановление магнитного потока происходит неравномерно и не сразу, что обуславливает возникновение переходного процесса, в течение которого образуются два потока – установившийся ФУ и свободный ФСВ. Для определения общего значения используется формула:

ФТО = ФУ + ФСВ

В точке отсчета, характеризующей начальный момент времени при t = 0, ФТО также приравнивается к нулю, поэтому справедливым представляется равенство ФСВ = – ФУ. Знаки полярности магнитных потоков совпадают во втором полупериоде, и, соответственно, результирующая величина достигает пикового максимума (ФТмакс).

Рис. 2. Магнитные потоки в сердечнике под нагрузкой

Схематически наблюдается отставание ФУ от UТ на 90 градусов, что говорит о зависимости ФСВ и ФТмакс от фазы напряжения. Данные величины достигают наибольших значений при включении – в момент прохождения UТ через ноль

Если не брать во внимание постепенное затухание, ФТмакс ≈ 2ФУ. Но пиковая величина потока может быть и выше, когда в толще сердечника присутствует остаточное намагничивание Фост, по знаку совпадающее с ФСВ

Тогда:

ФТмакс = (2ФУ + Фост)> 2ФУ

Сердечник насыщается при значениях потоков, приближенных к 2ФУ, вызывая резкий бросок Iнам. Ток намагничивания образуется только в той обмотке цепи, на которую подается напряжение при включении. Он преобразуется через защитное устройство и поступает на реле, заставляя его срабатывать при соблюдении неравенства Iнам > Iс.з..

Уравнения Максвелла для магнитного поля в веществе

Наличие материи заставляет учитывать токи Ампера в уравнениях Максвелла для магнитного поля:

При вводе выражения уравнение изменяется:

и выделение оператора ротора:

аргумент ротора идентифицируется как вектор магнитного поля в веществе:

Уравнение Максвелла можно переписать эквивалентно:

Плотность тока в предыдущем уравнении относится исключительно к электрическим токам, определяемым движением только свободных электронов, а не к атомным токам намагничивания.

В случае, когда поле имеет нулевую дивергенцию, уравнения для поля в отсутствие вещества и поля в присутствии вещества формально эквивалентны, что позволяет определять поле в широком классе задач, начиная с расстановки свободных токов.

Кроме того, в нестационарном случае четвертое уравнение имеет вид:

где последний член у второго члена есть плотность тока смещения .

Молекулярные токи и индукция магнитного поля

Для того, чтобы вычислить индукцию макроскопического поля молекулярные токи заменяют макроскопическими токами, которые непрерывно изменяются в пространстве. Такие токи имеют название токов намагничивания. Дальше эти плотность этих токов будем обозначать $overrightarrow{j_m}$. Плотность токов проводимости будем обозначать $overrightarrow{j}$. Так получаем, что магнитное поле порождается токами проводимости и токами намагничивания. Если известны эти токи, то можно вычислять индукцию поля $overrightarrow{B},$ используя формулы для вакуума. В таком случае теорема о циркуляции вектора индукции магнитного поля будет иметь вид:

или в дифференциальной форме:

где I — ток проводимости, $I_m$ — ток намагничивания, полные токи, которые пронизывают контур L.

Итак, возникновение магнитных моментов связано с наличием круговых токов. Токи в элементарных объемах, которые приводят к возникновению магнитных моментов, назвали молекулярными токами. Однако не следует воспринимать этот термин буквально. Молекулярные токи, строго говоря, могут течь только внутри молекулы. При определении намагниченности и других параметров имеют в виду усредненные величины. Магнитные моменты представляют размазанными по объему вещества, а молекулярные токи текущими по всему объему.

Разворот

Перемагничивание, также известное как переключение, относится к процессу, который приводит к переориентации вектора намагниченности на 180 ° (дуга) относительно его начального направления с одной стабильной ориентации на противоположную. Технологически это один из наиболее важных процессов в магнетизме, который связан с процессом хранения магнитных данных , который используется в современных жестких дисках . Как известно сегодня, есть только несколько возможных способов обратить намагничивание металлического магнита:

1. приложенное магнитное поле
2. инжекция спина через пучок частиц со спином
3. перемагничивание циркулярно поляризованным светом ; то есть падающее электромагнитное излучение с круговой поляризацией

3.2. Взаимодействие параллельных токов

Закон Фарадея:

, где µ — магнитная характеристика среды, называемая магнитной проницаемостью.

Направление токов влияет на силу взаимодействия.

По аналогии с электростатикой, где сила определяет напряженность, а напряженность — индукцию, в магнетизме напряженность и индукция — силовые характеристики. Принято в электростатике основной силовой характеристикой считать напряженность, а в магнетизме — индукцию.

Правило буравчика:

Если ток направлен по закрутке буравчика, то шляпка вращается по силовой линии. В каждой точке пространства направление силовых линий совпадает с направление касательной. Таким образом, силовые линии магнитного поля являются замкнутыми.

Как происходит процесс

При подаче нагрузки намагничивание прибора из-за включения рассматривается как негативное явление, способное спровоцировать БТН максимальной амплитуды. При отключении ток намагничивания сокращается до нулевой отметки, а магнитная индукция корректируется в зависимости от степени намагничивания стального сердечника, в результате чего в магнитопроводе сохраняется остаточная индукция.

Если через время повторить включение токопреобразующего устройства под напряжение, подчиненное синусоидальному закону изменения, магнитная индукция меняется со смещением остаточной величины до 90% от номинального значения. В результате возникает высокая амплитуда намагничивания и изменение формы кривой.

Рис. 3. Кривая БНТ классического типа

Уровень намагничивающего тока затухает на десятые доли секунды, но полное «сглаживание» кривой наступает в течение нескольких секунд, а при определенных условиях – через несколько минут. Длительность затухания апериодической составляющей осциллограммы БТН обусловлена высокой амплитудой тока в начальный (нулевой) момент времени и содержанием разных гармоник. Пиковая величина зависит от нагрузочного напряжения и его параметров, а также от значения и полярности остаточного магнитного потока в сердечнике.

Пик тока может быть выше номинального значения для высокомощных агрегатов в 10-15 раз, а для приборов мощностью (<50 кВА) – больше в 20-25 раз. Период затухания – от нескольких миллисекунд до секунд.

Природа молекулярных токов

Все атомы состоят из положительного ядра, в котором сосредотачивается почти вся масса атома и некоторого числа электронов. Суммарный отрицательный заряд электронов в атоме равен положительному заряду ядра, атом в нормальном состоянии электрически нейтрален.

Электроны в атоме непрерывно движутся. При объяснении многих явлений считают, что орбиты движения электронов вокруг ядра представляют собой окружности (или в крайнем случае эллипсы). Каждый электрон в атоме перемещается по собственной орбите, разные орбиты электронов находятся в разных плоскостях.

Электроны, вращающиеся по орбитам, образуют замкнутые токи, поэтому и предполагают, что именно они являются молекулярными токами.

Сила Лоренца

Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.

Формула для нахождения силы Лоренца:

где ​\( q \)​ – заряд частицы, ​\( v \)​ – скорость частицы, ​\( B \)​ – модуль вектора магнитной индукции, ​\( \alpha \)​ – угол между вектором скорости частицы и вектором магнитной индукции.

Направление силы Лоренца определяют по правилу левой руки: если ладонь левой руки расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции ​\( B_\perp \)​ входила в ладонь, а четыре вытянутых пальца указывали направление скорости положительно заряженной частицы, то отогнутый на 90° большой палец покажет направление силы Лоренца.

Если заряд частицы отрицательный, то направление силы изменяется на противоположное.

Важно!
Если вектор скорости сонаправлен с вектором магнитной индукции, то частица движется равномерно и прямолинейно. В однородном магнитном поле сила Лоренца искривляет траекторию движения частицы

В однородном магнитном поле сила Лоренца искривляет траекторию движения частицы.

Если вектор скорости перпендикулярен вектору магнитной индукции, то частица движется по окружности, радиус которой равен:

где ​\( m \)​ – масса частицы, ​\( v \)​ – скорость частицы, ​\( B \)​ – модуль вектора магнитной индукции, ​\( q \)​ – заряд частицы.

В этом случае сила Лоренца играет роль центростремительной и ее работа равна нулю. Период (частота) обращения частицы не зависит от радиуса окружности и скорости частицы. Формула для вычисления периода обращения частицы:

Угловая скорость движения заряженной частицы:

Важно!
Сила Лоренца не меняет кинетическую энергию частицы и модуль ее скорости. Под действием силы Лоренца изменяется направление скорости частицы

Если вектор скорости направлен под углом ​\( \alpha \)​ (0° < \( \alpha \) < 90°) к вектору магнитной индукции, то частица движется по винтовой линии.

В этом случае вектор скорости частицы можно представить как сумму двух векторов скорости, один из которых, ​\( \vec{v}_2 \)​, параллелен вектору \( \vec{B} \), а другой, \( \vec{v}_1 \), – перпендикулярен ему. Вектор \( \vec{v}_1 \) не меняется ни по модулю, ни по направлению. Вектор \( \vec{v}_2 \) меняется по направлению. Сила Лоренца будет сообщать движущейся частице ускорение, перпендикулярное вектору скорости \( \vec{v}_1 \). Частица будет двигаться по окружности. Период обращения частицы по окружности – ​\( T \)​.

Таким образом, на равномерное движение вдоль линии индукции будет накладываться движение по окружности в плоскости, перпендикулярной вектору \( \vec{B} \). Частица движется по винтовой линии с шагом ​\( h=v_2T \)​.

Важно!
Если частица движется в электрическом и магнитном полях, то полная сила Лоренца равна:

Особенности движения заряженной частицы в магнитном поле используются в масс-спектрометрах – устройствах для измерения масс заряженных частиц; ускорителях частиц; для термоизоляции плазмы в установках «Токамак».

Алгоритм решения задач о действии магнитного (и электрического) поля на заряженные частицы:

• сделать чертеж, указать на нем силовые линии магнитного (и электрического) поля, нарисовать вектор начальной скорости частицы и отметить знак ее заряда;
• изобразить силы, действующие на заряженную частицу;
• определить вид траектории частицы;
• разложить силы, действующие на заряженную частицу, вдоль направления магнитного поля и по направлению, ему перпендикулярному;
• составить основное уравнение динамики материальной точки по каждому из направлений разложения сил;
• выразить силы через величины, от которых они зависят;
• решить полученную систему уравнений относительно неизвестной величины;
• решение проверить.

3.13. Явление электромагнитной индукции. ЭДС электромагнитной индукции

Проводник, по которому не пропускают ток, помещаем в магнитное поле. Будем перемещать проводник перпендикулярно вектору магнитного поля. По закону Лоренца так как . Мы получили, что свободные заряды, которые, по определению, имеются в проводнике, будут перемещаться вдоль проводника. В результате перераспределения зарядов в проводнике при их движении на концах проводника возникает разность потенциалов, которая создает электрическое поле в проводнике: . Тогда напряженность электрического поля в проводнике

Если подключим гальванометр, то можно выразить напряженность через напряжение . В равновесии Fл=Fк. То есть: . Если закон перемещения проводника в магнитном поле произволен, то разбиваем все перемещение на отрезки dr: , где dS=drℓ — площадь, заметаемая проводником при перемещении. Правило Фарадея: величина разности потенциалов, возникающих на концах проводника при его перемещении в магнитном поле прямо пропорциональна скорости изменения магнитного потока.

Если концы проводника замкнуты между собой, то в цепи протекает ток так, если бы проводник являлся источником тока. Тогда по закону Ампера сила, действующая на проводник с током в магнитном поле (правило левой руки) направлена в сторону, противоположную перемещению проводника в магнитном поле, то есть эта сила препятствует перемещению. Тогда:

1. разность потенциалов, возникающих на концах проводника, называют ЭДС магнитной индукции.
2. поскольку ЭДС вызывает силы, препятствующие движению проводника, то в законе Фарадея ставят знак “минус” (правило Ленца):

Размагничивание

Размагничивание

Размагничивание — это уменьшение или устранение намагниченности. Один из способов сделать это — нагреть объект выше его температуры Кюри, когда тепловые флуктуации имеют достаточно энергии, чтобы преодолеть обменные взаимодействия, источник ферромагнитного порядка, и разрушить этот порядок. Другой способ — вытащить его из электрической катушки с переменным током, протекающим через него, создавая поля, противодействующие намагничиванию.

Одно из применений размагничивания — устранение нежелательных магнитных полей. Например, магнитные поля могут мешать электронным устройствам, таким как сотовые телефоны или компьютеры, а также механической обработке, заставляя обрезки цепляться за свои родительские части.

В уравнениях Максвелла

Поведение магнитных полей ( B, H), электрических полей ( E, D), плотности заряда ( ρ) и плотности тока ( J) описывается уравнениями Максвелла. Роль намагничивания описана ниже.

Отношения между B, H и M

Магнитное поле

Намагниченность определяет дополнительное магнитное поле H как

Bзнак равноμ(ЧАС+M){\ Displaystyle \ mathbf {B} = \ mu _ {0} (\ mathbf {H + M})}( Единицы СИ )

Bзнак равноЧАС+4πM{\ Displaystyle \ mathbf {B} = \ mathbf {H} +4 \ pi \ mathbf {M}}( Гауссовские единицы )

что удобно для различных расчетов. Вакуума проницаемость μ 0, по определению,4π × 10 −7 В с / ( А м ) (в единицах СИ).

Связь между M и H существует во многих материалах. В диамагнетиках и парамагнетиках зависимость обычно линейная:

Mзнак равноχЧАС,Bзнак равноμЧАСзнак равноμ(1+χ)ЧАС,{\ Displaystyle \ mathbf {M} = \ chi \ mathbf {H}, \, \ mathbf {B} = \ mu \ mathbf {H} = \ mu _ {0} (1+ \ chi) \ mathbf {H},}

где χ называется объемной магнитной восприимчивостью, а μ называется магнитной проницаемостью материала. Потенциал магнитной энергии на единицу объема (т.е. магнитной плотности энергии ) парамагнетика (или диамагнетика) в магнитном поле:

-M⋅Bзнак равно-χЧАС⋅Bзнак равно-χ1+χB2μ,{\ displaystyle — \ mathbf {M} \ cdot \ mathbf {B} = — \ chi \ mathbf {H} \ cdot \ mathbf {B} = — {\ frac {\ chi} {1+ \ chi}} {\ гидроразрыв {\ mathbf {B} ^ {2}} {\ mu _ {0}}},}

отрицательный градиент которого представляет собой на парамагнетик (или диамагнетик) на единицу объема (т.е. плотность силы).

В диамагнетиках () и парамагнетиках () обычно, и поэтому. χlt;{\ Displaystyle \ чи lt;0}χgt;{\ displaystyle \ chigt; 0}|χ|≪1{\ displaystyle | \ chi | \ ll 1}M≈χBμ{\ displaystyle \ mathbf {M} \ приблизительно \ chi {\ frac {\ mathbf {B}} {\ mu _ {0}}}}

В ферромагнетиках нет взаимно однозначного соответствия между M и H из-за магнитного гистерезиса.

Магнитная поляризация

В качестве альтернативы намагниченности, можно определить магнитную поляризацию, I (часто символ J используется, чтобы не путать с плотностью тока).

Bзнак равноμЧАС+я{\ Displaystyle \ mathbf {B} = \ mu _ {0} \ mathbf {H} + \ mathbf {I}}( Единицы СИ ).

Это по прямой аналогии с электрической поляризацией,. Таким образом, магнитная поляризация отличается от намагниченности в μ 0 раз: Dзнак равноεE+п{\ Displaystyle \ mathbf {D} = \ varepsilon _ {0} \ mathbf {E} + \ mathbf {P}}

язнак равноμM{\ Displaystyle \ mathbf {I} = \ mu _ {0} \ mathbf {M}}( Единицы СИ ).

В то время как намагниченность обычно измеряется в амперах на метр, магнитная поляризация измеряется в теслах.

Ток намагничивания

Намагниченность M вносит вклад в плотность тока J, известную как ток намагничивания.

Jмзнак равно∇×M{\ Displaystyle \ mathbf {J} _ {\ mathrm {m}} = \ набла \ раз \ mathbf {M}}

а для связанного поверхностного тока:

Kмзнак равноM×п^{\ displaystyle \ mathbf {K} _ {\ mathrm {m}} = \ mathbf {M} \ times \ mathbf {\ hat {n}}}

так что полная плотность тока, которая входит в уравнения Максвелла, определяется как

Jзнак равноJж+∇×M+∂п∂т{\ displaystyle \ mathbf {J} = \ mathbf {J} _ {\ mathrm {f}} + \ nabla \ times \ mathbf {M} + {\ frac {\ partial \ mathbf {P}} {\ partial t} }}

где J F является плотностью электрического тока свободных зарядов (также называемая свободным током), второй член представляет собой вклад от намагниченности, а последний член связан с электрической поляризацией P.

Магнитостатика

Магнитостатика

В отсутствие свободных электрических токов и зависящих от времени эффектов уравнения Максвелла, описывающие магнитные величины, сводятся к

∇×ЧАСзнак равно∇⋅ЧАСзнак равно-∇⋅M{\ Displaystyle {\ begin {выровнено} \ mathbf {\ nabla \ times H} amp; = 0 \\\ mathbf {\ nabla \ cdot H} amp; = — \ nabla \ cdot \ mathbf {M} \ end {выровнено}} }

Эти уравнения могут быть решены аналогично электростатическим задачам, где

∇×Eзнак равно∇⋅Eзнак равноρϵ{\ displaystyle {\ begin {align} \ mathbf {\ nabla \ times E} amp; = 0 \\\ mathbf {\ nabla \ cdot E} amp; = {\ frac {\ rho} {\ epsilon _ {0}}} \ конец {выровнено}}}

В этом смысле −∇⋅ M играет роль фиктивной «плотности магнитного заряда», аналогичной плотности электрического заряда ρ ; (см. также размагничивающее поле ).

Сообщений 14

• tosha37
• Пользователь
• Неактивен

• Зарегистрирован: 2011-05-03
• Сообщений: 102
• Репутация :

Тема: Расчет бросков тока намагничивания трансформаторов

Добрый день уважаемые коллеги. Возникли вопросы про расчет отстройки ТО или ТНЗНП от бросков тока намагничивания:

1) Правильно ли я понимаю, что при расчете ТНЗНП согласно руководящим указаниям по релейной защите выпуск 12 для линий с односторонним питанием: «Условия “а” и “б” рассматриваются при расчете защит линий, оборудованных выключателями с пофазным приводом; указанные условия не учитываются, если первая ступень защиты отстроена по времени от одновременного включения фаз выключателя». Из паспорта на выключатель ВГТ-110 кВ: разновременность работы полюсов, с, не более 0,002 с при включении в то время как время срабатывания реле тока ТНЗНП защит, выполненных на МП элементной базе, не превышает 0,025 с. Т.е. можно говорить, что время разновременности включения фаз выключателя практически не превышает собственного времени срабатывания защиты, поэтому условие отстройки от броска тока намагничивания трансформаторов можно не учитывать.

Или все-таки каким-то образом отстраиваются от бросков тока намагничивания трансформаторов в таких ситуациях?

2) Вопрос определения Сб. Каким образом его взять применительно для защит на МП элементной базе? Ведь в «Руководящих указаниях по релейной защите. Вып.9. Дифференциально –фазная высокочастотная защита линий 110 – 330 кВ. М., “Энергия”, 1972. 114 с. с ил.» и в «Руководящих указаниях по релейной защите. Вып.12. Токовая защита нулевой последовательности от замыканий на землю линий 110 – 500 кВ. Расчеты. М., “Энергия”, 1980. 88 с. с ил.». таблицы П-6 и таблицы ПV-4 соответственно даны значения Сб для реле, выполненных на электромеханической элементной базе.

3) И еще такой вопрос касаемо параметрирования. У ЭКРы есть дополнительные ступени ТНЗНП V и VI, если мне не изменяет память, и там есть возможность завести разрешить работу ТНЗНП от устройства БТНТ (например в шкафе ШЭ2607 021_200), которое как я понимаю, блокирует действие ТНЗНП при бросках тока намагничивания, следовательно, это условие можно не учитывать получается?

Спасибо за ответы

БТНТ.png

58.63 Кб, 1 скачиваний с 2016-08-29

You don’t have the permssions to download the attachments of this post.

Источник