Вынесение за скобку
Пример:
Разложить на множители многочлен
Решение:
Здесь можно заметить, что все три члена многочлена имеют общий множитель ab. Действительно,
![]()
На основании распределительного закона данный многочлен можно записать в виде произведения суммы первых множителей его членов на одночлен ab. Итак,
![]()
Ответ :
Прием, примененный в рассмотренном примере, называется вынесением за скобку. Этот прием тесно связан с правилом умножения многочлена на одночлен. Так же как правило умножения многочлена на одночлен, вынесение за скобку основывается на распределительном законе. При умножении многочлена на одночлен распределительный закон применяется для того, чтобы представить в виде суммы произведение суммы на число. При вынесении за скобку, наоборот, сумма нескольких слагаемых, имеющих общий множитель, преобразовывается в произведение некоторой суммы на этот множитель.
При вынесении за скобку следует руководствоваться следующим правилом:
Правило. .Если все члены многочлена содержат некоторую букву в каких-либо степенях, то можно вынести за скобку степень этой буквы с наименьшим из показателей, с которыми буква входит в отдельные члены многочлена. Если таких букв имеется несколько, то выносится за скобку произведение степеней этих букв с надлежащими показателями.
Точно так же можно выносить за скобку числовой коэффициент. Вообще говоря, этот коэффициент может быть взят каким угодно. Например,
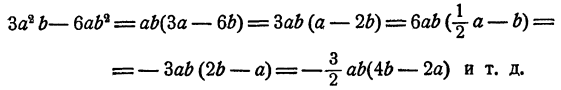
Однако наиболее удобно так выбирать коэффициент, чтобы многочлен, остающийся в скобке, имел целые коэффициенты, не имеющие общего целого множителя, например,
или
При преобразовании алгебраических выражений вынесение за скобку играет вспомогательную роль. Поэтому выбор знака коэффициента, а иногда и его величины, должен производиться в соответствии с целью, для достижения которой делается вынесение за скобку. В частности, часто бывает нужно вынести за скобку численный множитель, например,
![]()
Отметим, наконец, что вынесение за скобку возможно во всяком алгебраическом выражении, представляющем собой сумму нескольких слагаемых, имеющих общий множитель, например,
![]()
Иногда при этом наличие общего множителя становится очевидным только после некоторых преобразований.
Пример:
Разложить на множители многочлен
Решение:
Здесь мы видим, что если из выражения, находящегося в первой скобке, вынести число 3, то в скобке останется двучлен, члены которого только знаками отличаются от членов второй скобки. Поэтому преобразование нужно вести так:
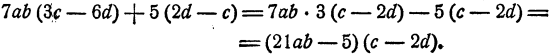
Формулы сокращенного умножения
При выполнении различных алгебраических преобразований встречаются часто некоторые частные случаи умножения. Получающиеся при этом произведения полезно запомнить наизусть, чтобы в дальнейшем, когда эти случаи встретятся, можно было сразу написать результат, не производя каждый раз почленного умножения. Равенства, выражающие эти частные случаи умножения, называются формулами сокращенного умножения.
1. Квадрат суммы. Возведем в квадрат сумму двух чисел a и b.
(a + b)2 = (a+b)(a+b) = a2 + ab + ab + b2
Приведя подобные члены получим:
(a + b)2 = a2 + 2ab + b2.
Эту формулу следует запомнить как в приведенной записи, так и в словесном выражении.
Квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа.
Примеры:
1)
(3a + 2b)2 = (3a)2 + 2 * 3a * 2b + (2b)2 = 9a2 + 12ab + 4b2.
Следует приобрести навык писать сразу окончательный результат, не проводя промежуточной записи, которая показана в этом примере.
2) Эта формула применяется при устном возведении в квадрат чисел, немного больших «круглого» числа, например:
412 = (40 + 1)2 = 402 + 2 * 40 * 1 + 12 = 1681;
322 = (30 + 2)2 = 302 + 2 * 2 * 30 + 22 = 900 + 120 + 4 = 1024.
3) Особенно легко запомнить прием возведения в квадрат чисел, оканчивающихся пятеркой. Положим, число имеет a десятков и 5 единиц. Тогда его можно записать так:
10a + 5.
Возведем это число в квадрат по формуле:
(10a + 5)2 = 100a2 + 2 * 5 * 10a + 52 = 100a2 + 100a + 25 = 100a(a + 1) + 25.
Полученное выражение показывает, что для возведения в квадрат числа, оканчивающегося пятеркой, надо число его десятков умножить на число, единицей большее, и к произведению приписать 25. Например:
652 = 6 * 7 * 100 + 25 = 4225;
852 = 8 * 9 (сотен) + 25 = 7225;
3,52 = 3 * 4 + 0,25 = 12,25.
Последний пример можно записать так:
Значит, чтобы возвести в квадрат смешанное число, дробная которого равна , достаточно целую часть умножить на число, единицей большее, и к произведению прибавить .2. Квадрат разности.
(a – b)2 = (a – b)(a – b) = a2 – ab – ab + b2.(a – b)2 = a2 – 2ab + b2.
Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа.
Эта формула отличается от ранее выделенной формулы только знаком среднего члена. Поэтому часто пишут сразу обе формулы так:Примеры:
1)
(4a2b – ab)2 = 16a4b2 – 8a2b * ab + a2b2 = 16a4b2 – 8a3b2 + a2b2.
И здесь следует стараться написать сразу результат, производя промежуточные вычисления в уме.
2) Эта формула применяется при устном возведении в квадрат чисел, немного меньших «круглого» числа, например:
392 = (40 – 1)2 = 402 – 2 * 40 + 1 = 1521;
482 = (50 – 2)2 = 2500 – 2 * 2 * 50 + 4 = 2304;
792 = (80 – 1)2 = 6400 – 160 + 1 = 6241.
3. Произведение суммы двух чисел на их разность.
(a + b)(a – b) = a2 + ab – ab – b2.(a + b)(a – b) = a2 – b2.
Произведение суммы двух чисел на их разность равно разности квадратов этих чисел.
Примеры.
1) (5a + 2b)(5a – 2b) = 25a2 – 4b2.
2) (2a2 + 3b3)(2a2 – 3b3) = 4a4 – 9b6.
3) Эта формула применяется при устном умножении двух чисел, из которых одно на несколько единиц больше «круглого» числа, на сколько другое меньше его, например: 47 и 53, 68 и 72.
47 * 53 = (50 – 3)(50 + 3) = 502 – 32 = 2491;
68 * 72 = 702 – 4 = 4896;
33 * 27 = 900 – 9 = 891.
4) Но иногда бывает полезно поступить наоборот: для вычисления разности квадратов двух чисел заменить эту разность произведением суммы оснований на их разность, например:
1022 — 1012 = (102 – 101)(102 + 101) = 203;
542 — 462 = (54 – 46)(54 + 46) = 800;
4. Куб суммы.
(a + b)3 = (a + b)2(a + b) = (a2 + 2ab + b2)(a + b) = a3 + 2a2b + ab2 + a2b + 2ab2 + b3;(a + b)3 = a3 + 3a2b + 3ab2 + b3.
Куб суммы двух чисел равен кубу первого числа, плюс утроенное произведение квадрата первого на второе, плюс утроенное произведение первого на квадрат второго, плюс куб второго числа.
Примеры.
1) (2a + 3b)3 = 8a3 + 3 * 4a2 * 3b + 3 * 2a * 9b2 + 27b3 = 8a3 + 36a2b + 54ab2 + 27b3.
2) 113 = 103 + 3 * 102 + 3 * 10 + 1 = 1331.
5. Куб разности.
(a – b)3 = (a – b)2(a – b) = (a2 – 2ab + b2)(a – b).
Произведя умножение и приведя подобные члены, получим:
(a – b)3 = a3 – 3a2b + 3ab2 – b3.
Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого на второе, плюс утроенное произведение первого на квадрат второго, минус куб второго числа.
Примеры.
1) (x – 2)3 = x3 – 6×2 + 12x – 8.
2) (3a – 2b)3 = 27a3 – 54a2b + 36ab2 – 8b3.
Если Вам нравится этот сайт…
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Для того что бы упростить алгебраические многочлены, существуют формулы сокращенного умножения
. Их не так уж и много и они легко запоминаются, а запомнить их нужно. Обозначения которые используются в формулах, могут принимать любой вид (число или многочлен).
Первая формула сокращенного умножения называется разность квадратов
. Она заключается в том что из квадрата одного числа отнимается квадрат второго числа равен величине разности данных чисел, а также их произведению.
а 2 — b 2 = (а — b)(a + b)
Разберем для наглядности:
22 2 — 4 2 = (22-4)(22+4)=18 * 26 = 468
9а 2 — 4b 2 c 2 = (3a — 2bc)(3a + 2bc)
Вторая формула о сумме квадратов
. Звучит она как, сумма двух величин в квадрате равняется квадрату первой величины к ней прибавляется двойное произведение первой величины умноженное на вторую, к ним прибавляется квадрат второй величины.
(а + b) 2 = a 2 +2ab + b 2
Благодаря данной формуле, становится намного проще вычислять квадрат от большого числа, без использования вычислительной техники.
Так к примеру:
квадрат от 112 будет равен
1) В начале разберем 112 на числа квадраты которых нам знакомы
112 = 100 + 12
2) Вписываем полученное в скобки возведенные в квадрат
112 2 = (100+12) 2
3) Применяя формулу, получаем:
112 2 = (100+12) 2 = 100 2 + 2 * 100 * 12 + 122 = 10000 + 2400+ 144 = 12544
Третья формула это квадрат разности
. Которая гласит о том, что две вычитаемые друг друга величины в квадрате равняются, тому что, от первой величины в квадрате отнимаем двойное произведение первой величины умноженное на вторую, прибавляя к ним квадрат второй величины.
(а +b) 2 = а 2 — 2аb + b 2
где (а — b) 2 равняется (b — а) 2 . В доказательство чему, (а-b) 2 = а 2 -2аb+b 2 = b 2 -2аb + а 2 = (b-а) 2
Четвертая формула сокращенного умножения называется куб суммы
. Которая звучит как: две слагаемые величины в кубе равны кубу 1 величины прибавляется тройное произведение 1 величины в квадрате умноженное на 2-ую величину, к ним прибавляется тройное произведение 1 величины умноженной на квадрат 2 величины, плюс вторая величина в кубе.
(а+b) 3 = а 3 + 3а 2 b + 3аb 2 + b 3
Пятая, как вы уже поняли называется куб разности
. Которая находит разности между величинами, как от первого обозначения в кубе отнимаем тройное произведение первого обозначения в квадрате умноженное на второе, к ним прибавляется тройное произведение первого обозначения умноженной на квадрат второго обозначения, минус второе обозначение в кубе.
(а-b) 3 = а 3 — 3а 2 b + 3аb 2 — b 3
Шестая называется — сумма кубов
. Сумма кубов равняется произведению двух слагаемых величин, умноженных на неполный квадрат разности, так как в середине нет удвоенного значения.
а 3 + b 3 = (а+b)(а 2 -аb+b 2)
По другому можно сказать сумму кубов можно назвать произведение в двух скобках.
Седьмая и заключительная, называется разность кубов
(ее легко перепутать с формулой куба разности, но это разные вещи). Разность кубов равняется произведению от разности двух величин, умноженных на неполный квадрат суммы, так как в середине нет удвоенного значения.
а 3 — b 3 = (а-b)(а 2 +аb+b 2)
И так формул сокращенного умножения всего 7, они похожи друг на друга и легко запоминаются, единственно важно не путаться в знаках. Они так же рассчитаны на то, что их можно использовать в обратном порядке и в учебниках собрано довольно много таких заданий
Будьте внимательны и все у вас получится.
Применяют для упрощения вычислений, а также разложение многочленов на множители, быстрого умножения многочленов. Большинство формул сокращенного умножения можно получить из бинома Ньютона — в этом Вы скоро убедитесь.
Формулы для квадратов
применяют в вычислениях чаще. Их начинают изучать в школьной программе начиная с 7 класса и до конца обучения формулы для квадратов и кубов школьники должны знать на зубок.
Формулы для кубов
не сильно сложные и их нужно знать при сведении многочленов к стандартному виду, для упрощения подъема суммы или разности переменной и числа к кубу.
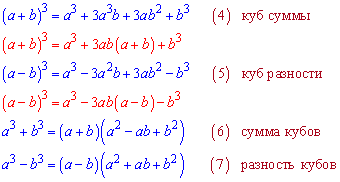
Формулы обозначены красным получают из предыдущих группировкой подобных слагаемых.
Формулы для четвертого и пятого степени
в школьном курсе мало кому пригодятся, однако есть задачи при изучении высшей математики где нужно вычислять коэффициенты при степенях.
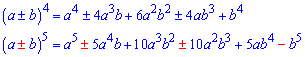
Формулы для степени
n
расписаны
через биномиальные коэффициенты с использованием факториалов следующие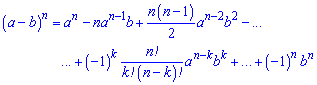
Квадрат разности двух выражений
Формула квадрата разности двух выражений выглядит следующим образом:
(a − b)2 = a2 − 2ab + b2
Эту формулу можно прочитать так:
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Формула квадрата разности двух выражений выводится таким же образом, как и формула квадрата суммы двух выражений. Выражение (a − b)2 представляет собой произведение двух многочленов, каждый из которых равен (a − b)
(a − b)2 = (a − b)(a − b)
Если выполнить это умножение, то получится многочлен a2 − 2ab + b2
(a − b)2 = (a − b)(a − b) = a2 − ab − ab + b2 = a2 − 2ab + b2
Пример 1. Преобразовать выражение (7x − 5)2 в многочлен.
Воспользуемся формулой квадрата разности двух выражений:
(a − b)2 = a2 − 2ab + b2
(7x − 5)2 = (7x)2 − 2 × 7x × 5 + 52 = 49×2 − 70x + 25
Значит, (7x − 5)2 = 49×2 − 70x + 25.
Попробуем решить данный пример, не пользуясь формулой квадрата разности. У нас должен получиться тот же результат:
(7x − 5)2 = (7x − 5)(7x − 5) = 49×2 − 35x − 35x + 25 = 49×2 − 70x + 25.
Формула квадрата разности двух выражений тоже имеет геометрический смысл. Если площадь квадрата со стороной a равна a2, то площадь квадрата, сторона которого уменьшена на b, будет равна (a − b)2
Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке уменьшили на b. У квадрата все стороны равны. Если одну сторону уменьшить на b, то остальные стороны тоже уменьшатся на b
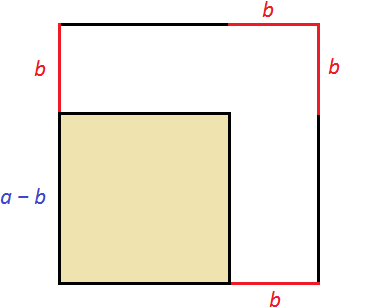
Получился новый квадрат, который меньше предыдущего. На рисунке он выделен жёлтым. Сторона его равна a − b, поскольку старая сторона a уменьшилась на b. Чтобы вычислить площадь этого квадрата, можно из первоначальной площади квадрата a2 вычесть площади прямоугольников, которые получились в процессе уменьшения сторон старого квадрата. Покажем эти прямоугольники:
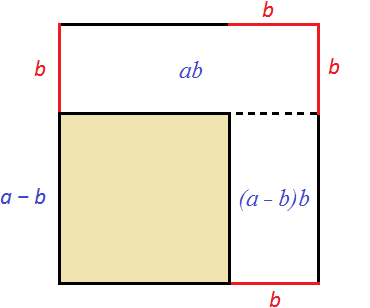
Тогда можно написать следующее выражение: старая площадь a2 минус площадь ab минус площадь (a − b)b
a2 − ab − (a − b)b
Раскроем скобки в выражении (a − b)b
a2 − ab − ab + b2
Приведем подобные слагаемые:
a2 − 2ab + b2
В результате получается выражение a2 − 2ab + b2, которое является правой частью формулы квадрата разности двух выражений:
(a − b)2 = a2 − 2ab + b2
Формулы квадрата суммы и квадрата разности в общем называют формулами сокращённого умножения. Эти формулы позволяют значительно упростить и ускорить процесс перемножения многочленов.
Ранее мы говорили, что рассматривая член многочлена по отдельности, его нужно рассматривать вместе со знаком, который перед ним располагается.
Но применяя формулы сокращённого умножения, знак исходного многочлена не следует рассматривать в качестве знака самого этого члена.
Например, если дано выражение (5x − 2y)2, и мы хотим воспользоваться формулой (a − b)2 = a2 − 2ab + b2, то вместо b нужно подставлять 2y, а не −2y. Это особенность работы с формулами, которую не следует забывать.
(5x − 2y)2a = 5xb = 2y(5x − 2y)2 = (5x)2 − 2 × 5x × 2y + (2y)2 = 25×2 − 20xy + 4y2
Если подставлять −2y, то это будет означать, что разность в скобках исходного выражения была заменена на сумму:
(5x − 2y)2 = (5x + (−2y))2
и в таком случае нужно применять не формулу квадрата разности, а формулу квадрата суммы:
(5x + (−2y)2a = 5xb = −2y(5x + (−2y))2 = (5x)2 + 2 × 5x × (−2y) + (−2y)2 = 25×2 − 20xy + 4y2
Исключением могут быть выражения вида (x − (−y))2. В данном случае, применяя формулу (a − b)2 = a2 − 2ab + b2 вместо b следует подставить (−y)
(x − (−y))2 = x2 − 2 × x × (−y) + (−y)2 = x2 + 2xy + y2
Но возводя в квадрат выражения вида x − (−y), удобнее будет заменять вычитание на сложение x + y. Тогда первоначальное выражение примет вид (x + y)2 и можно будет воспользоваться формулой квадрата суммы, а не разности:
(x + y)2 = x2 + 2xy + y2
Формулы для кубов
До этого мы познакомились с тождествами, в которых величины возводились во вторую степень. Их будет достаточно почти для всех школьных заданий, в том числе и на ЕГЭ, поэтому необходимо сосредоточиться именно на их изучении.Однако в алгебре есть и более сложные формулы сокращенного умножения, в которых переменные возводятся в куб.Их использование может пригодиться в задачах повышенной сложности. Выведем их.
Найдем значение куба суммы двух слагаемых. Для этого возведем в куб выражение a + b:
(a + b)3 = (a + b)2(a + b) = (a2 + 2ab + b2)(a + b) = a3 + a2b + 2a2b + 2ab2 + ab2 + b3 = a3 + 3a2b + 3ab2 + b3
Получили тождество
(a + b)3 = a3 + 3a2b + 3ab2 + b3
которое называют формулой куба суммы.
Пример. Вычислите 1013
Решение.
1013 = (100 + 1)3 = 1003 + 3*1002*1 + 3*100*12 + 1 = 1000000 + 30000 + 300 + 1 = 1030301
Ответ: 1030301.
Пример. Представьте в виде многочлена выражение (4p + 3k)3.
Решение. Воспользуемся формулой куба суммы:
(4p + 3k)3 = (4p)3 + 3*(4p)2*3k + 3*4p*(3k)2 + (3k)3 = 64p3 + 144p2k + 108pk2 + 27k3
Выведем аналогичным образом и формулу куба разности чисел:
(a — b)3 = (a — b)2(a — b) = (a2 — 2ab + b2)(a — b) = a3 — a2b — 2a2b + 2ab2 — b3 = a3 — 3a2b + 3ab2 — b3
Итак, мы получили ещё одно тождество
(a — b)3 = a3 — 3a2b + 3ab2 — b3
Пример. Вычислите 4983.
Решение. Представим число 498 как разность 500 – 2. Тогда для вычисления можно воспользоваться выражением для вычисления куба разности:
4983 = (500 — 2)3 = 5003 — 3*5002*2 + 3 * 500 * 22 — 23 = 125000000 — 1500000 + 6000 — 8 = 123505992
Ответ: 123505992.
Сложнее получить тождества для суммы и разности кубов, ведь напрямую найти разложить на множители выражение a3 + b3 довольно тяжело. К счастью, математикам удалось подобрать новые множители.
Сначала рассмотрим выражение
a2 + ab + b2
Оно отличается от квадрата суммы только одним слагаемым. Вместо 2ab стоит ab. Из-за этой схожести его называют неполным квадратом суммы.
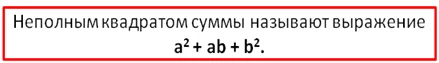
Аналогично определяют и такое понятие, как неполный квадрат разности.
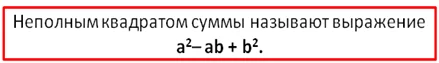
Теперь попробуем перемножить неполный квадрат суммы чисел a и b и их разность:
(a — b)(a2 + ab + b2) = a3 + a2b + ab2 — a2b — ab2 — b3 = a3 — b3
В результате нам удалось получить формулу разности кубов:
a3 — b3 = (a — b)(a2 + ab + b2)

Теперь попробуем умножить сумму двух величин на неполный квадрат разности:
(a + b)(a2 — ab + b2) = a3 — a2b + ab2 + a2b — ab2 + b3 = a3 + b3
Получили формулу суммы кубов:
a3 + b3 = (a + b)(a2 — ab + b2)

Понятно, что запомнить все эти тождества нелегко, однако их всегда можно посмотреть в любом математическом справочнике.
Пример. Разложите на множители полином 8p3 + 0,001q3.
Решение. Здесь можно воспользоваться тождеством для куба суммы:
8p3 + 0.001q3 = (2p)3 + (0.1q)3 = (2p + 0.1q)((2p)2 — 2p*0.1q + (0.1q)2) = (2p + 0.1q)(4p2 — 0.2pq +0.01q2)
Применять формулы с кубами для вычислений значительно сложнее, чем со вторыми степенями, однако всё же иногда они могут помочь. Пусть надо вычислить значение выражения 553 + 453, не используя калькулятор или компьютер. Разложим его на множители:
533 + 453 = (55 + 45)(552 — 55*45 + 452) = 100(552 — 55*45 + 452)
Далее для упрощения расчетов добавим к значению в скобке произведение 55•45 и тут же отнимем его. Это позволит сделать «дополнить» неполный квадрат разности и воспользоваться соответствующей формулой сокращенного умножения:
100(552 — 55*45 + 452) = 100((552 — 55*45 — 55*45 + 452 + 55*45) = 100((552 — 2*55*45 + 452) + 55*45) = 100((55 — 45)2 55*45) = 100((10)2 + 55*45) = 100(100 + 55*45)
В свою очередь произведение 55•45 можно также упростить:
100(100 + 55*45) = 100(100 + (50 + 5)*(50 — 5)) = 100(100 + (502 — 52)) = 100(100 + 2500 — 25) = 100*2575 = 257500
Полученный результат можно проверить с помощью калькулятора:
553 + 453 = 257500
Примеры задач для 7−8 класса
В заключение разберём и решим два задания на применение формул сокращённого умножения по алгебре.
Задача 1. Упростить выражение:
(m + 3)² + (3m + 1)(3m — 1) — 2m (5m + 3).
Решение. В условии задания требуется упростить выражение, т. е. раскрыть скобки, выполнить действия умножения и возведения в степень, а также привести все подобные слагаемые. Условно разделим выражение на три части (по числу слагаемых) и поочерёдно раскроем скобки, применяя ФСУ там, где это возможно.
-
(m + 3)² = m² + 6m + 9
(квадрат суммы); -
(3m + 1)(3m — 1) = 9m² — 1
(разность квадратов); - В последнем слагаемом необходимо выполнить перемножение: 2m (5m + 3) = 10m² + 6m
.
Подставим полученные результаты в исходное выражение:
(m² + 6m + 9) + (9m² — 1) — (10m² + 6m)
.
С учётом знаков раскроем скобки и приведём подобные слагаемые:
m² + 6m + 9 + 9m² 1 — 10m² — 6m = 8.
Задача 2. Решить уравнение, содержащее неизвестное k в 5 степени:
k⁵ + 4k⁴ + 4k³ — 4k² — 4k = k³.
Решение. В этом случае необходимо воспользоваться ФСУ и методом группировки. Нужно перенести последнее и предпоследнее слагаемое в правую часть тождества.
k⁵ + 4k⁴ + 4k³ = k³ + 4k² + 4k.
Из правой и из левой части выносится общий множитель (k² + 4k +4)
:
k³(k² + 4k + 4) = k (k² + 4k + 4)
.
Всё переносится в левую часть уравнения, чтобы в правой остался 0:
k³(k² + 4k + 4) — k (k² + 4k + 4) = 0
.
Снова необходимо вынести общий множитель:
(k³ — k)(k² + 4k + 4) = 0.
Из первого полученного сомножителя можно вынести k
. По формуле краткого умножения второй множитель будет тождественно равен (k + 2)²
:
k (k² — 1)(k + 2)² = 0.
Использование формулы разности квадратов:
k (k — 1)(k + 1)(k + 2)² = 0.
Поскольку произведение равно 0, если хотя бы один из его множителей нулевой, найти все корни уравнения не составит труда:
- k = 0;
- k — 1 = 0; k = 1;
- k + 1 = 0; k = -1;
- (k + 2)² = 0; k = -2.
На основании наглядных примеров можно понять, как запомнить формулы, их отличия, а также решить несколько практических задач с применением ФСУ. Задачи простые, и при их выполнении не должно возникнуть никаких сложностей.
Среди различных выражений, которые рассматриваются в алгебре, важное место занимают суммы одночленов.
Приведем примеры таких выражений:
\(5a^4 — 2a^3 + 0,3a^2 — 4,6a + 8 \)
\(xy^3 — 5x^2y + 9x^3 — 7y^2 + 6x + 5y — 2 \)
Сумму одночленов называют многочленом. Слагаемые в многочлене называют членами многочлена. Одночлены также относят к многочленам,
считая одночлен многочленом, состоящим из одного члена.
Например, многочлен
\(8b^5 — 2b \cdot 7b^4 + 3b^2 — 8b + 0,25b \cdot (-12)b + 16 \)
можно упростить.
Представим все слагаемые в виде одночленов стандартного вида:
\(8b^5 — 2b \cdot 7b^4 + 3b^2 — 8b + 0,25b \cdot (-12)b + 16 = \)
\(= 8b^5 — 14b^5 + 3b^2 -8b -3b^2 + 16 \)
Приведем в полученном многочлене подобные члены:
\(8b^5 -14b^5 +3b^2 -8b -3b^2 + 16 = -6b^5 -8b + 16 \)
Получился многочлен, все члены которого являются одночленами стандартного вида, причем среди них нет подобных.
Такие многочлены называют многочленами стандартного вида
.
За степень многочлена
стандартного вида принимают наибольшую из степеней его членов.
Так, двучлен \(12a^2b — 7b \) имеет третью степень, а трехчлен \(2b^2 -7b + 6 \) — вторую.
Обычно члены многочленов стандартного вида, содержащих одну переменную, располагают в порядке убывания показателей ее степени.
Например:
\(5x — 18x^3 + 1 + x^5 = x^5 — 18x^3 + 5x + 1 \)
Сумму нескольких многочленов можно преобразовать (упростить) в многочлен стандартного вида.
Иногда члены многочлена нужно разбить на группы, заключая каждую группу в скобки. Поскольку заключение в скобки — это
преобразование, обратное раскрытию скобок, то легко сформулировать правила раскрытия скобок:
Если перед скобками ставится знак «+», то члены, заключаемые в скобки, записываются с теми же знаками.
Если перед скобками ставится знак «-», то члены, заключаемые в скобки, записываются с противоположными знаками.
Краткое описание
В алгебре большим спросом пользуются различные формулы и соответствующие правила сокращённого умножения. При правильном подходе ученик может максимально быстро и правильно решать большие уравнения. Универсальные формулы были получены специалистами для умножения и вычитания сразу нескольких многочленов. Только подготовленные ученики могут максимально быстро решать поставленные задачи, существенно упростив используемое выражение. Базовые правила востребованных преобразований позволяют выполнять определённые манипуляции с уравнениями.
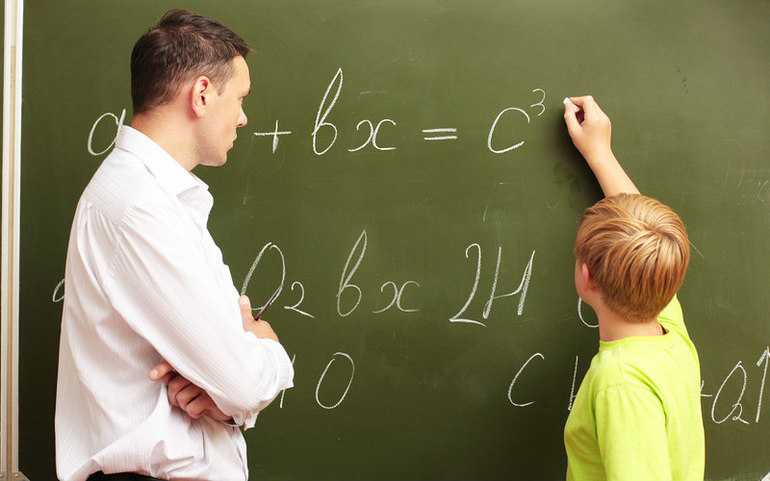
Если максимально придерживаться основных рекомендаций, то можно будет получить в левой части примера равенство выражения, расположенное с правой стороны. Ученик должен хорошо владеть теми формулами, которые применяются для сокращённого умножения, используемого во время решения задач, а также уравнений. Но даже в этом случае нужно соблюдать ряд нюансов, чтобы можно было избежать допущения грубых ошибок.
Интересным фактом является то, что некоторые формулы для быстрого умножения были выведены экспертами ещё в конце четвёртого тысячелетия до нашей эры. Именно целеустремлённые греки максимально развили идеи своих предшественников, из-за чего им удалось разработать сразу несколько важных и полезных правил. Но в те времена математики мыслили совершенно иначе, так как они стремились воссоздать числа с помощью подручных материалов или геометрических фигур. К примеру: специально обтёсанные камни на счётной доске из дерева.
Ещё несколько лет назад формулы для определения суммы различных величин выводились исключительно геометрическим методом. Эксперты практиковали рассечение квадрата на разные фрагменты. Настоящий подъём науки пришёлся на времена Ньютона и других учёных. Именно эти целеустремлённые люди смогли внести огромный вклад в развитие формул для алгебры, представив обществу усовершенствованный вариант.
Умножение разности двух выражений на неполный квадрат их суммы
Встречаются задачи, в которых требуется умножить разность двух выражений на неполный квадрат их суммы. Выглядит это произведение следующим образом:
(a − b)(a2 + ab + b2)
Первый многочлен (a − b) является разностью двух выражений, а второй многочлен (a2 + ab + b2) является неполным квадратом суммы этих двух выражений.
Неполный квадрат суммы это многочлен вида a2 + ab + b2. Он похож на обычный квадрат суммы a2 + 2ab + b2 за исключением того, что в нём произведение первого и второго выражений не удваивается.
Например, выражение 4×2 + 6xy + 9y2 является неполным квадратом суммы выражений 2x и 3y.
Действительно, первый член выражения 4×2 + 6xy + 9y2, а именно 4×2 является квадратом выражения 2x, поскольку (2x)2 = 4×2. Третий член выражения 4×2 + 6xy + 9y2, а именно 9y2 является квадратом выражения 3y, поскольку (3y)2 = 9y2. Член находящийся в середине 6xy, является произведением выражений 2x и 3y.
Итак, умножим разность (a − b) на неполный квадрат суммы a2 + ab + b2
(a − b)(a2 + ab + b2) = a(a2 + ab + b2) − b(a2 + ab + b2) =a3 + a2b + ab2 − a2b − ab2 − b3 = a3 − b3
То есть выражение (a − b)(a2 + ab + b2) равно a3 − b3
(a − b)(a2 + ab + b2) = a3 − b3
Это тождество называют формулой умножения разности двух выражений на неполный квадрат их суммы. Эту формулу можно прочитать так:
Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений.
Пример 1. Выполнить умножение (2x − 3y)(4×2 + 6xy + 9y2)
Первый многочлен (2x − 3y) это разность двух выражений 2x и 3y. Второй многочлен 4×2 + 6xy + 9y2 это неполный квадрат суммы двух выражений 2x и 3y. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a − b)(a2 + ab + b2) = a3 − b3. В нашем случае умножение (2x − 3y)(4×2 + 6xy + 9y2) можно заменить на разность кубов 2x и 3y
(2x − 3y)(4×2 + 6xy + 9y2) = (2x)3 − (3y)3 = 8×3 − 27y3
Попробуем решить этот же пример, не пользуясь формулой (a − b)(a2 + ab + b2) = a3 − b3. У нас получится тот же результат, но решение станет длиннее:
(2x − 3y)(4×2 + 6xy + 9y2) = 2x(4×2 + 6xy + 9y2) − 3y(4×2 + 6xy + 9y2) =8×3 + 12x2y + 18xy2 − 12x2y − 18xy2 − 27y3 = 8×3 − 27y3
Пример 2. Выполнить умножение (3 − x)(9 + 3x + x2)
Первый многочлен (3 − x) является разностью двух выражений, а второй многочлен является неполным квадратом суммы этих двух выражений. Это позволяет воспользоваться формулой (a − b)(a2 + ab + b2) = a3 − b3
(3 − x)(9 + 3x + x2) = 33 − x3 = 27 − x3
Дополнительные формулы сокращенного умножения
Есть три основные дополнительные ФСУ – это бином Ньютона, формула возведения в квадрат суммы трех, четырех и более слагаемых, а также формула разности n-ых степеней двух слагаемых. Коротко о каждой из них.
Бином Ньютона
Бином Ньютона – это формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Выглядит она следующим образом:
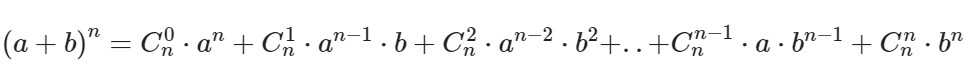
Ck в степени n – это биноминальные коэффициенты, стоящие в строке под номером n в треугольнике Паскаля. Вычисляются эти коэффициенты по формуле:
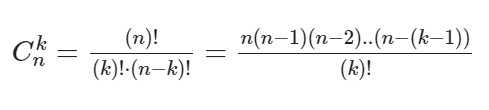
Иначе говоря, ФСУ для квадрата и куба разности и суммы являются частными случаями формулы бинома Ньютона при n=2 и n=3 соответственно.
Однако может быть так, что слагаемых в сумме, которую нужно возвести в степень, больше, чем два. В таком случае подойдет формула квадрата суммы трех, четырех и более слагаемых.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Как и было сказано, формула возведения в квадрат суммы трех, четырех и более слагаемых нужна, когда слагаемых в сумме, которую нужно возвести в степень, больше, чем два.
Выглядит она так:
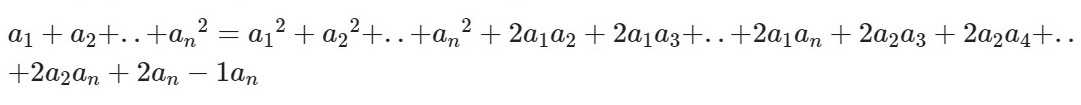
Читать и запоминать эту формулу нужно следующим образом: квадрат суммы n слагаемых равен сумме квадратов всех слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
И последняя формула – это формула разности n-ых степеней двух слагаемых, выглядящая вот так:
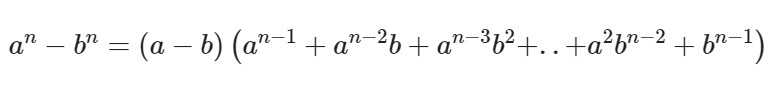
Как правило, данную формулу разделяют на две отдельные: для четных и нечетных степеней.
Формула для четных показателей 2m:
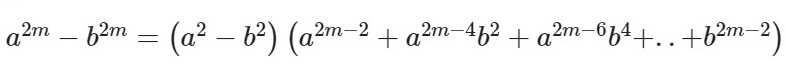
Формула для нечетных показателей 2m + 1:
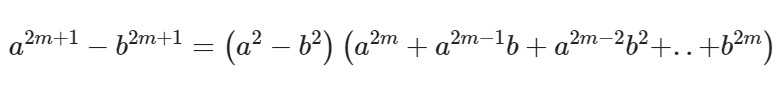
Несложно догадаться, что ФСУ разности квадратов и кубов являются частными случаями данной формулы при n=2 и n=3 соответственно. А для разности кубов b заменяется на –b.
Рассмотренные нами ФСУ и дополнительные ФСУ обязательно помогут вам быстрее справляться с математическими задачами и занимать свой мозг полезной деятельностью.
Вопросы и ответы
И напоследок несколько ответов на часто задаваемые вопросы.
Для чего нужны формулы сокращенного умножения?
Формулы сокращенного умножения нужны, чтобы упростить и ускорить вычисления, а также для улучшения наглядности и понимания математических выражений.
В настоящее время ФСУ широко используются в образовании и науке, а также в практической жизни. Они применяются в различных областях, таких как математика, физика, химия и инженерия, плюс могут применяться к решению различных задач, например, в области финансов, менеджмента и исследования данных.
Как появились формулы сокращенного умножения?
Формулы сокращенного умножения появились в результате исследований математиков в области алгебры и арифметики и основаны на использовании их свойств, таких как коммутативность, ассоциативность и дистрибутивность.
Если обратиться к истории, можно узнать, что такими формулами пользовались еще в Древнем Вавилоне и Древнем Египте. Первым же, кто доказал математическую закономерность квадрата суммы, был древнегреческий ученый Евклид, живший в III веке до н.э. А на общепринятом языке математические формулы были обоснованы Исааком Ньютоном.
Сколько всего формул сокращенного умножения?
Не существует точного количества формул сокращенного умножения, т.к. их можно создавать неограниченное количество. Но в основном изучают и используют семь основных формул. Это квадрат суммы, квадрат разности, разность квадратов, сумма кубов, разность кубов, куб суммы и куб разности. Также распространено применения трех дополнительных ФСУ, таких как бином Ньютона, формула возведения в квадрат суммы трех, четырех и более слагаемых и формула разности n-ых степеней двух слагаемых.
Почему формулы сокращенного умножения изучают на алгебре в 7 классе?
Формулы сокращенного умножения изучаются на алгебре в 7 классе, потому что именно на этом этапе школьники знакомятся с понятием многочлена и действиям с ним. Кроме того, ФСУ являются важным и основным инструментом для решения математических задач и упрощения вычислений.
Формулы помогают ученикам развить навыки в решении простых задач, а также дают им навыки для решения более сложных задач в будущем, что в перспективе способно помочь молодым людям в их дальнейшем обучении и карьере.
Можно ли не использовать формулы сокращенного умножения?
Конечно, при решении математических задач можно и не использовать формулы сокращенного умножения. Однако без них процесс решения может оказаться очень трудоемким и долгим. ФСУ же заметно упрощают его и помогают справляться с заданиями намного быстрее.
Помимо прочего, ФСУ входят в обязательную школьную программу, вследствие чего преподаватели часто требуют от учеников, во-первых, знать эти формулы наизусть, а во-вторых, решать задания именно с их помощью.






























