Формула и удивительная история её возникновения
Самая обычная формула для большинства случаев имеет вид: m = pV , где m – масса тела, p и V – плотность вещества и его объём, занимаемый в пространстве соответственно. Можно, конечно, не заморачиваться и посчитать всё на онлайн-ресурсах, но знать формулу всё же полезно. Соответственно V = m / p , p = m / V .
Самое интересное – это то, что формулу нашёл мужик, который бегал голышом по улице и был при этом другом царя. Интересно? Тогда следующие три абзаца для вас.
Был в Древней Греции такой царь-тиран, как Гиерон II. Он начал подозревать, что его корону сделали не из чистого золота и ювелиры его облапошили. Но Гиерон не знал, как можно это доказать. Тогда он обратился к умнейшему человеку того времени – Архимеду
Получив приказ разобраться с делами государственной важности, Архимед день за днём стал искать решение вопроса
Ох, и нелёгкая же задачка выпала учёному. Ведь на то время не было ни нужных формул, ни современных девайсов, ни гугла, чтобы быстренько найти решение. И вот однажды, придя в баню и погрузившись в неё, Архимед заметил, что выливающаяся вода равна по объёму тому, что погружено в воду.
Эврика! – Прокричал Архимед и нагишом поспешил в свою лабораторию проводить опыты. Учёный сложил все данные в своей голове и позже проделал следующий опыт: он взял корону и опустил её в воду. Затем он взял кусок золота такого же веса и опустил его также в воду. Объём вытесненной воды получился разным. Если бы корона была сделана из чистого золота, то её объём и слитка совпали. Это доказывало то, что ювелиры обманули царя. Кто бы мог подумать, что одно из величайших открытий появилось благодаря обманщикам, тирану и учёному.
Примеры расчета плотности формулы
Расчет плотности формулы может быть полезным при изучении и анализе химических реакций, рассмотрении физических процессов и определении концентраций растворов. Вот несколько примеров расчета плотности формулы.
-
Пример 1: Расчет плотности раствора с известной массой и объемом.
Пусть у нас есть раствор, в котором содержится 50 г вещества и его объем составляет 100 мл. Чтобы расчитать плотность такого раствора, необходимо разделить массу вещества на объем раствора.
Плотность = Масса / Объем
Плотность = 50 г / 100 мл = 0.5 г/мл
-
Пример 2: Расчет массы вещества по известной плотности и объему.
Пусть у нас есть раствор с плотностью 1.2 г/мл и объемом 75 мл. Чтобы расчитать массу вещества в этом растворе, необходимо умножить плотность на объем.
Масса = Плотность * Объем
Масса = 1.2 г/мл * 75 мл = 90 г
-
Пример 3: Расчет объема раствора по известной массе и плотности.
Пусть у нас есть раствор массой 60 г и плотностью 0.8 г/мл. Чтобы расчитать объем такого раствора, необходимо разделить массу на плотность.
Объем = Масса / Плотность
Объем = 60 г / 0.8 г/мл = 75 мл
-
Пример 4: Расчет плотности газа.
Плотность газа можно рассчитать по формуле:
Плотность = (Масса газа * Молярная масса газа) / (Объем газа * Универсальная газовая постоянная)
Для расчета плотности газа необходимо знать его массу, молярную массу, объем и универсальную газовую постоянную.
Определение плотности
Определение плотности газов, жидкостей и твердых веществ осуществляется с целью исследования свойств веществ, идентификации и определения степени их чистоты, определения концентрации двухкомпонентных растворов спиртов, кислот и оснований.
Плотность однородного вещества р — физическая величина, равная отношению массы т вещества к занимаемому им объему V:
Единицей плотности в Международной системе единиц (СИ) является килограмм на кубический метр; в единицах СГС плотность выражается в граммах на кубический сантиметр.
Относительная плотность вещества — величина, равная отношению его плотности к плотности некоторого другого вещества при определенных физических условиях. Такими стандартными веществами служат вода при температуре 3,98 °С и нормальном атмосферном давлении (760 мм рт. ст., или 1013 гПа) или сухой воздух при 20 °С и нормальном атмосферном давлении:
где р — плотность данного вещества, р0 — плотность стандартного вещества.
Относительная плотность — безразмерная величина. Относительную плотность жидкости принято относить к температуре 20 °С и к плотности воды при 3,98 °С (4°С). В этом случае относительная плотность обозначается d204.
В тех случаях, когда плотность жидкости по условиям опыта определяют не при 20 °С, а при другой температуре t, ее значение dt4 может быть пересчитано на нормальное значение по формуле:
где dt4 — относительная плотность исследуемой жидкости при температуре испытания t°С; a — средняя температурная поправка на 1 °С, находимая по табл. 14.
Относительная плотность является одной из важнейших физико-химических характеристик веществ (особенно жидкостей), наряду с температурой плавления и кипения.
Плотность веществ определяют с помощью пикнометров, ареометров и гидростатических весов.
Обозначения и термины
Далее будет приведён список понятий и их определение в условиях понятий об измерениях плотности:
- Масса – плотность тела, помноженная на его объём, занимаемый в пространстве. Это также величина, определяющая силу воздействия гравитационного поля на объект.
- Объём – физическая величина, характеризующая количество пространства, занимаемое объектом.
- Плотность определяет то, какое количество вещества умещается в объёме при определённом весе в стандартных условиях.
- Нормальные/стандартные условия в разных организациях имеют свои значения. К таким условиям относятся температура окружающей среды, атмосферное давление и в отдельных случаях прочие параметры.
- Атмосферное давление – понятие, применяемое больше для газов, так как на их объём имеет большое влияние, нежели на твёрдые вещества. Атмосферное давление можно определить как силу, с которой воздействует воздух на Землю под действием гравитационного поля.
- Температура – физический показатель степени нагрева вещества. Чем больше температура, тем больше объём тела.
Атомная и ядерная физика
К оглавлению…
Энергия кванта электромагнитной волны (в т.ч. света) или, другими словами, энергия фотона вычисляется по формуле:
Импульс фотона:
Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ):
Максимальная кинетическая энергия вылетающих электронов при фотоэффекте может быть выражена через величину задерживающего напряжение Uз и элементарный заряд е:
Существует граничная частота или длинна волны света (называемая красной границей фотоэффекта) такая, что свет с меньшей частотой или большей длиной волны не может вызвать фотоэффект. Эти значения связаны с величиной работы выхода следующим соотношением:
Второй постулат Бора или правило частот (ЗСЭ):
В атоме водорода выполняются следующие соотношения, связывающие радиус траектории вращающегося вокруг ядра электрона, его скорость и энергию на первой орбите с аналогичными характеристиками на остальных орбитах:
На любой орбите в атоме водорода кинетическая (К) и потенциальная (П) энергии электрона связаны с полной энергией (Е) следующими формулами:
Общее число нуклонов в ядре равно сумме числа протонов и нейтронов:
Дефект массы:
Энергия связи ядра выраженная в единицах СИ:
Энергия связи ядра выраженная в МэВ (где масса берется в атомных единицах):
Формула альфа-распада:
Формула бета-распада:
Закон радиоактивного распада:
Ядерные реакции
Для произвольной ядерной реакции описывающейся формулой вида:
Выполняются следующие условия:
Энергетический выход такой ядерной реакции при этом равен:
Примеры решения задач
Прежде чем приступить к примерам, следует понимать, что если данные даны в килограммах и кубических сантиметрах, то нужно либо сантиметры перевести в метры, либо килограммы перевести в граммы. По такому же принципу надо переводить и остальные данные – миллиметры, тонны и так далее.
Задача 1. Найти массу тела, состоящего из вещества, плотность которого равна 2350 кг/м³ и имеет объём 20 м³. Применяем стандартную формулу и с лёгкостью находим значение. m = p*V= 2 350 * 20 = 47 000 кг.
Задача 2. Уже известно, что плотность чистого золота без примесей равна 19,32 г/см³. Найти массу драгоценной цепочки из золота, если объём составляет 3,7 см³. Воспользуемся формулой и подставим значения. p = m / V = 19,32/3,7 = 5,22162162 гр.
Задача 3. На склад поставили металл с плотностью 9250 кг/м³. Масса составляет 1,420 тонн. Нужно найти занимаемый металлом объём. Тут нужно сначала перевести либо тонны в килограммы, либо метры в километры. Проще будет воспользоваться первым методом. V = m / p = 1420/9250 = 0.153513514 м³.
Как найти плотность в физике
Для того, чтобы найти плотность, нужно знать массу и объем вещества. Формула для расчета плотности выглядит следующим образом:
Плотность = Масса / Объем
Массу можно определить с помощью весов или на основе известной плотности и объема. Объем может быть найден путем измерений или вычислений в зависимости от конкретной задачи.
Приведем пример расчета плотности. Предположим, у нас есть стальной шар с массой 2 кг и объемом 0,1 м³. Чтобы найти плотность, нужно поделить массу на объем:
Плотность = 2 кг / 0,1 м³ = 20 кг/м³
Таким образом, плотность стального шара равна 20 кг/м³.
Плотность имеет важное значение при изучении свойств вещества и его поведения в различных условиях. Она помогает определить, насколько плотное или редкое вещество, как оно будет взаимодействовать с другими веществами, а также каковы будут его физические и химические свойства
Важно помнить, что плотность может изменяться в зависимости от температуры и давления. Поэтому в некоторых задачах может потребоваться учет этих факторов
Теперь, когда вы знаете как найти плотность в физике, вы сможете успешно решать множество задач и понимать мир вокруг себя с точки зрения науки.
Что есть плотность
В первом приближении определение плотности кажется простым и понятным: плотность есть скалярная физическая величина (характеристика вещества), задаваемая как отношение собственной массы тела к общему объёму, этим телом занимаемому. Однако намётанный глаз сразу подметит «скользкое» место, а именно: о каком именно состоянии тела идёт речь, насколько оно однородно? Действительно, газ или жидкость (с некоторыми ограничениями) — тела в бытовом понимании по сути своей изотропные (то есть с характеристиками, одинаковыми в пределах интересующего физического объёма и не зависящими от выбранного направления в этом объёме), однако как быть с твёрдыми телами?
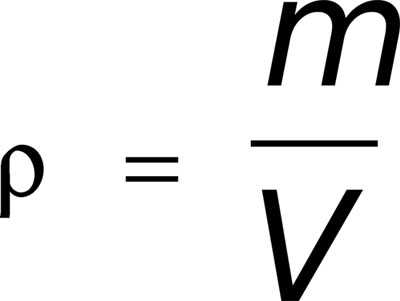
В предельном случае это можно продемонстрировать на твёрдом сыпучем материале, где в одном общем объёме находятся и частички самого материала, и пустоты между ними (хорошо учившие физику в школе попутно возразят, что примерно такую же картину можно получить и с газами/жидкостями, если начать «дробить» их до молекулярного/атомного уровня). Поэтому вышеприведённое определение подразумевает среднюю (иначе — усреднённую) характеристику тела для выбранного характеристического размера, а для сыпучих тел отдельно вводятся понятия «истинной плотности» (усреднённая характеристика, рассчитываемая только по фактическому объёму самих частиц) и «насыпной плотности» (расчётная характеристика для сыпучего материала с учётом всех его пустот — но без дополнительного уплотнения).
Перед переходом ко второму интересующему определению не лишним будет напомнить, что также существует и иногда практически используется на производстве термин «удельная плотность«, задаваемый как отношение плотности интересующего объекта к плотности вещества-эталона (для газов и жидкостей таковыми эталонами типично служат вода и воздух)
Для оперирования удельной плотностью важно, чтобы и объект, и эталон находились при одинаковой температуре/давлении (причина в том, что в различных системах измерений эти «стандартные величины» могут браться за условную «точку отсчёта» по-разному)
Работа, мощность, энергия
Механическая работа рассчитывается по следующей формуле:
Самая общая формула для мощности (если мощность переменная, то по следующей формуле рассчитывается средняя мощность):
Мгновенная механическая мощность:
Коэффициент полезного действия (КПД) может быть рассчитан и через мощности и через работы:
Формула для кинетической энергии:
Потенциальная энергия тела поднятого на высоту:
Потенциальная энергия растянутой (или сжатой) пружины:
Полная механическая энергия:
Связь полной механической энергии тела или системы тел и работы внешних сил:
Закон сохранения механической энергии (далее – ЗСЭ). Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):
Электричество и магнетизм
Электрическое поле
| Сила Кулона: | `F=k(q_1*q_2)/r^2` |
| Поле точечного заряда: | `E=kq/r^2` | |
| Сила, действующая на заряд в эл.поле: | `F=q*E` | |
| Потенциал поля: | `varphi=W/q` | где `W` — потенциальная энергия заряда в поле |
| Работа по перемещению заряда: | `A=DeltaW=qDeltavarphi=qU` | |
| Напряжение в однородном поле: | `U=Ed` | |
| Ёмкость конденсатора (любого): | `C=q/U` | |
| Ёмкость плоского конденсатора: | `C=(epsilonepsilon_0S)/d` | |
| Параллельное соединение конденсаторов: | `C_(общ)=C_1+C_2+…` | |
| Последовательное соединение конденсаторов: | `1/C_(общ)=1/C_1+1/C_2+…` | |
| Энергия конденсатора: | `W_c=(CU^2)/2=(qU)/2=q^2/(2C)` |
Постоянный ток
| Сила тока: | `I=(Deltaq)/(Deltat)` | |
| Переменный ток: | `I(t)=q'(t)` | |
| Сопротивление: | `R=rhol/S` | где `rho` — удельное сопротивление |
| Закон Ома для участка цепи: | `I=U/R` | |
| Закон Ома для полной цепи: | `I=varepsilon/(R+r)` | |
| Параллельное соединение проводников: | `1/R=1/R_1+1/R_2+…` | |
| `R=(R_1*R_2*…)/(R_1+R_2+…)` | ||
| `I=I_1+I_2+…` | ||
| `U=U_1=U_2=…` | ||
| Последовательное соединение проводников: | `R=R_1+R_2+…` | |
| `I=I_1=I_2=…` | ||
| `U=U_1+U_2+…` | ||
| Мощность тока: | `P=UI=I^2R=U^2/R` | |
| Закон Джоуля-Ленца: | `Q=I^2Rt` |
Электромагнитная индукция:
| Магнитный поток: | `Ф=BScosalpha` |
| Закон электромагнитной индукции: | `varepsilon_i=-(DeltaФ)/(Deltat)=-Ф’_t` |
| ЗДС в движущемся проводнике: | `varepsilon_i=Blvsinalpha` |
| Индуктивность: | `L=Ф/I` |
| ЭДС самоиндукции: | `varepsilon_(si)=-L(DeltaI)/(Deltat)=-LI’_t` |
| Энергия катушки с током: | `W_L=(LI^2)/2` |
Электромагнитные колебания и волны:
| `q(t)=q_0sin(omegat+varphi_0)` |
| `I(t)=q'(t)=q_0omegacos(omegat+varphi_0)=I_0cos(omegat+varphi_0)` |
| Формула Томсона: | `T=2pisqrt(LC)` |
| `omega=(2pi)/T=1/sqrt(LC)` | |
| Скорость электромагнитной волны: | `c=lambdanu` |
Что такое плотность формула?
Плотность формула — это математическое выражение, которое позволяет определить плотность вещества. Плотность — это физическая величина, которая характеризует массу вещества, занимающего определенный объем. Другими словами, плотность показывает, насколько концентрировано или плотно расположены молекулы или атомы вещества.
Плотность формула обычно записывается как:
Плотность = масса / объем
где масса обозначает массу вещества в граммах или килограммах, а объем обозначает объем вещества в литрах или кубических сантиметрах.
Плотность формула позволяет вычислить плотность различных материалов и веществ, таких как жидкости, газы, твердые вещества и пр. Например, с помощью плотности формулы можно определить, как плотно расположены молекулы воды или свинца.
Значение плотности может использоваться для проведения различных расчетов и изучения свойств вещества. Также, с помощью плотности формулы можно определить, будет ли объект плавать или тонуть в жидкости, их будет ли происходить смешивание различных веществ и пр.
Важно отметить, что плотность формула может быть разной для различных веществ и материалов. К примеру, плотность жидкости будет отличаться от плотности газа или твердого материала, так как у них разная масса и объем
Использование плотности в расчётах
Плотность вещества — это табличная величина, и она позволяет по известной массе вычислить объём тела, или наоборот, получить массу тела известного объёма.
Рис. 2. Таблица плотности разных веществ.
Например, в приведённом примере с шариками из различных веществ не требуется изготавливать шарики, чтобы знать их массу. Достаточно измерить диаметр шарика (для настольного тенниса он составляет 0,04 м) и по геометрическим формулам вычислить его объём (он составит 0,0000335 куб. м). Умножая полученный объём на плотность вещества, взятую из таблицы, можно получить вес шарика, не изготавливая и не взвешивая его. Например, стеклянный шарик такого размера будет весить около 85 г, а золотой шарик — 647 г.
Плотность можно измерить не только для твёрдых, но и для жидких и газообразных тел. Например, плотность воздуха составляет 1,29 кг на кубический метр. А значит, воздух, находящийся в комнате средних размеров (например, $6 \times 3.5 \times 3$м) весит около 80 кг! Вполне заметная масса, хотя обычно кажется, что воздух ничего не весит. Масса и плотность воздуха впервые была определена Г. Галилеем путём взвешивания сосуда до и после откачивания из него воздуха.
Рис. 3. Взвешивание воздуха.
Что мы узнали?
Плотность — это физическая величина, показывающая, насколько сильно «упаковано» вещество в данном объёме. Она равна отношению массы вещества к объёму, занимаемому этой массой, и измеряется в килограммах на кубический метр.
-
/10
Вопрос 1 из 10
Почему тела одинаковых размеров имеют одинаковую массу?
- Размер равен массе.
- Размер и масса — это одно и то же.
- Масса всех тел одинакова.
- Это не так, масса тел одинакового размера неодинакова.
Электростатика
Электрический заряд может быть найден по формуле:
Линейная плотность заряда:
Поверхностная плотность заряда:
Объёмная плотность заряда:
Закон Кулона (сила электростатического взаимодействия двух электрических зарядов):
Где: k — некоторый постоянный электростатический коэффициент, который определяется следующим образом:
Напряжённость электрического поля находится по формуле (хотя чаще эту формулу используют для нахождения силы действующей на заряд в данном электрическом поле):
Принцип суперпозиции для электрических полей (результирующее электрическое поле равно векторной сумме электрических полей составляющих его):
Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра:
Напряженность электрического поля, которую создает заряженная плоскость:
Потенциальная энергия взаимодействия двух электрических зарядов выражается формулой:
Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:
В однородном электрическом поле существует связь между напряженностью поля и напряжением:
Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:
Работа электрического поля в общем случае может быть вычислена также и по одной из формул:
В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:
Определение потенциала задаётся выражением:
Потенциал, который создает точечный заряд или заряженная сфера:
Принцип суперпозиции для электрического потенциала (результирующий потенциал равен скалярной сумме потенциалов полей составляющих итоговое поле):
Для диэлектрической проницаемости вещества верно следующее:
Определение электрической ёмкости задаётся формулой:
Ёмкость плоского конденсатора:
Заряд конденсатора:
Напряжённость электрического поля внутри плоского конденсатора:
Сила притяжения пластин плоского конденсатора:
Энергия конденсатора (вообще говоря, это энергия электрического поля внутри конденсатора):
Объёмная плотность энергии электрического поля:
Как вычислить плотность формулы?
Вычисление плотности формулы является важным этапом при решении различных задач и проблем в науке, инженерии и других областях. Плотность формулы позволяет определить количество информации, содержащейся в формуле, с учетом объема занимаемого места. Как правило, плотность формулы выражается в битах на символ.
Для вычисления плотности формулы необходимо выполнить следующие шаги:
- Определите количество символов в формуле. Символом может быть буква, цифра, математический знак или любой другой элемент, имеющий значение в контексте формулы.
- Определите объем занимаемого места формулой. Объем может быть представлен в виде числа символов или же может быть измерен в байтах.
- Разделите количество символов на объем занимаемого места. Полученное значение будет являться плотностью формулы.
Например, если в формуле содержится 100 символов и она занимает 10 байт, то плотность формулы будет равна 10 символам на байт.
Вычисление плотности формулы имеет практическое применение в различных областях. Например, в информационной технологии плотность формулы может использоваться для оптимизации хранения и передачи данных. Чем выше плотность формулы, тем более компактно можно представить информацию и тем быстрее можно будет передать или сохранить ее.
Примеры расчета плотности формулы
Количество символов
Объем занимаемого места
Плотность формулы
300
50 байт
6 символов на байт
200
100 байт
2 символа на байт
500
200 байт
2.5 символа на байт
Таким образом, вычисление плотности формулы является важным инструментом для определения эффективности использования места при хранении и передаче информации. Зная плотность формулы, можно выбрать наиболее оптимальные способы представления данных.
Динамика
Второй закон Ньютона:
Здесь: F — равнодействующая сила, которая равна сумме всех сил действующих на тело:
Второй закон Ньютона в проекциях на оси (именно такая форма записи чаще всего и применяется на практике):
Третий закон Ньютона (сила действия равна силе противодействия):
Сила упругости:
Общий коэффициент жесткости параллельно соединённых пружин:
Общий коэффициент жесткости последовательно соединённых пружин:
Сила трения скольжения (или максимальное значение силы трения покоя):
Закон всемирного тяготения:
Если рассмотреть тело на поверхности планеты и ввести следующее обозначение:
Где: g — ускорение свободного падения на поверхности данной планеты, то получим следующую формулу для силы тяжести:
Ускорение свободного падения на некоторой высоте от поверхности планеты выражается формулой:
Скорость спутника на круговой орбите:
Первая космическая скорость:
Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:
Диапазон плотностей в природе
Для различных природных объектов плотность меняется в очень широком диапазоне.
- Самую низкую плотность имеет межгалактическая среда (2·10 −31 ÷5·10 −31 кг/м³) .
- Плотность межзвёздной среды приблизительно равна 10 −23 ÷10 −21 кг/м³.
- Средняя плотность Солнца примерно в 1,5 раза выше плотности воды.
- Средняя плотность красных гигантов на много порядков меньше, чем у Солнца, из-за того, что их радиус в сотни раз больше.
- Средняя плотность Земли равна 5520 кг/м³.
- Жидкий водород при атмосферном давлении и температуре −253 °C имеет плотность 70 кг/м³.
- Плотность жидкого гелия при атмосферном давлении равна 130 кг/м³.
- Плотность пресной воды составляет 1000 кг/м³.
- Гранит имеет плотность 2600 кг/м³.
- Плотность железа равна 7874 кг/м³.
- Наибольшую плотность среди металлов имеет осмий (22 587 кг/м³).
- Плотность атомных ядер приблизительно равна 2·10 17 кг/м³.
- Плотность белых карликов составляет 10 8 ÷10 12 кг/м³.
- Плотность нейтронных звёзд имеет порядок 10 17 ÷10 18 кг/м³.
- Теоретически верхнюю границу представляет планковская плотность (современная физика оценивает её в 5,1·10 96 кг/м³, хотя не исключено, что она очень сильно завышена).
Масса и плотность вещества
Шарик для настольного тенниса весит 2,7 г.
Но такой же по размеру шарик из дерева будет весить 15–20 г, а из железа — 260 г. Если же шарик изготовить из свинца, его масса достигнет 380 г.
Столь большая разница в массе одинаковых по размеру тел объясняется тем, что элементарные частицы внутри различных веществ имеют различное пространственное расположение, и в одном и том же объёме помещается разное их количество. Например, в ядрах атомов свинца в среднем 208 нуклонов, составляющих основную массу. А в ядрах железа — только 56 нуклонов. В ядрах элементов, из которых состоят молекулы дерева и воздуха, нуклонов ещё меньше.
Мало того, в составе молекул и кристаллических решёток атомы могут находиться на разных расстояниях, и в одном и том же объёме будет помещаться их различное количество. Наконец, в газах молекулы находятся друг от друга на относительно больших расстояниях, это и объясняет лёгкость газов (и малую массу шарика от пинг-понга, на 99 % заполненного воздухом).
Возникает вопрос: как учесть эту разницу?
В физике для этого используется специальная величина — плотность, которая показывает, насколько сильно «упаковано» вещество в данном объёме.
В приведённом примере наивысшая плотность будет у свинцового шарика, наименьшая — у шарика для пинг-понга.
Молекулярная физика
Химическое количество вещества находится по одной из формул:
Масса одной молекулы вещества может быть найдена по следующей формуле:
Связь массы, плотности и объёма:
Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:
Определение концентрации задаётся следующей формулой:
Для средней квадратичной скорости молекул имеется две формулы:
Средняя кинетическая энергия поступательного движения одной молекулы:
Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом:
Следствия из основного уравнения МКТ:
Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева):
Газовые законы. Закон Бойля-Мариотта:
Закон Гей-Люссака:
Закон Шарля:
Универсальный газовый закон (Клапейрона):
Давление смеси газов (закон Дальтона):
Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:
Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:
Формулы по физике за 7 класс
Скорость при равномерном движении
\
Средняя скорость при неравномерном движении. Количество отрезков пути и промежутков времени зависят от условия задачи
\
Плотность вещества. Плотность – это физическая величина, характеризующаяся отношением массы тела к занимаемому этим телом объёму:
\
Сила тяжести. Рядом с поверхностью Земли все тела обладают одинаковым коэффициентом ускорения свободного падения \
\
\
Равнодействующая сил. Равнодействующая сила – это сила, которая может заменить несколько приложенных к телу сил. В зависимости от их направленности по отношению друг к другу различают две формулы.
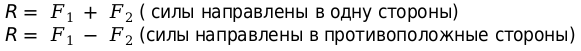
Вес тела
\
Сила трения
Зависимость плотности от температуры
Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность ведёт себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого значения.
При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Вода, кремний, германий и некоторые другие вещества являются исключениями из данного правила, так как их плотность при переходе в твердую фазу уменьшается.






























