Формула массы куба от длины его ребра

Задачи на плотность, массу и объем с решением

Формулы, используемые в задачах по физике на плотность, массу и объем.

Плотность равна отношению массы тела к его объёму. Плотность обозначают греческой буквой ρ (ро).

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1. Найдите плотность молока, если 206 г молока занимают объем 200 см3?

Задача № 2. Определите объем кирпича, если его масса 5 кг?

Задача № 3. Определите массу стальной детали объёмом 120 см3

Задача № 4. Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?

Решение: Из таблицы плотности веществ (см. в конце страницы) определим, что плотность чугуна (ρ₂ = 7000 кг/м3) меньше плотности стали (ρ₁ = 7800 кг/м3). Следовательно, в единице объема чугуна содержится меньшая масса, чем в единице объема стали, так как чем меньше плотность вещества, тем меньше его масса, если объемы тел одинаковы.

Задача № 5. Определите плотность мела, если масса его куска объемом 20 см3 равна 48 г. Выразите эту плотность в кг/м3 и в г/см3.

Ответ: Плотность мела 2,4 г/см3, или 2400 кг/м3.

Задача № 6. Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м2 ?

ОТВЕТ: 160 кг.

РЕШЕНИЕ. Из формулы для плотности получаем m = p • V. С учетом того, что объем балки V = S • l , получаем: m = p • S • l.

Вычисляем: m = 800 кг/м3 • 0,04 м2 • 5 м = 160 кг.

Задача № 7. Брусок, масса которого 21,6 г, имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.

ОТВЕТ: Брусок сделан из алюминия.

Задача № 8 (повышенной сложности). Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?

ОТВЕТ: 5 мм.

РЕШЕНИЕ: Объем кубика V_K= а3 = 216 см3. Объем стенок V_С можно вычислить, зная массу кубика m_К и плотность меди р: V_С = m_К / р = 91 см3. Следовательно, объем полости V_П = V_K — V_C = 125 см3. Поскольку 125 см3 = (5 см)3, полость является кубом с длиной ребра b = 5 см. Отсюда следует, что толщина стенок куба равна (а — b)/2 = (6 – 5)/2 = 0,5 см.

Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.

ОТВЕТ: 8000 кг/м3

РЕШЕНИЕ: Если бы часть воды из пробирки не вылилась, то в этом случае общая масса пробирки, воды и куска металла в ней была бы равна 50 г + 12 г = 62 г. По условию задачи масса воды в пробирке с куском металла в ней равна 60,5 г. Следовательно, масса воды, вытесненной металлом, равна 1,5 г, т. е. составляет 1/8 массы куска металла. Таким образом, плотность металла в 8 раз больше плотности воды.

Задачи на плотность, массу и объем с решением. Таблица плотности веществ.

Как, зная только массу, рассчитать плотность?

Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть: Vпар. = a • b • c, где Vпар. – объем прямоугольного параллелепипеда, а a, b, c — значения его длины, ширины и высоты (толщины), соответственно.
Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.

Конспект урока «Задачи на плотность, массу и объем с решением».

Следующая тема: «Задачи на силу тяжести и вес тела».

Функции

«Понятие функции» — Логическая трактовка понятия «функция». Основные подходы к введению понятия «функции». Методические особенности изучения прямой и обратной пропорциональной зависимости. Построение первой из рассматриваемых функций проводится методом «загустения» точек. Ввести термин «угловой коэффициент». Опора на знания о пропорции и пропорциональной зависимости величин.

«Графики функций» — Графиком функции является кубическая парабола. Функция. Графиком функции является прямая, проходящая через начало координат. Графиком функции является ветвь параболы. Область значений функции – все значения зависимой переменной у. Графиком функции является парабола. Графиком функции является гипербола.

«Функции 9 класс» — Приложение 3. Приложение11. В таких случаях говорят о графическом задании функции. Допустимые арифметические действия над функциями. – сложение, – вычитание, – умножение, – деление. Приложение 16. Функцию можно задать с помощью формулы, например: y=2x+5, S=at2/2, S=vt. К элементарным функциям относятся практически все функции, встречающиеся в школьном учебнике.

«Определение числовой функции» — Способы задания функции. Словесная формулировка. Y=f(x). Функция задана аналитически. Определение числовой функции. Функция задана таблично. Графический способ. Графы удобно описывать матрицами. Выразите каждую переменную через две другие. Функция задана графически. Дана функция y=f(x). Числовое множество Х и правило f.

«Способы задания функции» — Способ задания функции таблицей. Зависимость атмосферного давления p от высоты h над уровнем моря: Способы задания функции. Способ задания функции графиком. 1. Зависимость температуры воздуха t от времени суток Т. формулой графиком Таблицей Словесный. 2.Графики движения автомобиля и автобуса. Существует три способа задания функции:

Единицы измерения ребра куба

Ребро куба, как и любого другого геометрического объекта, может быть измерено в различных единицах.

Самые распространенные единицы измерения длины, которые могут использоваться для измерения ребра куба:

Миллиметры (мм) — это наименьшая общепринятая единица измерения длины. Измерения ребра куба в миллиметрах могут быть полезны, когда требуется высокая точность измерений, например при работе с микроэлементами или изготовлении моделей.
Сантиметры (см) — это единица измерения длины, часто используемая в повседневной жизни. Измерение ребра куба в сантиметрах будет удобно для большинства практических задач, таких как строительство, дизайн интерьера или изучение геометрии в школе.
Метры (м) — это родительская единица измерения длины в системе СИ. Измерение ребра куба в метрах будет полезно при работе с крупными объектами, как например в строительстве зданий или измерении размеров комнат.

Важно помнить, что при выборе единицы измерения ребра куба следует руководствоваться конкретной задачей и требуемой точностью. Также полезно учитывать единицы измерения, используемые в контексте других измерений или приложений, с которыми может быть связана данная задача

Определение массы куба по формуле: шаги и инструкция

Для определения массы куба необходимо знать его объем и плотность материала, из которого он изготовлен. Формула для расчета массы куба выглядит следующим образом:

Масса = Объем × Плотность

Шаги для определения массы куба:

Определите объем куба. Объем куба можно вычислить, умножив длину каждой из его сторон друг на друга: V = a × a × a, где a — длина стороны куба.
Установите плотность материала, из которого изготовлен куб. Плотность может быть известна или требуется ее измерение с помощью специальных приборов или методов.
Подставьте полученные значения в формулу для определения массы куба: Масса = V × Плотность.
Вычислите полученное выражение, чтобы получить массу куба в соответствующих единицах измерения.

Например, если сторона куба равна 5 см, а плотность материала равна 2 г/см³, то:

Объем = 5 см × 5 см × 5 см = 125 см³

Масса = 125 см³ × 2 г/см³ = 250 г

Теперь вы знаете, как определить массу куба по формуле. Следуйте указанным шагам и используйте данную инструкцию при необходимости. Запомните — формулы позволяют быстро расчитывать различные величины, делая нашу работу более эффективной и точной!

Примеры расчета массы куба по формуле

Пример 1:
Допустим, у нас есть куб со стороной 5 см. Найдем его массу, используя формулу.

Сторона куба (a) = 5 см

Воспользуемся формулой для расчета массы куба:

Масса куба = плотность x объем

Масса куба = плотность x (сторона куба x сторона куба x сторона куба)

Здесь плотность — это физическая величина, которая зависит от материала, из которого сделан куб.

Допустим, плотность куба составляет 2 г/см^3. Тогда:

Масса куба = 2 г/см^3 x (5 см x 5 см x 5 см)

Масса куба = 2 г/см^3 x 125 см^3

Масса куба = 250 г

Получаем, что масса куба составляет 250 г.
Пример 2:
Предположим, у нас есть куб со стороной 10 м. Давайте найдем его массу, используя формулу.

Сторона куба (a) = 10 м

Заданная плотность материала куба составляет 3 кг/м^3. Тогда:

Масса куба = 3 кг/м^3 x (10 м x 10 м x 10 м)

Масса куба = 3 кг/м^3 x 1000 м^3

Масса куба = 3000 кг

Таким образом, масса куба составляет 3000 кг.
Пример 3:
Предположим, у нас есть куб со стороной 8 дюймов. Найдем его массу, используя формулу.

Сторона куба (a) = 8 дюймов

Плотность куба равна 1 фунту/кубический дюйм. Тогда:

Масса куба = 1 фунт/куб. дюйм x (8 дюймов x 8 дюймов x 8 дюймов)

Масса куба = 1 фунт/куб. дюйм x 512 куб. дюймов

Масса куба = 512 фунтов

Таким образом, масса куба составляет 512 фунтов.

Объем цилиндра

Цилиндр не получится разбить на несколько призм, поэтому для вычисления его объема используется другой метод. Впишем цилиндр в правильную n-угольную призму. Одновременно построим и другую правильную n-угольную призму, которая сама будет вписана в цилиндр. Объем вписанной призмы обозначим как V_в, а объем описанной призмы как V_о. Объем самого цилиндра – это V_ц. При этом высоты всех трех фигур одинаковы:

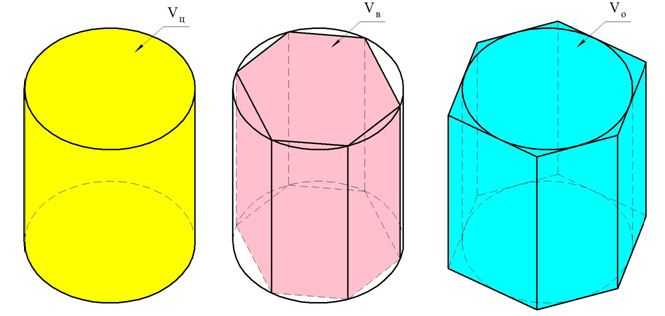
Ясно, что объем вписанной призмы меньше объема цилиндра, а тот в свою очередь меньше объема описанной призмы:

Теперь будем неограниченно увеличивать число n. При этом площади S_в и S_о будут стремиться к площади основания цилиндра, равной величине πr2, где r– радиус основания цилиндра. Это возможно лишь в том случае, если справедливо равенство

Задание. Найдите объем цилиндра с высотой 5 см и радиусом 6 см.

Решение. Сначала находим площадь основания:

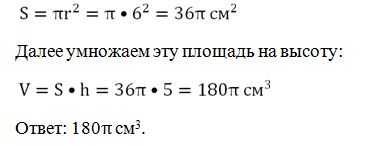
Задание. Известно, что высота цилиндра вдвое больше его радиуса, а объем цилиндра равен 54π. Найдите радиус цилиндра.

Решение. Обозначим радиус цилиндра буквой х. Тогда по условию высота будет вдвое больше, то есть она составит 2х. Вычислим объем цилиндра:

Ответ: 3.

Задание. Труба изготовлена из металла с плотностью 11,4 г/см3. Внутренний диаметр трубы равен 13 мм, а ее стенка имеет толщину 4 мм. Длина трубы – 25 метров. Какова ее масса?

Решение. Для расчета массы необходимо сперва вычислить объем трубы. Ясно, что если к объему трубы прибавить объем внутреннего отверстия, то в итоге получится объем большого цилиндра, чей диаметр равен наружному диаметру трубы:

Легко найти объем отверстия, ведь оно имеет форму цилиндра. Его радиус вдвое меньше диаметра, то есть он равен 13/2 = 6,5 мм

При расчете важно не забыть перевести высоту в миллиметры:

Сегодня мы узнали о такой характеристике тел, как объем. Если объем куба и прямоугольного параллелепипеда мы умели находить ещё в средней школе, то определять объем цилиндра и прямой призмы мы научились только сейчас. Однако все эти случаи по сути одинаковы – надо перемножить высоту фигуры и площадь ее основания. В будущем мы научимся вычислять объемы более сложных фигур – пирамиды, конуса, шара.

Примеры расчета массы куба

Для наглядности рассмотрим несколько примеров расчета массы куба.

Пример 1:

Пусть данными являются следующие значения:

Ребро куба: 3 см

Плотность материала: 2 г/см³

Масса куба равна произведению плотности материала на объем куба:

Масса = плотность × объем

Объем куба равен ребру, возведенному в куб:

Объем = 3 см × 3 см × 3 см = 27 см³

Таким образом, масса куба будет:

Масса = 2 г/см³ × 27 см³ = 54 г

Пример 2:

Пусть данными являются следующие значения:

Ребро куба: 5 м

Плотность материала: 7 кг/м³

Масса куба равна произведению плотности материала на объем куба:

Масса = плотность × объем

Объем куба равен ребру, возведенному в куб:

Объем = 5 м × 5 м × 5 м = 125 м³

Таким образом, масса куба будет:

Масса = 7 кг/м³ × 125 м³ = 875 кг

Заметьте, что во втором примере масштаб измерений изменился с сантиметров на метры, поэтому и значения плотности и объема также изменились.

Рассмотрим более сложный пример расчета

Слиток из двух металлов с плотностями ρ1 и ρ2 , имеет массу m и объём V. Определить объём этих металлов в слитке.

Решение.
Пусть V1 объём первого металла, V2 объём второго металла. Тогда V1 + V2 = V; V1 = V V2; ρ1V1 + p2V2 = ρ1V1 + ρ2 (V V1) = m

Класс:

7

Цели урока.

1. Образовательные:
систематизировать
знания, имеющиеся у учащихся о понятиях:
“плотность”, “масса”, “объем”, расширить
область знаний о данных понятиях, выработка
умения применять изученный материал для решения
практических задач.

2. Развивающие: формирование логического
мышления, продолжать развивать навык решения
физических задач.

3. Воспитательные: привития учащимся к
доброжелательному общению, взаимопомощи.

Тип урока: комбинированный.

Оборудование: 15 комплектов таблиц 1 и 2.

Ход урока

1. Организационный этап.

2. Актуализация знаний.

Деятельность учителя	Деятельность учеников
— Что такое плотность?	Физическая величина, которая показывает, какое количество вещества, содержится в единице объема.
— Что означает, плотность железа равна 6800 кг/м 3 ? Как можно найти плотность вещества? От чего зависит масса тела?	Это означает, что масса 1 м 3 железа равна 6800 кг. Чтобы найти плотность вещества нужно массу разделить на объем.
— Как найти массу тела?	Масса тела зависит от его объема и плотности вещества, из которого состоит данное тело.
— Как найти объем тела, если известна его масса и вещество, из которого состоит тело?	Чтобы найти массу тела нежно его плотность умножить на объем. Чтобы найти объем тела, нужно его массу разделить на плотность.

3. Решение задач
1. Как будем выставлять оценку за работу на уроке по принципу сложения или вычитания?	По принципу сложения.
2. Таблица 1 (Приложение №1). На складе имеются грузы: мел, пробка, береза, лед, сталь. Каждый груз упакован в контейнеры по 2 м 3 . для перевозки этих грузов были вызваны пять автомобилей. Ваша задача распределить грузы по автомобилям.	Найти массу грузов.
— Что нужно сделать, чтобы распределить грузы по автомобилям?
— Как найти массу вещества, если известна его плотность и объём?	кг/м 3
— В каких единицах измерена плотность вещества?	В килограммах
— В каких единицах будет вычислена масса?	В тоннах и килограммах
— В каких единицах выражена грузоподъемность автомобилей?	В тоннах, а для москвича в килограммах
— В каких единицах нужно получить массу грузов? Решите данную задачу и распределите грузы по автомобилям. Учитель проверяет правильность выполненного задания у первого решившего ученика, и назначает его своим ассистентом. В карточках (Приложение № 3) учеников делаются записи количества набранных баллов.	Ученики решают задачи и распределяют грузы.
3. Таблица 2 (Приложение № 2). Имеются пять различных жидкостей, которые имеют одинаковую массу. Эти жидкости нужно разлить по пяти различным сосудам. Что нужно сделать, чтобы разлить жидкости по сосудам?	Найти объём жидкостей.
— Как найти объем, если известна масса вещества и его плотность?
— В каких единицах получится вычисленный объём?	в м 3 .
— В каких единицах дан объём сосудов?	В литрах и миллилитрах
— В каких единицах нужно получить объём жидкостей?	В литрах и миллилитрах
Решите данную задачу и распределите жидкость по сосудам. Учитель проверяет правильность выполненного задания у первого решившего ученика, и назначает его своим ассистентом. В карточках учеников делаются записи количества набранных баллов.	Ученики решают задачу.
4. Рефлексия.
— Какие физические понятия Вы использовали для выполнения заданий? Сравните количество баллов, которые вы выставили сами себе, с количеством баллов, которые вам выставили проверяющие. Какой вы можете для себя сделать вывод? Готовы ли вы к контрольной работе?	Масса, плотность, объем.

Домашнее задание:
повторить 18-22.

Масса

Решение.

Задание.
Какова масса 2м 3 меди?

Ответ.
(кг)

Свойства объема

Свойства объема во многом совпадают со свойствами площади. Ясно, что у равных тел будут одинаковы и объемы.

Второе свойство объема связано с тем, что он является аддитивной величиной. Это значит, что если тело можно разбить на несколько тел, то его объем будет равен сумме объемов этих тел.

Это свойство аддитивности объема уже позволяет решать некоторые стереометрические задачи.

Задание. Тело состоит из цилиндра объемом 12 см3 и конуса объемом 4 см3. Каков объем этого тела?

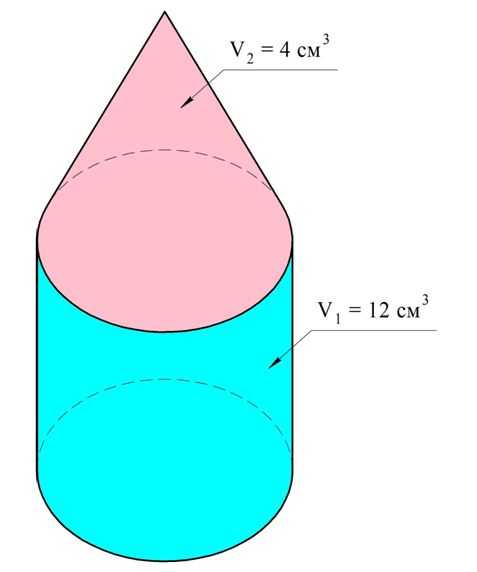
Решение. Здесь надо просто сложить объемы цилиндра и конуса, чтобы найти общий объем всей фигуры:

Ответ: 16 см3.

Задание. Найдите объем фигуры, показанной на рисунке:

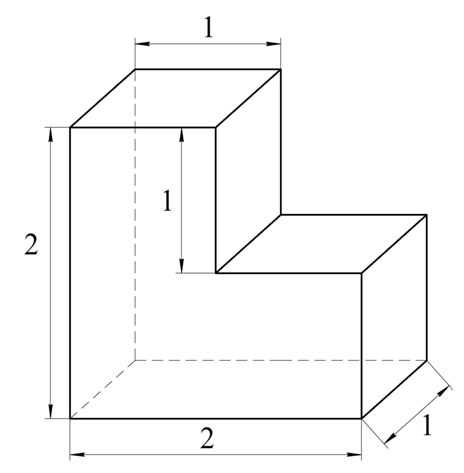
Решение. Данную фигуру несложно разбить на три единичных куба:

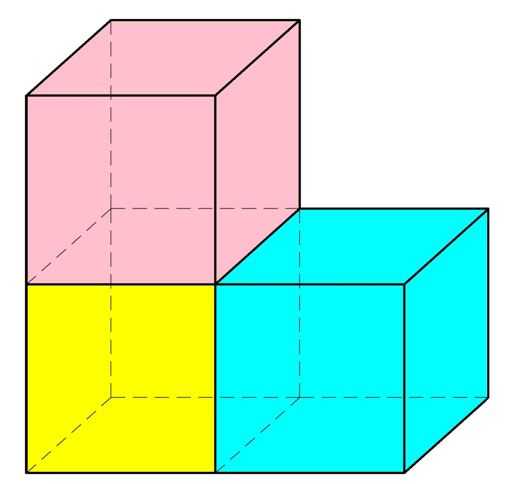
Тогда объем тела будет равен сумме объемов трех единичных кубов, то есть трем:

Ответ: 3.

Задание. Вычислите объем фигуры, получающейся при рассечении куба плоскостью, проходящей через два его ребра.

Решение. Ясно, что такая секущая плоскость будет делить куб на две равные фигуры (иначе просто не удастся провести плоскость через два ребра):

Также понятно, что два получившихся многогранника равны друг другу. Обозначим объем каждого из них как V. Тогда в сумме их объем должен быть равен 1, ведь вместе эти фигуры образуют единичный куб. Это позволяет составить уравнение, из которого можно вычислить величину V:

Формулы для куба

Примем следующие обозначения, которые будут использоваться далее:

Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.

Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.

Площадь полной поверхности

Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.

Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.

Объем куба равен длине его ребра, возведенной в куб.

Радиус шара, описанного около куба, равняется половине его диагонали.

Объем прямой призмы

Рассмотрим сначала прямую призму, в чьем основании располагается прямоугольный треугольник. Ее можно достроить до прямоугольного параллелепипеда:

Ясно, что объем параллелепипеда будет вдвое больше объема исходной призмы, ведь он состоит из двух таких призм. Аналогично и площадь основания у параллелепипеда будет вдвое больше. Обозначим площадь основания призмы буквой S, а ее высоту как h, тогда площадь основания параллелепипеда будет 2S, а его объем составит 2S•h. Тогда объем призмы будет вдвое меньше, то есть он окажется равным S•h.

Далее рассмотрим прямую призму, в основании которой лежит уже произвольный треугольник. Проведем в этом треугольнике высоту, которая упадет на противоположную сторону (такую высоту всегда можно провести). Далее через эту высоту проведем плоскость, перпендикулярную основанию. В результате мы разделим призму на две прямых призмы, в основании каждой из которых будет лежать прямоугольный треугольник:

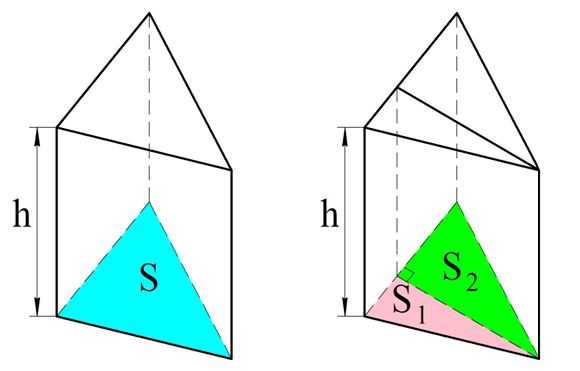
Пусть площади получившихся прямоугольных треугольников обозначены как S₁и S₂, а общая площадь основания исходной призмы – это S. Мы можем вычислить объемы этих призм:

Теперь, наконец, рассмотрим прямую призму, чье основание – произвольный многоугольник. Этот многоугольник можно разбить на несколько треугольников с площадями S₁, S₂, S₃…, а призма соответственно будет разбита на несколько треугольных призм с объемами V₁, V₂, V₃и. т. д.

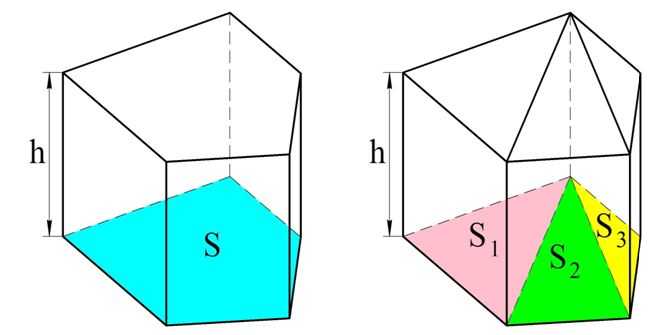
Объем каждой треугольный призмы мы можем рассчитать:

Задание. Все ребра правильной шестиугольной призмы одинаковы, их длина обозначена буквой а. Найдите объем такой призмы.

Решение. Сначала необходимо найти площадь основания призмы, то есть площадь правильного шестиугольника. Напомним формулы для правильных многоугольников, изученные ещё в девятом классе:

Для вычисления объема надо лишь умножить полученную площадь на высоту призмы, а она также равна а:

Задание. В кубе АВСDА₁В₁С₁D₁ через середины ребер СD и BC проведено сечение, параллельное ребру СС₁. Это сечение отсекает от куба треугольную призму, чей объем равен 19. Найдите объем куба.

Решение. Ясно, что и куб, и треугольная призма будут прямыми призмами, причем у них одинаковая высота СС₁. Тогда можно утверждать, что отношение их объемов равно отношению площадей их оснований:

Пусть сторона АВ имеет длину а. Тогда площадь квадрата АВСD будет составлять а2. Отрезки ЕС и FC будут вдвое короче АВ, то есть их длина составляет a/2. ∆EFC – прямоугольный, и его площадь может быть рассчитана как половина произведения его катетов:

Плотность тела — зависимость массы и объема

Например, железный куб с ребром 10 см имеет массу 7,8 кг, алюминиевый куб тех же размеров имеет массу 2,7 кг, а масса такого же куба изо льда 0,9 кг. Величина, характеризующая массу, приходящуюся на единичный объём данного вещества, называется плотностью. Плотность равна частному от массы тела и его объёма, т.е.

ρ = m/V, где ρ (читается «ро») плотность тела, m — его масса, V объём.

В Международной системе единиц СИ плотность измеряется в килограммах на кубический метр (кг/м3); также часто используются внесистемные единицы, например, грамм на кубический сантиметр (г/см3). Очевидно, 1 кг/м3 = 0,001 г/см3. Заметим, что при нагревании веществ их плотность уменьшается или (реже) увеличивается, но это изменение так незначительно, что при расчётах им пренебрегают.

Сделаем оговорку, что плотность газов непостоянна; когда говорится о плотности какого-нибудь газа, обычно имеется ввиду его плотность при 0 градусов по Цельсию и нормальном атмосферном давлении (760 миллиметров ртутного столба).

Объемы фигур. Объем куба.

Куб — трехмерная геометрическая фигура, у которой все ребра равны (длина равна ширине и равна высоте).

У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны.

Вычислить объем куба легко – нужно перемножить длину, ширину и высоту. Так как у куба длина равна

ширине и равна высоте, то объем куба равен s 3 ,

где s – длина одного (любого) ребра куба.

Воспользуйтесь онлайн калькулятором для расчета объема куба: объем куба, онлайн расчет.

Для расчета объемов других тел воспользуйтесь этим калькулятором: калькулятор объемов фигур.

Метод 1 из 3: Возведение в куб ребра куба

Найдите длину одного ребра куба. Как правило, длина ребра куба дана в условии задачи. Если вы

вычисляете объем реального объекта кубической формы, измерьте его ребро линейкой или рулеткой.

Рассмотрим пример. Ребро куба равно 5 см. Найдите объем куба.

Возведите в куб длину ребра куба. Другими словами, умножьте длину ребра куба саму на себя три раза.

Если s — длина ребра куба, то

и, таким образом, вы вычислите объем куба.

Этот процесс аналогичен процессу нахождения площади основания куба (равна произведению длины на

ширину квадрата в основании) и последующему умножению площади основания на высоту куба (то есть,

другими словами, вы умножаете длину на ширину и на высоту). Так как в кубе длина ребра равна ширине и

равна высоте, то это процесс можно заменить возведением ребра куба в третью степень.

В нашем примере объем куба равен:

К ответу припишите единицы измерения объема. Так как объем – это количественная

характеристика пространства, занимаемого телом, то единицами измерения объема являются кубические

В нашем примере размер ребра куба давался в сантиметрах, поэтому объем будет измеряться в кубических

сантиметрах (или в см 3 ). Итак, объем куба равен 125 см 3 .

Если размер ребра куба дается в других единицах, то и объем куба измеряется в соответствующих

Например, если ребро куба равно 5 м (а не 5 см), то его объем равен 125 м 3 .

Метод 2 из 3: Вычисление объема по площади поверхности

В некоторых задачах длина ребра куба не дана, но даны другие величины, с помощью которых вы

можете найти ребро куба и его объем. Например, если вам дана площадь поверхности куба, то разделите

ее на 6, из полученного значения извлеките квадратный корень и вы найдете длину ребра куба. Затем

возведите длину ребра куба в третью степень и вычислите объем куба.

Площадь поверхности куба равна 6s 2 ,

где s – длина ребра куба (то есть вы находите площадь одной грани куба, а затем умножаете ее на 6, так

как у куба 6 равных граней).

Рассмотрим пример. Площадь поверхности куба равна 50 см 2 . Найдите объем куба.

Разделите площадь поверхности куба на 6 (так как у куба 6 равных граней, вы получите площадь

одной грани куба). В свою очередь площадь одной грани куба равна s 2 , где s – длина ребра куба.

В нашем примере: 50/6 = 8,33 см 2 (не забывайте, что площадь измеряется в квадратных единицах — см 2 ,

Так как площадь одной грани куба равна s 2 , то извлеките квадратный корень из значения площади

одной грани и получите длину ребра куба.

В нашем примере, √8,33 = 2,89 см.

Возведите в куб полученное значение, чтобы найти объем куба.

В нашем примере: 2,89 * 2,89 * 2,89 = 2,893 = 24,14 см 3 . К ответу не забудьте приписать кубические

Метод 3 из 3: Вычисление объема по диагонали

Разделите диагональ одной из граней куба на √2, чтобы найти длину ребра куба. Таким образом,

если в задаче дана диагональ грани (любой) куба, то вы можете найти длину ребра куба, разделив

Рассмотрим пример. Диагональ грани куба равна 7 см. Найдите объем куба. В этом случае длина ребра куба

равна 7/√2 = 4,96 см. Объем куба равен 4,963 = 122,36 см 3 .

где d — диагональ грани куба, s – ребро куба. Эта формула вытекает из теоремы Пифагора, согласно

которой квадрат гипотенузы (в нашем случае диагональ грани куба) прямоугольного треугольника равен

сумме квадратов катетов (в нашем случае ребер), то есть:

Разделите диагональ куба на √3, чтобы найти длину ребра куба. Таким образом, если в задаче

дана диагональ куба, то вы можете найти длину ребра куба, разделив диагональ на √3.

Диагональ куба — отрезок, соединяющий две вершины, симметричные относительно центра куба, равный

(где D — диагональ куба, s – ребро куба).

Эта формула вытекает из теоремы Пифагора, согласно которой квадрат гипотенузы (в нашем случае

диагональ куба) прямоугольного треугольника равен сумме квадратов катетов (в нашем случае один катет –

это ребро, а второй катет – это диагональ грани куба, равная 2s 2 ), то есть

Рассмотрим пример. Диагональ куба равна 10 м. Найдите объем куба.