Как найти объем куба: варианты задач и их решение

Понятие геометрического тела

Геометрическое тело – это объемная фигура, ограниченная плоскими гранями и имеющая как минимум три измерения: длину, ширину и высоту.

В геометрии существует множество различных геометрических тел, таких как куб, параллелепипед, цилиндр, конус, пирамида и др. Каждое из этих тел имеет свои уникальные свойства и характеристики.

Основные понятия, связанные с геометрическими телами:

1. Грань – это плоская поверхность, ограничивающая тело.
2. Ребро – это линия пересечения двух граней.
3. Вершина – это точка пересечения трех и более ребер.
4. Объем – это трехмерная величина, равная количеству пространства, занимаемого телом.
5. Площадь поверхности – это сумма площадей всех граней тела.

Знание понятий и свойств геометрических тел важно в многих областях, таких как архитектура, инженерия, дизайн и другие. Понимание форм и структуры этих тел помогает в решении различных задач и создании новых объектов

Например, куб – это особый вид параллелепипеда, у которого все грани являются квадратами. Куб очень часто встречается в повседневной жизни: коробки, игрушки, кубики для игры – все они имеют форму куба. Знание свойств куба позволяет легко решать задачи, связанные с вычислением объема и площади поверхности данного тела.

Таким образом, геометрические тела играют важную роль в нашей жизни и обладают множеством интересных свойств и связей.

Вычисление объема прямоугольного параллелепипеда

Итак, вы знаете, что нужно рассчитать объем, но не забывайте, что обязательно нужно уточнить о какой именно фигуре идет речь: объем куба, или же объемного прямоугольника. Ведь расчет этих, казалось бы, одинаковых фигур, абсолютно разный.

Для начала рассмотрим само понятие объемного прямоугольника. Это параллелепипед. В его основании находится параллелограмм. Так как таковых у него шесть, следовательно все параллелограммы являются гранями параллелепипеда.

Что касается его граней, они могут отличаться, то есть, если прямые боковые грани представляют собой прямоугольники, тогда это прямой параллелепипед, ну, а если все шесть граней являются прямоугольниками, то перед нами прямоугольный параллелепипед.

1. После прочтения задачи, нужно определить что именно следует найти; длину фигуры, объем или же площадь.
2. Какая именно часть фигуры рассматривается в задаче — ребро, вершина, грань, сторона, а может быть, вся фигура целиком?

Определив все поставленные задачи, можно переходить непосредственно к вычислениям. Для этого нам понадобятся специальные формулы. Итак, для того чтобы найти объем прямоугольного параллелепипеда перемножается между собой длина, ширина и высота (то есть толщина фигуры). Формула вычисления объема прямоугольного параллелепипеда следующая:

V=a*b*h,

V является объемом параллелепипеда, где a — его длина b — ширина и h — высота соответственно.

Важно! Перед началом перевести все измерения в одну единицу исчисления. Ответ должен получится непременно в кубических единицах

Пример первый

Определим объем бака для спирта, при следующих размерах:

• длина три метра;
• ширина два метра пятьдесят сантиметров;
• высота триста сантиметров.

Для начала обязательно согласовываем единицы измерения и перемножаем их:

Перемножив данные, мы получим ответ в кубических метрах, то есть 3*2.5*3= 22.5 метра в кубе.

Пример второй

Шкаф имеет высоту четыре метра, ширину семьдесят сантиметров и глубину 80 сантиметров.

Зная формулу вычисления можно произвести умножение. Но не стоит торопиться, как и было сказано вначале, следует согласовать между собой единицы, то есть при желании вычислять в сантиметрах перевести все исчисления в сантиметры, ежели в метрах, то в метры. Сделаем оба варианта.

Итак, начнем с сантиметров. Переводим метры в сантиметры:

V = 2240000 сантиметров в кубе.

V = 2.24 метра в кубе.

Исходя из вышеперечисленных манипуляции, очевидно, что работа с кубическими метрами более легка и понятна.

Пример третий

Дана комната, объем которой должен быть вычислен. Длина этой комнаты равна пяти метрам, ширина — трем, а высота потолка 2,5. Опять используем известную нам формулу:

V = a * b * h;

где, а длина комната и равна 5, b- ширина и равна 3 и h высота, которая равна 2.5

Так как все единицы даны в метрах, можно сразу приступать к вычислениям. Перемножая между собой a, b и h:

V = 37.5 метра в кубе.

Итак, в качестве заключения, можно сказать, что зная основные математические правила для вычисления объема или же площади фигур, а также правильно определив фигуры (плоские или же объемные), умея переводить сантиметры в метры и наоборот — можно облегчить изучение геометрии вашему ребенку, что не может не сделать этот процесс более интересным и привлекательным, ведь все накопленные знания в школе, могут быть успешно использованы в самой обычной бытовой жизни в будущем.

Источник

Примеры задач

Пример 1

Найти куб выражения $(2x-3y)$

Решения

Из формулы куба разности, получаем:

$(2x-3y)^3=(2x)^3-3\cdot (2x)^2\cdot 3y+3\cdot 2x\cdot (3y)^2-(3y)^3=8x^3-36x^2 y+54xy^2-27y^3$

Замечание 1

Замечание: Особое внимание нужно обращать на то, что формулу необходимо применять к одночленам, входящим в сумму, целиком. Частой ошибкой в таком случае бывает, что в куб возводится только часть одночлена (к примеру, возводят не $3y$ целиком, а только $y$, что приводит к ошибке!!!). Пример 2

Пример 2

Возвести в куб:

а) $(-8α+5β)^3$

б) $(q^2+7)^3$

Решение.

а) $(-8α+5β)^3$

Так как у нас нечетная степень, то мы можем вынести знак «минус» за скобки, получим:

$(-8α+5β)^2=-(8α-5β)^3$

Используем формулу куба суммы:

$(8α-5β)^3=(8α)^3-3\cdot (8α)^2\cdot 5β+3\cdot 8α\cdot (5β)^2-(5β)^3=512α^3-960α^2 β+600αβ^2-125β^3$

Окончательно

$(-8α+5β)^3=125β^3-512α^3+960α^2 β-600αβ^2$

б) $(q^2-7)^2$

Используем формулу куба суммы:

$(q^2-7)^2=(q^2)^3-3\cdot (q^2)^2\cdot 7+3\cdot q^2\cdot 7^2-7^3=q^6-21q^4+147q^2-343$

Пример 3

Представить в виде куба $8x^3-12x^2+6x-1$

Решение.

Это выражение можно записать следующим образом:

$8x^3-12x^2+6x-1=(2x)^3-3\cdot (2x)^2\cdot 1+3\cdot 2x\cdot 1-1^3$

Следовательно, по формуле куба суммы

$8x^3-12x^2+6x-1=(2x-1)^3$

Пример 4

Вывести формулу куба разности трех выражений.

Решение.

По условию задачи нам нужно раскрыть скобки в следующем выражении

$(α-β-γ)^3$

Считая $(α-β)$ за первый член суммы, а γ за второй, по формуле куба имеем

$(α-β-γ)^3=(α-β)^3-3(α-β)^2 γ+3(α-β) γ^2-γ^3$

По формулам куба и квадрата разности, подставляя и раскрывая скобки, будем получать

$(α+β+γ)^3=α^3-3α^2 β+3aβ^2-β^3-3α^2 γ+6αβγ-3β^2 γ+3αγ^2-3βγ^2-γ^3$

Окончательно

$(α-β-γ)^3=α^3-β^3-γ^3-3α^2 β-3α^2 γ-3β^2 γ-3βγ^2+3aβ^2+3αγ^2+6αβγ$

Таким образом, используя различные такие формулы можно вывести еще множество формул для сокращенного умножения и рационального преобразования выражений. В частности они помогают и при решений конкретных математический уравнений и задач.

Понятие объема тела

Объем является количественным параметром пространства, занятого телом или веществом.

Термин объема можно рассматривать совместно с понятием вместимости. Это обозначение для объема какого-то внутреннего пространства сосуда, коробки и тому подобного. Объем тела, как и вместимость некой емкости, зависит от таких характеристик, как:

• форма;
• линейные размеры.

Главным свойством объема принято считать аддитивность.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Аддитивность означает равенство объема какого-либо тела сумме объемов частей этого тела, которые не пересекаются между собой.

Согласно СИ, единицей измерения объема является метр кубический (м³). В процессе решения задач можно встретить единицы измерения объемов тел в виде см³, дм³, или литров. В иностранной литературе также используются указания объемов веществ, находящихся в жидком или сыпучем состоянии, в таких единицах измерения, как, например, галлон, баррель и другие.

Величина объема используется при составлении различных уравнений и неравенств. При этом данный параметр обозначают с помощью буквы V. Это сокращение от латинского слова volume, которое в переводе означает объем или наполнение.

Разложение суммы кубов

Посмотрим, как можно разложить суммированные кубы. Запишем еще раз полученную формулу:

\((a+b)^3 = a^3+3a^2 b+3ab^2+b^3\)

Вычислим с ее помощью сумму пары кубов:

\(a^3+b^3 = (a+b)^3-3a^2 b-3ab^2 = (a+b)^3-3ab(a+b) = (a+b)((a+b)^2-3ab) = (a+b)(a^2+2ab+b^2-3ab) = (a+b)(a^2-ab+b^2 )\)

Рассмотрим следующий многочлен:

\((a^2-ab+b^2 )\)

Данное выражение носит название неполного квадрата разности и имеет знак минуса. Для понимания запишем соотношение полного квадрата разности, которое имеет следующий вид:

\((a^2-2ab+b^2 ) = (a-b)^2\)

В результате получилось соотношение, подходящее для упрощения задачи по разложению суммы пары кубов на несколько множителей:

\(a^3+b^3 = (a+b)(a^2-ab+b^2 )\)

Кубы пары выражений в сумме дают произведение суммы данных выражений и неполного квадрата разности этих же выражений, то есть:

\(a^3+b^3 = (a+b)(a^2-ab+b^2 )\)

Дополнительные формулы сокращенного умножения

Есть три основные дополнительные ФСУ – это бином Ньютона, формула возведения в квадрат суммы трех, четырех и более слагаемых, а также формула разности n-ых степеней двух слагаемых. Коротко о каждой из них.

Бином Ньютона

Бином Ньютона – это формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Выглядит она следующим образом:

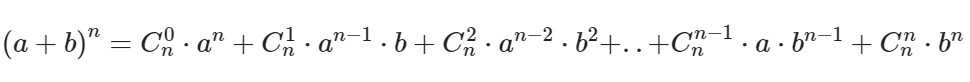
Ck в степени n – это биноминальные коэффициенты, стоящие в строке под номером n в треугольнике Паскаля. Вычисляются эти коэффициенты по формуле:

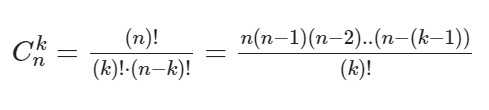
Иначе говоря, ФСУ для квадрата и куба разности и суммы являются частными случаями формулы бинома Ньютона при n=2 и n=3 соответственно.

Однако может быть так, что слагаемых в сумме, которую нужно возвести в степень, больше, чем два. В таком случае подойдет формула квадрата суммы трех, четырех и более слагаемых.

Формула возведения в квадрат суммы трех, четырех и более слагаемых

Как и было сказано, формула возведения в квадрат суммы трех, четырех и более слагаемых нужна, когда слагаемых в сумме, которую нужно возвести в степень, больше, чем два.

Выглядит она так:

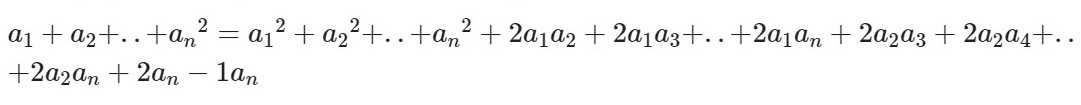
Читать и запоминать эту формулу нужно следующим образом: квадрат суммы n слагаемых равен сумме квадратов всех слагаемых и удвоенных произведений всех возможных пар этих слагаемых.

Формула разности n-ых степеней двух слагаемых

И последняя формула – это формула разности n-ых степеней двух слагаемых, выглядящая вот так:

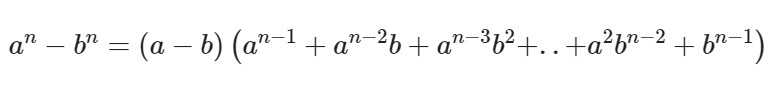
Как правило, данную формулу разделяют на две отдельные: для четных и нечетных степеней.

Формула для четных показателей 2m:

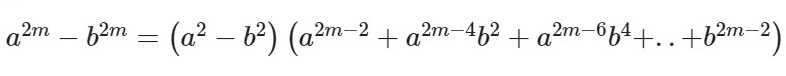
Формула для нечетных показателей 2m + 1:

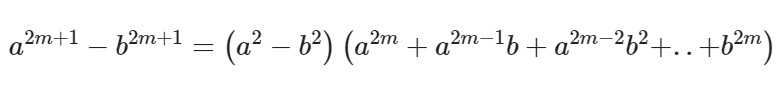
Несложно догадаться, что ФСУ разности квадратов и кубов являются частными случаями данной формулы при n=2 и n=3 соответственно. А для разности кубов b заменяется на –b.

Рассмотренные нами ФСУ и дополнительные ФСУ обязательно помогут вам быстрее справляться с математическими задачами и занимать свой мозг полезной деятельностью.

Вопросы и ответы

И напоследок несколько ответов на часто задаваемые вопросы.

Для чего нужны формулы сокращенного умножения?

Формулы сокращенного умножения нужны, чтобы упростить и ускорить вычисления, а также для улучшения наглядности и понимания математических выражений.

В настоящее время ФСУ широко используются в образовании и науке, а также в практической жизни. Они применяются в различных областях, таких как математика, физика, химия и инженерия, плюс могут применяться к решению различных задач, например, в области финансов, менеджмента и исследования данных.

Как появились формулы сокращенного умножения?

Формулы сокращенного умножения появились в результате исследований математиков в области алгебры и арифметики и основаны на использовании их свойств, таких как коммутативность, ассоциативность и дистрибутивность.

Если обратиться к истории, можно узнать, что такими формулами пользовались еще в Древнем Вавилоне и Древнем Египте. Первым же, кто доказал математическую закономерность квадрата суммы, был древнегреческий ученый Евклид, живший в III веке до н.э. А на общепринятом языке математические формулы были обоснованы Исааком Ньютоном.

Сколько всего формул сокращенного умножения?

Не существует точного количества формул сокращенного умножения, т.к. их можно создавать неограниченное количество. Но в основном изучают и используют семь основных формул. Это квадрат суммы, квадрат разности, разность квадратов, сумма кубов, разность кубов, куб суммы и куб разности. Также распространено применения трех дополнительных ФСУ, таких как бином Ньютона, формула возведения в квадрат суммы трех, четырех и более слагаемых и формула разности n-ых степеней двух слагаемых.

Почему формулы сокращенного умножения изучают на алгебре в 7 классе?

Формулы сокращенного умножения изучаются на алгебре в 7 классе, потому что именно на этом этапе школьники знакомятся с понятием многочлена и действиям с ним. Кроме того, ФСУ являются важным и основным инструментом для решения математических задач и упрощения вычислений.

Формулы помогают ученикам развить навыки в решении простых задач, а также дают им навыки для решения более сложных задач в будущем, что в перспективе способно помочь молодым людям в их дальнейшем обучении и карьере.

Можно ли не использовать формулы сокращенного умножения?

Конечно, при решении математических задач можно и не использовать формулы сокращенного умножения. Однако без них процесс решения может оказаться очень трудоемким и долгим. ФСУ же заметно упрощают его и помогают справляться с заданиями намного быстрее.

Помимо прочего, ФСУ входят в обязательную школьную программу, вследствие чего преподаватели часто требуют от учеников, во-первых, знать эти формулы наизусть, а во-вторых, решать задания именно с их помощью.

Технический рисунок

Технический рисунок – это наглядное изображение, выполненное по правилам аксонометрических проекций от руки, на глаз. Им пользуются в тех случаях, когда нужно быстро и наглядно показать на бумаге форму предмета. Обычно в этом возникает необходимость при конструировании, изобретательстве и рационализации, а также при обучении чтению чертежей, когда с помощью технического рисунка нужно пояснить форму детали, представленной на чертеже.

Выполняя технический рисунок, придерживаются правил построения аксонометрических проекций: под теми же углами располагают оси, так же сокращают размеры по осям, соблюдают форму эллипсов и последовательность построения.

Как найти элементы куба по его стороне?

Поскольку грань фигуры — это квадрат, то ее площадь определится по формуле №1, в которой известную величину нужно возвести в квадрат:

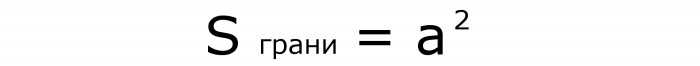
А диагональ любой грани вычисляется по формуле №2, в которой сторона умножается на корень из 2:

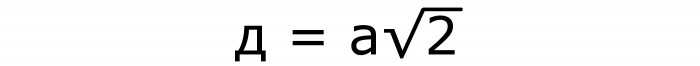
Предыдущая формула получается из теоремы Пифагора. Это легко понять, если увидеть, что диагональ грани — это гипотенуза прямоугольного треугольника. А катетами его становятся стороны квадрата.

Чтобы определить диагональ куба, нужна будет следующая формула №3, содержащая известную сторону и квадратный корень из 3:

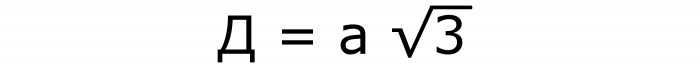
Она тоже получается из теоремы Пифагора. Только в качестве гипотенузы выступает искомая диагональ. Катетами же становятся сторона квадрата и его диагональ.

Иногда требуется знать формулу для вычисления площади боковой поверхности этой фигуры. В ней квадрат стороны умножается на 4. Вот она (№4):

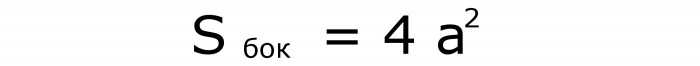
Понять, как получается эта формула, несложно. Боковых граней — 4. А это значит, что их общая площадь — учетверенное значение площади одного квадрата.

Если нужно определить площадь всей поверхности, то используют эту запись, в которой ушестеряется квадрат ребра (формула №5):

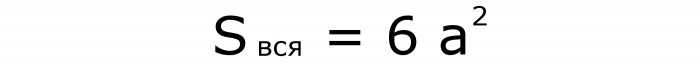
Она получается аналогично предыдущей формуле, только число квадратов увеличилось до 6.

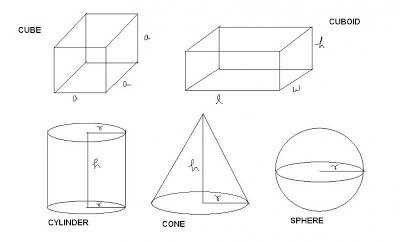
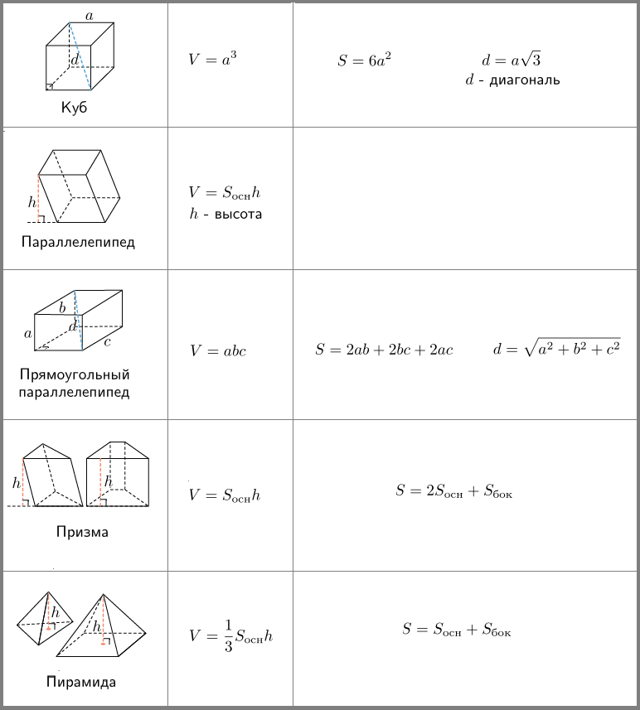
Формулы объема и площади поверхности. Призма, пирамида — материалы для подготовки к ЕГЭ по Математике

Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:

1. Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
2. Элементарная логика.

Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.

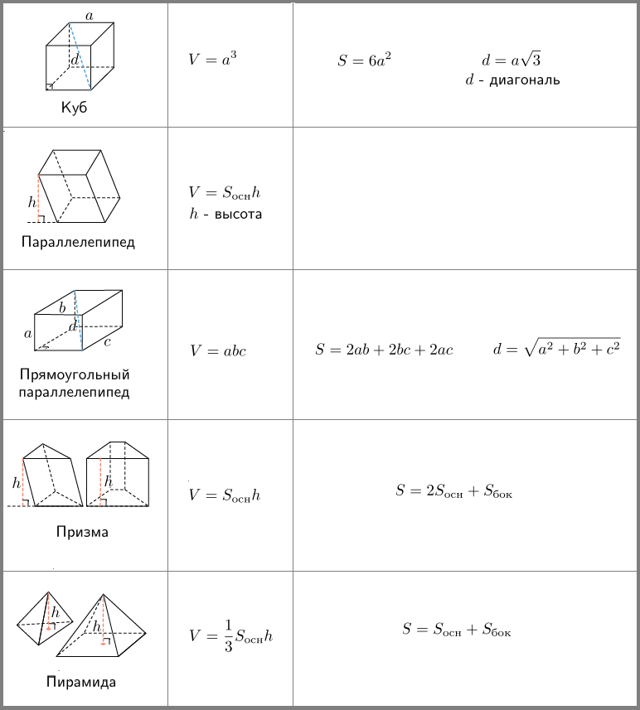
Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».

Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.

Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.

Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.

Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.

Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб

Очевидно, их 6, поскольку у куба 6 граней.

Иногда в задаче  надо посчитать площадь поверхности куба или призмы.

Напомним, что площадь поверхности многогранника — это сумма площадей всех его граней.

В некоторых задачах каждое ребро многогранника увеличили, например, в три раза. Очевидно, что при этом площадь поверхности увеличится в девять раз, а объём — в раз.

Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.

Cube Formula — Что такое Cube Formula? Примеры

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Куб числа непосредственно отражает объем куба, имеющего длину ребра, равную данному числу.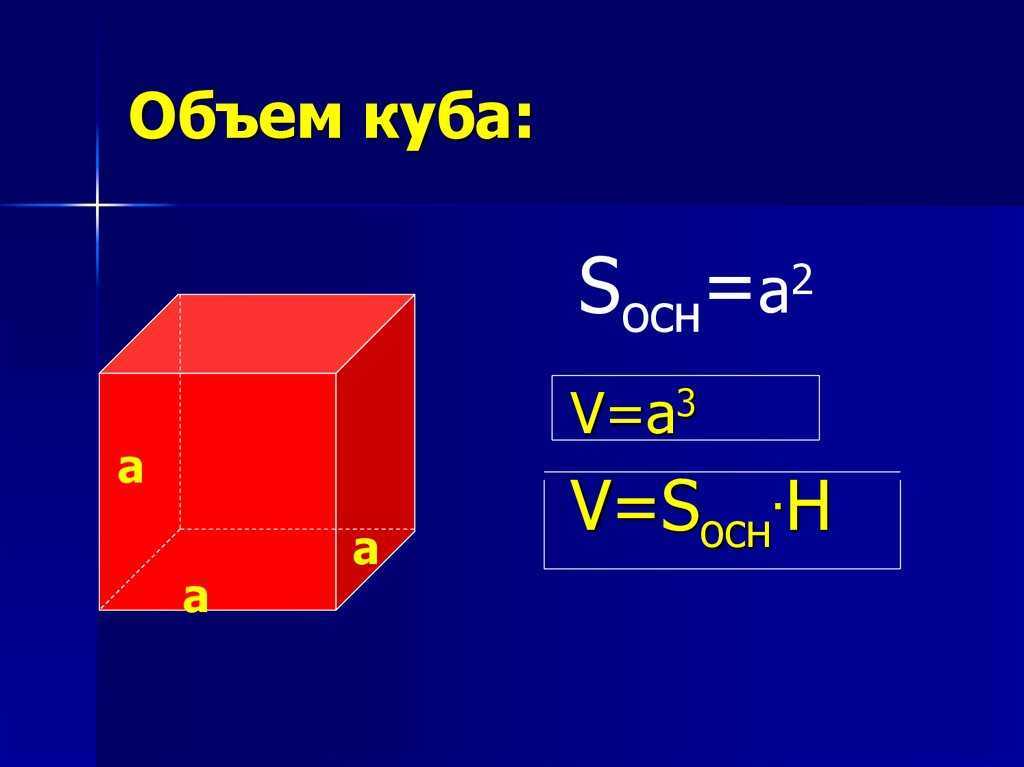

Что такое формула куба?

Куб является одним из пяти платоновых тел и также известен как правильный шестигранник.

Формула куба

Объем куба

Объем куба можно рассчитать с использованием различных формул на основе заданных параметров. Его можно рассчитать, используя длину стороны, а также размер диагонали куба.

• Объем куба (на основе длины стороны) = a 3  кубических дюймов, где a – длина стороны куба
• Объем куба (по диагонали) = (√3×d 3 )/9кубических дюймов, где d — длина диагонали куба

Боковая площадь куба

Боковая площадь куба равна сумме площадей всех боковых граней куба.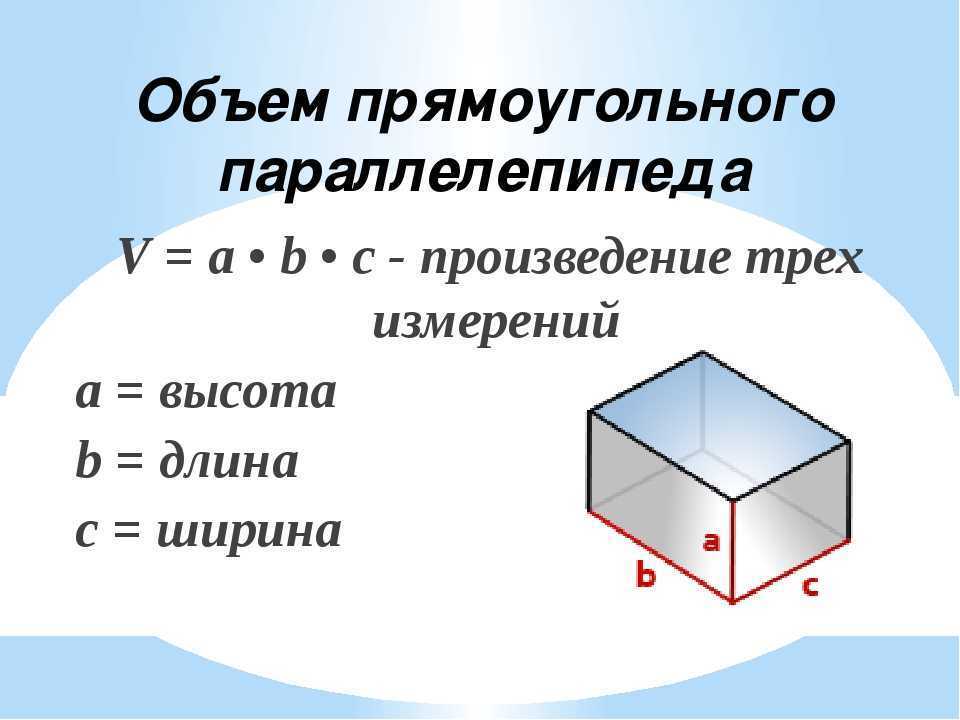

LSA куба = 4a 2

, где a — длина стороны.

Общая площадь куба

Общая площадь поверхности куба будет равна сумме площади основания и площади вертикальных поверхностей куба. Поскольку все грани куба состоят из квадратов одинакового размера, то общая площадь поверхности куба будет равна площади поверхности одной грани, сложенной с самой собой в пять раз. Таким образом, формула для нахождения площади поверхности куба:

Общая площадь поверхности (TSA) куба = 6a 2

, где a — длина стороны.

Диагональ куба

Куб имеет диагонали двух разных длин, более короткие лежат на квадратных гранях, а более длинные проходят через центр. Главной диагональю куба называется та, которая проходит через центр, который можно найти, умножив длину одной стороны на квадратный корень из 3.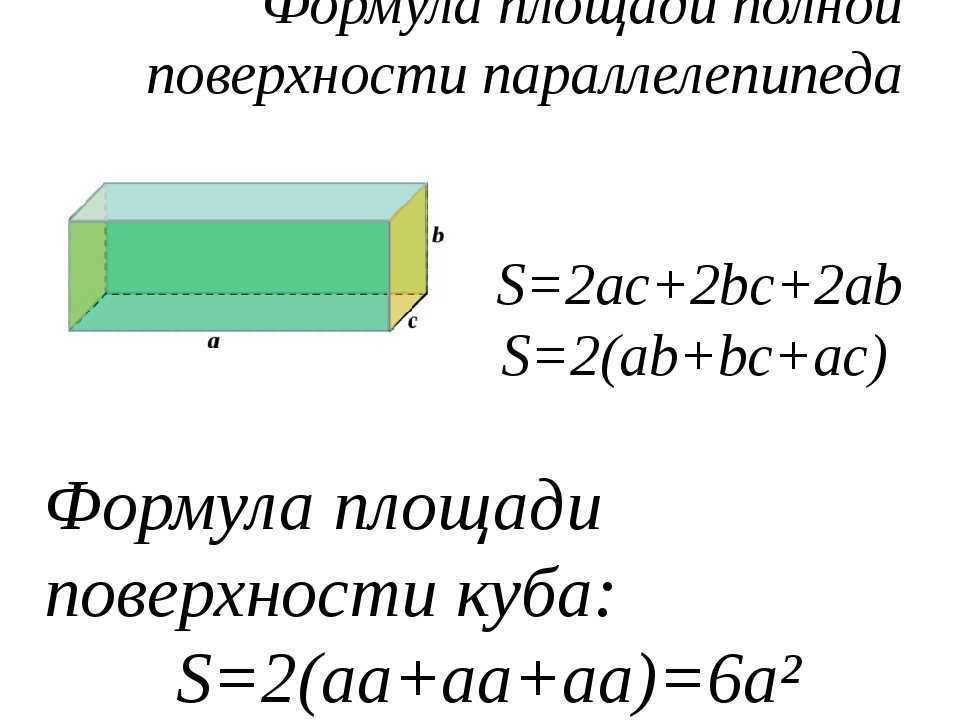

Диагональ куба = a√3

Давайте лучше разберемся с формулами куба на нескольких решенных примерах.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запись на бесплатный пробный урок

Примеры с использованием формулы куба

Пример 1: Найдите объем кубика Рубика длиной 4 дюйма. Решение:

Чтобы найти объем кубика Рубика: кубик Рубика0003

Длина стороны куба = 4 дюйма (дано)

Используя формулу куба, объем = с × с × с = с 3

Поместите значения,

объем = 4 × 4 × 4 = 4 3  = 64

Ответ: Объем кубика Рубика составляет 64 кубических дюйма.

Пример 2: Размеры куба – 64 дюйма. Найдите его диагональ по формуле куба. Решение: 

Чтобы найти диагональ куба:

Размеры куба: длина (l) = ширина (w) = высота (h) = 64 дюйма (данные)

Используя формулу куба,

диагональ = a√3 

Поместите значения,

Диагональ = 64√3 = 110,848 дюйма

Ответ: Диагональ куба равна 110,848 дюйма

Пример 3: Найдите общую площадь поверхности куба, если длина стороны куба равна 25 дюймам.

Решение:

Длина стороны куба, a = 25 дюймов 

Используя формулу площади куба, а именно: A = 6a 2

Поместите значения,

A = 6 × 25 × 25 = 3750 квадратных дюймов

Ответ: Площадь поверхности куб равен 3750 квадратных дюймов.

Часто задаваемые вопросы о формуле куба

Что такое формула куба?

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Это простые формулы, зависящие в основном от одного параметра — длины ребра или стороны куба.

Как рассчитать диагональ куба по формуле куба?

Главную диагональ куба , пересекающую центр, можно найти, умножив длину одной стороны на квадратный корень из 3. Таким образом, диагональ куба = a√3, где a – ребро куба. .

Что такое s в формуле куба?

В формуле куба s относится к ребру куба. Все формулы куба — объем, площадь поверхности и диагонали — зависят от ребра куба, представленного как s, так и a.

Как вывести формулу куба?

Чтобы вычислить объем по формуле куба,

• Шаг 1: Рассмотрим любой квадратный лист бумаги.
• Шаг 2: Теперь площадь, покрытая этим квадратным листом, будет равна площади его поверхности, т. е. его длине, умноженной на его ширину. Оба одинаковы в случае куба. Таким образом, площадь поверхности будет равна «s 2 ».
• Шаг 3: Куб получается путем складывания нескольких квадратных листов таким образом, чтобы высота стала равной длине и ширине, т. е. единицам «s». Таким образом, высота или толщина куба равна «s».

Таким образом, можно сделать вывод, что общее пространство, занимаемое кубом, то есть объем, равно площади основания, умноженной на высоту. Объем куба = s 2  × s = s 3

Чтобы вывести формулу поверхности куба,

• Шаг 1. Рассмотрим любой лист бумаги квадратной формы.
• Шаг 2: В случае квадрата, поскольку длина и ширина равны, площадь поверхности будет равна «s 2 » (длина, умноженная на ширину).
• Шаг 3: Поскольку у куба 6 граней, общая площадь поверхности куба равна площади одной грани, умноженной на 6 = 6s 2

Измерение объема жидкости

В международной системе единиц (СИ) за единицу объема принят кубический метр (м3) — объем куба со стороной 1 м, — и образованные от него производные:

• кубический километр;
• кубический дециметр ;
• кубический сантиметр ;
• кубический миллиметр .

Литр является внесистемной метрической единицей объема и вместимости, которая допускается к применению наравне с единицами СИ во всех областях.

Измерение объема жидкости с помощью мензурки

Для измерения объема жидкости используют измерительные приборы — мензурку, или измерительный цилиндр.

Правила пользования мензуркой:

1. Мензурку располагают таким образом, чтобы поверхность жидкости в ней находилась на уровне глаз.
2. Поверхность жидкости в мензурке должна быть строго горизонтальной, угол наклона недопустим.
3. Вода у стенок сосуда немного приподнимается (краевой эффект объясняется явлением смачивания), в средней же части сосуда поверхность жидкости почти плоская. Глаз следует направить на деление, совпадающее с плоской частью поверхности.

Погрешность измерения объема жидкости гидростатическим методом

Чем выше точность измерения датчика, тем больше рассчитываемый объем будет соответствовать реальному. Например, если используется датчик с классом точности 0,5 % и пределом измерения 0,4 бар, установленный в цилиндрической емкости с площадью дна 1 м² и высотой 4 м, полностью заполненной водой, вычисление абсолютной погрешности измерения объема имеет вид: .

Квадрат разности двух выражений

Формула квадрата разности двух выражений выглядит следующим образом:

(a − b)2 = a2 − 2ab + b2

Эту формулу можно прочитать так:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Формула квадрата разности двух выражений выводится таким же образом, как и формула квадрата суммы двух выражений. Выражение (a − b)2 представляет собой произведение двух многочленов, каждый из которых равен (a − b)

(a − b)2 = (a − b)(a − b)

Если выполнить это умножение, то получится многочлен a2 − 2ab + b2

(a − b)2 = (a − b)(a − b) = a2 − ab − ab + b2 = a2 − 2ab + b2

Пример 1. Преобразовать выражение (7x − 5)2 в многочлен.

Воспользуемся формулой квадрата разности двух выражений:

(a − b)2 = a2 − 2ab + b2

(7x − 5)2 = (7x)2 − 2 × 7x × 5 + 52 = 49×2 − 70x + 25

Значит, (7x − 5)2 = 49×2 − 70x + 25.

Попробуем решить данный пример, не пользуясь формулой квадрата разности. У нас должен получиться тот же результат:

(7x − 5)2 = (7x − 5)(7x − 5) = 49×2 − 35x − 35x + 25 = 49×2 − 70x + 25.

Формула квадрата разности двух выражений тоже имеет геометрический смысл. Если площадь квадрата со стороной a равна a2, то площадь квадрата, сторона которого уменьшена на b, будет равна (a − b)2

Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке уменьшили на b. У квадрата все стороны равны. Если одну сторону уменьшить на b, то остальные стороны тоже уменьшатся на b

Получился новый квадрат, который меньше предыдущего. На рисунке он выделен жёлтым. Сторона его равна a − b, поскольку старая сторона a уменьшилась на b. Чтобы вычислить площадь этого квадрата, можно из первоначальной площади квадрата a2 вычесть площади прямоугольников, которые получились в процессе уменьшения сторон старого квадрата. Покажем эти прямоугольники:

Тогда можно написать следующее выражение: старая площадь a2 минус площадь ab минус площадь (a − b)b

a2 − ab − (a − b)b

Раскроем скобки в выражении (a − b)b

a2 − ab − ab + b2

Приведем подобные слагаемые:

a2 − 2ab + b2

В результате получается выражение a2 − 2ab + b2, которое является правой частью формулы квадрата разности двух выражений:

(a − b)2 = a2 − 2ab + b2

Формулы квадрата суммы и квадрата разности в общем называют формулами сокращённого умножения. Эти формулы позволяют значительно упростить и ускорить процесс перемножения многочленов.

Ранее мы говорили, что рассматривая член многочлена по отдельности, его нужно рассматривать вместе со знаком, который перед ним располагается.

Но применяя формулы сокращённого умножения, знак исходного многочлена не следует рассматривать в качестве знака самого этого члена.

Например, если дано выражение (5x − 2y)2, и мы хотим воспользоваться формулой (a − b)2 = a2 − 2ab + b2, то вместо b нужно подставлять 2y, а не −2y. Это особенность работы с формулами, которую не следует забывать.

(5x − 2y)2a = 5xb = 2y(5x − 2y)2 = (5x)2 − 2 × 5x × 2y + (2y)2 = 25×2 − 20xy + 4y2

Если подставлять −2y, то это будет означать, что разность в скобках исходного выражения была заменена на сумму:

(5x − 2y)2 = (5x + (−2y))2

и в таком случае нужно применять не формулу квадрата разности, а формулу квадрата суммы:

(5x + (−2y)2a = 5xb = −2y(5x + (−2y))2 = (5x)2 + 2 × 5x × (−2y) + (−2y)2 = 25×2 − 20xy + 4y2

Исключением могут быть выражения вида (x − (−y))2. В данном случае, применяя формулу (a − b)2 = a2 − 2ab + b2 вместо b следует подставить (−y)

(x − (−y))2 = x2 − 2 × x × (−y) + (−y)2 = x2 + 2xy + y2

Но возводя в квадрат выражения вида x − (−y), удобнее будет заменять вычитание на сложение x + y. Тогда первоначальное выражение примет вид (x + y)2 и можно будет воспользоваться формулой квадрата суммы, а не разности:

(x + y)2 = x2 + 2xy + y2

Как найти объем прямоугольного параллелепипеда

Найдем объем прямоугольного параллелепипеда. На рисунке изображены куб, являющийся единицей измерения объема, и прямоугольный параллелепипед, объем которого надо измерить. Единицей длины служит ребро куба.Рассмотрим сначала случай, когда длины ребер параллелепипеда a, b и c выражаются конечными десятичными дробями и число десятичных знаков после запятой не более n.

Произведем следующую операцию: разобьем ребра куба, исходящие из одной вершины, на  равных частей и проведем через точки деления плоскости, перпендикулярные этим ребрам. При этом куб разобьется на  малых кубов с ребрами, равными .

Найдем объем малого куба. По свойству объема объем большого куба равен сумме объемов малых кубов. Так как объем большого куба равен единице, а число малых кубов равно , то объем малого куба равен .

Так как числа: — целые, то ребра параллелепипеда можно разбить на целое число частей, равное .

На ребре a их будет , на ребре , на ребре .

Проведем через точки деления ребер перпендикулярные ребрам плоскости. При этом мы получаем разбиение параллелепипеда на малые кубы со стороной .

Число их равно: .

Объем параллелепипеда равен сумме объемов содержащихся в нем малых кубов.

Так как объем малого куба равен , а их число равно , то объем параллелепипеда равен .

Рассмотрим теперь случай, когда длина хотя бы одного из ребер a, b, c выражается бесконечной десятичной дробью.

Обозначим через  приближенные значения числа a с недостатком и с избытком с точностью до n десятичных знаков.

Приближенные значения чисел b и с с той же точностью обозначим через 

Параллелепипед с ребрами имеет объем меньший, чем данный параллелепипед, так как его можно поместить внутрь данного. Параллелепипед с ребрами  имеет объем больший, чем данный параллелепипед, так как данный параллелепипед можно поместить внутрь него.

Таким образом, объем данного параллелепипеда заключен между  дают приближенное значение числа abc с любой наперед заданной точностью, если n достаточно велико, то отсюда следует: .

Как читать формулы сокращенного умножения

Научитесь произносить формулы сокращенного выражения:

1. Разность между квадратами двух выражений равна произведению их разности на их сумму.
2. Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого и второго плюс квадрат второго.
3. Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого и второго плюс квадрат второго.
4. Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.
5. Разность кубов двух выражений равна произведению разности первого и второго выражений на неполный квадрат их суммы.
6. Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второй.
7. Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого и второго плюс утроенное произведение первого на квадрат второго минус куб второго.

Формула куба – объяснение, свойства и примеры решения

Нас окружают разные предметы, которые состоят из разных геометрических форм. Подумайте о детской игре с кубиками, игральными костями или кубиком льда. Что вы замечаете общего среди всего этого? Все они имеют форму куба, не так ли? В этой статье мы изучим, что такое куб? Объем формулы куба, площадь формулы куба, площадь поверхности формулы куба. Некоторыми из распространенных примеров кубика являются кубик льда, игральные кости, кубик Рубика.

Введение. Что такое куб?

Куб — это трехмерная фигура, состоящая из граней квадратной формы одинакового размера.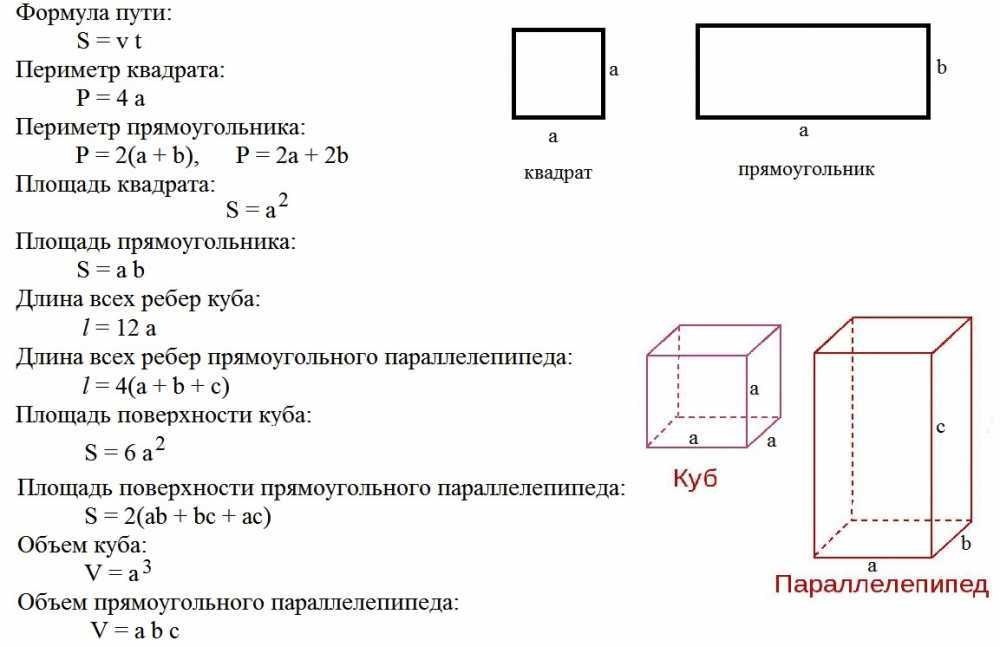

На приведенном ниже рисунке изображен куб, где l — длина, b — ширина, h — высота, и l = b = h. Длина, ширина и высота представляют ребра куба. И когда три ребра встречаются в точке, это называется вершиной.

(Изображение будет загружено в ближайшее время)

Свойства куба

1.  Все грани куба имеют квадратную форму.

2. Все грани и ребра равны.

3. Углы куба прямые.

4. Каждая из граней встречается с четырьмя соседними гранями.

5. Каждая из вершин встречается с тремя гранями и тремя ребрами.

6. Ребра, противоположные друг другу, параллельны и также равны.

7. Все 12 диагоналей на поверхности имеют площадь одинаковой величины

8. Все 4 внутренние диагонали равны

Например, куб имеет шесть граней. Следовательно, площадь его поверхности будет равна сумме площадей всех шести граней.

В основном площадь поверхности можно классифицировать как:

Площадь изогнутой поверхности объекта – это площадь всех криволинейных поверхностей объекта.

Боковая поверхность предмета – это площадь всех граней предмета, за исключением площади его основания и вершины. Для куба площадь боковой поверхности будет равна сумме площадей четырех сторон, то есть умноженной на 4 стороны.

Площадь боковой поверхности = 4 × (край) 2

902

Куб — это трехмерный объект, поэтому пространство, занимаемое кубом, будет трехмерным.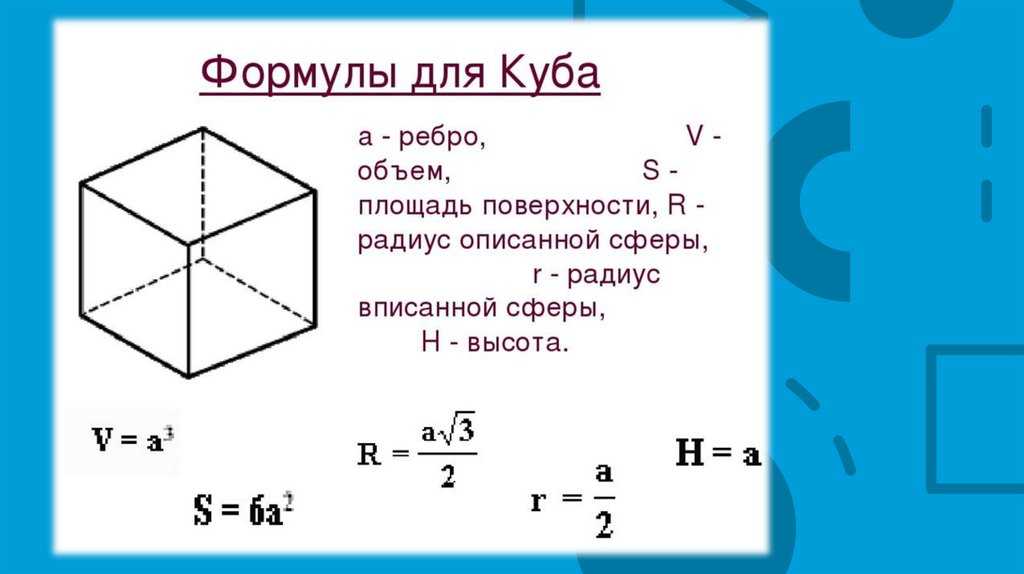

Куб ограничен шестью квадратными гранями, поэтому площадь поверхности будет вычисляться путем сложения площадей всех шести квадратных граней. Следовательно, площадь поверхности куба по формуле равна 9.0003

Площадь поверхности куба = 6 (сторона) 2

Внутренняя часть полого объекта может быть заполнена воздухом или какой-либо жидкостью, которая принимает форму объекта. В таких случаях объем вещества, который может вместить внутренность предмета, называется вместимостью полого предмета. Таким образом, мы можем сказать, что объем объекта — это мера занимаемого им пространства, а вместимость объекта — это объем вещества, которое может вместить его внутренность.

А объем куба — это занимаемое им пространство. Объем формулы куба будет рассчитан как:

Volume = (side) 3

Length of Diagonal of Face of the Cube = √2(edge)

Длина диагонала из куба = √3 (Edge)

3

3

3

3 9000

Периметр = 12 (ребро)

Решаемые примеры

Пример 1. Найдите площадь поверхности куба, длина стороны которого равна 7 см.

Решение:

Указанная длина = края = 7 см

Ум.

        = 6 × 49

        =  294 см 2

Пример 2: Сторона кубического ящика равна 9 м. Найдите объем кубического ящика.

Решение:

DED, сторона = A = 9m

по формуле объема A Cube, мы знаем, что

V = A 3 11963

9

v = 3 1113

9

v = 3 1113

9

v = 3 1113

V = 3 111996469

v = 3 11996469

v = 3 113

V = 3 x 9 x 9

V = 729 кв.

2

Значение кубов в математике

Кубы — это трехмерные квадраты, которые многие считают символом геометрического совершенства. С какой стороны на него ни посмотри, он выглядит одинаково. Это часть геометрии в математике и чрезвычайно важна как глава. Понимание этого является ключом к пониманию других связанных концепций. Учащиеся должны быть внимательны при изучении кубиков, так как из этой главы возникнет много вопросов. Они могут перейти к формуле куба — объяснение, свойства и примеры решений и подробно разобраться в этом. На этой странице Веданту каждая концепция упрощена для понимания учеником.