Диагональ куба вывод формулы

Cube Formula — Что такое Cube Formula? Примеры

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Куб числа непосредственно отражает объем куба, имеющего длину ребра, равную данному числу.

Что такое формула куба?

Куб является одним из пяти платоновых тел и также известен как правильный шестигранник.

Формула куба

Объем куба

Объем куба можно рассчитать с использованием различных формул на основе заданных параметров. Его можно рассчитать, используя длину стороны, а также размер диагонали куба.

Объем куба (на основе длины стороны) = a 3 кубических дюймов, где a – длина стороны куба
Объем куба (по диагонали) = (√3×d 3 )/9кубических дюймов, где d — длина диагонали куба

Боковая площадь куба

Боковая площадь куба равна сумме площадей всех боковых граней куба.

LSA куба = 4a 2

, где a — длина стороны.

Общая площадь куба

Общая площадь поверхности куба будет равна сумме площади основания и площади вертикальных поверхностей куба. Поскольку все грани куба состоят из квадратов одинакового размера, то общая площадь поверхности куба будет равна площади поверхности одной грани, сложенной с самой собой в пять раз. Таким образом, формула для нахождения площади поверхности куба:

Общая площадь поверхности (TSA) куба = 6a 2

, где a — длина стороны.

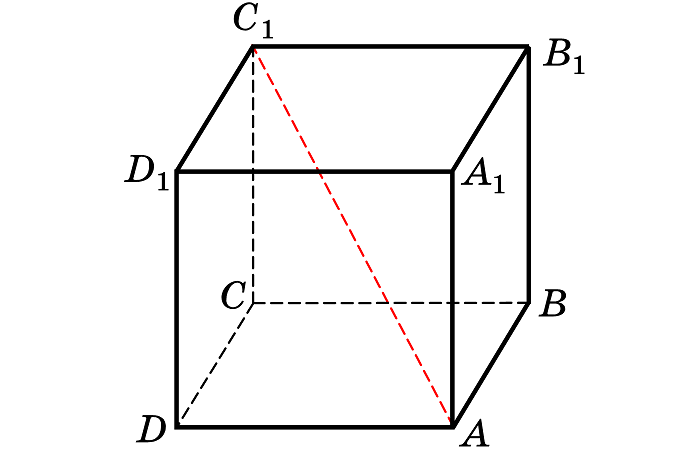
Диагональ куба

Куб имеет диагонали двух разных длин, более короткие лежат на квадратных гранях, а более длинные проходят через центр. Главной диагональю куба называется та, которая проходит через центр, который можно найти, умножив длину одной стороны на квадратный корень из 3.

Диагональ куба = a√3

Давайте лучше разберемся с формулами куба на нескольких решенных примерах.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запись на бесплатный пробный урок

Примеры с использованием формулы куба

Пример 1: Найдите объем кубика Рубика длиной 4 дюйма. Решение:

Чтобы найти объем кубика Рубика: кубик Рубика0003

Длина стороны куба = 4 дюйма (дано)

Используя формулу куба, объем = с × с × с = с 3

Поместите значения,

объем = 4 × 4 × 4 = 4 3 = 64

Ответ: Объем кубика Рубика составляет 64 кубических дюйма.

Пример 2: Размеры куба – 64 дюйма. Найдите его диагональ по формуле куба. Решение:

Чтобы найти диагональ куба:

Размеры куба: длина (l) = ширина (w) = высота (h) = 64 дюйма (данные)

Используя формулу куба,

диагональ = a√3

Поместите значения,

Диагональ = 64√3 = 110,848 дюйма

Ответ: Диагональ куба равна 110,848 дюйма

Пример 3: Найдите общую площадь поверхности куба, если длина стороны куба равна 25 дюймам.

Решение:

Длина стороны куба, a = 25 дюймов

Используя формулу площади куба, а именно: A = 6a 2

Поместите значения,

A = 6 × 25 × 25 = 3750 квадратных дюймов

Ответ: Площадь поверхности куб равен 3750 квадратных дюймов.

Часто задаваемые вопросы о формуле куба

Что такое формула куба?

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Это простые формулы, зависящие в основном от одного параметра — длины ребра или стороны куба.

Как рассчитать диагональ куба по формуле куба?

Главную диагональ куба , пересекающую центр, можно найти, умножив длину одной стороны на квадратный корень из 3. Таким образом, диагональ куба = a√3, где a – ребро куба. .

Что такое s в формуле куба?

В формуле куба s относится к ребру куба. Все формулы куба — объем, площадь поверхности и диагонали — зависят от ребра куба, представленного как s, так и a.

Как вывести формулу куба?

Чтобы вычислить объем по формуле куба,

Шаг 1: Рассмотрим любой квадратный лист бумаги.
Шаг 2: Теперь площадь, покрытая этим квадратным листом, будет равна площади его поверхности, т. е. его длине, умноженной на его ширину. Оба одинаковы в случае куба. Таким образом, площадь поверхности будет равна «s 2 ».
Шаг 3: Куб получается путем складывания нескольких квадратных листов таким образом, чтобы высота стала равной длине и ширине, т. е. единицам «s». Таким образом, высота или толщина куба равна «s».

Таким образом, можно сделать вывод, что общее пространство, занимаемое кубом, то есть объем, равно площади основания, умноженной на высоту. Объем куба = s 2 × s = s 3

Чтобы вывести формулу поверхности куба,

Шаг 1. Рассмотрим любой лист бумаги квадратной формы.
Шаг 2: В случае квадрата, поскольку длина и ширина равны, площадь поверхности будет равна «s 2 » (длина, умноженная на ширину).
Шаг 3: Поскольку у куба 6 граней, общая площадь поверхности куба равна площади одной грани, умноженной на 6 = 6s 2

Диагональ куба

Куб является базовым геометрическим телом, когда речь заходит об объеме и объемных телах. Недаром третья степень, которая получается умножением трех одинаковых чисел друг на друга (как при нахождении объема куба — трех его измерений одинаковых измерений) названа в его честь.

Основным и единственным параметром куба является его ребро a,так как все ребра у куба конгруэнтны, и представляют собой одновременно и длину, и ширину, и высоту. Соответственно, всего одно значение определяет все возможные характеристики куба, связанные с его измерениями.

Помимо ребер, вершины куба можно соединить диагоналями. Диагонали могут проходить через грани куба, тогда они будут просто диагональю основания или диагональю квадрата в плоскости, либо диагонали могут быть проведены внутри самого куба, соединяя противоположные основания в крайних точках (вершинах).

Чтобы найти диагональ куба через его ребро, необходимо сначала провести дополнительное построение в виде диагонали одного из соединяемых оснований, тогда диагональ куба станет гипотенузой новоиспеченного прямоугольного треугольника, катетами которого являются ребро куба и диагональ основания. Если ребро куба задано условиями задачи, то диагональ квадрата в основании придется сначала вычислить по формуле: d=a√2

Тогда диагональ куба можно будет выразить через теорему Пифагора, и она примет следующий вид:

Свойства куба

В куб можно вписать тетраэдр двумя вариантами, причем вершины тетраэдра, а их четыре, будут совпадать с четырьмя вершинами куба. Все шесть ребер тетраэдра будут располагаться на всех шести гранях куба и будут равны диагонали грани квадрата.
Четыре сечения куба это правильные шестиугольники, они проходят по центру куба перпендикулярно четырем диагоналям.
В куб вписывается октаэдр, причем все шесть вершин октаэдра совместятся с центрами шести граней куба.
Куб вписывается в октаэдр, причем все восемь вершин куба расположатся в центрах восьми граней октаэдра.
В куб можно вписать икосаэдр, так, что шесть взаимно параллельных ребер икосаэдра расположатся на шести гранях куба, остальные двадцать четыре ребра внутри куба, все 12 вершин икосаэдра лягут по шести граням куба.

Немного теории о кубе

Этот многогранник относится сразу к прямым параллелепипедам и призмам. Он — частный случай того и другого. В основании куба лежит квадрат, и боковые ребра его равны стороне данного квадрата. Таким образом, все три измерения имеют одинаковые значения.

Все шесть граней куба представляют собой квадраты. Длина каждого из 12 ребер одинаковая.

В каждой из граней можно провести диагональ, длину которой легко найти по формуле Пифагора. Кроме того, сам куб имеет диагонали. Их всего четыре. Проводится диагональ куба так, чтобы начинаться из вершины нижнего основания. Конец этого отрезка оказывается в вершине верхнего основания, но так, чтобы не совпасть с диагональю квадрата.

Особенности использования формулы для расчета больших и маленьких кубов

При расчете диагонали куба по его объему, есть несколько важных особенностей, которые необходимо учитывать, особенно при работе с большими и маленькими кубами. Следующие аспекты помогут вам более точно определить длину диагонали:

Точность измерений: Для получения точного результата, очень важно иметь точные измерения объема куба. Используйте наиболее точные инструменты и следите за правильностью измерений.

Единицы измерения: Убедитесь, что используете одну и ту же систему измерений как для объема, так и для диагонали

Например, если объем выражен в кубических сантиметрах, то диагональ также должна быть выражена в сантиметрах.

Формула для больших кубов: При расчете диагонали больших кубов, формула для нахождения длины диагонали будет состоять из извлечения кубического корня из утроенного объема куба. Такая формула правильно учтет отношения между объемом и длиной диагонали.

Формула для маленьких кубов: Для маленьких кубов, можно использовать более простую формулу для расчета диагонали. Просто возведите объем куба в степень 1/3 и получите длину диагонали.

Дополнительные измерения: Если у вас есть возможность, измерьте еще одну сторону куба, чтобы получить более точный результат. Используя формулу для нахождения длины диагонали, с учетом измеренной стороны, получите более точный результат.

Следуя этим особенностям, вы сможете более точно определить длину диагонали как для больших, так и для маленьких кубов по их объему. Имейте в виду, что в некоторых случаях может потребоваться округление до нужного числа знаков после запятой для получения более удобного значения.

Угол между ребром и гранью куба

Угол между ребром и гранью куба зависит от их взаимного положения. Если ребро и грань куба пересекаются или лежат в одной плоскости, то угол между ними равен 0 градусов. В этом случае ребро проходит через грань куба и является ее противоположной стороной.

Если же ребро и грань куба не пересекаются, то угол между ними будет 90 градусов. В этом случае ребро и грань куба образуют прямой угол, а ребро является одной из сторон грани.

В таблице ниже приведены математические обозначения и описания углов, в зависимости от положения ребра и грани куба:

Угол	Описание
0°	Ребро проходит через грань куба
90°	Ребро и грань образуют прямой угол

Что такое многогранник

Простейшей геометрической фигурой является прямая. Ею называется линия, которая имеет свое продолжение вправо и влево. Если эту прямую ограничить с двух сторон, получится отрезок. Для определения его величины достаточно одного измерения — длины. Прямая, ограниченная с одной стороны, имеет свое название. Это отрезок.

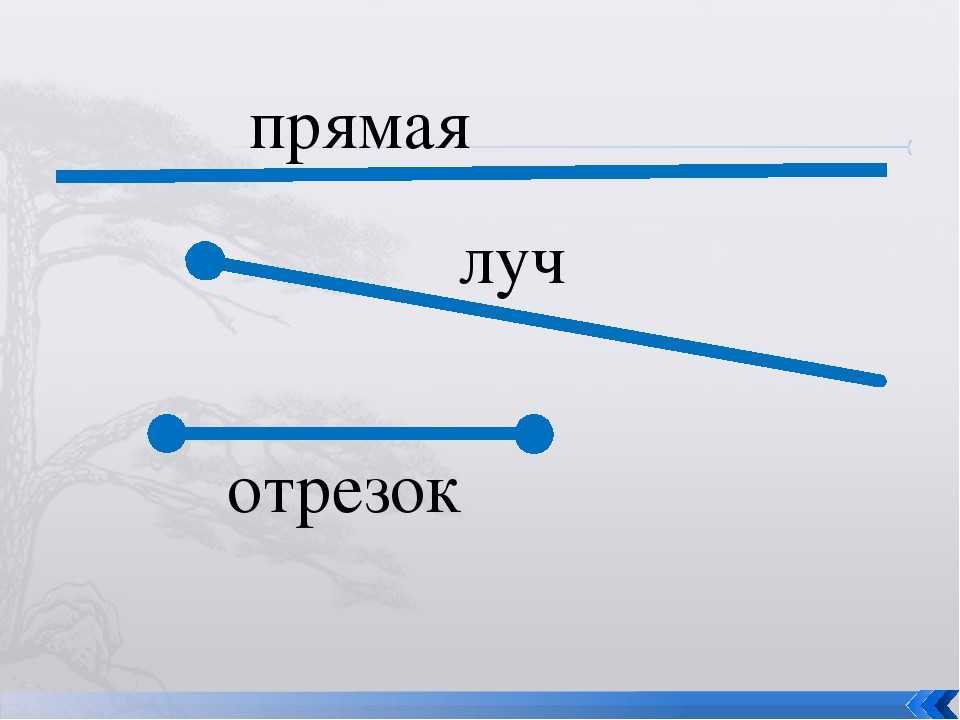
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут. В пределах одной плоскости, кроме прямой, которую можно измерить одной величиной, существуют геометрические фигуры, измеряемые длиной и шириной

Это многоугольники

В пределах одной плоскости, кроме прямой, которую можно измерить одной величиной, существуют геометрические фигуры, измеряемые длиной и шириной. Это многоугольники.

Они могут иметь различное количество углов и характеризуются таким понятием как площадь.

Фигура, которая располагается в нескольких плоскостях, характеризуется пространственными величинами или трехмерным измерением. К таким фигурам относят многогранники.

Многогранник — геометрическая фигура, имеющая замкнутую поверхность, которую можно представить совокупностью многоугольников.

Для полной характеристики многогранника необходимо назвать следующие свойства:

стороны обязательно являются смежными с одной соседней стороной;
при необходимости можно, начав движение от одного из многоугольников, достигнуть любого другого, используя принцип смежности;
площадь поверхности многогранника равна сумме площадей многоугольников, ограничивающих фигуру.

При этом каждый многоугольник — это грань, сторона — ребро, а вершина — вершина многогранника.

Многогранник, как геометрическое тело, может быть представлен несколькими параллелепипедами, которые соединены по одной из граней. В таком случае их площадь будет равна сумме площадей свободных сторон и одной стороны, по которой произошло соединение. Объем такого тела будет равен сумме объемов каждого из параллелепипедов.

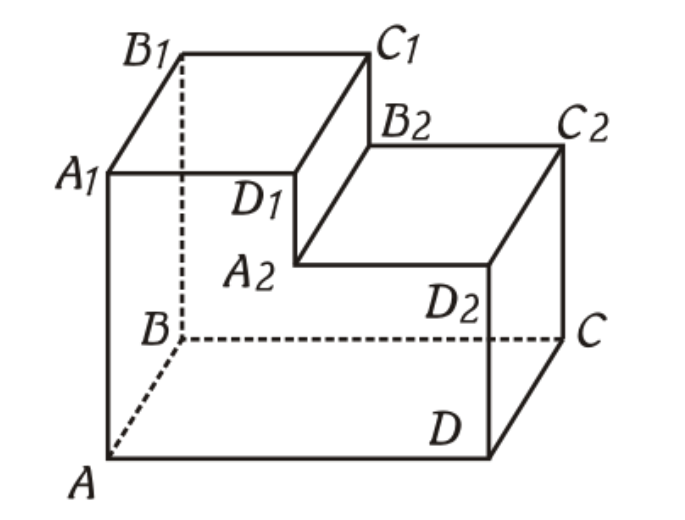
Многогранники бывают:

выпуклыми (каждая из точек фигуры находится по одну сторону от плоскости);
невыпуклыми (не все точки располагаются по одну сторону плоскости).

Проще говоря, выпуклый многогранник можно поставить на одну из сторон, и он будет на ней «уверенно стоять». С невыпуклым такого действия совершить нельзя.

Примечание 1

Важно помнить, что многогранник — это не только поверхность, состоящая из нескольких многоугольников. Это еще и тот внутренний объем, который ограничивает данная поверхность. Именно поэтому в стереометрии отделяют два понятия: площадь многогранника и его объем

Именно поэтому в стереометрии отделяют два понятия: площадь многогранника и его объем.

Параллелепипед и его виды

Если дословно перевести его название с древнегреческого, то получится, что это фигура, состоящая из параллельных плоскостей. Существуют такие равносильные определения параллелепипеда:

призма с основанием в виде параллелограмма;
многогранник, каждая грань которого — параллелограмм.

Его виды выделяются в зависимости от того, какая фигура лежит в его основании и как направлены боковые ребра. В общем случае говорят о наклонном параллелепипеде
, у которого основание и все грани — параллелограммы. Если у предыдущего вида боковые грани станут прямоугольниками, то его нужно будет называть уже прямым
. А у прямоугольного
и основание тоже имеет углы по 90º.

Причем последний в геометрии стараются изображать так, чтобы было заметно, что все ребра параллельны. Здесь, кстати, наблюдается основное отличие математиков от художников

Последним важно передать тело с соблюдением закона перспективы. И в этом случае параллельность ребер совсем незаметна

Немного теории о кубе

Все шесть граней куба представляют собой квадраты. Длина каждого из 12 ребер одинаковая.

Немного теории о кубе

Все шесть граней куба представляют собой квадраты. Длина каждого из 12 ребер одинаковая.

Трехгранный угол

Выберем в пространстве произвольную точку K. Далее из нее проведем три луча КА, КВ и КС так, чтобы они не находились в одной плоскости:

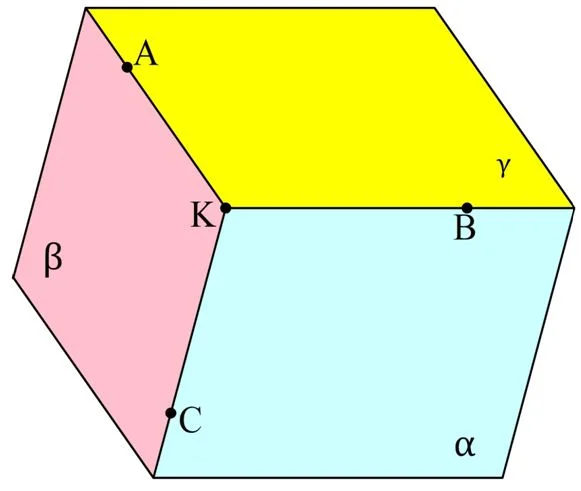
В результате мы получили фигуру, которую именуют трехгранным углом. Она состоит их трех плоских углов: ∠АКС, ∠АКВ и ∠ВКС. Эти углы так и называются – плоские углы трехгранного угла. Сам же трехгранный угол обозначают четырьмя буквами: КАВС

Обратите внимание, что через каждую пару лучей КА, КВ и КС можно провести плоскость. Таким образом, название «трехгранный» угол показывает, что в точке К сходятся три грани

Чаще всего в стереометрии такой угол возникает при рассмотрении вершин тетраэдра, в котором есть сразу четыре трехгранных угла:

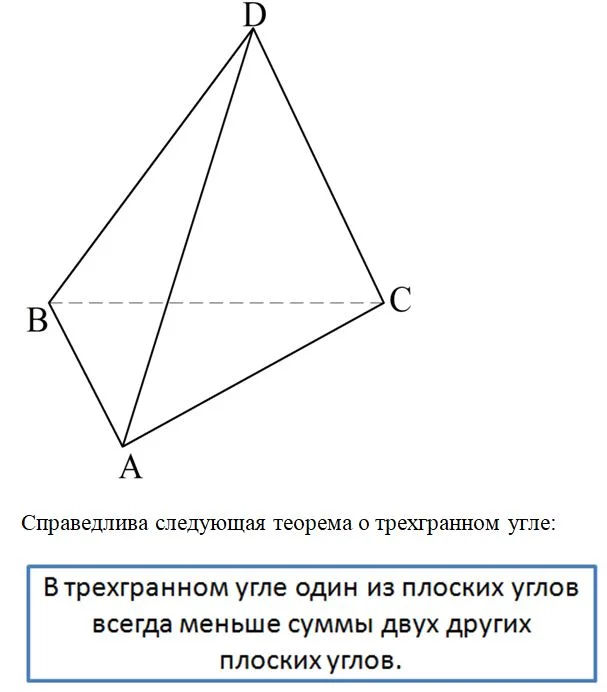
Доказательство. Пусть в пространстве из точки D выходят лучи AD, BD и CD

Важно понимать, что мы можем свободно «передвигать» точки А, В и С по лучам, и величина плоских углов при этом меняться не будет. Если среди плоских углов нет наибольшего, то теорема очевидно выполняется

Поэтому надо рассмотреть лишь случай, когда один из углов – наибольший. Пусть им будет ∠BDC:

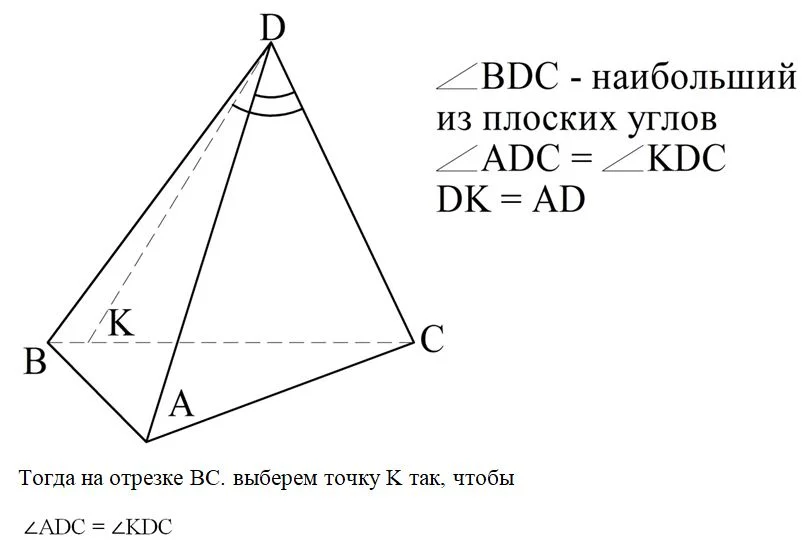
Это возможно сделать, ведь ∠BDC > AD, поэтому внутри ∠BDC можно провести луч DK. Далее «сместим» точку А на луче АD так, чтобы DK = AD. Естественно, что при этом плоские углы трехгранного угла никак не изменятся, также как останется верным равенство

Сравним ∆ADC и ∆DKC. У них есть общая сторона DC, одинаковы стороны DK и AD, а также совпадают углы между ними. Значит, эти треугольники равны, и тогда можно записать, что:

Теперь сравним ∆ABD и ∆DBK. У них BD – общая сторона, а DK = AD. При этом BK < AB. В таком случае против меньшей стороны будет лежать меньший угол (смотри примечание после доказательства), то есть

Именно это неравенство и необходимо было доказать.

Примечание. В ходе доказательства было использовано утверждение, что если у двух треугольников две стороны одинаковы, в третьи стороны отличаются, то против меньшей третьей стороны будет располагаться меньший угол:

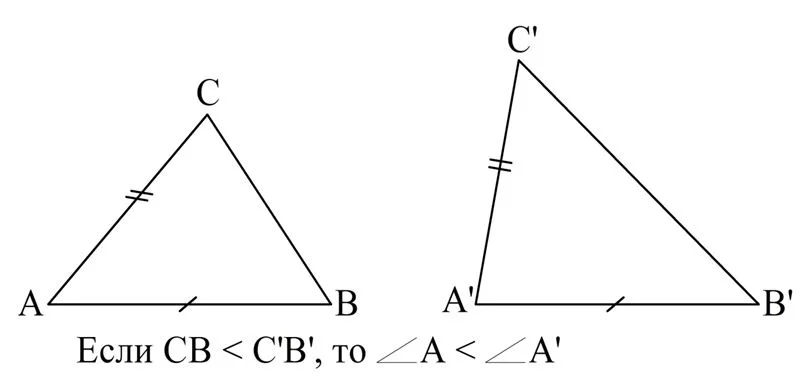
Это утверждение часто не рассматривается в курсе планиметрии, поэтому есть смысл доказать его отдельно. Действительно, пусть есть ∆АВС и ∆А’B’C’, АС = А’C’ и АВ = A’B’, а СВ < C’B’. Надо показать, что ∠А <∠A’. Для этого выразим стороны СВ и C’B’ (а точнее говоря, их квадраты) с помощью теоремы косинусов:

Из последнего неравенства на основе определения косинуса для углов из интервала от 0° до 180° вытекает, что и

Куб — свойства, виды и формулы

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.

Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;

прямая призма, все грани которой есть квадраты;

прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

Понятие двугранного угла и угла между плоскостями

Напомним, что в планиметрии углом называют фигуру, состоящую из точки и двух лучей, выходящих из нее. Сама точка именуется вершиной угла, а лучи – сторонами угла.

По аналогии в стереометрии рассматривается схожая фигура – двугранный угол. Он состоит из двух полуплоскостей, которые исходят из одной прямой. Каждая из этих полуплоскостей именуется гранью двугранного угла, а их общая прямая – это ребро двугранного угла.

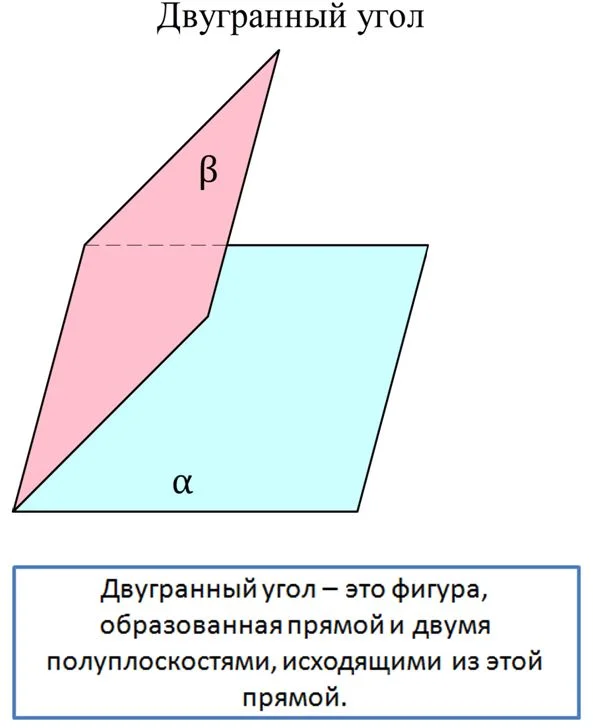
Для обозначения двугранного угла достаточно указать две точки на его ребре, а также ещё по одной точке на каждой грани. Например, на следующем рисунке показан угол САВD:

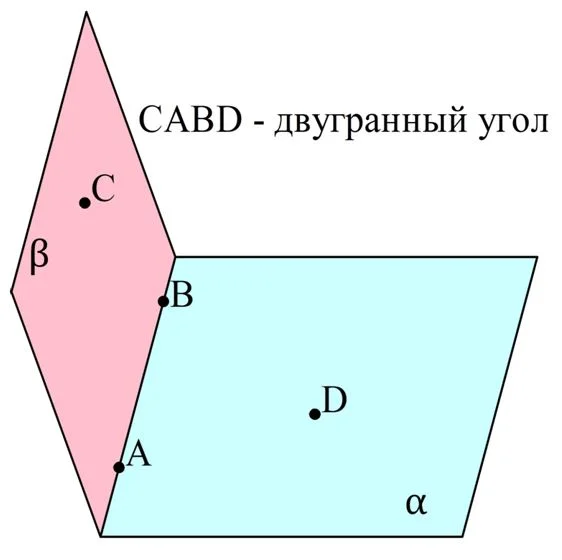
Двугранные углы часто встречаются в обычной жизни. Например, его образуют двухскатные крыши домов. В стереометрии двугранные угла можно найти в любом многограннике.

Двугранные углы можно измерять. Для этого надо выбрать произвольную точку на ребре угла и на каждой грани построить перпендикуляр, проходящий через эту точку. Через эти два перпендикуляра можно построить единственную плоскость. Угол между двумя перпендикулярами и принимается за величину двугранного угла.

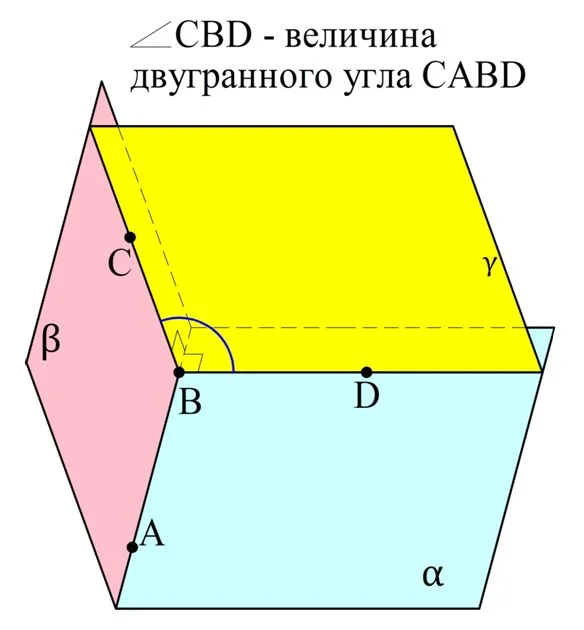
Отдельно отметим, что плоскость, проходящая через перпендикуляры (на рисунке выше это γ) перпендикулярна ребру угла АВ. Это вытекает из признака перпендикулярности прямой и плоскости. Действительно, АВ⊥ВС и АВ⊥BD, поэтому и АВ⊥γ. Построенный угол ∠СBD называют линейным углом двугранного угла.

Понятно, что в каждом двугранном угле можно построить сколько угодно линейных углов:

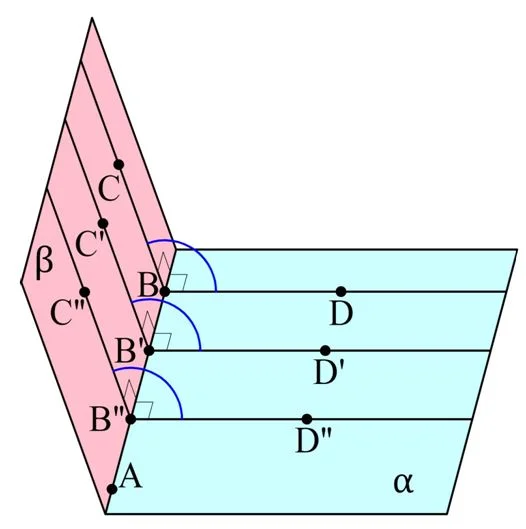
Здесь помимо ∠ВСD построены линейные углы ∠В’С’D’ и ∠В’’С’’D’’. Однако все эти углы имеют одинаковую градусную меру. Сравним, например, ∠ВСD и ∠В’С’D’. Так как BD⊥AB и B’D’⊥АВ, то BD||B’D’. Аналогично можно прийти к выводу, что ВС||B’C’. Получаем, что стороны углов ∠ВСD и ∠В’С’D’ – это сонаправленные лучи, а потому ∠ВСD и ∠В’С’D’ одинаковы.

Двугранные углы, как и обычные углы, можно разделить на острые (их градусная мера меньше 90°), прямые (они в точности равны 90°) и тупые (которые больше 90°).

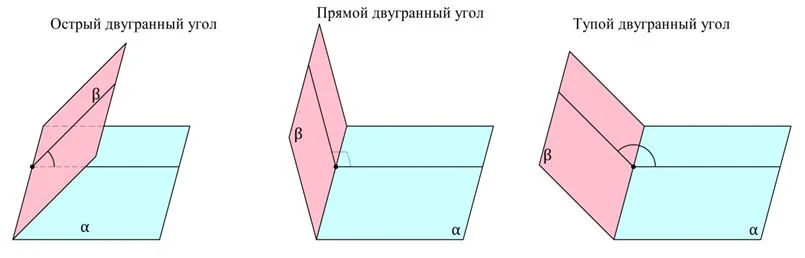
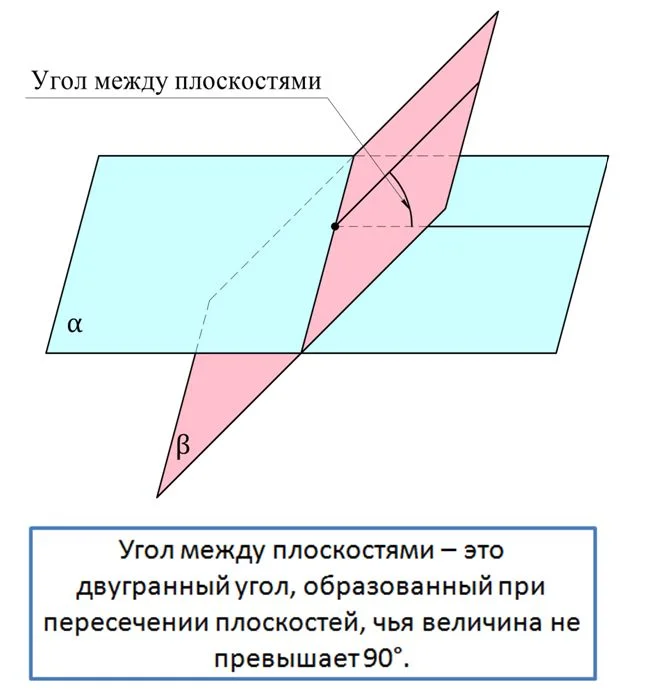
Если две плоскости пересекаются, то они образуют сразу 4 двугранных угла. Если среди них есть острый угол, то его величина считается углом между плоскостями. Если же все образуется 4 прямых двугранных угла, то угол между плоскостями принимается равным 90°.

Как бы вы записали формулу площади поверхности и объема куба через длину его диагонали?

Геометрия Площадь поверхности Куб Диагональ

Рэйчел М.

Мне дана переменная d, которая представляет собой диагональ куба. Других чисел или переменных не указано. Я должен написать формулу, чтобы найти площадь поверхности куба

Подробнее

Отчет

3 ответа от опытных наставников

КРУЗ С.

Репетитор

4.9
(80)

Опытный заведующий кафедрой математики, стаж преподавания более 7 лет

См. таких репетиторов

Посмотреть таких репетиторов

Куб состоит из конгруэнтных сторон, и каждая грань куба является квадратом.

Площадь квадрата равна 2 , а поскольку у куба шесть сторон, площадь поверхности куба равна 6 (a 2 ) или 6a 2

Диагональ на грани куба будет создайте два треугольника 45-45-90, где катет = x и гипотенуза = x√2.

Диагональ d также является гипотенузой

d=x√2

Решение для x даст длину каждой стороны .

d/√2=x√2/√2

x = d/√2

x= (d)(√2) / (√2)(√2) = d√2/2

вычислить площадь одной стороны, определить x 2

(d√2 / 2) 2 = 2d 2 / 4 = (1/2)d 2

Площадь 6 стороны равна ( 6)(1/2)d 2 = 3d 2 , что является площадью поверхности.

SA = 3d 2

Объем равен 3 или x 3 = (d)(√2) / 2 * (d)(√2) / 2 * . (г)(√2) / 2 . = д 3 * . 2√2/8 =

V = d 3 √ 2/4

Объем равен d, умноженному на квадратный корень из 2, деленному на 4

Голосовать за 0 Понизить

Подробнее

Отчет

Исаак С.
ответил 04/29/19

Репетитор

4.9
(748)

Репетитор по физике, химии, математике и компьютерному программированию

Об этом репетиторе ›

Отношение диагонали к одной из сторон равно sqrt 3.

поэтому, чтобы найти объем, возьмите длину диагонали и разделите ее на sqrt 3, чтобы найти длину одной стороны.

Диагональ куба

Тогда диагональ куба можно будет выразить через теорему Пифагора, и она примет следующий вид:

Геометрия 10 класс

«Аксиомы стереометрии 10 класс» — Аксиомы стереометрии. А, В, С ? одной прямой А, В, С ? ? ? — единственная плоскость. 1. Лежат ли на плоскости ? точки В и С? 2. Найдите длину отрезка CF и площадь треугольника АВС. 2. Объясните, как построить линию пересечения плоскостей (AB1K) и (ADD1)? В любой плоскости пространства справедливы все аксиомы и теоремы планиметрии. 3. Назовите линию пересечения плоскостей (МОВ) и (ADO). Через две пересекающиеся прямые проходит плоскость, и притом только одна.

«Основные аксиомы стереометрии» — Древняя китайская пословица. Аксиомы стереометрии. Источники и ссылки. Изображения пространственных фигур. Геометрические тела. Геометрия. Пирамида Хеопса. Основные фигуры в пространстве. Следствия из аксиом стереометрии. Предмет стереометрии. Плоскость. Первые уроки стереометрии. Следствия из аксиом. Плоскости имеют общую точку. Аксиома. Четыре равносторонних треугольника. Точки прямой лежат в плоскости.

«Сечения фигур» — Пирамида. Значение. Многогранники в архитектуре. Точка. Воздух. Проведем прямую МК. Прямые в плоскостях. Пчёлы. Точка пересечения прямых. Построить сечение куба. Сечение куба плоскостью. Точки, лежащие в плоскости сечения. Мир многогранников. Построение сечений многогранника. Земля. Определение. Сечение куба. Искомое сечение. Сечение. Глубины различных наук. Сечение пирамид. Решение. Отметим точки.

«Сечение призмы» — Сечение призмы. Плоскость сечения параллельна боковому ребру призмы. Построение методом «следов». Определение сечения призмы. Плоскость сечения. Определение сечения. Диагональное сечение. Построение. Виды сечений. Построение сечений. Самостоятельная работа. Сечение призмы плоскостью. Сечения призмы.

«Предмет стереометрии» — Теорема Пифагора. Невидимая сторона. Неопределяемые понятия. Наглядные представления. Планиметрия. Стереометрия. Из истории. Вселенная. Сегодня на уроке. Геометрия. Пространственные представления. Египетские пирамиды. Помните ли вы теорему Пифагора. Точки. Пифагор. Аксиомы стереометрии. Пентаграмма. Понятие науки стереометрии. Указания. Правильные многогранники. Евклид. Философская школа. Основные понятия стереометрии.

«Декартова система» — Декартова система координат. Вопросы для заполнения. Прямоугольная система координат. Понятие системы координат. Введение декартовых координат в пространстве. Определение декартовой системы. Координаты точки. Координаты любой точки. Координаты вектора. Рене Декарт.

«Геометрия 10 класс»

Гексаэдр. Куб.

Каждое ребро куба соединяет две вершины и имеет два конца. Один конец ребра принадлежит одной грани куба, а другой конец — соседней грани. Каждое ребро пересекается с другими ребрами под прямыми углами, образуя сетку ребер, которая характерна для куба. Ребра куба являются важными элементами, которые определяют его форму и структуру. Изучение свойств и характеристик ребер куба позволяет лучше понять геометрические особенности этой фигуры и использовать их в решении задач и заданий. Определение ребра куба Длина ребра куба одинакова для всех его ребер и является основной характеристикой этой геометрической фигуры. Длина ребра обозначается символом «a» и определяет размеры куба. Ребро куба является прямым отрезком, а его направление может быть любым в пространстве.

Оно может быть горизонтальным, вертикальным или наклонным.

Радиус вписанной сферы куба Сферу можно вписать в куб таким образом, что она коснется поверхностью всех рёбер куба. Такая сфера именуется — полувписанная в куб. Радиус полувписанной сферы можно определить по формуле: Площадь поверхности куба Для наглядности площадь поверхности куба можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон куба это площадь правильного четырехугольника — квадрата умноженной на 6.

Куб является одним из основных геометрических тел, широко используемых в науке, технике и архитектуре.

Свойства рёбер куба 1. Длина ребра: Все ребра куба имеют одинаковую длину. Если длина одного ребра равна a, то длина каждого ребра куба будет равна a. Количество ребер: Куб имеет 12 ребер. Каждая из 8 вершин куба соединена с 3 ребрами, а каждое ребро связано с 4 ребрами. Геометрическая форма: Ребра куба являются прямыми отрезками, которые параллельны осям координат.

Ориентация: Каждое ребро имеет начальную и конечную вершины. Порядок соединения вершин определяет ориентацию ребра. Взаимное расположение: Ребра куба пересекаются под прямым углом. Каждое ребро соединяет две вершины, которые находятся на каждой из трех осей координат, и пересекает одну или две грани куба. Таким образом, ребра куба определяют его структуру, форму и связи между вершинами и гранями. Они являются важными элементами в геометрии и математике, а также имеют применение в различных областях науки и техники.

Примеры использования вершин, граней и ребер куба Определение объема и площади поверхности куба. Для этого необходимо знать длину ребра куба и использовать соответствующие формулы. Создание трехмерной модели куба. При построении модели используются вершины, грани и ребра, которые определяют размеры и форму куба. Расчет диагонали куба.

Куб имеет 9 осей симметрии. Три оси симметрии это прямые проходящие через центр параллельных граней куба: Шесть осей симметрии это прямые соединяющие центры противолежащих рёбер куба: Куб имеет 9 плоскостей симметрии Три плоскости проходят через центр параллельно граням Шесть плоскостей проходят через центр по диагонали Куб может быть помещен в сферу вписан , так, что каждая из его вершин будет касаться внутренней стенки сферы. Радиус описанной сферы куба Сфера может быть вписана внутрь куба. Радиус вписанной сферы куба Сферу можно вписать в куб таким образом, что она коснется поверхностью всех рёбер куба.

Итог

Представлен простейший калькулятор онлайн для заданных величин рассматриваемого здесь геометрического тела. Объем его – вне зависимости от единицы, дозволяющей сделать его измерения.

Вычисления производят в:

метрах;
сантиметрах;
миллиметрах.

Итог выводят в сантиметрах, метрах кубических.

Ожидая получение расчета, пользователь также может указать желаемую точность выводимого результата, то есть число знаков, идущих за запятой и до которого нужно округлить уже подсчитанный показатель.

Найти заданную величину абсолютно несложно посредством простого помощника, которым является представляемый калькулятор онлайн. Необходимое значение он выдает мгновенно, в расчетах никогда нет ошибок. Поэтому пользователь может быть стопроцентно уверен в выданных калькуляцией результатах.

Рассчитывающий объем куба калькулятор действует следующим образом: при каждом указанном значении, все прочие будут найдены автоматически. Следовательно, при вводе в ячейку (поле калькулятора онлайн), например, показателя длины грани нашей фигуры либо ее диагонали, радиуса вписываемого шара или площади, нажимают «Расчет», и все необходимые данные об иных величинах будут тотчас получены. Для удобства итоги выводятся вместе с расчетными формулами.

Cube Formula — Что такое Cube Formula? Примеры

Что такое формула куба?

Формула куба

Примеры с использованием формулы куба

Часто задаваемые вопросы о формуле куба

Что такое формула куба?

Как рассчитать диагональ куба по формуле куба?

Что такое s в формуле куба?

Как вывести формулу куба?

Диагональ куба

Свойства куба

Немного теории о кубе

Особенности использования формулы для расчета больших и маленьких кубов

Угол между ребром и гранью куба

Что такое многогранник

Параллелепипед и его виды

Немного теории о кубе

Немного теории о кубе

Трехгранный угол

Куб — свойства, виды и формулы

Понятие двугранного угла и угла между плоскостями

Как бы вы записали формулу площади поверхности и объема куба через длину его диагонали?

3 ответа от опытных наставников

Диагональ куба

Геометрия 10 класс

Гексаэдр. Куб.

Итог

Похожие записи:

Похожие записи: