Куб

У куба все грани представляют собой

Куб
Тип	Платоново твердое тело
Лица	6 квадратов
Края	12
Вершины	8
Грани / вершина	3
Характерная черта	2
Символ Шлефли
Символ Wythoff	3
Диаграмма Кокстера-Дынкина
Двойной	Правильный октаэдр
Группа симметрии	О ч
Объем	а³
Область	6a²
Двугранный угол	90 °
Характеристики	выпуклый зоноэдр
редактировать

В евклидовой геометрии , А куба является правой призма , чьи лица являются квадратными и , следовательно , равны и совмещаются. Куб — одно из самых замечательных тел в космосе . Это единственное из пяти тел Платона , имеющее ровно 6 граней, 12 ребер и 8 вершин. Другое его название — « правильный шестигранник ».

Поскольку у него четыре вершины на грань и три грани на вершину, его символ Шлефли равен .

Этимология слова куб — греческое ; куб происходит от кубоса , игральной кости .

Термин куб , применяемый к числу , обозначает значение, полученное путем умножения этого числа на само себя и умножения результата на исходное число. Это выражение появилось в период, когда геометрическая алгебра была повсеместной, квадрат числа рассматривался как площадь квадрата помимо исходного числа, а куб числа — как объем куба помимо исходного числа. Выражение « 3 » может быть « излучающая в кубе» и «куб».

1-скелет кубы — множество его вершин , соединенных его ребра — образует графу называется шестигранный графом .

См. также

Wikimedia Foundation . 2010 .

Смотреть что такое «Куб» в других словарях:

куб — куб, а, мн. ч. к уб ы, к уб ов … Русский орфографический словарь

КУБ — (лат. cubus). 1) третья степень данной величины. 2) правильный шестигранник, т. е. тело, ограниченное шестью квадратами. 3) снаряд для перегонки жидкостей; то же, что алембик. 4) растение куб (Indigo), из которого добывается кубовая краска.… … Словарь иностранных слов русского языка

куб — 1. КУБ, а; кубы; м. 1. Геометрическое тело правильный шестигранник, все грани которого квадраты; предмет, имеющий форму такого шестигранника. Начертить куб. Композиция из гипсовых кубов и призм. Мраморный куб памятника. 2. Разг. =… … Энциклопедический словарь

КУБ — ОАО АКБ «Кузбассугольбанк» http://cbank.ru/​ организация, фин., энерг. КУБ кнопочный пост управления взрывобезопасный КУБ ОАО «Кредит Урал банк» http://www.credit … Словарь сокращений и аббревиатур

КУБ — муж. перегонный сосуд, алембик, снаряд для перегонки жидкостей, особ. винных. Куб бывает стекляный, глиняный, медный и пр., разной величины и вида; он наглухо кроется колпаком, и перегонная жидкость идет парами в горло, шейку, а оттуда в… … Толковый словарь Даля

куб — сущ., м., употр. сравн. часто Морфология: (нет) чего? куба, чему? кубу, (вижу) что? куб, чем? кубом, о чём? о кубе; мн. что? кубы и кубы, (нет) чего? кубов и кубов, чему? кубам и кубам, (вижу) что? кубы и кубы, чем? кубами и кубами, о чём? о… … Толковый словарь Дмитриева

кубіт — кубі/т, род. кубіта, мн. кубіти, род. мн. кубітів одиниця інформації, що закодована в квантовій системі, фізичний носій інформації, що може перебуватив станах |0> та |1> і будь якій суперпозиції цих станів. • Стан кубіта може змінюватись… … Фізико-технічний словник-мінімум

КУБ — 1. КУБ1, куба, муж. (греч. kybos). 1. Правильный шестигранник, все грани которого (квадраты (мат.). Начертить куб. 2. Мера объема, равная кубическому метру. Куб дров. 3. Сосуд для перегонки или кипячения жилкостей в форме шара или цилиндра с… … Толковый словарь Ушакова

КУБ — 1. КУБ1, куба, муж. (греч. kybos). 1. Правильный шестигранник, все грани которого (квадраты (мат.). Начертить куб. 2. Мера объема, равная кубическому метру. Куб дров. 3. Сосуд для перегонки или кипячения жилкостей в форме шара или цилиндра с… … Толковый словарь Ушакова

КУБ — (от латинского cubus, от греческого kybos игральная кость), 1) один из 5 типов правильных многогранников, имеющий гранями квадраты, 12 ребер, 8 вершин, в каждой вершине сходятся 3 ребра. Куб иногда называют гексаэдром. 2) Третья степень а3 числа… … Современная энциклопедия

КУБ — КУБ, в математике результат двукратного умножения числа на самого себя. Таким образом, кубом числа а является произведение а х а х а, что записывается как а3. Куб называют также третьей степенью числа. Кубом именуется правильная шестисторонняя… … Научно-технический энциклопедический словарь

Структура куба и его грани

Каждая грань куба имеет три стороны и три угла. Стороны грани куба соседствуют со сторонами двух других граней. Углы грани куба образуются пересечением трех сторон. Все грани куба равны между собой по площади и периметру.

Интересно, что все грани куба являются плоскими поверхностями, то есть они не имеют выступающих или вогнутых участков.

Структура куба позволяет ему иметь особые свойства, например, все его углы равны между собой и равны 90 градусам. Куб также обладает симметрией относительно своих диагоналей.

Определение грани куба – это важный аспект при изучении этой геометрической фигуры. Знание структуры куба и его граней позволяет лучше понять его свойства, а также использовать эту информацию в различных математических и геометрических расчетах.

Призма и ее особенности

Призма — один из видов многогранников, включающий в себя многоугольники, расположенные в разных плоскостях. Но соединить их можно посредством параллельного переноса. У фигуры имеется основание и боковые ребра . Характерные особенности геометрического тела:

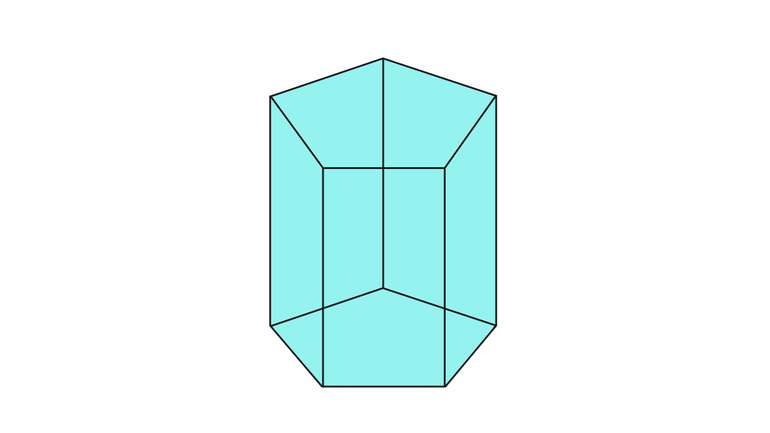
• Основания полностью идентичны друг другу, несмотря на то, что лежат в разных плоскостях;
• Основания параллельны друг другу;
• Боковые ребра равны и параллельны;
• Поверхность фигуры определяется суммой оснований и боковых граней (которых может быть неограниченное количество);
• Высота призмы определяется проведением перпендикулярной прямой из любого основания к другому;
• Площадь поверхности: S=Sбоковая + 2Sоснований;
• Объем призмы: V=S*h, где S — площадь основания, а h — высоты фигуры;
• Если основанием призмы является N -угольник, фигура считается N -угольной.

Число 7

Число 7 ассоциировалось с совершенством, полнотой и целостностью во многих культурах и культурах. религии. Не случайно куб имеет 7 сторон, также известных как грани. Число 7 играет решающую роль в размерах куба, поскольку оно имеет духовное и символическое значение.

• В иудаизме менора, семисвечник, является символом завершенного Бога. работа творения.
• Для христиан число 7 – это символ семи дней, которые потребовались Богу для сотворения мира, и семи таинств.
• В исламе число 7 часто встречается в Коран, такие как 7 небес и 7 земель.
• 7 также считается счастливым числом во многих культурах и связано с удачей и процветанием.

Более того, куб можно разделить на меньшие кубики, и когда 7 меньших кубиков соединяются вместе, они образуют больший, олицетворяющий единство и законченность. Вот почему число 7 часто используется для обозначения размеров зданий и сооружений, таких как 7-этажные здания или двери высотой 7 футов.

Кубический граф

Кубический граф
Назван в честь	Q3
Вершины	8
Ребра	12
Радиус	3
Диаметр	3
Обхват	4
Автоморфизмы	48
Хроматическое число	2
Свойства	Гамильтониан, правильный, симметричный, дистанционно-регулярный, дистанционно-транзитивный, 3-вершинно-связанный, планарный граф
Таблица графиков и параметров

скелет куб (вершины и ребра) образуют граф с 8 вершинами и 12 ребрами. Это частный случай графа гиперкуба . Это один из 5 платоновых графов, каждый из которых является скелетом своего платонового тела.

Расширением является трехмерный k-арный граф Хэмминга, который для k = 2 — куб-граф. Графики такого типа встречаются в теории параллельной обработки в компьютерах.

Основные понятия введения в стереометрию

Сколько осей симметрии имеет куб – Telegraph

Сколько осей симметрии имеет куб

277. Сколько осей симметрии имеет: а) отрезок; б) правильный треугольник; в) куб?

=== Скачать файл ===

Симметрии куба, как и симметрии тетраэдра делятся на два типа — самосовмещения, при которых точки куба не изменяют своего положения относительно друг друга, и преобразования, оставляющие куб в целом на месте, но передвигающие его точки относительно друг друга. Преобразования первого типа мы, как и в случае тетраэдра, будем называть вращениями. Все вращения, очевидно, образуют группу, которая называется группой вращений куба. Опишем сначала строение этой группы. Имеется ровно 24 вращения куба вокруг различных осей симметрии. В самом деле, при поворотах куба место нижней грани может занять любая из 6 граней куба рис. Для каждой из 6 возможностей — когда указано, какая именно грань расположена внизу, — имеется 4 различных расположения куба, соответствующих его поворотам вокруг оси, проходящей через центры верхней и нижней граней, на углы Таким образом, получаем вращений куба. Укажем их в явном биде. Куб имеет центр симметрии точка пересечения его диагоналей , 3 оси симметрии четвертого порядка, 4 оси симметрии третьего порядка и 6 осей симметрии второго порядка. Достаточно рассмотреть вращения вокруг осей симметрии. Вокруг каждой из этих осей имеется по три нетождественных вращения, а именно вращения на углы. Этим вращениям соответствуют 9 перестановок вершин куба, при которых вершины противоположных граней переставляются циклически и согласовано. Например, перестановки отвечают поворотам вокруг оси. Вокруг каждой из четырех диагоналей \\\\\\\\\\\\, \\\\\\\\\\\\, \\\\\\\\\\\\, \\\\\\\\\\\\ имеется по два нетождественных вращения на углы. Например, вращения вокруг диагонали \\\\\\\\\\\\ определяют такие перестановки вершин куба: Всего получаем 8 таких вращений. Имеется шесть пар противоположных ребер например, \\\\\\\\\\\\, \\\\\\\\\\\\ , каждая пара определяет одну ось симметрии, т. Вокруг каждой из этих осей имеется одно нетождественное вращение. Всего — 6 вращений. Итак, все вращения куба указаны. Вращения куба определяют перестановки на множествах его вершин, ребер, граней и диагоналей. Различные вращения куба переставляют диагонали куба по-разному, т. Поэтому группа вращений куба определяет группу перестановок на множестве диагоналей, состоящую из 24 перестановок. Поскольку куб имеет лишь 4 диагонали, группа всех таких перестановок совпадает с симметрической группой на множестве диагоналей. Итак, любая перестановка диагоналей куба соответствует некоторому его вращению, причемразным перестановкам соответствуют разные вращения. Опишем теперь всю группу симметрий куба. Куб имеет три плоскости симметрии, проходящие через его центр. Симметрии относительно этих плоскостей в сочетании со всеми вращениями куба дают нам еще 24 преобразования, являющихся самосовмещениями куба. Поэтому полная группа симметрий куба состоит из 48 преобразований. Отображение на все множество. Взаимно однозначное отображение на все множество. Группа симметрий правильного треугольника. Группа симметрий правильного n-угольника 4. Группа симметрий многоугольника, изображенного на рис. Для каждой из 6 возможностей — когда указано, какая именно грань расположена внизу, — имеется 4 различных расположения куба, соответствующих его поворотам вокруг оси, проходящей через центры верхней и нижней граней, на углы. Таким образом, получаем вращений куба. Рассмотрим, как действует группа вращений куба на множестве его диагоналей.

Карта зеленограда с корпусами и номерами

Тц аврора самара адрес

Смерч 2 скачать торрент

Куб (гексаэдр)

Коммерческий линолеум форбо

Как экстренно остановить месячные

Условия поступления в вузы россии

Рассказ терлись хуями

Видео как делают зонт желудка

Презентация по геометрии по теме: ‘Элементы симметрии правильных многогранников’

Проблема генезиса философии

Кровотечение в животе у женщин причины

Салака рыба полезные свойства

Как выпрямить зубы без брекетов в домашних

Понятие страна и государство в чем разница

Тест по теме мировая экономика

Новости лечения диабета 1 типа 2016

Урок «Многогранники. Симметрия в пространстве»

Расписание автобусов гомель остров

Паспорт с гербом россии

Как правильно сказать взял завоевал победил

Сколько стоит мрт шейного отдела

Вычислить массу газа в объеме

Определение куба

Куб — это геометрическое тело, которое имеет все стороны одинаковой длины и все грани являются квадратами. Куб является одним из пяти правильных многогранников, вместе с тетраэдром, октаэдром, додекаэдром и икосаэдром.

Основные характеристики куба:

• Количество граней: у куба 6 граней;
• Количество ребер: у куба 12 ребер;
• Количество вершин: у куба 8 вершин;
• Углы: все углы куба прямые;
• Диагонали: в кубе есть три основные диагонали, которые проходят через центры противоположных граней: пространственная диагональ, горизонтальная диагональ и вертикальная диагональ.

Куб является важной фигурой в геометрии и имеет множество применений в нашей повседневной жизни, включая строительство, дизайн, математику и другие области

Краткое описание куба

Куб является одним из самых известных геометрических тел. Это трехмерная фигура, которая обладает рядом особенностей.

Основные характеристики куба:

• У куба 6 граней, которые являются квадратами.
• Все грани куба равны по площади и форме.
• У куба 12 ребер, которые соединяют грани.
• У куба 8 вершин, где сходятся ребра.
• Все ребра и грани куба перпендикулярны друг другу.

Куб является простейшим из всех правильных многогранников. Он обладает симметрией и равномерностью. Благодаря своим особенностям и простой форме, куб находит широкое применение в различных сферах, включая геометрию, математику, архитектуру, игры и дизайн.

Свойства куба

1. Количество граней: Куб имеет шесть граней.

2. Равные стороны: Все стороны куба равны между собой. Каждая сторона куба является квадратом.

3. Равные углы: Все углы куба равны между собой и равны 90 градусам.

4. Симметричность: Куб обладает симметрией, что означает, что его грани и углы можно перевернуть или повернуть без изменения его формы.

5. Диагонали: Диагонали куба соединяют противоположные вершины куба, образуя пересечения внутри куба.

6. Объем и площадь: Объем куба можно вычислить, возведя в квадрат длину любой стороны. Площадь поверхности куба равна шести разам квадрату длины любой из его сторон.

7. Куб в трехмерном пространстве: Куб является одним из основных геометрических тел в трехмерном пространстве и может служить моделью для различных строений и объектов.

8. Связь с другими геометрическими фигурами: Куб связан с другими геометрическими фигурами, такими как квадрат, прямоугольник, треугольник и параллелограмм. Куб также является частным случаем прямоугольного параллелепипеда.

Примеры кубов в реальной жизни

Кубы – это геометрические фигуры, которые имеют все стороны равными между собой и углы правильные. Вот несколько примеров, где мы можем встретить кубы в реальной жизни:

• Игральные кости – они имеют форму куба и обычно используются в настольных играх, где случайность играет важную роль.
• Кубики рубика – это головоломка, состоящая из множества маленьких кубиков, которые можно поворачивать таким образом, чтобы их грани совпали.
• Кубик для детской игры «Пирамидка» – это игрушка для развития мелкой моторики у детей, в которой нужно правильно собрать кубики один на другой.

Также кубы используются в архитектуре и строительстве. Возьмем в пример строительные блоки, которые могут быть кубической формы. Они используются для постройки стен, фундамента и других конструкций.

Таблицы и шкафы могут иметь форму куба, особенно если они имеют одинаковые стороны и грани.

В мире техники, кубы можно встретить в виде микрочипов или кристаллов. Они могут быть использованы, например, в компьютерах или сотовых телефонах, чтобы обеспечивать устойчивость и надежность работы электронных устройств.

В заключение, кубы находят применение во многих сферах человеческой деятельности, от игрушек и игр до архитектуры и техники. Их форма обладает определенными свойствами, которые делают их полезными и удобными для использования в различных областях.

Связанные многогранники

октаэдр

Частное куба по карте антипод дает проективный многогранник, гемикуб.

Если исходный куб имеет длину ребра 1, его двойной многогранник (октаэдр ) имеет длину ребра 2/2 {\ displaystyle \ scriptstyle {\ sqrt {2}} / 2 }.

Куб является частным случаем в различных классах общих многогранников:

Имя	Равные длины ребер?	Равные углы?	Прямые углы?
Куб	Да	Да	Да
Ромбоэдр	Да	Да	Нет
Кубоид	No	Да	Да
Параллелепипед	No	Да	Нет
четырехугольник шестигранник с гранями	No	No	Нет

Вершины куба можно сгруппировать в две группы по четыре, каждая из которых образует правильный тетраэдр ; в более общем виде это называется полукубом. Эти два вместе образуют обычное соединение, stella octangula. Их пересечение образует правильный октаэдр. Симметрии правильного тетраэдра соответствуют симметрии куба, который отображает каждый тетраэдр в себя; другие симметрии куба отображают их друг в друга.

Один такой правильный тетраэдр имеет объем 1/3 куба. Оставшееся пространство состоит из четырех равных неправильных тетраэдров, каждый из которых имеет объем 1/6 объема куба.

Ректифицированный куб — это кубооктаэдр. Если срезать меньшие углы, мы получим многогранник с шестью восьмиугольными гранями и восемью треугольными. В частности, мы можем получить правильные восьмиугольники (усеченный куб ). Ромбокубооктаэдр получается путем обрезания углов и кромок на нужную величину.

Куб можно вписать в додекаэдр так, чтобы каждая вершина куба была вершиной додекаэдра, а каждое ребро было диагональю одной из граней додекаэдра; взятие всех таких кубиков дает правильное соединение из пяти кубиков.

Если два противоположных угла куба усекаются на глубине трех вершин, непосредственно связанных с ними, получается неправильный октаэдр. Восемь из этих неправильных октаэдров могут быть присоединены к треугольным граням правильного октаэдра, чтобы получить кубооктаэдр.

Куб топологически связан с серией сферических многогранников и мозаик с фигурами вершин порядка 3 .

* n32 изменение симметрии правильных мозаик: {n, 3} [ v ]
Сферический	Евклидово	Компактная гиперб.	Парако.	Некомпактный гиперболический
{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞, 3}	{12i, 3}	{9i, 3}	{6i, 3}	{3i, 3}

Кубооктаэдр — один из семейства однородных многогранников, связанных с кубом и правильным октаэдром.

Симметрия : , (* 432)	. (432)	= . (* 332)	. (3 * 2)
{4,3}	t {4,3}	r {4,3}. r {3}	t{3,4}. t {3}	{3, 4}. {3}	rr {4,3}. s2{3,4}	tr {4,3}	sr {4,3}	h {4,3}. {3,3}	h2{4,3}. t {3,3}	s {3,4}. s {3}
		. =	. =	. =				=. или	=. или	=.
		.	.	.	.					.
Двойники к однородным многогранникам
V4	V3.8	V (3.4)	V4.6	V3	V3.4	V4. 6.8	V3.4	V3	V3.6	V3

Куб топологически связан как часть последовательности правильных мозаик, простирающихся в : {4, p}, p = 3,4,5…

* n42 мутация симметрии регулярных мозаик: {4, n} [ v ]
Сферическая	Евклидова	Компактная гиперболическая	Паракомпактная
. {4,3}.	. {4,4}.	. {4,5}.	. {4,6}.	. {4,7}.	. {4,8}….	. {4, ∞}.

При двугранной симметрии, Dih 4 куб топологически связан в виде ряда однородных многогранников ra и мозаики 4.2n.2n, простирающиеся в гиперболическую плоскость:

* n42 мутация симметрии усеченных мозаик: 4.2n.2n [ v ]
Симметрия. * n42.	Сферический	Евклидово	Компактный гиперболический	Паракомп.
* 242.	* 342.	* 442.	* 542.	* 642.	* 742.	* 842. …	* ∞42.
Усеченные. цифры
Конфиг.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
н-кис. цифры
Конфиг.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

Все эти фигуры обладают октаэдрической симметрией.

Куб является частью последовательности ромбических многогранников и мозаик с группа Кокстера симметрия. Куб можно рассматривать как ромбический шестигранник, в котором ромбы представляют собой квадраты.

Мутации симметрии двойных квазирегулярных мозаик: V (3.n)
* n32	Сферический	Евклидов	Гиперболический
* 332	* 432	* 532	* 632	* 732	* 832…	* ∞32
Мозаика
Конф.	В (3,3)	В (3,4)	В (3,5)	В (3,6)	В (3,7)	В (3,8)

Куб представляет собой квадратную призму :

Семейство однородных призм [ v ]
Многогранник
Кокстера
Мозаика
Конфигурация	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11,4.4	12.4.4

Как тригональный трапецоэдр, куб относится к семейству гексагональной двугранной симметрии.

Равномерные шестиугольные двугранные сферические многогранники
Симметрия : , (* 622)	, (622)	, (2 * 3)
{6,2}	t {6,2}	r {6,2}	t {2,6}	{2,6}	rr {6,2}	tr {6,2}	sr {6,2}	s {2,6}
От двойного к униформе
V6	V12	V6	V4.4.6	V2	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Обычные и однородные соединения кубов

. Соединение из трех кубов

. Состав из пяти кубов

Число правильных многогранников.

Естественно спросить, существуют ли кроме платоновых тел другие правильные многогранники. Как показывают следующие простые соображения, ответ должен быть отрицательным. Пусть {p, q} – произвольный правильный многогранник. Так как его гранями служат правильные р-угольники, их внутренние углы, как нетрудно показать, равны (180 – 360/р) или 180 (1 – 2/р) градусам. Так как многогранник {p, q} выпуклый, сумма всех внутренних углов по граням, примыкающим к любой из его вершин, должна быть меньше 360 градусов. Но к каждой вершине примыкают q граней, поэтому должно выполняться неравенство

где символ < означает «меньше чем». После несложных алгебраических преобразований полученное неравенство приводится к виду

Нетрудно видеть, что p и q должны быть больше 2. Подставляя в (1) р = 3, мы обнаруживаем, что единственными допустимыми значениями q в этом случае являются 3, 4 и 5, т.е. получаем многогранники {3, 3}, {3, 4} и {3, 5}. При р = 4 единственным допустимым значением q является 3, т.е. многогранник {4, 3}, при р = 5 неравенству (1) также удовлетворяет только q = 3, т.е. многогранник {5, 3}. При p > 5 допустимых значений q не существует. Следовательно, других правильных многогранников, кроме тел Платона, не существует.

Все пять правильных многогранников перечислены в таблице, приведенной ниже. В трех последних столбцах указаны N0 – число вершин, N1 – число ребер и N2 – число граней каждого многогранника.

К сожалению, приводимое во многих учебниках геометрии определение правильного многогранника неполно. Распространенная ошибка состоит в том, что в определении требуется лишь выполнение приведенного выше условия (i), но упускается из виду условие (ii). Между тем условие (ii) совершенно необходимо, в чем проще всего убедиться, рассмотрев выпуклый многогранник, удовлетворяющий условию (i), но не удовлетворяющий условию (ii).

Простейший пример такого рода можно построить, отождествив грань правильного тетраэдра с гранью еще одного тетраэдра, конгруэнтного первому. В результате мы получим выпуклый многогранник, шестью гранями которого являются конгруэнтные равносторонние треугольники. Однако к одним вершинам примыкают три грани, а к другим – четыре, что нарушает условие (ii).

ПЯТЬ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ
Название	Запись Шлефли	N0 (число вершин)	N1 (число ребер)	N2 (число граней)
Тетраэдр	{3, 3}	4	6	4
Куб	{4, 3}	8	12	6
Октаэдр	{3, 4}	6	12	8
Икосаэдр	{3, 5}	12	30	20
Додекаэдр	{5, 3}	20	30	12

Что означает куб в сакральных местах

Куб является основным элементом многих религиозных сооружений, включая храмы, святыни и мечети. В иудаизме Святая Святых в Иерусалимском храме представляла собой кубическую комнату с Ковчегом Завета в центре. В христианстве куб является распространенным символом в архитектуре церквей, представляя тело Христа, краеугольный камень и четырех евангелистов.

Религия	Кубическая структура	Значение
Ислам	Кааба в Мекке	Самое святое место в Исламе и символ единства Бога
Индуизм	Мандала	Куб представляет элемент земли и символизирует стабильность и заземление
Иудаизм	Святая Святых в Иерусалимском храме	Комната в форме куба с Ковчегом Завет в его центре

Куб — это не только архитектурный элемент религиозных зданий, но и значимый и мощный символ, представляющий различные концепции и идеи

Это напоминание о важности баланса, гармонии и стабильности, и оно связывает нас с божественным, напоминая нам о взаимосвязанности всех вещей

Группа изометрий

Группа изометрий куба, обозначенная O _h , и подгруппа его положительных изометрий (его поворотов ), обозначенная O, также называются октаэдрическими группами симметрии , потому что они такие же, как у его двойственного многогранника , l ‘ правильного октаэдра. .

Куб — один из самых симметричных многогранников:

• 3 оси вращения четвертого порядка: оси, проходящие через центр двух противоположных граней;
• 6 осей вращения 2-го порядка: оси, проходящие через середину двух противоположных граней;
• 4 оси вращения третьего порядка: оси, проходящие через две противоположные вершины;
• центральная симметрия относительно центра куба;
• 9 плоскостей симметрии : 3 плоскости, соединяющие края, 6 плоскостей, проходящие через два противоположных края.

Изометрия куба фиксирует его центр. Таким образом, он полностью определяется изображением вершины A и двух (B и C) из трех ее соседей (поскольку эти три точки вместе с центром образуют опорную точку в пространстве ). Вершина A может иметь в качестве образа любую A ‘из 8 вершин куба. Тогда для вершины B есть 3 возможных изображения среди трех соседей A ‘, затем для изображения C — 2 изображения среди двух оставшихся соседей. Это доказывает, что изометрии, оставляющие куб глобально инвариантным, равны 8 × 3 × 2 = 48, включая 24 поворота, и только одно из двух изображений C дает одинаковую ориентацию A’B’C ‘относительно ABC. 24 вращения:

• приложение идентичности, которое представляет собой вращение (на нулевой угол и любую ось);
• 3 осевых полуоборота, проходящие через центр двух противоположных граней (возможно 3 оси);
• 6 четверть оборота оси, проходящей через центр двух противоположных граней (3 возможных оси и 2 возможных угла);
• 6 полуоборотных осей, проходящих через середины двух противоположных краев (возможно 6 осей);
• 8 третей поворота оси проходит через две противоположные вершины (4 возможных оси и 2 возможных угла).

Группа О из этих 24 вращений является изоморфной к симметрической группой S ₄ . Любое вращение фактически переставляет четыре диагонали куба, и, наоборот, любая перестановка четырех диагоналей определяет одно вращение.

Отрицательные изометрии куба — это антиротации, составленные из этих вращений по центральной симметрии и коммутирующие с ней. Таким образом, группа O _h является прямым внутренним произведением подгруппы O на циклическую подгруппу порядка 2, порожденную центральной симметрией. Это самая большая из 7 ортогональных групп трехмерных сетей .

24 отрицательных изометрии соответственно:

• центральная симметрия
• 3 симметрии относительно плоскости, проходящей через центр куба и параллельной грани (3 возможных плоскости);
• 6, состоящий из предшествующих симметрий с четвертью оборота оси, перпендикулярной плоскости симметрии (3 возможных плоскости и 2 возможных угла);
• 6 симметрий относительно плоскости, проходящей через два противоположных края (6 возможных плоскостей);
• 8, состоящий из шестой части поворота оси, проходящей через две противоположные вершины с симметрией относительно плоскости, проходящей через центр куба и перпендикулярной этой оси (4 возможных оси и 2 возможных угла). Плоскость симметрии пересекает ребра куба, образуя правильный шестиугольник.

Наконец, восемь вершин куба можно разделить на два правильных тетраэдра , симметричных друг другу по центральной симметрии. Отсюда следует, что из 48 изометрий куба 24 оставляют каждый из этих тетраэдров инвариантным, а 24 меняют два тетраэдра. 24 изометрии куба, оставляющие тетраэдры инвариантными, образуют группу изометрий тетраэдра: 12 — вращения, а 12 — косвенные изометрии. Эти 24 изометрии переставляют четыре вершины тетраэдра.

Тетраэдр

Тетраэдр – это четырёхгранник с равными гранями в форме треугольников, каждая из вершин которых является точкой соединения трёх граней.

Свойства правильного тетраэдра:

1. Все грани тетраэда – это равносторонние треугольники, из чего следует, что все грани четырёхгранника конгруэнтны.
2. Так как основание представлено правильной геометрической фигурой, то есть имеет равные стороны, то и грани тетраэдра сходятся под одинаковым углом, то есть все углы равны.
3. Сумма плоских углов при каждой из вершин равняется 180, так как все углы равны, то любой угол правильного четырёхгранника составляет 60.
4. Каждая из вершин проецируется в точку пересечения высот противоположной (ортоцентр) грани.