Примеры расчетов
Чтобы наглядно продемонстрировать применение приведенных выше правил, рассмотрим несколько конкретных примеров.
В кубометрах
Примеры:
- Бассейн диаметром 3 м планируется наполнить на глубину 1,5 м. Чтобы определить объем, воспользуемся формулой: V = π * D2/4 * H = 3,14 *32 /4 * 1,5 = 10,5975 м3.
- При величине радиуса круглой чаши 5 м и высоте бортов 2 м в резервуар можно максимально залить: V = π * R2 * H = 3,14 * 52 * 2 = 157 м3.
- Допустим, что минимальная высота наполнения составляет 80 см, а глубина на другой стороне 120 см. При диаметре бассейна 300 см получаем: Hср = (H1 + H2)/2 = (80 + 120)/2 = 100 см, V= 3002 * 100 * 0,78 = 7 020 000 (см3) = 7,020 м3.
Справка. В одном кубометре (1 м3) содержится 106 кубических сантиметров воды.
В литрах
Линейные величины традиционно измеряют в метрах и сантиметрах, а жидкости в литрах. Один литр воды теоретически представляет собой кубик со стороной 10 см. В 1 м3 таких кубиков 1000 штук. Таким образом: 1м3 = 1000 литров.
Масса такого объема воды равна 1 тонне.
Примеры:
- Определим вместимость конструкции диаметром 1 м и глубиной 0,5 м: V = π * D2/4 * H = 3,14 * 12 /4 * 0,5 = 0,3925 м3. Чтобы получить объем в литрах, умножаем на тысячу: V = 392,5 л.
- Большой резервуар шириной 500 см и глубиной 200 см способен принять: V = D2 * H * 0,78 = 5002 * 200 * 0,78 = 39 000 000 (см3) = 39 тыс.л.
- Овальный бассейн с длиной 10 м и шириной 4 м, заполненный на 1,5 м, обсчитывается следующим образом: S =π*ab = 3,14 * (10/2) * (4/2) = 31,4 (м2), V = S * H = 31,4 * 1,5 = 47,1 (м3) = 47 100 л.
Рассчитываем число досок в кубометре

Сколько же? Примерно 64 штуки в кубе, в зависимости от размеров вагонки.
Напомним читателю, что вагонка – это тонкий пласт дерева, отлично выглядящий и очень удобный для монтирования.
Ее название происходит от слова вагон. Первоначально железнодорожные вагоны обшивали тонкой деревянной доской, которую и назвали вагонкой.
Стандартная толщина — от двенадцати до пятнадцати миллиметров, а иногда и двадцать — если нужна внешняя отделка. Они достаточно прочны, чтобы не ломаться и не продавливаться, и именно такие габариты стоит учитывать при расчетах.
Длина стандартной доски составляет около двух-трех метров, хотя существуют и шестиметровые элементы. Также для расчета объема нужно знать полезную ширину, обычно около восьмидесяти миллиметров, хотя, опять же, существуют и более широкие доски. Более широкую и более толстую применяют для обделывания снаружи зданий.
Зная все габариты доски в миллиметрах, необходимо, переведя известные числа в метры, перемножить их, получив объем одной доски. Следующим шагом раздели один куб на наш результат. Итак, мы выяснили, сколько в кубе вагонки.
Поскольку ее используют для обшивки плоских поверхностей, для расчетов необходимого количества материала также используют квадратные метры. Таблица — сколько вагонки в кубе для нескольких стандартных размеров:
| Размеры (мм) | Объем одной доски (м3) | Сколько кв. м. в м3 |
| 16х88х6 | 0.0084 | 62.5 |
| 16х88х3 | 0.0042 | 62.5 |
| 12.5х90х3 | 0.0034 | 80 |
Удивительная форма: куб
Куб – это фигура, с которой мы сталкиваемся не только на уроках геометрии и искусства, но и в повседневной жизни. Другое название куба – обычный куб. Куб – это правильный многогранник, каждая грань которого представляет собой квадрат. Куб можно назвать объемным, трехмерным или даже трехмерным квадратом. Куб имеет 8 вершин, 6 граней и 12 ребер. Куб – это удивительная геометрическая фигура, в которой могут быть спрятаны или установлены другие фигуры, такие как октаэдр, тетраэдр, икосаэдр и другие.
Удивительная форма: куб
Куб или гексаэдр также называют кубом Неккера, по имени швейцарского кристаллографа Луи Альберта Неккера. В 1832 году Неккер предложил иллюзию: если смотреть в куб со стенками, то можно увидеть, что маленькая черная точка появляется то на переднем плане, то на заднем, то в углу, то в середине. Он перемещается с одного места на другое, как будто движется. Еще одна особенность куба Неккера заключается в том, что его параллельные боковые грани как бы расходятся. Вы можете покрасить один из краев в другой цвет и посмотреть, как этот цветной край причудливо движется.
Еще один необычный куб – куб художника Маурица Эшера. Этот куб невозможен.
Еще одно интересное открытие, связанное с кубом, было сделано в 1966 году фотографом Чарльзом Ф. Кокраном. Он сделал фотографию, которую назвали “сумасшедшей коробкой”. Что такое “сумасшедший язык”? Это внутренний и внешний каркас гексаэдра (куба). Сумасшедший ящик” основан на неправильных связях, которые были допущены при рисовании фигуры.
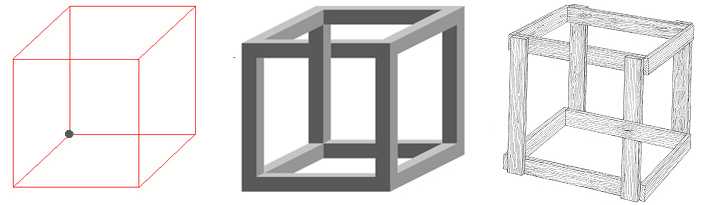
| Куб Неккера | Куб Эшера | “Сумасшедший ящик |
В список самых удивительных и причудливых форм входят интегральный куб, расширяющийся куб (также называемый бесконечным кубом), повторяющиеся кубы, кубическая снежинка, плавающие кубы, двухэтажный куб и многие, многие другие. Все эти фигуры завораживают, от них невозможно оторвать взгляд. Каждый, кто их видит, хочет понять, как они создаются.
Куб всегда таил в себе множество загадок – это чрезвычайно сложная и в то же время чрезвычайно простая геометрическая фигура, которая помогает нам заглянуть в глубины сознания. В древности Платон называл его священной фигурой и ассоциировал со знаком Земли, потому что это самая стабильная фигура из всех. Куб – это фигура сакральной геометрии. Уже в 16 веке немецкий математик и астроном Иоганн Кеплер создал модель Солнечной системы, в которую вписал куб.
Где вы можете найти куб? Здания обычно имеют форму куба, поэтому достаточно выглянуть из окна, и вы сразу увидите куб. Самая известная игрушка-головоломка, которую каждый ребенок хотя бы раз в жизни держал в руках, а некоторые даже смогли собрать, – это кубик Рубика. Название говорит само за себя. В 1975 году венгерский архитектор Эрне Рубик создал головоломку “Кубик Рубика”, которая стала популярной во всем мире. Кубик Рубика – это кубик из пластика, который, в свою очередь, состоит из 26 кубиков. Когда кубик Рубика собран, каждая из его граней окрашивается в один определенный цвет.
Многие вещества кристаллизуются в виде кубиков, например, поваренная соль и минерал флюорит.
Сколько граней у кубика ?
Что такое ребра и грани куба? Ребром куба называется место соединения или стыка граней. У куба всегда есть двенадцать рёбер. Все ребра куба равны между собой. Ребро связано отношениями с площадью и диагональю квадрата. Сколько граней у куба ответ? Для того чтобы решить эту задачу, нужно изучить свойства куба. Всего в кубе 6 граней, 8 вершин и 12 рёбер. В каждой вершине есть по 3 грани и 3 ребра. Каждая грань граничит с 4-мя другими, так как у квадрата 4 ребра.
Что такое грань квадрата? Квадрат — это четырехугольник, у которого все стороны равны и все углы прямые, то есть по 90 градусов. Следовательно у квадрата четыре вершины четыре угла. У квадрата одна грань одна плоскость. У квадрата четыре ребер ребра — это тоже самое, что стороны. Что такое вершина и что такое грань?
Сколько граней имеет куб. Сколько граней у Куба. Куб грани вершины. Куб и грани Куба. Куб все грани квадраты. Элементы Куба. Сколько у Куба граней вершин и ребер. Параллельные грани Куба. Сколько граней у кубика. Ребро Куба Куба. Грань в Кубе. Кубр грани вершины ребра. Параллелепипед грани вершины ребра. Сечения многогранника, Призмы, параллелепипеда и Куба. Куб ребро. Правильный многогранник каждая грань которого представляет квадрат. Куб является правильным многогранником. Невидимая грань Куба. Невидимые грани. Куб видимые и невидимые грани. Куб с невидимыми гранями. Вершины Куба. Вершина и грани Куба. Число вершин Куба. Куб параллелепипед ребра грани вершины. Гексаэдр грани вершины ребра. Куб гексаэдр. Правильный гексаэдр. Форма грани гексаэдра. Куб или правильный гексаэдр. Ребра и грани в Кубе. Куб сумма плоских углов. Куб сумма плоских углов при вершине. Параллелограмм ребра и грани.
Во 2-м случае ребра тетраэдра, которые попарно скрещиваются принадлежат попарно противоположным граням куба. Такой тетраэдр будет правильным, а его объём будет составлять треть от объёма куба. В куб вписывают октаэдр , при этом все 6 вершин октаэдра совмещаются с центрами 6-ти граней куба.
Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей. На рисунке куба видимые ребра изображены сплошными линиями, а невидимые — штриховыми? На рисунке куба видимые ребра изображены сплошными линиями, а невидимые — штриховыми. Записать обозначения вершин этого куба. Записать обозначения видимых ребер куба ; невидимых ребер куба. Записать обозначения видимых граней куба ; невидимых граней куба. Начерти в тетрадь куб изображенный на рисунке так чтобы грань MNPK была 1 видимой 2 невидимой. Какие из них являются видимыми ребрами? Есть ли среди них невидимые грани? Начертите пятиугольную грань многогранника, если ребро куба 4 см, а разрез проходит через середины ребер куба? Начертите пятиугольную грань многогранника, если ребро куба 4 см, а разрез проходит через середины ребер куба. Как нарисовать не видимые грани куба? Как нарисовать не видимые грани куба. Сколько ребер, граней, вершин у куба? Дан куб? Ребро куба 4 см, найти сумму длин всех ребер, сумму площадей всех граней куба? Перечерти в тетрадь куб, изображенный на рисунке, так, чтобы грань MNPK была : 1 видимой ; 2 невидимой? Перечерти в тетрадь куб, изображенный на рисунке, так, чтобы грань MNPK была : 1 видимой ; 2 невидимой. Построить прямоугольный параллелепипед и найти длину видимых ребер, закрасить невидимые грани в синий цвет? Построить прямоугольный параллелепипед и найти длину видимых ребер, закрасить невидимые грани в синий цвет. Что такое куб, сколько у него ребер и граней?
Задания для самостоятельного решения
Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.
Решение
P = 2(a + b)
a = 6, b = 2P = 2(6 + 2) = 12 + 4 = 16 см
Ответ: периметр прямоугольника равен 16 см.
Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.
Решение
S = aba = 6, b = 2S = 6 × 2 = 12 см2
Ответ: площадь равна 12 см2.
Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.
Решение
S = abS = 12, a = 6, b = x12 = 6 × xx = 2
Ответ: ширина прямоугольника составляет 2 см.
Задача 4. Вычислите площадь квадрата со стороной 8 см
Решение
S = a2a = 8S = 82 = 64 см2Ответ: площадь квадрата со стороной 8 см равна 64 см2
Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.
Решение
V = abca = 6, b = 4, c = 3V = 6 × 4 × 3 = 72 см3.
Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3
Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см
Решение
V = abcV = 200, a = 10, b = 5, c = x200 = 10 × 5 × x200 = 50xx = 4
Ответ: высота прямоугольного параллелепипеда равна 4 см.
Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га
Решение
Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.
Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.
Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза
4 × 3 = 12 га
Ответ: пшеницей засеяно 12 га.
Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.
Решение
a — длинаb — ширинаc — высота
a = 42 мb = мc = 42 × 0,1 = 4,2 м
Определим объем зернохранилища:
V = abc = 42 × 30 × 4,2 = 5292 м3
Определите сколько тонн зерна вмещает зернохранилище:
5292 × 740 = 3916080 кг
Переведём килограммы в тонны:
Ответ: зернохранилище вмещает 3916,08 тонн зерна.
Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.
Решение
Определим сколько литров в минуту вливается через вторую трубу:
25 л/мин × 0,75 = 18,75 л/мин
Определим сколько литров в минуту вливается в бассейн через обе трубы:
25 л/мин + 18,75 л/мин = 43,75 л/мин
Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин
43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л
1 л = 1 дм3
35 525 л = 35 525 дм3
Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:
35 525 дм3 : 1000 дм3 = 35,525 м3
Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
V = 35,525a = 5.8b = 3.5c = x
35,525 = 5,8 × 3,5 × x35,525 = 20,3 × xx = 1,75 м
с = 1,75
Ответ: высота (глубина) бассейна составляет 1,75 м.
Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Площадь прямоугольника
В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.
Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.
Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.
Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:
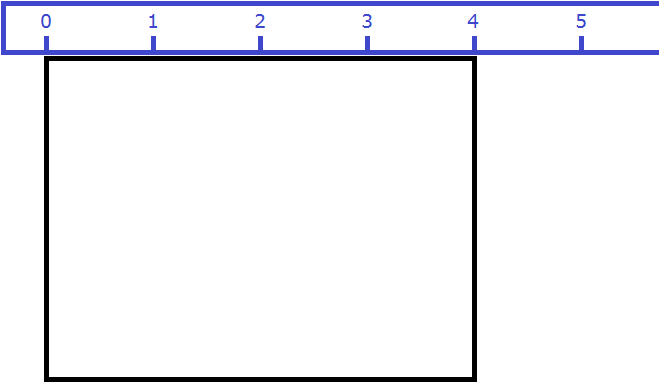
Теперь измерим ширину. Пусть она составила 3 метра:
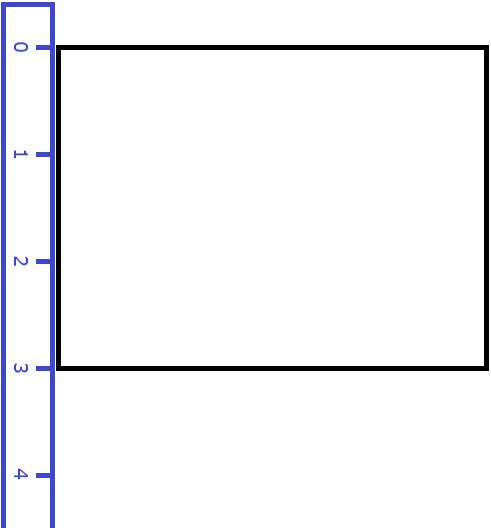
Умножим длину (4 м) на ширину (3 м).
4 × 3 = 12
Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:
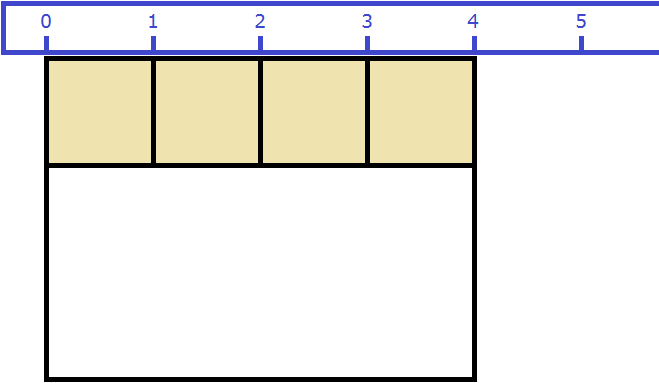
Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:
Сколько квадратных метров в кубическом метре
Всем известно, что в России действуют непомерно высокие процентные ставки по ипотечному кредитованию.
Зарубежная недвижимость Сколько стоит жилье в Германии
На сегодня наибольший интерес для инвестиций в немецкие объекты недвижимости представляют такие города как Берлин, Мюнхен, Гамбург, Дюссельдорф, Штутгарте, Нюрнберг, Лейпциг.
В нашей жизни часто встречаются ситуации, когда необходимо перевести одни единицы измерения в другие. Например, килограммы нам, порой, требуется перевести в граммы, километры — в метры и т.д. Это так называемые кратные единицы. Но зачастую, возникает необходимость перевести несхожие единицы измерения, например квадратные метры перевести в кубические метры и наоборот. Соответственно, возникает вопрос: сколько квадратных метров в кубическом метре?
Напоминаем, что кубические метры применяются для вычисления объема, а квадратные метры используются для вычисления площади. Однако при строительстве и закупке строительных материалов часто необходимо произвести конвертацию одних единиц в другие, чтобы понять, сколько по площади нам необходимо материалов, чтобы заполнить тот или иной объем.
Например, нам нужно перевести квадратные метры в кубометры. Кроме таких параметров, как длина и ширина, которые используются для исчисления площади, вам понадобится знать еще и толщину (высоту, глубину) изделия или материалов.
Чтобы узнать объем, необходимо перемножить длину, ширину и высоту, или зная уже площадь изделия, умножить ее на высоту(глубину, толщину).
V = а х в х с, где
а, в, с — соответственно длина, ширина, высота.
Например, вы делаете ремонт в доме и вам требуется застелить пол площадью 500 квадратных метров доской, у которой толщина 2 сантиметра. Доски продаются в кубометрах. Сколько вам понадобится кубометров доски для решения поставленной задачи?
Для начала, нужно толщину, которая указана в сантиметрах, перевести в метры:
2/100 = 0,02 метра
Теперь площадь умножаем на толщину:
500 х 0,02 = 10 метров кубических
Получается, чтобы застелить пол площадью в 500 квадратных метров доской с толщиной 0,02 метра, вам потребуется приобрести 10 кубометров доски. А сколько квадратных метров в кубическом метре? В одном кубометре, исходя из условий нашего примера, 50 квадратных метров. Как мы это посчитали? Нужно 1 куб.метр разделить на толщину в метрах:
1 / 0,02 = 50 кв. метров
В одном кубометре стройматериалов с различной толщиной будет абсолютно различное количество метров квадратных. В нашем примере, если для установки пола будет использоваться доска не 2 см, а предположим 3 см, то понадобится 15 кубических метров такой доски (500 х 0,03), а в одном кубическом метре такой доски будет 33,33 квадратных метра
1 / 0,03 = 33,33
Игорь Воропаев Комментарий эксперта
Игорь Воропаев — ведущий юрист «Проспер-Консалтинг» Консультант портала PropertyExperts
На самом деле, несмотря на то, что с математическими единицами мы знакомы с самого детства, определить, как правильно следовать, чтобы переводить их, иногда бывает довольно тяжело. Для того, чтобы понимать, как выполняется расчет, необходимо представить, что именно можно рассчитать с помощью этой величины. Например, если это жидкое вещество (например, вода), то ее величину можно измерить в миллилитрах, литрах, децилитрах, сантилитрах, а также в декалитрах, тоннах, кубических метрах и т.д. в зависимости от условной цели определения.
Для бруса, древесины, пиломатериала, вагонки используется метрическая система, включающая миллиметры, дециметры, кубы, из которых также стоит выбирать по ситуации и размеру. Например, возможно найти длину доски не в метрах, а в км, но такой путь не будет являться быстрым и не сможет помочь так, как это сделает калькулятор, которому под силу перед тысяч знаков одновременно. Также существуют калькуляторы, в которых может содержаться функция конвертера, которая помогает перемножать еще быстрее, чем прежде, а, значит, получать лучшие результаты.
Практическое применение куба и квадрата
Куб и квадрат — это геометрические фигуры, которые имеют свое особое применение не только в математике, но и в повседневной жизни.
Что касается квадрата, то его применение можно встретить во многих сферах, например:
- Строительство: квадрат используется для определения прямых углов, проверки перпендикулярности и выравнивания поверхностей.
- География: квадраты могут использоваться для построения сетки координат на географических картах, что помогает в навигации и определении точных координат.
- Графика и дизайн: квадрат может быть использован как основная форма в создании дизайна логотипов, упаковки продуктов и других графических элементов.
Что касается куба, то его применение также можно найти в различных сферах:
- Механика: кубы используются для моделирования и расчета механических систем, включая машинные детали и конструкции, например, при проектировании автомобилей или самолетов.
- Кристаллография: кубические кристаллы широко применяются в научных исследованиях и промышленности для создания оптических приборов, лазеров и полупроводниковых материалов.
- Информационные технологии: кубы используются в алгоритмах и структурах данных, таких как кубы данных, для анализа, обработки и хранения больших объемов информации.
Таким образом, куб и квадрат имеют широкое практическое применение и являются неотъемлемой частью различных областей, включая науку, технологии, строительство и дизайн.
Перевод в другие единицы
Для перевода в необходимое значение надо помнить довольно простые пропорции перевода метров в сантиметры и миллиметры.
Единицы длины:
1 м = 100 см = 1 000 мм
Единицы площади:
1 м² = 10 000 см² = 1 000 000 мм²
Единицы объема:
1 м³ = 1 000 000 см³ = 1 000 000 000 мм³
Количество жидкости очень часто измеряется в литрах, тут достаточно знать, что:
- 1 л = 1 000 см³
- 1 000 л = 1 м³
Довольно часто приходится рассчитывать объем, исходя из веса, и тут нужно знать плотность вещества. Проще всего с водой, плотность которой 1т/1м³. То есть тонна воды займет один м³ (куб), а тонна молока, например, займет примерно 1,030 куба.
Песок имеет плотность от 1,3 т/м³ до 1,8 т/м³. Это значит, что один м³ весит от 1,3 до 1,8 тонны.
Расчет кубатуры пиломатериалов имеет тонкости. Если доска обрезная и одинаковая, достаточно взять одну, измерить длину, толщину, ширину, перемножить эти параметры, а затем получившееся значение умножить на общее количество. Это и будет искомое значение.
Бывает также, что приходится высчитывать вместимость цилиндрических объектов (бочек, цистерн и подобных). Основанием здесь служит круг, а площадь его равна произведению числа пи (π = 3.14) на квадрат радиуса (половины диаметра) или S=πR².
В практической жизни можно применить и такой достаточно простой способ определения объема жидкостей или сыпучих веществ — в кубометре содержится 1 тыс. литров или 100 десятилитровых ведер. Кому-то покажется хлопотным таскать и пересчитывать ведра с песком или водой, но этот способ точен и общедоступен.
Определение количества досок в одном кубометре леса
Для строительства лес, как правило, продают в строительных магазинах кубами. Свои подсчеты хозяева обычно ведут в штуках. Для того, чтобы понимать:
- Сколько кубов леса заказывать;
- Или наоборот, сколько досок получится в одном кубе, надо предварительно сделать некоторые расчеты.
Перед тем, как начинать их, уточните у продавца длину одной доски. Разные поставщики предлагают разный лес. У кого-то это шестиметровый брус, у кого-то трехметровый, а у кого-то могут быть и 1 метр 20 сантиметров. А также узнайте стандартную высоту и ширину. Обычно она около 2 – 2,5 сантиметров.
Зная исходную длину, считаем сколько таких досок в кубическом метре:
- Умножаем длину бруса на необходимую вам и согласованную заранее с магазином ширину. При этом помним, что расчеты производятся в метрах. Так мы узнаем площадь одной доски;
- Делим один квадрат на площадь одного бруса. Получаем количество досок в одном квадрате;
- Делим один квадрат на высоту бруска, переведенную в метры. В нашем случае 2,5 см = 0,025 м. Получаем число квадратов в кубе;
- Умножаем количество досок в одном квадрате на число квадратных метров в кубе.
Таким образом, определив количество необходимых досок в кубе вы сможете заказать нужное вам число кубометров для строительства.
Презентация к уроку по математике на тему: Презентация к уроку “Объемные геометрические фигуры”
Наталья НиколаевнаПирамидаСказка про параллелограмм
и его дружную семейкуЖил был параллелограммсо своей женой трапецией. У параллелограммабыли такие свойства: противоположные стороны и углы равны; диагонали пересекаются и точкой пересечения делятся пополам. А у его жены трапециитолько то, что две противоположные стороны параллельны, а две другие нет. И вот у них родился долгожданный сын прямоугольник. По наследству ему передавались те же свойства, что у папы и добавилось еще одно свойство: диагонали равны. Так он рос год за годом и, к удивлению родителей, все его стороны и он стал четырехугольником, у которого все углы и стороны равны. И стали звать его квадратом. При этом он приобрел еще два свойства: диагонали взаимно перпендикулярны и являются биссектрисами его углов. Так проходили годы, и когда квадратстал юношей, он снова стал меняться, вытянулся…его углы изменились, и родители назвали его ромбом. Свойства у него остались те же кроме одного, что углы прямые
Назови имена членов дружной семейкиЦилиндр– в элементарной геометрии, геометрическое тело, образованное вращением прямоугольника около одной стороны.ЦилиндрКуб – это один из пяти правильных многогранниковПравильный прямоугольный параллелепипед имеет 6 граней, 12 ребер, 8 вершин.КубСпасибо за внимание!Шар; СфераПирамида– многогранник, основание которого многоугольник, а остальные грани – треугольники, имеющие общую вершину.ПирамидаГеометрия вокруг нас, нужно только присмотреться!ПараллелепипедНазови плоские геометрические фигурыШар — геометрическое тело;совокупность всех точек пространства, находящихся от центра на расстоянии,не больше заданного. Это расстояние
называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра.Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой: замкнутый шарвключает эту сферу, открытый шар — исключает.Шар; СфераПараллелепипед– это призма, основанием которой служит параллелограмм,или многогранник, у которого шесть граней и каждая из них — параллелограмм.Параллелепипед
КонусВзгляд на геометрию со стороны….Биолог:«…Квадраты— вид – фигура рода Прямоугольники, семейства Параллелограммы, отряда Четырёхугольники, класса Многоугольники, типа Плоские фигуры, царства Фигуры. Некоторые биологи также относят квадрат к роду Ромбы, что, конечно же, ошибочно. Любой школьник знает, что стороны ромба, в отличие от квадрата, проводятся не по горизонтали и по вертикали, а по диагонали. В зависимости от формата окружающей среды размер фигуры может варьировать от нескольких миллиметров до нескольких миль и даже больше, если начертить её на карте мира»
Куб и его свойства

В настоящее время видеоуроки нельзя просматривать или распространять среди студентов.
Чтобы получить доступ к этому и другим видеоурокам из комплекта, добавьте его в свой личный кабинет через покупку в каталоге.



Конспект урока “Куб и его свойства”
На предыдущем уроке мы узнали о таких многогранниках, как Прямоугольный параллелограмм..
Решив задачу со спичками, мы получили геометрическую фигуру под названием пирамида.
Перед этим вас познакомят и с другими многогранниками. Теперь вернемся к параллелепипеду.
Таким образом, поверхность параллелепипеда состоит из шести прямоугольников. Эти прямоугольники называются лица параллелограмм.
Обратите внимание, что два соседних прямоугольника имеют общую сторону, которую мы называем край прямоугольного параллелепипеда. Концы ребер называются вершины прямоугольного параллелепипеда
Таким образом, прямоугольный параллелепипед имеет 6 граней, 12 ребер и 8 вершин.
Обратите внимание, что хотя многогранники различны, поверхность каждого многогранника состоит из правильных многоугольников, которые мы называем гранями многогранника. Два соседних правильных многоугольника имеют общую сторону – ребро многогранника
Концы ребер являются вершинами многогранника.
Этот многогранник называется октаэдр. Он имеет 8 ребер, которые являются треугольниками, 12 граней и 6 вершин.
Куб – это прямоугольный параллелограмм, у которого все ребра равны
Обратите внимание, что мы рисуем пунктирные линии для граней куба, которые не видны. Это дает полное представление о фигуре и ее положении относительно нас
Все грани куба – равные квадраты. Поверхность куба состоит из 6 равных квадратов. Убедитесь, что грани напротив друг друга не имеют общих ребер. Эти называются напротив.
лицакоторые имеют общее ребро, называются прилегающая территория.
Теперь давайте проведем небольшой эксперимент. Возьмите коробку, имеющую форму куба. Мы раскрываем его, затем разрезаем вдоль четырех вертикальных ребер, а затем разворачиваем.
Форма, которую мы имеем, называется Разворачивание куба.. Он состоит из 6 равных квадратов.
Фигуры ниже также являются взрывающимися кубами.
Используя каждую из разверток, вы можете сделать модель куба. Для этого выполните следующие действия. Нарисуйте чертеж куба на листе бумаги. Выключите его. Согните его вдоль секций, соответствующих граням куба, и склейте.
Теперь нарисуйте отрезок, который соединит самые удаленные вершины куба. Мы называем эти вершины противоположными вершинами.
Отрезок, соединяющий две противоположные вершины куба, называется диагональю куба.
Теперь давайте решим несколько задач.
Проблема первая. Определите, какой кубик мы получим из данной сборки.
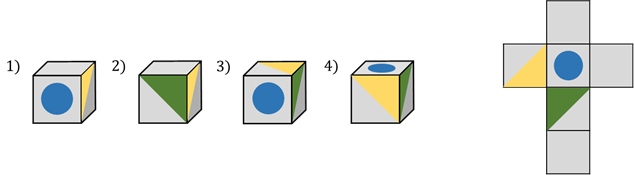
Давайте представим, какие грани куба являются смежными, то есть имеют общее ребро, и сравним с предложенными вариантами, чтобы найти правильный. Для этого нам удобнее всего сравнивать лица, которые отличаются в зависимости от рисунка на них
Обратите внимание на лицо с желтым треугольником и лицо с зеленым треугольником. Конечно, при сборке куба эти грани будут примыкать друг к другу
Следовательно, при различных поворотах куба возможны четыре варианта взаимного расположения этих граней.
Давайте теперь сравним четыре предложенных варианта. Сразу видно, что первый вариант неверен. Второй вариант неверен. Конечно, третий вариант также неверен. Однако вариант четыре является правильным, поскольку грани, на которых изображены треугольники, правильные. В этом случае на верхней поверхности должен быть синий круг. Это правильно.
Таким образом, мы выяснили, что из данного расширения получится куб с числом 4.
Вы можете решить эту проблему другим способом. Вы можете нарисовать этот контур на бумаге. Удобнее это делать на листе бумаги с квадратами, тогда вам не придется пользоваться линейкой, чтобы соблюсти размеры куба. Вы просто посчитаете количество квадратов, которое вам необходимо.
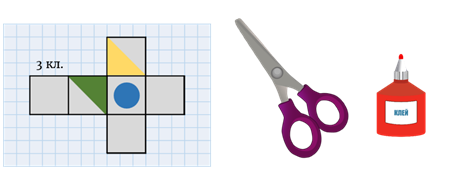
Затем вам нужно будет раскрасить и вырезать нарисованный контур. Затем скатайте его в кубик и склейте. После этого вы можете легко сравнить полученный куб с любым из предложенных вариантов и выбрать подходящий.
Вторая задача. Модель куба с длиной ребра 4 см была окрашена серой краской и разрезана вдоль ребра на кубики с длиной ребра 1 см. Сколько кубиков получилось: а) окрашенных по трем граням; б) окрашенных по двум граням?

Третья проблема. На рисунке показан скелет куба. Затем нарисуйте видимые грани так, чтобы на куб можно было смотреть: a) сверху слева; b) снизу справа.
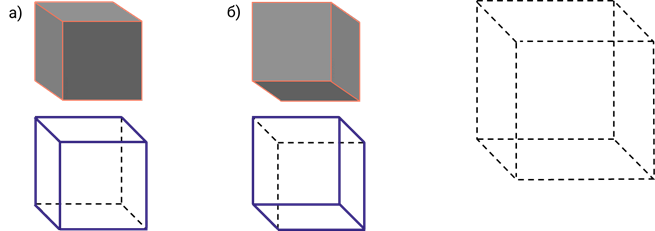
Проблема четвертая .. Фигура, показанная на рисунке, состоит из пяти кубиков. Какой формы фигура, если смотреть на нее: a) спереди; b) слева; c) сверху?
Пример расчета
Допустим, нужно залить ленточный фундамент под сооружение размером 8 на 12 метров, разделенное на три помещения стенами длиной 8 и 6 метров. Примем ширину фундамента 40 см, высоту в метр. Длина составит 54 метра, а объем фундамента будет 0,4*1*54 = 21,6 м³. Это значение можно смело округлить до 22 м³.
Приготовление кубометра бетонной смеси для заливки фундамента требует примерно 350 кг цемента, 800 кг песка, 1200 кг щебня и 140 л воды. Значит, на весь фундамент нужно 154 мешка цемента по 50 кг (7,7 тонн), 17,6 тонн песка, 26,4 тонн щебня и примерно 3 кубометра воды.
Это совершенно приблизительный подсчет, навскидку, позволяющий просто прикинуть размер предстоящих материальных и трудовых затрат. Кстати, количество вынутого под фундамент грунта будет сопоставимо, а то и выше объема самого фундамента, хотя тот и не полностью находится в земле. Объясняется это тем, что траншея под фундамент роется шире для установки опалубки и сопутствующих работ.
Точно так же приходится рассчитывать потребный объем при, допустим, переезде или отправке каких-то товаров или грузов. Ведь переплачивать за лишний объем кузова заказанного автомобиля, транспортного контейнера или железнодорожного вагона никому не хочется.
Достаточно просто вспомнить (посмотреть в интернете) элементарные геометрические формулы из школьной программы и приложить здравый смысл. Ведь всегда можно приблизительно рассчитать объем мебели при переезде или коробок при отправке товара и оценить предстоящие усилия и затраты. А для более точных, окончательных расчетов всегда можно прибегнуть к помощи специалистов. Тем более что предварительный итог более или менее известен, и это может служить некоторой проверкой при согласовании условий.
Формулы
Для куба с длиной ребра a {\ displaystyle a}:
| площадь поверхности | 6 a 2 {\ displaystyle 6a ^ {2} \,} | объем | a 3 {\ displaystyle a ^ {3} \,} |
| диагональ лица | 2 a {\ displaystyle {\ sqrt {2}} a} | диагональ пространства | 3 a {\ textstyle {\ sqrt {3}} a} |
| радиус описанной сферы | 3 2 a {\ displaystyle {\ frac {\ sqrt {3}} {2}} a} | радиус сферы, касательной к краям | a 2 {\ displaystyle {\ frac {a} {\ sqrt {2}}}} |
| радиус вписанной сферы | a 2 {\ displaystyle { \ frac {a} {2}}} | углы между гранями (в радианах ) | π 2 {\ displaystyle {\ frac {\ pi} {2}}} |
В качестве объем куба — третья степень его сторон a × a × a {\ displaystyle a \ times a \ times a}, третьи степени называются кубиками, по аналогии с квадратами и вторыми степенями.
Куб имеет наибольший объем среди кубоидов (прямоугольных блоков) с заданной площадью поверхности. у куба есть ла Самый большой объем среди кубоидов с одинаковым общим линейным размером (длина + ширина + высота).
Точка в пространстве
Для куба, описывающая сфера которого имеет радиус R, и для данной точки в его трехмерном пространстве с расстояниями d i от восьмерки куба вершин, имеем:
- ∑ i = 1 8 di 4 8 + 16 R 4 9 = (∑ i = 1 8 di 2 8 + 2 R 2 3) 2. {\ displaystyle {\ frac {\ sum _ {i = 1} ^ {8} d_ {i} ^ {4}} {8}} + {\ frac {16R ^ {4}} {9}} = \ left ({\ frac {\ sum _ {i = 1} ^ {8} d_ {i} ^ {2}} {8}} + {\ frac {2R ^ {2}} {3}} \ right) ^ { 2}.}






















