Куб ℹ️ определение, свойства геометрических фигур, виды, обозначение

Куб — свойства, виды и формулы

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.

Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;

прямая призма, все грани которой есть квадраты;

прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

Как сделать цилиндр из бумаги?

Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

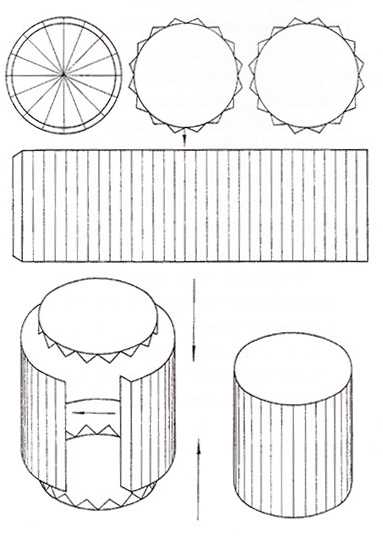
Рисование развертки:

1. Рисуем прямоугольник на бумаги, в котором ширина — это высота цилиндра, а длина определит диаметр будущей фигуры. Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
2. Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
3. Вырезаем все детали будущего бумажного цилиндра.
4. Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.
5. Цилиндр готов!

Необычная головоломка

Хотите порадовать любимых деток необычной головоломкой или сделать незабываемый фотоальбом? Тогда вам пригодится небольшой мастер-класс по созданию куба-трансформера. На каждой грани такого кубика можно расположить картинку или фотографию, а внутри еще целых шесть картинок.

Для изготовления такого кубика вам понадобится:

• 12 картинок или фотографий;
• Клей;
• 8 кубиков с гранями по 4 см;
• Скотч.

Кубики можно взять самые обычные детские или склеить самому по такой развертке:

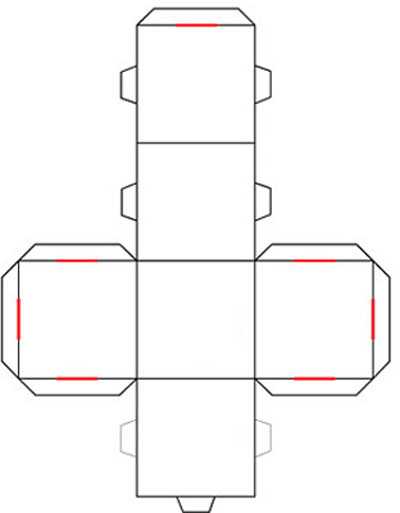
Для начала посмотрите места крепления кубиков:

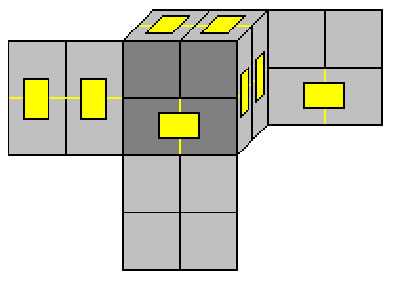
Чтобы было более понятно, рассмотрим этот процесс пошагово. Сначала склейте две пары кубиков так, как показано желтыми полосками на схеме:

Расположите эти четыре кубика рядом и склейте в местах, указанных синим цветом:

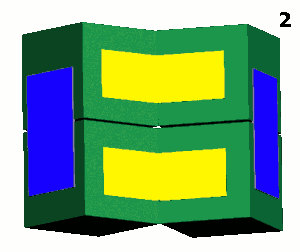
Поставьте кубики так, как показано на схеме. При этом желтая склейка окажется со стороны противоположной красной. Склейте по красным линиям:

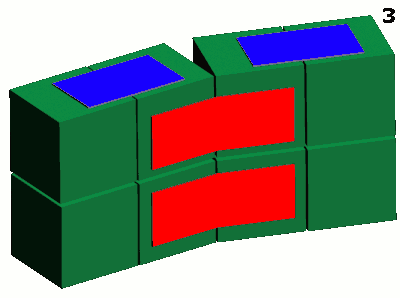
Фото нужно расположить на четверке кубиков. Размер фотографий 8 на 8 см.

Необычный фотоальбом из кубика-трансформера готов! Как его можно раскладывать и просматривать картинки, вы можете увидеть на фото.

Куб является, многогранной фигурой, стороны, которой представлены квадратом. Если вы или ваш малыш любит загадки, то прочитав статью, узнаете, как сделать кубик из бумаги. Также узнаете о разнообразных вариантах кубов и подробный процесс изготовления, каждого из видов.

Простой бумажный кубик

Объемный шестигранный куб 3Д складывают из квадратного листка бумаги без клея. И даже ножницы здесь не потребуются. Разве что отрезать лишний «хвостик» от листа А4, чтобы получить заготовку-квадрат. Зато пригодится навык надувания воздушных шариков, ведь мы сейчас научим вас тому, как сделать надувной кубик. Заинтригованы? Тогда начнем:

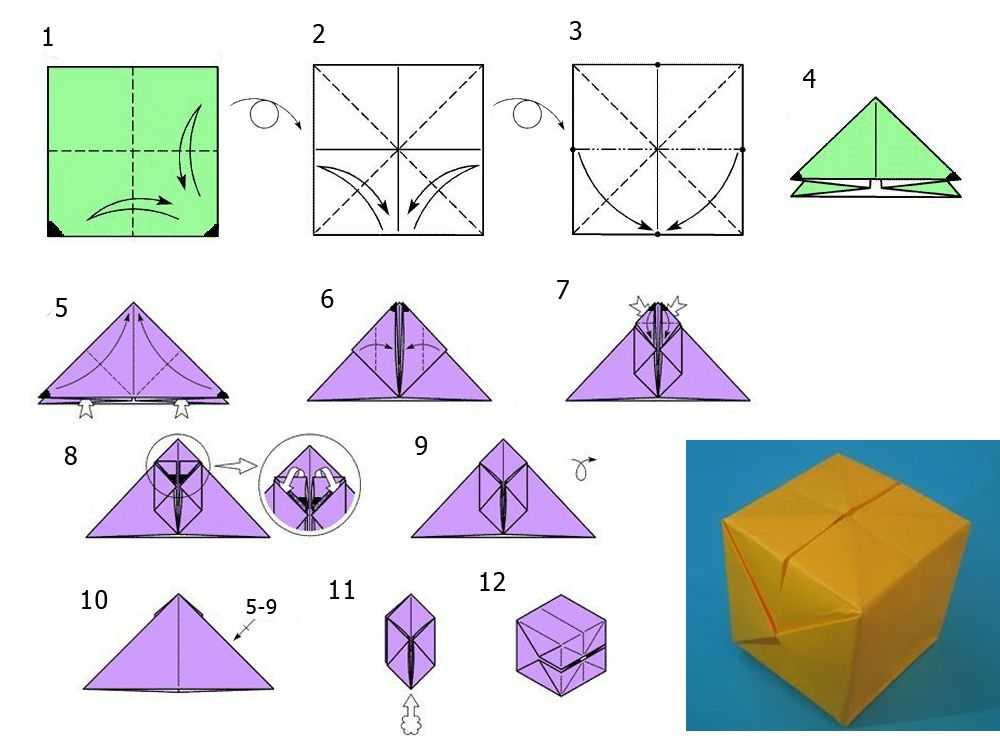
• Схема 1 — ваш наглядный ориентир. К нему следует прибегать каждый раз, когда алгоритм складывания кажется сложным. Возьмите бумажный квадрат и сложите его по диагоналям, затем пополам — все это просто разметка;
• Ориентируясь на диагонали-сгибы, сформируйте треугольник, подгибая внутрь боковые плоскости заготовки (см. схему). 4 гуляющих угла у основания треугольника нужно подогнуть к вершине по 2 с каждой стороны заготовки;
• Боковые противоположные уголки подогните к центру — у вас здесь есть вертикальная ось-ориентир. Повторите действие с другой стороны. Гуляющие уголки одного из конических выступов (на втором углы «закрыты») дважды подгибают, чтобы их можно было аккуратно заправить в срединные уголки-кармашки;
• Аналогично заправьте дважды сложенные уголки в кармашки с обратной стороны заготовки. Модель куба готова, осталось дать ей объем. Найдите открытый уголок и через него надуйте макет.

Формула куба – объяснение, свойства и примеры решения

Нас окружают разные предметы, которые состоят из разных геометрических форм. Подумайте о детской игре с кубиками, игральными костями или кубиком льда. Что вы замечаете общего среди всего этого? Все они имеют форму куба, не так ли? В этой статье мы изучим, что такое куб? Объем формулы куба, площадь формулы куба, площадь поверхности формулы куба. Некоторыми из распространенных примеров кубика являются кубик льда, игральные кости, кубик Рубика.

Введение. Что такое куб?

Куб — это трехмерная фигура, состоящая из граней квадратной формы одинакового размера.

На приведенном ниже рисунке изображен куб, где l — длина, b — ширина, h — высота, и l = b = h. Длина, ширина и высота представляют ребра куба. И когда три ребра встречаются в точке, это называется вершиной.

(Изображение будет загружено в ближайшее время)

Свойства куба

1.  Все грани куба имеют квадратную форму.

2. Все грани и ребра равны.

3. Углы куба прямые.

4. Каждая из граней встречается с четырьмя соседними гранями.

5. Каждая из вершин встречается с тремя гранями и тремя ребрами.

6. Ребра, противоположные друг другу, параллельны и также равны.

7. Все 12 диагоналей на поверхности имеют площадь одинаковой величины

8. Все 4 внутренние диагонали равны

Например, куб имеет шесть граней. Следовательно, площадь его поверхности будет равна сумме площадей всех шести граней.

В основном площадь поверхности можно классифицировать как:

Площадь изогнутой поверхности объекта – это площадь всех криволинейных поверхностей объекта.

Боковая поверхность предмета – это площадь всех граней предмета, за исключением площади его основания и вершины. Для куба площадь боковой поверхности будет равна сумме площадей четырех сторон, то есть умноженной на 4 стороны.

Площадь боковой поверхности = 4 × (край) 2

902

Куб — это трехмерный объект, поэтому пространство, занимаемое кубом, будет трехмерным.

Куб ограничен шестью квадратными гранями, поэтому площадь поверхности будет вычисляться путем сложения площадей всех шести квадратных граней. Следовательно, площадь поверхности куба по формуле равна 9.0003

Площадь поверхности куба = 6 (сторона) 2

Внутренняя часть полого объекта может быть заполнена воздухом или какой-либо жидкостью, которая принимает форму объекта. В таких случаях объем вещества, который может вместить внутренность предмета, называется вместимостью полого предмета. Таким образом, мы можем сказать, что объем объекта — это мера занимаемого им пространства, а вместимость объекта — это объем вещества, которое может вместить его внутренность.

А объем куба — это занимаемое им пространство. Объем формулы куба будет рассчитан как:

Volume = (side) 3

Length of Diagonal of Face of the Cube = √2(edge)

Длина диагонала из куба = √3 (Edge)

3

3

3

3 9000

Периметр = 12 (ребро)

Решаемые примеры

Пример 1. Найдите площадь поверхности куба, длина стороны которого равна 7 см.

Решение:

Указанная длина = края = 7 см

Ум.

        = 6 × 49

        =  294 см 2

Пример 2: Сторона кубического ящика равна 9 м. Найдите объем кубического ящика.

Решение:

DED, сторона = A = 9m

по формуле объема A Cube, мы знаем, что

V = A 3 11963

9

v = 3 1113

9

v = 3 1113

9

v = 3 1113

V = 3 111996469

v = 3 11996469

v = 3 113

V = 3 x 9 x 9

V = 729 кв.

2

Значение кубов в математике

Кубы — это трехмерные квадраты, которые многие считают символом геометрического совершенства. С какой стороны на него ни посмотри, он выглядит одинаково. Это часть геометрии в математике и чрезвычайно важна как глава. Понимание этого является ключом к пониманию других связанных концепций. Учащиеся должны быть внимательны при изучении кубиков, так как из этой главы возникнет много вопросов. Они могут перейти к формуле куба — объяснение, свойства и примеры решений и подробно разобраться в этом. На этой странице Веданту каждая концепция упрощена для понимания учеником.

Cube Formula — Что такое Cube Formula? Примеры

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Куб числа непосредственно отражает объем куба, имеющего длину ребра, равную данному числу.

Что такое формула куба?

Куб является одним из пяти платоновых тел и также известен как правильный шестигранник.

Формула куба

Объем куба

Объем куба можно рассчитать с использованием различных формул на основе заданных параметров. Его можно рассчитать, используя длину стороны, а также размер диагонали куба.

• Объем куба (на основе длины стороны) = a 3  кубических дюймов, где a – длина стороны куба
• Объем куба (по диагонали) = (√3×d 3 )/9кубических дюймов, где d — длина диагонали куба

Боковая площадь куба

Боковая площадь куба равна сумме площадей всех боковых граней куба.

LSA куба = 4a 2

, где a — длина стороны.

Общая площадь куба

Общая площадь поверхности куба будет равна сумме площади основания и площади вертикальных поверхностей куба. Поскольку все грани куба состоят из квадратов одинакового размера, то общая площадь поверхности куба будет равна площади поверхности одной грани, сложенной с самой собой в пять раз. Таким образом, формула для нахождения площади поверхности куба:

Общая площадь поверхности (TSA) куба = 6a 2

, где a — длина стороны.

Диагональ куба

Куб имеет диагонали двух разных длин, более короткие лежат на квадратных гранях, а более длинные проходят через центр. Главной диагональю куба называется та, которая проходит через центр, который можно найти, умножив длину одной стороны на квадратный корень из 3.

Диагональ куба = a√3

Давайте лучше разберемся с формулами куба на нескольких решенных примерах.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запись на бесплатный пробный урок

Примеры с использованием формулы куба

Пример 1: Найдите объем кубика Рубика длиной 4 дюйма. Решение:

Чтобы найти объем кубика Рубика: кубик Рубика0003

Длина стороны куба = 4 дюйма (дано)

Используя формулу куба, объем = с × с × с = с 3

Поместите значения,

объем = 4 × 4 × 4 = 4 3  = 64

Ответ: Объем кубика Рубика составляет 64 кубических дюйма.

Пример 2: Размеры куба – 64 дюйма. Найдите его диагональ по формуле куба. Решение: 

Чтобы найти диагональ куба:

Размеры куба: длина (l) = ширина (w) = высота (h) = 64 дюйма (данные)

Используя формулу куба,

диагональ = a√3 

Поместите значения,

Диагональ = 64√3 = 110,848 дюйма

Ответ: Диагональ куба равна 110,848 дюйма

Пример 3: Найдите общую площадь поверхности куба, если длина стороны куба равна 25 дюймам.

Решение:

Длина стороны куба, a = 25 дюймов 

Используя формулу площади куба, а именно: A = 6a 2

Поместите значения,

A = 6 × 25 × 25 = 3750 квадратных дюймов

Ответ: Площадь поверхности куб равен 3750 квадратных дюймов.

Часто задаваемые вопросы о формуле куба

Что такое формула куба?

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Это простые формулы, зависящие в основном от одного параметра — длины ребра или стороны куба.

Как рассчитать диагональ куба по формуле куба?

Главную диагональ куба , пересекающую центр, можно найти, умножив длину одной стороны на квадратный корень из 3. Таким образом, диагональ куба = a√3, где a – ребро куба. .

Что такое s в формуле куба?

В формуле куба s относится к ребру куба. Все формулы куба — объем, площадь поверхности и диагонали — зависят от ребра куба, представленного как s, так и a.

Как вывести формулу куба?

Чтобы вычислить объем по формуле куба,

• Шаг 1: Рассмотрим любой квадратный лист бумаги.
• Шаг 2: Теперь площадь, покрытая этим квадратным листом, будет равна площади его поверхности, т. е. его длине, умноженной на его ширину. Оба одинаковы в случае куба. Таким образом, площадь поверхности будет равна «s 2 ».
• Шаг 3: Куб получается путем складывания нескольких квадратных листов таким образом, чтобы высота стала равной длине и ширине, т. е. единицам «s». Таким образом, высота или толщина куба равна «s».

Таким образом, можно сделать вывод, что общее пространство, занимаемое кубом, то есть объем, равно площади основания, умноженной на высоту. Объем куба = s 2  × s = s 3

Чтобы вывести формулу поверхности куба,

• Шаг 1. Рассмотрим любой лист бумаги квадратной формы.
• Шаг 2: В случае квадрата, поскольку длина и ширина равны, площадь поверхности будет равна «s 2 » (длина, умноженная на ширину).
• Шаг 3: Поскольку у куба 6 граней, общая площадь поверхности куба равна площади одной грани, умноженной на 6 = 6s 2

Квадрат из бумаги: схема изготовления

Геометрические фигурки полюбят изготавливать дети и взрослые — процесс настолько увлекательный, что очень скоро у вас появится целая коллекция разнообразных кубиков. Перед началом работы необходимо запастись нужным количеством бумаги, которой хватит на все стороны, чтобы впоследствии не пришлось доклеивать к имеющемуся каркасу недостающие элементы. Развертка выполняется на ватмане или картоне. Материал должен быть в меру плотным, чтобы фигура не помялась при сборке, но слишком толстый лист бумаги также не подойдет. Особое условие — наличие дополнительных граней по бокам некоторых сторон, при помощи которых будет происходить склеивание куба. Объемный квадрат состоит из восьми одинаковых сторон. Чтобы не ошибиться с выбором ватмана, выполните все расчеты до нанесения чертежа на лист бумаги.

Как сделать из бумаги или картона куб-трансформер

Для того чтобы выполнить куб-трансформер, потребуются лист картона, линейка, карандаш, скотч или клей.

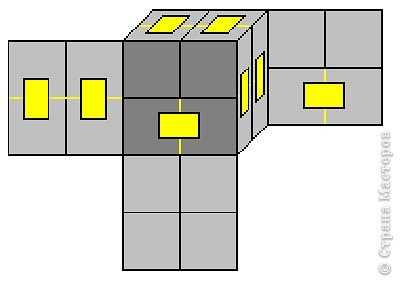
Первым делом, надо обозначить на листе картона восемь разверток кубиков со сторонами три сантиметра. Затем каждую развертку следует вырезать и сложить из них кубики. После того, как кубики будут готовы, их необходимо соединить, используя кусочки скотча. На фото, размещенном ниже, будет показано, где должны располагаться места соединения. Кубики склеивать между собой необходимо с двух сторон.

Кубик можно украсить, наклеив на каждую сторону кубика картинки одной тематики. Чаще всего такие кубики используют в качестве календаря, меню или памятного сувенира, например, для туристов, обклеив кубик изображениями достопримечательностей города.

Дополнительные материалы

Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Геометрия и куб

Куб — это фигура, которые мы встречаем не только на уроках геометрии и изобразительного искусства, но и в нашей повседневной жизни. Другое название куба — правильный гексаэдр. Кубом называется правильный многогранник, каждая грань которого является квадратом. Куб можно назвать объемный, трехмерным или даже 3D квадратом. Куб имеет 8 вершин, 6 граней, 12 ребер. Куб — это удивительная геометрическая фигура, в которую можно спрятать или вписать другие фигуры, например такие: октаэдр, тетраэдр, икосаэдр и другие.

Удивительная фигура «куб»

Куб или гексаэдр также называют кубом Неккера, назван он так в честь швейцарского кристаллографа Луиса Альберта Неккера. В 1832 году Неккер предложил иллюзию, вглядываясь в куб с гранями можно заметить, что маленькая черная точка появляется то на переднем, то на заднем плане, то в углу или в центре. Она перемещается из одного места в другое, как бы движется. Еще одна особенность куба Неккера в том что, его параллельные боковые ребра кажутся расходящимися. Можно перекрасить одну из граней в другой цвет, и посмотреть, как эта цветная грань фантастическим образом перемещается.

Еще один необычный куб — это куб художника Маурица Эшера. Это куб, который невозможен.

Еще одно интересное открытие, имеющие отношение к кубу, было сделано в 1966 году благодаря фотографу Чарльзу Ф. Кокрану. Он сделал фотографию, которую окрестили «сумасшедший ящик». Что же из себя представляет «сумасшедший язык»? Это вывернутый наизнанку каркас фигуры гексаэдра (куба). «Сумасшедший ящик» основывается на неправильных соединениях, которые допустили при рисовании фигуры.

Куб Неккера

«Сумасшедший ящик»

В список самых удивительных и странных фигур можно занести: интегральный куб, разрастающийся куб (также может называться бесконечным кубом), повторяющиеся кубы, кубическую снежинку, парящие кубы, двухэтажный куб и многие, многие другие. Все эти фигуры завораживают, от них не возможно оторвать глаз. Каждый, кто их видит, хочет понять, как они устроены.

Куб всегда таил в себе много загадок — удивительно сложная и в тоже время удивительно простая геометрическая фигура, помогающая заглянуть в глубины сознания. Еще в древности Платон называл ее священной фигурой и относил к знаку Земли, потому что это самая устойчивая фигура из всех других. Куб является фигурой сакральной геометрии. Еще в 16 веке немецкий математик и астроном Иоганн Кеплер составил модель солнечной системы, в которую вписал куб.

Где можно встретить куб? Здания чаше всего имеют кубическую форму, так что можно просто выглянуть в окно, и вы сразу увидите куб. Самая знаменитая игрушка-головоломка, которую хотя бы раз в жизни каждый ребенок держал в руках, а некоторым даже удалось ее собрать, это кубик Рубика. Название говорит само за себя. В 1975 году венгерский архитектор Эрне Рубик создал игрушку-головоломку, которая стала популярной во всем мире. Кубик-рубик представляет собой куб, сделанный из пластмассы, который в свою очередь состоит из 26 кубиков. И когда «Кубик-рубик» собран, каждая его грань окрашивается в один определенный цвет.

Различные вещества кристаллизуются в форме куба, например поваренная соль, минерал флюорит и другие.

Инструменты и материалы, чтобы сделать куб из бумаги

Чтобы комфортно и удобно работать с бумагой или картоном, в нашем случае вырезать и склеивать геометрические фигуры, вам понадобятся следующие инструменты:- ножницы (или канцелярский нож с железной линейкой и твердой поверхностью, которую не жалко испортить);- плотная бумага или картон (белый или цветной), формата А4;- клей.Так же вам необходим компьютер с принтером, лучше цветным, чтобы распечатать понравившуюся схему для дальнейшего склеивания фигуры.

Объем куба и прямоугольного параллелепипеда

Докажем важную вспомогательную теорему:

Действительно, пусть у двух параллелепипедов одинаковы основания. Тогда их можно совместить. Пусть общим основанием будет АВСD, а высотами параллелепипедов будут отрезки АР и АК, причем АР <АК. Объем меньшего параллелепипеда с высотой АР обозначим как V_Р, а большего – как V_K:

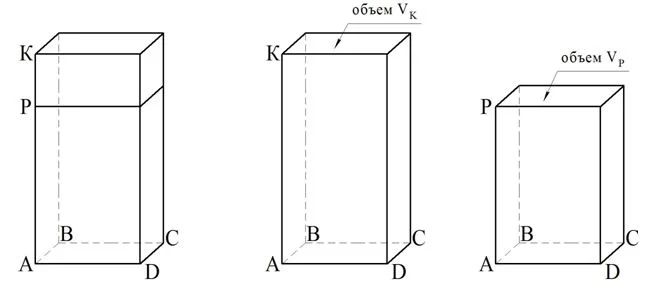
Нам надо доказать, что объемы фигур пропорциональны их высотам:

Для начала рассмотрим случай, когда отношение высот является рациональным числом. Это означает, что существует некоторая дробь m/n, такая, что

где m и n – натуральные числа. Тогда разобьем отрезок АК как раз на n равных отрезков. В этом случае отрезок АР будет состоять в точности из m таких отрезков. Далее через концы отрезков проведем плоскости, параллельные основанию:

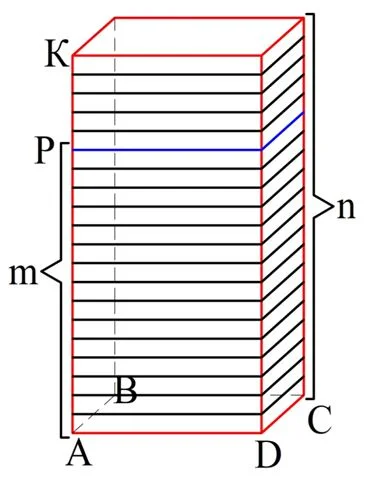
В результате мы получили n равных параллелепипедов («пластин»), которые все вместе образуют большой параллелепипед объемом V_K. Поэтому объем одной такой пластины равен величине V_K/n:

Итак, мы доказали теорему для случая, когда отношение высот является рациональным числом. Теперь перейдем к более сложному случаю, когда это отношение представляет собой иррациональное число. Здесь можно рассуждать от противного. Предположим, что теорема ошибочна, тогда для каких-нибудь двух параллелепипедов отношение их объемов будет равно не отношению их высот, а какому-то другому числу k:

Это значит, что k либо меньше, либо больше, чем отношение АР/АК. Рассмотрим случай, когда k< АР/АК (случай, когда k> АР/АК, рассматривается аналогичным образом). Тогда возьмем какое-нибудь рациональное число R, находящееся между числами k и АР/АК:

(Примечание. Здесь мы неявно используем утверждение, которое можно доказать в рамках алгебры – между любыми двумя различными действительными числами располагается хотя бы одно рациональное число).

Умножим это неравенство на длину АК:

Построим параллелепипеды с общим основанием АВСD и высотами АК и АР, а также с высотой АЕ = R•АК. Так как R•АК < АР, то точка Е будет лежать между А и Р:

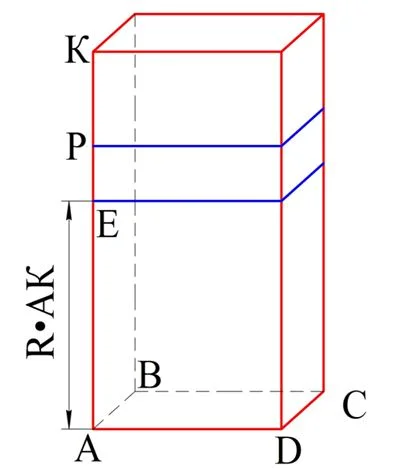
Объем параллелепипеда с высотой АЕ обозначим как V_Е. Ясно, что

ведь число k не может быть одновременно и больше, и меньше R. Полученное противоречие означает, что исходное предположение об ошибочности теоремы неверно, и на самом деле она справедлива, ч. т. д.

Теперь с помощью доказанной теоремы можно вывести известную ещё из младших классов формулу для расчета объема прямоугольного параллелепипеда.Пусть измерения прямоугольного параллелепипеда являются числами а, b и c. Построим:

• единичный куб;
• параллелепипед с габаритами а, 1, 1 с объемом V₁;
• параллелепипед с габаритами а, b, 1 с объемом V₂;
• параллелепипед с габаритами а, b, c с объемом V.

Тогда можно последовательно вычислить их объемы. Объем первого параллелепипеда будет в а раз больше объема единичного куба, то есть он будет равен а. Объем второго параллелепипеда будет больше ещё в bраз, а третьего – ещё в с раз:

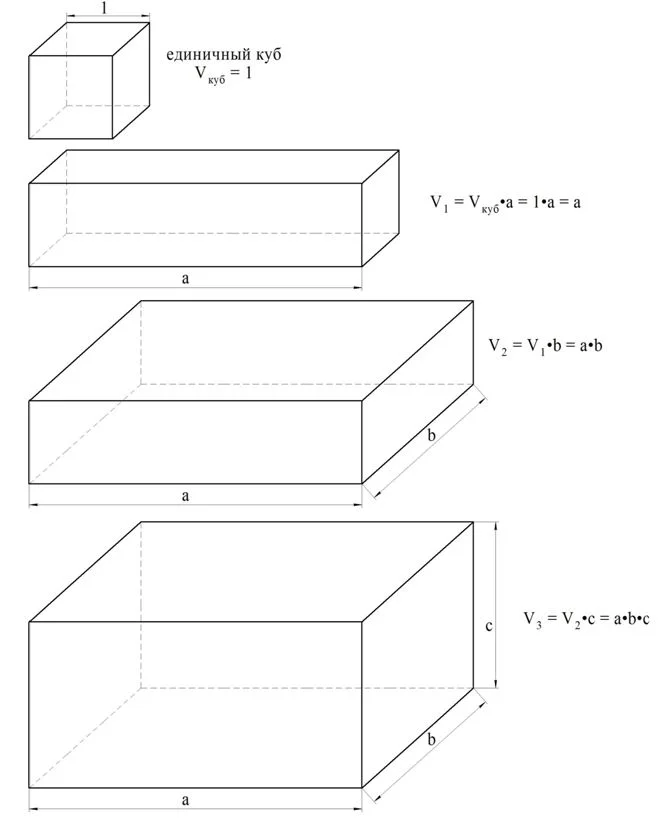
Соответственно, для расчета объема параллелепипеда используется формула

Иногда эту формулу формулируют несколько иначе: объем параллелепипеда – это произведение площади его основания на длину высоты, перпендикулярной этому основанию.

Задание. Три смежных ребра прямоугольного параллелепипеда имеют длины 9, 4 и 7 см. Каков объем параллелепипеда?

Решение. Здесь надо просто перемножить габариты параллелепипеда:

Ответ: 252 см3.

Куб можно рассматривать как прямоугольный параллелепипед с одинаковыми измерениями. Поэтому для вычисления его объема надо умножить ребро куба само на себя дважды, то есть возвести его в куб.

Задание. Вычислите объем куба с ребром 8 метров.

Решение. Просто возводим сторону ребро куба в третью степень:

Задание. Если ребро куба увеличить на 2 дм, то его объем вырастет на 98 дм3. Какова длина ребра этого куба?

Решение. Обозначим длину ребра буквой х. Тогда объем куба будет составлять х3 дм. Если ребро увеличить на 2 дм, то оно будет иметь длину х + 2 дм, и тогда объем куба будет равен уже (х + 2)3 дм. Условие задачи можно записать в виде уравнения:

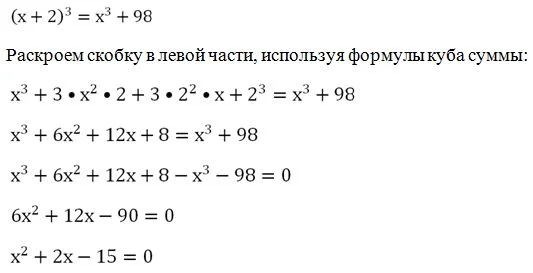
Это квадратное уравнение имеет два корня, 3 и (– 5), что можно проверить с помощью теоремы Виета. Корень х = – 5 не имеет геометрического смысла, поэтому остается ответ х = 3.

Ответ: 3 дм.

Далее рассмотрим перевод единиц измерения объема. Например, как перевести 1 м3 в кубические сантиметры? Рассмотрим куб с ребром 1 м. Ясно, что его объем будет равен 1 м3. С другой стороны, можно сказать, что длина ребра этого куба составляет 100 см:

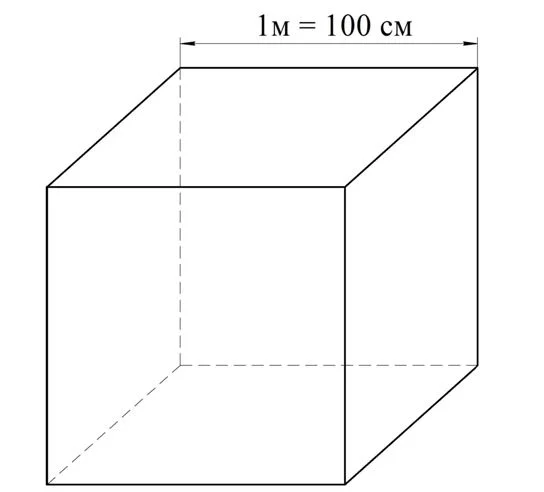
Тогда объем этого куба можно посчитать так:

Аналогично можно переводить и другие единицы измерения.

Модульный кубик

Имея знания, как сделать кубик из бумаги в технике оригами и изготовив поделку несколько раз, можно попробовать сконструировать кубик из модулей. Потребуется шесть листов цветной бумаги, желательно, чтобы листов было по 2 одинакового цвета. Что касается цветного картона, то для этой поделки его лучше не использовать.

Также нужно понимать, что подобная работа требует много времени, но в итоге получится прекрасная поделка. При изготовлении нужно соблюдать точную последовательность.

Изготовление модульных поделок, заключается в соединение отдельных элементов в цельную конструкцию. Подобные действия мы проводили при

Процесс изготовления кубика из модулей:

Потратив некоторое время, вы узнали, как сделать модульный кубик из бумаги. И наверняка убедились, что итоговый результат изготовления обладает прекрасным внешним видом.

Если желаете, чтобы поделка не распадалась, то во время конструирования, лучше использовать клей. Он обеспечит надежность крепления деталей.

Разные грани — разные формы

Многогранники — это особая сфера геометрии. Они бывают простые — к примеру кубики, которыми дети играют с раннего возраста, — а бывают очень и очень сложные. Простроение развертки многогранников для склеивания считаетсядостаточно сложной областью конструирования и творчества: нужно не только знать основы черчения, геометрические особенности пространства, но и иметь пространственное воображение, позволяющее оценить правильность решения еще на стадии проектирования. Но и одной фантазией не обойтись. Чтобы сделать развертки не достаточно просто представить, как в конце концов должна выглядеть работа. Нужно уметь правильно ее просчитать, сконструировать, а также грамотно начертить.

Правильные и неправильные звездчатые многогранники

Складывая платоновые тела между собой в определенном порядке, вы можете построить немало звездчатых многоранников — красивых, сложных, многокомпонентных. Но они будут называться «неправильными звездчатыми многогранниками». Правильных звездчатых многогранников всего четыре: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Развертки многогранников для склеивания не будут простыми чертежами. Они, как и фигуры, будут состоять из нескольких компонентов. Так, например, малый звездчатый додекаэдр строится из 12 пятиугольных равнобочных пирамид, сложенных по типу правильного додекаэдра. То есть для начала придется начертить и склеить 12 одинаковых штук правильных пирамид, состоящих из 5 равных граней. И только затем из них можно сложить звездчатый многогранник. Развертка самого малого звездчатого додекаэра — сложное и практически невыполнимое задание. Чтобы ее простроить, нужно суметь на одной плоскости уместить соединенные друг с другом 13 разверток разных геометрических объемных тел.

Элементы куба

Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.

Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Диагональ куба — одна из осей симметрии.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Как сделать куб из бумаги или картона: различие по технике изготовления

Сделать куб из бумаги или картона, как кажется на первый взгляд, элементарно. На практике же всё оказывается иначе. Особый страх появляется в глазах тех, кто узнаёт о том, что вариантов изготовления кубов достаточно много и все они различаются, как по сложности, так и по внешнему виду. Более подробно мы рассмотрим самые популярные из способов и покажем схемы их изготовления.

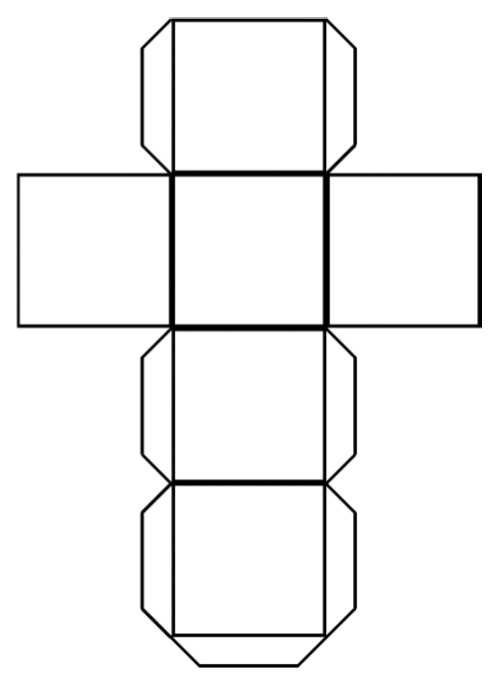
К наиболее простому из всех относится объемный куб, делающийся при помощи развертки. Для этого можно воспользоваться данной разверткой. Её достаточно распечатать, вырезать по контуру, согнуть по пунктирной линии и, смазав клапаны клеем, склеить.

На этом изготовление самого простого куба закончено.

Как сделать куб-трансформер.

Следующим по степени сложности и оригинальности стоит считать куб-трансформер. Такой куб сможет на долгое время занять ребёнка. К тому же, он является отличной поделкой, которую можно сделать вместе с детьми, поскольку сложного в нём ничего нет.

В качестве инструкции изготовления такого куба можно воспользоваться нашими фото, приведенными ниже.

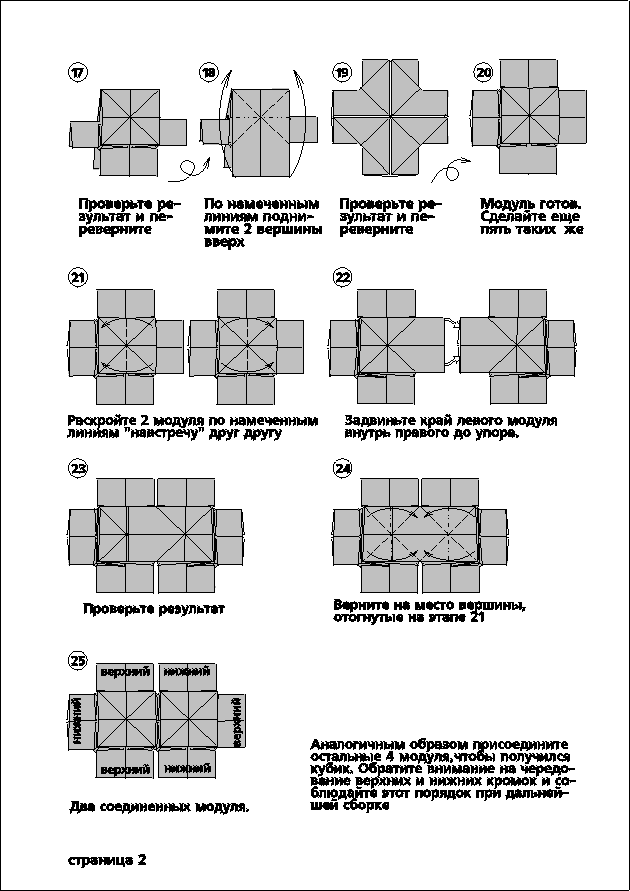
Для изготовления такого куба потребуется всего-навсего лист формата А4, карандаш, скотч и линейка.

Схема его изготовления весьма длинная, но оно того стоит:

1) Верхний угол сгибается и протягивается к нижнему краю;

2) Ненужная часть бумаги срезается по линии сгиба;

3) Полученный квадрат сворачивается пополам и разрезается пополам, нам понадобится только один прямоугольник, полученный в результате;

4) Вдоль листа делается изгиб, каждая сторона сворачивается, образуя «двойную дверь»;

5) Лист переворачивается на другую сторону и делается еще одна «дверь»;

6) Каждая сторона сворачивается аналогично;

7) Изгибы фальцуются, чтобы они были отчетливо видны;

Лист разворачивается и складывается в ширину;

9) При помощи линейки и карандаша прочерчиваются линии изгибов;

10) Делаются линии среза по чертежу;

11) От центральной линии среза отворачивается бумага и склеивается между собой скотчем;

12) Вторая часть склеивается аналогично 11 пункту;

13) Края фигуры протягиваются к центру и фиксируются посередине.

Так же инструкцию по изготовлению куба трансформера вы можете посмотреть в нашем видео:

Куб Йошимото.

Этот куб появился почти сразу же после появления известного во всем мире кубика Рубика и представляет собой аналогичную головоломку, которую подвластно сделать любому желающему.

Куб йошимото и по сей день вызывает недоумение, поскольку его можно крутить и вертеть в разные стороны, составляя его в различные конструкции вроде змейки или кольца. Нет предела удивлению, когда в руках данный куб распадается на две объемные остроугольные звезды.

Для его изготовления потребуется плотная бумага или картон, карандаш, линейка, ножницы и скотч.

Для начала нужно распечатать и вырезать заготовку в 16-ти экземплярах. Чтобы готовая поделка получилась больше, нужно просто увеличить изображение при печати. Так же можно собственноручно начертить чертежи исходя из этой схемы:

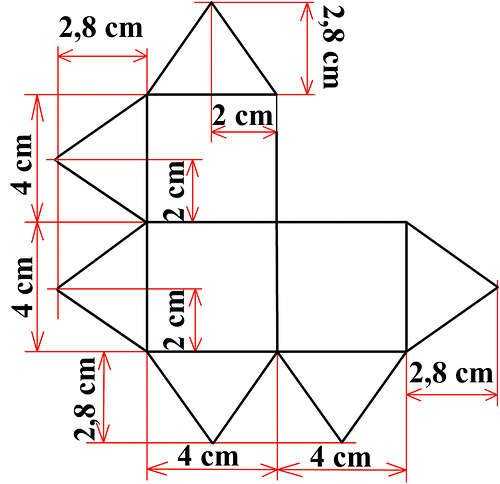
Затем, вырезанная заготовка складывается по линиям сгиба и склеивается скотчем (более подробно описано в видео под статьей). То же самое повторяется с оставшимися пятнадцатью деталями. Позже эти сегменты соединяются между собой. Одна «звезда» состоит из 8 соединенных между собой сегментов. Примечательно также то, что подвижная часть этих сегментов должна при соединении быть направлена внутрь.

Куб из бумаги схема развёртки

Заготовка шаблон для кубикаЗнания о том, как сделать кубик из бумаги помогут вам сконструировать, подарочную коробочку, или коробку для сладостей. Подробное в одной из предыдущих статей. Процесс изготовления куба с применением заготовки, начинается с конструирования развертки. Развертка является схемой, которая предназначена для изготовления объемного куба из картона либо бумаги.

Для работ, по изготовлению развертки (схемы) нам потребуется:

• лист бумаги;
• простой карандаш;
• линейка и ножницы.

Как сделать куб из бумаги по схеме:

Чертим квадрат. Следим за показателями: стороны должны быть равными, а углы соответствовать отметке девяносто градусов. Теперь вспоминаем школьную программу и узнаем, что у куба 6 граней. Это означает, что и на бумаге должно быть шесть квадратов.
Рисуем карандашом возле куба идентичные квадраты. Многим покажется, что остался один лишний и он не нужен, но это не так. Его нужно начертить рядом с любым из квадратов.
Итак, вроде 6 квадратов начерчены, теперь для их соединения, нужны небольшие припуски. Чертятся они по бокам 3-ёх квадратов. При этом их ширина должна быть до одного сантиметра. Вырезаем схему и приступаем к склеиванию поделки

Важно не забыть, подрезать уголки припусков, так как качественней и удобней проводить работу.

Проведя такие манипуляции у вас получится объемный куб, на котором можно написать буквы и нарисовать животных. Подобную конструкцию можно изготовить и без помощи черчения. Как сделать кубик из бумаги у которого 12 сторон, можно сделать по следующей схеме: