Функция плотности распределения

Дополнительные сведения

В отличие от вероятности функция плотности вероятности может принимать значения больше единицы; например, равномерное распределение на интервале имеет плотность вероятности f (x) = 2 для 0 ≤ x ≤ ½ и f (x) = 0 в другом месте.

Стандартное нормальное распределение имеет плотность вероятности

f (x) = 1 2 π e — x 2/2. {\ displaystyle f (x) = {\ frac {1} {\ sqrt {2 \ pi}}} \; e ^ {- x ^ {2} / 2}.}

Если задана случайная величина X и его распределение допускает функцию плотности вероятности f, то ожидаемое значение X (если ожидаемое значение существует) может быть вычислено как

E ⁡ = ∫ — ∞ ∞ xf (x) dx. {\ displaystyle \ operatorname {E} = \ int _ {- \ infty} ^ {\ infty} x \, f (x) \, dx.}

Не каждое распределение вероятностей имеет функцию плотности: распределения дискретных случайных величин — нет; равно как и распределение Кантора, даже при том, что оно не имеет дискретной составляющей, т.е. не присваивает положительную вероятность какой-либо отдельной точке.

Распределение имеет функцию плотности тогда и только тогда, когда его кумулятивная функция распределения F (x) абсолютно непрерывна. В этом случае: F почти всюду дифференцируемо, и его производная может использоваться как плотность вероятности:

d d x F (x) = f (x). {\ displaystyle {\ frac {d} {dx}} F (x) = f (x).}

Если распределение вероятностей допускает плотность, то вероятность каждого одноточечного набора {a} равна нулю; то же самое верно для конечных и счетных множеств.

Две плотности вероятности f и g представляют одно и то же распределение вероятностей, если они различаются только на наборе Лебега нулевой меры.

в поле в статистической физике, неформальная переформулировка приведенного выше отношения между производной кумулятивной функции распределения и функцией плотности вероятности обычно используется в качестве определения функции плотности вероятности. Это альтернативное определение выглядит следующим образом:

Если dt — бесконечно малое число, вероятность того, что X входит в интервал (t, t + dt), равна f (t) dt, или:

Pr (t

Суммы независимых случайных величин

Функция плотности вероятности суммы двух независимых случайных величин U и V, каждая из которых имеет функцию плотности вероятности, является свертка их отдельных функций плотности:

f U + V (x) = ∫ — ∞ ∞ f U (y) f V (x — y) dy = (f U ∗ f V) ( х) {\ displaystyle f_ {U + V} (x) = \ int _ {- \ infty} ^ {\ infty} f_ {U} (y) f_ {V} (xy) \, dy = \ left (f_ {U} * f_ {V} \ right) (x)}

Можно обобщить предыдущее соотношение на сумму N независимых случайных величин с плотностями U 1,…, U N:

е U 1 + ⋯ + UN (x) = (е U 1 * ⋯ * f UN) (x) {\ displaystyle f_ {U_ {1} + \ cdots + U_ {N}} (x) = \ left (f_ {U_ {1}} * \ cdots * f_ {U_ {N}} \ right) (x)}

Это можно получить из двухсторонней замены переменных с участием Y = U + V и Z = V, аналогично приведенному ниже примеру для частного независимых случайных величин.

Плотности, связанные с несколькими переменными

Для непрерывных случайных величин X1,…, X n также можно определить плотность вероятности функция, связанная с множеством в целом, часто называемая совместной функцией плотности вероятности . Эта функция плотности определяется как функция n переменных, так что для любой области D в n-мерном пространстве значений переменных X 1,…, X n, вероятность того, что реализация набора переменных попадет в область D, равна

Pr (X 1,…, X n ∈ D) = ∫ D f X 1,…, X n (x 1,…, xn) dx 1 ⋯ dxn. {\ displaystyle \ Pr \ left (X_ {1}, \ ldots, X_ {n} \ in D \ right) = \ int _ {D} f_ {X_ {1}, \ ldots, X_ {n}} (x_ {1}, \ ldots, x_ {n}) \, dx_ {1} \ cdots dx_ {n}.}

Если F (x 1,…, x n) = Pr (X 1 ≤ x 1,…, X n ≤ x n) — это кумулятивная функция распределения вектора (X 1,…, X n), тогда совместная функция плотности вероятности может быть вычислена как частная производная

f (x) = ∂ n F ∂ x 1 ⋯ ∂ xn | х {\ displaystyle f (x) = {\ frac {\ partial ^ {n} F} {\ partial x_ {1} \ cdots \ partial x_ {n}}} {\ bigg |} _ {x}}

Предельные плотности

Для i = 1, 2,…, n пусть f Xi(xi) будет функцией плотности вероятности, связанной только с переменной X i. Это называется функцией предельной плотности, и ее можно вывести из плотности вероятности, связанной со случайными величинами X 1,…, X n, путем интегрирования по всем значениям других n — 1 переменная:

f X i (xi) = ∫ f (x 1,…, xn) dx 1 ⋯ dxi — 1 dxi + 1 ⋯ dxn. {\ displaystyle f_ {X_ {i}} (x_ {i}) = \ int f (x_ {1}, \ ldots, x_ {n}) \, dx_ {1} \ cdots dx_ {i-1} \, dx_ {i + 1} \ cdots dx_ {n}.}

Независимость

Непрерывные случайные величины X 1,…, X n, допускающие плотность соединений все независимы друг от друга тогда и только тогда, когда

f X 1,…, X n (x 1,…, xn) = f X 1 (x 1) ⋯ f X n ( xn). {\ displaystyle f_ {X_ {1}, \ ldots, X_ {n}} (x_ {1}, \ ldots, x_ {n}) = f_ {X_ {1}} (x_ {1}) \ cdots f_ { X_ {n}} (x_ {n}).}

Следствие

Если совместная функция плотности вероятности вектора из n случайных величин может быть разложена на произведение n функций одной переменной

е Икс 1,…, Икс N (Икс 1,…, xn) = f 1 (x 1) ⋯ fn (xn), {\ displaystyle f_ {X_ {1}, \ ldots, X_ {n}} (x_ {1}, \ ldots, x_ {n}) = f_ {1} (x_ {1}) \ cdots f_ {n} (x_ {n}),}

(где каждое f i не обязательно является плотностью), то все n переменных в наборе независимы друг от друга, и функция предельной плотности вероятности каждой из них задается как

f X i (xi) = fi (xi) ∫ fi (x) dx. {\ displaystyle f_ {X_ {i}} (x_ {i}) = {\ frac {f_ {i} (x_ {i})} {\ int f_ {i} (x) \, dx}}.}

Пример

Этот элементарный пример иллюстрирует приведенное выше определение многомерных функций плотности вероятности в простом случае функции от набора двух переменных. Назовем R → {\ displaystyle {\ vec {R}}}двумерным случайным вектором координат (X, Y): вероятность получить R → {\ displaystyle {\ vec {R}}}в четверть плоскости положительных значений x и y равно

Pr (X>0, Y>0) = ∫ 0 ∞ ∫ 0 ∞ f X, Y ( х, у) dxdy. {\ displaystyle \ Pr \ left (X>0, Y>0 \ right) = \ int _ {0} ^ {\ infty} \ int _ {0} ^ {\ infty} f_ {X, Y} (x, y) \, dx \, dy.}

Математическое ожидание дискретной случайной величины.

Математическое ожидание случайной величины
задает ее «центральное» значение. Для дискретной случайной величины математическое ожидание вычисляется как сумма произведений значений $x_1,\dots ,\ x_n$ на соответствующие этим значениям вероятности $p_1,\dots ,\ p_n$, то есть: $M\left(X\right)=\sum^n_{i=1}{p_ix_i}$. В англоязычной литературе используют другое обозначение $E\left(X\right)$.

Свойства математического ожидания
$M\left(X\right)$:

1. $M\left(X\right)$ заключено между наименьшим и наибольшим значениями случайной величины $X$.
2. Математическое ожидание от константы равно самой константе, т.е. $M\left(C\right)=C$.
3. Постоянный множитель можно выносить за знак математического ожидания: $M\left(CX\right)=CM\left(X\right)$.
4. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий: $M\left(X+Y\right)=M\left(X\right)+M\left(Y\right)$.
5. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: $M\left(XY\right)=M\left(X\right)M\left(Y\right)$.

Пример 3

. Найдем математическое ожидание случайной величины $X$ из примера $2$.

$$M\left(X\right)=\sum^n_{i=1}{p_ix_i}=1\cdot {{1}\over {6}}+2\cdot {{1}\over {6}}+3\cdot {{1}\over {6}}+4\cdot {{1}\over {6}}+5\cdot {{1}\over {6}}+6\cdot {{1}\over {6}}=3,5.$$

Можем заметить, что $M\left(X\right)$ заключено между наименьшим ($1$) и наибольшим ($6$) значениями случайной величины $X$.

Пример 4

. Известно, что математическое ожидание случайной величины $X$ равно $M\left(X\right)=2$. Найти математическое ожидание случайной величины $3X+5$.

Используя вышеуказанные свойства, получаем $M\left(3X+5\right)=M\left(3X\right)+M\left(5\right)=3M\left(X\right)+5=3\cdot 2+5=11$.

Пример 5

. Известно, что математическое ожидание случайной величины $X$ равно $M\left(X\right)=4$. Найти математическое ожидание случайной величины $2X-9$.

Используя вышеуказанные свойства, получаем $M\left(2X-9\right)=M\left(2X\right)-M\left(9\right)=2M\left(X\right)-9=2\cdot 4-9=-1$.

Центр распределения случайной величины

Однозначное определение понятия центра распределения не существует. Обычно, в качестве понятия центра распределения используют три понятия:

• Медиана
• Мода
• Математическое ожидание

Медиана

Медиана определяется из принципа симметрии.

Медиана, это такая точка на оси x, что слева и справа от ней вероятности появления случайной величины одинаковы и равны 1/2.

Другими словами, площадь под кривой плотности распределения справа и слева от медианы равны друг другу.

В отличие от других центров распределения, медиана существует у любого распределения вероятностей.

Мода

Мода, это максимум кривой плотности распределения случайной величины.

Другими словами, мода, это самое наиболее вероятное значение случайной величины, максимально вероятное.

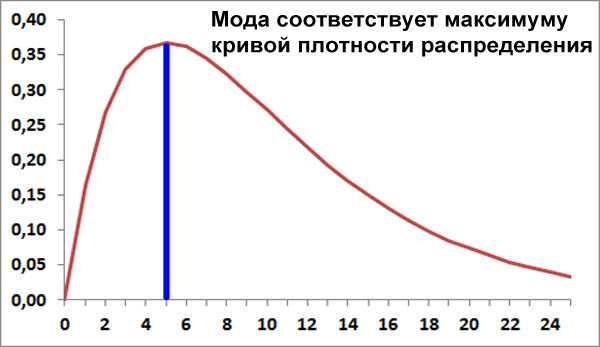
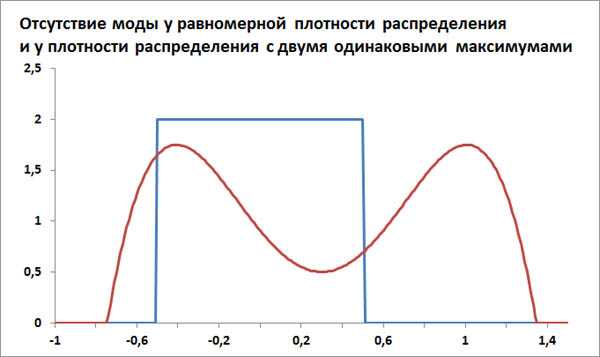
Исходя из такого определения, понятно, что мода существует не у всякого распределения. Мода не существует в случае, когда плотность распределения или не имеет максимума или у плотности распределения есть
несколько максимумов одинаковой высоты. Например, у равномерного распределения, когда функция плотности распределения выглядит, как прямоугольник, нет моды.

Математическое ожидание

Чаще всего в качестве центра распределения используется математическое ожидание. Причина этого в том, что математическое ожидание можно выразить аналитически с помощью формул.

Для дискретного распределения формула математического ожидания следующая.

Для непрерывного распределения формула математического ожидания следующая.

Теперь понятно, почему математическое ожидание может не существовать. Если, при стремлении x в бесконечность, плотность распределения падает как 1/x2 или ещё медленнее, то
интеграл в определении математического ожидания расходится.

Рассмотрим типичную задачу по вычислению математического ожидания на бинарных опционах. Допустим, брокер на выигрыш выплачивает 75% от размера ставки, а на проигрыш забирает всю ставку 100%. Найдем
матожидание для метода прогнозирования, который дает 65% успешных сделок.

В работе с бинарными опционами может быть два случайных события. Это выигрыш с вероятностью p=0.65 и проигрыш с вероятностью q=0.35. Случайная величина относительного дохода трейдера
(относительно величины его ставок) с вероятностью p принимает значение α=0.75 и с вероятностью q=0.35 принимает значение ß= -1.

Собираем это всё в сумму по формуле математического ожидания для дискретного распределения и получаем.

μ = αp + ßq = +0.1375

Положительное математическое ожидание говорит о том, что данный метод прогнозирования можно использовать на бинарных опционах. Трейдер будет в прибыли при большом количестве сделанных ставок, теоретически
при бесконечном числе ставок (и если у него хватит начального депозита на просадки в серии проигрышей).

А если метод прогнозирования трейдера дает только 65% прибыльных сделок?

В этом случае p=0.55, q=0.45. Подставляя эти данные в формулу математического ожидания для дискретного распределения, получаем μ=-0.0375.

Отрицательное матожидание говорит о том, что данный метод прогнозирования ни в коем случае нельзя применять. Если с таким методом прогнозирования трейдер получил прибыль на конечной серии ставок, то это
простое случайное везение.

Формула математического ожидания позволяет найти пограничное значение доли прибыльных сделок, которое необходимо получить от метода прогнозирования, и вывести
основную формулу бинарных опционов. Основная формула бинарных опционов
соответствует нулевому математическому ожиданию.

На Форексе и на фондовой бирже всё вычисляется аналогично. С той лишь разницей, что там параметры α и ß определяются через положения ордеров TakeProfit и StopLoss. Суть
параметров α и ß, это доли прибыли и убытка от размера собственных средств трейдера, участвующих в сделке.

Сравниваем точность представленных методов

Для сравнения точности представленных методов будем использовать расстояние Кульбака-Лейблера от априорной функции плотности распределения до получаемой оценки :

Для вычисления метрики уже, не мудрствуя лукаво, будем использовать numpy:

Получим оценки плотности распределения случайной величины для разных априорных распределений при разных соотношениях и сравним значений KL-дивергенции:

В результате ожидаемо в обоих случаях получаются монотонно возрастающие зависимости метрики от соотношения (Рисунок 2), однако, метод, основанный на численном дифференцировании функции распределения случайной величины дает на порядок меньшее расхождение кривой оценки плотности распределения с теоретической кривой, чем метод, основанный на построении гистограммы, что особенно заметно при больших значениях .

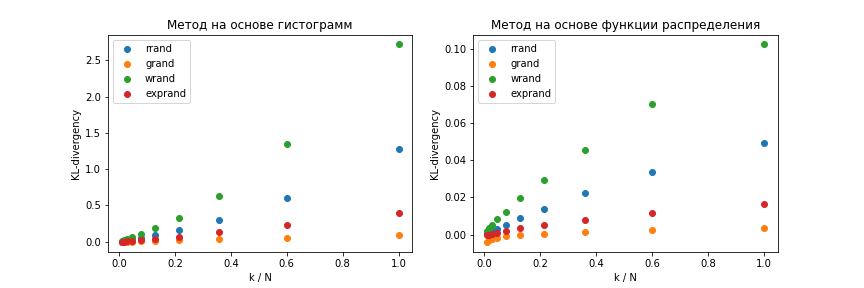Рисунок 2. Зависимость значения диверегенции Кульбака-Лейблера между априорным распределением и его оценкой от соотношения k / N для метода, основанного на бинаризации данных (слева) и метода, основанного на взятии произвоной от оценки функции распределения (справа).

Связь между дискретным и непрерывным распределениями

Можно представить определенные дискретные случайные величины, а также случайные величины, включающие как непрерывную, так и дискретную часть, с помощью обобщенного функция плотности вероятности с использованием дельта-функции Дирака. (Это невозможно с функцией плотности вероятности в смысле, определенном выше, это может быть выполнено с распределением.) Например,, рассмотрим двоичную дискретную случайную величину, имеющую распределение Радемахера, то есть принимающее -1 или 1 для значений с вероятностью 1/2 каждое. Плотность вероятности, связанная с этой переменной, равна:

е (t) = 1 2 (δ (t + 1) + δ (t — 1)). {\ Displaystyle f (t) = {\ frac {1} {2}} (\ delta (t + 1) + \ delta (t-1)).}

Более общие y, если дискретная переменная может принимать n различных значений среди действительных чисел, тогда соответствующая функция плотности вероятности имеет вид:

f (t) = ∑ i = 1 npi δ (t — xi), {\ displaystyle f (t) = \ sum _ {i = 1} ^ {n} p_ {i} \, \ delta (t-x_ {i}),}

где x 1…, xn {\ displaystyle x_ {1} \ ldots, x_ {n}}- дискретные значения, доступные для переменной, а p 1,…, pn {\ displaystyle p_ {1}, \ ldots, p_ {n}}- вероятности, связанные с этими значениями.

Это существенно унифицирует обработку дискретных и непрерывных распределений вероятностей. Например, приведенное выше выражение позволяет определять статистические характеристики такой дискретной переменной (такие как ее среднее, ее дисперсия и ее эксцесс ), начиная с приведены формулы для непрерывного распределения вероятности.

Свойства математического ожидания

Рассмотрим свойства математического ожидания.

Свойство 1. Математическое ожидание постоянной
величины равно этой постоянной:

Свойство 2. Постоянный множитель можно выносить за знак
математического ожидания:

Свойство 3. Математическое ожидание суммы (разности)
случайных величин равно сумме (разности) их математических ожиданий:

Свойство 4. Математическое ожидание произведения случайных
величин равно произведению их математических ожиданий:

Свойство 5. Если все значения случайной величины
X уменьшить (увеличить) на одно и то же число С, то её
математическое ожидание уменьшится (увеличится) на то же число:

Математическое ожидание и дисперсия непрерывной случайной величины

Для непрерывной случайной величины механическая интерпретация математического
ожидания сохранит тот же смысл: центр массы для единичной массы, распределённой непрерывно на оси
абсцисс с плотностью f(x). В отличие от дискретной случайной величиной, у которой
аргумент функции изменяется
скачкообразно, у непрерывной случайной величины аргумент меняется непрерывно. Но математическое ожидание
непрерывной случайной величины также связано с её средним значением.

Чтобы находить математическое ожидание и дисперсию непрерывной случайной величины,
нужно находить определённые интегралы. Если дана функция плотности непрерывной случайной величины, то
она непосредственно входит в подынтегральное выражение. Если дана функция распределения вероятностей, то,
дифференцируя её, нужно найти функцию плотности.

Арифметическое среднее всех возможных значений непрерывной случайной
величины называется её математическим ожиданием, обозначаемым
или .

Математическое ожидание
непрерывной случайной величины Х, плотностью вероятности которой является
функция f(x), находится как величина интеграла

,

если он сходится абсолютно.

Дисперсией непрерывной случайной величины называется величина интеграла

,

если он сходится.

Среднее квадратичное отклонение непрерывной случайной величины
определяется как арифметическое значение квадратного корня из дисперсии.

Оптимизируем алгоритм, основанный на бинаризации данных

В качестве алгоритма нахождения плотности распределения автор предлагает довольно широко распространенный метод, основанный на разбиении интервала значений переменной на заданное число бинов равной ширины и подсчет числа вхождений значений переменной в каждый бин, реализованный в ряде библиотек , а также собственную реализацию в соответствии с условиями (оригинальные комментарии сохранены):

Можно заметить, что сложность данного алгоритма составляет , т.к. внешний цикл пробегает значений, внутренний же, в худшем случае, пробегает значений. Грубо оценим время выполнения функции при различных значениях и

Вывод:

Разумеется, столь удручающие результаты не позволяют использовать данную реализацию метода, благо есть готовые реализации. Однако, можно добиться линейной сложности алгоритма подсчета значений в бинах по и константной по , существенно, тем самым, снизив вычислительное время, всего лишь добавив предварительную сортировку значений и заменив внутренний цикл по всем значениям случайной величины на цикл лишь по тем значениям, которые попадают в бин:

Выполним аналогичное тестирование времени выполнения оптимизированной функции при различных значениях и добавив некоторое число повторений:

Вывод:

С такими результатами гораздо приятнее иметь дело и такую нативную реализацию можно использовать в условиях, когда нет возможности устанавливать дополнительные пакеты. Следует, однако, заметить, что ассимптотическая сложность метода определяется алгоритмом сортировки, и в данном случае составляет .

Примечание:Представленные выше реализации используют нестрогое равенство для сравнения действительных чисел, что, вообще говоря, некорректно. Вследствие этого могут возникать граничные эффекты, поскольку вхождения минимального/максимального значений случайной величины в первый/последний бины не гарантировано. Следует немного модифицировать реализацию, добавив учет по умолчанию минимального и максимального значений случайной величины в первом и последнем бинах, соответственно, и пробегать в цикле по оставшимся значениям.

Подготовка данных

Тестировать методы будем с использованием данных, сгенерированных для 4-х распределений, для которых известны аналитические выражения плотности, как в оригинальной статье: Релея, гамма, Вейбулла и экспоненциального. Для этого используем код MilashchenkoEA с небольшими изменениями (для удобства дальнейшего использования изменены сигнатуры функций, возвращающих значения аналитической функции плотности вероятности на заданном массиве значений случайной переменной):

Сгенерируем для каждого распределения наборы случайных величин, и организуем их в словарь:

Далее, эти наборы данных будут использованы для тестирования целиком, либо срезами, содержащими значений случайной величины.

Примеры решения задач по теме «Закон распределения дискретной случайной величины»

Задача 1.

Выпущено 1000 лотерейных билетов: на 5 из них выпадает выигрыш в сумме 500 рублей, на
10 – выигрыш в 100 рублей, на 20 – выигрыш в 50 рублей, на 50 – выигрыш в 10 рублей. Определить
закон распределения вероятностей случайной величины X – выигрыша на один билет.

Решение.

По условию задачи возможны следующие значения случайной
величины X: 0, 10, 50, 100 и 500.

Число билетов без выигрыша равно 1000 – (5+10+20+50) = 915, тогда P(X=0) = 915/1000 = 0,915.

Аналогично находим все другие вероятности: P(X=0) = 50/1000=0,05, P(X=50) = 20/1000=0,02, P(X=100) = 10/1000=0,01,
P(X=500) = 5/1000=0,005. Полученный закон представим в виде таблицы:

Найдем математическое ожидание величины Х:
М(Х) = 1*1/6 + 2*1/6 + 3*1/6 + 4*1/6 + 5*1/6 + 6*1/6 = (1+2+3+4+5+6)/6 = 21/6 = 3,5

Задача 3.

Устройство состоит из трех независимо работающих элементов.
Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа
отказавших элементов в одном опыте, построить многоугольник распределения. Найти функцию распределения
F(x) и построить ее график. Найти математическое ожидание, дисперсию и среднее квадратическое
отклонение дискретной случайной величины.

Решение.

1.
Дискретная случайная величина X={число отказавших элементов в
одном опыте} имеет следующие возможные значения: х 1 =0 (ни один из элементов устройства не
отказал), х 2 =1 (отказал один элемент), х 3 =2 (отказало два элемента) и х 4 =3 (отказали три
элемента).

Отказы элементов независимы друг от друга, вероятности отказа каждого элемента равны между собой,
поэтому применима формула
Бернулли

. Учитывая, что, по условию, n=3, р=0,1, q=1-р=0,9, определим
вероятности значений:
P 3 (0) = С 3 0 p 0 q 3-0 = q 3 = 0,9 3 = 0,729;
P 3 (1) = С 3 1 p 1 q 3-1 = 3*0,1*0,9 2 = 0,243;
P 3 (2) = С 3 2 p 2 q 3-2 = 3*0,1 2 *0,9 = 0,027;
P 3 (3) = С 3 3 p 3 q 3-3 = р 3 =0,1 3 = 0,001;
Проверка: ∑p i = 0,729+0,243+0,027+0,001=1.

Таким образом, искомый биномиальный закон распределения Х имеет вид:

По оси абсцисс откладываем возможные значения х i , а по оси ординат –
соответствующие им вероятности р i . Построим точки М 1 (0; 0,729), М 2 (1; 0,243),
М 3 (2; 0,027), М 4 (3; 0,001). Соединив эти точки отрезками прямых, получаем искомый многоугольник распределения.

3.
Найдем функцию распределения F(x) = Р(Х

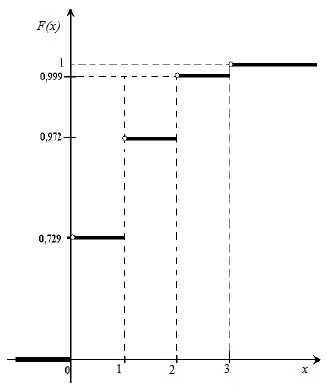График функции F(x)

4.
Для биномиального распределения Х:
— математическое ожидание М(X) = np = 3*0,1 = 0,3;
— дисперсия D(X) = npq = 3*0,1*0,9 = 0,27;
— среднее квадратическое отклонение σ(X) = √D(X) = √0,27 ≈ 0,52.

Случайной величиной
называют переменную величину, которая в результате каждого испытания принимает одно заранее неизвестное значение, зависящее от случайных причин. Случайные величины обозначают заглавными латинскими буквами: $X,\ Y,\ Z,\ \dots $ По своему типу случайные величины могут быть дискретными
и непрерывными
.

Дискретная случайная величина
— это такая случайная величина, значения которой могут быть не более чем счетными, то есть либо конечными, либо счетными. Под счетностью имеется ввиду, что значения случайной величины можно занумеровать.

Пример 1

. Приведем примеры дискретных случайных величин:

а) число попаданий в мишень при $n$ выстрелах, здесь возможные значения $0,\ 1,\ \dots ,\ n$.

б) число выпавших гербов при подкидывании монеты, здесь возможные значения $0,\ 1,\ \dots ,\ n$.

в) число прибывших кораблей на борт (счетное множество значений).

г) число вызовов, поступающих на АТС (счетное множество значений).

Функция распределения вероятностей. Плотность вероятностей

Определение . Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.

Для непрерывной случайной величины вводится понятие функции распределения.

Определение. Функцией распределения вероятностей случайной величины Х называют функцию F(х), определяющую для каждого значения x вероятность того, что случайная величина Х примет значение меньшее x, то есть:

3. Вероятность того, что случайная величина примет значение, заключенное в интервале [a; b), равна приращению функции распределения на этом интервале:

P(a ≤ X Определение . Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения:

Часто вместо термина «плотность распределения вероятностей» используют термин «плотность вероятностей» и «дифференциальная функция».

Свойства плотности распределения:

1. Плотность распределения неотрицательна в любой точке оси Ох:

2. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а, b), определяется равенством:

P(a Определение. Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством

где f(x) – плотность распределения случайной величины Х.

Предполагается, что интеграл сходится абсолютно. В частности, если все возможные значения принадлежат интервалу (a;b), то

Математическое ожидание обладает следующими свойствами:

1. Математическое ожидание постоянной величины равно самой постоянной:

2. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:

3. Постоянный множитель можно выносить за знак математического ожидания:

4. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:

Определение . Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством:

Как и в случае с дискретной случайной величиной, можно показать, что

В частности, если все возможные значения Х принадлежат интервалу (a;b), то

Дисперсия обладает следующими свойствами:

1. Дисперсия постоянной равна нулю:

2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:

3. Дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых:

4. Дисперсия произведения независимых случайных величин равна произведению дисперсий сомножителей:

5. Дисперсия суммы постоянной и независимой случайной величины равна квадрату постоянной на дисперсию независимой случайной величины:

Пример. Дана функция распределения непрерывной случайной величины Х

2.2 Функция распределения

После разговора о распределении вероятностей пришло время поговорить о функции распределения. Эта функция распределения является упрощенной версией! Должно называться полное имяФункция распределения понятий。

Посмотрите на закон распределения на рисунке ниже. Закон распределения здесь явно является «функцией вероятности», о которой мы только что говорили, и это всего лишь одно. Но я знаю, что многие учебники называются законами о распределении.

Функция распределения вероятностей — это накопление функций вероятности

Давайте посмотрим на формулу на графике, где F (x) представляет собой функцию распределения вероятностей. Справа от этого символа находится длинная формула, которая напоминает функцию вероятности, но знак равенства становится формулой, которая меньше или равна знаку. Если вы посмотрите вправо, это скопление функций вероятности одна за другой!

Вы открыли секрет функции распределения вероятностей? Это совсем не новость, это совокупный результат значения функции вероятности! Поэтому ее еще называют кумулятивной функцией вероятности!

Функция вероятности и функция распределения вероятности похожи на две стороны медали, они просто разные средства описания вероятности!

3 Функция вероятности и функция распределения непрерывных случайных величин

«Функция вероятности» непрерывных случайных величин имеет другое название.Это называется «Функция плотности вероятности».

Почему это так называется? Воспользуемся словами мастера, чтобы сказать вам, что в книге Чэнь Сиру «Теория вероятностей и математическая статистика»

Если вы все еще не понимаете этот анализ, взгляните на следующую формулу:

Функция плотности вероятности, выраженная математической формулой, является функцией определенного интеграла. Определенный интеграл используется для определения площади в математике, и здесь вы можете выразить вероятность как площадь!

Слева представлен график, построенный функцией распределения непрерывной случайной величины F (x), а справа — график, построенный функцией плотности вероятности непрерывной случайной величины f (x). Между ними существует следующее соотношение:Функция плотности вероятности — это производная функция функции распределения。

Сравнивая два изображения, вы обнаружите, что если вы используете область на правом рисунке для представления вероятности, вы можете использовать график, чтобы четко увидеть, какие значения имеют большую вероятность!Следовательно, когда мы выражаем вероятность непрерывной случайной величины, очень хорошо использовать функцию плотности вероятности f (x) для ее выражения!

Однако у читателей могут возникнуть такие вопросы:

В: Каково значение значения функции плотности вероятности в определенной точке?

A: Значение легче понять в определенный моментФункция плотности вероятности А именноСкорость изменения вероятности в этой точке(Или производная). В этом месте значение плотности вероятности легко принять за значение вероятности.

Например: соотношение между расстоянием (вероятностью) и скоростью (плотностью вероятности).

• Скорость определенной точки нельзя рассматривать как расстояние до определенной точки.
• Это не имеет смысла, потому что расстояние — это понятие от ХХ до ХХ.
• Следовательно, вероятность также должна иметь интервал.
• Этот интервал может быть окрестностью x (он может бесконечно приближаться к 0). Интегрируя f (x) в окрестности x, вы можете найти площадь этой окрестности, которая представляет вероятность возникновения этого события, представленного этой окрестностью.

Функция распределения дискретной случайной величины.

Способ представления дискретной случайной величины в виде ряда распределения не является единственным, а главное он не является универсальным, поскольку непрерывную случайную величину нельзя задать с помощью ряда распределения. Существует еще один способ представления случайной величины — функция распределения.

Функцией распределения
случайной величины $X$ называется функция $F\left(x\right)$, которая определяет вероятность того, что случайная величина $X$ примет значение, меньшее некоторого фиксированного значения $x$, то есть $F\left(x\right)=P\left(X

Свойства функции распределения
:

1. $0\le F\left(x\right)\le 1$.
2. Вероятность того, что случайная величина $X$ примет значения из интервала $\left(\alpha ;\ \beta \right)$, равна разности значений функции распределения на концах этого интервала: $P\left(\alpha
3. $F\left(x\right)$ — неубывающая.
4. ${\mathop{lim}_{x\to -\infty } F\left(x\right)=0\ },\ {\mathop{lim}_{x\to +\infty } F\left(x\right)=1\ }$.

Пример 9

. Найдем функцию распределения $F\left(x\right)$ для закона распределения дискретной случайной величины $X$ из примера $2$.

$\begin{array}{|c|c|}
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
\hline
\end{array}$

Если $x\le 1$, то, очевидно, $F\left(x\right)=0$ (в том числе и при $x=1$ $F\left(1\right)=P\left(X

Если $1

Если $2

Если $3

Если $4

Если $5

Если $x > 6$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)+P\left(X=5\right)+P\left(X=6\right)=1/6+1/6+1/6+1/6+1/6+1/6=1$.

Итак, $F(x)=\left\{\begin{matrix}
0,\ при\ x\le 1,\\
1/6,при\ 1
1/3,\ при\ 2
1/2,при\ 3
2/3,\ при\ 4
5/6,\ при\ 4
1,\ при\ x > 6.
\end{matrix}\right.$

Закон распределения вероятностей дискретной случайной величины.

Дискретная случайная величина $X$ может принимать значения $x_1,\dots ,\ x_n$ с вероятностями $p\left(x_1\right),\ \dots ,\ p\left(x_n\right)$. Соответствие между этими значениями и их вероятностями называется законом распределения дискретной случайной величины
. Как правило, это соответствие задается с помощью таблицы, в первой строке которой указывают значения $x_1,\dots ,\ x_n$, а во второй строке соответствующие этим значениям вероятности $p_1,\dots ,\ p_n$.

$\begin{array}{|c|c|}
\hline
X_i & x_1 & x_2 & \dots & x_n \\
\hline
p_i & p_1 & p_2 & \dots & p_n \\
\hline
\end{array}$

Пример 2

. Пусть случайная величина $X$ — число выпавших очков при подбрасывании игрального кубика. Такая случайная величина $X$ может принимать следующие значения $1,\ 2,\ 3,\ 4,\ 5,\ 6$. Вероятности всех этих значений равны $1/6$. Тогда закон распределения вероятностей случайной величины $X$:

$\begin{array}{|c|c|}
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
\hline
\end{array}$

Замечание
. Поскольку в законе распределения дискретной случайной величины $X$ события $1,\ 2,\ \dots ,\ 6$ образуют полную группу событий, то в сумме вероятности должны быть равны единице, то есть $\sum{p_i}=1$.