Теплопроводность через плоскую и цилиндрическую стенку

Тепловой поток

Количество тепла, проходящее через данную поверхность в единицу времени, называется тепловым потоком Q, Вт .

Количество тепла, через единицу поверхности в единицу времени, называется плотностью теплового потока или удельным тепловым потоком и характеризует интенсивность теплообмена.

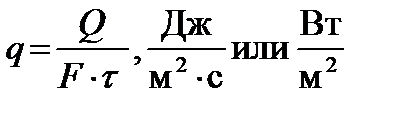
(9.4)

Плотность теплового потока q, направлена по нормали к изотермической поверхности в сторону, обратную градиенту температуры, т. е. в сторону уменьшения температуры.

Если известно распределение q по поверхности F, то полное количество тепла Q_τ, прошедшее через эту поверхность за время τ, найдется по уравнению:

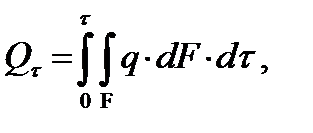
(9.5)

(9.5′)

Если величина q постоянна по рассматриваемой поверхности, то:

(9.5″)

Теплопроводность через цилиндрическую стенку (граничные условия первого рода)

Теплообменные аппараты в большинстве случаев имеют не плоские, а цилиндрические поверхности, например рекуператоры типа «труба в трубе», кожухотрубные водонагреватели и т.д. Поэтому возникает необходимость рассмотрения основных принципов расчета цилиндрических поверхностей.

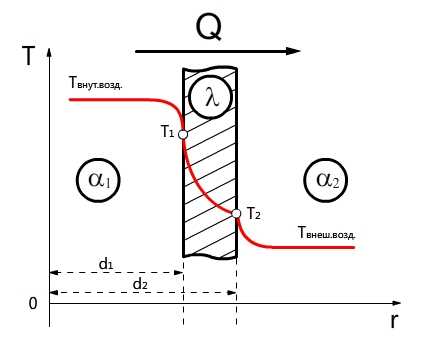
Согласно закону Фурье, количество теплоты, проходящее в единицу времени через этот слой, равно:

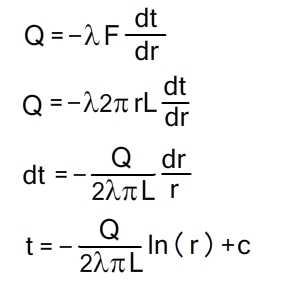
Подставим значения граничные значение и вспомним, что разность логарифмов равна логарифму отношению аргументов, получим:

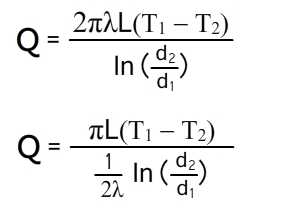
Распределение температур внутри однородной цилиндрической стенки подчиняется логарифмическому закону, и уравнение температурной кривой имеет вид:

Количество теплоты, проходящее через стенку трубы, может быть отнесено либо к единице длины трубы L, либо к единице внутренней F₁ или внешней F₂ поверхности трубы. При этом расчетные формулы принимают следующий вид:

q_L = Q/L = πΔT / (1/2λ * ln(d₂/d₁));

q₁ = Q/S₁ = Q/πd₁L

От чего зависит показатель теплопроводности

Показатель теплопроводности зависит от нескольких факторов:

Температура.
Условия эксплуатации того или иного материала.
Влажность. Высокий уровень влажности провоцирует вытеснение сухого воздуха капельками жидкости из пор, из-за чего значение увеличивается многократно.
Агрегатное состояние вещества. Самой высокой теплопроводностью обладают твердые тела, самой низкой — газы (в частности, вакуум).
Структура, пористость (поры говорят о неоднородности структуры: когда через них проходит тепло, охлаждение будет минимальным); плотность вещества (большая плотность способствует более активному взаимодействию частиц, теплообмен и уравновешивание температур протекает быстрее).

Нулевой закон термодинамики

Одно из положений так называемого нулевого закона термодинамики непосредственно сосредоточен на идее теплопроводности. Бейлин (1994) пишет, что «… можно сформулировать нулевой закон:

Все диатермальные стены эквивалентны».

A — это физическая связь между двумя телами, которая позволяет теплу между ними. Бейлин имеет в виду диатермальные стены, которые соединяют исключительно два тела, особенно проводящие стены.

Это утверждение «нулевого закона» принадлежит идеализированному теоретическому дискурсу, и реальные физические стены могут иметь особенности, не соответствующие его общности.

Например, материал стены не должен подвергаться фазовому переходу, например испарению или плавлению, при температуре, при которой он должен проводить тепло. Но когда учитывается только тепловое равновесие, а время не является актуальным, так что проводимость материала не имеет большого значения, один подходящий проводник тепла ничем не хуже другого. И наоборот, другой аспект нулевого закона состоит в том, что, опять же с учетом соответствующих ограничений, данная диатермальная стена безразлична к природе термостата, к которому она подключена. Например, стеклянная колба термометра действует как диатермическая стенка вне зависимости от того, подвергается ли она воздействию газа или жидкости, при условии, что они не разъедают и не плавят ее.

Эти различия относятся к числу определяющих характеристик теплопередачи. В некотором смысле это симметрии теплопередачи.

Понятие теплопроводности в физике

Перенос теплоты осуществляется 3 способами:

Конвекция.
Излучение.
Теплопроводность.

Совершая непрерывные хаотические движения, молекулы, атомы, электроны и другие микрочастицы, из которых состоят тела, сталкиваются друг с другом. При этом частицы, обладающие большей энергией, частично передают ее частицам с меньшей энергией.

Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния.

По отдельности в реальном мире виды переноса теплоты практически не встречаются. Чаще всего происходит совместный перенос.

Условная схема теплообмена:

Закон Фурье

Закон теплопроводности, также известный как закон Фурье, гласит, что скорость теплопередачи через материал пропорционален отрицательному градиенту в температуре и площади, перпендикулярной этому градиенту, через которую течет тепло. Мы можем указать этот закон в двух эквивалентных формах: в интегральной форме, в которой мы рассматриваем скорость потока или потоки локально.

Закон охлаждения Ньютона является дискретным аналогом закона Фурье, тогда как закон Ома является электрическим аналогом закона Фурье, а законы диффузии Фика являются его химическим аналогом.

Дифференциальная форма закона теплопроводности

Дифференциальная форма закона теплопроводности Фурье показывает, что локальный тепловой поток плотность, q {\ displaystyle \ mathbf {q}}, произведению теплопроводности, k {\ displaystyle k}, и отрицательного местного температурного градиента, — ∇ Т {\ Displaystyle — \ набла Т}. Плотность теплового потока — это количество энергии, которое проходит через единицу площади в единицу времени.

q = — К ∇ T {\ displaystyle \ mathbf {q} = -k {\ nabla} T}

где (включая единицы СИ )

q {\ displaystyle \ mathbf {q}}- локальная плотность теплового потока, W ·m

k {\ displaystyle {\ big.} k {\ big.}}- проводимость материала, W · М · K,

∇ T {\ displaystyle {\ big.} \ Nabla T {\ big.}}- температурный градиент, K · м.

Теплопроводность, k {\ displaystyle k}, часто рассматривается как постоянная величина, хотя это не всегда верно. Хотя теплопроводность материала обычно изменяется в зависимости от некоторых распространенных материалов, изменение может быть в значительном диапазоне температур. В анизотропных материалахлопроводность обычно изменяется в зависимости от теплопроводности; в этом случае к {\ displaystyle k}представлен тензором второго порядка. В неоднородных материалах k {\ displaystyle k}изменяется в зависимости от пространственного положения.

Для многих простых приложений закон Фурье используется в его одномерной форме. В направлении x

qx = — kd T dx {\ displaystyle q_ {x} = — k {\ frac {dT} {dx}}}

В изотропной среде закон Фурье приводит к :

∂ U ∂ T знак равно α (∂ 2 u ∂ Икс 2 + ∂ 2 u ∂ Y 2 + ∂ 2 u ∂ Z 2) {\ Displaystyle {\ frac {\ partial u} {\ partial t}} = \ альфа \ left ({\ frac {\ partial ^ {2} u} {\ partial x ^ {2}}} + {\ frac {\ partial ^ {2} u} {\ partial y ^ {2}}} + { \ frac {\ partial ^ {2} u} {\ partial z ^ {2}}} \ right)}

с , известным как тепловое ядро .

Интегральная форма

Интегрируя формулу по всей поверхности материала S {\ displaystyle S}, мы приходим к интегральной форме закона Фурье:

∂ Q ∂ T знак равно — k {\ displaystyle {\ frac {\ partial Q} {\ partial t}} = — k}S {\ displaystyle \ scriptstyle S}∇ T ⋅ d S {\ displaystyle {\ nabla} T \ cdot \, dS}

где (включая единицу СИ ):

∂ Q ∂ t {\ displaystyle {\ big.} {\ Fr ac {\ partial Q} {\ partial t}} {\ big.}}- количество тепла, полученное на единица времени (в Вт), и
d S {\ displaystyle dS}Элемент ориентированной площади поверхности (в м)

Вышеупомянутое дифференциальное уравнение, когда интегрированный для однородного материала с одномерной геометрией между двумя конечными точками при постоянной, дает скорость теплового поток как:

Q Δ T знак равно — К A Δ T Δ Икс {\ Displaystyle {\ большой. } {\ frac {Q} {\ Delta t}} = — kA {\ frac {\ Delta T} {\ Delta x}}}

где

Δ t {\ displaystyle \ Delta t}- временной интервал, в течение которого количество тепла Q {\ displaystyle Q}проходит через поперечное сечение материала,

A {\ displaystyle A}- площадь поперечного сечения,

Δ T {\ displaystyle \ Delta T}- разница температур между концами,

Δ x {\ displaystyle \ Delta x}- расстояние между концами.

Этот закон лежит в основе вывода уравнения теплопроводности.

Переходная теплопроводность

Передача тепла на границе раздела

Передача тепла на границе раздела считается переходным тепловым потоком

Для анализа этой проблемы важно число Био, чтобы понять, как ведет себя система. Число Био определяется следующим образом: Bi = h L k {\ displaystyle {\ textit {Bi}} = {\ frac {hL} {k}}}Коэффициент теплопередачи h {\ displaystyle h}, вводится в эту формуле и измеряется в Дж м 2 с K {\ displaystyle {\ frac {J} {m ^ {2} sK}}}

Если система имеет число Био менее 0,1, ведет материал в соответствии с ньютоновским охлаждением, то есть с незначительным градиентом температуры внутри тела. Если число Био больше 0,1, система ведет себя как последовательное решение. Температурный профиль во времени может быть получен из уравнения

q = — h Δ T, {\ displaystyle q = -h \, \ Delta T,}

, которое становится

T — T f T i — T f = ехр ⁡ . {\ displaystyle {\ frac {T-T_ {f}} {T_ {i} -T_ {f}}} = \ operatorname {exp} \ left .}

Коэффициент теплопередачи, ч измеряется в Вт м 2 К {\ displaystyle \ mathrm {\ frac {W} {m ^ {2} K}} }, и представляет собой передачу тепла на границе раздела между двумя материалами. Это различается для каждого интерфейса и представляет собой поток понимания понимания «теплового интерфейса».

Решение серии может быть проанализировано с помощью номограммы. Номограмма имеет относительную температуру как координаты y и Фурье, которое вычисляется как

Fo = α t L 2. {\ displaystyle {\ textit {Fo}} = {\ frac {\ alpha t} {L ^ {2}} }.}

Число Био увеличивается с уменьшением числа Фурье. Есть пять шагов, чтобы определить температурный профиль с точки зрения времени.

Вычислить число Био
Определить, какая относительная глубина имеет значение, x или L.
Преобразовать время в число Фурье.
Преобразовать T i {\ displaystyle T_ {i}}относительно относительной температуры с граничными условиями.
В сравнении требуется указать точку для начала числа Био на номограмме.

МАНТИЙНЫЕ ПЛЮМЫ

Мантийные плюмы были открыты почти 50 лет назад Морганом и Вильсоном. Они представляют
собой долгоживущие (до ~100 млн лет) струи горячего вещества, поднимающегося со дна
мантии и прожигающего в горячих точках движущиеся литосферные плиты и континенты,
образуя большие магматические провинции.

В серии работ на численных моделях тепловой конвекции подробно исследовались режимы тепловой конвекции
при разной степени нагрева и разных контрастах вязкости (см. видео http://rjes.wdcb.ru/v16/2016ES000569/plumes-hr. html). Показано, что с увеличением нагрева и контраста вязкости течения в виде ячеек сменяются
на совокупность нисходящих и восходящих конвективных потоков в виде холодных высоковязких
погружающихся плит и горячих плюмов.

Регулярные конвективные ячейки имеют место при Ra < 105. При Ra ~ 106 восходящие и нисходящие потоки становятся узкими, подобно струям. При Ra ~ 107 струи начинают пульсировать с периодом ~1 млн лет. Среднее время жизни отдельного
плюма в виде пульсирующей струи около 100 млн лет. Во время подъема со дна мантии
нового плюма он имеет форму гриба, после достижения поверхности ножка плюма становится
пульсирующей струей. При дальнейшем росте числа Рэлея (соответствующем ранней Земле)
тепловая конвекция переходит в режим упорядоченно поднимающихся термиков (частей разорванных
плюмов). При еще большей интенсивности тепловая конвекция становится турбулентной,
при которой термики зарождаются и поднимаются хаотично. На зарождение и пространственное
расположение плюмов в мантии большое влияние оказывают находящиеся на дне мантии гигантские
горячие скопления эклогита под Африкой и Тихим океаном [].

В реальной Земле при высокой интенсивности тепловой конвекции только часть восходящих
конвективных потоков находится в плюмовом режиме. Погружающиеся литосферные плиты
благодаря вязкому сцеплению должны вовлекать в циркуляционное движение большую долю
вещества мантии. В результате только часть восходящих конвективных потоков принимает
форму плюмов, а другая часть остается в виде восходящих мантийных струй, доставляющих
вещество в срединно-океанические хребты.

Поскольку плюмы зарождаются на границе ядро–мантия, то ранее [] полагалось, что плюмы охлаждают ядро, а погружающиеся плиты охлаждают низы мантии.
При этом предполагалось, что тепловой поток из ядра примерно равен потоку тепла, выносимого
на поверхность плюмами. В работе [] была оценена скорость роста массы топографических возвышенностей, порождаемых мантийными
плюмами. Эта масса соответствует тепловому разуплотнению вещества в плюмах, по которому
находится поток тепла, выносимый плюмами на поверхность. Такая оценка давала для полного
потока тепла, выносимого мантийными плюмами, и соответственно для потока из ядра значение
2.4–3.5 ТВт. Однако это значение теплового потока ядра почти в 5 раз ниже значения,
следуемого из вышеприведенного полного теплового баланса Земли. В работе [] значение тепла, выносимого в горячих точках, принимается еще меньшим, до 1 ТВт.

При таком малом значении потока из ядра для объяснения наблюдаемого полного потока
тепла Земли приходилось даже принимать [], что якобы обилие радиоактивных изотопов урана и тория в Земле значительно превышает
обилие в хондритовых метеоритах. В работе [] для объяснения недостающего тепла строилась модель эволюции конвекции с более медленным
остыванием в прошлом благодаря более прочным сухим литосферным плитам, которые теплоэкранировали
мантию в ранней Земле.

В работах процесс переноса тепла плюмами внутри мантии рассчитывался непосредственно на численных
сферических моделях мантийной конвекции без жестких плит. При этом был сделан вывод,
что плюмы могут выносить на поверхность лишь часть тепла, поступающего из ядра. Однако,
что происходит с другой частью потока из ядра, оставалось неизвестным, и эта часть
тепла ядра была названа невидимой. Предполагалось, например, что в мантии есть много
мелких невидимых плюмов []. По сферической трехмерной модели мантийной конвекции без плит [] плюмы забирают 60% тепла, идущего из ядра, но, поднимаясь, при адиабатическом расширении
теряют много тепла и в результате выносят на поверхность только 1/4–1/5 часть тепла
ядра.

Теплопередача через плоскую стенку в граничащую среду (граничные условия третьего рода)

Теплопередача — это более сложный процесс теплообмена между жидкими и газообразными средами, разделенными твердой стенкой. Теплопередача включает в себя и процесс теплопроводности, и процесс теплоотдачи.

Коэффициент теплоотдачи α, Вт/(м2·К) — это количество теплоты, отдаваемое в единицу времени единицей поверхности при разности температур между поверхностью и окружающей средой, равной одному градусу.

Коэффициент теплопередачи k, Вт/(м2·К), характеризует тепловой поток, проходящий через единицу площади поверхности стенки при разности температуры сред, равной одному градусу:

Коэффициент теплопередачи для n слойной стенки:

Термические сопротивления теплоотдаче на внешних поверхностях стенки будут равны:

Тогда общее термическое сопротивление теплопередаче будет равно:

Температуры на поверхности стенки можно определить по формулам:

Применение показателя теплопроводности на практике

Тепловая энергия широко используется в технике и в быту. Все способы ее применения можно разделить на два способа:

энергетический (для преобразования тепла в механическую работу);
технологический (для направленного изменения свойств различных тел).

Процессы преобразования теплоты в работу изучаются в технической термодинамике, а процессы непосредственного использования — в теплопередаче.

Правильная организация рабочих процессов в теплоэнергетике, в химической, пищевой промышленности, в технике холода, в металлургии, в строительной индустрии, электротехнике невозможна без знания законов теплопередачи и учета показателей теплопроводности в различных элементах машин и аппаратов, химической и других отраслей промышленности.

Теория теплообмена широко применяется на практике. Например, в строительстве важны значения теплопроводности различных утеплителей (минеральная вата, пенополистирол и т.д.).

Применение теплопроводности

Сплит-охлаждение

Сплит-охлаждение — это метод охлаждения мелких капель расплавленных материалов путем быстрого контакта с холодной гладкой. Частицы подвергаются характерному процессу охлаждения с тепловым профилем на t = 0 {\ displaystyle t = 0}для начальной температуры как максимальная при x = 0 {\ displaystyle x = 0}и T = 0 {\ displaystyle T = 0}в x = — ∞ {\ displaystyle x = — \ infty}и x = ∞ {\ displaystyle x = \ infty}, тепловой профиль при t = ∞ {\ displaystyle t = \ infty}для — ∞ ≤ x ≤ ∞ {\ displaystyle — \ infty \ leq x \ leq \ infty}в качестве граничных условий. Сплетенное охлаждение быстро заканчивается установкой температуры и по форме аналогично уравнению гауссовой диффузии. Профиль температуры в зависимости от положения и времени этого типа охлаждения изменяется в зависимости от:

T (x, t) — T i = T i Δ X 2 π α t exp ⁡ (- x 2 4 α t) {\ displaystyle T (x, t) -T_ {i} = {\ frac {T_ {i} \ Delta X} {2 {\ sqrt {\ pi \ alpha t}}}} \ operatorname {exp} \ left (- {\ frac {x ^ {2}} {4 \ alpha t}} \ right)}

Охлаждение Splat — это фундаментальная, концепция адаптирована для практического использования в форме термического напыления. коэффициент температуропроводности, представленный как α {\ displaystyle \ alpha}, можно записать как α = k ρ C p {\ displaystyle \ alpha = {\ frac { k} {\ rho C_ {p}}}}. Это зависит от материала.

Закалка металла

Закалка металла — это переходный процесс теплопередачи с точки зрения преобразования температуры во времени (TTT). Можно управлять процессом охлаждения, чтобы отрегулировать фазу подходящего материала. Например, соответствующая закалка стали может преобразовать желаемую долю в ней аустенита в мартенсит, создавая очень твердый и прочный продукт. Чтобы добиться этого, выполнить закалку на «носу» (или эвтектика ) диаграмму TTT. Временные материалы различаются по своему числу Био, время, необходимое для охлаждения материала, или число Фурье на практике рассматривается. Для стали диапазон температур закалки обычно составляет от 600 ° C до 200 ° C. Чтобы контролировать время закалки и выбрать подходящую закалочную среду, необходимо определить число Фурье по желаемому времени закалки, относительному перепаду температуры и соответствующему району Био. Обычно правильные цифры считываются со стандартной номограммы. Вычислив коэффициент теплопередачи по этой жидкости, подходящей для данной среды.

Количественные характеристики переноса теплоты

Тепловым потоком или мощностью теплового потока называется количество тепловой энергии, передаваемое в единицу времени через произвольную поверхность. Обозначается Q, размерность .

В литературных источниках могут быть другие обозначения этой величины.

Плотность теплового потока – это количество тепловой энергии, передаваемой в единицу времени через единичную площадь поверхности. Обозначается q, размерность .

Эта величина характеризует интенсивность теплового потока с поверхности теплообмена.

Количество теплоты – количество тепловой энергии, передаваемое за произвольное время через произвольную поверхность. Обозначается , размерность Дж.

Плотность теплового потока q может быть определена по формуле, :

где F – площадь поверхности, м 2 ,

Если задана плотность теплового потока q,можно определить мощность теплового потока Q и количество переданной тепловой энергии

В общем случае тепловой поток может изменяться во времени и по пространственным координатам. Тогда соотношения будут представлены в дифференциальной форме

Важнейшими понятиями теории теплообмена является температурное поле и градиент температуры.

Температурное поле – это совокупность значений температур в пространстве и во времени.

В общем случае температурное поле записывается как некоторая функция трех координат и времени:

Различают стационарное и нестационарное температурное поле. Температурное поле, когда оно зависит от времени, называется нестационарнымтемпературным полем.

Стационарноетемпературное поле имеет место, когда температура t не зависит от времени (остается неизменным):

Если температура зависит от двух координат — имеем двумерное стационарное температурное поле

Если температура зависит только от одной координаты — имеем одномерное стационарное температурное поле

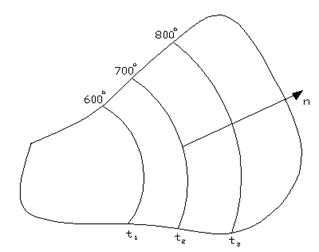
Рисунок 2.2 – Пример изотермических линий

Для иллюстрации температурного поля используются изотермические поверхности илиизотермические линии– это геометрическое место точек, температура в которых одинакова (см. рис. 2.2).

Характеристикой изменчивости температурного поля служит градиент температуры.

Градиент температуры grad t – это вектор, направленный по нормали к изотермической поверхности, и численно равный производной от температуры по этому направлению, т.е. по нормали. Обозначается , размерность .

Для одномерного температурного поля градиент температуры равен: .

Градиент температуры grad t направлен в сторону увеличения температуры, показывает направление тоста температуры:

Для линейного распределения температуры по толщине пластины, представленного на рис. 2.3 (одномерное температурное поле), градиент температуры может быть определен по формуле:

Пример: Определить градиент температуры, если известна температура поверхностей стенки ; и ее толщина ;

Решение: градиент температуры

Рисунок 2.3 – Распределение температуры по толщине стены

2.3 Закон Фурье – основной закон теплопроводности

Закон Фурье: вектор плотности теплового потока, передаваемого теплопроводностью , прямо пропорционален градиенту температур

где — коэффициент теплопроводности вещества, .

Знак «-» показывает, что вектор плотности теплового потока q и находятся на одной прямой линии, но направлены в разные стороны.

Тепловой поток всегда направлен в сторону уменьшения температур.

На практике широко используется выражение Фурье для одномерного температурного поля

Тепловой поток через произвольно ориентированную элементарную площадку dF равен скалярному произведению вектора плотности теплового потока на вектор элементарной площадки dF.

Количество теплоты, переданной через всю поверхность F, определяется интегрированием этого произведения по поверхности

Для постоянного во времени теплового потока q справедливо выражение

Коэффициент теплопроводности характеризует способность вещества проводить теплоту. Численно коэффициент теплопроводности равен плотности теплового потока при градиенте температуры 1 :

Например: коэффициент теплопроводности воздуха (воздух – лучший природный теплоизолятор), коэффициент теплопроводности водорода значительно больше .

В газах коэффициент теплопроводности зависит от скорости движения молекул и коэффициент теплопроводности возрастает при уменьшении массы молекулы, а также при увеличении температуры газа.

В металлах теплопроводность происходит в основном за счет теплового движения электронов (как и электропроводность).

Коэффициент теплопроводности жидкостей больше, чем у газов . Для неметаллов ; .

Вещества, у которых называются теплоизоляционными.

Приборы для измерения теплопроводности

Анализатор теплопроводности

Свойство теплопроводности любого газа при стандартных условиях давления и температуры является фиксированной величиной. Следовательно, это свойство известного эталонного газа или известных эталонных газовых смесей можно использовать для определенных сенсорных приложений, таких как анализатор теплопроводности.

Принцип работы этого прибора основан на мосте Уитстона, содержащем четыре нити, сопротивления которых согласованы. Всякий раз, когда определенный газ проходит через такую сеть нитей, их сопротивление изменяется из-за измененной теплопроводности нитей и, таким образом, изменения выходного напряжения на выходе моста Уитстона. Это выходное напряжение будет коррелировано с базой данных для идентификации пробы газа.

Датчик газа

Принцип теплопроводности газов также может использоваться для измерения концентрации газа в бинарной смеси газов.

Работа: если один и тот же газ присутствует вокруг всех нитей мостика Уитстона, то во всех нитях поддерживается одинаковая температура и, следовательно, одинаковое сопротивление; в результате получается сбалансированный мост Уитстона. Однако, если образец разнородного газа (или газовая смесь) проходит через один набор из двух нитей, а эталонный газ — через другой набор из двух нитей, мост Уитстона становится несбалансированным. И результат Выходное сетевое напряжение схемы будет коррелировано с базой данных для определения компонентов пробы газа.

Используя этот метод, можно идентифицировать многие неизвестные образцы газа, сравнивая их теплопроводность с другой эталонным газом с известной теплопроводностью. Наиболее часто используется эталонный газ — азот; как теплопроводность обычных обычных газов (кроме водорода и гелия).