Таблица квадратов натуральных чисел от 1 до 100

Таблица квадратов натуральных чисел 1 до 100

12 = 1 22 = 4 32 = 9 42 = 16 52 = 25 62 = 36 72 = 49 82 = 64 92 = 81 102 = 100	112 = 121 122 = 144 132 = 169 142 = 196 152 = 225 162 = 256 172 = 289 182 = 324 192 = 361 202 = 400	212 = 441 222 = 484 232 = 529 242 = 576 252 = 625 262 = 676 272 = 729 282 = 784 292 = 841 302 = 900	312 = 961 322 = 1024 332 = 1089 342 = 1156 352 = 1225 362 = 1296 372 = 1369 382 = 1444 392 = 1521 402 = 1600	412 = 1681 422 = 1764 432 = 1849 442 = 1936 452 = 2025 462 = 2116 472 = 2209 482 = 2304 492 = 2401 502 = 2500
512 = 2601 522 = 2704 532 = 2809 542 = 2916 552 = 3025 562 = 3136 572 = 3249 582 = 3364 592 = 3481 602 = 3600	612 = 3721 622 = 3844 632 = 3969 642 = 4096 652 = 4225 662 = 4356 672 = 4489 682 = 4624 692 = 4761 702 = 4900	712 = 5041 722 = 5184 732 = 5329 742 = 5476 752 = 5625 762 = 5776 772 = 5929 782 = 6084 792 = 6241 802 = 6400	812 = 6561 822 = 6724 832 = 6889 842 = 7056 852 = 7225 862 = 7396 872 = 7569 882 = 7744 892 = 7921 902 = 8100	912 = 8281 922 = 8464 932 = 8649 942 = 8836 952 = 9025 962 = 9216 972 = 9409 982 = 9604 992 = 9801 1002 = 10000

Игры для учебы таблицы умножения

Игровая форма – самая удобная для запоминания. Развлечения помогут понять ребенку, что математика – это весело. Играя вместе с детьми, родители получают способ, как помочь быстро выучить и запомнить таблицу умножения школьнику.

Снегопад

Делают из бумаги снежинки, в центре которых рисуют квадраты. Большие фигуры чертят на меньшие квадраты, по периметру их проставляют цифры. Ребенок собирает снежинки и считает количество квадратиков в каждой из них. Школьник быстро поймет, что умножать проще, чем пересчитывать каждую клетку.

Битва прямоугольников

Игра направлена на понимание законов умножения, выяснения площади прямоугольника. Берут 2 кубика, листы бумаги в клетку и фломастеры. Игроки выбирают цвет фломастера и начинают играть:

1. Первый кидает 2 кубика. Отмечает на листе прямоугольник или квадрат. Стороны фигур считает по клеткам, их будет по числам на кубиках.
2. В середине фигуры пишут площадь фигуры – количество клеток, которые она занимает.
3. Затем в игру вступает следующий игрок. Действия аналогичные.
4. Выигрывает тот, чьи фигуры занимают большую площадь листа.

Рыбалка

Игра подразумевает «вылавливание рыб» в количестве, кратном 2 или 3. Сначала подготавливают необходимые материалы:

• большой лист клетчатой бумаги с нарисованными рыбками и животными (или находят готовый);
• карточки – рыбки;
• кубик;
• фишки;
• листок бумаги с ручкой.

Действия игроков:

1. Бросают кубик, перемещая фишки по полю. Как только на клетку выпадает рыбка, игрок кладет себе количество «рыбок» – карточек по числу на нарисованной фигурке.
2. Если фишка останавливается на изображении животного, игрок не получает рыбок.
3. В конце игры подсчитывают «улов».

Карточки

На обычных квадратиках из картона пишут примеры умножения без ответов. Перемешивают и дают вытягивать ребенку. Если школьник ответил правильно, он забирает карточку, неверный ответ – возвращает в коробку. Разнообразит игру ответ на время, выдача призов за «рекорд дня» и пр. За неверные ответы тоже делать «наказание» – прочитать стишок или убрать игрушки.

Декартова таблица умножения

Декартовы таблицы умножения — это еще один способ представления таблиц умножения. Чтобы построить его, мы сначала строим таблица с 11 строками и 11 столбцамиs, пронумеровав по следующему рисунку:

×	1	2	3	4	5	6	7	8	9	10
1
2
3
4
5
6
7
8
9
10

Теперь, чтобы найти элементы, занимающие каждое место в таблице, мы умножаем значение строки на значение столбца:

Декартова таблица умножения

Записав только результаты произведений, мы получим следующую декартову таблицу:

×	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50
6	6	12	18	24	30	36	42	48	54	60
7	7	14	21	28	35	42	49	56	63	70
8	8	16	24	32	40	48	56	64	72	80
9	9	18	27	36	45	54	63	72	81	90
10	10	20	30	40	50	60	70	80	90	100

Квадратное уравнение и формула разложения квадратного трехчлена на множители

Пусть квадратное уравнение имеет вид:

Тогда дискриминант находят по формуле:

Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:

Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:

Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения может быть вычислено по формуле:

Парабола

График параболы задается квадратичной функцией:

При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:

Игрек вершины параболы:

Таблица умножения и деления

Файлы: 

Вложение	Размер
Таблица умножения и деления, картинка с пояснением	74.46 КБ
Таблица умножения и деления	105.44 КБ
Таблица умножения и деления без ответов	19.53 КБ

Чтобы скачать и рапсечатать таблицу умножения и деления, используйте ссылки выше или нажмите правую кнопку мышки над картинками ниже и выберите «сохранить картинку как».

Таблица умножения и деления без ответов.

Тип:

материал

• Все тесты. Проверка. Тренажер таблицы умножения.
  • Умножение на 1. Все тесты.
    • Умножение на 1 (ввести ответ
    • Умножение на 1 (двусторонние карточки
    • Умножение на 1 (двусторонние карточки
    • Умножение на 1 (карточки
    • Умножение на 1 (карточки
    • Умножение на 1 (найти ответ
    • Умножение на 1 (найти ответ
  • Умножение на 2. Все тесты.
    • Умножение на 2 (ввести ответ
    • Умножение на 2 (ввести ответ
    • Умножение на 2 (двусторонние карточки
    • Умножение на 2 (двусторонние карточки
    • Умножение на 2 (карточки
    • Умножение на 2 (карточки
    • Умножение на 2 (найти ответ
    • Умножение на 2 (найти ответ
  • Умножение на 3. Все тесты.
    • Умножение на 3 (ввести ответ
    • Умножение на 3 (ввести ответ
    • Умножение на 3 (двусторонние карточки
    • Умножение на 3 (двусторонние карточки
    • Умножение на 3 (карточки
    • Умножение на 3 (карточки
    • Умножение на 3 (найти ответ
    • Умножение на 3 (найти ответ
  • Умножение на 4. Все тесты.
    • Умножение на 4 (ввести ответ
    • Умножение на 4 (ввести ответ
    • Умножение на 4 (двусторонние карточки
    • Умножение на 4 (двусторонние карточки
    • Умножение на 4 (карточки
    • Умножение на 4 (карточки
    • Умножение на 4 (найти ответ
    • Умножение на 4 (найти ответ
  • Умножение на 5. Все тесты.
    • Умножение на 5 (ввести ответ
    • Умножение на 5 (ввести ответ
    • Умножение на 5 (двусторонние карточки
    • Умножение на 5 (двусторонние карточки
    • Умножение на 5 (карточки
    • Умножение на 5 (карточки
    • Умножение на 5 (найти ответ
    • Умножение на 5 (найти ответ
  • Умножение на 6. Все тесты.
    • Умножение на 6 (ввести ответ
    • Умножение на 6 (ввести ответ
    • Умножение на 6 (двусторонние карточки
    • Умножение на 6 (двусторонние карточки
    • Умножение на 6 (карточки
    • Умножение на 6 (карточки
    • Умножение на 6 (найти ответ
    • Умножение на 6 (найти ответ
  • Умножение на 7. Все тесты.
    • Умножение на 7 (ввести ответ
    • Умножение на 7 (ввести ответ
    • Умножение на 7 (двусторонние карточки
    • Умножение на 7 (двусторонние карточки
    • Умножение на 7 (карточки
    • Умножение на 7 (карточки
    • Умножение на 7 (найти ответ
    • Умножение на 7 (найти ответ
  • Умножение на 8. Все тесты.
    • Умножение на 8 (ввести ответ
    • Умножение на 8 (ввести ответ
    • Умножение на 8 (двусторонние карточки
    • Умножение на 8 (двусторонние карточки
    • Умножение на 8 (карточки
    • Умножение на 8 (карточки
    • Умножение на 8 (найти ответ
    • Умножение на 8 (найти ответ
  • Умножение на 9. Все тесты.
    • Умножение на 9 (ввести ответ
    • Умножение на 9 (ввести ответ
    • Умножение на 9 (двусторонние карточки
    • Умножение на 9 (двусторонние карточки
    • Умножение на 9 (карточки
    • Умножение на 9 (карточки
    • Умножение на 9 (найти ответ
    • Умножение на 9 (найти ответ
  • Умножение на 10. Все тесты.
    • Умножение на 10 (ввести ответ
    • Умножение на 10 (ввести ответ
    • Умножение на 10 (двусторонние карточки
    • Умножение на 10 (двусторонние карточки
    • Умножение на 10 (карточки
    • Умножение на 10 (карточки
    • Умножение на 10 (найти ответ
    • Умножение на 10 (найти ответ
  • Тест-тренажер онлайн! Таблица умножения
  • Тест-тренажер онлайн! Таблица умножения. 10 вопросов.
• Умножение
  • Умножение на 1
  • Умножение на 2
  • Умножение на 3
  • Умножение на 4
  • Умножение на 5
  • Умножение на 6
  • Умножение на 7
  • Умножение на 8
  • Умножение на 9
  • Умножение на 10
• Таблица умножения до 20 и до 100
• Таблица умножения и деления
• Умножение в столбик
• Еще
  • Таблица сложения
  • Линейка
  • Без ответов
  • Таблица кубов
  • Таблица степеней
  • Калькуляторы
    • Умножение
    • Найти неизвестный множитель
    • Деление
    • Сложение
    • Кубов
  • Шпаргалка

Таблица степеней первых натуральных чисел

Начнем с таблицы для нахождения степеней натуральных чисел от $2$ до $12$ по степеням от $1$ до $10$ (таблица 1)

Обратите внимание, что мы не приводим степени $1$, потому что единица будет равна самой себе в любой степени

Нужно найти значения из этой таблицы следующим образом: В первом столбце находим число, степень которого нас интересует. Запоминаем номер этой строки. Итак, в первом члене находим показатель степени и запоминаем найденный столбец. Пересечение найденной строки и столбца даст нам ответ.

Тренируйте свой мозг с удовольствием Развивайте память, внимание и мышление с помощью онлайн-тренажеров. Выберите программуПример 1. Найдите $8^7$

Найдите $8^7$

Решение.

Находим число $8$ в первом столбце: получаем восьмую строку.

Находим число $7$ в первой строке: получаем восьмой столбец.

Мы видим, что число $2097152$ находится на их пересечении. Поэтому

$8^7=2097152$

Игры при изучении таблицы умножения

Карточки

Чтобы использовать для изучения таблицы умножения карточки нужно подготовить их с примерами без ответов. Дальше вы их перемешиваете, и ребёнок тянет каждый раз по одной карточке. Он должен сказать правильный ответ на указанный пример, в этом случае карточку нужно отложить в сторону. Если ребёнок не ответил или дал неправильный ответ на карточку, то она возвращается в стопку.

К такой игре можно вносить изменения, например, давать ответы в течение определенного количества времени, или подсчитывать сколько каждый день был правильных ответов, чтобы ребёнок хотел увеличить количество правильных ответов.

Также за неправильный ответ на пример можно давать ребёнку небольшое задание

Например, рассказать какое-нибудь стихотворение или прибраться у себя в комнате. А вот тогда, когда ребёнок ответил на вопросы по всем карточкам, стоит вручить ему небольшой, но приятный подарок.

Когда ребёнок освоил основные правила и примеры таблицы умножения, можно организовать обратную игру с карточками. Вы также готовите карточки, только вместо примеров вы на них пишите ответы, например число 20. Ребёнок же должен вам назвать 2-3 примера, то есть те числа, которые при умножении дадут результат 20, например 2 умножить на 10, или 4 умножить на 5.

Для наглядности можно использовать примеры из жизни, и обсуждать с ребенком вещи, которыми он интересуется. Например, можно спросить, сколько колёс нужно 4 машинкам. Также можно взять палочки для счёта, фломастеры или кубики, которые также можно складывать и умножать.

Если ребёнок совсем не может выучить какой-то пример по умножению, и постоянно путает ответ, можно упростить процесс запоминания и использовать лёгкие стихи. Например, 8 медведей рубили дрова, 8 на 9 равно 72. Так ребенку будет легче постепенно запомнить пример из жизни.

Таблица пифагора от 1 до 20

×	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
2	2	4	6	8	10	12	14	16	18	20	22	24	26	28	30	32	34	36	38	40
3	3	6	9	12	15	18	21	24	27	30	33	36	39	42	45	48	51	54	57	60
4	4	8	12	16	20	24	28	32	36	40	44	48	52	56	60	64	68	72	76	80
5	5	10	15	20	25	30	35	40	45	50	55	60	65	70	75	80	85	90	95	100
6	6	12	18	24	30	36	42	48	54	60	66	72	78	84	90	96	102	108	114	120
7	7	14	21	28	35	42	49	56	63	70	77	84	91	98	105	112	119	126	133	140
8	8	16	24	32	40	48	56	64	72	80	88	96	104	112	120	128	136	144	152	160
9	9	18	27	36	45	54	63	72	81	90	99	108	117	126	135	144	153	162	171	180
10	10	20	30	40	50	60	70	80	90	100	110	120	130	140	150	160	170	180	190	200
11	11	22	33	44	55	66	77	88	99	110	121	132	143	154	165	176	187	198	209	220
12	12	24	36	48	60	72	84	96	108	120	132	144	156	168	180	192	204	216	228	240
13	13	26	39	52	65	78	91	104	117	130	143	156	169	182	195	208	221	234	247	260
14	14	28	42	56	70	84	98	112	126	140	154	168	182	196	210	224	238	252	266	280
15	15	30	45	60	75	90	105	120	135	150	165	180	195	210	225	240	255	270	285	300
16	16	32	48	64	80	96	112	128	144	160	176	192	208	224	240	256	272	288	304	320
17	17	34	51	68	85	102	119	136	153	170	187	204	221	238	255	272	289	306	323	340
18	18	36	54	72	90	108	126	144	162	180	198	216	234	252	270	288	306	324	342	360
19	19	38	57	76	95	114	133	152	171	190	209	228	247	266	285	304	323	342	361	380
20	20	40	60	80	100	120	140	160	180	200	220	240	260	280	300	320	340	360	380	400

Превращаем 100 примеров в 36

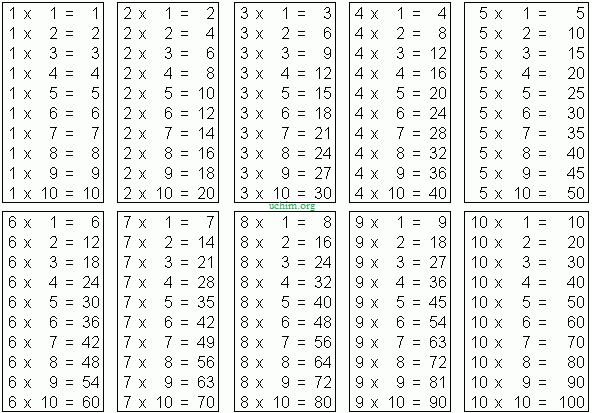
Таблица умножения на обратной стороне большинства тетрадок выглядит так:

На то, чтобы её выучить, может уйти целое лето. Понятно, что механическое заучивание правильных ответов к сотне примеров — самый трудоёмкий способ запомнить результаты умножения чисел до 10 друг на друга.

Процесс в разы ускоряется, когда мы показываем, как все эти 100 сочетаний можно сократить до 36. В этом деле куда более удачным наглядным пособием служит таблица Пифагора:

На её примере уже можно показать принципы умножения через площади небольших прямоугольников:

• 3 * 5 = 15, потому что в прямоугольник со сторонами длиной 3 и 5 клеточек помещается 15 маленьких квадратиков (считаем их вместе, чтобы убедиться).

• 5 * 3 = 15 по той же причине (считаем вместе).

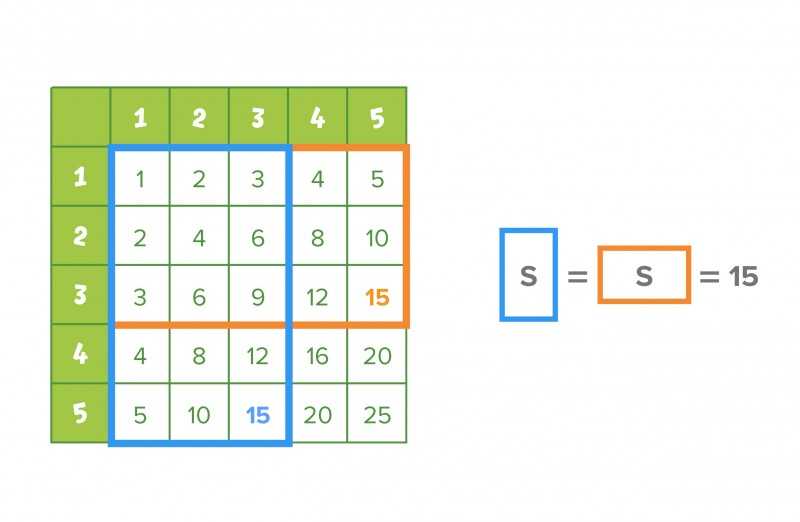
Здесь же наглядно демонстрируем свойство коммутативности: от перестановки мест множителей произведение не меняется. Разумеется, название этого свойства лучше придержать до Хеллоуина, чтобы не пугать никого раньше времени

Из-за этого таблица Пифагора симметрична относительно своей диагонали, поэтому из 100 примеров для запоминания остаётся уже 55: сама диагональ с значениями 1, 4, 9, …, 100 и всё, что находится выше или ниже.

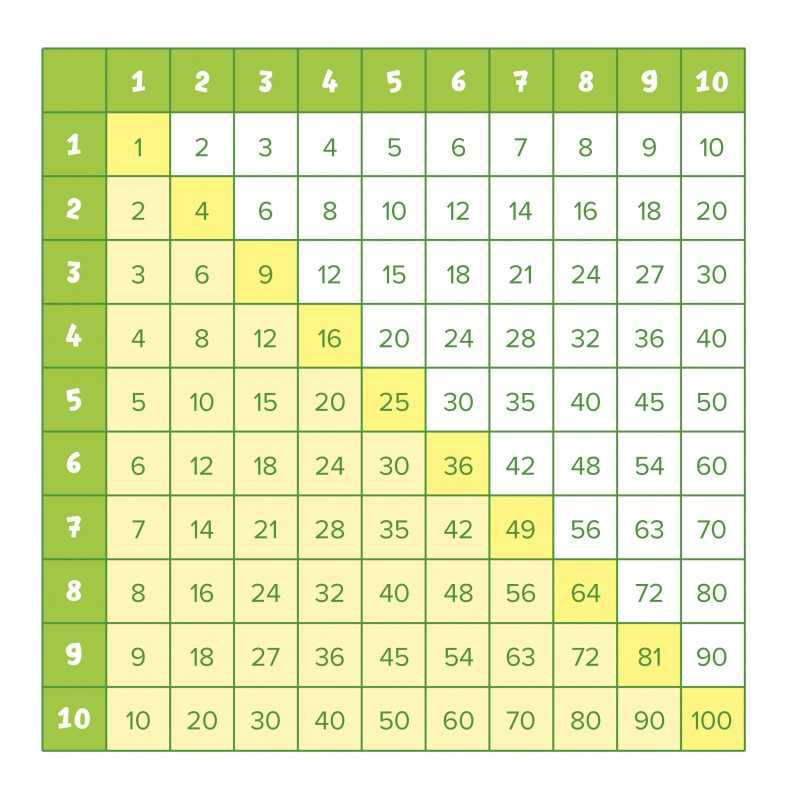
Это открытие можно сделать самостоятельно, заполнив часть пустой таблицы Пифагора, в которой изначально отмечены только множители:

 

Ребёнок может начать заполнять её, даже если ещё не знает правил умножения — складывать ведь он уже умеет, поэтому без труда посчитает сначала 2 + 2, потом 4 + 2, потом 6 + 2, и так, вплоть до 20. Потом ряд с тройками, и так далее.

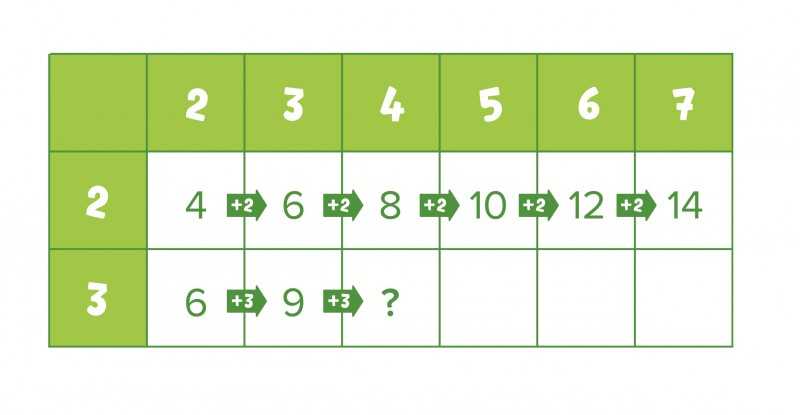
Заполнив только часть таблицы (например, квадрат 6 * 6 клеток), уже можно увидеть одинаковые числа и понять, что зубрить её целиком совсем не нужно.

После этого на той же таблице Пифагора демонстрируем два принципа, позволяющие «автоматизировать» ещё 19 операций на умножение: умножение на 1 и умножение на 10:

• Если число умножить на единицу, оно никак не меняется.

• Если число умножить на 10, у него появляется ноль на конце.

Отнимаем от оставшихся ранее 55 примеров на умножение ещё 19 «автоматизированных» и получаем всего 36 сочетаний, которые нужно запомнить. Почти втрое меньше, чем предлагают нам на обложках тетрадок!

Уже легче, не так ли?

Таблица квадратов натуральных чисел 200 до 300

2012 = 40 401 2022 = 40 804 2032 = 41 209 2042 = 41 616 2052 = 42 025 2062 = 42 436 2072 = 42 849 2082 = 43 264 2092 = 43 681 2102 = 44 100	2112 = 44 521 2122 = 44 944 2132 = 45 369 2142 = 45 796 2152 = 46 225 2162 = 46 656 2172 = 47 089 2182 = 47 524 2192 = 47 961 2202 = 48 400	2212 = 48 841 2222 = 49 284 2232 = 49 729 2242 = 50 176 2252 = 50 625 2262 = 51 076 2272 = 51 529 2282 = 51 984 2292 = 52 441 2302 = 52 900	2312 = 53 361 2322 = 53 824 2332 = 54 289 2342 = 54 756 2352 = 55 225 2362 = 55 696 2372 = 56 169 2382 = 56 644 2392 = 57 121 2402 = 57 600	2412 = 58 081 2422 = 58 564 2432 = 59 049 2442 = 59 536 2452 = 60 025 2462 = 60 516 2472 = 61 009 2482 = 61 504 2492 = 62 001 2502 = 62 500
2512 = 63 001 2522 = 63 504 2532 = 64 009 2542 = 64 516 2552 = 65 025 2562 = 65 536 2572 = 66 049 2582 = 66 564 2592 = 67 081 2602 = 67 600	2612 = 68 121 2622 = 68 644 2632 = 69 169 2642 = 69 696 2652 = 70 225 2662 = 70 756 2672 = 71 289 2682 = 71 824 2692 = 72 361 2702 = 72 900	2712 = 73 441 2722 = 73 984 2732 = 74 529 2742 = 75 076 2752 = 75 625 2762 = 76 176 2772 = 76 729 2782 = 77 284 2792 = 77 841 2802 = 78 400	2812 = 78 961 2822 = 79 524 2832 = 80 089 2842 = 80 656 2852 = 81 225 2862 = 81 796 2872 = 82 369 2882 = 82 944 2892 = 83 521 2902 = 84 100	2912 = 84 681 2922 = 85 264 2932 = 85 849 2942 = 86 436 2952 = 87 025 2962 = 87 616 2972 = 88 209 2982 = 88 804 2992 = 89 401 3002 = 90 000

Учить таблицу умножения – игра

Попробуйте нашу обучающую электронную игру. Используя её, вы уже завтра сможете решать математические задачи в классе у доски без ответов, не прибегая к табличке, чтобы умножить числа. Стоит только начать играть, и уже минут через 40 будет отличный результат. А для закрепления результата тренируйтесь несколько раз, не забывая о перерывах. В идеале – каждый день (сохраните страницу, чтобы не потерять). Игровая форма тренажера подходит как для мальчиков, так и для девочек.

Таблица умножения – таблица, где строки и столбцы озаглавлены множителями (1, 2, 3, 4, 5…), а ячейки таблицы содержат их произведение. Применяется таблица для обучения умножению. Здесь есть игра и картинка для печати.

Как на калькуляторе посчитать в квадрате?

Найти с помощью калькулятора квадрат числа 11052:

1. Шаг 1. Набрать на калькуляторе число, которое нужно возвести в квадрат. В нашем случае — это число 11052.
2. Шаг 2. Нажать кнопку умножить: «*».
3. Шаг 3. Нажать кнопку равно: «=». Полученное число и будет квадратом числа.

Чтобы найти квадрат числа, введите это число в калькулятор, а затем нажмите кнопку “x 2 “. “1/X” – деление числа 1 на текущее число. Чтобы разделить число 1 на текущее число, введите это число в калькулятор, а затем нажмите кнопку “1/X”.”%” – вычисление процента от числа.” √” – вычисление квадратного корня. Чтобы найти квадратный корень числа, введите это число в калькулятор, а затем нажмите кнопку “√”.

Дополнительные формулы сокращенного умножения

Есть три основные дополнительные ФСУ – это бином Ньютона, формула возведения в квадрат суммы трех, четырех и более слагаемых, а также формула разности n-ых степеней двух слагаемых. Коротко о каждой из них.

Бином Ньютона

Бином Ньютона – это формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Выглядит она следующим образом:

Ck в степени n – это биноминальные коэффициенты, стоящие в строке под номером n в треугольнике Паскаля. Вычисляются эти коэффициенты по формуле:

Иначе говоря, ФСУ для квадрата и куба разности и суммы являются частными случаями формулы бинома Ньютона при n=2 и n=3 соответственно.

Однако может быть так, что слагаемых в сумме, которую нужно возвести в степень, больше, чем два. В таком случае подойдет формула квадрата суммы трех, четырех и более слагаемых.

Формула возведения в квадрат суммы трех, четырех и более слагаемых

Как и было сказано, формула возведения в квадрат суммы трех, четырех и более слагаемых нужна, когда слагаемых в сумме, которую нужно возвести в степень, больше, чем два.

Выглядит она так:

Читать и запоминать эту формулу нужно следующим образом: квадрат суммы n слагаемых равен сумме квадратов всех слагаемых и удвоенных произведений всех возможных пар этих слагаемых.

Формула разности n-ых степеней двух слагаемых

И последняя формула – это формула разности n-ых степеней двух слагаемых, выглядящая вот так:

Как правило, данную формулу разделяют на две отдельные: для четных и нечетных степеней.

Формула для четных показателей 2m:

Формула для нечетных показателей 2m + 1:

Несложно догадаться, что ФСУ разности квадратов и кубов являются частными случаями данной формулы при n=2 и n=3 соответственно. А для разности кубов b заменяется на –b.

Рассмотренные нами ФСУ и дополнительные ФСУ обязательно помогут вам быстрее справляться с математическими задачами и занимать свой мозг полезной деятельностью.

Вопросы и ответы

И напоследок несколько ответов на часто задаваемые вопросы.

Для чего нужны формулы сокращенного умножения?

Формулы сокращенного умножения нужны, чтобы упростить и ускорить вычисления, а также для улучшения наглядности и понимания математических выражений.

В настоящее время ФСУ широко используются в образовании и науке, а также в практической жизни. Они применяются в различных областях, таких как математика, физика, химия и инженерия, плюс могут применяться к решению различных задач, например, в области финансов, менеджмента и исследования данных.

Как появились формулы сокращенного умножения?

Формулы сокращенного умножения появились в результате исследований математиков в области алгебры и арифметики и основаны на использовании их свойств, таких как коммутативность, ассоциативность и дистрибутивность.

Если обратиться к истории, можно узнать, что такими формулами пользовались еще в Древнем Вавилоне и Древнем Египте. Первым же, кто доказал математическую закономерность квадрата суммы, был древнегреческий ученый Евклид, живший в III веке до н.э. А на общепринятом языке математические формулы были обоснованы Исааком Ньютоном.

Сколько всего формул сокращенного умножения?

Не существует точного количества формул сокращенного умножения, т.к. их можно создавать неограниченное количество. Но в основном изучают и используют семь основных формул. Это квадрат суммы, квадрат разности, разность квадратов, сумма кубов, разность кубов, куб суммы и куб разности. Также распространено применения трех дополнительных ФСУ, таких как бином Ньютона, формула возведения в квадрат суммы трех, четырех и более слагаемых и формула разности n-ых степеней двух слагаемых.

Почему формулы сокращенного умножения изучают на алгебре в 7 классе?

Формулы сокращенного умножения изучаются на алгебре в 7 классе, потому что именно на этом этапе школьники знакомятся с понятием многочлена и действиям с ним. Кроме того, ФСУ являются важным и основным инструментом для решения математических задач и упрощения вычислений.

Формулы помогают ученикам развить навыки в решении простых задач, а также дают им навыки для решения более сложных задач в будущем, что в перспективе способно помочь молодым людям в их дальнейшем обучении и карьере.

Можно ли не использовать формулы сокращенного умножения?

Конечно, при решении математических задач можно и не использовать формулы сокращенного умножения. Однако без них процесс решения может оказаться очень трудоемким и долгим. ФСУ же заметно упрощают его и помогают справляться с заданиями намного быстрее.

Помимо прочего, ФСУ входят в обязательную школьную программу, вследствие чего преподаватели часто требуют от учеников, во-первых, знать эти формулы наизусть, а во-вторых, решать задания именно с их помощью.

Геометрия на плоскости (планиметрия)

Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника:

Площадь треугольника через две стороны и угол между ними:

Площадь треугольника через сторону и высоту опущенную на неё:

Полупериметр треугольника находится по следующей формуле:

Формула Герона для площади треугольника:

Площадь треугольника через радиус описанной окружности:

Формула медианы:

Свойство биссектрисы:

Формулы биссектрисы:

Основное свойство высот треугольника:

Формула высоты:

Еще одно полезное свойство высот треугольника:

Теорема косинусов:

Теорема синусов:

Радиус окружности, вписанной в правильный треугольник:

Радиус окружности, описанной около правильного треугольника:

Площадь правильного треугольника:

Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):

Радиус окружности, вписанной в прямоугольный треугольник:

Радиус окружности, описанной вокруг прямоугольного треугольника:

Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:

Длина средней линии трапеции:

Площадь трапеции:

Площадь параллелограмма через сторону и высоту опущенную на неё:

Площадь параллелограмма через две стороны и угол между ними:

Площадь квадрата через длину его стороны:

Площадь квадрата через длину его диагонали:

Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):

Площадь прямоугольника через две смежные стороны:

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):

Свойство касательных:

Свойство хорды:

Теорема о пропорциональных отрезках хорд:

Теорема о касательной и секущей:

Теорема о двух секущих:

Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):

Свойство центральных углов и хорд:

Свойство центральных углов и секущих:

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:

Сумма углов n-угольника:

Центральный угол правильного n-угольника:

Площадь правильного n-угольника:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь сектора:

Площадь кольца:

Площадь кругового сегмента:

Таблица квадратов двузначных чисел

0 2 = 0 1 2 = 1 2 2 = 4 3 2 = 9 4 2 = 16 5 2 = 25 6 2 = 36 7 2 = 49 8 2 = 64 9 2 = 81	10 2 = 100 11 2 = 121 12 2 = 144 13 2 = 169 14 2 = 196 15 2 = 225 16 2 = 256 17 2 = 289 18 2 = 324 19 2 = 361	20 2 = 400 21 2 = 441 22 2 = 484 23 2 = 529 24 2 = 576 25 2 = 625 26 2 = 676 27 2 = 729 28 2 = 784 29 2 = 841	30 2 = 900 31 2 = 961 32 2 = 1024 33 2 = 1089 34 2 = 1156 35 2 = 1225 36 2 = 1296 37 2 = 1369 38 2 = 1444 39 2 = 1521	40 2 = 1600 41 2 = 1681 42 2 = 1764 43 2 = 1849 44 2 = 1936 45 2 = 2025 46 2 = 2116 47 2 = 2209 48 2 = 2304 49 2 = 2401
50 2 = 2500 51 2 = 2601 52 2 = 2704 53 2 = 2809 54 2 = 2916 55 2 = 3025 56 2 = 3136 57 2 = 3249 58 2 = 3364 59 2 = 3481	60 2 = 3600 61 2 = 3721 62 2 = 3844 63 2 = 3969 64 2 = 4096 65 2 = 4225 66 2 = 4356 67 2 = 4489 68 2 = 4624 69 2 = 4761	70 2 = 4900 71 2 = 5041 72 2 = 5184 73 2 = 5329 74 2 = 5476 75 2 = 5625 76 2 = 5776 77 2 = 5929 78 2 = 6084 79 2 = 6241	80 2 = 6400 81 2 = 6561 82 2 = 6724 83 2 = 6889 84 2 = 7056 85 2 = 7225 86 2 = 7396 87 2 = 7569 88 2 = 7744 89 2 = 7921	90 2 = 8 100 91 2 = 8281 92 2 = 8464 93 2 = 8649 94 2 = 8836 95 2 = 9025 96 2 = 9216 97 2 = 9409 98 2 = 9604 99 2 = 9801

02=0=0

Таблица квадратов натуральных чисел от $10$ до $99$

Другой популярной таблицей является таблица квадратов чисел от $10$ до $99$ (табл. 4), то есть всех десятичных чисел.

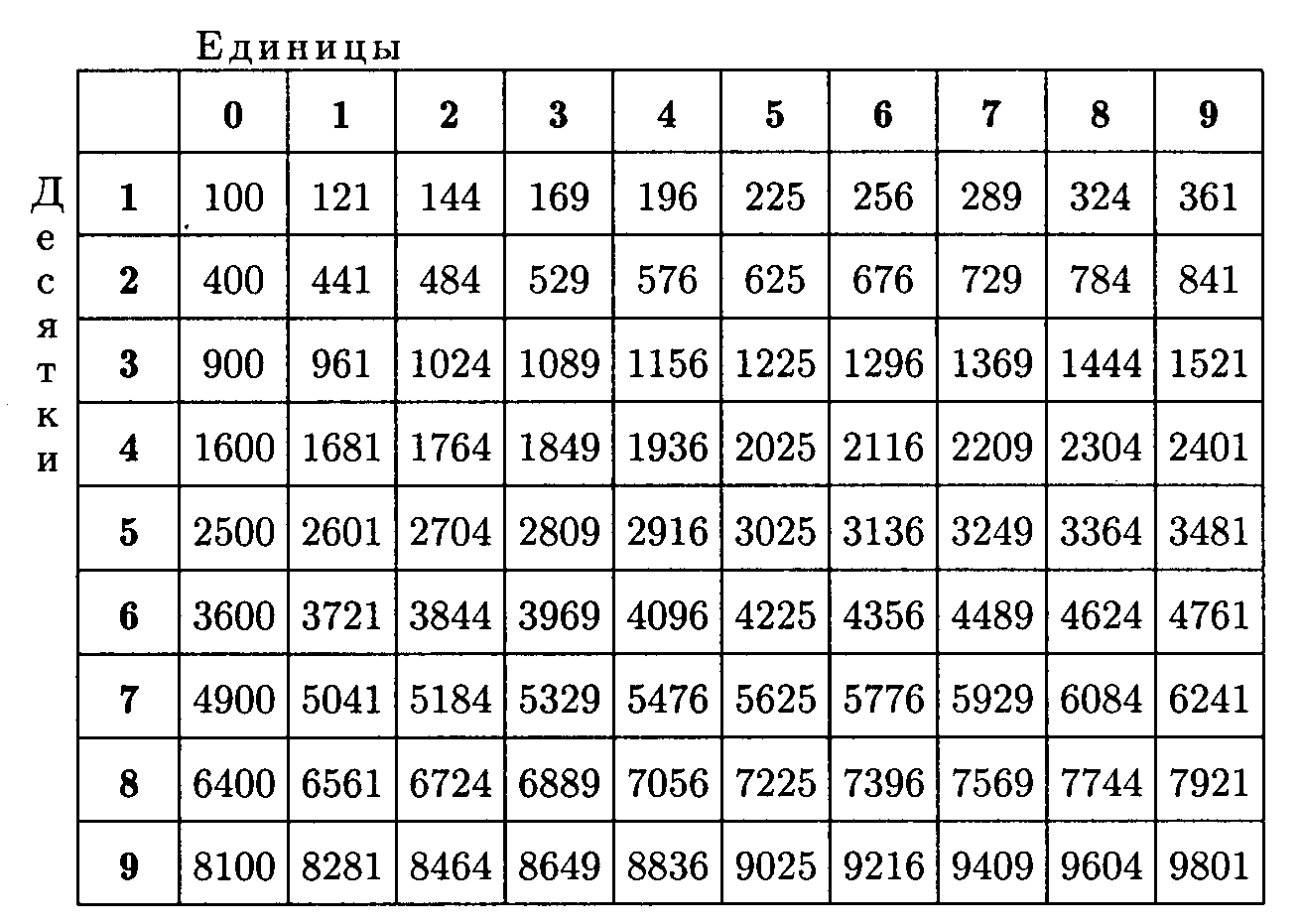
Необходимо найти значения из этой таблицы следующим образом: В первом столбце находим количество десятков интересующего нас числа. Запомните число в этой строке. Итак, в первом слагаемом находим количество единиц интересующего числа и запоминаем найденный столбец. Пересечение найденной строки и столбца даст нам ответ.

Пример 3

Найдите $37^2$

Решение.

Находим число $3$ в первом столбце: получаем 4 строку.

Находим число $7$ в первой строке: получаем восьмой столбец.

Мы видим, что на их пересечении число $1369$. Поэтому

37$^2=1369$

Кто создал таблицу квадратов?

Иногда изобретение таблицы умножения приписывают Пифагору, в честь которого она названа в различных языках, включая французский, итальянский и русский. В 493 году Викторий Аквитанский создал таблицу из 98 столбцов, которая представляла в римских числах результат перемножения чисел от 2 до 50.

Пифагор изучил в Египте, а потом привез в Европу цифровые матрицы, известные ранее только узкому кругу избранных. В адаптированном варианте тайные таблицы дошли до наших дней и ныне известны как квадрат Пифагора. Пифагор не оставил после себя собрания сочинений, он держал своё учение в тайне и передавал ученикам устно. Учёные утверждают, что квадрат Пифагора дает возможность точно определить сильные и слабые стороны человеческой натуры.

Таблица степеней чисел до 100 в кубе

Часто в примерах требуется возвести двузначное число в куб. Сделать это будет проще со следующей таблицей:

_{*Для лучшего понимания примеры подсвечены голубым.}

Пример 4. Работаем с таблицей натуральных степеней чисел в кубе.

Задача. Найти 453.

Решение. Делим число на десятки и единицы. Находим 4 десятка (левый столбец) и 5 единиц (верхняя полоса) и ищем значение их пересечения.

Ответ. 157464.

Пример 5. Вычисляем квадрат по таблице.

Задача. Найти 403.

Решение. Найти значение можно двумя способами. Первый — руководствуясь таблицей. 4 — десятки, 0 — единицы. Ищем пересечение этих цифр. Результат — 6400. Второй способ: возводим 4 в куб и прибавляем два нуля (т.к. 10 в кубе = 100). 43=64. Прибавляем «00» и получаем идентичный ответ: 6400.

Ответ. 6400.

Пользоваться таблицами степеней по математике несложно. Но только в том случае, если речь идет о небольших цифрах. В длинных примерах, состоящих из множества чисел в степенях, можно использовать онлайн калькуляторы. Это позволит избежать ошибок, которые могут быть вызваны просмотром не той ячейки.