Ii. молекулярная физика

Уравнение идеального газа в термодинамике

Понятие «Идеальный газ» в термодинамике используется для обозначения некой идеализации по аналогии с материальной точкой.

Молекулы элемента в этом случае являются материальными точками. При этом соударения частиц признаются абсолютно упругими и постоянными. Для решения многих задач в термодинамике реальные газы целесообразно принимать за идеальные.

Благодаря этому появляется возможность составлять формулы в упрощенном виде, поскольку не приходится вводить в уравнение большое количество новых величин.

Итак, все молекулы идеального газа находятся в движении. Для того чтобы определить с какой скоростью и массой они движутся, можно применить уравнение состояния идеального тела.

Формула

Формула Клайперона-Менделеева имеет следующий вид:

Где:

m – масса исследуемого газа;

R – универсальная постоянная, равная 8,3144598 Дж/(моль*кг)

M – начальная молекулярная масса.

Для вычисления точной массы идеального газа используется произведение его объема и плотности. Формула выглядит так:

\

Между давлением газа и средней кинетической энергией существует некая взаимосвязь. В термодинамике ее называют основным уравнением молекулярно-кинетической теории и представляют в следующем виде:

\

Где:

n – концентрация молекул, находящихся в движении, по отношению к объему газа;

E – коэффициент средней кинетической энергии.

Определение

Параметры состояния, или термодинамические параметры, — это ряд физических величин, которые все вместе и каждая в отдельности могут дать характеристику наблюдаемой системе. К ним относятся такие понятия, как:

• температура и давление;
• концентрация, магнитная индукция;
• энтропия;
• энтальпия;
• энергии Гиббса и Гельмгольца и многие другие.

Выделяют интенсивные и экстенсивные параметры. Экстенсивными называются те, которые находятся в прямой зависимости от массы термодинамической системы, а интенсивными — которые определяются другими критериями. Не все параметры одинаково независимы, поэтому для того, чтобы вычислить равновесное состояние системы, необходимо определять сразу несколько параметров.

Кроме того, среди физиков существуют некоторые терминологические разногласия. Одна и та же физическая характеристика у разных авторов может называться то процессом, то координатой, то величиной, то параметром, а то и просто свойством. Все зависит от того, в каком контенте ученый ее использует. Но в некоторых случаях существуют стандартизированные рекомендации, которых должны придерживаться составители документов, учебников или приказов.

Классификация величин

Явления, которые характеризируют всю систему целиком, называют макроскопическими. В разных источниках классификация величин отличается, но основные группы все же можно выделить. 

Группы параметров:

1. Переменных состояний: экстенсивные и интенсивные величины.
2. Фазовые или химические реакции.
3. Термо- механические, химические и физические.
4. Функционалов процессов: энергия переноса массы, теплота, работа.

В некоторых случаях в литературе используются также такие определения, как внешние и внутренние величины. К первым относят экстенсивные свойства, а ко вторым — внутреннюю энергию, температуру или химсостав.

Термодинамическими параметрами называют и величины, которые поддаются и не поддаются измерению приборами. Давление, температура и объем легко измеряется, а внутреннюю энергию уже нужно вычислять по формулам.

Наряду с термическими параметрами свойств в термодинамике также широко используются и калорические. К ним относятся, в частности энтальпия и энтропия. 

Основные величины 

К основным термодинамическим параметрам относятся: удельный объем, давление и температура. Если меняется хотя бы одна из этих величин, происходит процесс. Совокупность генеральных свойств системы соответственно определяет ее состояние. 

Основные термодинамические параметры состояния:

1. Удельный объем. Речь идет о массе вещества, которая обратна плотности. Измеряется в кубических метрах (м3), а масса — в килограммах. Затем рассчитывается удельный объем как объем, деленный на массу.
2. Давление. Представляет собой количество силы, прилагаемой к площади. Для измерения используют разные единицы (например, Паскаль). Чтобы создать большое давление, прикладывают большую силу либо применяют ее к небольшой площади.
3. Температура. Показатель теплоты по температурной шкале Цельсия, Фаренгейта, Кельвина. Мера средней кинетической энергии атомов или молекул в системе. Нулевой закон термодинамики гласит, что тепло не передается между двумя объектами в тепловом равновесии. Следовательно они одинаковой температуры.
4. Плотность. Отношение массы вещества к объему. Физическое свойство материи (каждый элемент и соединение имеет уникальную плотность). Плотность определяется как мера относительной тяжести предметов с постоянным объемом.

Основным термодинамическим параметром являются также удельная теплоемкость вещества (объем теплоты, поглощаемой в процессе нагревания на 1 кельвин).

Количество теплоты. Удельная теплоемкость вещества

Количество теплоты – это скалярная физическая величина, равная энергии, которую тело получило или отдало при теплопередаче.

Обозначение – ​\( Q \)​, в СИ единица измерения – Дж.

Удельная теплоемкость – это скалярная физическая величина, численно равная количеству теплоты, которое тело массой 1 кг получает или отдает при изменении его температуры на 1 К.

Обозначение – ​\( c \)​, в СИ единица измерения – Дж/(кг·К).

Удельная теплоемкость определяется не только свойствами вещества, но и тем, в каком процессе осуществляется теплопередача. Поэтому выделяют удельную теплоемкость газа при постоянном давлении – ​\( c_P \)​ и удельную теплоемкость газа при постоянном объеме – ​\( c_V \)​. Для нагревания газа на 1 К при постоянном давлении требуется большее количество теплоты, чем при постоянном объеме – ​\( c_P > c_V \)​.

Формула для вычисления количества теплоты, которое получает тело при нагревании или отдает при охлаждении:

где ​\( m \)​ – масса тела, ​\( c \)​ – удельная теплоемкость, ​\( T_2 \)​ – конечная температура тела, ​\( T_1 \)​ – начальная температура тела.

Важно!
При решении задач на расчет количества теплоты при нагревании или охлаждении можно не переводить температуру в кельвины. Так как 1К=1°С, то​\( \Delta T=\Delta t \)​

Циклические процессы

В термодинамике и практических приложениях важную роль играют замкнутые циклы, состоящие из
равновесных процессов. Изменяясь в этих процессах, система периодически возвращается в исходное состояние.

Напомним, что, если $Q\gt 0$, то тепловая энергия получается системой,
а при $Q\lt 0$ — отдаётся наружу. Положительная работа $\delta A~=~P\,dV$
означает, что её производит система (а не «мы»),
а если $A \lt 0$ — работа совершается над системой, т.е. «нами».
Для замкнутого цикла $\Delta U = 0$ (возвращаемся в тоже состояние), поэтому $A=Q$, где:
$$
A ~=~ \oint P\,dV,~~~~~~~~~~~~~~~~=~~~~~~~~~~~~~~~Q~=~\oint T\,dS.
$$

Если обход контура равновесного процесса производится по часовой стрелке (см. стрелки на рисунках),
то выполняемая системой работа $A$ на плоскости $(P,V)$ равна площади, окружаемой кривой цикла,
а получаемая системой теплота $Q$ — площади для этого же процесса на плоскости $(T,S)$.

Действительно, интеграл от $P\,dV$ по верхней кривой между точками $(1-2)$
положителен и равен площади под этой кривой. Движение в обратную сторону
$(2-1)$ по нижней кривой приводит к «отрицательной площади» под этой кривой.
Сумма этих площадей равна площади закрашенной области. Аналогично для плоскости $(T,S)$.

Если направление контура меняется на противоположный, то меняются и знаки.
Тепло система отдаёт $Q\lt 0$,
и чтобы такой цикл был возможен, необходимо затрачивать «внешнюю» работу: $A = Q\lt 0$.

В силу того, что энтропия $dS=\delta Q/T$ является переменной состояния,
интеграл от неё по замкнутой кривой, как и для внутренней энергии,
равен нулю:
$$
\oint \frac{\delta Q}{T}~=~0.
$$
Это соотношение называют вторым началом термодинамики для равновесных процессов.

Интенсивные и экстенсивные параметры

Термодинамические параметры состояния делятся на две группы: экстенсивные (суммирующиеся) и интенсивные (выравнивающиеся). В первом случае свойство прямо пропорционально массе системы и обладает аддитивностью. Во втором: параметры таким свойством не обладают и не зависят от массы.

Экстенсивные или аддитививные параметры при фиксированных значениях интенсивных параметров пропорциональны числу частиц в системе (или ее массе). Интенсивные параметры принимают одинаковые значения для любой части равновесной системы, даже когда она не является пространственно однородной.

Экстенсивные величины — величины, значения которых для всей системы равны аналогичному показателю для отдельных ее частей.

• внутренняя энергия;
• масса;
• энтропия и энтальпия;
• объём.

Интенсивные величины — величины, которые не изменяются при разделении системы на части.

В отличие от них экстенсивные величины зависят от размеров системы и ее массы.

Интенсивные термодинамические параметры:

• температура;
• плотность;
• объем на массу;
• молярный объем (который является объемом на моль);
• средняя молекулярная масса (или молекулярная масса);
• магнитная индукция.

Разновидности по свойствам веществ, вступающих в реакцию

Любая химическая реакция сопровождается изменениями функций состояния системы, определяющихся переменными состояниями системы (объемом, давлением и температурой, количеством молей химических компонентов). Реакция возможна, если вещества имеют более низкую свободную энергию, чем реагенты.

1. Внутренняя энергия. Под этим термином понимают совокупность изменяемых составных частей полной энергии системы. Внутренняя энергия уменьшится, если система будет выделять тепло. Следовательно, она растет при увеличении тепла. Поскольку энергия никогда не создается и не разрушается (первый закон термодинамики), изменение внутренней энергии всегда равно нулю.
2. Энтропия. Эта мера энергии в системе, которую нельзя использовать для выполнения работы. Генерация энтропии в обратимом процессе равна нулю.
3. Энтальпия . Сумма внутренней энергии и произведения давления и объема термодинамической системы. Единицей измерения в Международной системе единиц является джоуль. Иногда также используются британскую тепловую единицу (БТЕ) ​​и калорию.

К характеристикам параметров состояния термодинамической системы относятся разные величины (в том числе температура, состав или плотность и многое другое). Именно они описывают ее в определенный момент времени в зависимости от набора состояний.

Цикл Карно

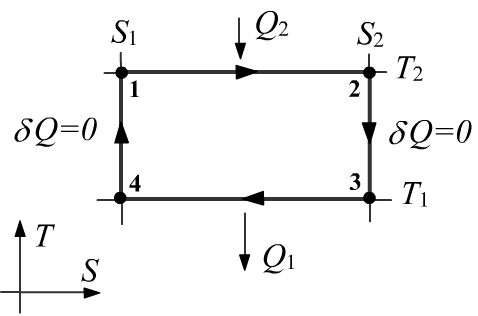
Рассмотрим в качестве примера цикл Карно, состоящий из
двух изотерм $T_1\lt T_2$ и двух
адиабат $S_1 \lt S_2$.
На изотерме $1-2$ система расширяясь,
получает тепло $Q_2 \gt 0$ от термостата с температурой $T_2$, а при сжатии на изотерме $3-4$
отдаёт его $Q_1 \lt 0$ термостату c температурой $T_1 \lt T_2 $.

На плоскости $(T,S)$ цикл Карно имеет форму прямоугольника. Так как $\delta Q = T\,dS$,
на изотермах имеем $Q_2~=~T_2\,(S_2-S_1)\gt 0$ и $Q_1~=~T_1\,(S_1-S_2)\lt 0$,
откуда сразу следует равенство Карно-Клаузиуса:
$$
\frac{Q_1}{T_1} + \frac{Q_2}{T_2} = 0.
$$

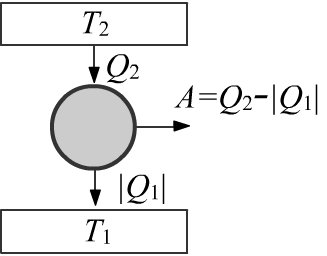Коэффициентом полезного действия (КПД) цикла называют отношение выполненной работы
к полученному от более горячего термостата тепла:
$$
\eta ~=~ \frac{A}{Q_2} ~=~ \frac{Q_1+Q_2}{Q_2} ~=~ 1-\frac{T_1}{T_2}.
$$
Так как $T_1 \lt T_2$, КПД всегда меньше единицы. Тепловая машина, работающая
по циклу Карно, производит работу благодаря градиенту температур в термостатах.
При наличии только одного термостата циклически производить работу нельзя.

Чуть более сложно выглядит анализ цикла Карно в переменных $(P,V)$.
Для получаемого $Q_2$ и отдаваемого $Q_1$ тепла можно воспользоваться
результатом анализа изотермического процесса:

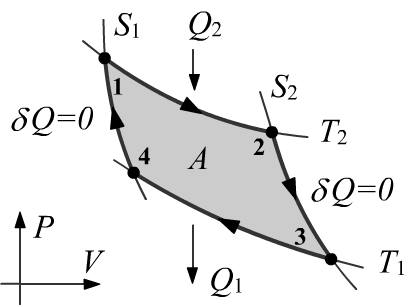
$$
Q_2 ~=~ k\,N\,T_2\,\ln \frac{V_2}{V_1},~~~~~~~~~~~~~~~~~~~~
Q_1 ~=~ k\,N\,T_1\,\ln \frac{V_4}{V_3}.~~~~~~~~~~~~
$$

На адиабатах $P\,V^\gamma ~=~ T\,V^{\gamma-1}~=~\text{const}$,
откуда
$T_1\,V^{\gamma-1}_3=T_2\,V^{\gamma-1}_2$ и
$T_1\,V^{\gamma-1}_4=T_2\,V^{\gamma-1}_1$,
или
$$
\frac{V_2}{V_1}~=~\frac{V_3}{V_4}.
$$
Отсюда уже несложно получить связь $Q_1/T_1+Q_2/T_2=0$.
Замечательным является то, что в это соотношение не входит параметр $\gamma$,
т.е. оно должно выполнятся любого идеального газа.
Более того, природа используемой в цикле системы (рабочего тела)
вообще роли не играет. Именно это наблюдение исторически привело к понятию энтропии.

◊ Дом отапливается при помощи холодильной машины, работающей по обратному циклу Карно.
Она «охлаждает» улицу ($T_1$)
и нагревает дом ($T_2$).
Работа для этой машины поступает
от тепловой машины (прямой цикл Карно) с нагревателем ($T_3$) и отдачей тепла в дом ($T_2$).
Во сколько раз такая схема даёт больше тепла, чем тепло $Q_3$, требуемое
для поддержания температуры нагревателя?

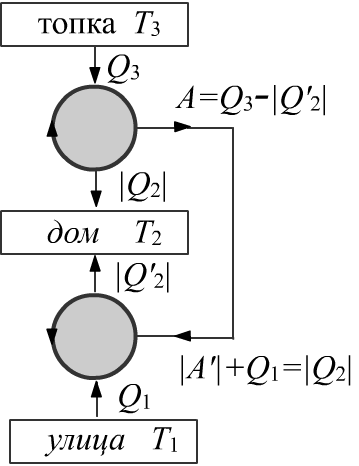
Тепловая машина производит работу $A$. Холодильная машина эту работу потребляет:
$$
A=Q_3+Q_2\gt 0,~~~~~~~~~~~~~A’~=~Q_1+Q’_2 ~=~ -A \lt 0
$$
Откуда $Q_1+Q’_2+Q_2+Q_3~=~0$. Кроме этого: $Q_3/T_3+Q_2/T_2~=~Q_1/T_1+Q’_2/T_2=0$.
Тепло, приходящее в дом, равно $Q_\text{get}~=~|Q_2|+|Q’_2|~=~Q_1+Q_3$. В результате:
$$
\frac{Q_\text{get}}{Q_3} ~=~ \frac{T^{-1}_1-T^{-1}_3}{T^{-1}_1-T^{-1}_2}.
$$
Пусть в градусах Цельсия $t_1=0\,°$, $t_2=20\,°$ и $t_3=100\,°$. Тогда $Q_\text{get}/Q_3=3.9$.

Шкала температур Цельсия

Для практического употребления по решению IX Генеральной конференции по мерам и весам в 1948 году была принята международная стоградусная температурная шкала – шкала Цельсия.

Шведский физик и астроном Андерс Цельсий (1701 – 1744) в 1742 году предложил шкалу термометра, в которой за ноль градусов (начало отсчёта температуры) принял температуру таяния льда, а за сто градусов – температуру кипения воды при нормальном атмосферном давлении в 1,01325 * 105 Па. Изменение длины столба жидкости в термометре на одну сотую долю длины между отметками 0 и 100 °С соответствует изменению температуры на 1 °С. По данной шкале единица измерения температуры – градус Цельсия.

Однако, несмотря на указанную выше конференцию, в некоторых странах (например, в США) до сих пор активно используется другая шкала – шкала Фаренгейта. На шкале Фаренгейта точка таяния льда равна +32 °F, а точка кипения воды равна +212 °F. При этом один градус Фаренгейта равен 1/180 разности этих температур.

Перевести градусы из Цельсия в Фаренгейт можно так:

Перевод из Фаренгейта в Цельсий:

Здесь t_F – температура по Фаренгейту, t_C – температура по Цельсию

Перевести градусы по Цельсию в градусы по Фаренгейту и обратно вы можете ниже.

Первый закон термодинамики

Закон сохранения и превращения энергии, распространенный на тепловые явления, называется первым законом (началом) термодинамики.

Можно дать формулировку этого закона исходя из способов изменения внутренней энергии.

Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:

Если рассматривать работу самой системы над внешними телами, то закон может быть сформулирован так:

количество теплоты, переданное системе, идет на изменение ее внутренней энергии и совершение системой работы над внешними телами:

Если система изолирована и над ней не совершается работа и нет теплообмена с внешними телами, то в этом случае внутренняя энергия не изменяется. Если к системе не поступает теплота, то работа системой может совершаться только за счет уменьшения внутренней энергии. Это значит, что невозможно создать вечный двигатель – устройство, способное совершать работу без каких-либо затрат топлива.

Первый закон термодинамики для изопроцессов

Изотермический процесс: ​\( Q=A’\,(T=const, \Delta U=0) \)​Физический смысл: все переданное газу тепло идет на совершение работы.

Изобарный процесс: \( Q=\Delta U+A’ \)​Физический смысл: подводимое к газу тепло идет на увеличение его внутренней энергии и на совершение газом работы.

Изохорный процесс: \( Q=\Delta U\,(V=const, A’=0) \)​Физический смысл: внутренняя энергия газа увеличивается за счет подводимого тепла.

Адиабатный процесс: ​\( \Delta U=-A’ \)​ или ​\( A=\Delta U\,\mathbf{(Q=0)} \)​Физический смысл: внутренняя энергия газа уменьшается за счет совершения газом работы. Температура газа при этом понижается.

Задачи об изменении внутренней энергии тел

Такие задачи можно разделить на группы:

• При взаимодействии тел изменяется их внутренняя энергия без совершения работы над внешней средой.
• Рассматриваются явления, связанные с превращением одного вида энергии в другой при взаимодействии двух тел. В результате происходит изменение внутренней энергии одного тела вследствие совершенной им или над ним работы.

При решении задач первой группы:

• установить, у каких тел внутренняя энергия уменьшается, а у каких – возрастает;
• составить уравнение теплового баланса ​\( (\Delta U=0) \), при записи которого в выражении ​\( Q =cm(t_2 – t_1) \)​ для изменения внутренней энергии нужно вычитать из конечной температуры тела начальную и суммировать члены с учетом получающегося знака;
• решить полученное уравнение относительно искомой величины;
• проверить решение.

При решении задач второй группы:

• убедиться, что в процессе взаимодействия тел теплота извне к ним не подводится, т.е. действительно ли ​\( Q = 0 \)​;
• установить, у какого из двух взаимодействующих тел изменяется внутренняя энергия и что является причиной этого изменения – работа, совершенная самим телом, или работа, совершенная над телом;
• записать уравнение ​\( Q = \Delta U + A \)​ для тела, у которого изменяется внутренняя энергия, учитывая знак перед работой и КПД рассматриваемого процесса;
• если работа совершается за счет уменьшения внутренней энергии одного из тел, то ​\( А= -\Delta U \)​, а если внутренняя энергия тела увеличивается за счет работы, совершенной над телом, то ​\( A=\Delta U \)​;
• найти выражения для ​\( \Delta U \)​ и ​\( A \)​;
• подставить в исходное уравнение вместо \( \Delta U \) и \( A \) выражения для них, получить окончательное соотношение для определения искомой величины;
• решить полученное уравнение относительно искомой величины;
• проверить решение.

Первое начало термодинамики

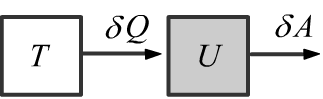
Любая замкнутая система характеризуется своей внутренней энергией $U$.
Внутренняя энергия увеличивается при получении тепловой энергии $\delta Q$
и уменьшается при совершении системой работы $\delta A=P\,dV$:
$$
dU ~=~\delta Q ~-~\delta A.~~~~~~~~~~~~~
$$

Тепловая энергия поступает ($\delta Q \gt 0$) в систему при её контакте с более горячим телом
или покидает ($\delta Q \lt 0$) систему при контакте с более холодным телом (если $\delta A=0$).
Работа $\delta A= P\,dV$, выполненная системой при расширении газа,
уменьшает внутреннюю энергию (если $\delta Q=0$).
При сжатии газа ($\delta A \lt 0$) внутренняя энергия увеличивается
(для этого необходимо затратить работу со стороны внешних сил).

Закон сохранения энергии, записанный в такой форме, называют первым началом термодинамики.
Он имеет очень широкую область применимости
и справедлив для любой системы находящейся, как в равновесии, так и вдали от него.

Принципы действия тепловых машин

Тепловым двигателем называют устройство, преобразующее внутреннюю энергию топлива в механическую энергию.

Основные части теплового двигателя:

• Нагреватель – тело с постоянной температурой, преобразующее внутреннюю энергию топлива в энергию газа. В каждом цикле работы двигателя нагреватель передает рабочему телу некоторое количество теплоты.
• Рабочее тело – это газ, совершающий работу при расширении.
• Холодильник – тело с постоянной температурой, которому рабочее тело передает часть тепла.

Любая тепловая машина получает от нагревателя некоторое количество теплоты ​\( Q_1 \)​ и передает холодильнику количество теплоты ​\( Q_2 \)​. Так как ​\( Q_1 > Q_2 \)​, то совершается работа ​\( A’ = Q_1 – Q_2 \)​.

Тепловой двигатель должен работать циклически, поэтому расширение рабочего тела должно сменяться его сжатием. Работа расширения газа должна быть больше работы сжатия, совершаемой внешними силами (условие совершения полезной работы). Температура газа при расширении должна быть выше, чем температура при сжатии. Тогда давление газа во всех промежуточных состояниях при сжатии будет меньше, чем при расширении.

В реальных тепловых машинах нагревателем является камера сгорания. В них рабочее тело нагревается за счет тепла, выделяющегося при сгорании топлива. Количество теплоты, выделяющееся при сгорании топлива, вычисляется по формуле:

где ​\( q \)​ – удельная теплота сгорания топлива, ​\( m \)​ – масса топлива.

Холодильником чаще всего у реальных двигателей служит атмосфера.

Виды тепловых двигателей:

• паровой двигатель;
• турбина (паровая, газовая);
• двигатель внутреннего сгорания (карбюраторный, дизельный);
• реактивный двигатель.

Тепловые двигатели широко используются на всех видах транспорта: на автомобилях – двигатели внутреннего сгорания; на железнодорожном транспорте – дизельные двигатели (на тепловозах); на водном транспорте – турбины; в авиации – турбореактивные и реактивные двигатели. На тепловых и атомных электростанциях тепловые двигатели приводят в движение роторы генераторов переменного тока.

Второй закон термодинамики

Все процессы в природе протекают только в одном направлении. В обратном направлении самопроизвольно они протекать не могут. Необратимым называется процесс, обратный которому может протекать только как составляющая более сложного процесса.

Примеры необратимых процессов:

• переход тепла от более нагретого тела к менее нагретому телу;
• переход механической энергии во внутреннюю энергию.

Первый закон термодинамики ничего не говорит о направлении процессов в природе.

Второй закон термодинамики выражает необратимость процессов, происходящих в природе. Существует несколько его формулировок.

Второй закон термодинамики (формулировка Клаузиуса):
невозможно перевести тепло от более холодной системы к более горячей при отсутствии одновременных изменений в обеих системах или окружающих телах.

Второй закон термодинамики (формулировка Кельвина):
невозможно осуществить такой периодический процесс, единственным результатом которого было бы получение работы за счет теплоты, взятой от одного источника.

Эта формулировка говорит также и о том, что невозможно построить вечный двигатель второго рода, то есть двигатель, совершающий работу за счет охлаждения какого-либо одного тела.

Важно!
В формулировке второго закона термодинамики большое значение имеют слова «единственным результатом». Если процессы, о которых идет речь, не являются единственными, то запреты снимаются

Например, в холодильнике происходит передача тепла от более холодного тела к нагретому и при этом осуществляется компенсирующий процесс превращения механической энергии окружающих тел во внутреннюю энергию.

Второй закон термодинамики выполняется для систем с огромным числом частиц. В системах с малым количеством частиц возможны флуктуации – отклонения от равновесия.

Давление

Давлением называется величина, характеризующая силу, воздействующую на тело, перпендикулярно его поверхности. Для того чтобы вычислить этот параметр, необходимо все количество силы разделить на площадь объекта. Единицами измерения этой силы будут паскали.

В случае с термодинамическими параметрами газ занимает весь доступный ему объем, и, кроме того, молекулы, его составляющие, непрерывно хаотично двигаются и сталкиваются друг с другом и с сосудом, в котором находятся. Именно эти удары и обуславливают давление вещества на стенки сосуда либо на тело, которое помещено в газ. Сила распространяется во всех направлениях одинаково именно из-за непредсказуемого движения молекул. Чтобы увеличить давление, необходимо повысить температуру системы, и наоборот.

Первое начало термодинамики

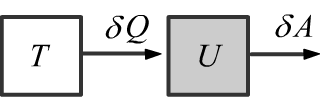
Любая замкнутая система характеризуется своей внутренней энергией $U$.
Внутренняя энергия увеличивается при получении тепловой энергии $\delta Q$
и уменьшается при совершении системой работы $\delta A=P\,dV$:
$$
dU ~=~\delta Q ~-~\delta A.~~~~~~~~~~~~~
$$

Тепловая энергия поступает ($\delta Q \gt 0$) в систему при её контакте с более горячим телом
или покидает ($\delta Q \lt 0$) систему при контакте с более холодным телом (если $\delta A=0$).
Работа $\delta A= P\,dV$, выполненная системой при расширении газа,
уменьшает внутреннюю энергию (если $\delta Q=0$).
При сжатии газа ($\delta A \lt 0$) внутренняя энергия увеличивается
(для этого необходимо затратить работу со стороны внешних сил).

Закон сохранения энергии, записанный в такой форме, называют первым началом термодинамики.
Он имеет очень широкую область применимости
и справедлив для любой системы находящейся, как в равновесии, так и вдали от него.

Энтропия

Второе начало термодинамики гласит, что энтропия не уменьшается. Другая формулировка постулирует, что энергия никогда не переходит от тела с более низкой температурой к более нагретому. Это, в свою очередь, отрицает возможность создания вечного двигателя, так как нельзя всю энергию, имеющуюся у тела, перевести в работу.

Само понятие «энтропия» было введено в обиход еще в середине 19 века. Тогда оно воспринималось как изменение количества тепла к температуре системы. Но такое определение подходит только к процессам, которые постоянно находятся в состоянии равновесия. Из этого можно вывести следующее заключение: если температура тел, составляющих систему, стремится к нулю, то и энтропия будет равна нулю.

Энтропия как термодинамический параметр состояния газа используется в качестве указания на меру беспорядочности, хаотичности движения частиц. Ее используют, чтобы определить распределение молекул в определенной области и сосуде, либо чтобы посчитать электромагнитную силу взаимодействия между ионами вещества.

Микроскопические и макроскопические параметры

Микроскопическое состояние (или микросостояние) — это состояние системы, определяемое заданием координат и импульсов всех составляющих систему частиц.

Макроскопическое состояние (или макросостояние) — это состояние системы, характеризуемое небольшим числом величин (Р, V, T) и, быть
может, еще некоторыми другими).

Величины, характеризующие макросостояние, называются макроскопическими параметрами. Те из них, которые характеризуют внутреннее
состояние системы, называются внутренними параметрами, а те, которые описывают внешнюю среду (внешние тела, поля), — внешними параметрами.

Смысл разделения на микро- и макросостояния состоит в следующем. Хаотическая динамика на микроскопическом уровне (молекулярный
хаос) проявляется как упорядоченное изменение состояния на макроскопическом уровне. Точное описание поведения системы на языке
микросостояний чрезвычайно сложно, если вообще возможно. Вместе с тем достаточно полное описание макроскопического поведения системы большого числа частиц может быть получено с помощью небольшого числа макроскопических параметров — давления Р, температуры Т, объема V и, быть может, еще нескольких других существенных характеристик. Если не интересоваться внутренним строением вещества, то достаточно ограничиться описанием на уровне макросостояния. При необходимости можно уточнить это описание, вводя в рассмотрение те или иные дополнительные параметры (например, те из них, которые характеризуют форму тела, его заряд, магнитный момент и т. д.).

Микроскопические и макроскопические параметры

Микроскопическое состояние (или микросостояние) — это состояние системы, определяемое заданием координат и импульсов всех составляющих систему частиц.

Макроскопическое состояние (или макросостояние) — это состояние системы, характеризуемое небольшим числом величин (Р, V, T) и, быть
может, еще некоторыми другими).

Величины, характеризующие макросостояние, называются макроскопическими параметрами. Те из них, которые характеризуют внутреннее
состояние системы, называются внутренними параметрами, а те, которые описывают внешнюю среду (внешние тела, поля), — внешними параметрами.

Смысл разделения на микро- и макросостояния состоит в следующем. Хаотическая динамика на микроскопическом уровне (молекулярный
хаос) проявляется как упорядоченное изменение состояния на макроскопическом уровне. Точное описание поведения системы на языке
микросостояний чрезвычайно сложно, если вообще возможно. Вместе с тем достаточно полное описание макроскопического поведения системы большого числа частиц может быть получено с помощью небольшого числа макроскопических параметров — давления Р, температуры Т, объема V и, быть может, еще нескольких других существенных характеристик. Если не интересоваться внутренним строением вещества, то достаточно ограничиться описанием на уровне макросостояния. При необходимости можно уточнить это описание, вводя в рассмотрение те или иные дополнительные параметры (например, те из них, которые характеризуют форму тела, его заряд, магнитный момент и т. д.).

Интенсивные и экстенсивные параметры

Термодинамические параметры состояния делятся на две группы: экстенсивные (суммирующиеся) и интенсивные (выравнивающиеся). В первом случае свойство прямо пропорционально массе системы и обладает аддитивностью. Во втором: параметры таким свойством не обладают и не зависят от массы.

Экстенсивные или аддитививные параметры при фиксированных значениях интенсивных параметров пропорциональны числу частиц в системе (или ее массе). Интенсивные параметры принимают одинаковые значения для любой части равновесной системы, даже когда она не является пространственно однородной.

Экстенсивные величины — величины, значения которых для всей системы равны аналогичному показателю для отдельных ее частей.

• внутренняя энергия;
• масса;
• энтропия и энтальпия;
• объём.

Интенсивные величины — величины, которые не изменяются при разделении системы на части.

В отличие от них экстенсивные величины зависят от размеров системы и ее массы.

Интенсивные термодинамические параметры:

• температура;
• плотность;
• объем на массу;
• молярный объем (который является объемом на моль);
• средняя молекулярная масса (или молекулярная масса);
• магнитная индукция.