Возможно ли, чтобы площадь сечения куба представляла собой правильный пятиугольник?

Описания свойств куба и пятиугольника

У куба есть несколько особенностей:

1. Все ребра куба имеют одинаковую длину.
2. Углы между гранями куба всегда равны 90 градусам.
3. Объем куба можно вычислить по формуле: V = a^3, где a — длина ребра.
4. Площадь поверхности куба можно вычислить по формуле: S = 6a^2, где a — длина ребра.

Пятиугольник — это многоугольник, состоящий из пяти отрезков, называемых сторонами, и пяти вершин, в которых стыкуются эти стороны. В пятиугольнике все стороны и углы могут быть разной длины и размера.

У пятиугольника такие свойства:

1. Углы внутри пятиугольника могут быть произвольными.
2. Сумма внутренних углов пятиугольника всегда равна 540 градусам.
3. Если стороны пятиугольника равны, то пятиугольник называется правильным.
4. Для правильного пятиугольника можно вычислить площадь по формуле: S = (a^2 * sqrt(25 + 10 * sqrt(5))) / 4, где a — длина стороны.

Задача № 4

Во сколько раз периметр сечения, имеющего форму треугольника, проходящего через вершины куба, больше периметра сечения, ему параллельного, но проходящему через середины сторон данного куба.

1. Рассмотрев собранную Вами модель зеленного цвета, а именно, его внешнюю разметку, выразите периметры необходимых сечений количеством диагоналей клеток. Периметр большего сечения вмещает в себя 18 диагоналей, а периметр меньшего – 9. Таким образом, получаем отношение: 18:9=22. Воспользовавшись определение коэффициента подобия, получим ответ: периметр большего сечения в 2 раза больше периметра меньшего сечения.

Примеры применения сечений куба в реальной жизни

1. Архитектура:

Сечения куба находят применение в архитектуре для создания интересных и необычных форм зданий. Изначально общежитие на территории Молжанского кадетского корпуса стало первым примером архитектурного решения с использованием сечений куба — его углы обеспечивают дополнительное освещение и общую динамику строения.

2. Дизайн:

Сечения куба используются в дизайне для создания оригинальных и необычных форм предметов интерьера, мебели и элементов декора. Например, сечение куба может быть использовано в качестве основы для дизайна столика или стула, придавая ему современный и стильный вид.

3. Инженерия:

В инженерии сечение куба применяется для проектирования и создания кубических объектов, таких как контейнеры или модульные сооружения. Например, используя сечение куба, можно создать эффективную систему хранения, упаковки или транспортировки товаров.

4. Математика и геометрия:

Сечения куба широко применяются в математике и геометрии для изучения объемов, площадей и форм кубических объектов. Сечения куба используются для демонстрации основных принциповтрехмерной геометрии и выпуклых многогранников, а также для решения различных геометрических задач.

Примеры применения сечений куба в реальной жизни
Область применения
Пример
Архитектура
Дизайн общежития с использованием сечений куба
Дизайн
Оригинальный дизайн столика на основе сечений куба
Инженерия
Создание контейнеров с использованием сечения куба
Математика и геометрия
Изучение объемов, площадей и форм кубических объектов

Это лишь некоторые примеры применения сечений куба в реальной жизни. В целом, сечения куба могут быть использованы в различных областях, где требуется создание объемных и геометрически правильных форм.

Дистанционные курсы для педагогов

Выдаём документы установленного образца! Учителя о ЕГЭ: секреты успешной подготовки В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных Курские власти перевели на дистант школьников в районах на границе с Украиной В приграничных пунктах Брянской области на день приостановили занятия в школах В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной Новые курсы: функциональная грамотность, ФГОС НОО, инклюзивное обучение и другие Университет им. Герцена и РАО создадут портрет современного школьника

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи. Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов. Источник

Реальные примеры пятиугольных сечений в других фигурах

Пятиугольник, являющийся правильным выпуклым плоским многоугольником, встречается не только в сечении куба. Он также может быть сформирован в других геометрических фигурах.

Например, одним из интересных примеров является правильный пятиугольник, который можно получить в сечении ромбоэдра. Ромбоэдр — это выпуклый многогранный полиэдр, у которого все грани являются ромбами. Пятиугольник образуется при сечении ромбоэдра плоскостью, которая проходит через его вершины.

Другим примером является сечение додекаэдра — многогранника, состоящего из 12 правильных пятиугольников. Пятиугольник образуется при плоскостном сечении додекаэдра через его вершины.

Эти реальные примеры пятиугольных сечений в других фигурах демонстрируют, что пятиугольники могут встречаться не только в кубе, но и в других геометрических фигурах. Изучение таких сечений позволяет расширить понимание свойств и возможностей геометрии и ее применение в реальной жизни.

Презентация на тему: » Доказать, что если в сечение куба получится треугольник, то этот треугольник остроугольный. Пусть ABCDA1B1C1D1 – куб, MNP – сечение куба плоскостью. Обозначим:» — Транскрипт:

3

Доказать, что если в сечение куба получится треугольник, то этот треугольник остроугольный. Пусть ABCDA1B1C1D1 – куб, MNP – сечение куба плоскостью. Обозначим: AN=x, AP=y, AM=z. Тогда. Рассмотрим треугольник MNP с углами,, и применим теорему косинусов: Переписав ее иначе: Имеем Из последнего равенства, очевидно, что cos >0, следовательно,

4

Построить сечение куба плоскостью, проходящей через концы трех ребер куба, выходящих из одной вершины. Вычислить периметр и площадь сечения, если ребро куба равно а. Сечение будет являться правильный треугольник, т.к. его стороны будут являться диагоналями граней куба. Соответственно периметр будет равен а площадь равна АВ С D A B C D

5

шестиугольник с одной осью симметрии: правильный шестиугольник: равнобедренная трапеция: Какую форму может иметь сечение куба плоскостью, проходящей через середины двух смежных ребер?

6

Диагональ куба выбрана в той диагональной плоскости, которая параллельна прямой МN. По условию MN параллельна АС. Построим MP параллельно DD и NL параллельно DD. Тогда PL параллельно MN. Плоскость MPLN параллельна диагональной плоскости ACCA, поскольку проходит через две пересекающиеся прямые, параллельные двум пересекающимся прямым плоскости ACCA. Диагональ АС принадлежит плоскости AACC, значит, AC параллельно (PMN). D B A B C A C D N P L M

7

Провести сечение куба через M и N двух смежных сторон основания и центр О грани верхнего основания. Вычислить площадь сечения, если ребро куба равно а Решение: Плоскость сечения пересекает грань ABCD по прямой, которая параллельна NM и проходит через точку О. Это прямая AC. Трапеция ACNM- равнобедренная стороны которой AC равно NM=, AM=CN=. Зная стороны трапеции и высоту, площадь равна. A A B C D B C D M N O

8

Плоскость параллельна диагонали куба, выходящей из общей вершины указанных сторон основания. Пусть M и N – середины двух смежных сторон грани ABCD. Отрезки MN и BD пересекаются в точке Р. Проводим отрезок РК параллельно диагоналям BD. Через две пересекающиеся прямые PK и MN проводим плоскость KLMNT. Она параллельна диагонали BD. B A B C D A C D M N K T L

9

H Правильный шестиугольник получается, когда сечение проходит через середины трех пар противоположных ребер. Докажем, что шестиугольник MNPKQL правильный. MN=MP=PK=QK=QL=ML= B D A B C A C D M N L P Q K

10

PP Плоскость параллельна диагонали BD. Пусть точка Р – пересечение отрезков BD и MN. В диагональной плоскости BDDB проводим отрезок PQ параллельный диагонали BD. Искомое сечение представляет собой треугольник MQN. B A B C D A C D M N Q

11

шестиугольник с одной осью симметрии: правильный шестиугольник: равнобедренная трапеция: Какую форму может иметь сечение куба плоскостью, проходящей через середины двух смежных ребер?

12

равнобедренный треугольник: прямоугольник: пятиугольник с одной осью симметрии: Построить сечение куба плоскостью, проходящей через середины двух смежных сторон основания параллельных диагоналей куба Задача интересна тем, что в условии не указано, о какой диагонали идет речь. Значит, возможны три случая:

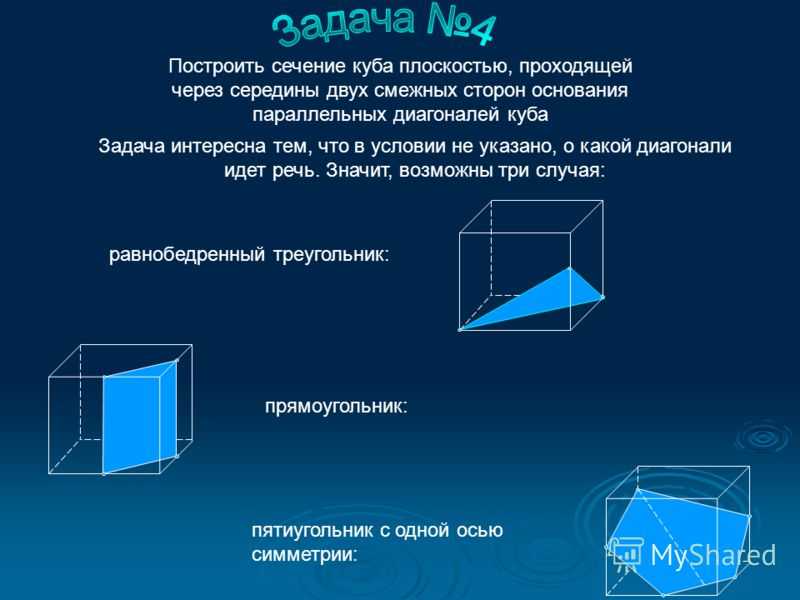
Разрешение мифа: правильное пятиугольное сечение куба — возможно или нет?

Давайте разберемся в данном вопросе. Во-первых, что такое правильный пятиугольник? Это такой пятиугольник, у которого все стороны и углы равны между собой. Правильные пятиугольники хорошо известны и хорошо изучены математиками.

Но что насчет куба? Куб — это трехмерная фигура, у которой все грани являются квадратами, все углы прямые, и все стороны имеют одинаковую длину. Такой объем можно представить себе как состоящий из совокупности одинаковых квадратных граней, смежные стороны которых образуют прямые углы.

Следует отметить, что если мы сделаем простое сечение куба, полученная плоскость будет содержать квадратную форму. Однако, как мы уже говорили ранее, пятиугольник — это фигура с пятью сторонами, а у куба — только шесть граней-квадратов и двенадцать ребер.

Таким образом, получение правильного пятиугольника путем сечения куба невозможно согласно свойствам имеющихся фигур. Математические модели и правила геометрии не позволяют нам получить форму пятиугольника из куба, только плоские пятиугольники могут быть получены.

Тем не менее, это не значит, что из куба нельзя получить другую форму пятиугольника. Если сделать более сложное сечение куба, возможно получение пятиугольника неправильной формы. Однако, в данном случае мы говорим о пятиугольниках, у которых стороны и углы не равны между собой.

Итак, мы разобрались с мифом о возможности правильного пятиугольного сечения куба. Математические правила и свойства геометрических фигур не позволяют нам получить такую форму, но более сложные сечения вполне могут привести к появлению пятиугольников неправильной формы.

Меч ниндзя разрезает математический куб пополам

Итак, вопрос.Разрезав куб на две равные половинки, мы получим в сечении …?— A: квадрат;— B: прямоугольник;— C: ромб;— D: шестиугольник.

Если вы думаете, что ответ A (квадрат) очевиден и отбрасываете все другие ответы, то делаете большую ошибку. Может показаться, что например, такой вариант ответа как D: (шестиугольник) здесь заведомо лишний. Но это не так. Здесь все варианты ответов верные!

В качестве идеи для этой статьи послужила популярная игра «Fruit ninja». Где необходимо разрезать мечом летящие фрукты. Допустим, что фрукты в большинстве, имеют круглую или овальную форму

Разрезая такие фрукты на половинки, обратите внимание, что будет в месте разреза. Какая геометрическая форма? Если мы разрезаем точно и быстро, то будет сечение в форме круга или овала

А как вам предложение разрезать классический куб ? Здесь уже придется подумать.Но мы ещё усложним задачу. Задача разрезать куб таким образом, чтобы после разреза получились равные половинки.

Как продемонстрировать, что это возможно? Как доказать, что куб можно разрезать на две равные половинки?Для этого мы рассмотрим каждый вариант ответа и изготовим модели кубов состоящие из двух половинок.У нас будет развёртка только одной половинки, чтобы исключить всякие сомнения.А как же вторая половинка?Вторая половинка должна быть точно такая же, как и первая. Тогда утверждение будет доказано.Просто ещё раз соберите половинку из этой же развёртки.Сложите половинки вместе, и вы получите исходный куб!

Математическая модель

Для ответа на вопрос о том, может ли сечение куба быть правильным пятиугольником, необходимо применить математическую модель. Для начала рассмотрим свойства правильного пятиугольника и куба.

Правильный пятиугольник — это пятиугольник, у которого все стороны равны и все углы между ними равны. Следовательно, вершины пятиугольника расположены на одной окружности.

Куб — это правильный многогранник, у которого все грани являются квадратами и все углы между гранями равны. Также все ребра и диагонали граней куба имеют равную длину.

Для решения задачи рассмотрим множество точек пересечения ребер куба. Найдем пересечение трех ребер, образующих грань, и соединим эти точки прямыми линиями. Получим плоскость, в которую вписан правильный пятиугольник.

Однако, поскольку все ребра куба имеют равную длину, а у правильного пятиугольника все стороны равны, такая плоскость не может быть построена внутри куба. Математически это можно проверить с помощью геометрических вычислений и формул.

Таким образом, сечение куба не может быть правильным пятиугольником. Это можно объяснить простыми геометрическими свойствами правильных пятиугольников и кубов.

• Сечение куба не может быть правильным пятиугольником.
• Правильный пятиугольник имеет углы, равные 108 градусам, в то время как куб имеет прямые углы, равные 90 градусам.
• Куб имеет 6 граней, в то время как пятиугольник имеет 5.
• Поэтому, геометрически невозможно получить правильный пятиугольник в результате сечения куба.

Таким образом, ответ на вопрос «Может ли сечение куба быть правильным пятиугольником» является отрицательным.

Виды и свойства сечения куба

Куб — это геометрическое тело, имеющее шесть граней, все из которых являются квадратами. В процессе сечения куба можно получить различные фигуры, которые обладают особыми свойствами и интересными характеристиками.

В зависимости от положения плоскости сечения, можно выделить несколько основных видов сечения куба:

1. Горизонтальное сечение: плоскость проходит параллельно основанию куба. В результате получаются два полукруга и прямоугольник.

2. Вертикальное сечение: плоскость проходит перпендикулярно основанию куба. В результате получается круг и прямоугольник.

3. Диагональное сечение: плоскость проходит по диагонали куба. В результате получается равнобедренные треугольники.

4. Сечение под углом: плоскость проходит под углом к основанию куба. В результате получаются различные сложные фигуры, могут быть треугольники, прямоугольники и многоугольники.

Сечение куба имеет ряд интересных свойств:

• Площадь сечений куба увеличивается пропорционально площади выбранной плоскости. Так, чем больше площадь плоскости сечения, тем больше площадь полученной фигуры.

• Сечение куба может быть симметричным или несимметричным, в зависимости от положения плоскости относительно центра куба. При симметричном сечении полученная фигура будет иметь оси симметрии.

• В случае горизонтального и вертикального сечений площадь полученных фигур будет равна сумме площадей двух квадратов, на которые разделился куб.

• Сечение куба всегда будет иметь ребра или стороны. Количество и форма ребер будут зависеть от вида сечения.

Изучение различных видов и свойств сечения куба позволяет лучше понять его геометрические характеристики и особенности. Это помогает применять знания о сечении куба в различных областях, таких как строительство, дизайн и математика.

Экспериментальные исследования

Одним из подходов к экспериментальному исследованию может быть изготовление модели куба и попытка его сечения правильным пятиугольником. В ходе эксперимента можно измерять углы и длины сторон полученного пятиугольника, а также сравнивать их со значениями углов и сторон правильного пятиугольника. Это позволит оценить, насколько точно исследуемый сечение соответствует правильному пятиугольнику.

Важно отметить, что экспериментальные исследования могут потребовать использования специальных инструментов и материалов, таких как лазерные уровни, точные измерительные приборы и материалы, позволяющие создать точное сечение куба. Кроме того, для получения достоверных результатов могут потребоваться повторные эксперименты и усреднение полученных данных

Сечения куба ⁠

• пра­виль­ный шести­уголь­ник;
• пяти­уголь­ник (непра­виль­ный);
• раз­лич­ные четырёх­уголь­ники (вклю­чая квад­рат, прямо­уголь­ник, ромб);
• а также раз­лич­ные тре­уголь­ники (вклю­чая пра­виль­ный).

Учащимся пред­лага­ется разме­стить (как сече­ние) каж­дый много­уголь­ник в кубе.

Можно пред­ложить и самим учащимся выре­зать много­уголь­ник, являющийся сече­нием куба.

Инте­ресно обсу­дить, почему у куба не бывает сече­ния в виде пяти­уголь­ника пра­виль­ного. Плос­кость, высе­кающая пяти­уголь­ник, пере­се­ка­ется с пятью гра­нями куба, а зна­чит, среди них будут две парал­лель­ные грани (а на самом деле — две пары). Пере­се­ка­ясь с одной плос­ко­стью, они дадут парал­лель­ные отрезки, а у пра­виль­ного пяти­уголь­ника нет парал­лель­ных сто­рон.

Такой же вопрос — какие пра­виль­ные много­уголь­ники можно полу­чить как сече­ние — инте­ресно рас­смот­реть и для других пра­виль­ных многогран­ни­ков, начи­ная с тет­раэдра и закан­чи­вая доде­каэд­ром.

Модель, демон­стри­рующую сече­ние куба в виде пра­виль­ного шести­уголь­ника, можно сде­лать в виде «ворот­ника» на куб.

Докажите, что сечением куба может быть правильный треугольник, квадрат, правильный шестиугольник, но не может быть правильный пятиугольник и правильный многоугольник с числом сторон более шести

Задачи повышенной трудности → номер 774

Если ABCDA1B1C1D1— куб с ребром a, то его сечение ACD1 — правильный треугольник, а любое сечение — параллельное грани — квадрат (рис. 574).

Проведем через середину Е ребра АВ плоскость α || ACD1 Она пересечет ВС в некоторой точке F.

Так как EF || АС, то по теореме Фалеса F — середина ВС и

Рассуждая аналогично, получим последовательно, что α

Пройдет также через середины G, Н, К, L ребер куба, и все стороны шестиугольника EFGHKL равны

Его углы равны между собой

Как соответственные углы треугольников KLE, LEF, EFG, FGH, GHK, HKL, равных друг другу по трем сторонам.

Таким образом — сечение — правильный шестиугольник. Пятиугольное сечение правильным быть не может. Так как в сечении AMNKL AL || MN, то

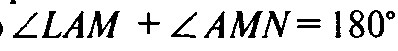
Равны, то они — прямые и не равны 108°.

Сечений с семью и более сторонами быть не может, так как граней у куба только шесть.

Основные принципы геометрии

Первым принципом геометрии является определение точки. Точка – это наименьшая единица пространства, не имеющая ни длины, ни ширины, ни толщины. Она представляет собой математическую абстракцию, которую мы используем для обозначения местоположения объектов.

Вторым основным принципом геометрии является линия. Линия – это бесконечно тонкая и прямая структура, составленная из бесконечного числа точек. Линия имеет длину, но не имеет ширины или толщины.

Третий принцип геометрии – это плоскость. Плоскость – это двумерная поверхность, состоящая из бесконечного числа линий. Она обладает шириной и длиной, но не имеет толщины.

Четвертый принцип – это фигуры и формы. Фигуры – это ограниченные области плоскости или пространства, которые могут быть описаны геометрическими фигурами, такими как круги, треугольники, прямоугольники и другие. Форма – это общее определение для всех фигур и объектов в геометрии.

Пятый и последний принцип геометрии – это отношения и свойства. Геометрия изучает отношения между объектами и их свойства, такие как длина, углы, площадь и объем. Эти свойства позволяют нам измерять и анализировать различные аспекты геометрических фигур и форм.

Благодаря основным принципам геометрии мы можем исследовать мир вокруг нас, строить и измерять объекты, анализировать пространственные формы и решать различные задачи, связанные с геометрией.

Особенности пересечения плоскости с ребрами куба

Пересечение плоскости с ребрами куба может иметь несколько особенностей, которые следует учитывать при изучении этого вопроса. Рассмотрим некоторые из них:

1. Типы пересечений: Плоскость может пересечь ребра куба в различных точках и под разными углами. В зависимости от положения плоскости относительно куба можно выделить следующие типы пересечений: пересечение внутри куба, пересечение на границе куба, пересечение по диагонали и пересечение на углах.
2. Количество пересечений: Положение плоскости может варьироваться от ситуации к ситуации, что влияет на количество пересечений с ребрами куба. Плоскость может пересечь как одно ребро, так и несколько ребер одновременно.
3. Форма пересечения: Пересечение плоскости с ребрами куба может образовывать различные формы и фигуры. Например, плоскость может разделить ребро на две части или образовать треугольник или трапецию на ребре.
4. Границы пересечения: Когда плоскость пересекает ребра куба, возникают границы пересечения. Эти границы могут быть прямыми линиями, кривыми или даже окружностями, в зависимости от формы пересечения плоскости и ребра куба.
5. Свойства пересечения: Пересечение плоскости с ребрами куба может обладать различными свойствами. Например, могут возникать симметричные пересечения, когда плоскость разделяет ребро на две равные части. Также могут возникать пересечения с дополнительными точками пересечения или с точками пересечения других ребер куба.

Изучение особенностей пересечения плоскости с ребрами куба позволяет лучше понять геометрию и свойства этой фигуры, а также применить полученные знания в решении различных математических задач.

Куб и несколько задач по стереометрии с ЕГЭ

В пособии “ЕГЭ 2005. Математика. Типовые тестовые задачи” (Корникова Т. А. и др. ) Содержит 10 задач (С4) по стереометрии, объединенных общей идеей: дана треугольная призма АВСА1В1С1 стороны основания АВ и ВС взаимно перпендикулярны и перпендикулярны ребру ВВ1, АВ=ВС=ВВ1, вершина А является вершиной конуса (или центром одного из оснований цилиндра, или центром сферы), основание конуса (сфера или второе основание цилиндра) проходит через середину одного ребра призмы, длина его известна. Надо найти объем или поверхность конуса (сферы, цилиндра).

Общий пример решения:

Данную призму дополнить до куба. Шестиугольник DEFKLM – сечение куба плоскостью основания конуса , окружность которого проходит через середину А1В1, А – вершина конуса, или

DEFKLM – сечение куба плоскостью основания цилиндра, окружность которого проходит через середину А1В1, А – центр второго основания цилиндра, или это сечение куба плоскостью большого круга сферы с центром А, сфера которого проходит через середину А1В1.

Шестиугольник DEFKLM – сечение куба плоскостью, проходящей через середину рёбер А1В1, ВВ1, ВСЖ при построении получаются точки K, L, M, которые являются серединами соответствующих рёбер. Стороны этого шестиугольника являются гипотенузами треугольников DB1E, EBF, FCK, KQL, LRM, MA1D, катеты которых равны половине ребра куба. Тогда центр этого шестиугольника является центром описанной около него окружности, которая пересекает рёбра куба в точках D,E, F, K, L и М, радиус этой окружности , где А1В1=а.

AO EL, т. к. EAL – равнобедренный: AL=AE.

(ABE u EAL – прямоугольные, AB=AQ= а, BE=LQ=)

EO=OL как середина диагонали ЕL шестиугольника DEFKLM, т. е. АО – медиана ,а по свойствам равнобедренного треугольника и высота. Аналогично доказывается АО DK. Так как АО перпендикулярна к двум пересекающимся прямым плоскости шестиугольника, то АО перпендикулярна ко всей плоскости.

Если А – вершина конуса то АО – его высота, если А – центр второго основания цилиндра, то АО- высота цилиндра.

АВС: АС=, P – точки пресечения диагоналей основания куба, АР=, РР1=АА1= а. ОР=РР1= , тогда из прямоугольного РОА АО=. И так АО=.

Тогда, если идёт речь о конусе:

Если речь идёт цилиндре:

Если речь идёт о сфере:

Корникова Т. А. и др. типовые тестовые задания. ЕГЭ – 2005

Вариант 6.

Задача. Даны призма АВСА1В1С1 и цилиндр. Стороны АВ и ВС основания призмы перпендикулярны ребру ВВ1 и взаимно перпендикулярны. Центром основания цилиндра служит точка А1 окружность второго основания проходит через середину ребра А1В1.

Найдите площадь полной поверхности цилиндра, если ВВ1=АВ=ВС=10. Найдите его объём.

Решение:

Так как стороны АВ и ВС основания призмы перпендикулярны ребру ВВ1 и взаимно перпендикулярны и АВ=ВС=ВВ1, то призма АВСА1В1С1 – это половина куба с ребром АВ. Окружность второго основания цилиндра проходит через середину А1В1. Эта окружность пересекает и другие рёбра куба. И эти точки пересечения окружности второго основания цилиндра и рёбер куба лежит в одной плоскости (плоскость сечения) и равноудалены от центра второго основания цилиндра. Плоскость второго основания цилиндра образует в сечении куба шестиугольник DEFKLM, все вершины которого являются вершинами соответствующих рёбер. Тогда ED=АР=R, ЕВ1D, В=900 (по условию), B1E=DB1=, тогда по теореме Пифагора ED=, R=.

Докажем, что АО перпендикулярно к сечению DEFKLM,так как является его высотой цилиндра.

РОА , Р=900 РА=, РО=.

По теореме Пифагора ОА= (ОА=h=).

SPO, P=900 PS= SO

в AOS: AO2=75 SO2=

AS2=AO2+SO2. AOS – прямоугольный АОSO.

Корникова Т. А. и др. типовые тестовые задания. ЕГЭ – 2005

Вариант 10.

Задача. Даны призма АВСА1В1С1 и конус. Стороны АВ и ВС основания перпендикулярны ребру ВВ1 и взаимно перпендикулярны. Вершина конуса располагается в точке А, окружность основания проходит через середину ребра А1В1.

Найдите площадь полной поверхности конуса, если ВВ1=АВ=ВС=8. Найдите объём этого конуса.

Решение:

Так как по условию дана прямая призма, в которой ВВ1=АВ=ВС, то эта призма является половиной куба. Вершина куба А является и вершиной конуса, основание которого пересекает А1В1 в точке D, следовательно AD – образующая конуса AD=. Сечение куба плоскостью основания конуса – это правильный шестиугольник DEFKLM, т. к. АD, AE, AF, AK, AL, AM – это образующие конуса, вершины D, E, F, K, L, M – равноудалены от основания высоты конуса в точке О, являются серединами рёбер куба. R=ED, EB1D, B1D =B1E=4, ED=4.

AA1D, A1=900, AD=.

AC= (из ОАН, ОН АН, НО=4, АН=4).