Интересные факты о разных единицах плотности
Единицы измерения плотности используются для определения плотности материалов и веществ. Вот некоторые интересные факты о различных единицах плотности:
| Единица измерения | Описание |
|---|---|
| Килограмм на кубический метр (кг/м³) | Самая распространенная единица измерения плотности. Используется для измерения плотности самых разных материалов, от воздуха до металлов. |
| Грамм на кубический сантиметр (г/см³) | Используется для измерения плотности более плотных материалов, таких как металлы и некоторые сплавы. В сравнении с кг/м³, значения плотности в г/см³ будут значительно больше. |
| Фунты на кубический фут (lb/ft³) | Хотя большинство стран метрической системы предпочитают использовать кг/м³, в США и некоторых других странах популярна единица измерения плотности в фунтах на кубический фут. Используется для измерения плотности газов и жидкостей. |
| Унции на галлон (oz/gal) | Единица измерения плотности жидкостей, часто используемая в США. Значения плотности в унциях на галлон будут значительно меньше, чем в кг/м³ или г/см³. |
Это лишь некоторые из множества единиц измерения плотности, которые существуют в мире. Каждая единица предназначена для измерения плотности в определенной системе и имеет свои конкретные применения.
Значение слова «кубический метр»
Как правильно перевести кубические метры в литры Перевести кубические метры в литры достаточно просто. Однако при частом конвертировании можно и ошибиться. Поэтому настоятельно рекомендуем использовать наш онлайн конвертер м3 в л. Это бесплатно, быстро и легко.
Их необходимо будет перемножить в уме, или по таблице умножения, или на калькуляторе. И полученное число будет площадью, которую надо будет покрывать краской или еще чем-нибудь. Это интересно! Иногда нужно знать как правильно высчитываются размеры. Сколько же дюймов в мм? Об этом можно прочесть в нашей статье. Бывает, что форма пола не стандартная, а, например, трапециевидная.
Тогда сложнее, особенно тем людям, кто не знает, что такое треугольник такое тоже есть в природе. Чтобы рассчитать размер трапеции, необходимо посчитать сначала площадь прямоугольника в середине, потом величину каждого треугольника по бокам, потом эти три числа сложить. Не легче ли сразу позвать бригаду рабочих? Пускай они думают, как рассчитать квадратные метры комнаты. Если на этом этапе возникло непонимание, то лучше сразу позвать учителя математики и попросить подсчитать, сколько кв. Площадь комнаты в квадратных метрах Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут: Рулетка. Лучше — с фиксатором, но подойдет и обычная. Бумага и карандаш или ручка. Калькулятор или считайте в столбик или в уме.
Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно. Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше. Прямоугольная комната Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м 430 см , ширина 3,25 м 325 см. Как высчитать площадь комнаты Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах.
В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров. Помещение неправильной формы Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам есть в таблице чуть ниже. Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно. Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.
Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник как на рисунке ниже. Как видите, для данного случая требуется иметь пять размеров.
L — длина коробки или комнаты в тех же единицах, что и объем W — ширина коробки или комнаты в тех же единицах, что и объем H — высота коробки или комнаты в тех же единицах, что и объем S — площадь коробки или комнаты в тех же единицах, что и объем Онлайн калькулятор кубов — расчета объема: быстрый и простой способ узнать объем фигуры или предмета.
Используйте калькулятор для расчета объема комнаты, офиса, нежилого помещения, коробки, и других аналогичных объектов.
Это заготовка статьи по физике. Вы можете помочь проекту, дополнив её. Отрывок, характеризующий Кубический метр Сын вздохнул, признаваясь этим вздохом в том, что отец понял его. Старик, продолжая складывать и печатать письма, с своею привычною быстротой, схватывал и бросал сургуч, печать и бумагу. Я всё сделаю.
Ты будь покоен, — говорил он отрывисто во время печатания. Андрей молчал: ему и приятно и неприятно было, что отец понял его. Старик встал и подал письмо сыну.
Как вывести формулу кубического метра?
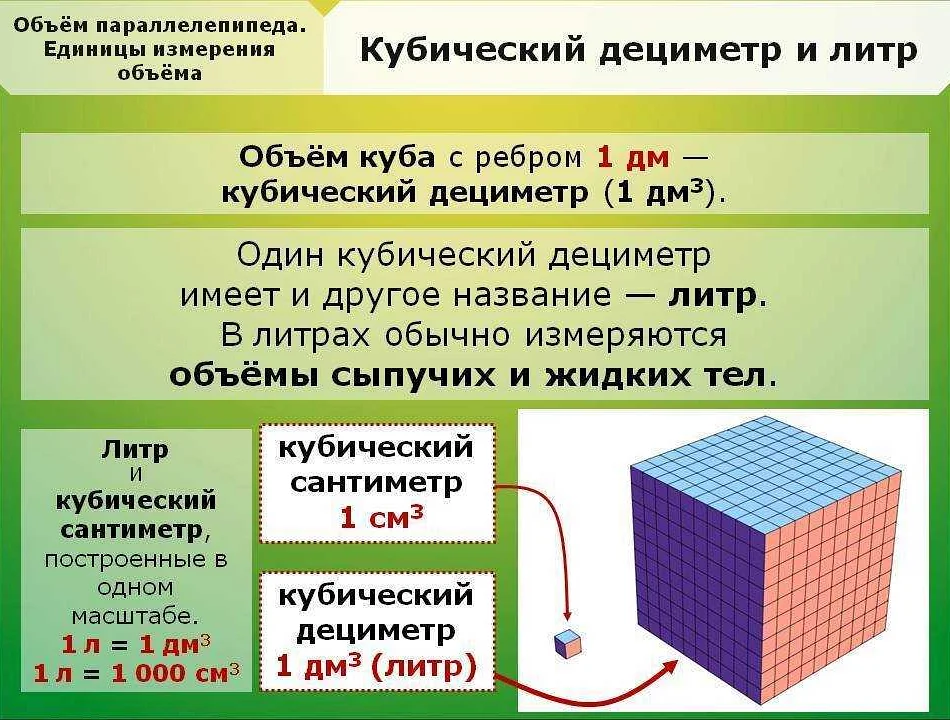
Кубический метр — это единица измерения объема, которую можно представить в виде формулы. Формула кубического метра выглядит следующим образом:
Объем = длина х ширина х высота
- Объем — объем тела в кубических метрах (м3).
- Длина — длина тела в метрах (м).
- Ширина — ширина тела в метрах (м).
- Высота — высота тела в метрах (м).
Например, если у нас есть прямоугольный параллелепипед длиной 2 м, шириной 3 м и высотой 4 м, то его объем можно рассчитать по формуле:
Объем = 2 м х 3 м х 4 м = 24 м3
Таким образом, формула кубического метра позволяет рассчитывать объем различных геометрических фигур и тел в единицах измерения метра кубического.
Единица измерения куба
Куб считается распространенной геометрической фигурой, используемой для измерения объема и определения других показателей. Однако она не может использоваться для определения площади, так как для расчета требуется только длина и ширина. Особенности кубометра заключаются в следующем:
- В качестве стандарта используется фигура, которая имеет метровые грани. Для обозначения применяется символ «³», сокращение в письменном виде «куб. м».
- При необходимости можно провести перевод полученного показателя в дециметры или сантиметры, миллиметры, километры и литры.
- В некоторых странах вычисления проводятся в футах, баррелях и ярдах. При этом перевод приблизительный, так как целое число при конвертации не получается.
- Кубометр является производной в Международной системе единиц и системе МКГСС и МТС. Поэтому в большинстве случаев производить перевод не нужно.
Единица измерения встречается в различных программах для компьютера, калькуляторах и другой вычислительной технике. Кубометровый показатель указывается на этикетке производителями материала, на емкостях и в иных случаях.
Conversions[edit]
Some SI units of volume to scale and approximate corresponding mass of water
-
1 cubic metre = 1000 litres (exactly) ≈ 35.3 cubic feet ≈ 1.31 cubic yards ≈ 6.29 oil barrels ≈ 220 imperial gallons ≈ 264 US fluid gallons
A cubic metre of pure water at the temperature of maximum density (3.98 °C) and standard atmospheric pressure (101.325 kPa) has a mass of 1000 kg, or one tonne. At 0 °C, the freezing point of water, a cubic metre of water has slightly less mass, 999.972 kilograms.
A cubic metre is sometimes abbreviated to m^3, M3, m**3, cu m, m3, CBM, cbm when superscript characters or markup cannot be used (e.g. in some typewritten documents and postings in Usenet newsgroups). The «cubic metre» symbol is encoded by Unicode at code point U+33A5 ㎥ SQUARE M CUBED.
В 1 тонне сколько кубометров?
Если вам нужно перевести одну единицу в другую, то есть массу в объем, то следует знать плотность вещества. Пойдем от обратного: чтобы узнать, сколько тонн в куб. метре — умножьте объем вещества на его плотность. К примеру:
- Плотность воды примерно 1000 кг/м3, а плотность золота 19621 кг/м3.
- В 1 кубометре воды будет 1000 кг или 1 тонна, то есть в 1 тонне 1 кубометр воды.
- В 1 кубометре золота 19,621 тонны (1 кубометр х 1 тонну / 19,621 = 0,059658 куб. метра), то есть в 1 тонне золота 0,05 кубометра.
Плотность веществ можно посмотреть в общепринятых таблицах. Вот одна из таких таблиц, которой пользуются строители и другие специалисты:
Также существует таблица расчета кубов.
Как считать кубические метры?
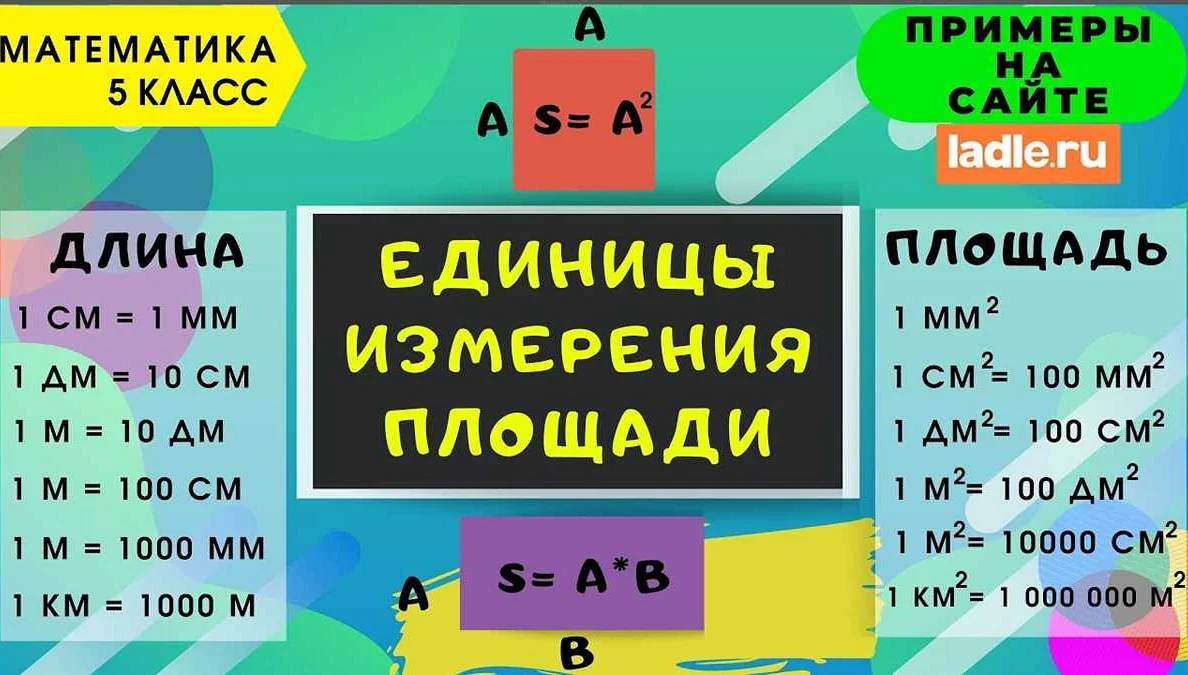
Кубический метр — это единица измерения объема тела в трехмерном пространстве. Для вычисления объема тела необходимо умножить длину, ширину и высоту тела и полученный результат измерить в кубических метрах.
При работе с некоторыми материалами, такими как бетон или кирпич, объем обычно измеряется в кубических метрах. Допустим, вы хотите построить забор длиной 12 метров, высотой 2 метра и толщиной 0,3 метра, то необходимо вычислить объем материала (12м x 2м x 0,3м = 7,2м³).
Для удобства вычислений можно использовать таблицы объемов различных фигур, таких как куб, параллелепипед и цилиндр.
- Объем куба = a³ (a — длина ребра)
- Объем параллелепипеда = abh (a, b — длины сторон, h — высота)
- Объем цилиндра = πr²h (r — радиус основания, h — высота)
Использование этих формул поможет точно вычислить объем тела и получить нужное количество кубических метров.
История
Государства мира по эпохам принятия международной системы
Предшественником СИ измерения является метрическая система, разработанная комиссией под председательством Лагранжа с 1791 г. Эта система медленно распространяется в Европе, включая Италию.
Единицы СИ, терминология и рекомендации устанавливаются Генеральной конференцией мер и весов ( GFCM ), «Генеральной конференцией мер и весов», органом, связанным с Международным бюро мер и весов (BIPM), «Международным бюро мер и весов». Меры « мер», органы, созданные на Метрополитен — конвенте года .
Система родилась в году во Франции с 1-й GFCM : тогда она называлась «Система МКС», потому что включала только основные единицы длины ( метр ), массы ( килограмм ) и времени ( секунда ).
В году по предложению физика Джованни Джорджи система была расширена за счёт включения единиц электрических величин. Первой попыткой была «Система MKS-Ω», принятая Международной электротехнической комиссией , в которой электрическое сопротивление изначально было выбрано в качестве основной величины , а единицей измерения был ом . После войны, в году, опять же по предложению Джорджи, GFCM одобрила переход от выбора электрического сопротивления в качестве основной величины к электрическому току , определив ампер в качестве его основной единицы . Так родилась «Система MKSA», также называемая «Система Гиорги».
В году 10-й GFCM добавил абсолютную температуру (и связанную с ней единицу измерения: кельвин ) и силу света (позже определив свечу как единицу измерения ) в качестве пятой и шестой фундаментальных величин.
В году 11-я ГКФК окончательно санкционировала рождение Международной системы (СИ).
В году 14-я ГКФК добавила количество вещества в качестве фундаментальной величины и определила моль числом Авогадро .
В 2018 году 26-я GFCM переопределила фундаментальные единицы с точки зрения физических констант , окончательно обновив себя с учетом результатов, достигнутых за годы в дисциплине размерного анализа .
Итак, сегодня ядро SI состоит в логическом порядке из:
- выбор основных физических величин на основе фундаментальных физических законов физических теорий считается универсальным.
- выбор значений фундаментальных физических констант, фигурирующих в этих законах
- определение названий единиц измерения основных величин, называемых основными единицами для семи основных физических величин, и их определение, исходя из физических констант.
Исходя из ядра Международной системы, мы можем определить все остальные величины, которые называются производными. Они связаны с основными величинами рассматриваемыми физическими законами и, соответственно, таковы их единицы измерения.
Международная система определяет единую единицу измерения для каждой производной величины (к которой применяются префиксы), которая всегда является простым произведением степеней основных единиц. Это позволяет исключить переводные коэффициенты и максимально облегчить расчеты зависимостей между значениями физических величин в задаче. Международная система измерения определяется как согласованная система , поскольку производные единицы измерения могут быть выражены как простое произведение и отношение между фундаментальными физическими величинами.
Наконец, SI определил десятичные
и двоичные префиксы , которые должны быть добавлены к единицам измерения для идентификации кратных и дольных единиц.
Использование кубического метра в строительстве
В строительстве кубический метр играет ключевую роль при расчете объемов материалов и площадей помещений. Он используется для измерения объема зданий, фундаментов, комнат, и других строительных конструкций.
Когда строители приступают к разработке проекта и планированию строительства, они ориентируются на объемы в кубических метрах. Это позволяет точно определить потребность в материалах, таких как бетон, кирпичи, дерево и другие.
При возведении стен и перекрытий строители проверяют, что они соответствуют заданному объему в кубических метрах. Это помогает контролировать качество и размеры выполняемых работ.
Кубический метр также используется при проведении замеров и расчете площадей помещений. Например, для определения площади пола или стен может использоваться формула: ширина x длина x высота = кубический метр.
В строительной индустрии эффективное использование кубического метра помогает достичь оптимальной структуры строительного объекта и снизить затраты на материалы. Более точные расчеты объемов и площадей помогают сэкономить время и ресурсы при строительстве, а также создать комфортные и безопасные условия для жильцов или пользователей построенного объекта.
Правила написания
Чтобы стандартизировать написание и избежать ошибок толкования, в СИ предусмотрены некоторые правила написания единиц измерения и связанных с ними символов.
Пишущие единицы
Единицы измерения должны быть указаны полностью, если они вставлены в дискурсивный текст; написание должно быть строчным круглым шрифтом , и следует избегать графических знаков, таких как ударения или диакритические знаки . Например, вы должны писать amps , а не amps или amps.
Написание символов
Обозначения (без префикса) должны быть указаны со строчной инициальной, за исключением тех, в которых единица измерения является одноименной, т. е. происходит от имени ученого, и тех, в которых символ мультипликативной приставки является верхний регистр. Например, обозначение единицы измерения давления, посвященное Блезу Паскалю , — Па , вместо этого единица измерения пишется полностью строчными буквами: паскаль . Второе — это если не сек, то грамм г и не гр, метр ме не мт. Единственным исключением является литр , символ которого может быть либо l, либо L.
Символы префиксов и единиц СИ являются математическими единицами, поэтому, в отличие от аббревиатур , символы СИ не должны сопровождаться точкой (для метра : m, а не m.); они также должны стоять после числового значения (например, вы пишете20 см , а не 20 см ) с пробелом между цифрой и символом:2,21 кг ,7,3 × 10 2 м² . В составных единицах (например, ньютон-метр : Н·м) символы единиц должны быть разделены пробелом или точкой на половине высоты, также называемой средней точкой (·). Использование других символов, например дефиса, не допускается: например, можно писать Н м или Н · м, но не Н м. В случае деления между единицами измерения можно использовать символ /, или горизонтальная черта, или отрицательная экспонента: например, Дж/кг или Дж кг- 1 или Дж кг — 1 .
Префикс является неотъемлемой частью единицы измерения и должен быть помещен на символе единицы без пробелов (например, k в км, M в МПа, G в ГГц, µ в мкг). Комбинации префиксов не допускаются (например, mµm следует записывать как nm). Единица с префиксом представляет собой одно символьное выражение (например, км 2 эквивалентно (км) 2 ).
При необходимости в скобки могут быть помещены группы единиц измерения: Дж/К·моль или Дж/К·моль или Дж·К — 1 ·моль- 1 или Дж (К·моль) -1 .
Для символов рекомендуется избегать курсива и полужирного шрифта , чтобы отличать их от математических и физических переменных (например, m для массы и l для длины).
Следует также помнить, что, хотя система СИ допускает употребление множественного числа для наименований единиц измерения (джоули, ватты,…), правила итальянского языка устанавливают, применительно к иностранным терминам, вошедшим в итальянский словарь , что раз они стали его частью, то должны быть приняты как застывшие в своей сущности элементы, несводимые к основным морфологическим структурам именной флективной системы итальянского языка. Поэтому не допускается написание джоули или ватти (как это было бы сделано с литрами и метрами), но ни джоулей и ватт, потому что в итальянском языке не предусмотрено образование множественного числа существительных путем добавления окончания -so — Эс .
Написание чисел
Чтобы сгруппировать цифры целой части числа от трех до трех, начиная справа, используйте пробел. Например 1 000 000 или 342 142 (в других системах записывается как 1 000 000 или 1 000 000 ). Запятая используется как разделитель между целой и десятичной частями, например 24,51. В году GFCM разрешила использовать точки в английских текстах.
Правовые положения
SI является эталоном для многих государств, таких как Италия , где использование было принято законом в DPR n. 802/1982 в соответствии с Директивой Совета ЕЭС от 18 октября 1971 г. (71/354/ЕЕС) с поправками от 27 июля 1976 г. (76/770/ЕЕС). Его использование является обязательным при составлении актов и документов, имеющих юридическую ценность, настолько, что в противном случае акты могут быть признаны недействительными.
Ход урока
I. Организационный момент
II. Постановка задач и целей урока
1. – Для того, чтобы наш урок прошёл успешно какие задачи поставим перед собой?
(Познакомиться с новой темой; продолжать учиться решать задачи; учиться правильно вычислять, сравнивать; внимательно слушать и слышать и т. д.)
— К нам на урок пришла точка. Как вы думаете в связи с чем она пришла сегодня на урок? О чём узнаем?
(Будем говорить о геометрических фигурах)
— Какие геометрические фигуры вы уже знаете?
— На какие группы их можно разделить?
(Плоские и объёмные (пространственные)
2. –Сегодня мы познакомимся с одной объёмной фигурой. Чтобы узнать с какой фигурой познакомимся выполним математический диктант.
Математический диктант
1. 240-65 +65= (240)
2. 18+19+2+21+22= (100)
3. 2*18*5= (180)
4. 528-(428+60)= (40)
5. Найдите Р треугольника, у которого все стороны равны. Длина одной стороны 9 см. (27см)
6. Найдите Р квадрата со стороной 6см. (36см)
7. Найдите площадь прямоугольника со сторонами 6м и 40м. (240м)
8. Найдите Р прямоугольника со сторонами 9см и 15см. (48см)
9. Найдите сторону прямоугольника, одна сторона которого 20м, а площадь 180м. кв. (9м)
ПРОВЕРКА
Соединяем последовательно точки
. 180 .100
240.
40.
27. 36.
— Что за фигура у нас получилась? (Куб)
— Какая это фигура? (Объёмная)
Ш. Работа над темой урока
1. — Тема нашего урока : КУБ И ЕГО ИЗОБРАЖЕНИЕ
(Открываю запись темы урока на доске и раздаю кубы на парты)
2. – У вас на партах кубы. Рассмотрите их. Что можете сказать об этой геометрической фигуре? Можете провести измерение.
(Все стороны равны)
— Эти стороны – грани. Посчитайте сколько всего граней у куба? (6)
— Сколько всего вершин? (8)
— Сколько всего рёбер? (12)
3. Проблемная ситуация.
— Посмотрите на изображение куба на чертеже. Сколько всего граней, вершин, рёбер вы видите на чертеже?
(3-грани, 7-вершин, 9-рёбер)
— Почему же их меньше? (ответы детей)
— Стороны, которые мы не можем увидеть, обозначаются на чертеже пунктирной линией. Сейчас попробуем достроить правильное изображение куба.
На чертеже есть точка 9. попробуйте её соединить с точками, чтобы завершить построение куба.
— Кто знает с какими точками надо соединить точку 9? (27, 40, 180)
— Сколько теперь граней получилось? Вершин? Рёбер?
4. – Куб – это геометрическая фигура. Значит, что мы можем измерить? (длину, ширину рёбер)
— Измерьте. Что вы заметили?
(Они равны – 4см)
— Если рёбра все равны, то какой фигурой является каждая грань?
(Квадрат)
— Найдите площадь одной грани.
(4*4=16 см. кв.)
— Чему равна площадь всей поверхности куба? Как быстро посчитать?
(16*6=96 см. кв.)
ФИЗМИНУТКА
1.– Если я называю плоские фигуры – приседаем, если объёмные – делаем хлопок над головой.
2. – Подпрыгните столько раз:
а) сколько сторон у треугольника (3)
б) сколько вершин у круга (0)
в) сколько углов у квадрата (4)
г) сколько осей симметрии у прямоугольника (4)
5. Практическая работа
— Из трубочек (для коктейля) и пластилина сделаем модель куба. (каркас)
— Вычислите: Сколько потребуется проволоки, если этот каркас делать из проволоки?
— Какие измерения для этого надо сделать? Что надо знать?
(длину ребра)
— Как будем вычислять?
(Количество рёбер умножить на длину ребра)
6. Постановка задач на следующий урок.
Показываю параллелепипед.
— Кто знает как называется эта фигура?
— Чем она похожа с кубом?
— На эти вопросы мы ответим на следующем уроке.
7. «Точка» на приготовила ещё одно интересное задание.
— Рассмотрите сколько всего четырёхугольников изображено на рисунке? (треугольников)
IV. Подведение итогов урока
— Что нового узнали на уроке?
— Что было интересным?
— Всё ли получилось?
— Что вызвало затруднения?
— Кто доволен своей работой?
_ Оцените на шкале успеха свои достижения. Если всё удалось, получилось – красным цветом; если всё было хорошо, но что – то не получилось– зелёным цветом; если не очень старался – синим.
Кратные и дольные единицы: что это
Вообще, мы часто используем некоторые приставки для обозначения кратных и дольных единиц. Возможно, ежедневно. Самые простые примеры — КИЛОграмм, МИЛИметр, САНТИметр. Привычные и распространенные единицы измерения, которые помогут понять механику применения приставок для обозначения приставок.

Приставки кратных и дольных единиц нужны не только во время учебы
Приставка «кило»
Все знают что килограмм — это тысяча грамм. И эта «тысяча» заменяется на приставку «кило», которая в математике обознается как 1000 или 10³. И это и есть одна из кратных приставок. В ней зашифровано количество нулей, которые надо поставить после цифры, к которой приставка относится. Когда говорим 2 килограмма, это значит, что нам надо 2000 граммов. То есть «2» надо умножить на 10³. Фактически это означает, что после двойки надо дописать три нуля. Вот и весь перевод.

Некоторые мы часто встречаем в повседневной жизни
Точно также переводится килоом, который обозначается как кОм. Это тоже тысяча, но не грамм, а Ом. Чтобы перевести килоомы в омы, просто цифру, после которой указана эта единица измерения, умножаем на 1000. Например, 1,2 кОм это 1200 Ом. 3 кОм (три килоома) — это 3000 Ом.
Если приставка «кило» встречается с любыми другими единицами измерения, обозначается она всегда одно и то же. Указанную цифру надо умножить на тысячу. Например, киловатт — тысяча ватт. Соответственно, мощность в 1,8 кВт — 1800 Вт. Или 8 кВ (киловольт) — это 8000 вольт.
Приставки «милли» и «санти»
Второй общеизвестный пример применения приставок — миллиметр. Но «милли» — это уже дольная часть. Это одна тысячная метра. В одном метре тысяча миллиметров. И миллиметр — это 10-3 или 0,001 метра. Фактически это значит, что указанную цифру надо разделить на 1000.

На самом деле их намного больше чем десяток, которые мы сразу можем вспомнить))
Из той же «оперы» сантиметры. Приставка «санти» обозначает, что указанная цифра является сотыми долями от целого. И сантиметр — это одна сотая метра. Мы к этому привыкли и не задумываемся. Иногда еще применяют дециметры, хоть это и не такая распространенная мера длины. Это одна десятая метра, и приставка «деци» указывает, что размер указан в десятых долях.
Что такое кубический метр (кубометр)
Кубический метр – термин, который получил название от слов куб и метр. Для указания куба применяется специальный символ «³». В большинстве случаев он используется для определения объема. Куб считается фигурой трехмерного пространства, то есть он характеризуется тремя основными показателями: длиной, шириной и высотой. Поэтому стандартный кубометр –это небольшой кубик.
Один кубический метр равен 1000 литров. Высота, ширина и длина составляют по одному метру, в результате чего получается фигура для вычисления объема. Термин использовался для создания распространенного показателя Еврокуб, который сегодня активно применяется в промышленности при перевозке сыпучих и других грузов.
Подобное понятие получило широкое распространение. Его часто используют на рынке строительных материалов или в других случаях, к примеру, в квитанциях на оплату коммунальных платежей.






























