Одночлены и многочлены

Тождества

Рассмотрим равенство

a+(a+5)=2a+5.

В данном случае переменная a, содержащаяся в равенстве, может принимать любое значение. Подставим значение a, равное 1:

1+(1+5)=2•1+5;

1+6=2+5;

7=7.

Получили верное равенство. Подставим другое значение переменной, например, а=2, снова получим верное равенство (9=9). Вообще при любом допустимом значении переменной a всегда будет получаться верное равенство. Такое равенство называют тождеством.

Иногда в тождествах вместо знака равенства используют особый значок «≡». Основные тождества алгебры, которые вы уже встречали ранее – это переместительные законы сложения и умножения:

• a+b=b+a;
• ab=b•a;

сочетательные законы сложения и умножения:

(a+b)+c = a+(b+c);

(a•b)•c = a•(b•c);

а также распределительный закон, позволяющий раскрывать скобки:

(a+b)•c = a•c+b•c.

Иногда в понятие тождества включают также и равенства, вовсе не содержащие никаких переменных, например:

62 =36.

В качестве примера равенства, не являющегося тождеством, можно привести 5d+10 = 50. Оно будет выполняться только при значении переменной, равной 8, а при всех остальных значениях не выполняться.

Если два выражения равны друг другу при любых значениях переменных, то их называют тождественно равными.Тождественным преобразованием называют замену выражения на другое, тождественно ему равное. В качестве примера тождественного преобразования можно привести запись:

a5+a6 =a11.

Упрощение на онлайн-калькуляторе

Привести одночлены к удобному виду, значит, упростить их до стандартной записи. Однако зачастую приходится иметь дело с выражениями большого порядка. При этом они могут включать в себя одновременно различные арифметические операции. Выполнять тождественные преобразования самостоятельно бывает довольно трудно, причём возникает вероятность допущения ошибки.

Поэтому использовать специализированные сайты, которые умеют быстро и безошибочно упрощать одночлены любого вида, не зазорно. Порталы предлагают свои услуги бесплатно и для решения примеров не требуют даже регистрации. Что интересно, кроме быстрого расчёта, пользователь, зашедший на такой ресурс, сможет увидеть всю цепочку упрощения, а при желании на страницах онлайн-калькулятора ознакомиться с теорией и основными определениями.

Из всего множества сайтов можно выделить следующие три:

1. Kontrolnaya-rabota. Сервис хоть и ориентирован на учащихся старших классов, но по своим возможностям довольно функционален. Так, с его помощью можно преобразовать даже комплексные выражения. Всё, что требуется от пользователя, это правильно ввести выражение и нажать кнопку «Упростить».
2. Umath. Программа даёт возможность упростить любое алгебраическое выражение. На сайте можно найти всю необходимую теорию. Ограничений в размере формулы нет.
3. Mathforyou. Используя этот онлайн-калькулятор, пользователь сможет выполнить различные действия над выражением, содержащим числовое и символьное обозначение. Для правильного вычисления нужно предварительно ознакомиться с правилами ввода математической формулы, указанными тут же на сайте.

Рекомендованные сайты имеют российский домен, а программы написаны русскими программистами. Поэтому проблем с пониманием, как пользоваться приложениями, возникнуть не должно. Интерфейс онлайн-калькуляторов не содержит нагромождения ненужной информации и интуитивно понятен. Ответ вычисляется буквально за несколько секунд, а используемые алгоритмы исключают возникновение ошибки.

Принцип преобразования

Пусть имеется сложный одночлен, состоящий из ненулевых степеней, квадратов, дробных чисел и букв следующего вида: 5 * 7 * a * m * c7 * 3 *2/9 * 2 (1/7) * am * bn * c * x5 * 120

Тут следует обратить внимание, что дроби в выражении могут быть любого типа, кроме случая, когда в знаменателе будет стоять буква. Такая запись неудобна для восприятия и дальнейшего использования из-за хаотично расставленных подобных членов

Поэтому нужно преобразовать её к стандартному виду.

В основе способа упрощения одночлена лежат следующие принципы:

1. Если в записи встречается число, то оно обязательно пишется впереди и должно быть единственным в выражении.
2. Каждая буква, встречающаяся в формуле, должна повторяться только один раз, записанная в своей степени.
3. Буквы в одночлене записывают в алфавитном порядке.

Что такое квадрат одночлена?

Квадратом одночлена называется выражение, полученное путем умножения одночлена самого на себя. Одночленом называется выражение, содержащее только одну переменную и ее степень.

Для вычисления квадрата одночлена нужно умножить каждый член одночлена на самого себя и затем сложить все полученные слагаемые. Квадрат одночлена может быть положительным или отрицательным в зависимости от знака одночлена.

Например, для одночлена 5x его квадрат будет выглядеть следующим образом:

5x * 5x = 25x^2

Если одночлен имеет отрицательный знак, его квадрат будет также содержать отрицательный знак. Например, для одночлена -3y его квадрат будет выглядеть следующим образом:

-3y * -3y = 9y^2

Знание и понимание понятия квадрата одночлена является важным для решения различных математических задач и упрощения выражений.

Действие над одночленами и приведение одночлена к стандартному виду

Одночлены можно складывать друг с другом и вычитать друг из друга. Поясним на примерах.

Пример 1

Сложим одночлены ${3ab}^5,\ {6b}^6,{13ab}^5$

Запишем вначале сумму:

${(3ab}^5)+\left(\ {6b}^6\right)+({13ab}^5) $

Раскроем скобки:

${3ab}^5+\ {6b}^6+{13ab}^5$

Приведем подобные слагаемые, в результате получим:

${16ab}^5+\ {6b}^6$

Пример 2

Вычтем из одночлена ${6b}^6$ одночлен ${-12b}^6$

Запишем вначале разность:

$\left(\ {6b}^6\right)-({-12b}^6) $

Раскроем скобки:

${6b}^6+{12b}^6$

Приведем подобные слагаемые, в результате получим:

${18b}^6$

Как мы видим, результатом сложения и вычитания может быть как одночлен, так и многочлен.

Умножение. Результатом перемножения одночленов всегда получается одночлен. Одночлены перемножаются по следующей схеме:

• составляется произведение.
• раскрываются скобки.
• группируются числа с числами, одинаковые переменные друг с другом.
• перемножаются числа и складываются степени соответствующих одинаковых переменных.

Пример 3

Умножим $3xzy^2$ и $5xz^3$

Составим произведение:

$\left(3xzy^2\right)\cdot (5xz^3)$

Раскроем скобки и сгруппируем числа и переменные:

$3\cdot 5xxz^3zy^2$

Перемножим, получим:

$15x^2y^2z^4$

Еще одна операция — возведение в степень. Так как по определению, чтобы возвести число в натуральную степень, необходимо умножить это число столько раз само на себя, какой показатель степени и множитель имеется. По такому же принципу перемножаются и одночлены.

Пример 4

Возвести одночлен ${3ab}^5$ в третью степень.

${\left({3ab}^5\right)}^3={3ab}^5\cdot {3ab}^5\cdot {3ab}^5=3\cdot 3\cdot {3a{a{ab}^5b}^5b}^5=27{a^3b}^{15}$

Последняя операция — деление одночлена на одночлен. Результатом такого деления часто выступает рациональная дробь и только иногда получается одночлен. Для выполнения деления одночленов записывается дробь и, при возможности, проводится сокращение.

Пример 5

Разделим одночлен $27{a^3b}^{15}$ на одночлен $9{ab}^{13}$

Запишем дробь:

$\frac{27{a^3b}^{15}}{9{ab}^{13}}$

Сократим, получим:

$\frac{27{a^3b}^{15}}{9{ab}^{13}}=3a^2b^2$

Пример задачи на действия над одночленами

Пример 6

Задача.

Даны два одночлена $15x^2y^2z^4$ и $3xy^2z^2$.

1. Найти степени обоих одночленов
2. Сложите эти одночлены.
3. Вычтите из первого одночлена второй.
4. Возведите второй одночлен в квадрат.
5. Перемножить одночлены.
6. Разделите первый одночлен на второй.

Решение:

Степень первого одночлена: $2+2+4=8$

Степень второго одночлена: $1+2+2=5$

$\left(15x^2y^2z^4\right)+\left(3xy^2z^2\right)=15x^2y^2z^4+3xy^2z^2$

$\left(15x^2y^2z^4\right)-\left(3xy^2z^2\right)=15x^2y^2z^4-3xy^2z^2$

${\left(3xy^2z^2\right)}^2=9x^2y^4z^4$

$\left(15x^2y^2z^4\right)\left(3xy^2z^2\right)=45x^3y^4z^6$

$\frac{15x^2y^2z^4}{3xy^2z^2}=5xz^2$

Определение степени с натуральным показателем

Периодически в математике приходится умножать число на само себя несколько раз. Пусть нам надо записать произведение десяти множителей, каждый из которых равен 2. Эта запись будет выглядеть так:

2*2*2*2*2*2*2*2*2*2

Однако существует и более компактная и удобная запись:

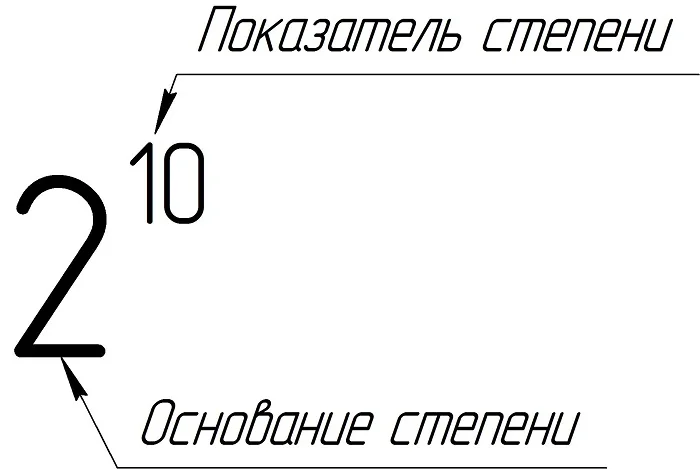
2*2*2*2*2*2*2*2*2*2 = 210

Говорят, что число 2 возвели в десятую степень. В данном случае двойка – это основание степени, а 10 – показатель степени:

Если показатель равен единице, то в произведении должен быть только один множитель, а потому само число не меняется:

21 = 2

Теперь сформулируем определение степени числа с натуральным показателем:

Важно понимать, что такое определение может использоваться только в том случае, если n – натуральное число. В старших классах будут рассматриваться примеры с дробными и отрицательными показателями, однако в таких случаях потребуются и более сложные определения этого понятия

Отметим, что основание может быть любым числом – целым, дробным, положительным, отрицательным.

Рассмотрим несколько простейших заданий.

1. Возведите в 5-ую степень число 3.

Решение:

35 = 3*3*3*3*3 = 9*3*3*3 = 27*3*3 = 81*3 = 243

2. Возведите во 2-ю степень число 0,7.

Решение:

0,72 = 0,7*0,7 = 0,49

3. Возведите в 3-ю степень дробь 3/4.

Решение:

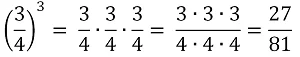
4. Возведите в 4-ую степень число – 4.

Решение:

(-4)4 = (-4)*(-4)*(-4)*(-4) = 16*(-4)*(-4) = (-64)*(-4) = 256

5. Возведите в третью степень – 5.

Решение:

(-5)3 = (-5)*(-5)*(-5) = 25*(-5) = -125

Обратите внимание, что при возведении отрицательного числа можно получить как отрицательное, так и положительное число. Здесь всё зависит от значения показателя

Если он четный, то получится положительное число, а если нечетный, то отрицательное.

6. Сравните выражения (–1,365)106 и (– 2,512)75.

Решение:

Число 106 – четное, поэтому при вычислении (–1,365)106 должно получиться положительное число:

(–1,365)106> 0.

Число 75 – нечетное, поэтому (– 2,512)75 – это отрицательное число:

(– 2,512)75<0.

Следовательно, можно записать следующее

(– 2,512)75< 0 <(–1,365)106, откуда

(– 2,512)75< (–1,365)106.

Ответ: (– 2,512)75< (–1,365)106.

Очевидно, что, сколько бы мы не умножали ноль на самого себя, в результате всегда будет получаться снова 0. Поэтому при любом натуральном значении n выражение 0n равно нулю.

Исторически сложилось, что для некоторых степеней в математике есть особое название. Квадратом числа называют его произведение на само себя. Например, квадрат шести (ещё говорят «шесть в квадрате») равен 36:

62 = 6*6 = 36

Кубом числа называют его третью степень. Так, куб пяти (ещё говорят «пять в кубе») равен 125:

53 = 5*5*5 = 25*5 = 125

Пример. Найдите сумму квадратов чисел (натуральных) от 1 до 5.

Решение:

12+22+32+42+52 = 1+4+9+16+25 = 55

Ответ: 55.

Такие названия связаны с тем, что, площадь квадрата со стороной, равной a, составляет a2, а объем куба с такой же длиной ребра равен a3. Квадраты и кубы чисел обладают множеством интересных свойств. Например, квадрат натурального числа n равен сумме первых n нечетных чисел:

12 = 1

22 = 1 + 3 = 4

32 = 1 + 3 + 5 = 9

42 = 1 + 3 + 5 + 7 = 16

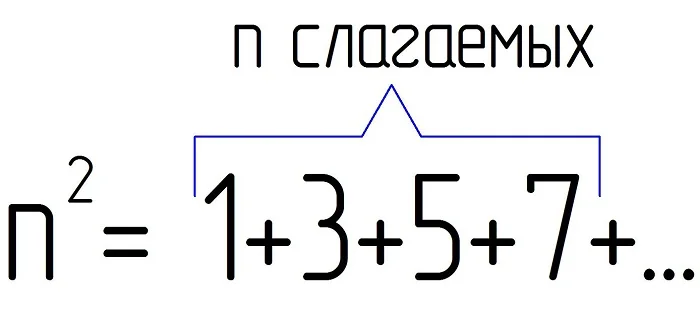
Попытайтесь привести доказательство этого факта. Если не получается, то просто посмотрите на следующую картинку:

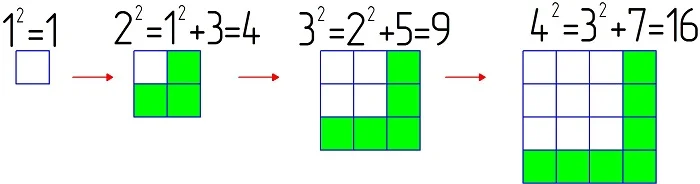
Количество клеточек под каждым числом соответствует его квадрату. Видно, что для получения каждого следующего квадрата нужно добавить к предыдущему нечетное количество клеточек (выделены зеленым цветом), чтобы «достроить» его до «полного» квадрата.

Важно отметить, что в арифметических выражениях операция возведения в степень выполняется до умножения и сложения. Рассмотрим пример

Пусть надо вычислить значение выражения:

-52 + 54/(-3)3

Решение:

Поставим последовательность выполнения операций:

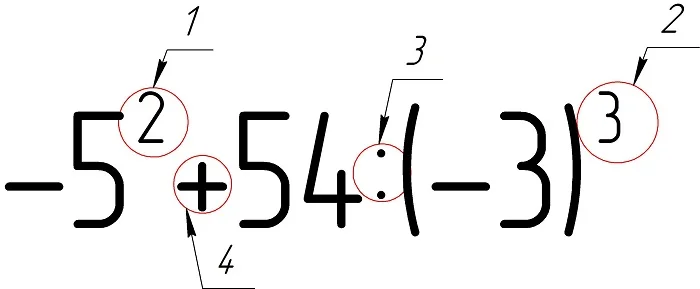
Выполним арифметические операции:

1) 52 = 5*5 = 25

2) (-3)3 = (-3)*(-3)*(-3) = -27

3) 54/(-27) = -2

4) -25+(-2) = -27

Ответ: – 27.

Обратите внимание, что самый первый минус в выражении относится не к пятерке, которую возводят в квадрат, а ко всему квадрату. То есть здесь сначала надо возвести 5 в квадрат, а потом изменить знак выражения. Если бы в этом примере была запись

Если бы в этом примере была запись

(-5)2 + 54/(-3)3

то тогда в первом действии мы получили бы

(-5)*(-5) = 25

А в четвертом выполняли бы сложение

25 + (-2) = 23

То есть, если необходимо возвести в степень отрицательное число, то его следует записать в скобках:

(-2)4 = (-2)*(-2)*(-2)*(-2) = 16

-24 = -2*2*2*2 = -16

Одночлены и многочлены от нескольких переменных

      Одночленом (мономом) от переменных   x₁ ,  x₂ , … , x_n   называют выражение вида:

где   c   – произвольное число, называемое коэффициентом одночлена, а символами

i₁ ,  i₂ , … i_n

обозначены целые неотрицательные числа.

      Таким образом, одночлен от нескольких переменных является произведением числа на несколько букв, каждая из которых входит в одночлен .

      Степенью одночлена называют сумму степеней всех входящих в него букв, т.е. сумму целых неотрицательных чисел:

i₁ +  i₂ + … + i_n .

      Число   c   называют коэффициентом одночлена.

      Пример. Степень одночлена

равна   3,   а коэффициент равен   – 0,83 .

      Два одночлена равны, если, во-первых, у них равны коэффициенты, а во-вторых, одночлены состоят из одних и тех же букв, которые входят в них с соответственно равными показателями степеней.

      Алгебраическая сумма одночленов от нескольких переменных носит название многочлена или полинома от нескольких переменных. Например,

      Степенью многочлена от нескольких переменных называют наивысшую степень входящих в него одночленов.

      В частности, степень многочлена

равна   8.

      Многочлен от нескольких переменных называют однородным многочленом, если степени всех входящих в него одночленов равны. В этом случае степень многочлена равна степени каждого входящего в него одночлена.

      Например, многочлен

является однородным многочленом степени   3.

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Приведение одночлена к стандартному виду

Рассмотрим следующий одночлен:

Этот одночлен выглядит не очень аккуратно. Чтобы сделать его проще, нужно привести его к так называемому стандартному виду.

Приведение одночлена к стандартному виду заключается в перемножении однотипных сомножителей, входящих в этот одночлен. То есть числа нужно перемножать с числами, переменные с переменными, степени со степенями. В результате этих действий получается упрощённый одночлен, который тождественно равен предыдущему.

Ещё один нюанс заключается в том, что в одночлене степени можно перемножать только в том случае, если они имеют одинаковые основания.

Итак, приведём одночлен 3a25a3b2 к стандартному виду. В этом одночлене содержатся числа 3 и 5. Перемножим их, получим число 15. Записываем его:

15

Далее в одночлене 3a25a3b2 содержатся степени a2 и a3, которые имеют одинаковое основание a. Из тождественных преобразований со степенями известно, что при , основание оставляют без изменений, а показатели складывают. Тогда перемножение степеней a2 и a3 даст в результате a5. Записываем a5 рядом с числом 15

15a5

Далее в одночлене 3a25a3b2 содержится степень b2. Её не с чем перемножать, поэтому она остаётся без изменений. Записываем её как есть к новому одночлену:

15a5b2

Мы привели одночлен 3a25a3b2 к стандартному виду. В результате получили одночлен 15a5b2

3a25a3b2 = 15a5b2

Числовой сомножитель 15 называют коэффициентом одночлена. Приводя одночлен к стандартному виду, коэффициент нужно записывать в первую очередь, и только потом переменные и степени.

Если коэффициент в одночлене отсутствует, то говорят, что коэффициент равен единице. Так, коэффициентом одночлена abc является 1, поскольку abc это произведение единицы и abc

abc = 1 × abc

А коэффициентом одночлена −abc будет −1, поскольку −abc это произведение минус единицы и abc

−abc = −1 × abc

Степенью одночлена называют сумму показателей всех переменных входящих в этот одночлен.

Например, степенью одночлена 15a5b2 является 7. Это потому что переменная a имеет показатель 5, а переменная b имеет показатель 2. Отсюда 5 + 2 = 7. Показатель числового сомножителя 15 считать не нужно, поскольку нас интересуют только показатели переменных.

Ещё пример. Степенью одночлена 7ab2 является 3. Здесь переменная a имеет показатель 1, а переменная b имеет показатель 2. Отсюда 1 + 2 = 3.

Если одночлен не содержит переменных или степеней, а состоит из числа, то говорят, что степень такого одночлена равна нулю. Например, степень одночлена 11 равна нулю.

Не следует путать степень одночлена и степень числа. Степень числа это произведение из нескольких одинаковых множителей, тогда как степень одночлена это сумма показателей всех переменных входящих в этот одночлен. В одночлене 11 нет переменных, поэтому его степень равна нулю.

Пример 1. Привести одночлен 5xx3ya2 к стандартному виду

Перемножим числа 5 и 3, получим 15. Это будет коэффициент одночлена:

15

Далее в одночлене 5xx3ya2 содержатся переменные x и x. Перемножим их, получим x2.

15×2

Далее в одночлене 5xx3ya2 содержится переменная y, которую не с чем перемножать. Записываем её без изменений:

15x2y

Далее в одночлене 5xx3ya2 содержится степень a2, которую тоже не с чем перемножать. Её также оставляем без изменений:

15x2ya2

Получили одночлен 15x2ya2, который приведён к стандартному виду. Буквенные сомножители принято записывать в алфавитном порядке. Тогда одночлен 15x2ya2 примет вид 15a2x2y.

Поэтому, 5xx3ya2 = 15a2x2y.

Пример 2. Привести одночлен 2m3n × 0,4mn к стандартному виду

Перемножим числа, переменные и степени по отдельности.

2m3n × 0,4mn = 2 × 0,4 × m3 × m × n × n = 0,8m4n2

Числа, переменные и степени при перемножении разрешается заключать в скобки. Делается это для удобства. Так, в данном примере перемножение чисел 2 и 0,4 можно заключить в скобки. Также в скобки можно заключить перемножение m3 × m и n × n

2m3n × 0,4mn = (2 × 0,4) × (m3 × m) × (n × n) = 0,8m4n2

Но желательно выполнять все элементарные действия в уме. Так, решение можно записать значительно короче:

2m3n × 0,4mn = 0,8m4n2

Но чтобы в уме приводить одночлен к стандартному виду, тема и должна быть изучена на хорошем уровне.

Одночлены и многочлены от одной переменной

      Одночленом (мономом) от переменной   x   называют   x ,  умноженную на число.

      , в которую возведена переменная   x,   называют степенью одночлена, а числовой множитель – коэффициентом одночлена.

      Если в одночлене степень переменной   x   не умножена ни на какое число, то считается, что коэффициент одночлена равен   1.

      Степень одночлена, являющегося числом, равняется нулю.

      Примеры одночленов от переменной   x:

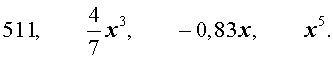
      Алгебраической суммой одночленов от переменной   x   называют один или несколько одночленов, соединенных между собой знаками сложения и вычитания. Аналогично определяется алгебраическая сумма чисел.

      Алгебраическую сумму одночленов от переменной   x   также называют многочленом или полиномом от переменной   x.   Например, многочленом является выражение

2×2 – 45x + 28×5 .

      Степенью многочлена называют наивысшую степень входящих в него одночленов.

      В частности, многочлен

ax + b ,

где буквами   a   и   b   обозначены произвольные числа, причем число   a    отлично от нуля, является многочленом первой степени.

      Многочлен

ax2 + bx + c ,

где буквами   a,   b   и   c   обозначены произвольные числа, причем число   a   отлично от нуля, является многочленом второй степени и называется квадратным трехчленом.

      Двучленом называется многочлен, состоящий из двух одночленов, трехчленом называется многочлен, состоящий из трех одночленов.

      Многочлен всегда можно расположить по возрастанию или по убыванию степеней входящих в него одночленов:

3 + 24x – 2×2 – x5 ;         – x5 – 2×2 + 24x + 3 .

      Число α называется корнем многочлена   p(x),   если

p(α) = 0.

      Например, квадратный трехчлен

x2 – 3x + 2

имеет два корня   x = 1   и   x = 2 .

Деление одночленов

Одночлен можно разделить на другой одночлен. Для этого нужно коэффициент первого одночлена разделить на коэффициент второго одночлена, а буквенную часть первого одночлена разделить на буквенную часть второго одночлена. При этом используется правило .

Например, разделим одночлен 8a2b2 на одночлен 4ab. Запишем это деление в виде дроби:

Первый одночлен 8a2b2 будем называть делимым, а второй 4ab — делителем. А одночлен, который получится в результате, назовём частным.

Разделим коэффициент делимого на коэффициент делителя, получим 8 : 4 = 2. В исходном выражении ставим знак равенства и записываем этот коэффициент частного:

Теперь делим буквенную часть. В делимом содержится a2, в делителе — просто a. Делим a2 на a, получаем a, поскольку a2 : a = a2 − 1 = a. Записываем в частном a после 2

Далее в делимом содержится b2, в делителе — просто b. Делим b2 на b, получаем b, поскольку b2 : b = b2 − 1 = b. Записываем в частном b после a

Значит, при делении одночлена 8a2b2 на одночлен 4ab получается одночлен 2ab.

Сразу можно выполнить проверку. При умножении частного на делитель должно получаться делимое. В нашем случае, если 2ab умножить на 4ab, должно получиться 8a2b2

2ab × 4ab = (2 × 4) × (aa) × (bb) = 8a2b2

Не всегда можно первый одночлен разделить на второй одночлен. Например, если в делителе окажется переменная, которой нет в делимом, то говорят, что деление невозможно.

К примеру, одночлен 6xy2 нельзя разделить на одночлен 3xyz. В делителе 3xyz содержится переменная z, которая не содержится в делимом 6xy2.

Проще говоря, мы не сможем найти частное, которое при умножении на делитель 3xyz дало бы делимое 6xy2, поскольку такое умножение обязательно будет содержать переменную z, которой нет в 6xy2.

Но если в делимом содержится переменная, которая не содержится в делителе, то деление будет возможным. В этом случае переменная, которая отсутствовала в делителе, будет перенесена в частное без изменений.

Например, при делении одночлена 4x2y2z на 2xy, получается 2xyz. Сначала разделили 4 на 2 получили 2, затем x2 разделили на x, получили x, затем y2 разделили на y, получили y. Затем приступили к делению переменной z на такую же переменную в делителе, но обнаружили, что такой переменной в делителе нет. Поэтому перенесли переменную z в частное без изменений:

Для проверки умножим частное 2xyz на делитель 2xy. В результате должен получиться одночлен 4x2y2z

2xyz × 2xy = (2 × 2) × (xx) × (yy) × z = 4x2y2z

Но в некоторых дробях, если невозможно выполнить деление, бывает возможным выполнить . Делается это с целью упростить выражение.

Так, в предыдущем примере нельзя было разделить одночлен 6xy2 на одночлен 3xyz. Но можно сократить эту дробь на одночлен 3xy. Напомним, что сокращение дроби это деление числителя и знаменателя на одно и то же число (в нашем случае на одночлен 3xy). В результате сокращения дробь становится проще, но её значение не меняется:

В числителе и знаменателе мы пришли к делению одночленов, которое можно выполнить:

Процесс деления обычно выполняется в уме, записывая над числителем и знаменателем получившийся результат:

Пример 2. Разделить одночлен 12a2b3c3 на одночлен 4a2bc

Пример 3. Разделить одночлен x2y3z на одночлен xy2

Дополнительно упомянем, что деление одночлена на одночлен также невозможно, если одна из степеней, входящая в делимое, имеет показатель меньший, чем показатель той же степени из делителя.

Например, разделить одночлен 2x на одночлен x2 нельзя, поскольку степень x, входящая в делимое, имеет показатель 1, тогда как степень x2, входящая в делитель, имеет показатель 2. Мы не сможем найти частное, которое при перемножении с делителем x2 даст в результате делимое 2x.

Конечно, мы можем выполнить деление x на x2, воспользовавшись свойством степени с целым показателем:

и такое частное при перемножении с делителем x2 будет давать в результате делимое 2x

Но нас пока интересуют только те частные, которые являются так называемыми целыми выражениями. Целые выражения это те выражения, которые не являются дробями, в знаменателе которых содержится буквенное выражение. А частное целым выражением не является. Это дробное выражение, в знаменателе которого содержится буквенное выражение.

Умножение и деление степеней

Пусть нам надо перемножить две выражения с одинаковым основанием, например, 54 и 53. Для этого представим их как произведение множителей:

54 = 5*5*5*5

53 = 5*5*5

Тогда их произведение можно записать как:

54*53 = (5*5*5*5)(5*5*5) = 5*5*5*5*5*5*5 = 57

Получается, что если перемножаются степени с одинаковым основанием, то в результате получается ещё одна степень с таким же основанием, чей показатель равен сумме показателей перемножаемых степеней. В виде формулы это записывается так:

an*am = an+m

Это правило умножения степеней называют основным свойством степени. Доказывается оно так:

Аналогично можно перемножить и более двух чисел. Например,

32*33*34 = 32+3+4 = 39

Теперь попробуем понять, как делить степени с одинаковыми основаниями.

Для этого запишем произведение чисел am–n и an:

am–n * an = am–n+n = am+(n-n) = am+0 = am

Получили, что am–n * an = am. Теперь поделим правую и левую часть равенства этого равенства на an:

Для наглядности рассмотрим случай с конкретными числами. Пусть надо надо вычислить 210:26. Можно записать, что

210-6*26 = 210-6+6 = 210

Поделим правую и левую часть этого равенства на 26:

Получается, что верно следующее правило деления степеней:

Данные правила действуют и в том случае, когда вместо показателя и/или основания используется переменная. Например:

Если в выражении есть и умножение, и деление, то следует сначала сложить показатели перемножаемых чисел, а потом вычесть из нее показатели делителей:

Теперь введем понятие нулевой степени числа. Для этого поделим an на само себя, учитывая уже сформулированные правила деления:

an : an = an-n = a

С другой стороны, любое число (кроме нуля), при делении на само себя дает единицу:

an : an = 1

Из этих двух равенств можно составить третье равенство:

a= 1

Получается, что любое число в нулевой степени равно единице.

К выражению 0 подобная логика неприменима, так как деление на ноль не допускается в алгебре. Поэтому считается, что выражение 0 не имеет смысла, так же как и деление на ноль.

Иногда приходится возводить в степень другую степень. Попытаемся вычислить выражение (23)4:

(23)4 = 23 * 23 * 23 * 23 = 23+3+3+3 = 23*4 = 212

Видно, что нам пришлось перемножить показатели. Верно следующее правило возведения степени в степень:

(an)m = anm

Рассмотрим пример. Необходимо вычислить значение выражения 910:318.

Решение. У делимого и делителя разные основания, поэтому сразу произвести деление не получится. Однако число 9 можно представить как квадрат тройки:

9 = 32

Тогда и выражение можно переписать:

910 : 318 = (32)10 : 318

Далее последовательно выполняем математические операции:

(32)10 : 318 = 32*10 : 318 = 32 : 318 = 320-18 = 32 = 9

Ответ: 9.

Ещё один пример. Необходимо сравнить числа 5300 и 3500.

Решение.

5300 = 53•100 =(53)100 =125100.

3500 =35•100 =(35)100 =243100.

125100<243100, значит, 5300< 3500.

Ответ: 5300< 3500.

Иногда приходится выполнять операции над степенями с разными основаниями, но одинаковыми показателями. Перемножим числа 24 и 34:

24*34 = (2*2*2*2)*(3*3*3*3)

Поменяем местами множители:

(2*2*2*2)*(3*3*3*3) = (2*3)*(2*3)*(2*3)*(2*3) = 6*6*6*6 = 64

Получается, что

24*34 = (2*3)4

Аналогичным образом для любых a и b, а также для любого натурального n справедливым будет равенство:

an•bn = (ab)n.

Такие же рассуждения помогают найти формулу и для деления чисел с одинаковыми показателями:

an:bn = (a:b)n.

Далее решим несколько примеров:

1. Вычислите 56•26.

Решение: 56•26 = (5*2)6 = 106 = 1 000 000

Ответ: 1 000 000.

2. Вычислите 4100•16150•0,5795.

Решение: Перепишем выражение с учетом того факта, что 4 = 22, а 16 = 24:

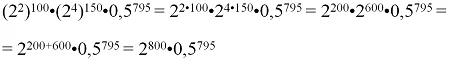
Заметим, что

а потому можно провести замену:

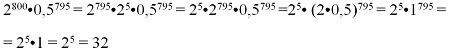
Ответ: 32.

Свойства квадрата одночлена

Свойства квадрата одночлена:

1. Знак не меняется: Квадрат любого одночлена имеет тот же знак, что и исходный одночлен.
2. Степень удваивается: Степень квадрата одночлена в два раза больше степени исходного одночлена.
3. Коэффициент возведения в квадрат: Квадрат одночлена получается путем возведения в квадрат каждого его коэффициента.
4. Произведение одночлена на его сопряженное значение: Умножение одночлена на его сопряженное значение (одночлена с противоположным знаком) приводит к образованию квадрата одночлена.

Примеры квадратов одночленов:

• Квадрат одночлена 2x равен 4x². Здесь коэффициент 2 возводится в квадрат (2² = 4), а степень переменной x удваивается (1 × 2 = 2).
• Квадрат одночлена -3a² равен 9a⁴. Здесь коэффициент -3 возводится в квадрат ((-3)² = 9), а степень переменной a удваивается (2 × 2 = 4).
• Квадрат одночлена 0,5y³ равен 0,25y⁶. Здесь коэффициент 0,5 возводится в квадрат (0,5² = 0,25), а степень переменной y удваивается (3 × 2 = 6).

Умножение одночленов

Одночлены можно перемножать. Чтобы перемножить одночлены, нужно перемножить их числовые и буквенные части.

Пример 1. Перемножить одночлены 5x и 8y

Перемножим числовые и буквенные части по отдельности. Для удобства перемножаемые сомножители будем заключать в скобки:

5x × 8y = (5 ×  × (x × y) = 40xy

Пример 2. Перемножить одночлены 5x2y3 и 7x3y2c

Перемножим числовые и буквенные части по отдельности. В процессе умножения будем применять правило перемножения степеней с одинаковыми основаниями. Перемножаемые сомножители будем заключать в скобки:

5x2y3 × 7x3y2c = (5 × 7) × (x2x3) × (y3y2) × c = 35x5y5c

Пример 3. Перемножить одночлены −5a2bc и 2a2b4

−5a2bc × 2a2b4 = (−5 × 2) × (a2a2) × (bb4) × c = −10a4b5c

Пример 4. Перемножить одночлены x2y5 и (−6xy2)

x2y5 × (−6xy2) = −6 × (x2x) × (y5y2) = −6x3y7

Пример 5. Найти значение выражения 

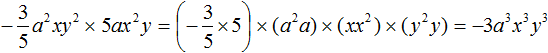
Коэффициент

Запомним: 

В случаях, когда коэффициент в результате вычислений оказался равен $1$, он обычно не записывается, но подразумевают, что он есть. Если коэффициент получился равным $-1$, то в стандартном виде минус без единицы записывают в самом начале.

Заметим, что после тождественных преобразований можно привести к стандартному виду абсолютно любой одночлен.

Пример

Запишем в стандартном виде выражение: $\frac {3}{7}\times {j^{13}}\times m^{29}\times c^{18}\times 0,25\times {j^2}$. 

Решение

При умножении числовых множителей сначала преобразуем десятичную дробь $0,25$ в простую и получим $\frac {1}{4}$. Тогда стандартный вид этого одночлена будет: $$\frac {3}{28}\times c^{18}\times {j^{15}}\times m^{29}$$

{"questions":}

Одночлен — что такое в алгебре

Выражения в алгебре бывают двух типов:

• буквенные, то есть те, что содержат буквы;
• числовые, в которых буквы отсутствуют.

Буквенные множители в некоторых случаях называют переменными.

В том случае, когда в одночлене числовой коэффициент отсутствует, этот числовой коэффициент считают равным единице (1). К примеру, для одночлена ас числовой коэффициент соответствует 1. Это объясняется тем, что при умножении одночлена на 1, его значение не меняется. Единицу не принято писать перед одночленом.

Не записывают и -1 перед одночленом. В качестве альтернативного варианта используют знак минуса без единицы. В результате по умолчанию числовой коэффициент составляет -1, хоть и не фигурирует в краткой записи. К примеру, одночлен -xyz имеет числовой коэффициент -1.

Примеры записей одночленов и их соответствующих коэффициентов: