Гетеродинный измеритель резонанса

Технологические Инновации и Будущее Резонанса напряжений

Резонанс напряжений остается актуальной технологией в мире электроники и электротехники, и его будущее обещает новые инновации и применения:

1. Сети Связи и Интернет вещей (IoT):
   С развитием Интернета вещей, резонансные цепи могут быть использованы для селективной фильтрации и усиления сигналов в сетях связи IoT. Это поможет в повышении эффективности передачи данных и увеличении дальности связи устройств.
2. Беспроводная Зарядка:
   Технологии беспроводной зарядки могут использовать резонансные цепи для оптимизации передачи энергии между источниками и приемниками. Это упростит зарядку устройств и расширит ее область применения.
3. Эффективность Солнечных Панелей:
   Резонансные цепи могут быть применены для увеличения эффективности солнечных батарей, что сделает солнечные системы более доступными и эффективными.
4. Электромобили и Электроника в Транспорте:
   В автомобильной и железнодорожной отраслях резонансные цепи могут использоваться для улучшения энергоэффективности и качества сигналов в системах безопасности и связи.
5. Медицинская Техника:
   В медицинской сфере резонансные цепи могут быть применены для усиления слабых биологических сигналов, таких как сигналы сердца или мозга, что улучшит точность и надежность диагностических устройств.
6. Квантовые Технологии:
   В квантовых вычислениях и связи резонанс может играть важную роль в манипулировании квантовыми состояниями и фотонами.
7. Сверхпроводимость:
   В области сверхпроводимости резонанс может применяться для создания более эффективных сверхпроводниковых устройств и схем.
8. Экологические Технологии: Резонансные цепи могут использоваться в области управления и мониторинга окружающей среды, например, для дистанционного зондирования и анализа данных о климате.
9. Космическая Техника:
   Резонансные цепи могут быть важными элементами в космических аппаратах и телекоммуникационных системах, где эффективность передачи данных и энергии играет критическую роль.

С учетом постоянного развития технологий и роста потребностей в эффективности и устойчивости, резонанс напряжений продолжит играть важную роль в электронике и электротехнике. Новые инновации будут способствовать расширению его применений и улучшению эффективности систем и устройств.

Применение на практике

Рассмотрим, какая польза и вред резонанса токов и напряжений. Наибольшую пользу явления резонанса принесли в радиопередающей аппаратуре. Простыми словами, а схеме приемника установлены катушка и конденсатор, подключенные к антенне. С помощью изменения индуктивности (например, перемещая сердечник) или величины емкости (например, воздушным переменным конденсатором) вы настраиваете резонансную частоту. В результате чего напряжение на катушке повышается и приемник ловит определенную радиоволну.

Вред эти явления могут на нести в электротехнике, например, на кабельных линиях. Кабель представляет собой распределенную по длине индуктивность и емкость, если на длинную линию подать напряжение в режиме холостого хода (когда на противоположном от источника питания конце кабеля нагрузка не подключена). Поэтому есть опасность того, что произойдет пробой изоляции, во избежание этого подключается нагрузочный балласт. Также аналогичная ситуация может привести к выходу из строя электронных компонентов, измерительных приборов и другого электрооборудования – это опасные последствия возникновения этого явления.

Емкость и индуктивность в цепи переменного тока

Если в цепях постоянного тока емкость в общем смысле представляет собой разорванный участок цепи, а индуктивность — проводник, то в переменном конденсаторы и катушки представляют собой реактивный аналог резистора.

Реактивное сопротивление катушки индуктивности определяется по формуле:

Векторная диаграмма:

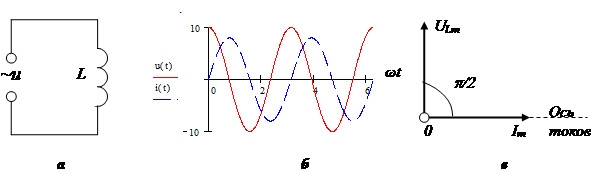
Реактивное сопротивление конденсатора:

Здесь w — угловая частота, f — частота в цепи синусоидального тока, L — индуктивность, C — емкость.

Векторная диаграмма:

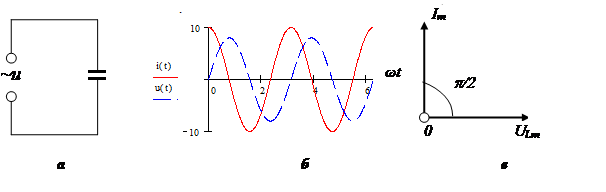
Стоит отметить, что при расчете соединенных последовательно реактивных элементов используют формулу:

Обратите внимание, что емкостная составляющая принимается со знаком минус. Если в цепи присутствует еще и активная составляющая (резистор), то складывают по формуле теоремы Пифагора (исходя из векторной диаграммы):. От чего зависит реактивное сопротивление? Реактивные характеристики зависят от величины емкости или индуктивности, а также от частоты переменного тока

От чего зависит реактивное сопротивление? Реактивные характеристики зависят от величины емкости или индуктивности, а также от частоты переменного тока.

Если посмотреть на формулу реактивной составляющей, то можно заметить, что при определенных значениях емкостной или индуктивной составляющей их разность будет равна нулю, тогда в цепи останется только активное сопротивление. Но это не все особенности такой ситуации.

Типы резонанса

В физике существует большое количество видов резонанса. Все они чем-то схожи и чем-то различны, а именно – своими признаками и природой появления. Среди них можно выделить:

• механический и акустический резонансы;
• электрический;
• оптический;
• орбитальные колебания;
• атомный, частичный и молекулярный.

График процесса в колебательном контуре

В следующих подразделах будет более подробно описан каждый из этих видов.

Механический и акустический

Наиболее популярным и очевидным механическим видом будут резонирующие качели, которые были упомянуты раньше. Если толкать их в определенные моменты с учетом их частоты, то размах их движения увеличится или затухнет, если силу не прикладывать.

Основаны механические резонаторы на преобразовании потенциальной энергии в кинетическую и обратно. Если рассматривать маятник, то вся его энергия – потенциальная в состоянии покоя. Она преобразуется в кинетическую, когда он проходит нижнюю точку на своей максимальной скорости.

Приборы для организации резонанса

Важно! Некоторые механические системы способны запасать потенциальную энергию и использовать ее в различных формах. В пример можно привести пружину, которая запасет сжатие, являющееся энергией связи атомов

Акустический тип резонирования можно встретить в некоторых музыкальных инструментах по типу гитары, скрипки, пианино

Они имеют основную резонансную частоту, которая зависит от длины, массы и силы натяжения струн

Акустический тип резонирования можно встретить в некоторых музыкальных инструментах по типу гитары, скрипки, пианино. Они имеют основную резонансную частоту, которая зависит от длины, массы и силы натяжения струн.

Акустическое резонирование помогает людям найти дефекты в трубопроводе

Кроме основной частоты, струны этих музыкальных инструментов обладают резонансом на высших гармонических колебаниях основной частоты. Если струну дернуть, то она начнет колебаться на всех частотах, которые присущи данному импульсу, но частоты, несовпадающие с резонансом, очень быстро затухнут, и человеческое ухо услышит только гармонические колебания, являющиеся нотами.

Акустические системы, микрофоны и громкоговорители не терпят резонанса отдельных частей своего корпуса, так как это снижает равномерность их амплитудно-частотной характеристики и ухудшает качество воспроизведения звуков.

Струны создают акустический резонанс

Резонанс электрический

В электронике резонанс также имеется. Им называется состояние или режим пассивной электроцепи, содержащей катушки и конденсаторы, при котором ее входное реактивное электросопротивление и проводимость будут нулевыми. Это означает, что при резонансе ток на входе в цепь, если он есть, будет совпадать по фазе с напряжением.

Колебательный контур

В электричестве резонирование достигается тогда, когда индукция и емкость реакции уравновешиваются. Это равенство и позволяет энергии производить циркуляцию между индуктивными элементами и их магнитным полем, и полем электрического типа в конденсаторе.

Сам механизм резонанса основан на том, что МП индуктивности создает электроток, который заряжает конденсатор, разрядка его и создает это магнитное поле. Простейшее устройство, основанное на этом взаимодействии, – колебательный контур, способный производить резонанс напряжений и токов.

Модель светового оптического резонирования

Оптический резонанс

И в оптическом диапазоне есть резонанс. Один из самых популярных его примеров – резонатор Фабри-Перо. Он образован несколькими зеркалами, между которыми устанавливается так называемая резонирующая стоячая волна. Кроме этого используются кольцевые системы резонирования с бегущей волной и микроскопические резонаторы со стоячими волнами.

Схема колебательного контура

Орбитальные колебания

Колебания в астрофизике представляют собой ситуации, когда есть два или более небесных объекта, которые имеют некоторые периоды обращения, соотносящиеся, как небольшие натуральные числа. В результате этого воздействия небесные объекты оказывают друг на друга постоянное гравитационное притяжение. Оно и производит стабилизацию их орбит.

Колебания есть и на орбитах небесных тел

Резонанс напряжений

Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:

и конденсатор в 1000 пФ

Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.

Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора  падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор — это не есть хорошо, но что не сделаешь ради науки!

Ну что же, приступим ;-). Давайте сначала посчитаем  резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.

Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:

Размах амплитуды 4 Вольта

Хотя на генераторе частоты  размах  более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.

Теперь небольшой прикол

Вот этот сигнал мы подаем на наш последовательный колебательный контур:

Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.

Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:

Смотрим напряжение на конденсаторе:

Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!

Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:

Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!

Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14,  и цепляю поочередно к ним лампочку:

Как видите — полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока — увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!

Объяснение резонанса напряжения

При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.

При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение U_L = IX_L , а на конденсаторе U_C = IX_C . А так как при резонансе у нас X_L = X_C , то получаем что U_L = U_C , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.

Резонанс в линейных системах с одной степенью свободы

К этой группе можно причислить рассмотренные последовательные и параллельные электрические схемы. Механический пример – пружина с грузом, который способен перемещаться только по вертикальной прямой. Исключены порывы ветра, вибрации, другие «паразитные» внешние воздействия. В подобных условиях можно применять типовые формулы для систем линейного типа.

Отмеченная выше добротность является определяющим фактором для избирательности по частоте. Сужение ширины резонансного диапазона помогает улучшить характеристики приемных и передающих устройств. Кроме экономного расходования электроэнергии, при правильном расчете схемы существенно улучшается помехозащищенность.

Последовательное соединение

Катушка индуктивности и последовательно включенный в цепь конденсатор вместе особенным образом воздействуют на генератор, от которого запитана цепь. Также они влияют на фазовые соотношения напряжения и тока:

1. Первый элемент сдвигает фазу, при этом напряжение начинает обгонять ток примерно на четверть периода.
2. Второй элемент действует иначе. Он заставляет ток обгонять напряжение также на одну четвертую часть периода фазы.

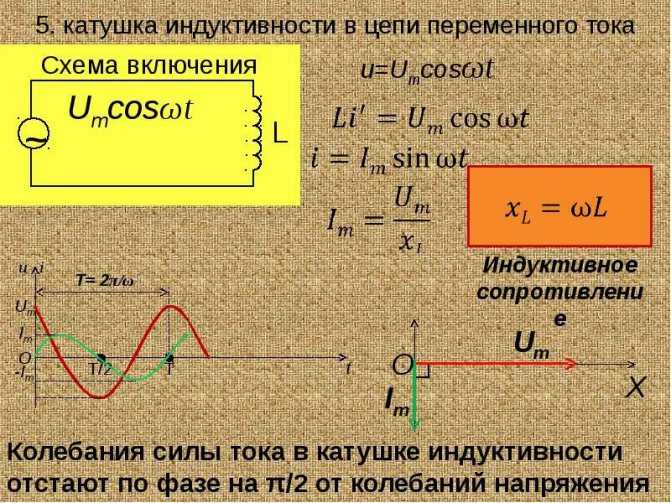
Индуктивное сопротивление действует на смещение фаз, из-за чего его можно считать противоположным работе емкостного сопротивления. В результате итоговый сдвиг фаз между напряжением и током в цепи зависит от суммарного действия индуктивного и емкостного сопротивлений, а также соотношения между ними. От этого тоже зависит характер цепи.

Общее реактивное сопротивление определить просто. Необходимо сложить два показателя сопротивления:

1. Индуктивное от катушки.
2. Емкостное от конденсатора.

Из-за того, что они оказывают противоположное воздействие, одному из них присваивается отрицательный знак (обычно ёмкостному сопротивлению конденсатора). Тогда общее реактивное сопротивление можно найти так: из показателя катушки вычесть конденсатор. Если общее напряжение разделить на найденный параметр, то по закону Ома получится сила тока. Эту формулу можно легко изменить, переведя на напряжение. Оно будет равно произведению силы тока и разности двух сопротивлений (индуктивное берется с катушки, а емкостное — с конденсатора).

Если раскрыть скобку, то первое значение отразит действительный показатель части общего напряжения, которая старается преодолеть сопротивление. Второе — слагающая всего напряжения, которая пытается преодолеть емкостный параметр. Так, общее напряжение можно рассматривать как сумму этих слагаемых.

Для определения этого значения нужно вычислить квадратный корень из суммы двух частей:

1. Общее активное сопротивление, возведенное в квадрат.
2. Квадрат разности индуктивного и емкостного сопротивлений, то есть общее реактивное.

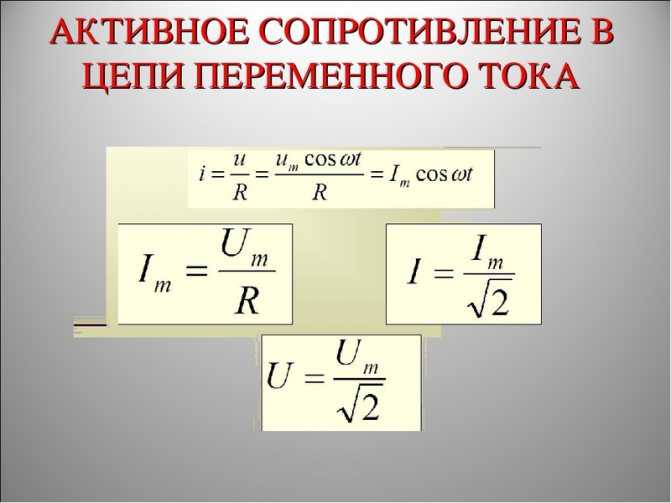
Общие сведения

Электрическим сопротивлением проводника является свойство проводить электрический ток. Для построения и расчета колебательного контура необходимо знать способы нахождения активного и реактивного сопротивлений. Сопротивление для цепей, питающихся от переменного тока (ЦПТ), бывает следующих видов: активное, реактивное и полное.

Активным сопротивлением является обыкновенный резистор. Реактивное состоит из следующих типов нагрузки: индуктивное и емкостное. Индуктивное (Xl) — сопротивление катушки индуктивности в цепи переменного тока, а емкостное (Xc) определяется наличием емкости в цепи (конденсатора).

Активное сопротивление

Активным сопротивлением в ЦПТ называется наличие любой нереактивной нагрузки. Его можно рассчитать следующими способами: при помощи измерения величины сопротивления и расчетным методом. Для измерения R применяется прибор, который называется омметром. Омметр входит в состав комбинированных приборов измерения электрических величин, которые называются мультиметрами. Он подключается параллельно нагрузке, причем для проведения измерений следует выключить электрическую цепь, поскольку наличие тока приведет прибор к выходу из строя.

Существует еще один способ, который является расчетным, однако он требует знаний в области физики. При вычислении величины R следует произвести измерения силы тока и напряжения, а точнее, их амплитудных значений (Uм и Iм соответственно). Это возможно сделать при помощи соответствующих приборов.

Для измерения величины напряжения применяется вольтметр, а силу тока можно измерить при помощи амперметра. Кроме того, эти приборы измеряют только действующие значения напряжения (Uд) и силы тока (Iд). Для расчета амплитудных значений следует воспользоваться следующими формулами:

1. Uм = Uд * sqrt (2).
2. Iм = Iд * sqrt (2).

​Для расчета R, которое можно найти, используя закон Ома для участка цепи (Iм = Uм / R): R = Uм / Iм. Воспользовавшись соотношениями зависимостей амплитудных значений от действующих, возможно рассчитать R: R = Uд * sqrt (2) / Iд * sqrt (2) = Uд / Iд. На практике применяют способ измерения сопротивления омметром.

Другие виды нагрузок

При наличии в ЦПТ катушки индуктивности возникает Xl, которую необходимо только рассчитывать. Индуктивное сопротивление рассчитывается по формуле, для которой необходимы циклическая частота (w) и индуктивность катушки (L): Xl = w * L.

Циклическая частота рассчитывается по следующей формуле, для которой необходимо только знать частоту переменного тока (f) и число ПИ (3,1416): w = 2 * 3,1416 * f. Индуктивность катушки рассчитывается, исходя из значений диаметра катушки (D в мм), числа витков (n) и длины намотки (l): L = (sqr (D/10) * sqr (n)) / (4,5 * D + 10 * l). Если подставить в формулу расчета индуктивного сопротивления все соотношения, то получается: Xl = 2 * 3,1416 * f * (sqr (D/10) * sqr (n)) / (4,5 * D + 10 * l).

Если в ЦПТ присутствует конденсатор с емкостью C, то добавляется еще и емкостное сопротивление — Xl, которое рассчитывается по следующей формуле: Xc = 1 / (w * C) = 1 / (2 * 3,1416 * f * C). Полное сопротивление в ЦПТ обозначается литерой Z и рассчитывается по формуле: Z = sqrt . Если подставить в формулу полного сопротивления соотношения, по которым находятся R, Xl и Xc, то получается следующая формула: Z = sqrt [sqr (Uд / Iд) +sqr ((1 / (2 * 3,1416 * f * C)) — (2 * 3,1416 * f * (sqr (D/10) * sqr (n)) / (4,5 * D + 10 * l))]. Для упрощения вычисления можно рассчитать отдельно значения R, Xc и Xl.

Применение резонанса напряжений

Одной из областей, где применяется резонанс напряжений, является электротехника. Например, это явление используется при проектировании и расчете резонансных контуров в электрических цепях, а также в резонансных инверторах и других устройствах, работающих на переменном токе. Резонанс напряжений позволяет достичь максимальной энергоэффективности и оптимальных рабочих характеристик таких систем.

Резонансное напряжение также активно используется в медицине. Например, в экстракорпоральной литотрипсии (разрушение камней в почках) применяется резонансная волна, которая разрушает камни без повреждения окружающих тканей. Также резонансное напряжение применяется в некоторых методах диагностики, например, в магнитно-резонансной томографии (МРТ).

Большое значение имеет применение резонанса напряжений в радиотехнике и связи. Резонансные контуры используются для выборки определенных частот из спектра сигналов, что позволяет передавать и принимать информацию с увеличенной эффективностью. Кроме того, резонаторы и резонансные фильтры используются в различных устройствах связи, таких как радиопередатчики и радиоприемники, для усиления и фильтрации сигналов.

Очень важным применением резонанса напряжений является область активного управления вибрациями и колебаниями. Резонансные системы используются для подавления и контроля нежелательных вибраций, например в автомобилях, самолетах и промышленных машинах. Также резонансные системы применяются в широком диапазоне устройств – от электронных гитар до мостов и зданий, позволяя обеспечить надежность и безопасность эксплуатации.

Таким образом, резонанс напряжений является важным явлением, которое находит широкое применение в различных областях науки и техники. Учитывая его особенности, его применение позволяет достичь высокой энергоэффективности, усилить или фильтровать сигналы, а также контролировать и подавлять нежелательные колебания и вибрации.

Резонанс напряжений

При последовательном соединении активного элемента $r$, емкостного $С$ и индуктивного $L$ в цепях переменного тока может возникать такое физическое явление, как резонанс напряжений. Колебания источника напряжения в этом случае будут равны по частоте колебаниям контура. При этом известна как полезность (например, в радиотехнике) этого явления, так и негативные последствия (для электрических установок большой мощности), например, при резком скачке напряжения в системах возможно возникновение неисправности или даже пожара.

Лень читать?

Задай вопрос специалистам и получи ответ уже через 15 минут!

Задать вопрос

Резонанс напряжений обычно достигается тремя способами:

• подбором индуктивности катушки;
• подбором емкости конденсатора;
• подбором угловой частоты $w_0$.

При этом все значения емкости, частоты и индуктивности определяются с использованием формул:

$L_0 = \frac{1}{w^2C}$

$C_0 = \frac{1}{w^2L}$

Частота $w_0$ считается резонансной. При условии неизменности в цепи и напряжения, и активного сопротивления $r$, сила тока при резонансе напряжения в ней окажется максимальной и равной:

$\frac{U}{r}$

Это предполагает полную независимость силы тока от реактивного сопротивления цепи. В ситуации, когда реактивные сопротивления $XC = XL$ по своему значению будут превосходить активное сопротивление $r$, на зажимах катушки и конденсатора появится напряжение, существенно превосходящее напряжение на зажимах цепи.

Кратность превышения на зажимах емкостного и индуктивного элемента напряжения по отношению к сети определяется выражением:

$Q = \frac{U_c0}{U}$

Величина $Q$ характеризует резонансные свойства контура, называясь при этом добротностью контура. Также резонансные свойства характеризуются величиной $\frac{1}{Q}$, то есть — затуханием контура.

Как определяется резонанс

На примере электричества и резонирования напряжений определить его можно специальными приборами: вольтметром или осциллографом. Для этого делают измерения напряжений во время настройки резонирования. При максимальном напряжении резонанс будет достигнут

Важно понимать, в какой именно системе достигается резонанирование. Например, в трансформаторе «Тесла» напряжение может достигать миллионов вольт и для настройки достаточно поднести щупы на небольшое расстояние к нему и менять параметры, смотря на изменение напряжения. Когда настройка будет достигнута и напряжение будет максимальным – это и будет резонирование

Когда настройка будет достигнута и напряжение будет максимальным – это и будет резонирование.

Вам это будет интересно Как рассчитать сопротивление цепи

Прибор для демонстрации резонанса маятников

Физическое обоснование резонанса напряжений

Основой физического обоснования резонанса напряжений является связь между силой, приложенной к системе, и реакцией системы на это воздействие. В колебательной системе, состоящей из масс и пружин, существуют собственные частоты колебаний. Если внешняя сила действует с частотой, близкой к собственной частоте системы, то возникает эффект резонанса.

Основной физический механизм возникновения резонанса напряжений связан с энергией, которая переносится в системе во время колебаний. Энергия переносится от внешней силы к системе через ее граничные элементы, например, пружины. Когда внешняя сила действует с частотой собственных колебаний системы, энергия переносится с максимальной эффективностью.

В резонансном состоянии энергия, переносимая в систему, не только компенсирует потери энергии, но и приводит к ее накоплению в системе. В результате амплитуда колебаний в системе растет, что может привести к резонансным напряжениям. Это происходит из-за недостаточной диссипации энергии в системе, вызванной ее особыми свойствами и соотношениями между массами и жесткостями элементов системы.

Пример	Объяснение
Колебания строительных конструкций под воздействием ветра	Под действием ветра на здание воздействуют пульсации воздушного потока с определенной частотой. Если частота пульсаций близка к собственным частотам колебаний здания, возникает резонанс, который приводит к увеличению амплитуды колебаний и резонансным напряжениям в конструкциях.
Работа двигателя, вызывающая колебания в автомобиле	Колебания, возникающие в автомобиле при работе двигателя, могут быть вызваны совпадением частоты двигателя с собственной частотой колебаний кузова. Это приводит к резонансу и усилению амплитуды колебаний, что может вызвать резонансные напряжения в автомобиле.
Колебания мостов при движении транспорта	Под воздействием движущегося транспорта на мосты возникают колебания с определенной частотой. Если эта частота близка к собственным частотам колебаний моста, возникает резонанс, который приводит к усилению колебаний и резонансным напряжениям.

Таким образом, физическое обоснование резонанса напряжений заключается в переносе энергии в колебательной системе, что приводит к усилению амплитуды колебаний и возникновению резонансных напряжений.

Положительные и отрицательные стороны резонанса

Высотные мачты и башни, небоскрёбы, мосты и смотровые площадки должны выдерживать возрастание амплитуды своих колебаний в результате внешних воздействий.

У явления резонанса есть плюсы:

• резонаторы на струнных инструментах усиливают гармонику, выполняя усиление стоячих волн;
• колебательный контур радиоприёмных устройств, при настройке на передающую станцию, усиливает принятый сигнал по амплитуде.

Разрушающие свойства этого явления используются при работе перфоратора – во время вибрации при сверлении бетонная стена вступает в резонанс с рабочим инструментом, и происходит разрушение бетона в точке применения.

Плюсы и минусы резонанса