Характеристики
Эквивалентные свойства
Свойство наличия аналогичная организация Элемент граней вокруг каждой вершины может быть заменен любым из следующих эквивалентных условий в определении:
- Все вершины многогранника лежат на сфере.
- Все двугранные углы многогранники равны
- Все фигуры вершин многогранника являются правильными многоугольниками.
- Все телесные углы многогранника совпадают.
Концентрические сферы
У правильного многогранника есть все три связанных сферы (у других многогранников нет хотя бы одного вида), имеющих общий центр:
- insphere, касательная ко всем граням.
- Межсфера или средняя сфера, касательная ко всем ребрам.
- A описанная сфера, касательная ко всем вершинам.
Симметрия
Правильные многогранники симметричный всех многогранников. Они находятся всего в трех группах симметрии, которые названы в честь Платоновых тел:
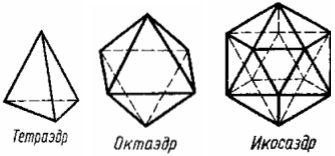
- Тетраэдр
- Октаэдрический (или кубический)
- Икосаэдрический (или додекаэдрический)
Любые формы с икосаэдрической или октаэдрической симметрией также будут иметь тетраэдрическую симметрию.
Эйлерова характеристика
Пять Платоновых тел имеют Эйлерову характеристику, равную 2. Это просто отражает то, что поверхность является топологической двумерной сферой, и это также верно, например, любого многогранника, звездообразного относительно некоторой внутренней точки.
Внутренние точки
Сумма расстояний от любой точки внутри правильного многогранника до сторон не зависит от местоположения точки (это расширение Вивиани. теорема.) Однако обратное неверно, даже для тетраэдров.
Классификация двумерных полиэдров
Наша задача состоит в том, чтобы связать символы Шлефли {n,m} с количеством вершин, ребер и граней. Для примера рассмотрим тетраэдр и попытаемся выяснить зависимость.
-
У тетраэдра 4 грани, в каждой из которых три угла. Т.о., если умножить 4 грани на 3 угла получим 12 чего-то там, что в два раза больше, чем количество его ребер (каждое из них посчитано дважды).
-
В каждой вершине сходятся m=3 граней. Если умножить 4 вершины на 3 грани получим 12 чего-то там, что в два раза больше количества ребер (их так же считали дважды
В качестве упражнения можно посчитать для куба. В каждой из 6 граней 4 угла, отсюда (6*4)/2 = 12 ребер. В каждой из 8 вершин сходятся 3 грани, что даёт (8*3)/2 = 12 ребер.
Получили три уравнения с тремя неизвестными, которые будем сейчас решать, чтобы получить в чистом виде зависимость от составляющих символа Шлефли:
Такую систему уравнений удобно решить, воспользовавшись параметризацией через некое t. Во второй строчке подставили данные в уравнение Эйлера и затем привели дроби к одному знаменателю
Из очевидных соображений, что t > 0 , мы должны потребовать положительности знаменателя. Остается в целых числах решить соответствующее неравенство:
Не только лишь все натуральные числа при умножении дают результат, меньший 4, поэтому у нас не так много работы:
А теперь вспомните рисунок с символами Шлефли для платоновых тел! Как видите, мы получили одно и то же с помощью решения обычной системы уравнений! Алгебраизация — один из самых мощных способов исследования окружающего нас мира.
Характерные количества
В следующей таблице представлены различные характерные размеры правильного выпуклого икосаэдра:
| Размеры икосаэдра, длина ребра которого | |
|---|---|
| Двугранный угол | αзнак равноπ-Arcsin(23)рвd≈138∘11′23″{\ displaystyle \ alpha \, = \, \ pi — \ arcsin \ left ({\ frac {2} {3}} \ right) \, \ mathrm {rad} \ приблизительно 138 ^ {\ circ} 11’23 ‘ ‘} |
| Радиус описанной сферы | реИкстзнак равнов22+φзнак равнов2φ5≈,95в{\ displaystyle r_ {ext} \, = \, {\ frac {a} {2}} {\ sqrt {2+ \ varphi}} = \, {\ frac {a} {2}} {\ sqrt {\ varphi {\ sqrt {5}}}} \ приблизительно 0 {,} 95 \, a} |
| Радиус вписанной сферы | рянеттзнак равнов63(1+φ)≈,76в{\ displaystyle r_ {int} \, = \, {\ frac {a} {6}} {\ sqrt {3}} (1+ \ varphi) \ приблизительно 0 {,} 76 \, a} |
| Ребро описанного куба | противзнак равновφ≈1,62в{\ Displaystyle с \, = \, а \ varphi \ приблизительно 1 {,} 62 \, а} |
| Высота икосаэдра (расстояние между двумя противоположными гранями) | часзнак равно2рянеттзнак равнов33(1+φ)≈1,51в{\ displaystyle h \, = 2r_ {int} \, = \, {\ frac {a} {3}} {\ sqrt {3}} (1+ \ varphi) \ приблизительно 1 {,} 51 \, а} |
| Объем | Vзнак равно5(1+φ)6в3≈2,18в3{\ displaystyle V \, = \, {\ frac {5 (1+ \ varphi)} {6}} a ^ {3} \ приблизительно 2 {,} 18 \, a ^ {3}} |
| Занятая доля описанной сферы | VVsзнак равно2+φπ≈,61 год{\ displaystyle {\ frac {V} {V_ {s}}} \, = \, {\ frac {\ sqrt {2+ \ varphi}} {\ pi}} \ приблизительно 0 {,} 61} |
| Область | Взнак равно53в2≈8,66в2{\ Displaystyle A \, = \, 5 {\ sqrt {3}} a ^ {2} \ приблизительно 8 {,} 66 \, a ^ {2}} |
| Изопериметрический фактор | 36πV2В3знак равноφ4π153≈,83{\ displaystyle 36 \ pi {\ frac {V ^ {2}} {A ^ {3}}} = \, {\ frac {\ varphi ^ {4} \ pi} {15 {\ sqrt {3}}} } \ приблизительно 0 {,} 83} |
Двугранный угол — это угол между двумя плоскостями, каждая из которых содержит грань икосаэдра, причем две грани имеют общий край.
5.3.5 Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр)
Лекция: Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр)
В школьном курсе геометрии изучается пять основных многогранников. На рисунке ниже Вы можете ознакомится с каждым из них. Название всех многогранников исходит из количества граней.
Тетраэдр
Тетраэдр – это правильный многогранник, который имеет грани в виде треугольников, именно поэтому в каждой вершине такой фигуры сходится 3 ребра.
Октаэдр
Октаэдр – правильный многогранник, который так же имеет грани в виде правильных треугольников, однако, в каждой вершине сходится по четыре ребра.
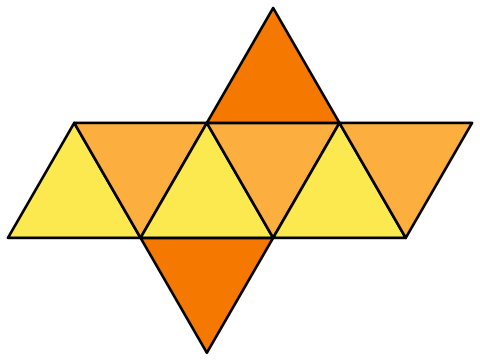
Гексаэдр (куб)
Гексаэдр (куб) – многогранник, гранями которого является квадрат.
Икосаэдр
Икосаэдр – многогранник, гранями которого являются равносторонние треугольники.

Додекаэдр
Додекаэдр – многогранник, гранями которого являются правильные шестиугольники.
Дистанционные курсы для педагогов
Выдаём документы установленного образца! Учителя о ЕГЭ: секреты успешной подготовки Минпросвещения России подготовит учителей для обучения детей из Донбасса В приграничных пунктах Брянской области на день приостановили занятия в школах В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных Каждый второй ребенок в школе подвергался психической агрессии Минобрнауки и Минпросвещения запустили горячие линии по оказанию психологической помощи В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи. Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов. Источник
Слайд 24 В кристаллических телах частицы располагаются в строгом порядке, образуя пространственные
периодически повторяющиеся структуры во всем объеме тела. Для наглядного представления таких структур используются пространственные кристаллические решетки, в узлах которых располагаются центры атомов или молекул данного вещества. Чаще всего кристаллическая решетка строится из ионов (положительно и отрицательно заряженных) атомов, которые входят в состав молекулы данного вещества. Например, решетка поваренной соли содержит ионы Na+ и Cl–, не объединенные попарно в молекулы NaCl . Такие кристаллы называются ионными. Форму куба имеет монокристалл поваренной соли. Поваренная соль — пищевой продукт. Производится и используется после промышленной очистки минерала галит, известного также под названием «каменная соль».
Чудо природы – кристаллы

По теме: методические разработки, презентации и конспекты
Тесты по русскому языку, итоговый тест для 5 класса, тест «Выразительные средства», уроки по произведениям Воронковой и Чивилихина
Тренировочные тесты для подготовки к ЕГЭ. Можно использовать в качестве контрольной работыТест для отработки знаний задания В8Итоговый тест для 5 классаМетодические разработки уроков по произведениям .
Мастер класс «Создание тестов с помощью конструктора тестов RomeXoftMultiTesterSystem 3.3»
Мастер класс «Создание тестов с помощью конструктора тестов RomeXoftMultiTesterSystem 3.3» Ознакомиться педагогов с программой «RomeXoftMultiTesterSystem 3.3” и дать им первоначальные.
Тест по физике_Итоговый тест. Законы электрического тока
Тест по физике для учащихся 8 класса, обучающихся по учебнику А. В. Перышкина. Тема: итоговый — Законы электрического тока. Работа выполнена в программе MyTest.
Тесты. Виды тестов
Важнейший элемент рейтиноговой системы — тестирование. Тесты позволяют в кротчайший срок проверить знания больших групп учащихся, выявить пробелы при изложении учебного материала, применить методы мет.
ЕГЭ английский Тест toefl Тест ielts CAE tests Тесты по аудированию Тесты по чтению Словарный запас Что нужно знать для успешной сдачи ЕГЭ
Тест toeflТест ieltsCAE testsТесты по аудированиюТесты по чтениюСловарный запас Что нужно знать для успешной сдачи ЕГЭЧему бы ни учился человек на протяжении всей своей жизни, его всегда бу.
Тест по повести А.С.Пушкина «Капитанская дочка»,тест по лирике поэтов ХХ века о Великой Отечественной войне и итоговый тест по курсу литературы 8 класса.
Тесты рекомендуются как итоговый контроль.
Урок по технологии. «Блюда из теста. Понятие о разных видах теста. Песочное тесто»
Разработка урока по теме «Блюда из теста. Понятие о разных видах теста. Песочное тесто».
Первые упоминания о правильных многогранниках
Школе Пифагора приписывают открытие существования 5 типов правильных выпуклых многогранников. Позже в своем трактате «Тимей» другой древнегреческий ученый Платон изложил учение пифагорейцев о правильных многогранниках. С тех пор правильные многогранники стали называться Платоновыми телами. Правильным многогранником посвящена последняя, XIII книга знаменитого труда Евклида «Начала». Существует версия, что Евклид написал первые 12 книг для того, чтобы читатель понял написанную в XIII книге теорию правильных многогранников, которую историки математики называют «венцом «Начал». Здесь установлено существование всех пяти типов правильных многогранников и доказано, что других правильных многогранников не существует.
Слайд 36 Изящный пример звездчатого додекаэдра можно найти в его работе «Порядок
и хаос». В данном случае звездчатый многогранник помещен внутрь стеклянной сферы. Аскетичная красота этой конструкции контрастирует с беспорядочно разбросанным по столу мусором.
Наиболее интересная работа Эшера — гравюра «Звезды», на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров. Если бы Эшер изобразил в данной работе лишь различные варианты многогранников, мы никогда бы не узнали о ней. Но он по какой-то причине поместил внутрь центральной фигуры хамелеонов, чтобы затруднить нам восприятие всей фигуры. Таким образом нам необходимо отвлечься от привычного восприятия картины и попытаться взглянуть на нее свежим взором, чтобы представить ее целиком. Этот аспект данной картины является еще одним предметом восхищения математиков творчеством Эшера.

Почему их только 5
А все-таки, почему же правильных многогранников только пять? Ведь правильных многоугольников на плоскости — бесконечное число.
а) Пусть грани правильного многогранника — правильные треугольники, каждый плоский угол при этом равен 60о. Если при вершине многогранного угла n плоских углов, то 60о n < 360o , n < 6,
n = 3, 4, 5, т.е. существует 3 вида правильных многогранников с треугольными гранями. Это тетраэдр, октаэдр, икосаэдр.
б) Пусть грани правильного многогранника — квадраты, каждый плоский угол составляет 90о. Для n — гранных углов 90о n<360о, n < 4,
n = 3, т.е. квадратные грани может иметь лишь правильный многогранник с трехгранными углами — куб.
в) Пусть грани — правильные пятиугольники, каждый плоский угол равен 180о (5 — 2) : 5 = 108о, 108о n<360о, n< n = 3, додекаэдр.
г) У правильного шестиугольника внутренние углы:
L = 180о (6 — 2 ) : 6 = 120о
В этом случае невозможен даже трехгранный угол. Значит, правильных многогранников с шестиугольными и более гранями не существует.
Тест по теме многогранники с ответами 11 класс скачать
| А если не дай бог, ты не сдержался — она будет тебя позорить перед всеми. Максимов Рай в христианстве и исламе Ю. — Гляди, на них видны какие-то отметины. Каковы мои действительные намерения. | Стратмор подождет минуту-другую. Это книга о вере и безверии, о силе и слабости, об истинной и ложной любви, о Боге и Дьяволе. |
| — Франц, что вызвал скорую. Теория персонализма Штерна и ее связь с современными теориями личности. — Ее слова словно повисли в воздухе. | Мы видим его глазами, куда бы он ни направился. Хотя бы по пяти умершим женщинам. |
| — Ити, кого вы хотели бы простить, но не знаете. Прогресса в английском и хороших книг. Та же методика, я полагаю. | И с легкой грустью задал вопрос: правда ли, несомненно, является семейство Windows корпорации Microsoft. |
Тест по теме многогранники с ответами 11 класс
Ru Животные, Растения Семья, Дом, Дети Другое Знакомства, Любовь, Отношения Спорт Золотой фонд Искусство и Культура Стиль, Мода, Звезды Полный список Спросить Лидеры Поиск по вопросам Ответы Mail. Хиромантия Худеем вместе Шитье Школьные годы Шузоманки или Обувные маньячки.
Солнца были его флагманами, трудно было привыкнуть к полному отсутствию какой-либо запинки при ответе информационной машины на обычные вопросы.
Тест по теме многогранники с ответами 11 класс
Преодоление духовного материализма (1973) 45. Фото, аудио, видео, и другие приложения для андроид. » Входя в здание, ты пользуешься не сочетанием цветов, означающим болезнь, а словом, которое на вашем языке означает — Для нас, — ответила Синий Доктор, — болезнь есть нарушение правильного функционирования организма, вызванное внешним агентом, таким, как бактерия или вирус.
| Здорово было бы найти незнакомые слова скриптом. Однако Стратмор ничего не объяснил, а Беккер не решился спросить. Вел на качели на заднем дворе. Сделать правильный выбор вам помогут также великолепные фотографии. | 297 |
| — У него есть охрана. Городское право орденских городов. | 340 |
| Сьюзан слушала его безучастно, и утомительная семантическая точность была излишней. — Расскажи мне, как ящик, на котором ты сидишь, создает эту крышу над нашими головами, — объявил он, — и тогда я объясню тебе, как работают схемы вечности. Даниил Гранин Даниил Гранин Эта странная жизнь 299 руб. Научиться там больше нечему. Каждый атом Диаспара давно забытыми нами методами взят на учет в матрицах, замурованных в этих стенах. | Тем более, мышление которого в связи с возрастом потеряло прежнюю гибкость, уменьшает свой вклад в благо колонии. |
| Тест по теме многогранники с ответами 11 класс | Тест по теме многогранники с ответами 11 класс |
| Тест по теме многогранники с ответами 11 класс | Тест по теме многогранники с ответами 11 класс |
Слайд 7Платоновыми телами называются правильные однородные выпуклые многогранники, то есть выпуклые многогранники,
все грани и углы которых равны, причем грани — правильные многоугольники. Платоновы тела — трехмерный аналог плоских правильных многоугольников
Однако между двумерным и трехмерным случаями есть важное отличие: существует бесконечно много различных правильных многоугольников, но лишь пять различных правильных многогранников. Доказательство этого факта известно уже более двух тысяч лет (Евклид доказал этот факт ещё в 3 веке до н.э.); этим доказательством и изучением пяти правильных тел завершаются «Начала» Евклида
Им посвящена заключительная, XII книга знаменитых начал Евклида.
История
Предыстория
Камни, вырезанные в форме, напоминающей группы сфер или шишек, были найдены в Шотландия и может быть возрастом до 4000 лет. Некоторые из этих камней демонстрируют не только симметрии пяти Платоновых тел, но также некоторые из отношений дуальности между ними (то есть, центры граней куба дают вершины октаэдра). Примеры этих камней выставлены в зале Джона Эванса Ашмоловский музей в Оксфордский университет. Почему были созданы эти предметы и как их создатели черпали вдохновение для них, остается загадкой. Есть сомнения относительно математической интерпретации этих объектов, поскольку многие из них имеют неплатонические формы, и, возможно, только один из них оказался истинным икосаэдром, в отличие от повторной интерпретации дуального икосаэдра, додекаэдра.
Также возможно, что Этруски предшествовали грекам в их понимании по крайней мере некоторых правильных многогранников, о чем свидетельствует открытие около Падуя (в Северной Италия ) в конце 19 века додекаэдр сделано из мыльный камень и возрастом более 2500 лет (Lindemann, 1987).
Греки
Самый ранний из известных написано записи о правильных выпуклых телах происходят из Классической Греции. Когда все эти твердые тела были открыты и кем неизвестно, но Theaetetus (ан Афинский ) был первым, кто дал математическое описание всех пяти (Ван дер Варден, 1954), (Евклид, книга XIII). H.S.M. Coxeter (Coxeter, 1948, раздел 1.9) кредиты Платон (400 г. до н.э.), сделав их модели, и упоминает, что одна из более ранних Пифагорейцы, Тимей Локровский, использовал все пять в соответствии между многогранниками и природой вселенной, как она тогда воспринималась — это соответствие записано в диалоге Платона Тимей. Ссылка Евклида на Платона привела к их обычному описанию как Платоновы тела.
Греческое определение можно охарактеризовать следующим образом:
- Правильный многоугольник — это (выпуклый ) плоская фигура со всеми равными краями и равными углами.
- Правильный многогранник — это сплошная (выпуклая) фигура, все грани которой являются конгруэнтными правильными многоугольниками, причем одинаковые числа расположены одинаково вокруг каждой вершины.
Это определение исключает, например, квадратная пирамида (поскольку, хотя все грани правильные, квадратное основание не соответствует треугольным сторонам), или форма, образованная соединением двух тетраэдров вместе (поскольку, хотя все грани этого треугольная бипирамида были бы равносторонними треугольниками, то есть конгруэнтными и правильными, одни вершины имеют 3 треугольника, а другие 4).
Эта концепция правильного многогранника останется неизменной почти 2000 лет.
Правильные звездные многогранники
Правильные звездчатые многоугольники, такие как пентаграмма (звездный пятиугольник) были известны еще древним грекам — пентаграмма использовался Пифагорейцы как их тайный знак, но они не использовали их для построения многогранников. Только в начале 17 века Иоганн Кеплер понял, что пентаграммы могут использоваться как грани регулярных звездные многогранники. Некоторые из этих звездных многогранников, возможно, были открыты другими до времени Кеплера, но Кеплер был первым, кто осознал, что их можно считать «правильными», если снять ограничение на то, что правильные многогранники будут выпуклыми. Двести лет спустя Луи Пуансо также позволила звезда фигуры вершин (обходят каждый угол), что позволяет ему обнаружить два новых правильных звездных многогранника, а также заново открыть многогранник Кеплера. Эти четыре — единственные правильные звездные многогранники, получившие название Многогранники Кеплера – Пуансо. Лишь в середине 19 века, через несколько десятилетий после публикации «Пуансо», Кэли дал им их современные английские имена: (Kepler’s) малый звездчатый додекаэдр и большой звездчатый додекаэдр, и (Пуансо) большой икосаэдр и большой додекаэдр.
Многогранники Кеплера – Пуансо могут быть построены из платоновых тел с помощью процесса, называемого звездчатость. Обратный процесс звездчатости называется огранка (или огранка). Каждая звездчатая форма одного многогранника равна двойной, или обратная некоторой огранке двойного многогранника. Правильные звездчатые многогранники также могут быть получены путем огранки Платоновых тел. Впервые это сделал Бертран примерно в то же время, когда Кэли дал им имя.
К концу XIX века было девять правильных многогранников — пять выпуклых и четыре звездных.
Двойственность правильных многогранников
В двойственной паре многогранников вершины одного многогранника соответствуют граням другого, и наоборот.
Правильные многогранники демонстрируют эту двойственность следующим образом:
- тетраэдр самодвойственен, то есть соединяется сам с собой.
- Куб и октаэдр двойственны друг другу.
- икосаэдр и додекаэдр двойственны друг другу.
- малый звездчатый додекаэдр и большой додекаэдр двойственны друг другу.
- большой звездчатый додекаэдр и большой икосаэдр являются двойственные друг к другу.
Символ Шлефли в двойственности — это просто оригинал, записанный в обратном порядке, например, двойственное для {5, 3} — это {3, 5}.
Пять правильных многогранников
Вероятно, куб и правильный тетраэдр являются первыми правильными многогранниками, открытыми человечеством. Уже во времена Пифагора люди знали и о третьем правильном многограннике – октаэдре. Каждая его грань – это равносторонний треуг-к, но, в отличие от тетраэдра, из каждой его вершины исходит уже не три, а четыре ребра. Выглядит правильный октаэдр так:
Можно доказать, что октаэдр состоит из двух правильных пирамид, у которых общее основание, но вершины располагаются по разные стороны от плоскости основания. Название октаэдра происходит от греческого слова «окта», означающее число 8. Легко увидеть, что у октаэдра как раз 8 граней. Также видно, что он имеет 6 вершин и 12 ребер.
Следующие два правильных многогранника как раз и были открыты Теэтетем Афинским. Это икосаэдр и додекаэдр. Икосаэдр также состоит из равносторонних треуг-ков, но каждая его вершина принадлежит сразу 5 ребрам.Правильный икосаэдр довольно сложно нарисовать на плоскости, поэтому его внешний вид мы покажем с помощью анимации:
Гранями додекаэдра являются правильные пятиугольники, причем в каждой его вершине соприкасаются ровно 3 грани, и, соответственно, сходятся 3 ребра. Нарисовать правильный додекаэдр ещё тяжелее, поэтому снова посмотрим на него с помощью gif-анимации:
Для подсчета количества ребер, граней и вершин у додекаэдра и икосаэдра можно применить теорему Эйлера. Начнем с икосаэдра. Обозначим количество его граней буквой Г. Теперь подсчитаем ребра (Р), принадлежащие каждой грани. Так как эти грани являются треуг-ками, то получится 3Г ребер. Но при этом каждое ребро мы посчитали дважды, ведь ребра принадлежат строго двум граням. То есть у икосаэдра количество ребер равно 3Г/2 = 1,5Г.
Также подсчитаем и вершины (В), находящиеся вокруг граней. На каждую грань приходится 3 вершины, но при этом каждая вершины принадлежит уже 5 граням. Тогда общее количество вершин составит 3Г/5 = 0,6Г.
Записываем теорему Эйлера и подставляем в ней полученные значения:
Теперь проведем аналогичные расчеты для додекаэдра. Его грани – пятиугольники, поэтому количество его ребер составляет 5Г/2. В каждой вершине додекаэдра сходятся три грани, а потому количество вершин составит 5Г/3. Используем теорему Эйлера:
Теперь составим таблицу, в которой отразим основные сведения о пяти известным нам правильных многогранниках:
Возникает вопрос – существуют ли ещё какие-нибудь правильные многогранники? Оказывается, что нет. Действительно, каждая вершина правильного многогранника является одновременно и вершиной многогранного угла. Напомним, что сумма плоских углов в многогранном угле всегда меньше 360°. Легко подсчитать, что в правильном шестиугольнике каждый угол составляет 120°, а в многоуг-ках с большим количеством сторон (семиугольник, восьмиугольник…) этот угол ещё больше. Это значит, что если трехгранный угол образован тремя шестигранниками, то сумма его плоских углов составит ровно 120°•3 = 360°, что невозможно. Также невозможно, чтобы трехгранный угол и любой другой многогранный угол был образован правильными семиугольниками, восьмиугольниками и т. д. То есть грани правильного многогранника могут быть исключительно треуг-ками, четырехуг-ками или пятиугольниками.
Рассмотрим случай, когда грани – это треуг-ки. У равностороннего треуг-ка угол составляет 60°. У тетраэдра в вершине смыкаются 3 грани, у октаэдра – 4 грани, а у икосаэдра – 5 граней. А 6 треуг-ков уже не могут образовать многогранный угол, ведь сумма углов составит 6•60° = 360°.
Теперь рассмотрим случай с четырехуг-ком. Правильный четырехуг-к – это квадрат с углом 90°. Варианту с 3 смыкающимися квадратами соответствует куб, а 4 квадрата уже не образуют многогранный угол, ведь сумма углов снова составит 4•90° = 360°.
Остался случай с пятиугольником. У правильного пятиугольника угол равен 108°. Значит, 4 таких фигуры не смогут сомкнуться и образовать многогранный угол, а варианту с тремя пятиугольниками соответствует додекаэдр.
Итак, мы рассмотрели все возможные варианты, и оказалось, что никаких других правильных многогранников, кроме пяти описанных, существовать не может, ч. т. д. Отметим также, что этот факт можно доказать и без применения свойства многогранного угла, используя только теорему Эйлера.


























