Прямоугольный параллелепипед

Слайды и текст этой презентации

Слайд 3

А

С

В

П-р

Н-я

П-я

Угол ВMN – линейный угол двугранного угла ВАСК

К

D

Повторение.

Слайд 4

Построить линейный угол двугранного угла ВАСК.

АВСD – четырехугольник, АС — диагональ.

А

В

П-р

Н-я

П-я

Угол ВСN – линейный угол двугранного угла ВАСК

К

С

D

2

1

Повторение.

Слайд 5

Построить линейный угол двугранного угла ВАСК.

АВСD – четырехугольник, АС – диагональ.

А

В

П-р

Н-я

П-я

Угол ВSN – линейный угол двугранного угла ВАСК

К

С

D

9

6

5

тупой

Повторение.

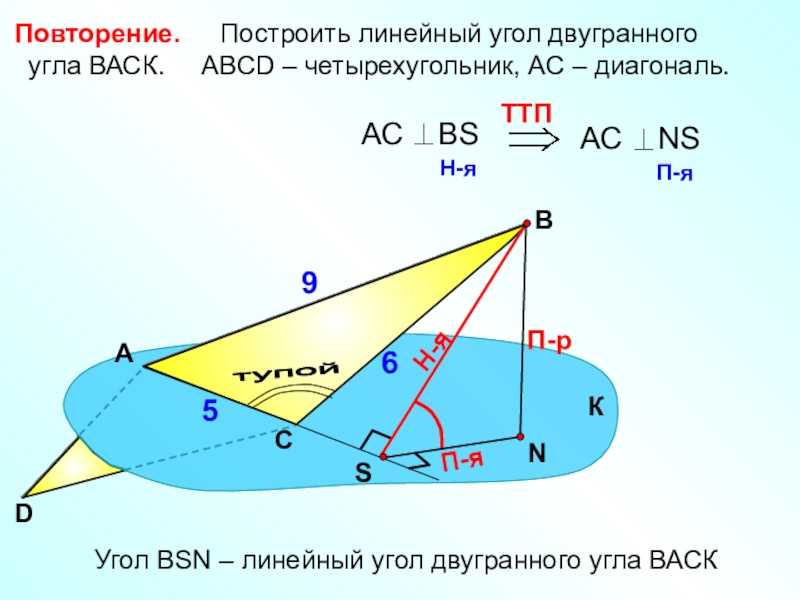
Слайд 7 Определение: Две пересекающиеся плоскости называются

Слайд 8 Примером взаимно перпендикулярных плоскостей

плоскости стены и потолка

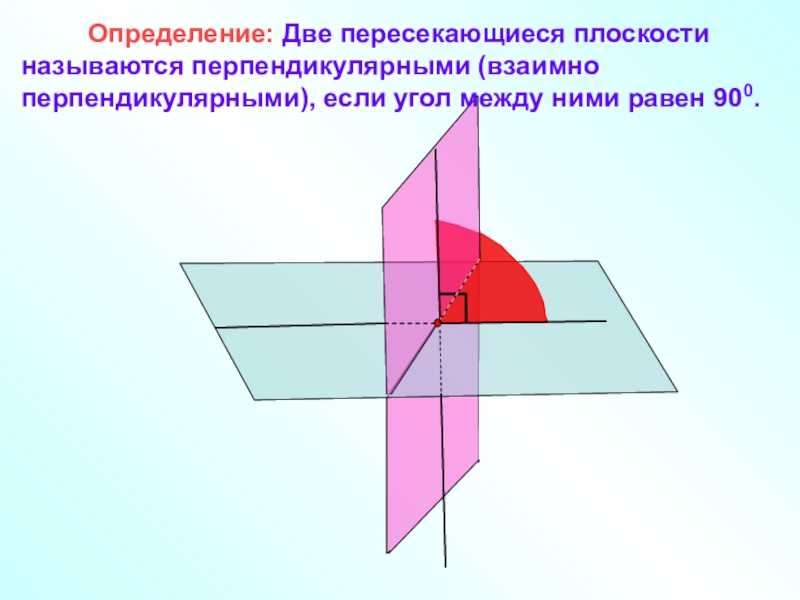
Слайд 9 Признак перпендикулярности двух плоскостей.

Если одна из двух плоскостей проходит через прямую,

перпендикулярную к другой плоскости, то такие плоскости перпендикулярны

А

С

Слайд 10Следствие. Плоскость, перпендикулярная к прямой, по которой пересекаются

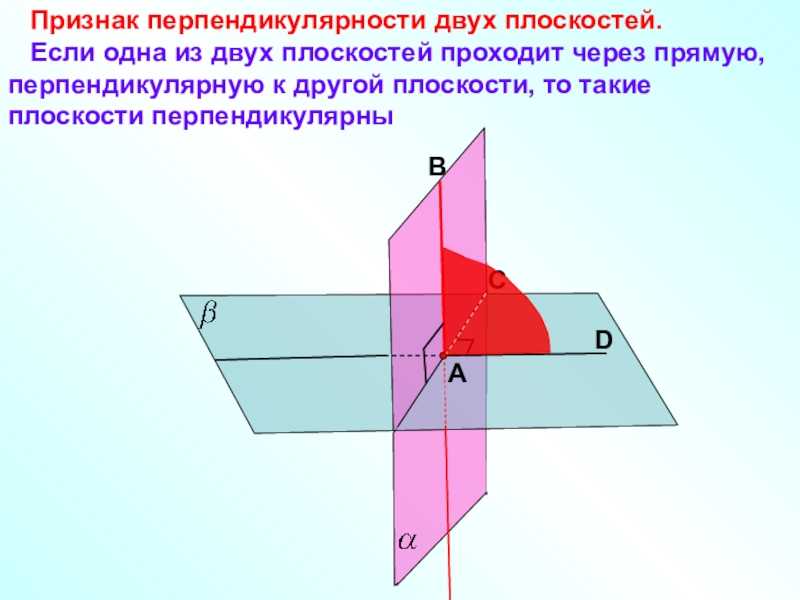
Слайд 11 Плоскости

и взаимно перпендикулярны пересекаются по прямой с. Докажите,

что любая прямая плоскости , перпендикулярная к прямой с, перпендикулярна к плоскости .

№ 178.

c

C

Подсказка

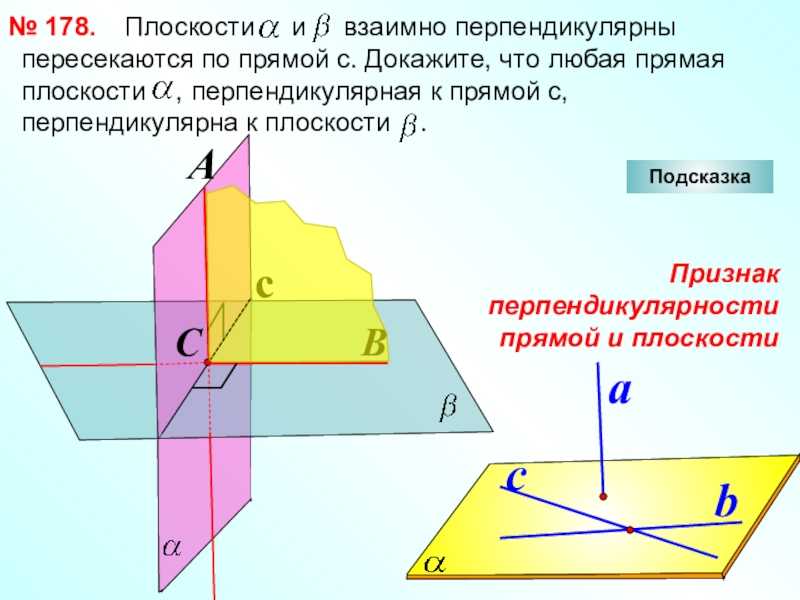
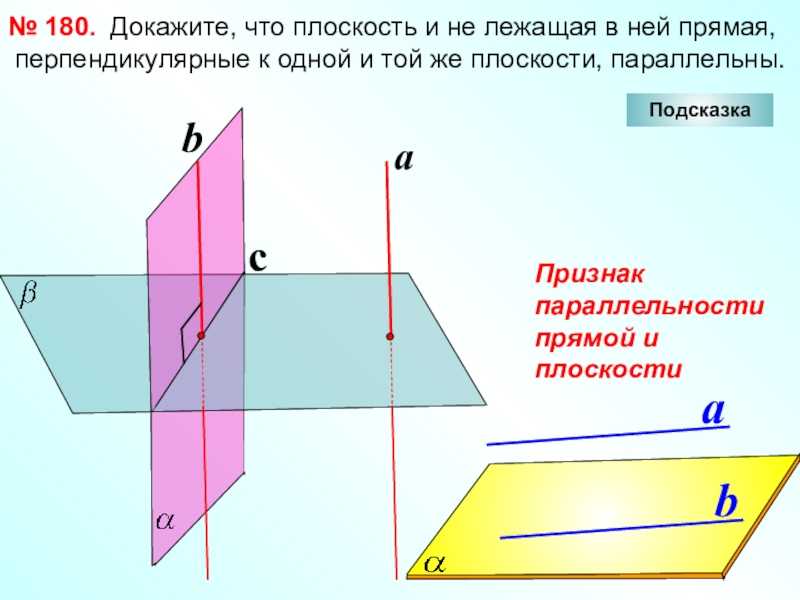
Слайд 12 Докажите, что плоскость

той же плоскости, параллельны.

№ 180.

c

Подсказка

Слайд 14 Плоскости

и взаимно перпендикулярны пересекаются по прямой a. Из

точки М проведены перпендикуляры МА и МВ к этим плоскостям. Прямая а пересекает плоскость АМВ в точке С. Докажите, что четырехугольник АСВМ – прямоугольник.

№ 182.

a

С

М

Слайд 15 Плоскости

и пересекаются по прямой a и перпендикулярны к

плоскости . Докажите, что прямая а перпендикулярна к плоскости .

№ 183.

Слайд 16 Прямоугольный параллелепипед Параллелепипед называется

прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания

представляют собой прямоугольники.

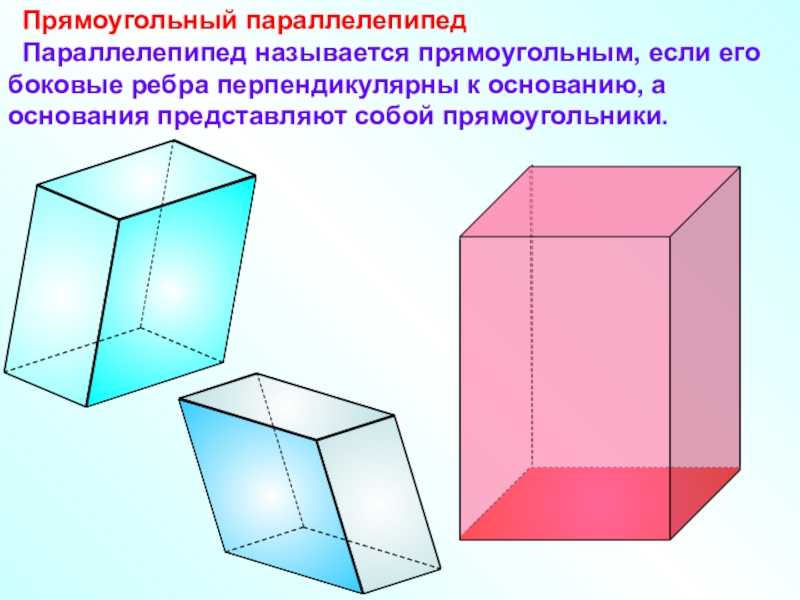
Слайд 18 10. В прямоугольном параллелепипеде все шесть

граней – прямоугольники. 20. Все

двугранные углы прямоугольного параллелепипеда – прямые.

Длины трех ребер, имеющих общую вершину, называются измерениями прямоугольного параллелепипеда.

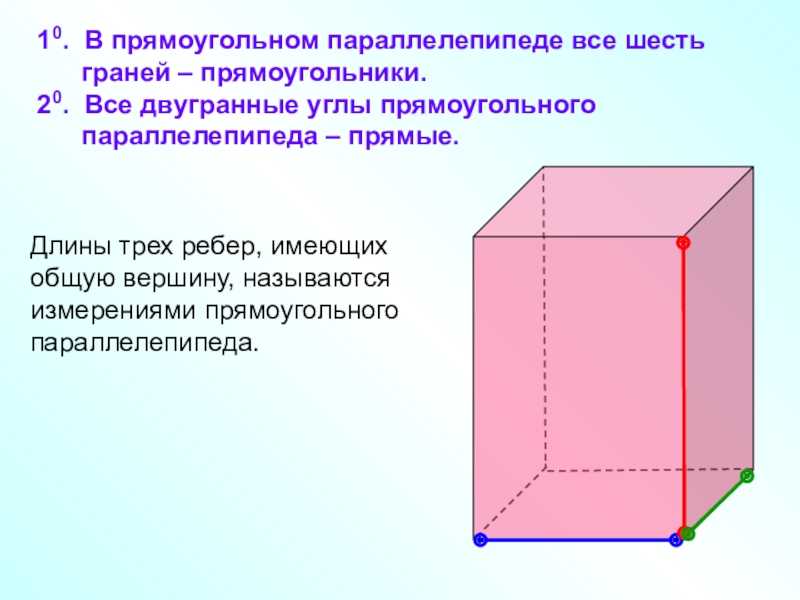
= a2 + b2Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов

трех его измерений.

d2 = a2 + b2 + с2

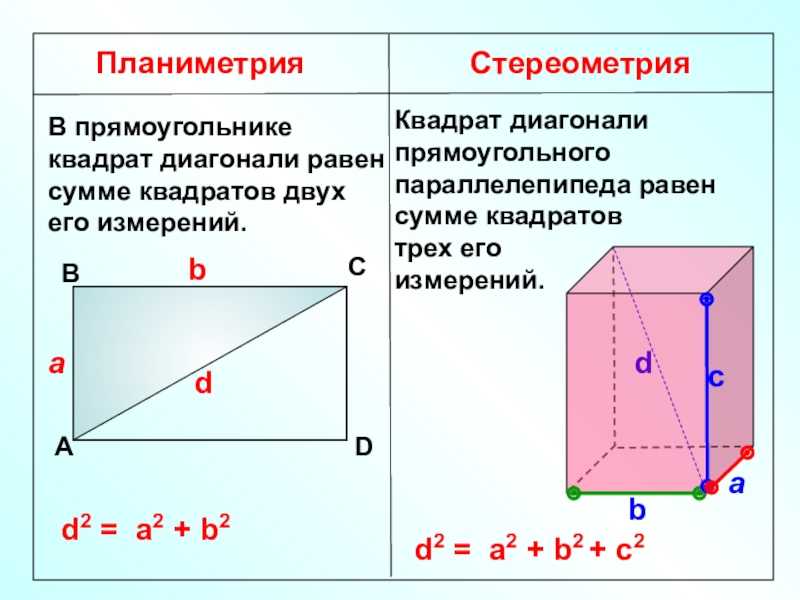
прямоугольного параллелепипеда равны.d2 = a2 + b2 + с2

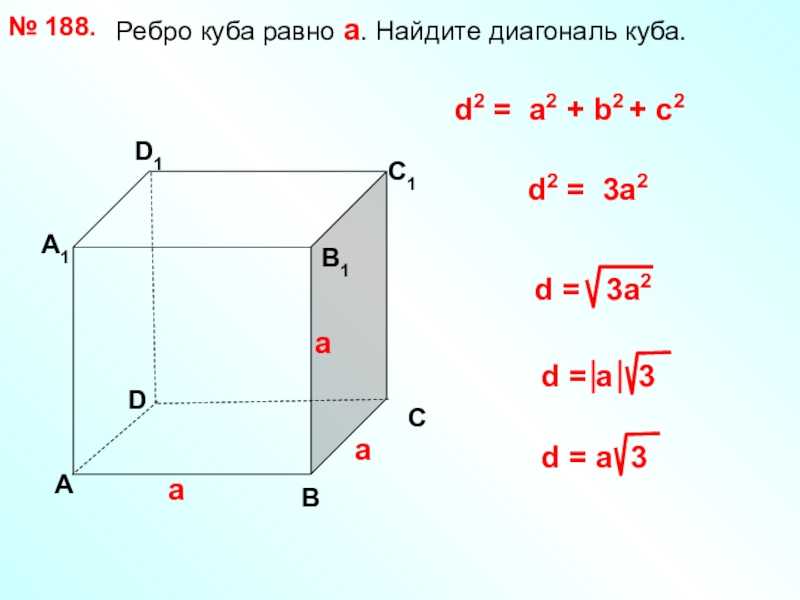
Слайд 21 Ребро куба равно а.

Найдите диагональ куба.№ 188.DАВСА1D1С1В1d2 = a2 + b2 + с2d2

= 3a2

а

а

а

Слайд 22 Найдите расстояние от вершины

куба до плоскости любой грани,

в которой не лежит эта вершина, если: а) диагональ грани куба равна m. б) диагональ куба равна d.

№ 189.

D

А

В

С

D1

С1

m

Подсказка

В1

А1

Слайд 23 Дан куб. Найдите следующие

двугранные углы: a) АВВ1С;

б) АDD1B; в) А1ВВ1К, где K – середина ребра А1D1.

№ 190.

D

А

В

С

А1

D1

С1

В1

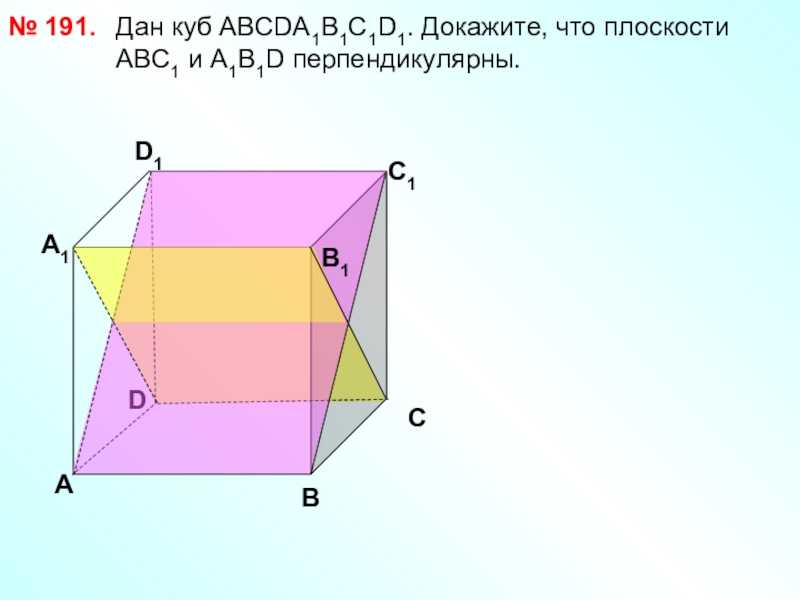
Слайд 24 Дан куб АВСDА1В1С1D1. Докажите,

что плоскости АВС1 и А1В1D

перпендикулярны.

№ 191.

D

А

В

С

А1

D1

С1

В1

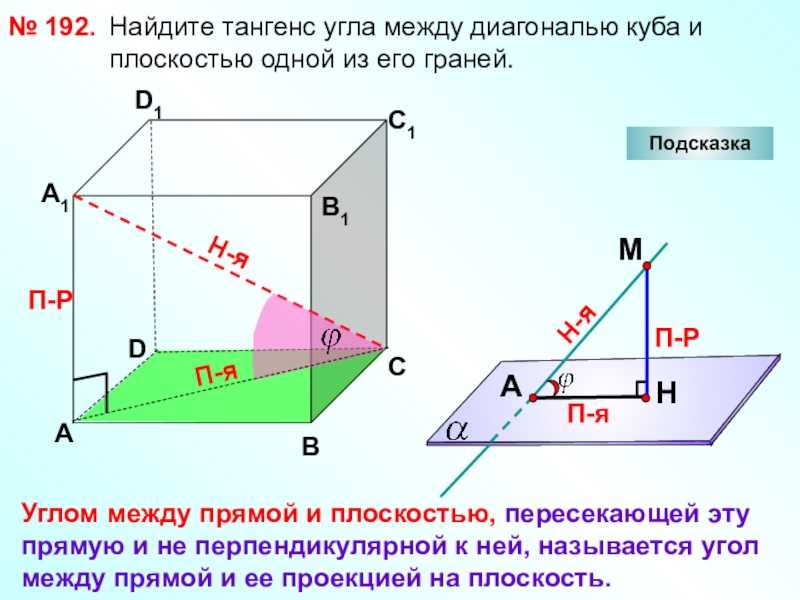
Слайд 25 Найдите тангенс угла между

диагональю куба и плоскостью одной

из его граней.

№ 192.

D

А

В

С

А1

D1

С1

В1

Подсказка

П-Р

Н-я

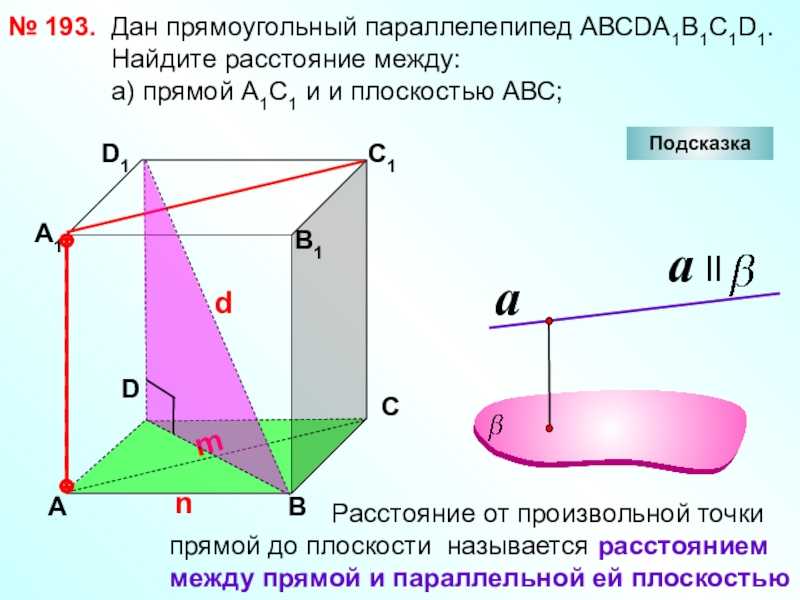
Слайд 26№ 193.DАВСА1D1С1В1Подсказка Дан

расстояние между: а) прямой А1С1 и и плоскостью АВС;

Слайд 27№ 193.DАВСА1D1С1В1Подсказка Дан

Найдите расстояние между: б) плоскостями АВВ1 и DCC1;

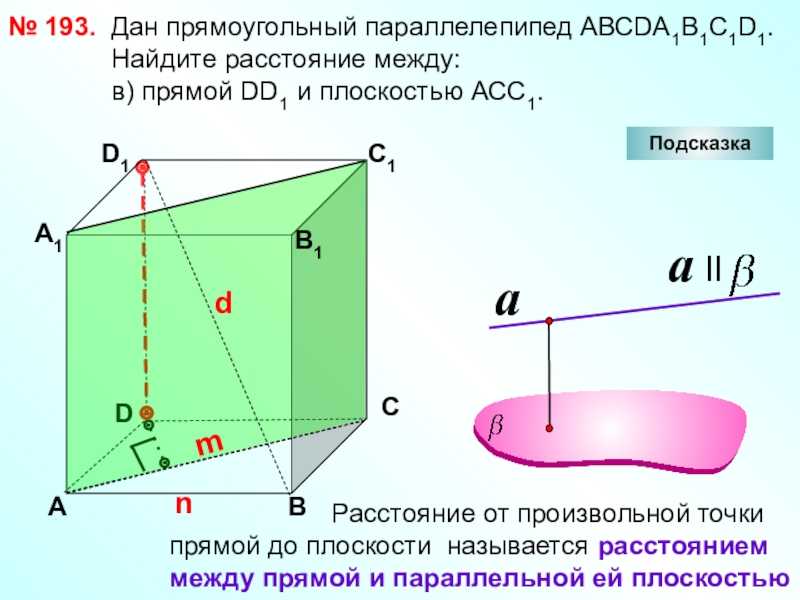
Слайд 28№ 193.DАВСА1D1С1 Дан прямоугольный

параллелепипед АВСDА1В1С1D1. Найдите расстояние

между: в) прямой DD1 и плоскостью АСС1.

Подсказка

В1

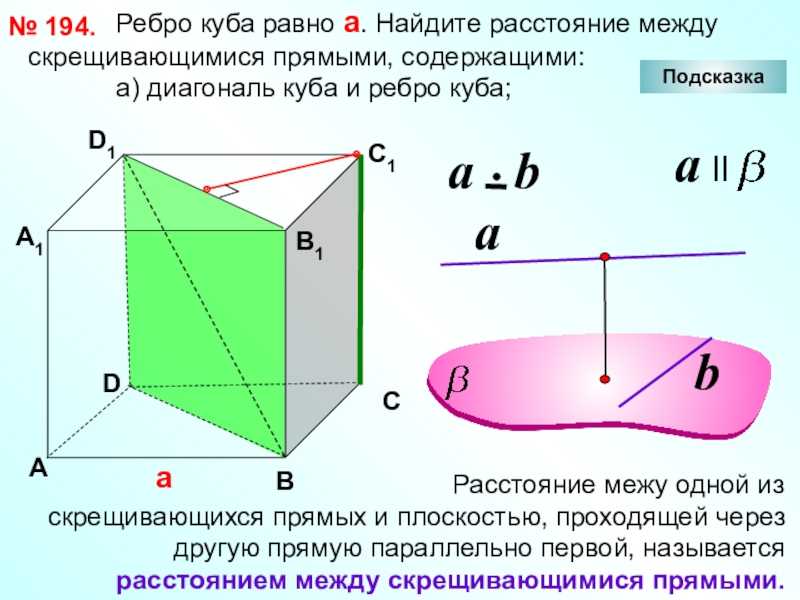
Слайд 29 Ребро куба равно а.

а) диагональ куба и ребро куба;

№ 194.

D

А

В

С

D1

С1

а

В1

А1

Подсказка

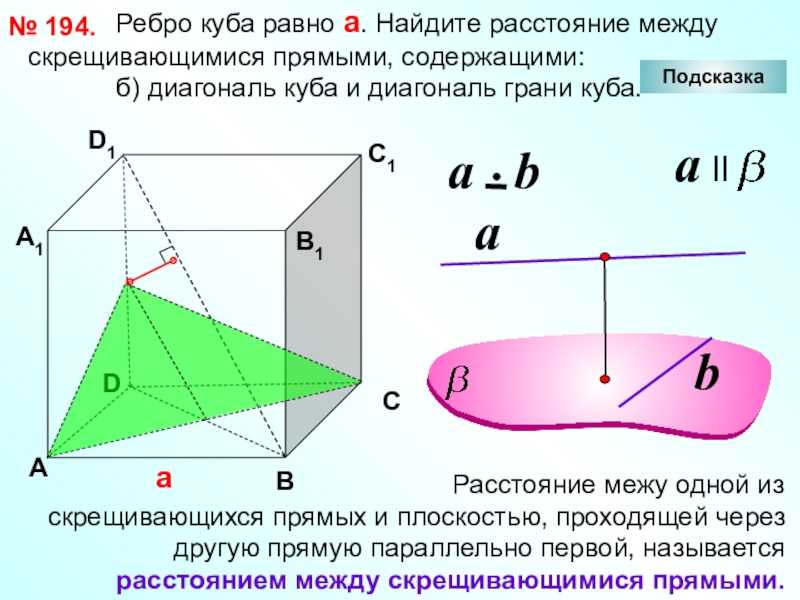
Слайд 30 Ребро куба равно а.

б) диагональ куба и диагональ грани куба.

№ 194.

D

А

В

С

D1

С1

а

В1

А1

Подсказка

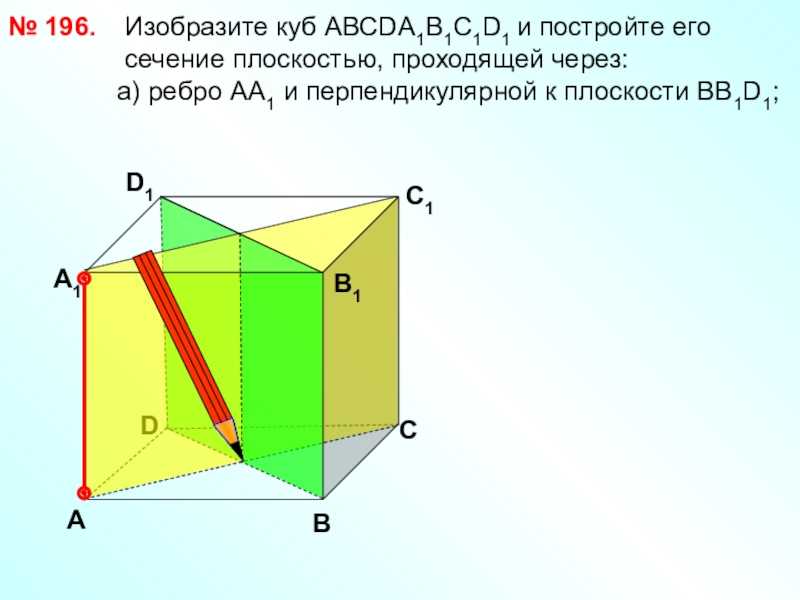
Слайд 31№ 196.DВD1С1 Изобразите куб

АВСDА1В1С1D1 и постройте его

сечение плоскостью, проходящей через: а) ребро АА1 и перпендикулярной к плоскости ВВ1D1;

А

А1

С

В1

Слайд 32№ 196. Изобразите куб

АВСDА1В1С1D1 и постройте его

сечение плоскостью, проходящей через: б) ребро АВ и перпендикулярной к плоскости СDA1.

D

В

D1

С1

А

А1

В1

С

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

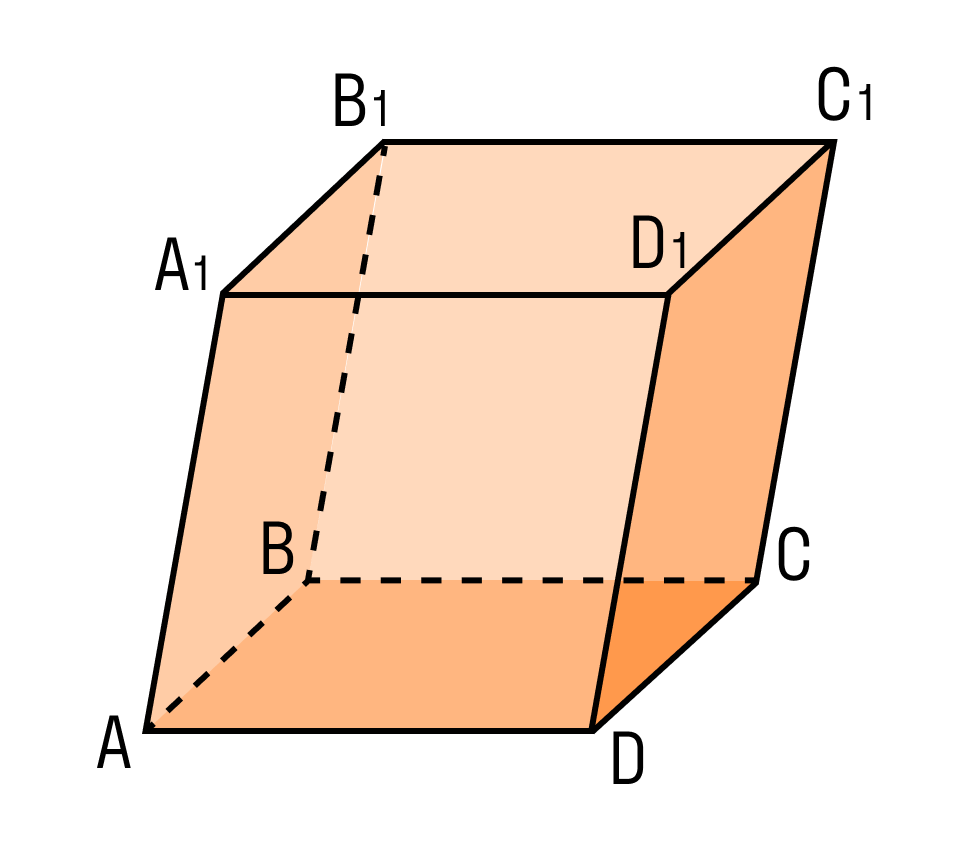
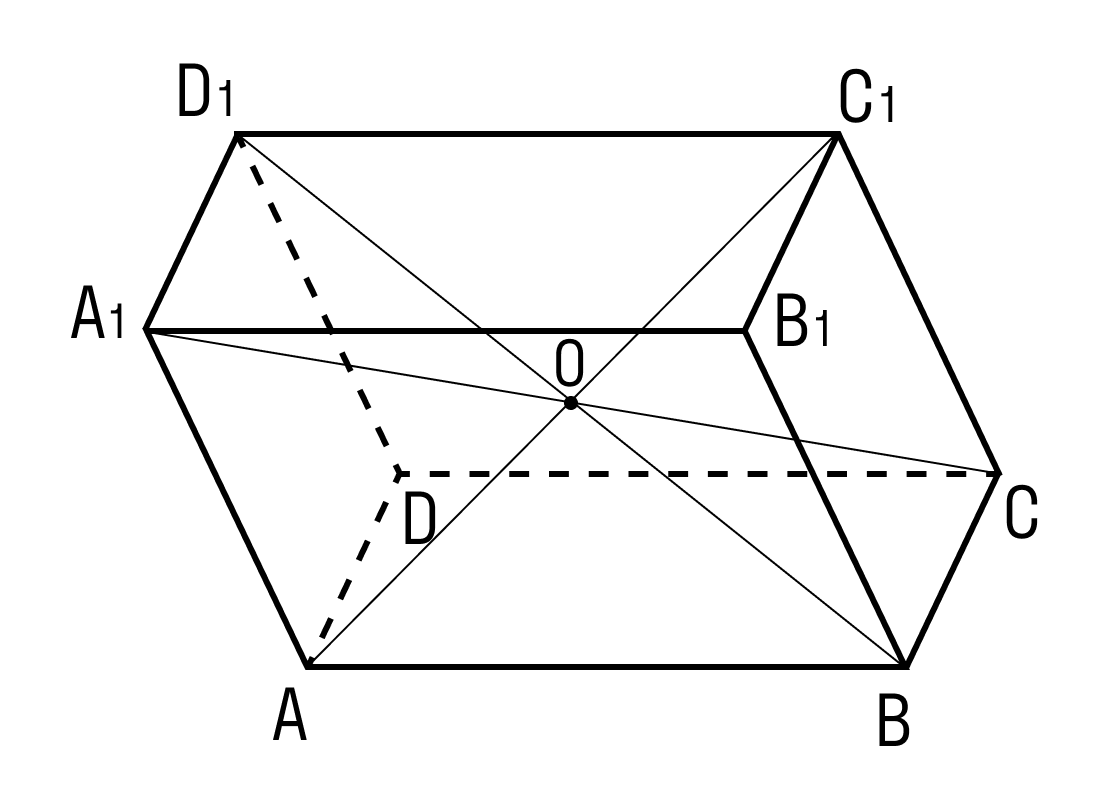
На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

1. Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
2. Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
3. Высота прямого параллелепипеда равна длине бокового ребра.
4. Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
5. Диагонали прямого параллелепипеда точкой пересечения делятся пополам.

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

• Площадь боковой поверхности прямого параллелепипеда Sб = Ро*hРо — периметр основания h — высота
• Площадь полной поверхности прямого параллелепипеда Sп = Sб+2SоSо — площадь основания
• Объем прямого параллелепипеда V = Sо*h

Свойства прямоугольного параллелепипеда

Измерениями прямоугольного параллелепипеда называются длины трёх рёбер с общей вершиной. Например,  в качестве измерений у прямоугольного параллелепипеда ABCDA1B1C1D1  можно взять длины рёбер D1D, D1C1 и D1A1, которые имеют общую вершину D1.

У прямоугольника два измерения — длина и ширина.При этом квадрат диагонали прямоугольника равен сумме квадратов двух его измерений (данное утверждение основывается на теореме Пифагора).

Свойство

Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

• Доказательство
• Дано: ABCDA1B1C1D1  — прямоугольный параллелепипед, В1В, В1С1, В1А1 — измерения
• Доказать: BD12 = В1В2 + В1С12 + В1А12
• Доказательство:

ВВ1 A1B1C1D1, т.е. данное ребро перпендикулярно любой прямой, которая принадлежит плоскости этой грани и проходит через точку В1. Следовательно, D1B1B = 900. По теореме Пифагора для D1B1B запишем:  BD12 = В1В2 + В1D12 . ABCDA1B1C1D1  — прямоугольный параллелепипед, то есть основание A1B1C1D1 является прямоугольником, значит, В1D1 есть диагональ прямоугольника и В1D12 = В1С12 + В1А12. Следовательно, BD12 = В1В2 + В1С12 + В1А12, что и требовалось доказать.

Мы знаем, что площадь прямоугольника равна произведению его измерений. По аналогии для прямоугольного параллелепипеда справедливо:

Объём  прямоугольного параллелепипеда равен произведению трёх его измерений.

Чтобы доказать данное утверждение воспользуемся принципом Кавальери:

Рассмотрим сначала прямоугольный параллелепипед с измерениями , и 1 и  куб с ребром 1, которые «стоят» на плоскости .

Нам известно, что данный куб будет являться единицей измерения объёмов, т.е. его объём равен 1. Любая секущая плоскость, параллельная плоскости , даёт в качестве сечения данного параллелепипеда прямоугольник, площадь которого равна , а куба — квадрат, площадь которого равна 1. То есть площадь сечения параллелепипеда в раз больше площади сечения куба, а, значит, согласно принципу Кавальери, объём рассматриваемого параллелепипеда больше объёма куба в раз, то есть равен .

Далее рассмотрим два прямоугольных параллелепипеда с измерениями  , , и , , 1, которые «стоят» на плоскости так, чтобы основания принадлежащие этой плоскости имели измерения , и , 1.

Объём второго параллелепипеда равен (см. доказано выше). Любая секущая плоскость, параллельная плоскости , даёт в качестве сечения первого параллелепипеда прямоугольник, площадь которого равна , а второго  — прямоугольник, площадь которого равна .

То есть площадь сечения первого параллелепипеда в раз больше площади сечения второго параллелепипеда, а, значит, согласно принципу Кавальери, объём первого параллелепипеда больше объёма второго параллелепипеда в раз, то есть равен V = , что и требовалось доказать.

В прямоугольном параллелепипеде с измерениями , , , который изображен выше, площадь основания S равна , а высота равна боковому ребру: = . Значит, формулу V = можно записать в виде: V = S.

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

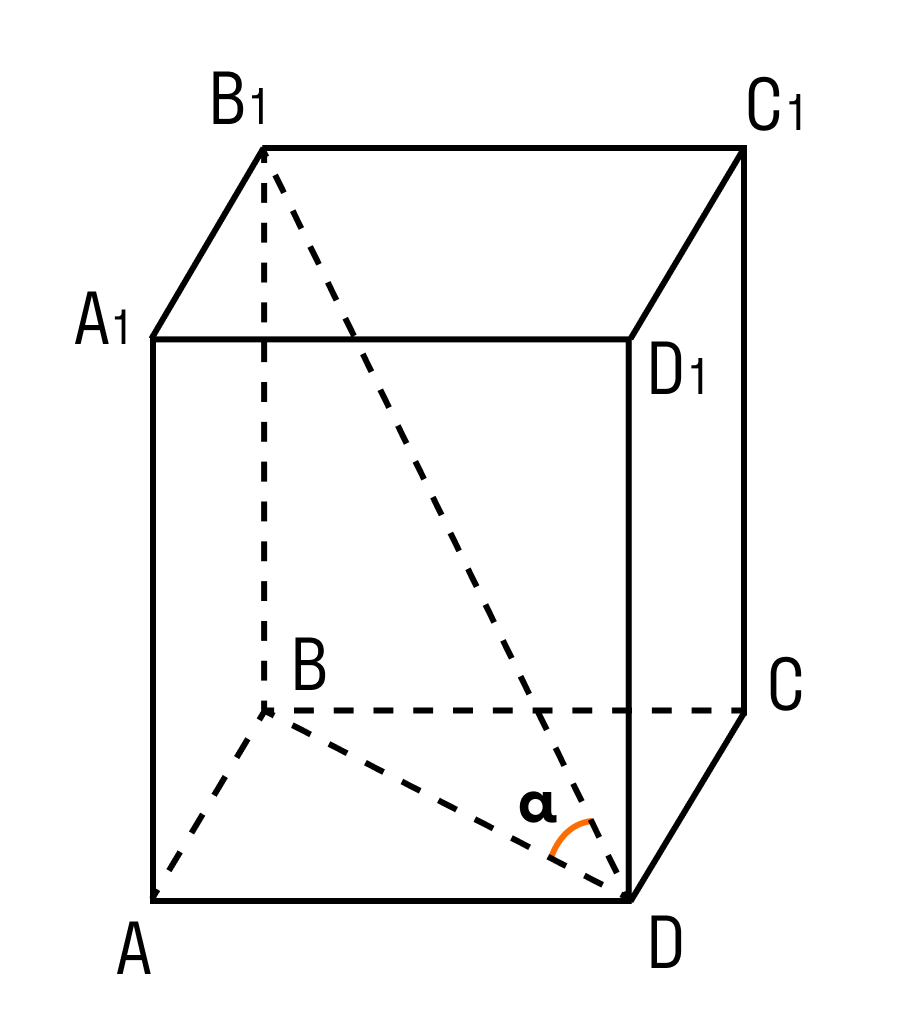
Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

• прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
• параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
• основание прямоугольного параллелепипеда — прямоугольник;
• три измерения прямоугольного параллелепипеда: длина, ширина, высота;
• диагональ параллелепипеда равна сумме квадратов его измерений.

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

1. Противолежащие грани параллелепипеда равны и параллельны друг другу.
2. Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
3. Параллелепипед симметричен относительно середины его диагонали.
4. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.

Какие виды параллелепипеда бывают?

Теперь разберёмся в том, какие параллелепипеды бывают. Как уже упомянуто выше, существует несколько типов этой фигуры: прямой, прямоугольный, наклонный параллелепипед, а также куб и ромбоэдр. Чем же они отличаются между собой? Все дело в образующих их плоскостях и углах, которые они образуют.

Разберемся более подробно с каждым из перечисленных видов параллелепипеда.

• Как уже понятно из названия, наклонный параллелепипед имеет наклонные грани, а именно такие грани, которые находятся по отношению к основанию не под углом 90 градусов.
• А вот у прямого параллелепипеда угол между основанием и гранью как раз составляет девяносто градусов. Именно по этой причине этот вид параллелепипеда имеет такое название.
• Если же все грани параллелепипеда – это одинаковые квадраты, то можно считать эту фигуру кубом.
• Прямоугольный параллелепипед получил такое название из-за образующих его плоскостей. Если все они являются прямоугольниками (и основание в том числе), то это прямоугольный параллелепипед. Такой вид параллелепипеда встречается не так часто. В переводе с греческого ромбоэдр означает грань или основание. Так называют трехмерную фигуру, у которой гранями являются ромбы.

Параллелепипед — это… Что такое Параллелепипед?

Параллелепи́пед (от греч. παράλλος — параллельный и греч. επιπεδον — плоскость) — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них параллелограмм.

Типы параллелепипеда

Различается несколько типов параллелепипедов:

• Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники;
• Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани прямоугольники;
• Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основания
• Куб — это прямоугольный параллелепипед с равными измерениями. Все шесть граней куба — равные квадраты.

Основные элементы

Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро — смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями.

Свойства

• Параллелепипед симметричен относительно середины его диагонали.
• Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
• Противолежащие грани параллелепипеда параллельны и равны.
• Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Прямой параллелепипед

• Площадь боковой поверхности Sб=Ро*h, где Ро — периметр основания, h — высота
• Площадь полной поверхности Sп=Sб+2Sо, где Sо — площадь основания
• Объём V=Sо*h

Прямоугольный параллелепипед

1. Основная статья: Прямоугольный параллелепипед
2. Площадь боковой поверхности Sб=2c(a+b), где a, b — стороны основания, c — боковое ребро прямоугольного параллелепипеда
3. Площадь полной поверхности Sп=2(ab+bc+ac)
4. Объём V=abc, где a, b, c — измерения прямоугольного параллелепипеда.

Произвольный параллелепипед

Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры.

Объём параллелепипеда равен абсолютной величине смешанного произведения трёх векторов, определяемых тремя сторонами параллелепипеда, исходящими из одной вершины.

Соотношение между длинами сторон параллалепипеда и углами между ними даёт утверждение, что определитель Грама указанных трёх векторов равен квадрату их смешанного произведения:215.

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

1. Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
2. Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
3. Высота прямого параллелепипеда равна длине бокового ребра.
4. Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
5. Диагонали прямого параллелепипеда точкой пересечения делятся пополам.

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

• Площадь боковой поверхности прямого параллелепипеда Sб = Ро*hРо — периметр основания h — высота
• Площадь полной поверхности прямого параллелепипеда Sп = Sб+2SоSо — площадь основания
• Объем прямого параллелепипеда V = Sо*h

Ход урока

I. Организационный момент

II. Постановка задач и целей урока

1. – Для того, чтобы наш урок прошёл успешно какие задачи поставим перед собой?

(Познакомиться с новой темой; продолжать учиться решать задачи; учиться правильно вычислять, сравнивать; внимательно слушать и слышать и т. д.)

— К нам на урок пришла точка. Как вы думаете в связи с чем она пришла сегодня на урок? О чём узнаем?

(Будем говорить о геометрических фигурах)

— Какие геометрические фигуры вы уже знаете?

— На какие группы их можно разделить?

(Плоские и объёмные (пространственные)

2. –Сегодня мы познакомимся с одной объёмной фигурой. Чтобы узнать с какой фигурой познакомимся выполним математический диктант.

Математический диктант

1. 240-65 +65= (240)

2. 18+19+2+21+22= (100)

3. 2*18*5= (180)

4. 528-(428+60)= (40)

5. Найдите Р треугольника, у которого все стороны равны. Длина одной стороны 9 см. (27см)

6. Найдите Р квадрата со стороной 6см. (36см)

7. Найдите площадь прямоугольника со сторонами 6м и 40м. (240м)

8. Найдите Р прямоугольника со сторонами 9см и 15см. (48см)

9. Найдите сторону прямоугольника, одна сторона которого 20м, а площадь 180м. кв. (9м)

ПРОВЕРКА

Соединяем последовательно точки

. 180 .100

240.

40.

27. 36.

— Что за фигура у нас получилась? (Куб)

— Какая это фигура? (Объёмная)

Ш. Работа над темой урока

1. — Тема нашего урока : КУБ И ЕГО ИЗОБРАЖЕНИЕ

(Открываю запись темы урока на доске и раздаю кубы на парты)

2. – У вас на партах кубы. Рассмотрите их. Что можете сказать об этой геометрической фигуре? Можете провести измерение.

(Все стороны равны)

— Эти стороны – грани. Посчитайте сколько всего граней у куба? (6)

— Сколько всего вершин? (8)

— Сколько всего рёбер? (12)

3. Проблемная ситуация.

— Посмотрите на изображение куба на чертеже. Сколько всего граней, вершин, рёбер вы видите на чертеже?

(3-грани, 7-вершин, 9-рёбер)

— Почему же их меньше? (ответы детей)

— Стороны, которые мы не можем увидеть, обозначаются на чертеже пунктирной линией. Сейчас попробуем достроить правильное изображение куба.

На чертеже есть точка 9. попробуйте её соединить с точками, чтобы завершить построение куба.

— Кто знает с какими точками надо соединить точку 9? (27, 40, 180)

— Сколько теперь граней получилось? Вершин? Рёбер?

4. – Куб – это геометрическая фигура. Значит, что мы можем измерить? (длину, ширину рёбер)

— Измерьте. Что вы заметили?

(Они равны – 4см)

— Если рёбра все равны, то какой фигурой является каждая грань?

(Квадрат)

— Найдите площадь одной грани.

(4*4=16 см. кв.)

— Чему равна площадь всей поверхности куба? Как быстро посчитать?

(16*6=96 см. кв.)

ФИЗМИНУТКА

1.– Если я называю плоские фигуры – приседаем, если объёмные – делаем хлопок над головой.

2. – Подпрыгните столько раз:

а) сколько сторон у треугольника (3)

б) сколько вершин у круга (0)

в) сколько углов у квадрата (4)

г) сколько осей симметрии у прямоугольника (4)

5. Практическая работа

— Из трубочек (для коктейля) и пластилина сделаем модель куба. (каркас)

— Вычислите: Сколько потребуется проволоки, если этот каркас делать из проволоки?

— Какие измерения для этого надо сделать? Что надо знать?

(длину ребра)

— Как будем вычислять?

(Количество рёбер умножить на длину ребра)

6. Постановка задач на следующий урок.

Показываю параллелепипед.

— Кто знает как называется эта фигура?

— Чем она похожа с кубом?

— На эти вопросы мы ответим на следующем уроке.

7. «Точка» на приготовила ещё одно интересное задание.

— Рассмотрите сколько всего четырёхугольников изображено на рисунке? (треугольников)

IV. Подведение итогов урока

— Что нового узнали на уроке?

— Что было интересным?

— Всё ли получилось?

— Что вызвало затруднения?

— Кто доволен своей работой?

_ Оцените на шкале успеха свои достижения. Если всё удалось, получилось – красным цветом; если всё было хорошо, но что – то не получилось– зелёным цветом; если не очень старался – синим.

Математика

Все двухгранные углы прямоугольного параллелепипеда —прямые Для следующего свойства нужно вспомнить, что в пространстве прямоугольный параллелепипед характеризуется шириной, длиной и высотой. Длины этих трех ребер назовем измерениями прямоугольного параллелепипеда На экране изображение и текст: Длины трёх рёбер, имеющих общую вершину называются измерениями прямоугольного параллелепипеда. В силу этих изменений, для основания длину и ширину можно назвать измерениями прямоугольника. И свойство диагонали прямоугольника сформулировать так: квадрат диагонали прямоугольника равен сумме квадратов двух его измерений.

Прямой параллелепипед может быть прямоугольным — основаниями являются прямоугольники. Наклонный параллелепипед — боковые грани не перпендикулярны основаниям. Куб — все грани фигуры являются равными квадратами. Если все грани параллелепипеда — это одинаковые ромбы, он называется ромбоэдром. Свойства параллелепипеда 1. Противоположные грани параллелепипеда взаимно параллельны и являются равными параллелограммами. Все диагонали параллелепипеда пересекаются в одной точке и в ней делятся пополам. Квадрат диагонали d прямоугольного параллелепипеда равен сумме квадратов трех его измерений: длины a , ширины b и высоты c. Прямоугольный параллелепипед. Что это такое? Определение параллелепипеда Начнем с того, что узнаем, что такое параллелепипед. Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

Каждый прямоугольник перпендикулярен тем, что имеет общий край. Они наиболее распространены в нашей повседневной жизни, так как это обычный способ обувных коробок и кирпичей.. Куб или правильный шестигранник Это частный случай предыдущего, где каждая из граней является квадратом. Куб также является частью геометрических тел, называемых платоновыми телами. Платоническое тело представляет собой выпуклый многогранник, так что его грани и внутренние углы равны друг другу. Эти алмазы все равны между собой, так как они имеют общие края. Romboiedro Его шесть граней — ромбоиды. Напомним, что ромбоид представляет собой многоугольник с четырьмя сторонами и четырьмя углами, которые равны от двух до двух. Ромбоиды — это параллелограммы, которые не являются ни квадратными, ни прямоугольниками, ни ромбами. С другой стороны, косые параллелепипеды — это те, в которых хотя бы одна высота не совпадает с ее краем. В эту классификацию мы можем включить ромбоэдры и ромбиэдры. Диагональный расчет Чтобы вычислить диагональ ортоэдра, мы можем использовать теорему Пифагора для R3. Напомним, что ортоэдр имеет характеристику, состоящую в том, что каждая сторона перпендикулярна сторонам, имеющим общий край. Из этого факта мы можем сделать вывод, что каждое ребро перпендикулярно тем, которые имеют общую вершину. Чтобы вычислить длину диагонали ортоэдра, действуем следующим образом: 1. Мы рассчитаем диагональ одной из граней, которую мы положим в качестве основы. Для этого мы используем теорему Пифагора.

Вот по этому в нашей задаче прямо говорится об этом. Если верить Священным Писаниям разных религий, то именно из одного такого ребра сотворены все прямоугольные параллелепипеды, задачи о которых решает вся прекрасная половина человечества. Следующая фраза «… равны 1, 2, 3» обозначает, что нам не нужно искать этот злополучный прямоугольный параллелепипед и свою линейку, чтобы измерить длины его граней, как это показано на рисунке. Тот, кто эту задачу придумал, уже сам всё измерил или выдумал эти размеры, что в данном случае принципиального значения не имеет. Кто есть кто в этом списке чисел? Где длина, ширина, высота нашего параллелепипеда? Нам это без разницы. Как бы мы этот прямоугольный параллелепипед не крутили, площадь его поверхности всегда будет оставаться неизменной. Предыдущие поколения математиков этот факт не единожды проверили. Когда мы доберемся до решения, мы сами в этом убедимся. Теперь вопрос, в чём же конкретно измеряется наш прямоугольный параллелепипед и площадь его поверхности? В каких единицах измерения? Ответ довольно прост — в любых единицах измерения длины. Англичане и американцы любят дюймы, футы, мили. Мы предпочитаем сантиметры, метры, километры. В чем измеряют длину инопланетяне? Мы вообще не знаем. Да нам эти единицы измерения и не важны. В чем бы мы не измеряли длину граней, циферки возле длин и площади будут одинаковыми. Циферки остаются, единицы измерения меняются.

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

1. В кубе 6 граней, каждая грань куба — квадрат.
2. Противолежащие грани параллельны друг другу.
3. Все углы куба, образованные двумя гранями, равны 90°.
4. У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
5. Диагонали куба равны.
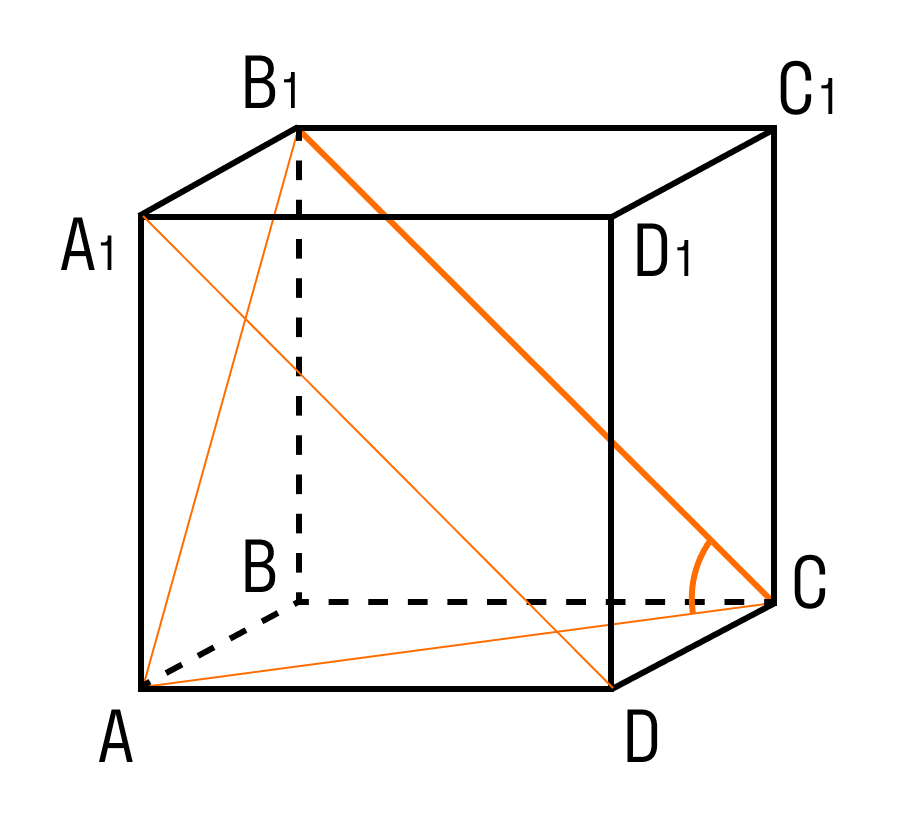
6. Диагональ куба в √3 раз больше его ребра.
7. Диагональ грани куба в √2 раза больше длины ребра.

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

• Объем куба через длину ребра a V = a3
• Площадь поверхности куба S = 6a2
• Периметр куба P = 12a

Вместо заключения

Слово ПРИЗМА используется не только в геометрии, хотя именно это значение считается главным. И именно оно первым записано во многих словарях. Но есть и другие варианты:

1. Физика– устройство для преломления световых лучей.
2. Риторика– оценка с учетом определенных факторов. Например, «Он смотрел на нее через призму прожитых лет» или «Он общался с ними через призму своего настроения».
3. Техника– элемент металлорежущего станка, который предназначен для закрепления на нем цилиндрической заготовки.

А еще «Призма» — это кодовое название советской радиостанции 5-АК. Есть такой хоккейный клуб в Латвии – «Призма-Рига». И наконец, в Финляндии существует сеть продуктовых магазинов «PRISMA».

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

• прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
• параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
• основание прямоугольного параллелепипеда — прямоугольник;
• три измерения прямоугольного параллелепипеда: длина, ширина, высота;
• диагональ параллелепипеда равна сумме квадратов его измерений.