График кубической функции: определение и примеры

График кубической функции. Построить кубическую функцию. Кубическая парабола график.

Как построить график кубических функций вида \(y = a (x − h)3 + k\). В этой статье мы покажем как построить график кубических функций путем построения точек. Общая формула кубической функции:

 где \(a, b, c\) и \(d\) являются действительными числами  и  \(a\) не равно нулю.

Построим график кубических функций путем построения точек.

Пример 1. Постройте график \(y = x^3 + 3\) на промежутке \(-3 ≤ x ≤ 3\).

Решение. 

Выберем произвольные точки \(x \) и посчитаем соответсвующие им значения \(y\):

Построим точки из таблицы и плавно соединим их:

Пример 2. Постройте график \(y = x^3-9x + 5\) на промежутке \(-4 ≤ x ≤ 4\):

Решение.  Строим график аналогично первому примеру:

1) когда  \(x = 1.6, \;y≈ –5.3\)

2) когда \(y = 12, \;x ≈ –0.8 \)  или  \( x ≈ –2.5\)

Теперь выведем правила построения графиков кубических функций вида \(y = a (x − h)^3 + k\).

• Если \(k > 0\), то график сдвигается на  \(k\) единиц вверх; если \(k < 0\), то график сдвигается на \(k\) единиц вниз.
• Если \(h > 0\),то график сдвигается  на \(h\) единиц вправо; если \(h < 0\), то график смещается на \(h\) единиц влево.
• Если \(a < 0\), график переворачивается.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Коллинеарности

Точки п₁, п₂, и п₃ (синим цветом) коллинеарны и принадлежат графику Икс3 + 32Икс2 − 52Икс + 54. Точки Т₁, Т₂, и Т₃ (красным) — точки пересечения (пунктирных) касательных к графику в этих точках с самим графиком. Они тоже коллинеарны.

Касательные к графику кубической функции в трех точках коллинеарные точки снова перехватить кубику в коллинеарных точках. Это можно увидеть следующим образом.

Поскольку это свойство инвариантно относительно жесткое движение, можно предположить, что функция имеет вид

ж(Икс)=Икс3+пИкс.{ displaystyle f (x) = x ^ {3} + px.}

Если α действительное число, то касательная к графику ж в момент (α, ж(α)) это линия

{(Икс, ж(α) + (Икс − α)ж ′(α)) : Икс ∈ р}.

Итак, точка пересечения этой линии и графика ж можно получить, решив уравнение ж(Икс) = ж(α) + (Икс − α)ж ′(α), то есть

Икс3+пИкс=α3+пα+(Икс−α)(3α2+п),{ displaystyle x ^ {3} + px = alpha ^ {3} + p alpha + (x- alpha) (3 alpha ^ {2} + p),}

который можно переписать

Икс3−3α2Икс+2α3=,{ displaystyle x ^ {3} -3 alpha ^ {2} x + 2 alpha ^ {3} = 0,}

и разложен на множители как

(Икс−α)2(Икс+2α)={ Displaystyle (х- альфа) ^ {2} (х + 2 альфа) = 0.}

Итак, касательная пересекает кубику в точке

(−2α,−8α3−2пα)=(−2α,−8ж(α)−10пα).{ displaystyle (-2 alpha, -8 alpha ^ {3} -2p alpha) = (- 2 alpha, -8f ( alpha) -10p alpha).}

Итак, функция, отображающая точку (Икс, у) графика в другую точку, где касательная пересекает график,

(Икс,у)↦(−2Икс,−8у−10пИкс).{ displaystyle (x, y) mapsto (-2x, -8y-10px).}

Это аффинное преобразование который преобразует коллинеарные точки в коллинеарные точки. Это подтверждает заявленный результат.

График логарифмической функции

Рассмотрим функцию с натуральным логарифмом .
Выполним поточечный чертеж:

Если позабылось, что такое логарифм, пожалуйста, обратитесь к школьным учебникам.

Основные свойства функции :

Область определения:

Область значений: .

Функция не ограничена сверху: , пусть и медленно, но ветка логарифма уходит вверх на бесконечность.
Исследуем поведение функции вблизи нуля справа: . Таким образом, ось  является вертикальной  асимптотой для графика функции при «икс» стремящемся к нулю справа.

Обязательно нужно знать и помнить типовое значение логарифма: .

Принципиально так же выглядит график логарифма при основании : , ,  (десятичный логарифм по основанию 10) и т.д. При этом, чем больше основание, тем более пологим будет график.

Случай  рассматривать не будем, что-то я не припомню, когда последний раз строил график с таким основанием. Да и логарифм вроде  в задачах высшей математики ооочень редкий гость.

В заключение параграфа скажу еще об одном факте: Экспоненциальная функция  и логарифмическая функция  – это две взаимно обратные функции. Если присмотреться к графику логарифма, то можно увидеть, что это – та же самая экспонента, просто она расположена немного по-другому.

Классификация

Кубические функции формы у=Икс3+пИкс.{ displaystyle y = x ^ {3} + px.}График любой кубической функции есть похожий к такой кривой.

В график кубической функции является кубическая кривая, хотя многие кубические кривые не являются графиками функций.

Хотя кубические функции зависят от четырех параметров, их график может иметь очень мало форм. На самом деле график кубической функции всегда похожий графику функции вида

у=Икс3+пИкс.{ displaystyle y = x ^ {3} + px.}

Это сходство можно построить как композицию переводы параллельно осям координат, a гомотия (равномерное масштабирование ), и, возможно, отражение (зеркальное изображение ) с уважением к у-ось. Дальше неравномерное масштабирование может преобразовать график в график одной из трех кубических функций

у=Икс3+Иксу=Икс3у=Икс3−Икс.{ displaystyle { begin {align} y & = x ^ {3} + x y & = x ^ {3} y & = x ^ {3} -x. end {выравнивается}}}

Это означает, что есть только три графика кубических функций вплоть до ан аффинное преобразование.

Вышесказанное геометрические преобразования можно построить следующим образом, исходя из общей кубической функции у=аИкс3+бИкс2+cИкс+d.{ displaystyle y = ax ^ {3} + bx ^ {2} + cx + d.}

Во-первых, если а < 0, то изменение переменной Икс → –Икс позволяет предположить а > 0. После этой замены переменной новый график является зеркальным отображением предыдущего по отношению к у-ось.

Тогда замена переменной Икс = Икс₁ – б3а предоставляет функцию формы

у=аИкс13+пИкс1+q.{ displaystyle y = ax_ {1} ^ {3} + px_ {1} + q.}

Это соответствует переносу, параллельному Икс-ось.

Изменение переменной у = у₁ + q соответствует переводу относительно у-оси, и дает функцию вида

у1=аИкс13+пИкс1.{ displaystyle y_ {1} = ax_ {1} ^ {3} + px_ {1}.}

Изменение переменной Икс1=Икс2а,у1=у2а{ displaystyle textstyle x_ {1} = { frac {x_ {2}} { sqrt {a}}}, y_ {1} = { frac {y_ {2}} { sqrt {a}}} } соответствует равномерному масштабированию и дают после умножения на а,{ displaystyle { sqrt {a}},} функция формы

у2=Икс23+пИкс2,{ displaystyle y_ {2} = x_ {2} ^ {3} + px_ {2},}

что является самой простой формой, которую можно получить подобием.

Тогда, если п ≠ 0, неравномерное масштабирование Икс2=Икс3|п|,у2=у3|п|3{ displaystyle textstyle x_ {2} = x_ {3} { sqrt {| p |}}, quad y_ {2} = y_ {3} { sqrt {| p | ^ {3}}}} дает после деления на |п|3,{ displaystyle textstyle { sqrt {| p | ^ {3}}},}

у3=Икс33+Икс3знак⁡(п),{ displaystyle y_ {3} = x_ {3} ^ {3} + x_ {3} operatorname {sign} (p),}

куда знак⁡(п){ displaystyle operatorname {знак} (p)} имеет значение 1 или –1, в зависимости от знака п. Если определить знак⁡()=,{ displaystyle operatorname {sign} (0) = 0,} последняя форма функции применяется ко всем случаям (с Икс2=Икс3{ displaystyle x_ {2} = x_ {3}} и у2=у3{ displaystyle y_ {2} = y_ {3}}).

Критические и переломные моменты

В корни, стационарные точки, точка перегиба и вогнутость из кубический многочлен Икс3 − 3Икс2 − 144Икс + 432 (черная линия) и его первая и вторая производные (красный и синий).

В критические точки кубической функции являются ее стационарные точки, то есть точки, в которых наклон функции равен нулю. Таким образом, критические точки кубической функции ж определяется

ж(Икс) = топор3 + bx2 + сх + d,

происходят при значениях Икс так что производная

3аИкс2+2бИкс+c={ displaystyle 3ax ^ {2} + 2bx + c = 0}

кубической функции равна нулю.

Решениями этого уравнения являются Икс-значения критических точек и даны с использованием квадратичная формула, к

Икскритический=−б±б2−3аc3а.{ displaystyle x _ { text {critical}} = { frac {-b pm { sqrt {b ^ {2} -3ac}}} {3a}}.}

Знак выражения внутри квадратного корня определяет количество критических точек. Если он положительный, то есть две критические точки, одна — локальный максимум, а другая — локальный минимум. Если б2 – 3ac = 0, то есть только одна критическая точка — точка перегиба. Если б2 – 3ac < 0, то (реальных) критических точек нет. В двух последних случаях, т. Е. Если б2 – 3ac неположительна, кубическая функция строго монотонный. См. Рисунок для примера корпуса Δ > 0.

Точка перегиба функции — это место, где она изменяется вогнутость. Точка перегиба возникает, когда вторая производная ж″(Икс)=6аИкс+2б,{ displaystyle f » (x) = 6ax + 2b,} равна нулю, а третья производная отлична от нуля. Таким образом, кубическая функция всегда имеет одну точку перегиба, которая встречается в

Иксперегиб=−б3а.{ displaystyle x _ { text {inflection}} = — { frac {b} {3a}}.}

Графики тригонометрических функций

С чего начинаются тригонометрические мучения в школе? Правильно. С синуса

Построим график функции

Данная линия называется синусоидой.

Напоминаю, что «пи» – это иррациональное число: , и в тригонометрии от него в глазах рябит.

Основные свойства функции :

Данная функция является периодической с периодом . Что это значит? Посмотрим на отрезок . Слева и справа от него бесконечно повторяется точно такой же кусок графика.

Область определения: , то есть для любого значения «икс» существует значение синуса.

Область значений: . Функция  является ограниченной: , то есть, все «игреки» сидят строго в отрезке .
Такого не бывает:  или , точнее говоря, бывает, но указанные уравнения не имеют решения.

Синус – это функция нечетная, синусоида симметричная относительно начала координат, и справедлив следующий факт: . Таким образом, если в вычислениях встретится, например, , то минус терять здесь ни в коем случае нельзя! Он выносится:

Как ведет себя синус на бесконечности? Попробуем провести исследование с помощью пределов:,  Чему равны такие пределы? Запомните, данных пределов не существует. По вполне понятным причинам, график синуса болтается как как неприкаянный, то дойдет единицы, то уйдет к минус единице и так до бесконечности.

Вот вам пример, когда предела не существует. В высшей математике это можно встретить не очень часто, но такое понятие, как «предела не существует» – существует!

В практических вычислениях желательно (и даже обязательно) знать и помнить следующие значения синуса: , , . Другие значения синуса (а также остальных тригонометрических функций) можно найти в методическом материале Тригонометрические таблицы.

График косинуса

Построим график функции

График косинуса – это та же самая синусоида, сдвинутая вдоль оси  на  влево
(см. также Пример 8 урока о геометрических преобразованиях графиков).

Поэтому почти все свойства синуса справедливы и для косинуса. За некоторым, но существенным исключением.

Косинус – это функция четная, ее график симметричен относительно оси  , и справедлив следующий факт: . То есть, минус перед аргументом косинуса можно безболезненно убирать (или наоборот, ставить). В отличие от синуса в косинусе минус «бесследно пропадает».

Для решения практических задач нужно знать и помнить следующие значения косинуса: , , .

Графики тангенса и котангенса

Построим график функции

Основные свойства функции :

Данная функция является периодической с периодом . То есть, достаточно рассмотреть отрезок , слева и справа от него ситуация будет бесконечно повторяться.

Область определения:  – все действительные числа, кроме …  , , , … и т. д. или коротко: , где  – любое целое число. Множество целых чисел (… -4, -3, -2, -1, 0, 1, 2, 3, 4, …) в высшей математике обозначают жирной буквой Z.

Область значений: . Функция  не ограничена. В этом легко убедиться и аналитически: – если мы приближаемся по оси  к значению  справа, то ветка тангенса уходит на минус бесконечность, бесконечно близко приближаясь к своей асимптоте . – если мы приближаемся по оси  к значению  слева, то «игреки» шагают вверх на плюс бесконечность, а ветка тангенса бесконечно близко приближается к асимптоте .

Тангенс – функция нечетная, как и в случае с синусом, минус из-под тангенса не теряется, а выносится: .

В практических вычислениях полезно помнить следующие значения тангенса: , , , а также те точки, в которых тангенса не существует (см. график).

График котангенса – это почти тот же самый тангенс, функции связаны тригонометрическим соотношением . Вот его график:

Свойства попробуйте сформулировать самостоятельно, они практически такие же, как и у тангенса.

Классификация

Кубические функции формы у=Икс3+пИкс.{ displaystyle y = x ^ {3} + px.}График любой кубической функции есть похожий к такой кривой.

В график кубической функции является кубическая кривая, хотя многие кубические кривые не являются графиками функций.

Хотя кубические функции зависят от четырех параметров, их график может иметь очень мало форм. На самом деле график кубической функции всегда похожий графику функции вида

у=Икс3+пИкс.{ displaystyle y = x ^ {3} + px.}

Это сходство можно построить как композицию переводы параллельно осям координат, a гомотия (равномерное масштабирование ), и, возможно, отражение (зеркальное изображение ) с уважением к у-ось. Дальше неравномерное масштабирование может преобразовать график в график одной из трех кубических функций

у=Икс3+Иксу=Икс3у=Икс3−Икс.{ displaystyle { begin {align} y & = x ^ {3} + x y & = x ^ {3} y & = x ^ {3} -x. end {выравнивается}}}

Это означает, что есть только три графика кубических функций вплоть до ан аффинное преобразование.

Вышесказанное геометрические преобразования можно построить следующим образом, исходя из общей кубической функции у=аИкс3+бИкс2+cИкс+d.{ displaystyle y = ax ^ {3} + bx ^ {2} + cx + d.}

Во-первых, если а < 0, то изменение переменной Икс → –Икс позволяет предположить а > 0. После этой замены переменной новый график является зеркальным отображением предыдущего по отношению к у-ось.

Тогда замена переменной Икс = Икс₁ – б3а предоставляет функцию формы

у=аИкс13+пИкс1+q.{ displaystyle y = ax_ {1} ^ {3} + px_ {1} + q.}

Это соответствует переносу, параллельному Икс-ось.

Изменение переменной у = у₁ + q соответствует переводу относительно у-оси, и дает функцию вида

у1=аИкс13+пИкс1.{ displaystyle y_ {1} = ax_ {1} ^ {3} + px_ {1}.}

Изменение переменной Икс1=Икс2а,у1=у2а{ displaystyle textstyle x_ {1} = { frac {x_ {2}} { sqrt {a}}}, y_ {1} = { frac {y_ {2}} { sqrt {a}}} } соответствует равномерному масштабированию и дают после умножения на а,{ displaystyle { sqrt {a}},} функция формы

у2=Икс23+пИкс2,{ displaystyle y_ {2} = x_ {2} ^ {3} + px_ {2},}

что является самой простой формой, которую можно получить подобием.

Тогда, если п ≠ 0, неравномерное масштабирование Икс2=Икс3|п|,у2=у3|п|3{ displaystyle textstyle x_ {2} = x_ {3} { sqrt {| p |}}, quad y_ {2} = y_ {3} { sqrt {| p | ^ {3}}}} дает после деления на |п|3,{ displaystyle textstyle { sqrt {| p | ^ {3}}},}

у3=Икс33+Икс3знак⁡(п),{ displaystyle y_ {3} = x_ {3} ^ {3} + x_ {3} operatorname {sign} (p),}

куда знак⁡(п){ displaystyle operatorname {знак} (p)} имеет значение 1 или –1, в зависимости от знака п. Если определить знак⁡()=,{ displaystyle operatorname {sign} (0) = 0,} последняя форма функции применяется ко всем случаям (с Икс2=Икс3{ displaystyle x_ {2} = x_ {3}} и у2=у3{ displaystyle y_ {2} = y_ {3}}).

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Конспект урока «Функции y=x2 и y=x3 и их графики»

· рассмотреть функцию y = x 2 , её свойства и график;

· рассмотреть функцию y = х 3 , её свойства и график.

На одном из предыдущих уроков мы с вами познакомились с линейной функцией, которую можно задать формулой вида:

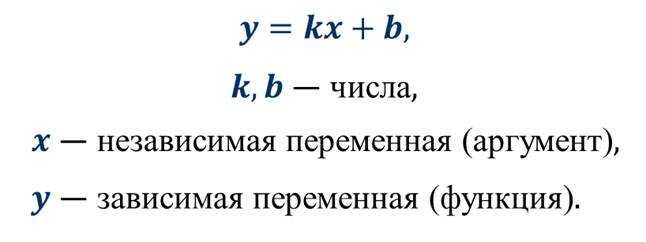
Также вспомним, что графиком линейной функции является прямая.

На этом уроке мы рассмотрим функции:

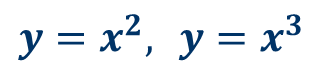
А точнее, мы научимся строить графики этих функций и выясним некоторые их свойства.

Начнём с того, что выразим формулой зависимость площади квадрата от длины его стороны.

Таким образом, зависимость площади квадрата от его стороны является примером функции.

Давайте построим график этой функции.

Составим таблицу значений x, y.

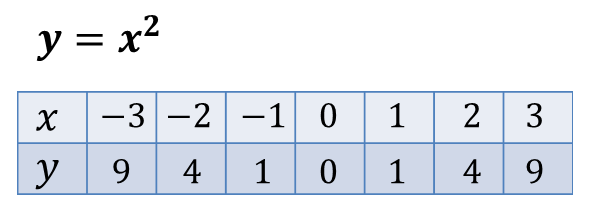
Далее полученные точки изобразим на координатной плоскости и проведём через них плавную линию.

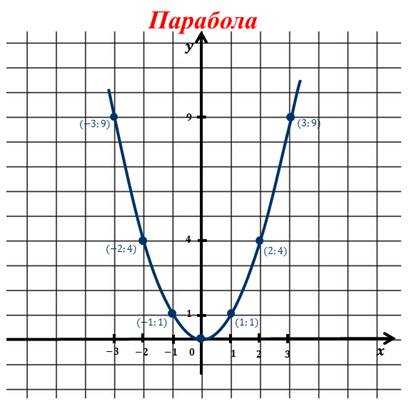
Обратите внимание, что этот график неограниченно продолжается вверх справа и слева от оси игрек. Теперь выясним некоторые свойства функции y = x 2

Теперь выясним некоторые свойства функции y = x 2 .

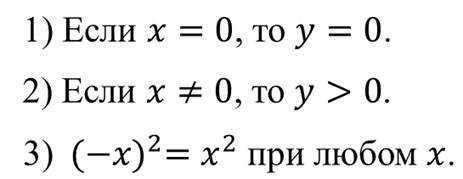
Из последнего свойства графика следует, что точки графика, имеющие противоположные абсциссы, симметричны относительно оси игрек.

Теперь давайте выразим формулой зависимость объёма куба от длины его ребра.

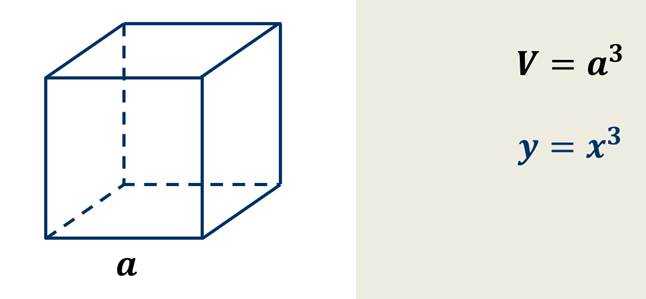
Если мы будем менять длину ребра, то и его объём будет меняться.

Зависимость объёма куба от длины его ребра является примером функции.

Построим график этой функции. Для этого придадим несколько значений аргументу икс и вычислим соответствующие значения функции.

Изобразим точки с полученными координатами на координатной плоскости и проведём через них плавную линию.

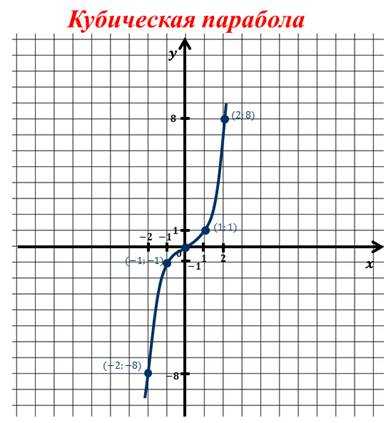
Обратите внимание, что этот график можно неограниченно продолжать справа от оси игрек вверх и слева от оси игрек вниз. Поговорим о свойствах функции игрек равняется икс в кубе

Поговорим о свойствах функции игрек равняется икс в кубе.

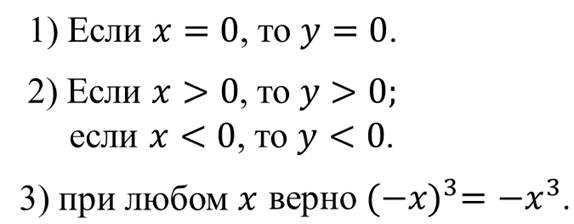
Следовательно, точки графика, которые имеют противоположные абсциссы, расположены симметрично относительно начала координат.

В повседневной жизни представление о параболе дают нам, например, траектории прыжков животных, радуга. Тросы висячего моста напоминают нам параболы.

Также параболу часто можно встретить в архитектуре.

Функция обратной пропорциональности

Функция обратной пропорциональности – это функция вида y = \(\frac{k}{x}\), где k – известное число и k ≠ 0, графиком которой является гипербола.

\(y = \frac{k}{x}\), где k – известное число k ≠ 0x – переменная

Рассмотрим пример такой функции \(y = \frac{2}{x}\)

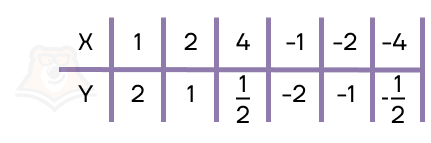
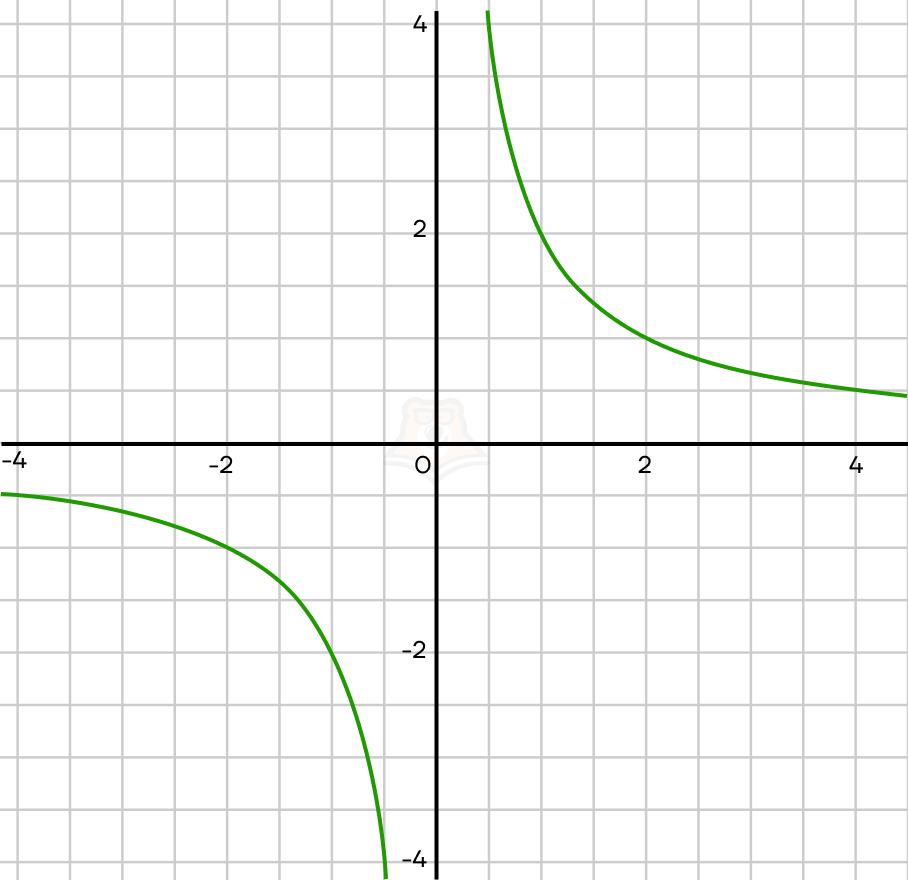
Как коэффициент k влияет на расположение гиперболы?

Как пронумерованы четверти на координатной плоскости?Вспомним четверти плоскостей. Они идут против часовой стрелки начиная с четверти, где и x, и y — положительные.

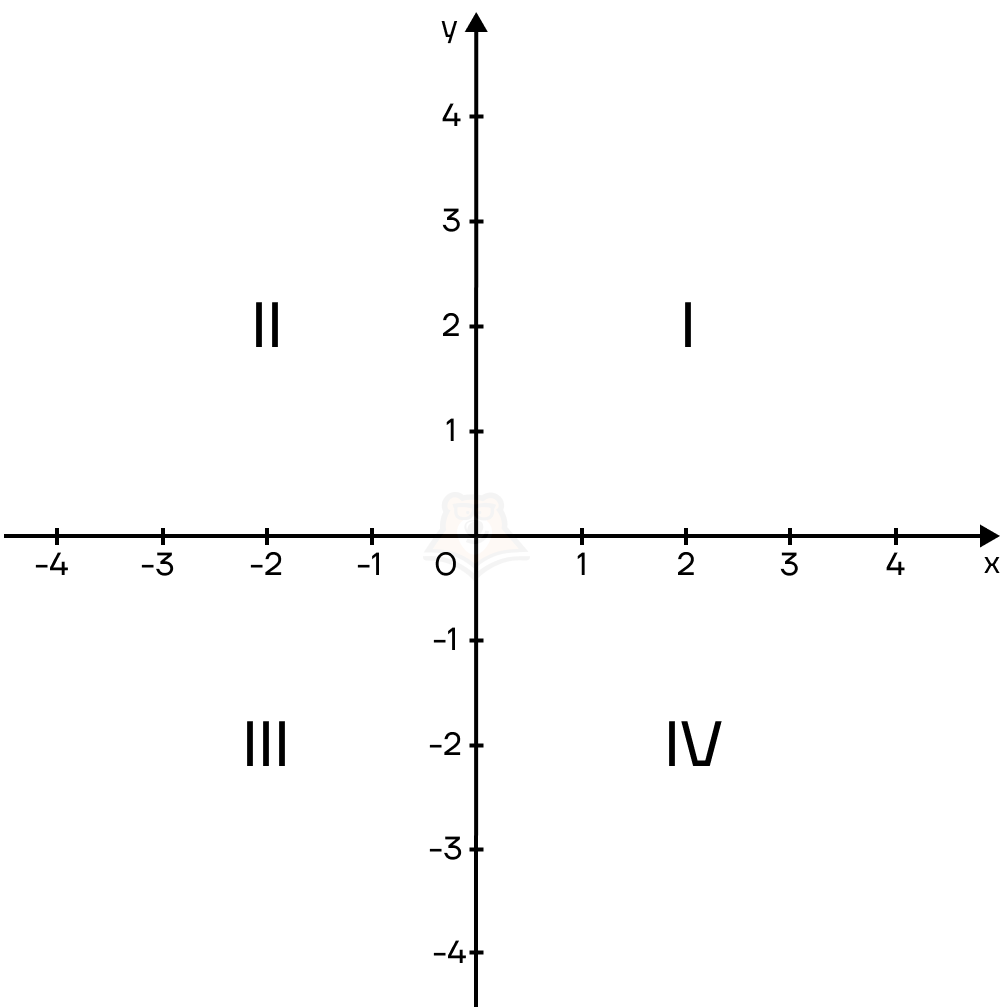
Гипербола при k > 0 – в первой и третьей плоскостях

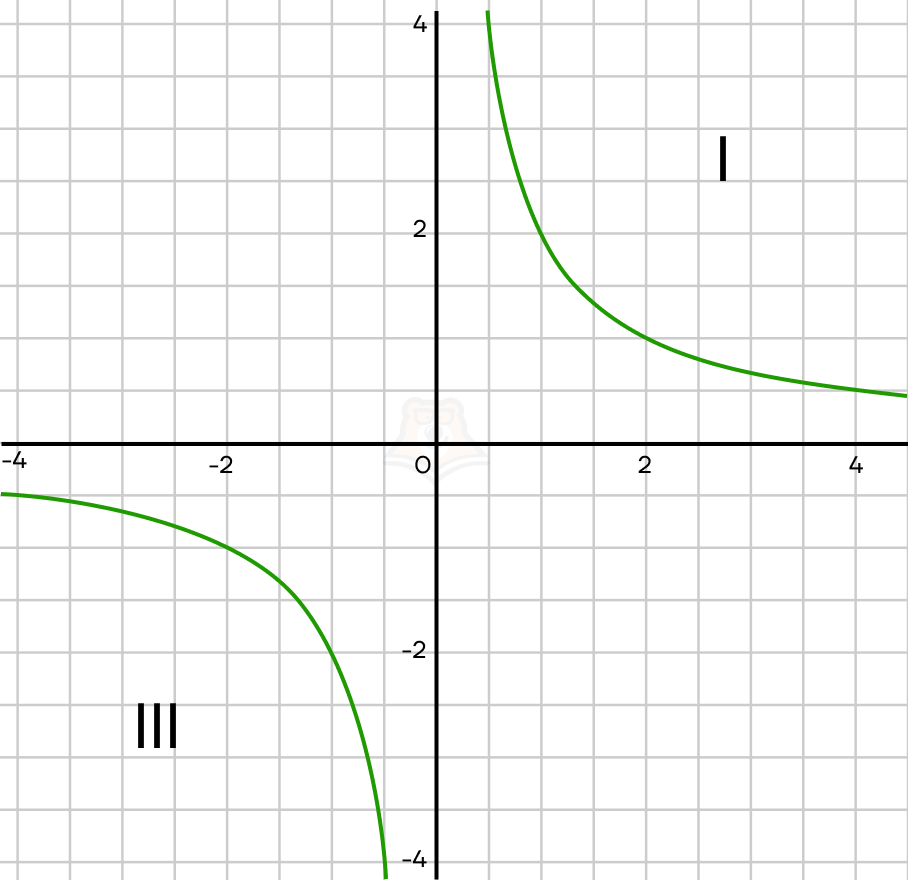
Гипербола при k< – во второй и четвертой плоскостях

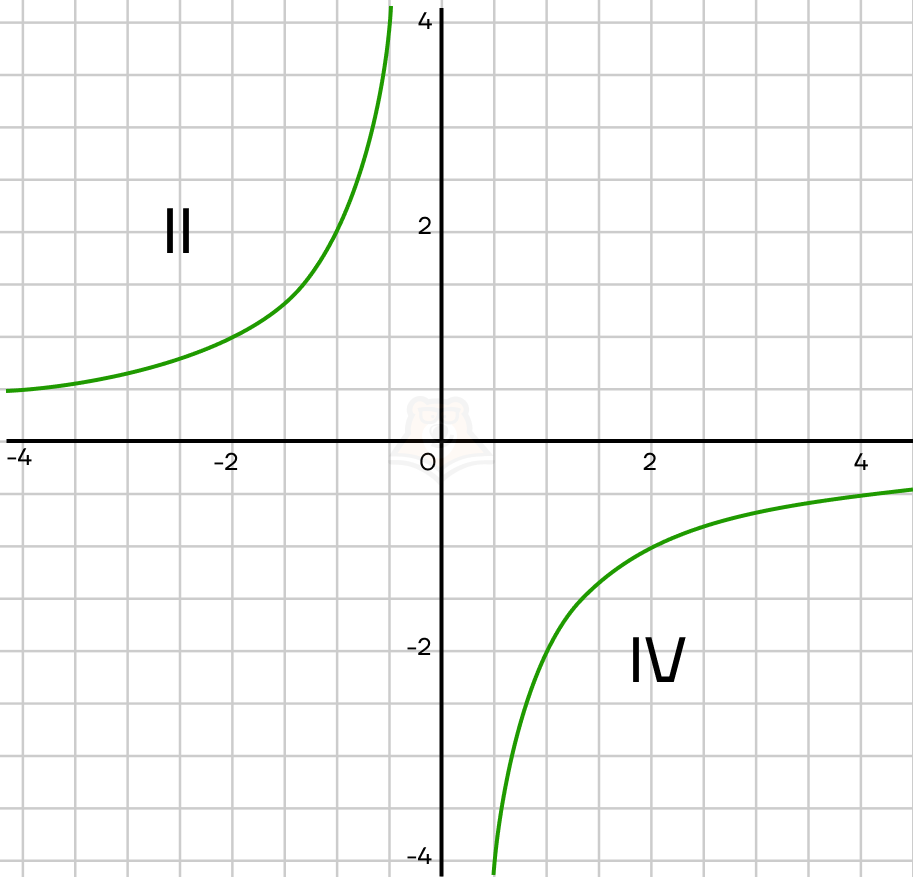
Гипербола может также двигаться по оси X или по оси Y

Движение графика по оси Y

\(y = \frac{k}{x} + n\) при k> 0

При n < 0, сдвиг внизПри n > 0, сдвиг вверх

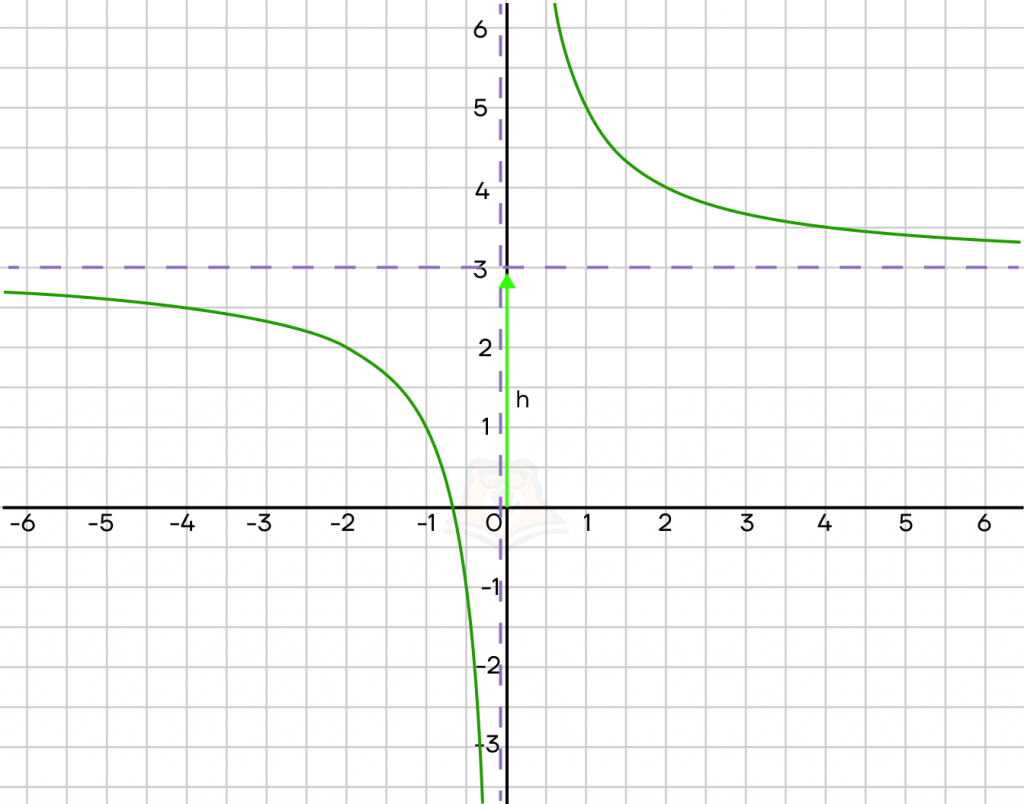
По графику выше можно сделать вывод, что n = 3.

Движение графика по оси X

\(y = \frac{k}{x + c}\) при k> 0

При c < 0, сдвиг вправоПри c > 0, сдвиг влево

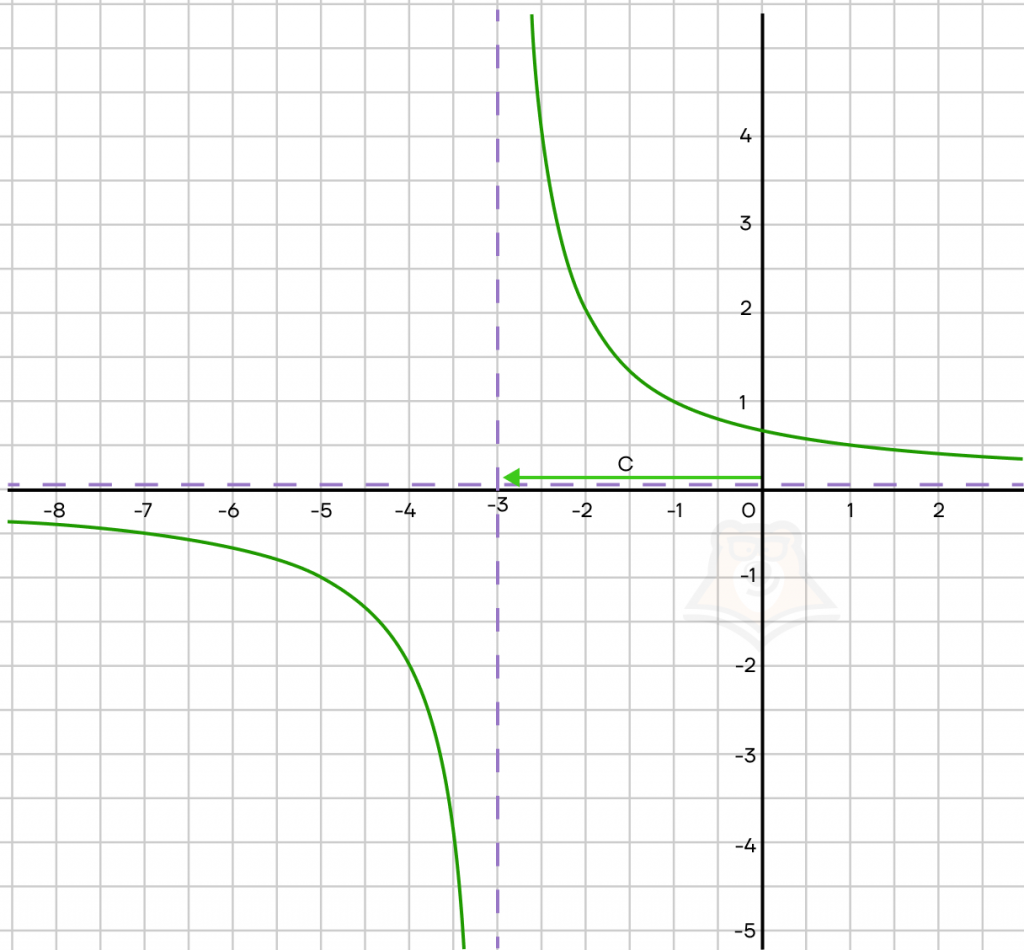
По графику выше можно сделать вывод, что c = 3.

Свойства функции обратной пропорциональности:

1. Область определения: D(y) = (-∞; 0) U (0; +∞)
2. Область значений функции: E(y) = (-∞; 0) U (0; +∞)
3. Наименьшего и наибольшего значений не существует.
4. Непериодическая.
5. При k > 0 убывает на (-∞;0) и (0; +∞).При k < 0 возрастает на (-∞; 0) и (0; +∞).
6. Нулей нет.
7. Нечетная.

Где же в реальной жизни мы можем встретить эту функцию? 

Самый простой пример – движение автомобиля: чем выше его скорость, тем меньше времени потребуется, чтобы преодолеть одно и то же расстояние.

Часто задаваемые вопросы о графике кубической функции

Как построить график кубических функций?

Чтобы построить график кубических многочленов, необходимо определить вершину, отражение, y-пересечение и x-пересечение.

Как выглядит график кубической функции?

Кубический график имеет две поворотные точки: точку максимума и точку минимума. Его кривая выглядит как холм, за которым следует впадина (или впадина, за которой следует холм).

Как построить график кубической функции в виде вершины?

Мы можем построить график кубической функции в виде вершины с помощью преобразований.

Что такое график кубической функции?

Кубический график — это график, иллюстрирующий многочлен степени 3. Он содержит две поворотные точки: максимум и минимум.

Как решить график кубической функции?

Чтобы построить график кубических многочленов, необходимо определить вершину, отражение, y-пересечение и x-пересечение.

Кубическая интерполяция

Учитывая значения функции и ее производной в двух точках, существует ровно одна кубическая функция, имеющая те же четыре значения, которая называется кубическим сплайном Эрмита..

Есть два стандартных способа использовать этот факт. Во-первых, если кто-то знает, например, путем физического измерения значения функции и ее производной в некоторых точках выборки, можно интерполировать функцию с помощью непрерывно дифференцируемой функции, которая является кусочно кубическая функция.

Если значение функции известно в нескольких точках, кубическая интерполяция заключается в приближении функции непрерывно дифференцируемой функцией, которая является кусочно куб. Для однозначно определенной интерполяции необходимо добавить еще два ограничения, например значения производных в конечных точках или нулевую кривизну в конечных точках.

Линейная функция

Любую функцию можно изобразить на графике (рисунке) и наглядно определить многие её свойства. Этим пользуются люди, составляя графики движения транспорта, посещения соцсетей или просмотра видеороликов на канале.  

Вспомним, что функция – это зависимость одной переменной от другой, а график функции – это представление данной зависимости на координатной плоскости. 

С помощью графика функции можно изучать поведение функции: возрастает или убывает, имеет ли нули, на каких промежутках значения положительные, а на каких отрицательные, наибольшее и наименьшее значение, является ли симметричной относительно OY.

Теперь давайте рассмотрим основные элементарные функции.

Что же такое линейная функция? 

Линейная функция – это функция вида y=kx+b, где k и b – известные числа, графиком которой является прямая.

y = kx + b, гдеk – коэффициентb – свободный членx – переменная

С линейной функцией мы встречаемся, когда оплачиваем проезд  в общественном транспорте.

Коэффициент и переменная определяют стоимость билета в зависимости от дальности поездки. Свободным членом может выступать доплата за комфортное место или за поезд-экспресс.

Пункт назначения	Станция 200 км	Станция 300 км	Станция 400 км
Цена поездки в обычном вагоне (kx)	500 руб.	750 руб.	1000 руб.
Цена за вагон “Люкс” (kx + b)	750 руб.	1000 руб.	1250 руб.

Рассмотрим пример такой функции и ее график:y = 2x + 3

Составим таблицу значений.

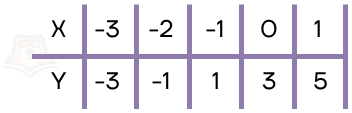
Теперь отметим найденные точки на координатной плоскости и проведём через них прямую.

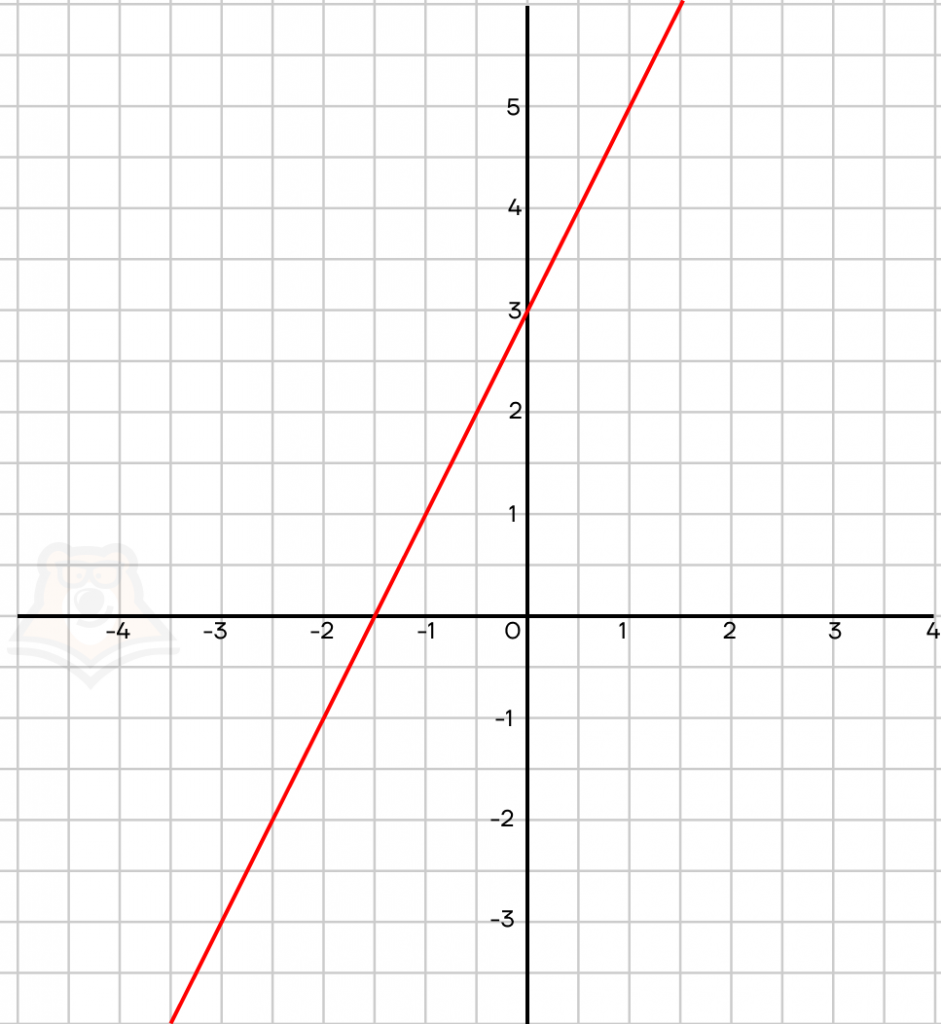
Полученный нами график является графиком данной линейной функции.

Также можно составить уравнение линейной функции самостоятельно при наличии графика.

За что отвечают коэффициенты в записи линейной функции?Коэффициент b – это длина отрезка по оси OY, на который происходит сдвиг от начала координат (может быть отрицательным, если пересечение графика с осью Y в точке с отрицательным значением).Коэффициент k – это угол наклона прямой, он равен отношению разностей координат двух произвольных точек.

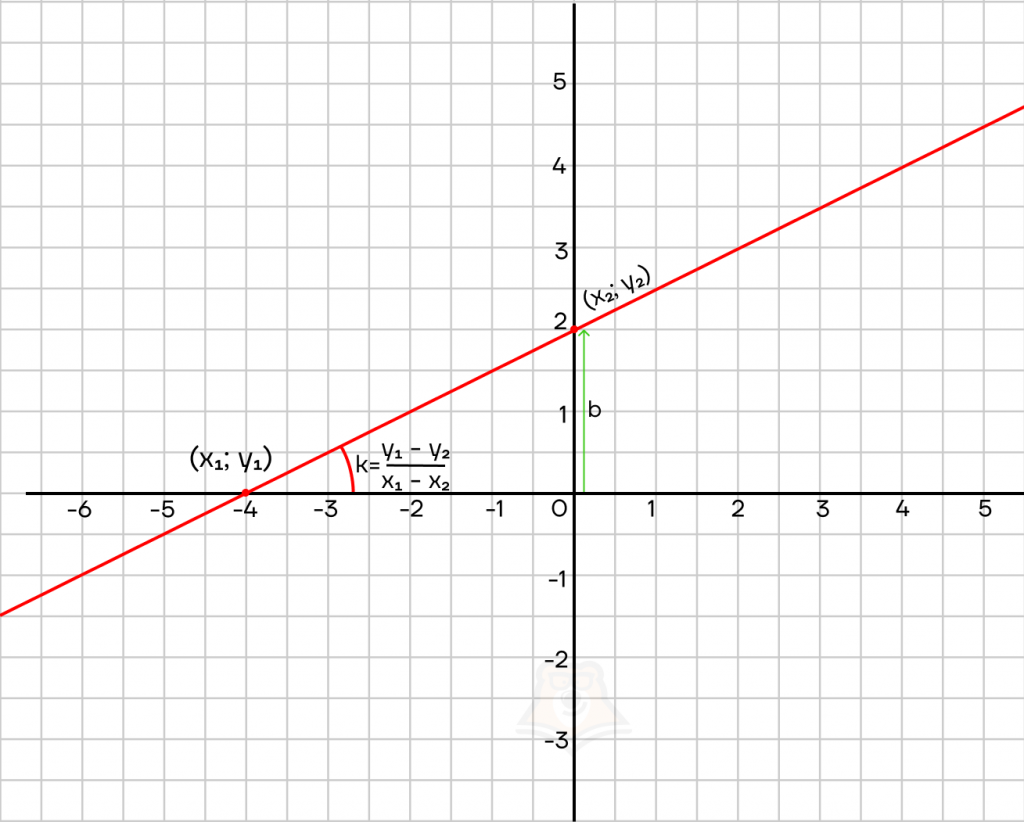
На графике найдем сначала коэффициент b , после определим координаты двух произвольных точек прямой и вычислим коэффициент k.

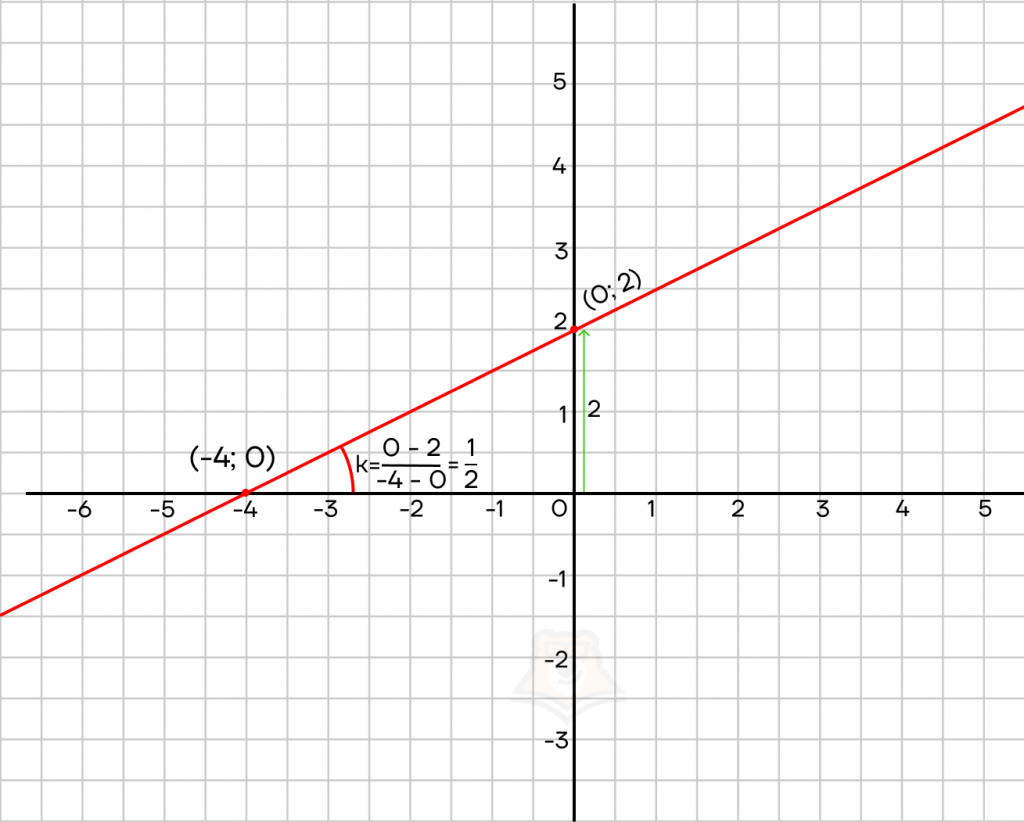
Подставим найденные коэффициенты в формулу линейной функции и получим\(y = \frac{1}{2}x + 2\)

Свойства линейной функции:

1. Область определения: D(y) = (-∞; +∞)
2. Область значений функции: E(y) = (-∞; +∞)
3. Наименьшего и наибольшего значения не существует.
4. Непериодическая.
5. Возрастает при  k > 0, убывает при k < 0.

Кубическая парабола

Кубическая парабола задается функцией . Вот знакомый со школы чертеж:

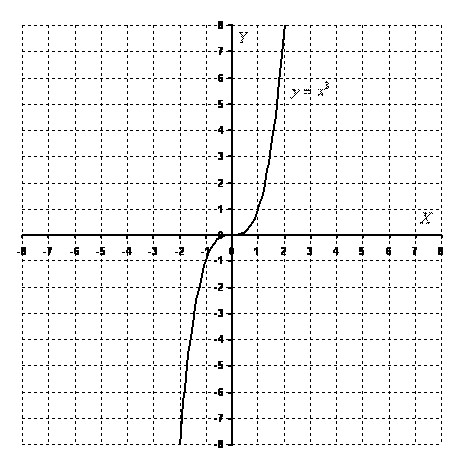
Перечислим основные свойства функции

Область определения – любое действительное число:.

Область значений – любое действительное число:.

Функция  является нечётной. Если функция является нечётной, то ее график симметричен относительно начала координат. Аналитически нечётность функции выражается условием . Выполним проверку для кубической функции, для этого вместо «икс» подставим «минус икс»: , значит, функция  является нечетной.

Функция  не ограничена. На языке пределов функции это можно записать так: ,

Кубическую параболу тоже удобнее строить с помощью алгоритма «челнока»:

Наверняка, вы заметили, в чем ещё проявляется нечетность функции. Если мы нашли, что , то при вычислении  уже не нужно ничего считать, автоматом записываем, что . Эта особенность справедлива для любой нечетной функции.

А теперь поговорим о графиках функций-многочленов высоких степеней чуть более подробно. График функции  () принципиально имеет следующий вид:

В этом примере коэффициент при старшей степени , поэтому график развёрнут «наоборот». Принципиально такой же вид имеют графики функций-многочленов 5-й, 7-й, 9-й и других нечетных степеней. Чем выше степень, тем больше промежуточных «загибулин».

Функции-многочлены 4-й, 6-й и других четных степеней имеют график принципиально следующего вида:

Эти знания полезны при исследовании графиков функций.