Закон ома для «чайников»: понятие, формула, объяснение

Где и как применяется формула P=U^2/R

Формула P=U^2/R используется для вычисления мощности в электрических цепях. Она связывает напряжение, сопротивление и мощность, позволяя определить количество электроэнергии, потребляемой или выделяющейся в цепи.

Электричество — это физическое явление, связанное с движением зарядов в проводниках. Оно является основным источником энергии для большинства бытовых приборов и промышленных установок.

Все электрические цепи состоят из источника электрического напряжения (обычно батареи или генератора), проводников, сопротивлений и потребителей. Напряжение обеспечивает движение электрического тока по цепи, а сопротивление ограничивает его поток.

Для определения мощности, выделяемой или потребляемой в цепи, используется формула P=U^2/R, где P — мощность, U — напряжение и R — сопротивление. При этом, напряжение измеряется в вольтах (В), сопротивление — в омах (Ω), а мощность — в ваттах (Вт).

Формула позволяет рассчитать мощность, выделяющуюся или потребляемую в цепи, когда известны напряжение и сопротивление. Например, при подключении бытовых приборов к сети, можно рассчитать мощность, потребляемую каждым из них, чтобы избежать перегрузки сети.

Также формула P=U^2/R применяется в электротехнике и электронике при проектировании и расчете электрических цепей. Зная значения напряжения и сопротивления, можно определить необходимую мощность и выбрать подходящие компоненты для цепи.

В общем, формула P=U^2/R является одной из основных формул в физике, связанной с электричеством. Она широко применяется для вычисления мощности в электрических цепях, помогая понять и контролировать энергию, проходящую через цепь.

Применение в электротехнике

PU2R – это формула, которая применяется в электротехнике для вычисления сопротивления электрической цепи. В электротехнике сопротивление является основным понятием, так как оно определяет электрический ток, протекающий через цепь.

Формула PU2R позволяет вычислить сопротивление (R), если известно напряжение (U) и ток (I), протекающий через цепь. Согласно формуле, сопротивление равно отношению напряжения к току: R = U / I.

Применение формулы PU2R в электротехнике позволяет определить сопротивление проводников, резисторов, диодов, транзисторов и других элементов электрических цепей. Расчет сопротивления осуществляется на основе измеренных значений напряжения и тока.

Зная сопротивление, можно рассчитать энергию, потребляемую или выделяемую в электрической цепи

Это важно для правильного выбора электрооборудования и расчета электрических сетей

Формула PU2R основывается на законах физики и применяется для решения различных задач в электротехнике и электронике. Она является одним из фундаментальных понятий в электротехнике и необходима для понимания работы электрических цепей и устройств.

Применение в физике

Формула PU2R широко применяется в физике для вычисления сопротивления в электрических цепях. Эта формула позволяет определить сопротивление в электрической цепи, основываясь на известных значениях напряжения и тока.

Сопротивление является важной характеристикой электрической цепи и определяет ее способность сопротивляться току. Чем выше сопротивление, тем меньше будет ток, протекающий через цепь при заданном напряжении

Формула PU2R выглядит следующим образом:

R = U / I

Где:

• R — сопротивление в электрической цепи (измеряется в омах)
• U — напряжение в электрической цепи (измеряется в вольтах)
• I — ток, протекающий через электрическую цепь (измеряется в амперах)

Как видно из формулы, сопротивление прямо пропорционально напряжению и обратно пропорционально току. Это позволяет вычислить сопротивление, если известны значения напряжения и тока.

Применение формулы PU2R в физике позволяет проводить расчеты и предсказывать поведение электрических цепей в различных условиях. Она является базовой формулой электрической цепи и используется во множестве прикладных областей физики и электротехники.

Объяснение действующего напряжения

Определение и формула — это хорошо. Но лучше все понять на наглядном примере. Объяснить все можно через мощность. Причем есть сложный для восприятия способ и более простой, который мы и рассмотрим далее.

Нам нужно взять один период синусоиды переменного напряжения, на этом промежутке построить синусоиду переменного тока и проанализировать мощность. Начнем с периода синусоиды переменного напряжения. Здесь же построим синусоиду переменного тока с учетом условной резистивной нагрузки (например, лампочки). По закону Ома сила тока равна напряжению, деленному на сопротивление.

Точные значения в конкретный момент при данном объяснении не принципиальны, поэтому все построения приблизительные. Естественно нужно понимать, что деля напряжение на сопротивление, мы получим синусоиду переменного тока с амплитудой в R раз меньшей, чем у напряжения. R – это значение сопротивления.

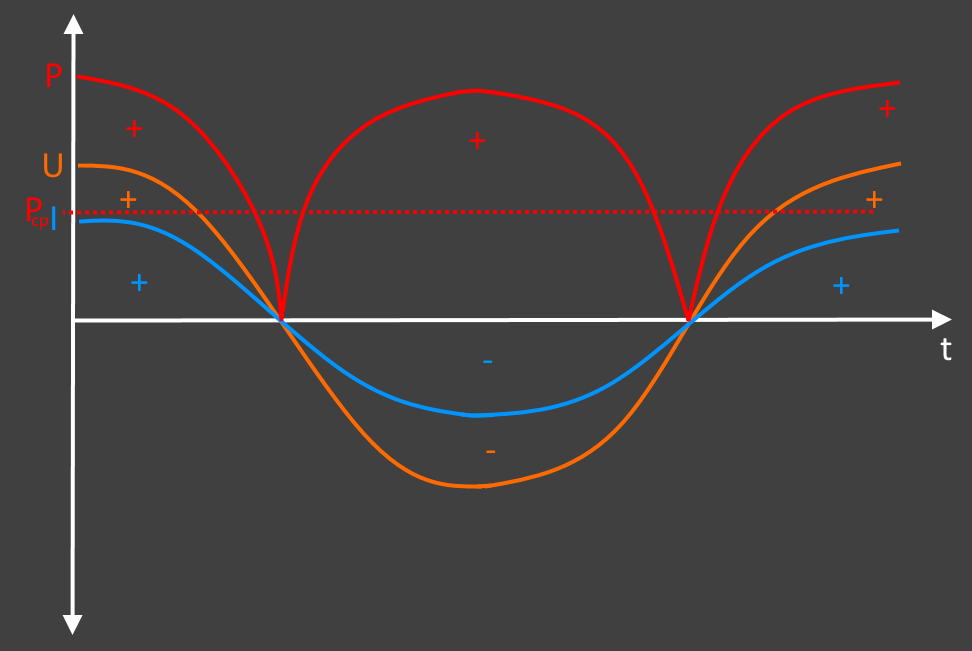
Теперь по двум синусоидам строим график мощности по формуле мощность равна силе тока умноженной на напряжение (P = I × U). Так как напряжение и ток имеют общие нулевые точки, то график мощности не будет заходить в отрицательную область. То есть сила тока со знаком «+» и напряжение со знаком «+» дадут мощность со знаком «+», так же как и сила тока со знаком «-» и напряжение со знаком «-» дадут мощность со знаком «+».

Анализируя полученный график можно отметить, что мощность пульсирующая. Она поднимается до максимального значения и падает до нуля, потом опять поднимается и снова падает. Как на эти колебания мощности реагируют электроприборы? Никак. Поскольку частота переменного тока 50 Герц, то эти колебания происходят очень быстро. Электроприборы откликаются не на максимальные и минимальные значения мощности, а на усредненные. То есть берется максимальное значение мощности и делится на два. Это значение называется действующим и находится по следующей формуле:

Pд = (Imax × Umax) / 2, где Pд — мощность действующая, Imax — сила тока максимальная, Umax — напряжение максимальное.

Двойку можно представить в виде корень из двух умножить на корень из двух. Получаем Действующее значение мощности = сила тока максимальная деленная на корень из двух умноженная на напряжение максимальное деленное на корень из двух (Pд = (Imax/√2) × (Umax/√2)).

И действительно, если мы возьмем максимальное напряжение из предыдущего примера 309,1 Вольт и разделим на корень из двух, то получим действующее напряжение (то, которое показывает вольтметр) 219,4 Вольт.

Применение формулы Е равно Мц квадрат в научных и технических расчетах

Эта формула имеет широкое применение в научных и технических расчетах. В физике она используется для определения энергии, высвободившейся в результате превращения массы. Это означает, что при расчете энергетических параметров реакций ядерного распада или ядерных синтезов можно применить формулу Е равно Мц квадрат.

Также формула применяется в технических расчетах. Например, в ядерной энергетике она используется для определения энергетического вывода реактора и расчета количества высвободившейся энергии при делении ядер атома.

Формула Е равно Мц квадрат также имеет важное значение в теории относительности, позволяя представить взаимосвязь массы и энергии в единой системе физических законов. Она послужила основой для развития атомной энергетики и дала возможность создания ядерного оружия

Важно отметить, что формула Е равно Мц квадрат имеет ограничения и не является универсальной для всех систем и процессов. Она применима только в условиях близких к покое и не может быть использована для высокоскоростных объектов, таких как быстрые частицы

В целом, формула Е равно Мц квадрат является важным инструментом для научных и технических расчетов, позволяя оценить энергетические характеристики и связи между массой и энергией в различных физических процессах.

Понятие выборочного наблюдения и область его применения.

Выборочное наблюдение применяется, когда применение сплошного наблюдения физически невозможно из-за большого массива данных или экономически нецелесообразно. Физическая невозможность имеет место, например, при изучении пассажиропотоков, рыночных цен, семейных бюджетов. Экономическая нецелесообразность имеет место при оценке качества товаров, связанной с их уничтожением, например, дегустация, испытание кирпичей на прочность и т.п.

Статистические единицы, отобранные для наблюдения, составляют выборочную совокупность или выборку, а весь их массив – генеральную совокупность (ГС). При этом числоединиц ввыборке обозначают n, а во всей ГС – N. Отношение n/N называется относительныйразмер или долявыборки.

Качество результатов выборочного наблюдения зависит от репрезентативности выборки, то есть от того, насколько она представительна в ГС. Для обеспечения репрезентативности выборки необходимо соблюдать принцип случайности отбора единиц, который предполагает, что на включение единицы ГС в выборку не может повлиять какой-либо иной фактор кроме случая.

Существует 4 способа случайного отбора в выборку:

1. Собственно случайный отбор или «метод лото», когда статистическим величинам присваиваются порядковые номера, заносимые на определенные предметы (например, бочонки), которые затем перемешиваются в некоторой емкости (например, в мешке) и выбираются наугад. На практике этот способ осуществляют с помощью генератора случайных чисел или математических таблиц случайных чисел.
2. Механический отбор, согласно которому отбирается каждая (N/n)-я величина генеральной совокупности. Например, если она содержит 100 000 величин, а требуется выбрать 1 000, то в выборку попадет каждая 100 000 / 1000 = 100-я величина. Причем, если они не ранжированы, то первая выбирается наугад из первой сотни, а номера других будут на сотню больше. Например, если первой оказалась единица № 19, то следующей должна быть № 119, затем № 219, затем № 319 и т.д. Если единицы генеральной совокупности ранжированы, то первой выбирается № 50, затем № 150, затем № 250 и так далее.
3. Отбор величин из неоднородного массива данных ведется стратифицированным (расслоенным) способом, когда генеральная совокупность предварительно разбивается на однородные группы, к которым применяется случайный или механический отбор.
4. Особый способ составления выборки представляет собой серийный отбор, при котором случайно или механически выбирают не отдельные величины, а их серии (последовательности с какого-то номера по какой-то подряд), внутри которых ведут сплошное наблюдение.

Качество выборочных наблюдений зависит и от типа выборки: повторная или бесповторная.

При повторном отборе попавшие в выборку статистические величины или их серии после использования возвращаются в генеральную совокупность, имея шанс попасть в новую выборку. При этом у всех величин генеральной совокупности одинаковая вероятность включения в выборку.

Бесповторный отбор означает, что попавшие в выборку статистические величины или их серии после использования не возвращаются в генеральную совокупность, а потому для остальных величин последней повышается вероятность попадания в следующую выборку.

Бесповторный отбор дает более точные результаты, поэтому применяется чаще. Но есть ситуации, когда его применить нельзя (изучение пассажиропотоков, потребительского спроса и т.п.) и тогда ведется повторный отбор.

Как правильно определить разность потенциалов в электрическом поле?

Разность потенциалов (также называемая напряжением) в электрическом поле представляет собой меру работы, которую нужно выполнить для перемещения единичного положительного заряда из одной точки второй в данном электрическом поле. Это фундаментальное понятие в электростатике и играет важную роль в понимании и анализе электрических цепей и систем.

Определение разности потенциалов

Разность потенциалов между двумя точками в электрическом поле обозначается символом «U» и измеряется в вольтах (В). Она характеризует работу, которую нужно совершить над единичным положительным зарядом, чтобы переместить его из одной точки второй.

Формула для расчёта разности потенциалов

Разность потенциалов между двумя точками в электрическом поле можно рассчитать с использованием следующей формулы:

UWq

где: U — разность потенциалов (вольты, В), W — работа, совершаемая над зарядом для перемещения его между точками (джоули, Дж), q — величина заряда (кулон, Кл).

Определение работы при перемещении заряда

Работа, которую нужно выполнить над положительным зарядом q для его перемещения в электрическом поле с разностью потенциалов U, определяется следующим образом:

W qU

где: W — работа (джоули, Дж), q — величина заряда (кулон, Кл), U — разность потенциалов (вольты, В).

Определение направления разности потенциалов

Разность потенциалов имеет направление от точки с более высоким потенциалом к точке с более низким потенциалом. Величина разности потенциалов показывает, насколько «выше» или «ниже» потенциал у данной точки по сравнению с другой.

Множественные разности потенциалов в цепи

В электрических цепях, состоящих из соединенных элементов, суммарная разность потенциалов в закольцованных цепях равна нулю (если нет изменений в магнитном поле). Это принцип известен как «закон Кирхгофа о напряжениях».

Измерение разности потенциалов

Разность потенциалов можно измерить с помощью вольтметра — прибора, предназначенного для измерения напряжения в электрических цепях. Вольтметры могут быть аналоговыми или цифровыми и имеют различные диапазоны измерения для разных приложений.

Что такое формула P=U^2/R?

Формула P=U^2/R является основной формулой в электричестве, которая используется для вычисления мощности электрической цепи. Эта формула связывает напряжение, сопротивление и мощность в электрической цепи.

В электрической цепи ток протекает через сопротивление, создавая энергию. Мощность, выражаемая в ваттах (W), показывает, сколько энергии используется в единицу времени. Используя формулу P=U^2/R, можно вычислить мощность, если известны значения напряжения и сопротивления.

В формуле P=U^2/R:

• P — мощность в ваттах (W)
• U — напряжение в вольтах (V)
• R — сопротивление в омах (Ω)

Формула говорит нам, что мощность равна квадрату напряжения, деленному на сопротивление. Это означает, что чем выше напряжение или чем меньше сопротивление в цепи, тем больше будет мощность.

Например, если у нас есть электрическая цепь с напряжением 10 вольт и сопротивлением 5 ом, тогда мы можем использовать формулу P=U^2/R, чтобы вычислить мощность:

P = (10^2) / 5 = 100 / 5 = 20 Вт

Таким образом, мощность этой электрической цепи равна 20 ваттам. Эта формула может быть очень полезной в применении электричества, так как она позволяет нам определить сколько энергии используется в электрической цепи и как это влияет на работу различных устройств.

Определение формулы

PU2R — это формула, которая используется для расчета энергии, потребляемой в электрической цепи, где P обозначает мощность, U — напряжение и R — сопротивление. Формула PU2R производится из формулы мощности P = UI, где P — мощность, U — напряжение и I — сила тока.

В физике сопротивление представляет собой сопротивление электрического тока в электрической цепи. Оно измеряется в омах (Ω). Разница потенциалов между двумя точками электрической цепи называется напряжением. Оно измеряется в вольтах (В).

Используя формулу PU2R, можно вычислить энергию, потребляемую в электрической цепи, зная значения напряжения и сопротивления. Формула PU2R является основой для расчета мощности и энергии в электротехнике и электронике.

Обозначение	Описание
P	Мощность (в ваттах)
U	Напряжение (в вольтах)
R	Сопротивление (в омах)

Формула PU2R позволяет узнать, сколько энергии будет потребляться в электрической цепи при заданных значениях напряжения и сопротивления

Знание этой формулы важно для проектирования электрических систем и устройств, а также для определения энергопотребления в домашних и промышленных сетях

Примеры использования

Формула PU2R используется для вычисления напряжения в электрической цепи, основываясь на известных значениях тока и сопротивления.

Напряжение (U) — это энергия, передаваемая в электрической цепи и измеряемая в вольтах.

Приведем пример использования формулы PU2R:

1. Известно значение тока в цепи (I) — 2 Ампера.
2. Известно значение сопротивления (R) — 5 Омов.
3. Используя формулу PU2R, можем вычислить напряжение (U):

Известные значения	Формула	Вычисление
Ток (I)	U = I * R	U = 2 * 5
Сопротивление (R)	U = 10 Вольт

Таким образом, если в электрической цепи протекает ток силой 2 Ампера и имеет сопротивление 5 Омов, то напряжение в этой цепи будет равно 10 Вольтам.

Формула PU2R является одной из основных формул в физике электричества и позволяет вычислить напряжение в электрической цепи на основе известных значений тока и сопротивления.

Напряжение: что это такое и зачем оно нужно

Напряжение – это одно из основных понятий в электротехнике, которое описывает разницу потенциалов между двумя точками в электрической цепи. Оно указывает на силу, с которой электрический ток будет протекать между этими точками.

Напряжение является неотъемлемой частью работы электрических систем и необходимо для передачи электрической энергии. Оно может быть источником электрического потенциала или результатом разницы напряжений между различными элементами цепи.

Зачем оно нужно? Напряжение используется для:

1. Подачи электрического тока к потребителям, таким как лампы, компьютеры, холодильники и другие устройства.
2. Передачи электрической энергии на большие расстояния через электроэнергетические сети.
3. Работы различных электрических устройств и систем: от простых переключателей и розеток до сложных промышленных систем.

Для измерения напряжения применяются специальные приборы, называемые вольтметрами или мультиметрами. Они позволяют определить значение напряжения между двумя точками в электрической цепи.

Напряжение обычно измеряется в вольтах (В) или киловольтах (кВ), в зависимости от масштаба системы и её потребностей.

Важно помнить, что неправильное использование или значительное увеличение напряжения может быть опасным и иметь серьёзные последствия. Поэтому рекомендуется обращаться к специалистам, если возникают сомнения или необходимо выполнить сложные электрические работы

Что такое напряжение и ток?

Кстати действительно что же такое электрический ток и напряжение? Я думаю, что никто на самом деле и не знает, ведь чтобы это знать это надо хотябы видеть. Кто может видеть ток, бегущий по проводам?

Да никто, человечество еще не достигло таких технологий, чтобы воочию наблюдать движения электрических зарядов.  Все что мы видим в учебниках и научных трудах это некая абстракция созданная в результате многочисленных наблюдений.

Ну ладно об этом можно много рассуждать… Так давайте попробуем разобраться, что такое электрический ток и  напряжение. Я не буду писать  определения, определения   не дают самого понимания сути.  Если интересно, возьмите любой учебник по физике.

Так как мы его не видим электрического тока и всех процессов протекающих в проводнике, тогда попробуем создать аналогию.

И традиционно электрический ток текущий в проводнике сравнивают с водой бегущей по трубам. В нашей аналогии  вода это электрический ток. Вода бежит  по трубам с определенной  скоростью, скорость это сила тока, измеряемая в амперах. Ну трубы это само собой проводник.

Хорошо, электрический ток мы себе представили, но а что такое напряжение? Сейчас помозгуем.

Вода  в трубе, в отсутствии каких-либо сил (сила тяжести, давления) теч не будет, она будет покоиться как и любая другая жижа вылитая на пол. Так вот эта сила или точнее  сказать энергия в нашей водопроводной аналогии и будет тем самым напряжением.

Но что происходит с водой бегущей из резервуара расположенного высоко над землей? Вода устремляется бурным потоком из резервуара к поверхности земли, гонимая силами тяготения. И чем выше от земли расположен резервуар тем с большей скоростью вытекает вода из шланга. Понимаете о чем я говорю?

Чем выше резервуар, тем больше сила (читай напряжение) воздействующая на воду. И тем больше скорость водного потока (читай сила тока). Теперь становится понятно и в голове начинает создаваться красочная картинка.

Разность потенциалов

А теперь давайте соединим эти бутылки между собой шлангом и поместим в шланг шарик, что будет?

Вода начнёт перетекать из бутылки, в которой уровень воды больше, в другую бутылку. И соответственно поток воды будет перемещать наш шарик по шлангу. Процесс перетекания воды прекратится тогда, когда уровень в бутылках станет одинаковым (принцип сообщающихся сосудов).

Когда уровень воды в бутылках стал одинаковым, разность потенциалов стала равна нулю, т.е. электродвижущая сила (ЭДС) равна нулю и наш шарик остаётся на месте.

Постоянное и переменное напряжение

Напряжение бывает бывает постоянным и переменным. В разговорной речи часто можно услышать “постоянный ток” и “переменный ток. Постоянный ток и постоянное напряжение – это синонимы, то же что и переменный ток и переменное напряжение.

На примере выше мы с вами рассмотрели постоянное напряжение. То есть давление воды на дно башни в течение времени постоянно. Пока в башне есть вода, она оказывает давление на дно башни. Вроде бы все элементарно и просто. Но какое же напряжение называют переменным?

Все любят качаться на качелях:

Сначала вы летите в одном направлении, потом происходит торможение, а потом уже летите обратно спиной и весь процесс снова повторяется. Переменное напряжение ведёт себя точно так же. Сначала “электрическое давление” давит в одну сторону, потом происходит процесс торможения, потом оно давит в другую сторону, снова происходит торможение и весь процесс снова повторяется, как на качелях.

Тяжко для понимания? Тогда вот вам еще один пример из знаменитой книжки “Первые шаги в электронике” Шишкова. Берем замкнутую систему труб с водой и поршень. Поршень у нас находится в движении. Следовательно, молекулы воды у нас отклоняются то в одну сторону:

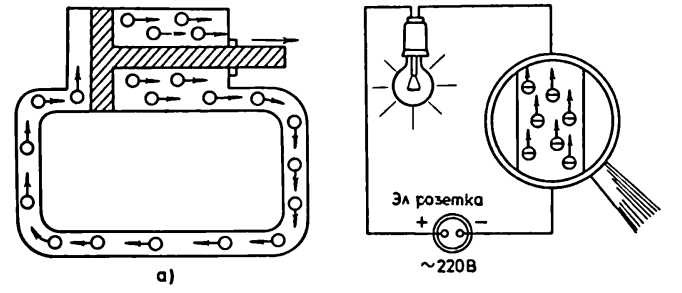
то в другую:

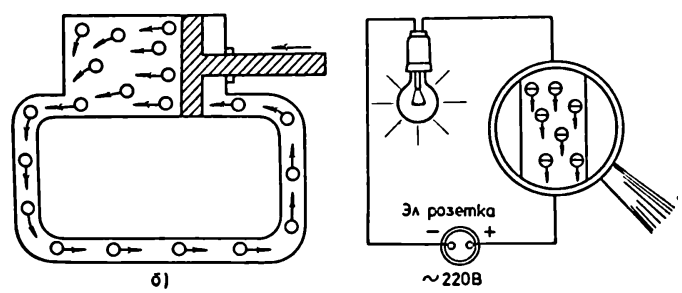
переменное напряжение

Так же ведут себя и электроны. В вашей домашней сети 220 В они колеблются 50 раз в секунду. Туда-сюда, туда-сюда. Столько-то колебаний в секунду называется Герцем. В литературе пишется просто “Гц”. Тогда получается, что колебание напряжения в наших розетках 50 Гц, а в Америке 60 Гц. Это связано со скоростью вращения генератора на электростанциях. В разговорной речи постоянное напряжение называют “постоянкой”, а переменное – “переменкой”.

Электрический ток

В наше время трудно себе представить жизнь без электричества. Телевизор не посмотреть, телефон не зарядить, чай не попить… Ни один электроприбор в доме не будет работать без электричества. А объявление об отключении электроэнергии, вызывает тихий ужас.

Электричество — это форма энергии, которая существует в виде статических или подвижных электрических зарядов.

Что общего у электрического тока с водой?Поток. И то и другое представляет собой направленное движение частиц. Из чего состоит вода? Из молекул. Когда эти молекулы движутся в одном направлении, то они образуют поток воды, который течет, например, по трубам.Так же и электрический ток. Он образуется потоком заряженных частиц, которые движутся по проводам.

Сформулируем определение:

Электрический ток — это упорядоченное движение заряженных частиц.

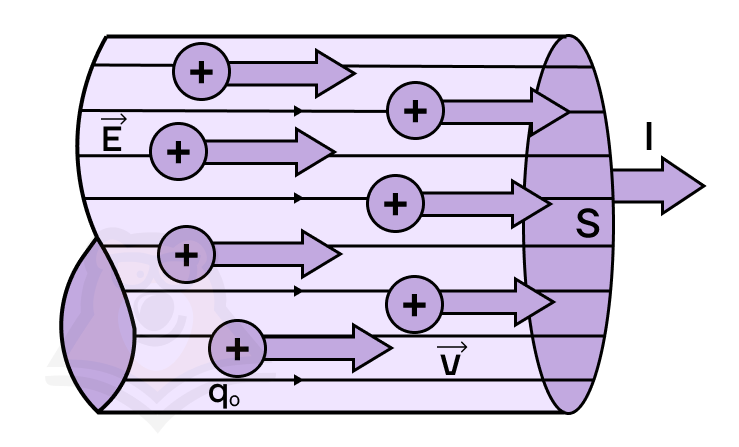
Чтобы электрический ток существовал, необходимо выполнение следующих условий:

• наличие свободных заряженных частиц;
• наличие электрического поля;
• наличие замкнутой электрической цепи.

Основными количественными характеристиками электрического тока являются сила тока и напряжение.

Электрическое напряжение: объяснение простыми словами

Электрическим напряжением обозначается физическая величина, равная разности потенциалов между двумя точками электрического поля при перемещении единичного заряда. Для простых пользователь такое обозначение не всегда понятно. Поэтому в этой статье мы попытаемся простым, доступным языком рассказать, что собой представляет электрическое напряжение, как оно измеряется и для чего это нужно.

Что такое разность потенциалов?

Для начала проанализируем рисунок:

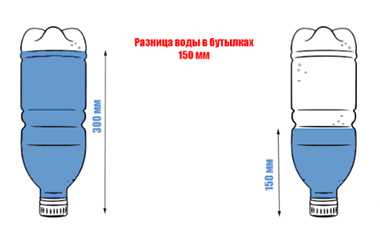
В первой бутылке вода находится на уровне 300 мм, а во второй – на отметке 150 мм. Разница между уровнями воды в обоих емкостях составляет 150 мм. Если рассматривать это с точки зрения науки об электричестве, это и есть разность потенциалов.

Однако, что будет, если соединить обе бутылки шлангом, а внутрь поместить обычный пластиковый шарик?

Из школьного урока физики о принципе соединяющихся сосудах знаем, что из бутылки, где уровень воды больше, жидкость постепенно перетечет в бутылку с более низким уровнем. Под воздействием потока воды шарик внутри соединяющего шланга будет перемещаться. Процесс перетекания завершится после того, как в обоих бутылках уровень жидкости уравновесится, станет одинаковым.

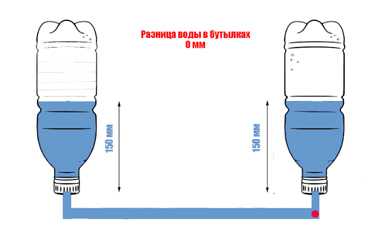
Иными словами, в ситуации, когда в соединенных между собой емкостях уровень жидкости станет одинаковым, результатом разности потенциалов станет ноль. Шарик останется на месте за счет электродвижущей силы, которая, по итогам эксперимента, равна нулю.

Что такое электродвижущая сила?

Аналогично напряжению, единицей измерения электродвижущей силы (ЭДС) является Вольт.

Для проведения следующего эксперимента понадобится вольтметр (прибор, измеряющий вольты) и обычная батарейка.

При исходном замере прибор покажет 1.5 В (Вольта). Однако это не является напряжением – значение указывает на величину электродвижущей силы.

На следующем этапе эксперимента к батарейке подключаются две лампочки. А напряжение измеряется в разных участках электроцепи.

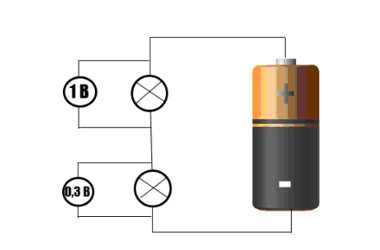
Внимание следует уделить следующим показателям: напряжение для одной лампочки составляет 1 Вольт, для другой же это значение 0.3 Вольта. Напряжение в используемых нами осветительных устройствах напрямую зависит от их мощности, измеряемой в Ваттах

Напряжение в используемых нами осветительных устройствах напрямую зависит от их мощности, измеряемой в Ваттах.

Мощность=Напряжение*ток (Р=U*I)

Из этого следует, что чем больше будет значение мощности лампы, тем большее напряжение будет на ней.

Однако, как же получается: если мощность батарейки 1.5 Вольта, к которой подключены лампочки, разделена на 1 Вольт и 0.3 Вольта, куда направились еще 0.2 Вольта? Дело в том, что каждая батарейка наделена своим внутренним сопротивлением, поэтому недостающие 0.2 Вольта были направлены именно сюда.

Резюме

Электродвижущей силой определена физическая величина, характеризующая в источниках тока работу сторонних силовых ресурсов. Посредством электродвижущей силы мы можем определять, как переносится заряд от источника тока по всей электрической цепи. Напряжение показывает этот процесс лишь на отдельном участке этой цепи. Если проще: напряжение – это внешнее силовое воздействие, способствующее перемещению шарика в шланге, соединяющим сосуды из выше приведенного примера. В электричестве напряжение обозначено силой, которая обеспечивает перемещение электронов между атомами.

Рассмотрим еще один пример

Представьте, что вам по силам будет поднять камень, вес которого составляет 40 кг. Это означает, что вы обладаете подъемной силой, равной 40 кг – в электричестве это обозначается как электродвижущая сила. Вы следуете и на своем пути вам попадается камень весом 20 кг. Вы его также берете и переносите на расстояние 10 метров. Для осуществления этого действия вам понадобилось определенное количество энергии, что в электричестве представляется как напряжение. Далее вам попадается камень весом в 30 кг. Следовательно, для его переноса из одного места в другое вам понадобится больше энергии, чем для камня, масса которого не превышала 20 кг. Однако подъемная сила (в электричестве ЭДС), независимо от веса переносимого вами камня, остается всегда одинаковой. При этом, вес камня определяет количество энергии, которая тратится на проведение этого действия (в электричестве это обозначено напряжением). Таким образом, на каждом отрезке вашего пути вы будете испытывать разное напряжение в зависимости от веса камня, который вы намерены перенести.

Определение и объяснение

В математике квадрат числа обозначается через символ «^2» и означает, что это число умножается само на себя. Например, «5 в квадрате», записывается как «5^2» и равно 25.

Таким образом, когда говорят, что число возведено в квадрат, это означает, что оно умножается само на себя. Результатом операции возведения числа в квадрат будет всегда положительное число или ноль, так как умножение положительного числа на положительное дает положительное число, а умножение нуля на ноль также дает ноль.

В квадрат можно возводить не только целые числа, но и десятичные, рациональные и иррациональные числа. Например, «2.5 в квадрате» равно 6.25, а «корень из двух в квадрате» равно 2.

Квадрат числа является важным понятием в алгебре и математическом анализе, который используется в различных математических выражениях, формулах и задачах. Например, квадраты чисел используются в алгебраических уравнениях, геометрических задачах, статистике и других областях математики.

Также стоит отметить, что есть и другие операции, связанные с возведением числа в степень, например, куб числа, когда число умножается само на себя два раза, обозначается через символ «^3».

Значение «в квадрате»

Понятие «в квадрате» часто используется в математике и означает умножение числа на само себя. Такой способ записи обозначается с помощью символа «^2». Например, число 4 в квадрате будет обозначаться как 4^2, что равно 4 * 4 = 16.

Квадрат числа имеет свою особенность: если число положительное, то его квадрат также будет положительным. Например, (-3)^2 = 9, а -3^2 = -9.

Значение «в квадрате» широко используется в различных областях, включая геометрию, физику и экономику. Например, при расчете площади квадрата или для определения квадратного корня.

Примеры чисел, возведенных в квадрат:

1. 2^2 = 2 * 2 = 4
2. (-5)^2 = (-5) * (-5) = 25
3. 10^2 = 10 * 10 = 100

Таким образом, значение «в квадрате» позволяет нам получить новое число путем умножения исходного числа на само себя.

Практические примеры использования

Простое объяснение того, что означает в квадрате, может быть полезно при решении математических задач. Рассмотрим несколько практических примеров использования этого понятия:

Пример	Описание
Вычисление площади квадрата	Для вычисления площади квадрата необходимо возвести длину его стороны в квадрат. Например, если сторона квадрата равна 5 см, то его площадь будет равна 5 в квадрате, то есть 25 квадратных сантиметров.
Нахождение суммы квадратов двух чисел	Чтобы найти сумму квадратов двух чисел, нужно возвести каждое число в квадрат, а затем сложить полученные значения. Например, сумма квадратов чисел 3 и 4 будет равна 3 в квадрате (9) плюс 4 в квадрате (16), что равно 25.
Разложение квадрата разности	Квадрат разности двух чисел можно разложить следующим образом: (а — b) в квадрате = а в квадрате — 2аб + b в квадрате. Например, разложим квадрат разности чисел 7 и 3: (7 — 3) в квадрате = 7 в квадрате — 2 * 7 * 3 + 3 в квадрате, что равно 16.

Все эти примеры демонстрируют, как простое объяснение в квадрате может быть использовано для решения различных математических задач.