Непрерывные случайные величины — определение и вычисление с примерами решения

Содержание

• 1 Пример
• 2 Абсолютно непрерывные одномерные распределения
• 3 Формальное определение
• 4 Дополнительные сведения
• 5 Связь между дискретным и непрерывным распределениями
• 6 Семейства плотности
• 7 Плотности, связанные с несколькими переменными
  • 7.1 Предельные плотности
  • 7.2 Независимость
  • 7.3 Следствие
  • 7.4 Пример
• 8 Функция случайных величин и изменение переменных в функции плотности вероятности
  • 8.1 Скаляр в скаляр
  • 8.2 Вектор в вектор
  • 8.3 Вектор в скаляр
• 9 Суммы независимых случайных величин
• 10 Произведения и частные независимых случайных величин
  • 10.1 Пример: распределение частных
  • 10.2 Пример: отношение двух стандартных норм
• 11 См. Также
• 12 Ссылки
• 13 Библиография
• 14 Внешние ссылки

Массовые функции вероятности: дискретные распределения вероятностей

Когда мы используем функцию вероятности для описания дискретного распределения вероятностей, мы называем еефункция вероятности(обычно сокращенно как pmf).

Функция вероятностной массы, которую мы назовем «f», возвращает вероятность результата. Поэтому функция вероятностной массы записывается как:

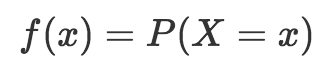
Я знаю, что это становится немного ужасно и математично, но терпите меня. Уравнение, которое мы видим выше, говорит, что массовая функция вероятности «f» просто возвращает вероятность результата x.

Итак, давайте вернемся к примеру честного шестистороннего кубика (вы, наверное, уже устали от этого примера). Функция вероятности, f, просто возвращает вероятность результата. Следовательно, вероятность броска 3 равна f (3) = 1/6. Это оно.

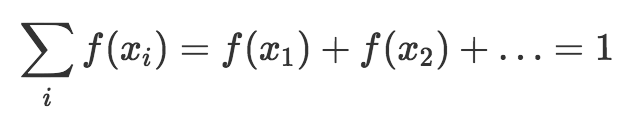
Итак, мы увидели, что можем записать дискретное распределение вероятностей в виде таблицы и функции. Мы также можем представить пример броска кубика графически

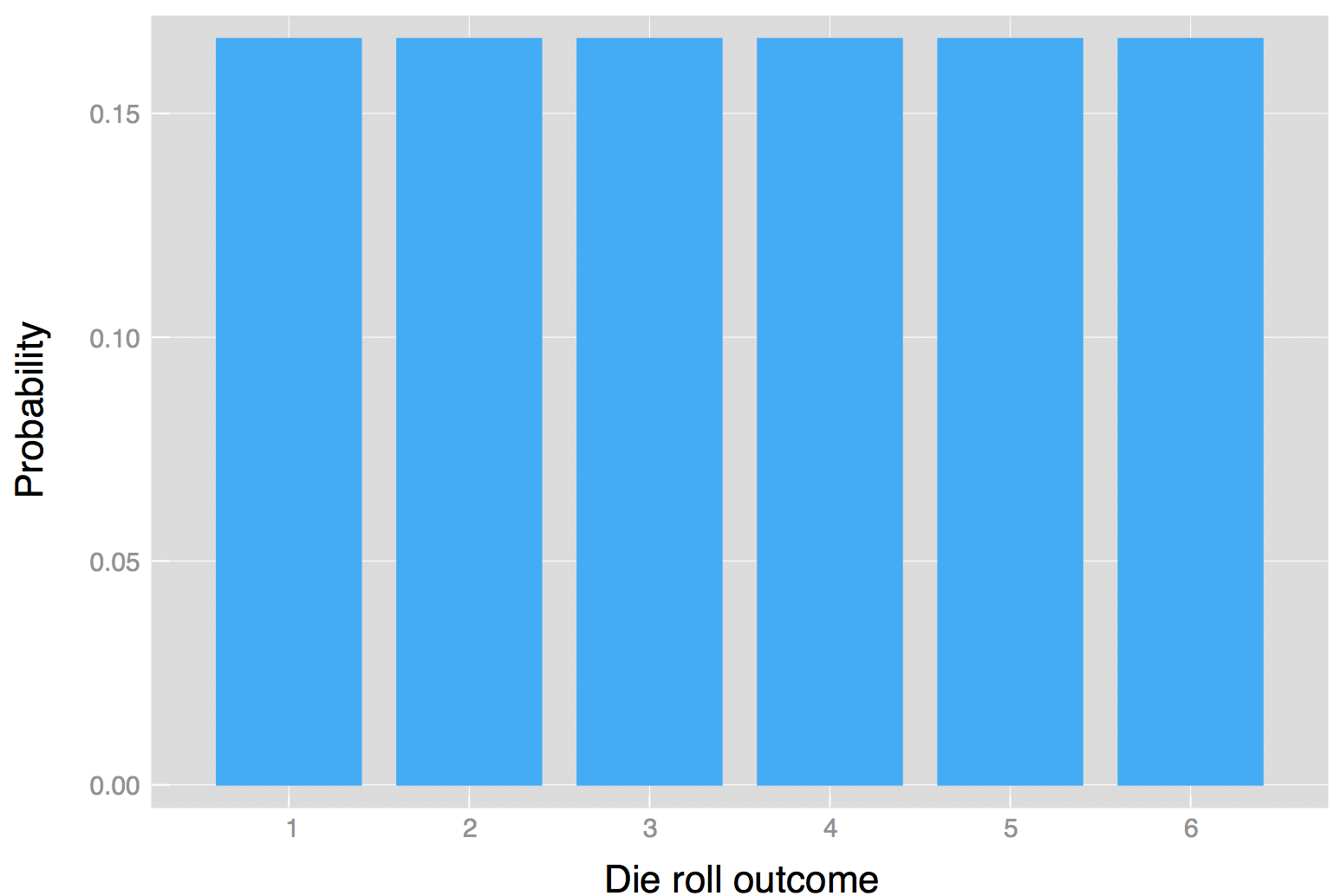Графическое представление распределения вероятностей для результатов бросания шестигранного кубика

Произведения и частные независимых случайных величин

Даны две независимые случайные величины U и V, каждая из которых имеет функцию плотности вероятности, плотность произведения Y = UV и частное Y = U / V можно вычислить заменой переменных.

Пример: частное распределение

Чтобы вычислить частное Y = U / V двух независимых случайных величин U и V, определите следующее преобразование:

Y = U / V {\ displaystyle Y = U / V}

Z = V {\ displaystyle Z = V}

Тогда совместная плотность p (y, z) может быть вычислена заменой переменных с U, V на Y, Z, и Y может быть получен путем маргинализации Z из плотности соединения.

Обратное преобразование:

U = YZ {\ displaystyle U = YZ}

V = Z {\ displaystyle V = Z}

Матрица Якоби J (U, V ∣ Y, Z) {\ displaystyle J (U, V \ mid Y, Z)}этого преобразования равно

| ∂ u ∂ y ∂ u ∂ z ∂ v ∂ y ∂ v ∂ z | = | z y 0 1 | = | z |. {\ displaystyle {\ begin {vmatrix} {\ frac {\ partial u} {\ partial y}} {\ frac {\ partial u} {\ partial z}} \\ {\ frac {\ partial v} {\ partial y}} {\ frac {\ partial v} {\ partial z}} \ end {vmatrix}} = {\ begin {vmatrix} z ​​y \\ 0 1 \ end {vmatrix}} = | z |.}

Таким образом:

p (y, z) = p (u, v) J (u, v ∣ y, z) = p (u) p (v) J (u, v ∣ y, z) = p U (yz) p V (z) | z |. {\ Displaystyle п (Y, Z) знак равно п (и, v) \, J (и, v \ середина у, г) = п (и) \, р (v) \, J (и, v \ середина у, z) = p_ {U} (yz) \, p_ {V} (z) \, | z |.}

И распределение Y может быть вычислено путем маргинализации Z:

p (y) = ∫ — ∞ ∞ p U (yz) p V (z) | z | dz {\ displaystyle p (y) = \ int _ {- \ infty} ^ {\ infty} p_ {U} (yz) \, p_ {V} (z) \, | z | \, dz}

Этот метод критически требует, чтобы преобразование из U, V в Y, Z было биективным. Вышеупомянутое преобразование соответствует этому, потому что Z может быть отображено непосредственно обратно в V, и для данного V отношение U / V является монотонным. То же самое и для суммы U + V, разности U — V и произведения UV.

Точно такой же метод можно использовать для вычисления распределения других функций от нескольких независимых случайных величин.

Пример: частное двух стандартных нормалей

Для двух стандартных нормальных переменных U и V, частное можно вычислить следующим образом. Во-первых, переменные имеют следующие функции плотности:

p (u) = 1 2 π e — u 2 2 {\ displaystyle p (u) = {\ frac {1} {\ sqrt {2 \ pi}}} е ^ {- {\ гидроразрыва {u ^ {2}} {2}}}}

p (v) = 1 2 π e — v 2 2 {\ displaystyle p (v) = {\ frac {1} {\ sqrt {2 \ pi}}} e ^ {- {\ frac {v ^ {2}} {2}}}}

Преобразуем, как описано выше:

Y = U / V {\ displaystyle Y = U / V}

Z = V {\ displaystyle Z = V}

Это приводит к:

p (y) = ∫ — ∞ ∞ p U (yz) p V (z) | z | d z = ∫ — ∞ ∞ 1 2 π e — 1 2 y 2 z 2 1 2 π e — 1 2 z 2 | z | d z = ∫ — ∞ ∞ 1 2 π e — 1 2 (y 2 + 1) z 2 | z | dz = 2 ∫ 0 ∞ 1 2 π e — 1 2 (y 2 + 1) z 2 zdz = ∫ 0 ∞ 1 π e — (y 2 + 1) uduu = 1 2 z 2 = — 1 π (y 2 + 1) е — (Y 2 + 1) U] U знак равно 0 ∞ = 1 π (Y 2 + 1) {\ Displaystyle {\ begin {align} p (y) = \ int _ {- \ infty} ^ { \ infty} p_ {U} (yz) \, p_ {V} (z) \, | z | \, dz \\ = \ int _ {- \ infty} ^ {\ infty} {\ frac {1} {\ sqrt {2 \ pi}}} e ^ {- {\ frac {1} {2}} y ^ {2} z ^ {2}} {\ frac {1} {\ sqrt {2 \ pi}}} e ^ {- {\ frac {1} {2}} z ^ {2}} | z | \, dz \\ = \ int _ {- \ infty} ^ {\ infty} {\ frac {1} {2 \ pi}} e ^ {- {\ frac {1} {2}} (y ​​^ {2} +1) z ^ {2}} | z | \, dz \\ = 2 \ int _ {0} ^ {\ infty} {\ frac {1} {2 \ pi}} e ^ {- {\ frac {1} {2}} (y ​​^ {2} +1) z ^ {2}} z \, dz \\ = \ int _ {0} ^ {\ infty} {\ frac {1} {\ pi}} e ^ {- (y ^ {2} +1)u}\,duu={\tfrac {1}{2}}z^{2}\\=\left.-{\frac {1}{\pi (y^{2} +1)}}e^{-(y^{2}+1)u}\right]_{u=0}^{\infty }\\={\frac {1}{\pi (y^{2}+1)}}\end{aligned}}}

This is the density of a standard Cauchy distribution.

Что такое плотность вероятности

Плотность вероятности — это производная от функции F(x), описывающей распределение случайной величины.

Двумерная, трехмерная, N-мерная плотность, иначе называемая совместной, определяет одновременное выполнение двух и более условий. Чтобы проанализировать взаимосвязь между характеристиками одного процесса, сдвинутыми на определенный интервал времени, или результаты одновременного броска двух игральных костей, нужно рассматривать двумерную плотность вероятности. Функция в таком случае должна определять одновременное выполнение двух условий: случайные величины (X) и (Y) одновременно принимают значения из интервалов (x_{1;}leq Xleq x_2\) и (y_{1;}leq Yleq y_2\).

Практические задачи, где требуется вычислить случайные величины, часто приходится решать в квантовой механике, например, рассчитывая коэффициенты отражения и прохождения квантовых частиц, движущихся в потенциальном поле. Также непрерывные случайные величины широко используют в генетике, ядерной физике.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Плотность (f(x)) аналогична таким понятиям, как плотность тока в теории электричества или плотность распределения масс на оси абсцисс.

Произведения и отношения независимых случайных величин

Учитывая две независимые случайные величины U и V, каждая из которых имеет функцию плотности вероятности, плотность произведения Y = УФ и частное Y=U/V можно вычислить заменой переменных.

Пример: частное распределение

Чтобы вычислить частное Y = U/V двух независимых случайных величин U и V, определите следующее преобразование:

Y=UV{ Displaystyle Y = U / V}

Z=V{ Displaystyle Z = V}

Тогда плотность стыков п(у,z) можно вычислить заменой переменных из U, V к Y, Z, и Y может быть получен маргинализация Z от плотности стыка.

Обратное преобразование:

U=YZ{ displaystyle U = YZ}

V=Z{ Displaystyle V = Z}

В Матрица якобиана J(U,V∣Y,Z){ Displaystyle J (U, V середина Y, Z)} этого преобразования

|∂ты∂у∂ты∂z∂v∂у∂v∂z|=|zу1|=|z|.{ displaystyle { begin {vmatrix} { frac { partial u} { partial y}} & { frac { partial u} { partial z}} { frac { partial v} { partial y}} & { frac { partial v} { partial z}} end {vmatrix}} = { begin {vmatrix} z ​​& y 0 & 1 end {vmatrix}} = | z |.}

Таким образом:

п(у,z)=п(ты,v)J(ты,v∣у,z)=п(ты)п(v)J(ты,v∣у,z)=пU(уz)пV(z)|z|.{ Displaystyle п (Y, Z) знак равно п (и, v) , J (и, v середина у, г) = п (и) , р (v) , J (и, v середина у , z) = p_ {U} (yz) , p_ {V} (z) , | z |.}

И распределение Y можно вычислить маргинализация Z:

п(у)=∫−∞∞пU(уz)пV(z)|z|dz{ displaystyle p (y) = int _ {- infty} ^ { infty} p_ {U} (yz) , p_ {V} (z) , | z | , dz}

Этот метод критически требует, чтобы преобразование из U,V к Y,Z быть биективный. Вышеупомянутое преобразование соответствует этому, потому что Z может быть напрямую отображен на V, и для данного V частное U/V является монотонный. То же самое и с суммой U + V, разница U − V и продукт УФ.

Точно такой же метод можно использовать для вычисления распределения других функций от нескольких независимых случайных величин.

Пример: частное двух стандартных нормалей

Учитывая два стандартный нормальный переменные U и V, частное можно вычислить следующим образом. Во-первых, переменные имеют следующие функции плотности:

п(ты)=12πе−ты22{ displaystyle p (u) = { frac {1} { sqrt {2 pi}}} e ^ {- { frac {u ^ {2}} {2}}}}

п(v)=12πе−v22{ displaystyle p (v) = { frac {1} { sqrt {2 pi}}} e ^ {- { frac {v ^ {2}} {2}}}}

Трансформируем как описано выше:

Y=UV{ Displaystyle Y = U / V}

Z=V{ Displaystyle Z = V}

Это ведет к:

п(у)=∫−∞∞пU(уz)пV(z)|z|dz=∫−∞∞12πе−12у2z212πе−12z2|z|dz=∫−∞∞12πе−12(у2+1)z2|z|dz=2∫∞12πе−12(у2+1)z2zdz=∫∞1πе−(у2+1)тыdтыты=12z2=−1π(у2+1)е−(у2+1)тыты=∞=1π(у2+1){ Displaystyle { begin {выровненный} p (y) & = int _ {- infty} ^ { infty} p_ {U} (yz) , p_ {V} (z) , | z | , dz & = int _ {- infty} ^ { infty} { frac {1} { sqrt {2 pi}}} e ^ {- { frac {1} {2 }} y ^ {2} z ^ {2}} { frac {1} { sqrt {2 pi}}} e ^ {- { frac {1} {2}} z ^ {2}} | z | , dz & = int _ {- infty} ^ { infty} { frac {1} {2 pi}} e ^ {- { frac {1} {2} } (y ^ {2} +1) z ^ {2}} | z | , dz & = 2 int _ {0} ^ { infty} { frac {1} {2 pi}} e ^ {- { frac {1} {2}} (y ​​^ {2} +1) z ^ {2}} z , dz & = int _ {0} ^ { infty} { frac {1} { pi}} e ^ {- (y ^ {2} +1) u} , du && u = { tfrac {1} {2}} z ^ {2} & = left .- { frac {1} { pi (y ^ {2} +1)}} e ^ {- (y ^ {2} +1) u} right] _ { u = 0} ^ { infty} & = { frac {1} { pi (y ^ {2} +1)}} end {выровнено}}}

Это плотность эталона Распределение Коши.

Система случайных величин

Глава 3 книги Дмитрия Трофимовича Письменного «Конспект лекций по теории вероятностей,
математической статистике и случайным процессам» рассказывает также о системе случайных величин.
Это понятие также нужно знать для успешного освоения предмета
«Статистическая динамика автоматических систем».

Упорядоченный набор (X₁, X₂, …, X_n) случайных
величин X_i, i = 1, 2, …, n, заданных на
одном и том же пространстве элементарных событий Ω, называется n-мерной
случайной величиной или системой n случайных величин.

Системы с.в. также могут быть дискретными, непрерывными и смешанными.

Графически случайный исход опыта с двумя случайными величинами (например, бросание сразу двух
игральных костей) можно изобразить случайной точкой M(x; y) или
случайным вектором OM (см. ). (Все
положения, касающиеся системы двух случайных величин, справедливы и для системы
из n > 2 случайных величин.)

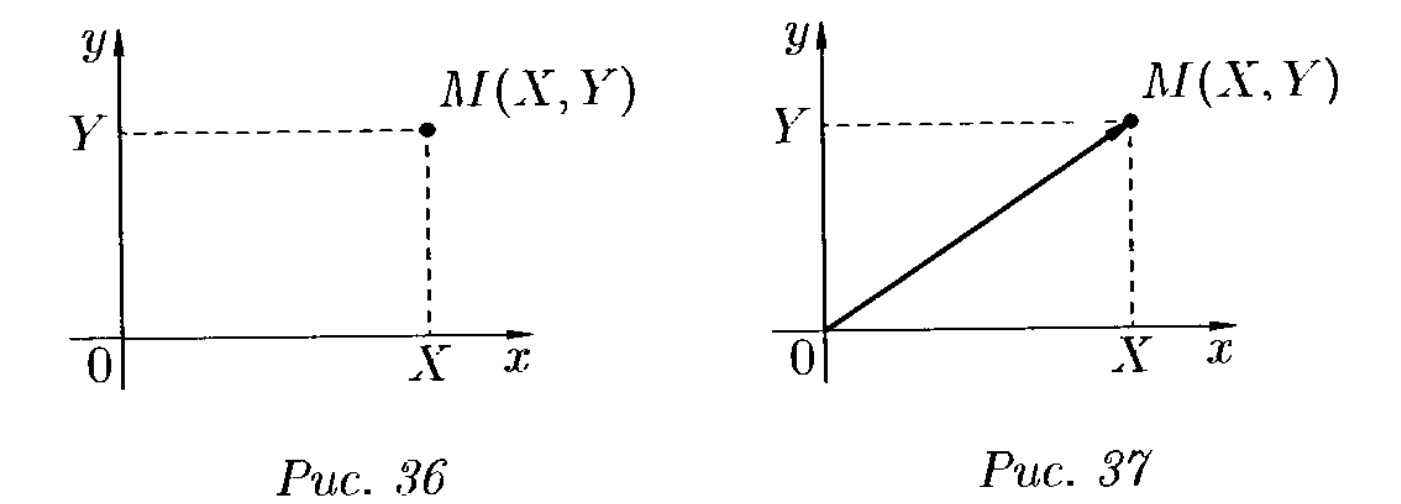Рисунок 3 — Изображение реализации опыта с двумя случайными величинами X и Y

Полной характеристикой системы случайных величин (X, Y) является её
закон распределения, который также, как и с ,
можно представить в виде формулы
p_ij = P{X = x_i, Y = y_j},
i = 1,…,n; j = 1,…,m;

или в виде таблицы с двойным входом:

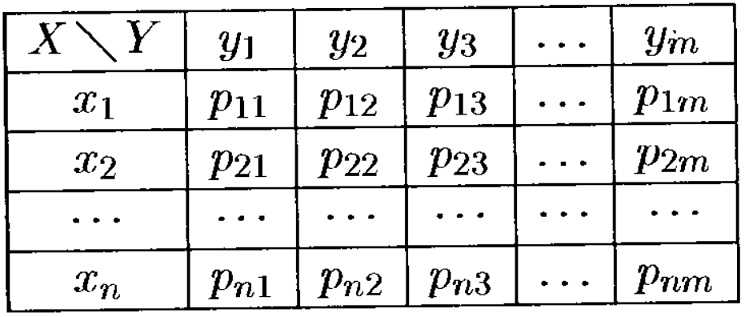Рисунок 4 — Таблица распределения системы двух с.в.

Причём сумма всех вероятностей p_ij, как сумма
вероятностей полной группы несовместных событий, равна единице.

График распределения двумерной дискретной случайной величины можно изобразить так, как
показано на Дмитрия Письменного.

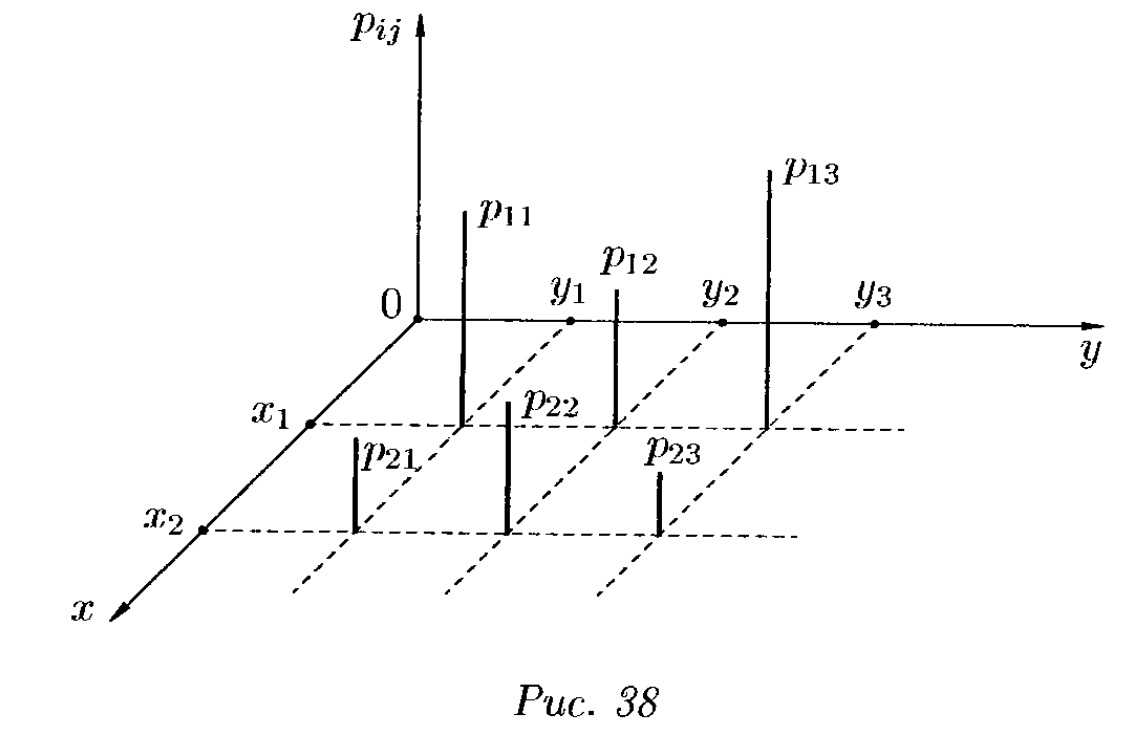Рисунок 5 — График распределения двумерной дискретной случайной величины

Функция распределения двумерной случайной величины

Универсальной формой задания распределения двумерной случайной величины
является функция распределения (или «интегральная функция»),
пригодная как для дискретной, так и для непрерывной случайной величины (с.в.).
Функция распределения системы с.в. обозначается как
F(x,y) или F_X,Y(x,y).

Эта функция по аналогии с
для любых действительных чисел x и
y равна вероятности совместного выполнения двух событий
{X < x} и {Y < y}. Т.е.:
F(x,y) = P{X < x, Y < y}.

Функция распределения двумерной дискретной с.в.
(X, Y) находится суммированием
всех вероятностей p_ij, для
которых x_i < x,
y_j < y:

F(x,y) =

∑

xi < x

∑

yj < y

p_ij .

А для непрерывной с.в. функция распределения выражается через плотность вероятности (см. параграф далее).

Абсолютно непрерывные одномерные распределения

Функция плотности вероятности чаще всего связана с абсолютно непрерывными одномерными распределениями. A случайная величина X {\ displaystyle X}имеет плотность f X {\ displaystyle f_ {X}}, где е Икс {\ displaystyle f_ {X}}- неотрицательная интегрируемая по Лебегу функция, если:

Pr = ∫ abf X ( х) dx. {\ displaystyle \ Pr = \ int _ {a} ^ {b} f_ {X} (x) \, dx.}

Следовательно, если FX {\ displaystyle F_ {X}}- кумулятивная функция распределения для X {\ displaystyle X}, тогда:

FX (x) = ∫ — ∞ xf X (u) du, {\ displaystyle F_ {X} (x) = \ int _ {- \ infty} ^ {x} f_ {X} (u) \, du,}

и (если е Икс {\ displaystyle f_ {X}}непрерывно в x {\ displaystyle x})

f X (x) = ddx FX (x). {\ Displaystyle f_ {X} (x) = {\ frac {d} {dx}} F_ {X} (x).}

Интуитивно можно представить себе f X (x) dx {\ displaystyle f_ {X } (x) \, dx}как вероятность попадания X {\ displaystyle X}в бесконечно малый интервал {\ displaystyle }.

Пример

Предположим, бактерии определенного вида обычно живут от 4 до 6 часов. Вероятность того, что бактерия живет ровно 5 часов, равна нулю. Многие бактерии живут приблизительно 5 часов, но нет никаких шансов, что какая-либо конкретная бактерия погибнет ровно в 5.0000000000… часов. Однако вероятность того, что бактерия погибнет в период от 5 часов до 5,01 часа, поддается количественной оценке. Предположим, ответ 0,02 (т.е. 2%). Тогда вероятность того, что бактерия погибнет в период от 5 часов до 5,001 часа, должна быть около 0,002, поскольку этот временной интервал в десять раз меньше предыдущего. Вероятность того, что бактерия погибнет в период от 5 часов до 5.0001 часа, должна быть около 0,0002 и так далее.

В этих трех примерах соотношение (вероятность смерти во время интервала) / (продолжительность интервала) приблизительно постоянное и равно 2 в час (или 2 часа). Например, вероятность смерти 0,02 в интервале 0,01 часа от 5 до 5,01 часа, а (вероятность 0,02 / 0,01 часа) = 2 часа. Это количество в 2 часа называется плотностью вероятности смерти примерно через 5 часов. Следовательно, вероятность того, что бактерия погибнет через 5 часов, может быть записана как (2 часа) dt. Это вероятность того, что бактерия погибнет в бесконечно малом временном окне около 5 часов, где dt — продолжительность этого окна. Например, вероятность того, что он живет дольше 5 часов, но меньше (5 часов + 1 наносекунда), составляет (2 часа) × (1 наносекунда) ≈ 6 × 10 (с использованием преобразования единиц измерения 3,6 × 10 наносекунд = 1 час).

Существует функция плотности вероятности f с f (5 часов) = 2 часа. интеграл от f для любого временного окна (не только бесконечно малых, но и больших окон) — это вероятность того, что бактерия погибнет в этом окне.

Дискретные и непрерывные случайные переменные

Чтобы это отложилось в голове, я повторю ещё раз: случайная переменная полностью задаётся распределением вероятностей своих значений. Есть 2 основных типа случайных переменных: дискретные (discrete) и непрерывные (continuous).

Дискретные переменные могут принимать набор чётко разделимых значений. Обычно я изображаю их как-нибудь так (probability mass function, pmf):

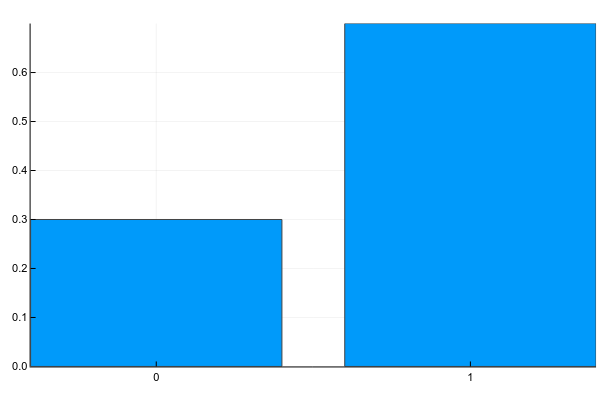
А текстом это обычно записывается так (g — gender):

Т.е. вероятность того, что случайно взятый человек из нашей выборки окажется женщиной () равна 0.3, а мужчиной () — 0.7, что эквивалентно тому, что в выборке было 30% женщин и 70% мужчин.

К дискретным же переменным относятся количество детей у человека, частота встречаемости слов в тексте, количество просмотров фильма и т.д. Результат классификации на конечное число классов, кстати, — это тоже дискретная случайная переменная.

Непрерывные переменные могут принимать любое значение в определённом интервале. Например, даже если мы записываем, что рост человека — 175см, т.е. округляем до 1 сантиметра, на самом деле он может быть 175.8231см. Изображают непрерывные переменные обычно с помощью кривой плотности вероятности (probability density function, pdf):

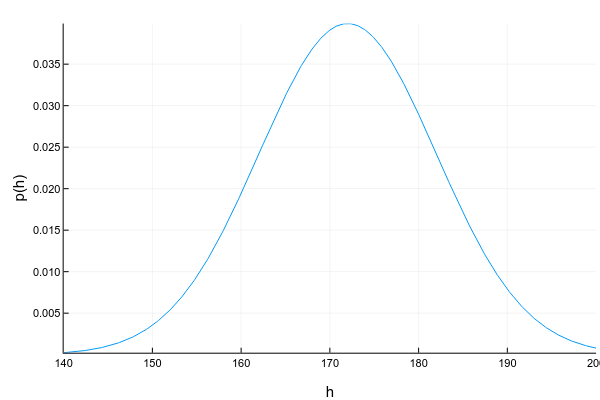
График плотности вероятности — штука хитрая: в отличие от графика массы вероятности для дискретных переменных, где высота каждой колонки показывает непосредственно вероятность получить такое значение, плотность вероятности показывает относительное количество вероятности вокруг некоторой точки. Саму же вероятность в этом случае можно посчитать только для интервала. Например, в этом примере вероятность, что случайно взятый человек из нашей выборки будет иметь рост от 160 до 170см равна примерно 0.3.

Вопрос: может ли плотность вероятности в какой-то точке быть больше единицы? Ответ — да, конечно, главное, чтобы общая площадь под графиком (или, говоря математически, интеграл плотности вероятности) был равен единице.

Ещё одна трудность с непрерывными переменными состоит в том, что их плотность вероятности не всегда возможно красиво описать. Для дискретных переменных у нас просто была таблица значение -> вероятность. Для непрерывных это уже не прокатит, поскольку значений у них, вообще говоря, бесконечное множество. Поэтому обычно стараются аппроксимировать набор данных каким-нибудь хорошо изученным параметрическим распределением. Например, график выше — это пример т.н. нормального распределения. Плотность вероятности для него задаётся формулой:

где (мат. ожидание, mean) и (дисперсия, variance) — параметры распределения. Т.е. имея всего 2 числа мы можем полностью описать распределение, посчитать его плотность вероятности в любой точке или суммарную веростность между двумя значениями. К сожалению, далеко не для любого набора данных найдётся распределение, которое сможет его красиво описать. Есть много способов бороться с этим (взять хотя бы смесь нормальных распределений), но это уже совсем другая тема.

Другие примеры непрерывного распределения: возраст человека, интенсивность пикселя на изображении, время ответа от сервера и т.д.

Построение графика нормального распределения

Прежде всего необходимо разбить наш массив на периоды. Для этого определяем минимальное и максимальное значение, размер каждого периода или шаг, с которым будет увеличиваться период.

Далее строим таблицу с категориями. Нижняя граница (B11) равняется округленному вниз ближайшему кратному числу. Остальные категории увеличиваются на значение шага. Формула в ячейке B12 и последующих будет выглядеть:

В столбце X будет производится подсчет количества переменных в заданном промежутке. Для этого воспользуемся формулой ЧАСТОТА(), которая имеет два аргумента: массив данных и массив интервалов. Выглядеть формула будет следующим образом =ЧАСТОТА(Data!A1:A175;B11:B20). Также стоит отметить, что в таком варианте данная функция будет работать как формула массива, поэтому по окончании ввода необходимо нажать сочетание клавиш Ctrl+Shift+Enter.

Таким образом у нас получилась таблица с данными, с помощью которой мы сможем построить диаграмму с нормальным распределением. Воспользуемся диаграммой вида Гистограмма с группировкой, где по оси значений будет отложено количество переменных в данном промежутке, а по оси категорий – периоды.

Осталось отформатировать диаграмму и наш график с нормальным распределением готов.

Итак, мы познакомились с вами с нормальным распределением, узнали, что Excel позволяет генерировать массив данных с помощью формулы НОРМ.ОБР() для определенного среднего значения и стандартного отклонения и научились приводить данный массив в графический вид.

Семейства плотностей

Обычно функции плотности вероятности (и функции массы вероятности ) параметризуются, то есть характеризуются неопределенными параметрами . Например, нормальное распределение параметризуется в терминах среднего и дисперсии, обозначенных μ {\ displaystyle \ mu}и σ 2 {\ displaystyle \ sigma ^ {2}}соответственно, что дает семейство плотностей

f (x; μ, σ 2) = 1 σ 2 π e — 1 2 (х — μ σ) 2. {\ displaystyle f (x; \ mu, \ sigma ^ {2}) = {\ frac {1} {\ sigma {\ sqrt {2 \ pi}}}} e ^ {- {\ frac {1} {2 }} \ left ({\ frac {x- \ mu} {\ sigma}} \ right) ^ {2}}.}

Важно помнить о различии между доменом семейства плотностей и параметров семейства. Разные значения параметров описывают разные распределения разных случайных величин на одном и том же пространстве выборки (один и тот же набор всех возможных значений переменной); это пространство выборки является областью семейства случайных величин, которое описывает это семейство распределений

Данный набор параметров описывает единичное распределение внутри семейства, разделяющее функциональную форму плотности. С точки зрения данного распределения параметры являются константами, а члены функции плотности, которые содержат только параметры, но не переменные, являются частью коэффициента нормализации распределения (мультипликативный коэффициент, который гарантирует, что площадь под плотностью — вероятность того, что что-то произойдет в области — равна 1). Этот коэффициент нормализации находится за пределами ядра распределения.

Поскольку параметры являются константами, повторная параметризация плотности в терминах различных параметров, чтобы дать характеристику другой случайной переменной в семействе, означает простую замену новых значений параметров в формулу вместо старых.. Однако изменение области определения плотности вероятности сложнее и требует дополнительных усилий: см. Раздел ниже, посвященный замене переменных.

Полная характеристика — случайная величина

Полная характеристика случайной величины дается ее распределением вероятностей. Однако исключительно полезны некоторые постоянные числовые характеристики случайной величины, дающие представление о ее свойствах. Среди таких характеристик особенно большую роль играет математическое ожидание. Оно определяется по распределению случайной величины.
 

Полными характеристиками случайных величин являются их функции распределения или плотности распределения вероятностей. Заметим, что при расчетах не всегда удобно пользоваться этими характеристиками, так как обычно их точные выражения неизвестны. Кроме того, расчеты с использованием функции распределения ( или плотности распределения) вероятностей часто оказываются весьма сложными или громоздкими.
 

Полными характеристиками случайных величин являются их законы распределения, характеризующие вероятность различных числовых значений погрешностей. Случайные погрешности характеризуются средним значением, дисперсией и среднеквадратичной ошибкой.
 

Полными характеристиками случайных величин являются их функции распределения или плотности распределения вероятностей. Заметим, что при расчетах не всегда удобно пользоваться этими характеристиками, так как обычно их точные выражения неизвестны.
 

Для полной характеристики случайной величины необходимо прежде всего знать те значения, которые она может принимать. Помимо этого нужно знать, с какой вероятностью случайная величина принимает то или иное значение.
 

Для полной характеристики случайной величины, кроме среднего значения, необходимо указать еще степень ее рассеивания или масштаб рассеивания около среднего значения.
 

Для полной характеристики случайной величины необходимо задать не только все возможные ее значения, но и закон ее распределения.
 

Самой универсальной и полной характеристикой случайной величины является закон ее распределения.
 

Вычисление вероятности получения значений величины в указанных границах, когда известна одна из полных характеристик случайной величины, — решается элементарно на базе теорем сложения вероятностей.
 

В процессе измерения случайная величина принимает какое-либо одно значение из их допустимого набора, поэтому для полной характеристики случайной величины необходимо знать не только ее возможные значения, но и как часто ( т.е. с какой вероятностью) следует ожидать каждое из этих значений. Математическое описание совокупности значений случайной величины с указанием вероятности появления каждого значения называется законом распределения этой величины. На основании опытных данных, как правило, принимают, что распределение совокупности результатов количественного химического анализа при содержании компонентов более 10 — 2 — 10 — 3 % соответствует так называемому закону нормального распределения. Распределение случайной величины определяется математическим ожиданием ( центром рассеяния значений случайной величины) и дисперсией, характеризующей степень рассеяния значений случайной величины вокруг ее математического ожидания.
 

Согласно теории вероятности, основной теоретической характеристикой случайного события является его вероятность. Закон распределения или распределение вероятностей случайной величины является полной характеристикой случайной величины, определяющей ее возможные значения и позволяющей сравнивать вероятности различных возможных значений.
 

Однако приведенная характеристика случайных величин тол-ько со стороны набора возможных значений далеко недостаточна. Понятие случайной величины неразрывно связано с понятием распределения. Для полной характеристики случайной величины наряду с ее возможными значениями следует указать, как часто она эти значения принимает.
 

Однако приведенная характеристика случайных величин только со стороны набора возможных значений далеко недостаточна. Понятие случайной величины неразрывно связано с понятием распределения. Для полной характеристики случайной величины наряду с ее возможными значениями следует указать, как часто она эти значения принимает.
 

Примеры использования функции вероятность для расчетов в Excel

Стоит отметить, что используются часто в Excel и другие статистические функции, к примеру:

Функция выполняет вычисление вероятности того, что значения с интервала находятся в заданных пределах. В случае, если верхний предел не будет задан, то будет возвращена вероятность того, что значения аргумента x_интервал будет равно значению аргумента под названием нижний_предел.

Вычисление процента вероятности события в Excel

Пример 1. Дана таблица диапазона числовых значений, а также вероятностей, которые им соответствуют:

Необходимо при использовании данной статистической функции вычислить вероятность события, что значение с указанного интервала входит в интервал .

Для этого введем функцию со следующими аргументами:

• х_интервал – это начальные данные (0, …, 4);
• интервал вероятностей является множеством вероятностей для начальных данных (0,15; 0,1; 0,15; 0,2; 0,4);
• нижний предел равен значению 1;
• верхний предел равен 4.

В результате выполненных вычислений получим:

Пример 2. В условии предыдущего примера нужно вычислить вероятность события «значение х равно 4».

Введем в ячейку С3 введем функцию с такими аргументами:

• х_интервал – начальные параметры (0, …, 4);
• интервал вероятностей – совокупность вероятностей для параметров (0,1; 0,15; 0,2; 0,15; 0,4);
• нижний предел – 4;

В данном примере верхний предел не указан, поскольку необходимо конкретное значение вероятности, а именно для значения 4.