ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Плотность железа 7,8 г/см3. Чему равна плотность железа в кг/м3?
1) 0,078 кг/м3 2) 7,8 кг/м3 3) 7800 кг/м3 4) 7 800 000 кг/м3
2. Две тележки массами 200 г и 400 г соединены сжатой пружиной и скреплены нитью. После того, как нить пережгли, пружина распрямилась, и тележки разъехались. Первая тележка приобрела скорость, равную 0,5 м/с. Какую скорость приобрела вторая тележка?
1) 0,25 м/с 2) 0,5 м/с 3) 1 м/с 4) 2 м/с
3. При взаимодействии двух тел каждое из них приобретает ускорение. Ускорение одного тела массой 200 г равно 1 м/с2. Ускорение другого тела массой 500 г равно
1) 2,5 м/с2 2) 1 м/с2 3) 0,5 м/с2 4) 0,4 м/с2
4. Массу тела измеряют,
А. взвешивая его на рычажных весах Б. приведя во взаимодействие с телом известной массы
Правильный ответ
1) только А 2) только Б 3) и А, и Б 4) ни А, ни Б
5. Три тела имеют одинаковый объём. Плотности веществ, из которых изготовлены эти тела, соотносятся как \( \rho_1<\rho_2<\rho_3 \). Как соотносятся массы этих тел?
1) \( m_1=m_2=m_3 \) 2) \( m_1>m_2>m_3 \) 3) \( m_1 4) \( m_1m_3 \)
6. На рисунке приведена столбчатая диаграмма, на которой представлены значения массы двух тел равного объёма. Какой вывод можно сделать из анализа диаграммы?
1) \( \rho_1=2\rho_2 \) 2) \( \rho_1=1,5\rho_2 \) 3) \( \rho_1=\rho_2 \) 4) \( \rho_1=0,5\rho_2 \)
7. Три кубика одинакового объёма сделаны из разных материалов. Плотности этих материалов соотносятся как \( \rho_1>\rho_2>\rho_3 \). Как соотносятся массы этих тел?
1) \( m_1 2) \( m_1=m_2=m_3 \) 3) \( m_1>m_2>m_3 \) 4) \( m_1>m_2
8. На рисунке приведены графики зависимости массы двух тел от их объёма. Сравните значения плотности этих тел.
1) \( \rho_1<\rho_2 \) 2) \( \rho_1=\rho_2 \) 3) \( \rho_1>\rho_2 \) 4) \( \rho_1\leq\rho_2 \)
9. Чему равна масса льдины объёмом 0,2 м3, если плотность льда 0,9 г/см3?
1) 0,18 кг 2) 4,5 кг 3) 18 кг 4) 180 кг
10. Отвечая на вопрос учителя о том, какую величину называют плотностью вещества, учащиеся давали разные ответы, среди которых были следующие:
А. Плотность вещества — физическая величина, прямо пропорциональная массе тела и обратно пропорциональная его объёму. Б. Плотность вещества — физическая величина, рав- ная отношению массы тела к его объёму.
Правильный ответ:
1) только А 2) только Б 3) и А, и Б 4) ни А, ни Б
11. Ниже приведены таблица плотности веществ и четыре утверждения. Из приведённых ниже утверждений выберите два правильных и запишите их номера
1) Масса 6 м3 машинного масла равна массе 2 м3 алюминия 2) Объём стальной детали больше объёма алюминиевой детали при их одинаковой массе 3) Объём 0,5 кг машинного масла примерно в 2 раза меньше объёма 0,8 кг спирта 4) Масса 5 м3 цинка меньше массы 30 м3 воды
12. Установите соответствие между физическими величинами в левом столбце и их зависимостью от выбора системы отсчёта в правом столбце. В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента из правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА A) масса Б) время B) скорость
ПОНЯТИЕ 1) относительная 2) инвариантная
Часть 2
13. Два мяча: один массой 200 г, другой массой 250 г после столкновения разлетелись в разные стороны. Мяч меньшей массы в результате столкновения приобрёл скорость 5 м/с. Чему равен путь, который пролетит за 2 с мяч большей массы? Считать, что скорость мяча за это время не изменится.
Что такое текс пряжи. Метрический номер № 32/2
С 1965 года вся страна СССР стала переходить на новую систему условного определения толщины пряжи.
На систему ТЕКС (от слова ТЕКСТИЛЬ). Это версия для запоминания слова.
А вообще определение ТЕКС (от лат. texo — тку, сплетаю).Толщина пряжи официально характеризуется линейной плотностью.
Линейная плотность пряжи определяется в системе ТЕКС (tex), массой в граммах, это вес одного километра нити.
Что такое Текс пряжи
ТЕКС – единица линейной плотности (грамм/километр), применяемая для измерения толщины волокон и нитей. Текс определяет вес одного километра нити.
Формула: 1000/Nm=tex
Что такое метрический номер № 32/2.
Но нас интересует метрический номер пряжи для машинного вязания № 32/2. Именно он (метрический номер пряжи) характеризует длину нити (м), вес которой равен 1 грамму,
а также показывает количество одинарных нитей, из которых скручена эта пряжа.
Например, для пряжи № 32/2:
32 — это длина одинарной нити, вес которой равен 1 г.
2 — это число скрученных вместе одинарных нитей.
Номер 32/2 означает, что 1 грамм одинарной нити имеет длину 32 метра, но т.к. пряжа скручена из двух нитей, получается 16 м на 1 г (или1600м/100г). Чем выше номер, тем тоньше и легче нить.
Пряжа № 32/2
Если взять одну нить этой пряжи и раскрутить её, то мы увидим, что она состоит из двух нитей.
А если эти две нити рассмотреть под микроскопом, то увидим, что каждая нить ещё состоит из 32 нитей!
Но, мы эти 64 нити (32х2) считаем как одно сложение пряжи!
Пряжа №32/2 рекомендована для машинного вязания.
 Пряжа — это очень тонкая, прочная, длинная нить которая получается посредством скручивания коротких волокон между собой.
Пряжа — это очень тонкая, прочная, длинная нить которая получается посредством скручивания коротких волокон между собой.
Пряжа для машинного вязания и пряжа для вязания на спицах имеет разную крутку. Крутка пряжи определяется числом кручений, приходящихся на 1 метр длины нитей. Число кручений зависит от вида, качества волокна, толщины и назначения пряжи.
Чем толще пряжа при прочих равных условиях, тем меньше кручений приходится на 1 метр длины.
Крутка изменяет свойства пряжи.
При увеличении крутки пряжа делается компактнее и жёстче, более упругой, диаметр уменьшается,
трение между волокнами увеличивается, волокна в пряже закрепляются прочнее, вследствие чего прочность пряжи повышается.
Пряжа №32/2 — «мобильная» пряжа.
Например.
Для изделия нам нужна пряжа в три сложения, а чтобы красиво выполнить кеттлёвку воротника, нам нужна ниточка в два сложения.
Если поиграться количеством сложений, то можно добиться потрясающих эффектов в вязании.
Повторим и запомним:ТЕКС линейной плотноститолщины
А метрический номер № 32/2 характеризует длину нити (м), вес которой равен 1 грамму,
а также показывает количество одинарных нитей, из которых скручена эта пряжа.
«Номер пряжи» — это количество метров пряжи в 1 грамме.
На этикетке мотка указан метраж пряжи в 100 граммах.
В 100 граммах 1600 метров.
Соотношение веса и длины пряжи определяется «номером пряжи» и количеством нитей.
Например производитель пишет: «пряжа 32/2».
Это значит, что номер одиночной пряжи 32.
Так как нитей две, то «суммарный» номер = 32 / 2 = 16
Х = 16 х 1000 = 16000 метров в 1 кг.
или 1600 метров в 100 граммах.
 километр пряжи №32/2детскому комплекту
километр пряжи №32/2детскому комплекту
- Обтяжка для пуговиц
- Работа с кеттлёвкой
Влияние массы на линейную плотность
Линейная плотность, также известная как линейная масса или плотность нити, представляет собой физическую величину, которая характеризует массу единицы длины материала. Влияние массы на линейную плотность может быть значительным и важным при анализе различных материалов и их свойств.
Чем больше масса материала на единицу длины, тем выше линейная плотность. Это означает, что материал с большей массой будет иметь более высокую линейную плотность, чем материал с меньшей массой при одинаковой длине. Например, у нити с массой 10 г и длиной в 1 метр будет более высокая линейная плотность, чем у нити с массой 5 г и той же длиной.
Влияние массы на линейную плотность может быть особенно важным при работе с текстильными материалами, волокнами и нитями. Нити с высокой линейной плотностью могут быть более прочными и устойчивыми к разрыву, поскольку они имеют более плотное внутреннее строение.
Кроме того, линейная плотность может влиять на определение размеров и веса изделий, созданных из материалов с различными линейными плотностями. Например, одежда из материала с высокой линейной плотностью может быть более плотной, иметь более тяжелый вес и обеспечивать лучшую защиту от холода, чем одежда из материала с низкой линейной плотностью.
Изучение влияния массы на линейную плотность является важной задачей в материаловедении и инженерии. Оно помогает определить оптимальные характеристики материалов и разработать новые материалы с требуемыми свойствами для различных приложений
Как измерить линейную плотность?
Линейная плотность – это величина, которая определяет, сколько чего-то находится на определенном участке линии или провода. Например, линейная плотность может указывать, сколько метров провода содержится в одном килограмме. Измерение линейной плотности может быть полезно в различных областях, таких как строительство, производство и наука.
Существует несколько способов измерить линейную плотность. Вот некоторые из них:
- Использование веса и длины: этот метод основан на измерении веса и длины исследуемого объекта. Для проведения измерений необходимо сначала измерить массу объекта с помощью весов, а затем измерить его длину с помощью линейки или мерной ленты. Линейная плотность вычисляется как отношение веса к длине объекта.
- Использование измерительной ленты или штанги: этот метод подразумевает непосредственное измерение длины объекта с помощью измерительной ленты или штанги. Затем необходимо измерить вес объекта с помощью весов. Линейная плотность вычисляется как отношение длины к весу объекта.
- Использование формулы: в некоторых случаях линейную плотность можно вычислить с использованием определенных формул. Например, для провода, линейная плотность может быть вычислена как отношение массы провода к его сечению.
При измерении линейной плотности важно учесть единицы измерения, которые используются. Например, линейная плотность провода может быть измерена в граммах на метр или в килограммах на метр, в зависимости от предпочтений и требований
Выбор метода измерения линейной плотности зависит от конкретной ситуации и свойств объекта
Важно учитывать, что точность измерений может быть подвержена ошибкам, поэтому необходимо применять адекватные инструменты и методы для достижения наиболее точных результатов
какой буквой в физике обозначается Плотность?
Зависимость показателей учитывается при расчете П. При повышении температуры П снижается из-за термического расширения, при котором объем вырастает, а масса остается прежней. Если температура снижается, П увеличивается, хотя имеются вещества, П которых при некоторых условиях температурного режима ведет себя иначе. Это вода, бронза, чугун. При фазовом переходе, модифицировании агрегатного состояния П меняется скачками. Условия вычисления зависят от свойств веществ, молекулярных элементов. Для разных природных объектов П изменяется в широком диапазоне. П воды ниже П льда из-за молекулярной структуры твердой формы жидкости. Вещество, переходя из жидкой в твердую форму, изменяет молекулярную структуру, расстояние между составными частицами сужается и плотность увеличивается. Зимой, если забыть слить воду из труб, их разрывает на части после замерзания. На П Н2О влияют примеси.
У морской воды знак П выше, чем у пресной. При соединении в одном стакане двух типов жидкости пресная останется на поверхности. Чем выше концентрация соли, тем больше П воды. Когда плотность вещества больше П воды, оно полностью погрузится в воду. Предметы, сделанные из материала по низкой П, будут плавать на поверхности воды. На практике эти свойства используются человеком. Сооружая суда, инженеры-проектировщики применяют материалы с высокой П. Корабли, теплоходы, яхты смогут затонуть во время плавания, в корпусах суден создают специальные полости, наполненные воздухом, ведь его П ниже плотности воды. Чтобы наживка для рыбалки погрузилась в воду, ее обременяют тяжелым по плотности материалом, например, грузиком из металла чаще свинца. Плотность сплава выше, чем у Н2О.
Жирные пятна масла, нефти, бензина остаются на поверхности воды из-за низкой П маслянистых веществ. Практическое применение Из учебников химии и физики вычисляют уровень плотности по формуле.
Известно, что мрамор объёмом 2 м3 имеет массу 5400 кг. Следовательно, 1 м3 мрамора будет иметь массу в 2 раза меньшую, т. Таким образом, плотность мрамора будет равна 2700 кг на 1 м3. Итак, если известна масса тела и его объём, можно определить плотность. Чтобы найти плотность вещества, надо массу тела разделить на его объём.
Плотность — это физическая величина, которая равна отношению массы тела к его объёму. Тогда получим формулу для вычисления плотности: Единицей плотности вещества в СИ является килограмм на кубический метр. Плотность вещества выражают очень часто и в граммах на кубический сантиметр рис. Плотность кубика, длина ребра которого равна 1 см, численно равна массе этого кубика Если плотность вещества выражена в , то её можно перевести в следующим образом. Плотность серебра 10 500.
Правда, вода является исключением из этого правила, её плотность при затвердевании уменьшается.
Средняя плотность Солнца примерно в 1,5 раза выше плотности воды. Средняя плотность красных гигантов на много порядков меньше, чем у Солнца, из-за того, что их радиус в сотни раз больше. Средняя плотность красных гигантов на много порядков меньше из-за того, что их радиус в сотни раз больше, чем у Солнца. Плотности некоторых газов.
Масса объекта — это внешнее свойство, которое зависит от вещества, присутствующего в веществе. Напротив, плотность объекта подразумевает внутреннее свойство объекта, которое не основано на количестве вещества, существующего в образце. Масса представляет количество вещества, присутствующего в объекте. В отличие от этого, плотность указывает массу, присутствующую на единицу объема. Единицей измерения массы является килограмм, тогда как стандартной единицей измерения плотности в соответствии с международным стандартом является килограмм на кубический метр. Нужна работа по низкой цене? У нас вы можете заказать статью по физике недорого! Тест по теме «Разница между массой и плотностью» 11 Апр 2019 в 09:09 7 422.
Таблица единиц измерения «Электричество и магнетизм»
| Физическая величина | Символ | Единица измерения физической величины | Ед. изм. физ. вел. | Описание | Примечания |
| Сила тока | I | ампер | А | Протекающий в единицу времени заряд. | |
| Плотность тока | j | ампер на квадратный метр | А/м2 | Сила электрического тока, протекающего через элемент поверхности единичной площади. | Векторная величина |
| Электрический заряд | Q, q | кулон | Кл = (А·с) | Способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии. | экстенсивная, сохраняющаяся величина |
| Электрический дипольный момент | p | кулон-метр | Кл•м | Электрические свойства системы заряженных частиц в смысле создаваемого ею поля и действия на неё внешних полей. | |
| Поляризованность | P | кулон на квадратный метр | Кл/м2 | Процессы и состояния, связанные с разделением каких-либо объектов, преимущественно в пространстве. | |
| Напряжение | U | вольт | В | Изменение потенциальной энергии, приходящееся на единицу заряда. | скаляр |
| Потенциал, ЭДС | φ, σ | вольт | В | Работа сторонних сил (некулоновских) по перемещению заряда. | |
| Напряженность электрического поля | E | вольт на метр | В/м | Отношение силы F, действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда q | |
| Электрическая емкость | C | фарад | Ф | Мера способности проводника накапливать электрический заряд | |
| Электрическое сопротивление | R, r | ом | Ом = (м2·кг/(с3·А2)) | сопротивление объекта прохождению электрического тока | |
| Удельное электрическое сопротивление | ρ | ом-метр | Ом•м | Способность материала препятствовать прохождению электрического тока | |
| Электрическая проводимость | G | сименс | См | Способность тела (среды) проводить электрический ток | |
| Магнитная индукция | B | тесла | Тл | Векторная величина, являющаяся силовой характеристикой магнитного поля | Векторная величина |
| Магнитный поток | Ф | вебер | Вб =
(кг/(с2·А)) |
Величина, учитывающая интенсивность магнитного поля и занимаемую им область. | |
| Напряженность магнитного поля | H | ампер на метр | А/м | Разность вектора магнитной индукции B и вектора намагниченности M | Векторная величина |
| Магнитный момент | pm | ампер-квадратный метр | А•м2 | Величина, характеризующая магнитные свойства вещества | |
| Намагниченность | J | ампер на метр | А/м | Величина, характеризующая магнитное состояние макроскопического физического тела. | векторная величина |
| Индуктивность | L | генри | Гн | Коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и полным магнитным потоком | |
| Электромагнитная энергия | N | джоуль | Дж = (кг·м2/с2) | Энергия, заключенная в электромагнитном поле | |
| Объемная плотность энергии | w | джоуль на кубический метр | Дж/м3 | Энергия электрического поля конденсатора | |
| Активная мощность | P | ватт | Вт | Мощность в цепи переменного тока | |
| Реактивная мощность | Q | вар | вар | Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока | |
| Полная мощность | S | ватт-ампер | Вт•А | Суммарная мощность с учетом активной и реактивной ее составляющих, а также отклонения формы тока и напряжения от гармонической |
Примеры линейной плотности
1. Примеры из физики:
Волна на струне: при изучении механики можно рассмотреть пример линейной плотности на примере волны на струне. Линейная плотность струны определяет ее массу на единицу длины. Например, если линейная плотность струны равна 0,05 кг/м, то на каждый метр длины приходится 0,05 кг массы струны.
2. Примеры из геометрии:
Нить или проволока: при изучении геометрии часто используют примеры линейной плотности для описания нитей или проволок. Например, если линейная плотность нити равна 0,1 кг/м, то на каждый метр длины нити приходится 0,1 кг массы нити.
3. Примеры из строительства:
Стальная балка: в строительстве линейную плотность можно использовать для расчета массы различных элементов конструкций, например стальных балок. Если линейная плотность стальной балки равна 0,5 кг/м, то на каждый метр длины стальной балки приходится 0,5 кг массы.
4. Примеры из текстильной промышленности:
Ткань или шнур: в текстильной промышленности линейную плотность можно использовать для расчета массы ткани или шнура. Например, если линейная плотность шнура равна 0,2 кг/м, то на каждый метр длины шнура приходится 0,2 кг массы шнура.
Таким образом, линейная плотность находит широкое применение в различных областях науки и техники. Она позволяет определить массу материала на единицу длины и использовать эту информацию для проведения расчетов и проектирования.
Примеры из физики
1. Тонкий стержень
Представим себе тонкий стержень, у которого масса равномерно распределена по его длине. Чтобы найти линейную плотность стержня, необходимо разделить массу стержня на его длину. Например, если масса стержня составляет 2 килограмма, а его длина равна 1 метру, то линейная плотность будет равна 2 кг/м.
2. Провод
В электрической схеме провода также может быть распределена зарядка по длине. Линейная плотность зарядки измеряется в Кулонах на метр. Например, если на проводе имеется зарядка 10 Кулонов, а его длина составляет 5 метров, то линейная плотность будет равна 2 Кулона/метр.
Из этих примеров становится понятно, как важна линейная плотность при рассмотрении распределения массы или заряда по длине. Она помогает определить, как равномерно или неравномерно распределены эти величины и каково их соотношение в пространстве.
Примеры из геометрии
Линейная плотность также находит свое применение в геометрии. Рассмотрим несколько примеров:
-
Считая длину проводника, можно использовать линейную плотность. Например, если проводник имеет длину 10 метров и массу 2 килограмма, то линейная плотность проводника будет равна 0,2 кг/м.
-
В геометрии примером использования линейной плотности может служить описание длины линии или кривой. Например, если имеется геометрическая фигура с линией длиной 20 сантиметров и массой 5 грамм, то линейная плотность этой линии будет равна 0,25 г/см.
-
Еще одним примером использования линейной плотности в геометрии может быть расчет плотности ограждения. Если ограждение имеет длину 15 метров и массу 10 килограмм, то линейная плотность этого ограждения будет равна 0,67 кг/м.
Определение плотности
Определение плотности газов, жидкостей и твердых веществ осуществляется с целью исследования свойств веществ, идентификации и определения степени их чистоты, определения концентрации двухкомпонентных растворов спиртов, кислот и оснований.
Плотность однородного вещества р — физическая величина, равная отношению массы т вещества к занимаемому им объему V:
Единицей плотности в Международной системе единиц (СИ) является килограмм на кубический метр; в единицах СГС плотность выражается в граммах на кубический сантиметр.
Относительная плотность вещества — величина, равная отношению его плотности к плотности некоторого другого вещества при определенных физических условиях. Такими стандартными веществами служат вода при температуре 3,98 °С и нормальном атмосферном давлении (760 мм рт. ст., или 1013 гПа) или сухой воздух при 20 °С и нормальном атмосферном давлении:
где р — плотность данного вещества, р0 — плотность стандартного вещества.
Относительная плотность — безразмерная величина. Относительную плотность жидкости принято относить к температуре 20 °С и к плотности воды при 3,98 °С (4°С). В этом случае относительная плотность обозначается d204.
В тех случаях, когда плотность жидкости по условиям опыта определяют не при 20 °С, а при другой температуре t, ее значение dt4 может быть пересчитано на нормальное значение по формуле:
где dt4 — относительная плотность исследуемой жидкости при температуре испытания t°С; a — средняя температурная поправка на 1 °С, находимая по табл. 14.
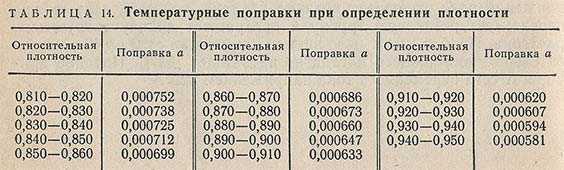
Относительная плотность является одной из важнейших физико-химических характеристик веществ (особенно жидкостей), наряду с температурой плавления и кипения.
Плотность веществ определяют с помощью пикнометров, ареометров и гидростатических весов.
Единицы измерения длины
Для измерения длины предназначены следующие единицы измерения:
- миллиметры;
- сантиметры;
- дециметры;
- метры;
- километры.
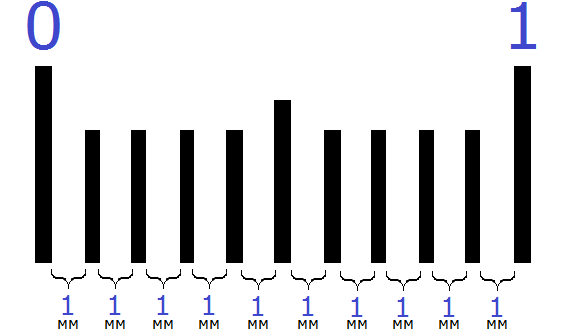
Самая маленькая единица измерения это миллиметр (мм). Миллиметры можно увидеть даже воочию, если взять линейку, которой мы пользовались в школе каждый день

Подряд идущие друг за другом маленькие линии это и есть миллиметры. Точнее, расстояние между этими линиями равно одному миллиметру (1 мм):
Следующая единица измерения это сантиметр (см). На линейке каждый сантиметр обозначен числом. К примеру наша линейка, которая была на первом рисунке, имела длину 15 сантиметров. Последний сантиметр на этой линейке выделен числом 15.
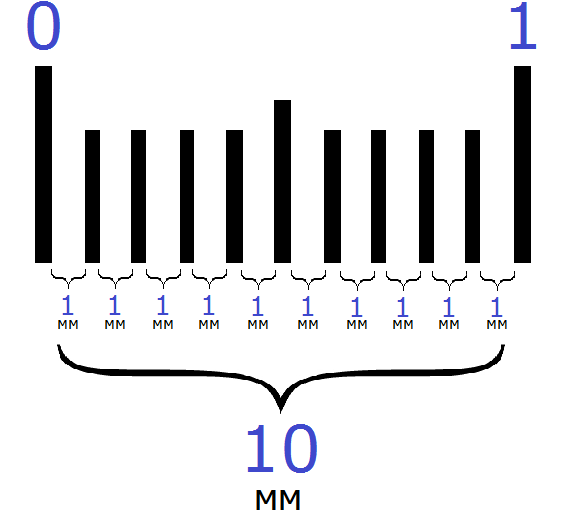
В одном сантиметре 10 миллиметров. Между одним сантиметром и десятью миллиметрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:
1 см = 10 мм
Вы можете сами убедиться в этом, если посчитаете количество миллиметров на предыдущем рисунке. Вы обнаружите, что количество миллиметров (расстояний между линиями) равно 10.
Следующая единица измерения длины это дециметр (дм). В одном дециметре десять сантиметров. Между одним дециметром и десятью сантиметрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:
1 дм = 10 см
Вы можете убедиться в этом, если посчитаете количество сантиметров на следующем рисунке:
Вы обнаружите, что количество сантиметров равно 10.
Следующая единица измерения это метр (м). В одном метре десять дециметров. Между одним метром и десятью дециметрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:
1 м = 10 дм
К сожалению, метр нельзя проиллюстрировать на рисунке, потому что он достаточно великоват. Если вы хотите увидеть метр в живую, возьмите рулетку. Она есть у каждого в доме. На рулетке один метр будет обозначен как 100 см. Это потому что в одном метре десять дециметров, а в десяти дециметрах сто сантиметров:
1 м = 10 дм = 100 см
100 получается путём перевода одного метра в сантиметры. Это отдельная тема, которую мы рассмотрим чуть позже. А пока перейдём к следующей единице измерения длины, которая называется километр.
Километр считается самой большой единицей измерения длины. Есть конечно и другие более старшие единицы, такие как мегаметр, гигаметр тераметр, но мы не будем их рассматривать, поскольку для дальнейшего изучения математики нам достаточно и километра.
В одном километре тысяча метров. Между одним километром и тысячью метрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:
1 км = 1000 м
В километрах измеряются расстояния между городами и странами. К примеру, расстояние от Москвы до Санкт-Петербурга около 714 километров.
Свойства массы
Эмпирически получены такие свойства массы, как:
- Масса — аддитивная скалярная величина, которая не зависит от места положения тела в пространстве. Аддитивность означает, что масса тела равна сумме масс частей тела. Это свойство в точности выполняется для макроскопических тел и нарушается, если энергия взаимодействия составных частей тела велика, например, при соединении протонов и нейтронов в ядро атома. То, что масса является скалярной величиной, значит, что инертные свойства тел одинаковы во всех направлениях.
- Масса тела не зависит от скорости, если она много меньше скорости света.
Массу можно определять при помощи взвешивания или используя динамический способ. Динамический способ нахождения массы заключается в следующем. Если один раз для рассматриваемого тела измерить ускорение и действующую на тело силу одновременно, то можно применяя формулу (1) вычислить массу. Зная массу тела можно рассчитывать ускорение тела по известной силе и по известному ускорению находить силу.
Единицы измерения линейной плотности
Линейная плотность является важной характеристикой материалов, определяющей количество массы, приходящееся на единицу длины. Единицы измерения линейной плотности могут быть различными в зависимости от системы мер и контекста, в котором используется данная характеристика
Наиболее распространенные единицы измерения линейной плотности:
- Килограмм на метр (кг/м) — это основная международная единица для измерения линейной плотности. Она используется в научных и инженерных расчетах, а также в производственных процессах.
- Грамм на сантиметр (г/см) — это одна из наиболее распространенных метрических единиц измерения линейной плотности. Она часто используется в текстильной и полимерной промышленности, а также в производстве нитей, шнуров и других материалов.
- Фунт на фут (lb/ft) — это американская единица для измерения линейной плотности. Она чаще всего используется в США и других странах, где применяется американская система мер, основанная на фунт-футах и дюймах.
Важно помнить, что при использовании разных единиц измерения линейной плотности может возникнуть путаница, поэтому перед началом измерений необходимо уточнить исходную систему мер и единицы, которые будут использоваться
Сатин

У сатина структура ткани отличается от предыдущих позиций. Здесь используется разновидность саржевого плетения с двойной скруткой нитей. Такая ткань имеет гладкую, шелковистую лицевую поверхность, на которой преобладают уточные нити, она довольно плотная и блестит. И чем больше скручены нити, тем больше ее блеск, и тем больше ткань похожа на шелк. Обратная сторона сатина — более матовая, иногда она чуть больше ворсится и по тактильным ощущениям становится похожа на фланель.
У обычного сатина-стандарт плотность 115-120 г/м 2 . Выделяют так же сатин De Luxe, где применяется активное крашение, и плотность ткани выше (она равна 130 г/м 2 ).
Вывод: важность линейной плотности в различных отраслях
Линейная плотность является одним из ключевых понятий в различных отраслях науки и техники. Ее определение и использование имеют большое значение в физике, инженерии, математике и других научных дисциплинах.
С помощью линейной плотности можно расчетно определить плотность распределения массы или энергии на протяжении некоторой линейной структуры. Это позволяет установить, как масса или энергия равномерно распределены по длине объекта или являются разнородными.
Линейная плотность имеет прямое применение в различных инженерных расчетах. Она позволяет определить, например, плотность электрического тока в проводнике или плотность зарядов на линии электрического поля. Эти параметры необходимы при проектировании и расчете схем электроэнергетических систем или электронных устройств.
Также линейная плотность применяется в физике для определения плотности магнитного потока или плотности магнитного поля на определенном участке. Эти характеристики необходимы для анализа и моделирования электромагнитных явлений и работы электротехнических устройств.
В математике линейная плотность используется для определения плотности распределения вероятности на прямой. Это позволяет описать статистическое распределение случайной величины или физического процесса на линии и провести анализ его свойств.
Вывод: понятие линейной плотности является фундаментальным для понимания распределения различных характеристик на протяжении линейной структуры. Ее применение необходимо во многих научных и технических областях для выполнения расчетов, моделирования и оптимизации различных процессов и систем.

























