Спектральная плотность

Радиосигналы, сформированные с помощью фильтра Найквиста

Для формирования сигнала, имеющего близкий к прямоугольному спектр мощности, Найквист предложил использовать сглаживающий фильтр, модуль коэффициента передачи (амплитудно-частотная характеристика, АЧХ) которого может быть записан в следующем виде:

где x_s = (ω — ω) Ts — нормированная к символьному интервалу Ts центрированная круговая частота, а варьируемый параметр сглаживания 0 ≤ α ≤ 1 (коэффициент roll-off) определяет степень прямоугольности фильтра, причем чем меньше значение а, тем «прямоугольнее» АЧХ фильтра, но и тем медленнее во временной области осуществляется затухание сигнала.

Импульсная характеристика может быть определена через обратное преобразование Фурье от коэффициента передачи фильтра. В случае идеальности фильтра, при условии, что коэффициент передачи описывается вещественной функцией, она имеет вид:

где Ts = t/Ts = т/n — нормированный к символьному интервалу параметр времени, причем символьный и двоичный тактовые интервалы связаны соотношением Ts = nT, n — целое положительное число.

Сигнал, сформированный с использованием фильтра Найквиста, характеризуется бесконечной длительностью и регулярностью (через символьный интервал) следования нулей функции, причем огибающая такого радиосигнала непостоянна. То есть в идеальном случае в тактовых точках следования символов отсутствует межсимвольная интерференция.

В то же время, как следует из теории оптимального приема радиосигналов в канале с аддитивным белым шумом, приемный фильтр должен иметь коэффициент передачи, комплексно сопряженный с формирующим фильтром. В результате прохождения такого сигнала через оптимальный приемный фильтр нарушается условие регулярности следования нулей в тактовых точках, возникает межсимвольная интерференция, вследствие чего снижается помехоустойчивость приема.

2.4.10 Спектральная плотность некоторых тестовых сигналов

Условие абсолютной интегрируемости функции ограничивает класс сигналов, для которых существует формула для спектральной плотности, выраженная обычными функциями. К таким сигналам относятся важные для анализа прохождения сигналов через электронные цепи функции, как гармоническое колебание, заданное при единичный скачок (функция Хевисайда), постоянный сигнал и др. Это позволяет сделать так называемая дельта-функция (функция Дирака)- бесконечно короткий импульс с единичной площадью.

а) Дельта-импульс во временной области.

При =0 дельта-импульс обозначается d (t) . Площадь импульса равна 1,т.е.

Одно из важных свойств d — функции – избирательность:

Спектральную плотность d -импульса определим обычным способом:

Таким образом, модуль спектральной плотности d — импульса равен 1[Сигн/Гц] на всех частотах и не зависит от положения на оси времени. ФЧХ спектральной плотности равна () , т.е. линейна (рис. 10).

Это означает, что бесконечное число гармонических составляющих с одинаковыми амплитудами и фазами, соответствующими ФЧХ, суммируясь, образуют пик очень большой величины в момент времени t, а в остальные моменты времени суммируются не в фазе, в результате чего получается ноль. Обратное преобразование Фурье может быть записано в виде

Понятие d — импульса широко используется при исследовании воздействия коротких импульсов на линейные цепи, при этом достаточно, чтобы амплитуда реального импульса была бы большой, а длительность – малой по сравнению с характерными параметрами цепи,

б) Дельта – функция в частотной области

В соответствии с теоремой взаимности можно записать (заменив t на w ):

Таким образом спектральной плотности d ( w ) соответствует постоянный сигнал, действующий при

в) Периодическая последовательность d -импульсов.

В соответствии со свойствами преобразований Фурье огибающая спектра периодического сигнала равна

Так как для одиночного d -импульса , то огибающая спектра периодической последовательности будет равна

Сигнал и его спектр при изображены на рис.11

При наличии сдвига относительно начала отсчета t=0 следует добавить ФЧХ, огибающая которой равна ( — w t ).

г) Единичный скачок.

Математически эта функция записывается следующим образом:

Запишем соотношение для спектральной плотности:

На рис.12 показаны временная и частотная характеристики единичного скачка при =0.

д) Спектральная плотность гармонического сигнала бесконечной длительности.

Такой сигнал на частотной плоскости легко отображается спектром с составляющими на частотах .

Найдем формально спектральную плотность такого сигнала Для этого запишем интеграл Фурье:

Таким образом, спектральная функция гармонического сигнала равна нулю везде, кроме w = , при которых она обращается в бесконечность. Аналогично можно ввести понятие спектральной плотности для любого периодического сигнала, состоящего из суммы гармонических составляющих. Действительно, пусть

Такое описание сигналов бывает полезным при рассмотрении смеси импульсного и периодического сигналов.

Андреевская Т.М., РЭ, МГИЭМ, 2004

Что такое спектральная плотность сигнала?

Спектральная плотность сигнала — это функция, которая описывает распределение энергии или мощности сигнала по его частоте. Она позволяет анализировать, на каких частотах содержится больше энергии или мощности сигнала.

Спектральная плотность сигнала широко используется в различных областях, таких как радиотехника, связь, аудиообработка, изображения и т.д. Она помогает выявить особенности сигнала, определить его составляющие частоты и применять соответствующую обработку.

Основными характеристиками спектральной плотности сигнала являются:

• Амплитуда: определяет мощность сигнала на каждой частоте. Чем больше амплитуда, тем больше энергии или мощности сигнала содержится на соответствующей частоте.

• Частота: указывает на то, на какой частоте находится энергия или мощность сигнала. Частота может быть непрерывной или разделенной на дискретные значения.

Примером спектральной плотности сигнала может быть анализ аудио сигнала. Предположим, у нас есть звуковая запись музыкальной композиции. С помощью спектральной плотности сигнала мы можем определить, на каких частотах содержится музыкальные инструменты и тембры, какая амплитуда на каждой частоте и как они изменяются со временем. Это позволяет выполнять такие операции, как equalizer, подавление шума и другие виды обработки звукового сигнала.

Анализ радиосигналов

Определение 1

Радиосигнал – это электромагнитное излучение, которое создается радиопередатчиком.

Основными характеристиками радиосигнала, на основе которых производится его анализ, являются:

1. Временные характеристики.
2. Спектральные характеристики.

Важнейшие временные характеристики радиосигналов — мощность, энергия, взаимная корреляционная функция, автокорреляционная функция. В любом радиотехническом устройстве сигнал должен выбираться таким образом, чтобы задачи всей системы выполнялись при минимальных затратах энергии. К энергетическим параметрам радиосигналов относятся: энергия сигнала на определенном промежутке времени, мгновенная мощность, средняя мощность на определенном промежутке времени.

Статья: Анализ радиосигналов и расчет характеристик согласованных фильтров

Найди решение своей задачи среди 1 000 000 ответов

Автокорреляционная функция предназначена для количественной оценки степени отличия сигнала от его копии, которая была сдвинута во времени:

Рисунок 1. Автокорреляционная функция. Автор24 — интернет-биржа студенческих работ

Если радиосигнал задается на бесконечном интервале, автокорреляционная функция определяется посредством понятия средней взаимной мощности сигнала и сдвинутой копии:

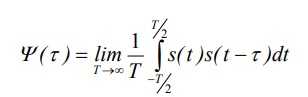Рисунок 2. Автокорреляционная функция. Автор24 — интернет-биржа студенческих работ

Взаимная корреляционная функция используется для определения степени подобия двух сигналов:

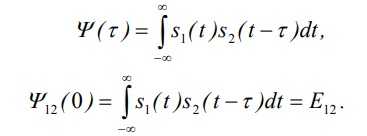Рисунок 3. Взаимная корреляционная функция. Автор24 — интернет-биржа студенческих работ

Взаимная корреляционная функция нечетная, поэтому может достичь своего максимума при любом сдвиге.

Спектральный анализ радиосигналов основан на представлении любого сигнала в виде совокупности элементарных колебаний, которые умножаются на коэффициенты Ск

Рисунок 4. Формула. Автор24 — интернет-биржа студенческих работ

Классический спектральный анализ основывается на преобразовании (обратном и прямом) Фурье:

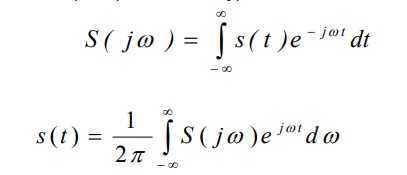Рисунок 5. Формула. Автор24 — интернет-биржа студенческих работ

Спектр представляет собой распределение сигнала по частотам. Он может быть фазовый и амплитудный. Когда известна зависимость сигнала от времени (форма сигнала), используется преобразование Фурье. Для периодического сигнала это ряд Фурье, а для непериодического — интегральное преобразование. Если известны частотные характеристики объекта, то можно получить выходной сигнал, задав его на входе. Для этого сначала получают спектр радиосигнала, после чего анализируется воздействие частотных характеристик на него. Результатом воздействия является получение спектра выходного сигнала, после чего, получают сам выходной сигнал, посредством обратного преобразования Фурье

Слайды и текст этой презентации

Слайд 1РАДИОТЕХНИЧЕСКИЕ ЦЕПИ
И СИГНАЛЫЛекционный курсЛекция 6Доцент Трухин М.П.

кривой, четной относительно начала отсчета времени. С увеличением верхней граничной

частоты спектра возрастают как центральный максимум, так и частота осцилляции.

Спектральной плотности

соответствует низкочастотный сигнал

кривой, четной относительно начала отсчета времени. С увеличением верхней граничной

частоты спектра возрастают как центральный максимум, так и частота осцилляции. При смещении на время to спектральной плотности

соответствует низкочастотный сигнал

сигнал

и v(t). Оба эти сигнала имеют одинаковые параметры So и

,, однако сигнал v(t) запаздывает по отношению к сигналу u(t) на время to, так что его спектральная плотность

Скалярное произведение этих сигналов

Минимально возможный сдвиг, приводящий к ортогонализации, получается при

Скалярное произведение обращается в нуль и два одинаковых по форме ИНС оказываются ортогональными, если временной сдвиг между ними удовлетворяет условию

Слайд 96.4. Теорема Котельникова Любые два сигнала с ограниченным спектром, принадлежащие

базиса может быть выполнена исходя из квадрата нормы одной из базисных функций

Базисные функции будут ортонормированными, если

соответствующую базисную функциюk-я отсчетная функция в пределах отрезка имеет

спектральную плотность, равную

выше может

быть полностью восстановлен, если известны отсчетные значения этого сигнала, взятые через равные промежутки времени

Слайд 12Временные диаграммы,
поясняющие работу дискретизатора

Слайд 13Временные диаграммы,
поясняющие восстановление сигнала

значения (выборки) для данного сигналаВ предельном случае, когда частота

стремится к ,на каждый период гармонического сигнала должно приходиться ровно две выборки.Если же условия теоремы Котельникова нарушаются и отсчеты во времени берутся недостаточно часто, то однозначное восстановление исходного сигнала принципиально невозможно.

Котельникова состоит в ее конструктивном характере: она не только указывает

на возможность разложения сигнала в соответствующий ряд, но и определяет способ восстановления непрерывного сигнала, заданного своими отсчетными значениями

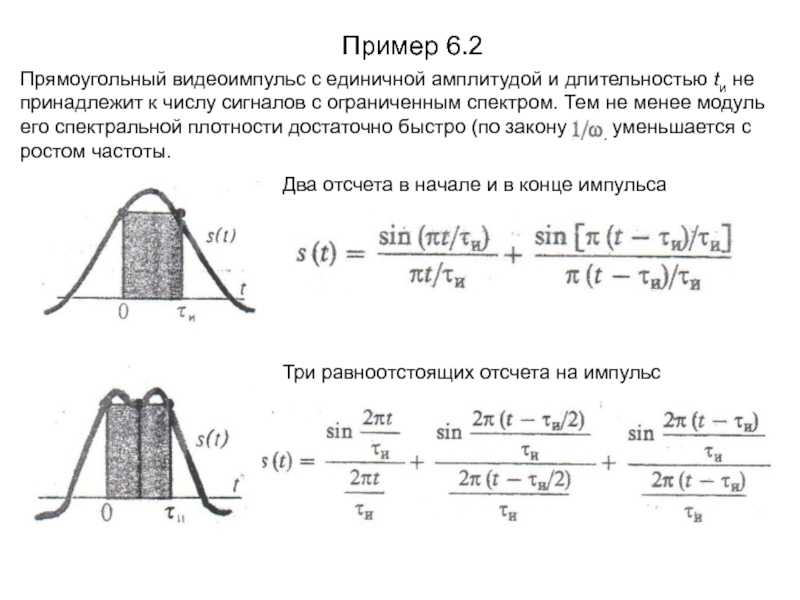
Слайд 16Пример 6.2Прямоугольный видеоимпульс с единичной амплитудой и длительностью tи не

принадлежит к числу сигналов с ограниченным спектром. Тем не менее

модуль его спектральной плотности достаточно быстро (по закону ) уменьшается с ростом частоты.

Два отсчета в начале и в конце импульса

Три равноотстоящих отсчета на импульс

Слайд 17Пример 6.3. Сравнение восстановление видеосигнала
по Котельникову и по ФурьеN

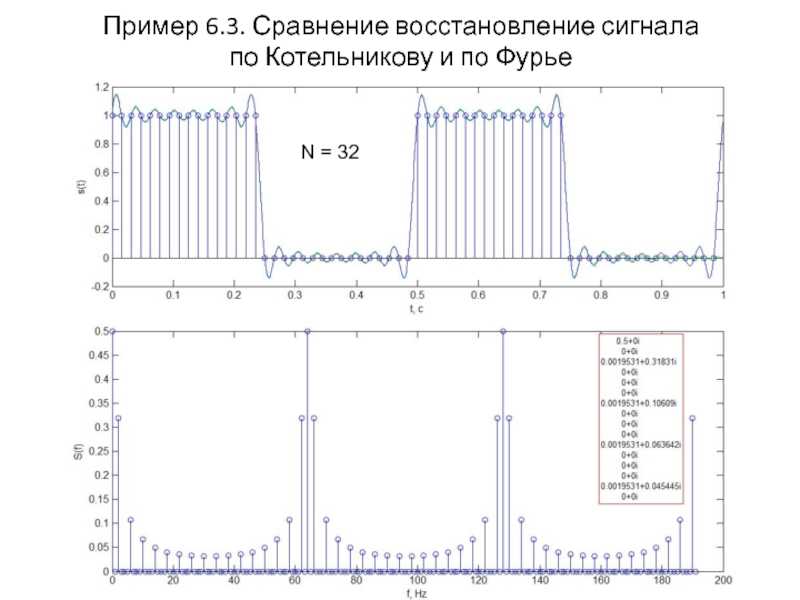
Слайд 18Пример 6.3. Сравнение восстановление сигнала
по Котельникову и по ФурьеN

= 32

сигнал можно представить суммой Если

— энергетический спектр сигнала s(t), то по теореме Рэлея

Спектры указанных сигналов не перекрываются, поэтому сигналы и ортогональны, а их энергии, т. е. квадраты норм, складываются:

Расчёт импульсной реакции и рекомендации к построению согласованного фильтра

Как известно, наряду с полезным сигналом, зачастую присутствуют шумы и поэтому при слабом полезном сигнале иногда трудно определить есть полезный сигнал или нет.

Для приёма сигнала сдвинутого во времени на фоне белого гауссовского шума (белый гауссовский шум «БГС» имеет равномерную плотность распределения) n (t) т.е. y (t) = + n (t), отношение правдоподобия при приёме сигнала известной формы имеет вид:

No

Поэтому приходим к выводу, что оптимальная обработка принимаемых данных — суть корреляционный интеграл

Полученная функция представляет собой ту существенную операцию, которую следует выполнить над наблюдаемым сигналом с тем, чтобы оптимальным (с позиции критерия минимума среднего риска) образом принять решение о наличии или отсутствии полезного сигнала.

Не вызывает сомнений тот факт, что данная операция может быть реализована линейным фильтром.

Действительно, сигнал на выходе фильтра с импульсной характеристикой g (t) имеет вид:

Как видно, при выполнении условия g (r-x) = KS (r-) эти выражения эквивалентны и тогда после замены t = r-x получаем:

где К — постоянная, а to — фиксированное время, при котором наблюдается выходной сигнал.

Фильтр с такой импульсной характеристикой g (t) (смотрите выше) называется согласованным.

Для того чтобы определить импульсную характеристику необходимо сигнал S (t) сместить на tо влево, т.е. получим функцию S (tо + t), а функцию S (tо — t) получить путём зеркального отображения сигнала относительно оси координат, т.е. импульсная характеристика согласованного фильтра будет равна входному сигналу, и при этом получаем на выходе согласованного фильтра максимальное отношение «сигнал-шум».

При нашем входном сигнале для построения такого фильтра необходимо сначала создать звено формирования одного трапецеидального импульса схема, которого изображена на (рис.9).

Рис. 10. Звено формирования радиоимпульса с заданной огибающей.

На вход звена формирования радиоимпульса с заданной огибающей (см. рис.9), подаётся сигнал огибающей радиосигнала (в нашем случае трапеция).

В колебательном звене формируется гармонический сигнал с несущей частотой о (в нашем случае 1,11МГц), поэтому на выходе этого звена имеем гармонический сигнал с частотой о.

С выхода колебательного звена сигнал подаётся на сумматор и на звено линии задержки сигнала на Ti (в нашем случае Ti =15 мкс), а с выхода звена задержки сигнал подаётся на фазовращатель (он нужен для того чтобы после окончания импульса отсутствовал радиосигнал на выходе сумматора).

После фазовращателя сигнал тоже подаётся на сумматор. На выходе сумматора, наконец, имеем трапецеидальные радиоимпульсы с частотой радиозаполнения о т.е. сигнал g (t).

Поскольку нам необходимо получить когерентную пачку из 9 трапецеидальных видеоимпульсов то необходимо сигнал g (t) подать на звено формирования такой пачки схема, которой имеет вид как на (рис 10):

Рис. 11. Звено формирования когерентной пачки.

На вход звена формирования когерентной пачки подаётся сигнал g (t), который представляет собой трапецеидальный радиоимпульс (или последовательность трапецеидальных радиоимпульсов).

Далее сигнал идёт на сумматор и на блок задержки, в котором реализуется задержка входного сигнала на период следования импульсов в пачке Tip умноженный на номер импульса минус единица, т.е. (N-1), а с выходабока задержки снова на сумматор.

Таким образом, на выходе звена формирования когерентной пачки (т.е. на выходе сумматора) имеем прямоугольную когерентную пачку трапецеидальных радиоимпульсов, что и требовалось реализовать.

Приложения

Электротехника

FM-радио

Концепция и использование спектра мощности сигнала является фундаментальным в электротехнике, особенно в системах электронной связи, включая радио связь, радары и связанные с ними системы, а также технология пассивного дистанционного зондирования. Электронные инструменты, называемые анализаторами спектра, используются для наблюдения и измерения спектров мощности сигналов.

Анализатор спектра измеряет величину кратковременного преобразования Фурье (STFT) входного сигнала. Если анализируемый сигнал можно рассматривать как стационарный процесс, STFT представляет собой хорошую сглаженную оценку его спектральной плотности мощности.

Космология

Изначальные флуктуации, вариации плотности в ранней Вселенной, количественно оцениваются спектром мощности, который дает мощность вариаций как функцию пространственного масштаба.

Анализ статистических данных

Статистические данные представляют собой количественную информацию, полученную в результате наблюдений, измерений или опросов

Анализ статистических данных является важной задачей при изучении различных явлений и процессов, так как позволяет найти закономерности и сделать выводы на основе фактических данных

Основные методы анализа статистических данных:

• Описательная статистика — представление основных характеристик исследуемой выборки, таких как среднее значение, медиана, размах, дисперсия и др.;
• Интервальные оценки — определение доверительных интервалов, в которых с заданной вероятностью находится истинное значение параметра;
• Корреляционный анализ — изучение взаимосвязей между различными переменными с помощью коэффициента корреляции;
• Регрессионный анализ — построение модели зависимости одной переменной от другой или нескольких переменных;
• Анализ дисперсии — проверка гипотез о равенстве средних значений в разных группах исследуемой выборки;
• Факторный анализ — выявление скрытых факторов, влияющих на исследуемое явление;
• Дискриминантный анализ — классификация объектов на основе их характеристик;
• Кластерный анализ — разделение объектов на группы схожих по своим характеристикам;
• Хронологический анализ — изучение изменения показателей в течение определенного времени;
• Прогнозирование — предсказание будущих значений на основе имеющихся данных.

Инструменты анализа статистических данных:

• Статистические пакеты — программное обеспечение, предназначенное для статистического анализа данных, такие как SPSS, R, Python (библиотеки NumPy, pandas, matplotlib и др.), Excel и др.;
• Графические методы — построение диаграмм, гистограмм, круговых диаграмм, ящиков с усами и др. для визуализации данных;
• Математические и статистические методы — различные математические модели и статистические тесты для выявления закономерностей в данных;
• Методы машинного обучения — алгоритмы, позволяющие автоматически находить закономерности в данных и делать прогнозы.

Анализ статистических данных позволяет сделать выводы и принять решения на основе фактической информации, что является важным в многих областях, таких как наука, бизнес, медицина, социология и др.

Примеры спектральной плотности сигнала

Спектральная плотность сигнала является мощным инструментом для анализа и понимания свойств различных сигналов. Ниже приведены несколько примеров спектральной плотности сигнала:

1. Звуковой сигнал

Для анализа и понимания звукового сигнала, спектральная плотность сигнала может показать, какие частоты присутствуют в этом сигнале и с какой интенсивностью. Например, при анализе музыкального трека можно увидеть, какие ноты или аккорды присутствуют в музыке и какая частота доминирует.

2. Радиосигнал

Спектральная плотность сигнала также применяется для анализа радиосигналов. Она позволяет определить, на каких частотах передаются разные радиостанции или сигналы, и с какой мощностью. Это помогает в выборе оптимальных частот для передачи радиосигнала и избегать помех от других радиостанций.

3. Электрический сигнал

В электронике и электротехнике спектральная плотность сигнала используется для анализа электрических сигналов. Например, для измерения шумов на линии передачи данных или для анализа гармоник в электрической сети. С помощью спектральной плотности сигнала можно определить, на каких частотах происходит наибольшее количество шумов или искажений и принять соответствующие меры для исправления проблемы.

4. Изображение

Для анализа изображений спектральная плотность сигнала может быть использована для определения частот, присутствующих в изображении. Например, при анализе фотографий можно определить, какие частоты отвечают за текстуры или какие частоты отвечают за различные детали в изображении. Это может быть полезно для обработки и улучшения качества изображения.

Все эти примеры демонстрируют, как спектральная плотность сигнала может помочь в анализе сигналов и понимании их структуры и свойств.

Спектральная плотность сигнала: как она рассчитывается?

Спектральная плотность сигнала является одним из важных инструментов анализа сигналов. Она позволяет изучать спектральную составляющую сигнала, то есть распределение энергии сигнала по различным частотам.

Чтобы рассчитать спектральную плотность сигнала, следуйте следующим шагам:

1. Закрепите сигнал, который вы хотите проанализировать. Сигнал может быть временным рядом амплитуд или последовательностью отсчетов. Например, это может быть звуковая волна, изображение или данные с датчика.
2. Примените преобразование Фурье к сигналу. Преобразование Фурье разлагает сигнал на его спектральные компоненты, представленные через амплитуды и фазы с различными частотами.
3. Измерьте амплитуды спектральных компонент с помощью преобразования Фурье. Вместо амплитуд в виде отсчетов вы получаете амплитуды в виде спектра энергии.
4. Рассчитайте энергию сигнала на каждой частоте. Для этого возьмите квадрат амплитуды каждой спектральной компоненты.
5. Нормализуйте энергию для каждой частоты, чтобы получить спектральную плотность сигнала. Это можно сделать, разделив энергию на ширину промежутка частоты или нормализуя ее по отношению к максимальной энергии сигнала.

В результате вы получаете спектральную плотность сигнала, представленную в виде графика или таблицы. Она показывает, какая часть энергии сигнала содержится в различных частотах и позволяет выявить особенности спектральной композиции сигнала.

Спектральная плотность сигнала применяется во многих областях, включая аудиообработку, обработку сигналов, радиоинженерию, телекоммуникации и другие. Этот инструмент позволяет выявлять частотные характеристики сигналов, изучать их распределение энергии и принимать решения на основе анализа спектра сигнала.

Спектральная плотность

В статистической радиотехнике и физике при изучении детерминированных сигналов и случайных процессов широко используется их спектральное представление в виде спектральной плотности, которая базируется на преобразовании Фурье.

Если процесс имеет конечную энергию и квадратично интегрируем (а это нестационарный процесс), то для одной реализации процесса можно определить преобразование Фурье как случайную комплексную функцию частоты:

((1))

Однако она оказывается почти бесполезной для описания ансамбля. Выходом из этой ситуации является отбрасывание некоторых параметров спектра, а именно спектра фаз, и построении функции, характеризующей распределение энергии процесса по оси частот. Тогда согласно теореме Парсеваля энергия

((2))

Функция характеризует, таким образом, распределение энергии реализации по оси частот и называется спектральной плотностью реализации. Усреднив эту функцию по всем реализациям можно получить спектральную плотность процесса.

Перейдем теперь к стационарному в широком смысле центрированному случайному процессу , реализации которого с вероятностью 1 имеют бесконечную энергию и, следовательно, не имеют преобразования Фурье. Спектральная плотность такого процесса может быть найдена на основании теоремы Винера-Хинчина как преобразование Фурье от корреляционной функции:

((3))

Если существует прямое преобразование, то существует и обратное преобразование Фурье, которое по известной определяет :

((4))

Если полагать в формулах (3) и (4) соответственно и , имеем

((5))

((6))

Формула (6) с учетом (2) показывает, что дисперсия определяет полную энергию стационарного случайного процесса, которая равна площади под кривой спектральной плотности. Размерную величину можно трактовать как долю энергии, сосредоточенную в малом интервале частот от до . Если понимать под случайный (флуктуационный) ток или напряжение, то величина будет иметь размерность энергии [В 2 /Гц] = . Поэтому иногда называют энергетическим спектром. В литературе часто можно встретить другую интерпретацию: – рассматривается как средняя мощность, выделяемая током или напряжением на сопротивлении 1 Ом. При этом величину называют спектром мощности случайного процесса.

Свойства спектральной плотности

Энергетический спектр стационарного процесса (вещественного или комплексного) – неотрицательная величина:

.

((7))

Энергетический спектр вещественного стационарного в широком смысле случайного процесса есть действительная и четная функция частоты:

.

((8))

Корреляционная функция и энергетический спектр стационарного в широком смысле случайного процесса обладают всеми свойствами, характерными для пары взаимных преобразований Фурье. В частности, чем «шире» спектр тем «уже» корреляционная функция , и наоборот. Этот результат количественно выражается в виде принципа или соотношения неопределенности.

См. также

• Преобразование Фурье
• Теорема Парсеваля
• Теорема Хинчина-Колмогорова
• Спектральная плотность мощности
• Спектральная плотность излучения

Литература

1. Зюко, А. Г. Теория передачи сигналов / А. Г. Зюко . — М .: Связь, 1980. — 288 с.
2. Тихонов, В. И. Статистический анализ и синтез радиотехнических устройств и систем / В. И. Тихонов, В. Н. Харисов. — М .: Радио и связь, 2004. — 608 с. — ISBN 5-256-01701-2
3. Тихонов, В. И. Статистическая теория радиотехнических устройств / В. И. Тихонов, Ю. Н. Бакаев. — М .: Академия им. проф. Н. Е. Жуковского, 1978. — 420 с.

• Обработка сигналов
• Преобразование Фурье

Wikimedia Foundation . 2010 .

Анализ спектральных характеристик

Анализ спектральных характеристик сигналов имеет важное значение в различных областях науки и техники, включая радиотехнику, телекоммуникации, медицину, физику и другие. С помощью спектрального анализа можно изучать спектральную плотность сигнала, выделить характеристические частоты, определить ширины спектральных линий и многое другое

Спектральная плотность сигнала предоставляет информацию о распределении мощности сигнала по различным частотам. Она выражается в единицах мощности или энергии на единицу частоты. Анализ спектральных характеристик позволяет определить основные параметры спектральной плотности сигнала, такие как пиковая частота, ширина спектра, отношение сигнал-шум и другие.

Одним из основных методов анализа спектральных характеристик является преобразование Фурье. Оно позволяет представить сигнал в частотной области и выделить его спектральные компоненты. Преобразование Фурье может использоваться для различных целей, начиная от простого отображения спектра до сложных алгоритмов обработки сигналов.

С помощью анализа спектральных характеристик можно также определить причину возникновения различных помех и искажений в сигнале. Например, с помощью спектрального анализа можно исследовать спектральные составляющие сигнала, вызванные шумами, интерференциями и другими искажениями. Это позволяет разработать эффективные методы фильтрации и подавления помех.

Также анализ спектральных характеристик позволяет исследовать динамические свойства сигнала. С помощью спектрального анализа можно определить периодические колебания, изменение спектральной плотности сигнала во времени, а также смещение в частоте и фазе сигнала. Это позволяет изучить различные динамические явления и подбирать наиболее подходящие методы обработки сигнала.

В целом, анализ спектральных характеристик является мощным инструментом для изучения сигналов и их свойств. Он позволяет получить информацию о распределении мощности сигнала по частотам, определить основные параметры спектральной плотности сигнала и использовать эту информацию для различных приложений, включая фильтрацию сигналов, обнаружение и подавление помех, исследование динамических свойств сигнала и другие.

Математические методы

Спектральная плотность сигнала является важным инструментом для анализа и обработки сигналов. Она позволяет определить распределение энергии сигнала в различных частотных областях. Для расчета спектральной плотности сигнала применяются различные математические методы.

Один из наиболее распространенных методов — преобразование Фурье. Оно позволяет перевести сигнал из временной области в частотную область. Преобразование Фурье находит коэффициенты спектра сигнала и позволяет определить его спектральную плотность.

Еще один важный метод — автокорреляция. Он позволяет определить степень похожести сигнала на самого себя при сдвиге на заданное время. Автокорреляционная функция используется для расчета спектральной плотности сигнала.

Математические методы также включают алгоритмы детектирования и фильтрации сигналов. Используя матричные операции и статистические методы, можно выделить нужные компоненты сигнала и избавиться от нежелательных помех.

Метод	Описание
Преобразование Фурье	Математический метод для перехода из временной области в частотную область
Автокорреляция	Математический метод для определения степени похожести сигнала на самого себя при сдвиге
Детектирование сигналов	Математический метод для выделения нужных компонентов сигнала
Фильтрация сигналов	Математический метод для избавления от нежелательных помех

Все эти методы позволяют анализировать сигналы и получать информацию о их спектральной плотности. Они широко используются в различных областях, таких как телекоммуникации, медицина, радиофизика и многое другое.

Заключение

Полученные результаты позволяют сопоставить спектральные характеристики классических фазомодулированных радиосигналов с постоянной огибающей и сигналов, сформированных на основе алгоритма Найквиста. Сигналы, используемые в спутниковой радиосвязи, обеспечивают существенную экономию частотного ресурса. В то же время реализация современных частотно-эффективных радиосистем предполагает применение высокоскоростных цифровых технологий, сложных принципов сигналообразования, линейных передающих и приемных трактов, не приводящих к разрушению сигналов. При возникновении заметной нелинейности в таком тракте возможно резкое снижение помехоустойчивости приема и изменение СПСМ, вплоть до предельного случая, когда при жестком амплитудном ограничении в тракте спектральные характеристики приближаются к соответствующим характеристикам сигналов с классической фазовой модуляцией.

Приведенные данные могут быть использованы при анализе и проектировании новых систем связи с эффективным использованием частотного ресурса. Представленные графики позволяют оценить влияние на спектральные характеристики радиосигналов, используемых в спутниковой связи, ряда параметров формирующего тракта.

Принципы экономного использования частотного ресурса, реализуемые в спутниковой связи, очевидно, будут востребованы и для других видов радиосвязи, в частности радиорелейной.

Дальнейшее совершенствование сигналов спутниковых радиосистем будет, по-видимому, происходить путем развития теории и практики создания новых адаптивных СКК при конвергенции методов модуляции и кодирования с целью повышения эффективности использования частотного ресурса.

Кроме того, данные результаты могут быть использованы для дальнейшего развития теории сложных импульсных процессов.

Литература

1. Шеннон К. Работы по теории информации и кибернетике / Пер. с англ. Под ред. Р.Л. Добрушина и О.Б. Лупанова. – М.: Издательство иностранной литературы, 1963. – 830 с.
2. Neves, A. An Algebraic Receiver for Full Response CPM Demodulation. VI International Telecommunications Symposium (ITS2006) / Aline Neves, Mamadou Mboup and Michel Fliess // Brazil: FORTALEZA-CE. – 2006. – 3–6 September.
3. Коновалов Г.В. Спектрально-корреляционный анализ сложных импульсных случайных процессов // Радиотехника и электроника. – 1980. – Т. XXV. – № 12. – С. 2566–2574.
4. Vokurka К. On the group pulse processes. I: classification // Kybernetika. – 1983. – Vol. 19. – № 5. – Р. 374–386 : http://dml.cz/dmlcz/125790.
5. Диденко М.Г. Спектральные характеристики радиосигналов цифровых систем передачи информации / М.Г. Диденко, С.В. Тян, Н.Д. Ханина // Техника средств связи.– 1988. – Вып. 2. – С. 73–88. – Техника радиосвязи.
6. F. de Jager and C.B Decker. Tamed frequency modulation, a novel method to achieve spectrum economy in digital transmissions / F. de Jager, C.B Decker // IEEE. Trans. on Comm.. – 1978, vol. COM-26, № 5, May. – Р. 534–542.
7. Диденко М.Г. Помехоустойчивость когерентного приема радиосигналов с управляемой частотной манипуляцией / М.Г. Диденко, С.В. Тян // Техника средств связи.– 1989. – Вып. 5. – С. 3–16. – Техника радиосвязи.
8. Диденко М.Г. Корреляционные и спектральные характеристики случайных импульсных сигналов сложной структуры / М.Г. Диденко, Г.В. Коновалов, С.В. Тян // Известия вузов. – 1990. – № 11. – С. 16–21. – Радиоэлектроника.

Опубликовано: Журнал «Технологии и средства связи» #1, 2014Посещений: 7943

Автор Всего статей:  2

Автор

В рубрику «Спутниковая связь» | К списку рубрик  |  К списку авторов  |  К списку публикаций