Полное понимание битовых операций за 7 минут

§3. Измерение информации

Что такое бит?

Рассмотрим электрическую лампочку, которая может находиться в двух состояниях: «горит» и «не горит». Тогда на вопрос «Горит ли сейчас лампочка» есть два возможных варианта ответа, которые можно обозначить цифрами 1 («горит») и 0 («не горит») (рис. 1.5). Поэтому ответ на этот вопрос (полученная информация) может быть записан как 0 или 1 1.

1 Конечно, вместо 0 и 1 можно использовать два любых знака.

Цифры 0 и 1 называют двоичными, и с этим связано название единицы измерения количества информации — бит. Английское слово bit — это сокращение от выражения binary digit — «двоичная цифра». Впервые слово «бит» в этом значении использовал американский инженер и математик Клод Шеннон в 1948 г.

Бит — это количество информации, которую можно записать (закодировать) с помощью одной двоичной цифры.

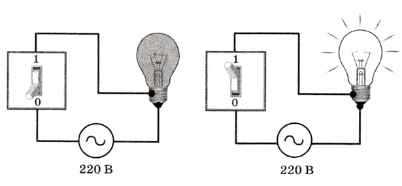
Рис. 1.5

Конечно, нужно договориться, что означают 0 и 1 (1 — это «горит» или «не горит»?), но для измерения количества информации это не важно.

Например, в сообщении «подброшенная монета упала гербом» содержится 1 бит информации, потому что монета могла упасть гербом (обозначим это через 0) или «решкой» (1). Сообщение «Дверь открыта» тоже содержит 1 бит, если считать, что дверь может быть в двух состояниях: открыта (0) или закрыта (1). Вот ещё пример диалога, в котором получена информация в 1 бит:

— Вы будете чай или кофе?

— Кофе, пожалуйста.

2 бита, 3 бита…

А если возможных вариантов не два, а больше? Понятно, что в этом случае количество информации будет больше, чем 1 бит. Представим себе, что на вокзале стоят 4 одинаковых поезда (рис. 1.6), причём только один из них проследует в Москву. Сколько битов понадобится для того, чтобы записать информацию о номере платформы, где стоит поезд на Москву?

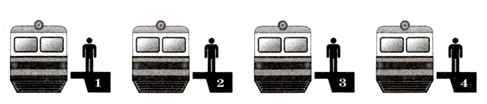
Рис. 1.6

Очевидно, что одного бита недостаточно, так как с помощью одной двоичной цифры можно закодировать только два варианта — коды 0 и 1. А вот два бита дают как раз 4 разных сообщения: 00, 01, 10 и 11. Теперь нужно сопоставить эти коды номерам платформ, например, так: 1 — 00, 2 — 01, 3 — 10, 4 — 11. Тогда сообщение 10 говорит о том, что поезд на Москву стоит на платформе № 3. Это сообщение несёт 2 бита информации.

Три бита дают уже 8 вариантов: 000, 001, 010, 011, 100, 101, 110 и 111. Таким образом, каждый бит, добавленный в сообщение, увеличивает количество вариантов в 2 раза (табл. 1.1).

Наверно, вы заметили, что все числа в нижней строчке таблицы — это степени числа 2: N = 2I.

Осталось выяснить, чему равно количество информации, если выбор делается, скажем, из 5 возможных вариантов (или из любого количества, не являющегося степенью числа 2). С точки зрения приведённого выше рассуждения случаи выбора из 5, 6, 7 и 8 вариантов не различаются — для кодирования двух двоичных цифр мало, а трёх — достаточно. Поэтому использование трёх битов для кодирования одного из 5 возможных вариантов избыточно, ведь три бита позволяют закодировать целых 8 вариантов! Значит, выбор из 5 вариантов даёт меньше трёх битов информации.

Чтобы количественно измерить разницу между, скажем, 5 и 8 вариантами, придется допустить, что количество информации в битах может быть дробным числом. При этом информация, полученная при выборе из 5 вариантов, больше, чем 2 бита, но меньше, чем 3 бита. Точную формулу для ее вычисления получил в 1928 г. американский инженер Ральф Хартли. Эта формула использует понятие логарифма, поэтому мы познакомимся с ней в 11 классе.

Тем не менее уже сейчас вы можете оценить количество информации при выборе из 5 вариантов. Допустим, на завтрак в лагере отдыха каждый день дают кашу одного из 5 видов. Чтобы закодировать вид каши, которую дают в понедельник, нужно, как мы знаем, 3 бита. Но меню на два дня может быть составлено 25 разными способами (5 • 5), поэтому для его кодирования достаточно 5 битов, ведь 25 < 32 = 25! Тогда получается, что количество информации при выборе информации из 5 вариантов меньше, чем 5/2 = 2,5 бита. Но и эту оценку можно уточнить. Для трёх дней получаем 5 • 5 • 5 = 125 вариантов. Так как 125 < 128 = 27, количество информации при выборе из 5 вариантов составляет не больше, чем 7/3 = 2,33 бита. И так далее. Попробуйте самостоятельно показать, что при выборе из 5 вариантов количество информации больше 2,25 бита. Верно ли, что при выборе из 6 вариантов количество информации менее 2,5 бита?

Следующая страница Другие единицы

Cкачать материалы урока

Практическое применение битов в компьютерных системах

Биты в компьютерных системах играют ключевую роль во множестве практических приложений. Они используются для кодирования и хранения информации, управления периферийными устройствами, обмена данными между устройствами и многих других задач.

Вот некоторые примеры практического применения битов:

Хранение данных: Биты используются для представления информации в компьютерных системах. Один бит может принять два значения: 0 или 1. С помощью множества битов можно представлять числа, символы, звук, изображения и другую информацию. Например, символ в компьютере может быть представлен с помощью 8 битов (байт).
Управление периферийными устройствами: Биты используются для управления периферийными устройствами компьютера, такими как клавиатура, мышь, принтер и др. Когда пользователь нажимает клавишу, манипулирует мышью или отправляет команду на принтер, компьютер использует биты для передачи информации о состоянии и действиях устройств.
Сетевое взаимодействие: Биты используются для передачи данных по сетям. Когда вы отправляете электронное письмо, загружаете веб-страницу или смотрите видео онлайн, информация передается в виде битов через сеть. Биты используются для кодирования и декодирования данных, обеспечивая их передачу и восстановление на другом конце.
Компьютерное видео и звук: Биты используются для представления видео и звука в компьютерных системах. Видео и звуковые файлы хранятся в форматах, которые кодируют информацию о цвете пикселей, амплитуде звука и других атрибутах с помощью битов. При проигрывании эти биты декодируются и воспроизводятся в виде видео и звука на экране и динамике.
Криптография: Биты используются для обеспечения безопасности данных. Криптографические алгоритмы используют биты для шифрования и дешифрования информации, защиты конфиденциальности и целостности данных. Биты служат основой для создания ключей шифрования, которые используются в схемах аутентификации и защите информации.

Это лишь некоторые примеры практического применения битов в компьютерных системах. Биты играют фундаментальную роль в работе и управлении информацией в компьютерах, их понимание и правильное использование является неотъемлемой частью работы в области информационных технологий.

2.2. Семантическая мера информации

Для измерения семантического содержания информации, т.е. ее количества на семантическом уровне, наиболее признанной мерой является тезаурус, который связывает семантические свойства информации со способностью пользователя принять полученное сообщение. Для этого используется понятие пользовательского тезауруса.

В зависимости от связи между семантическим содержанием информации S и тезаурусом пользователя S._pНабор семантической информации I_своспринимается пользователем и включается им в изменения своего тезауруса. Характер этой зависимости показан на рисунке 2.2:

при S_p=0 пользователь не воспринимает, не понимает поступающую информацию;
при S_p→ ∞ пользователь все знает, поступающая информация ему не нужна.

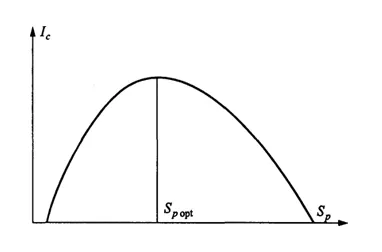
Рисунок 2.2: Зависимость количества семантической информации, воспринимаемой пользователем, от его тезауруса I_с= f ( S_p)

При оценке семантического аспекта (содержания) информации следует попытаться объединить значения S и S_p.

Соответствующей мерой количества семантической информации может быть коэффициент содержания S, который определяется как отношение количества семантической информации к ее объему:

Что такое сигнал?

Сигнал — это изменение физической величины в течение какого-либо времени. Человек приноровился использовать изменения для того, чтобы с помощью них кодировать информацию.

Каждое такое изменение называется состоянием сигнала.

Что может изменяться у электрического сигнала? — амплитуда, частота и фаза.

Фаза — это момент, с которого начинается сигнал.

На следующем графике изображено кодирование двоичной информации с использованием каждого из этих параметров.

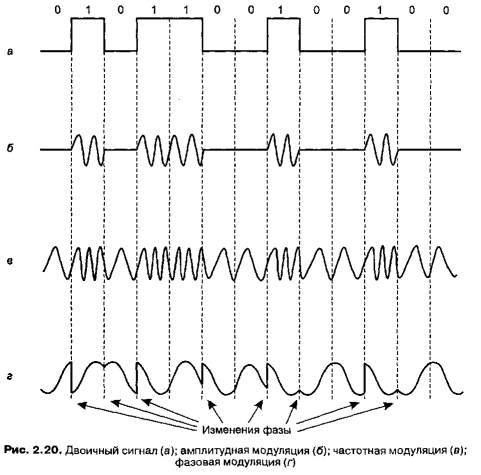график кодирования информации с помощью амплитуды, частоты и фазы.

Нужно учесть, что мы рассматриваем цифровой сигнал. Цифровой сигнал — это сигнал, который можно представить в виде последовательности дискретных (цифровых) значений.

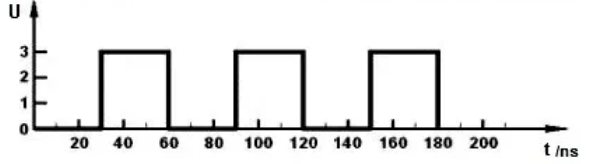пример бинарного цифрового сигнала.

А можно ли закодировать четыре значения? — можно! И тогда, на каждый сигнал будет приходиться один из вариантов сочетания нуля и единицы. Если нам дано 4 варианта сигнала, которыми нам нужно закодировать сигнал, то количество разрядов, необходимых для представления в двоичном виде будет log₂4 = 2.

Можно закодировать и больше значений.

Передача дискретной информации в телекоммуникационных сетях осуществляется тактировано, то есть изменение сигнала происходит через фиксированный интервал времени, называемый тактом.

Приемник (компьютер, который получает информацию) считает, что вначале каждого такта на его вход поступает новая информация. При этом независимо от того, повторяет ли сигнал состояние предыдущего такта или же он имеет состояние, отличное от предыдущего, приёмник получает новую информацию от передатчика. Например, если такт равен 0.3 с, а сигнал имеет два состояния и единица кодируется амплитудой 5 вольт, то присутствие на входе приёмника сигнала 5 вольт в течение 3 секунд означает получение информации, представленной двоичным числом 1111111111₂.

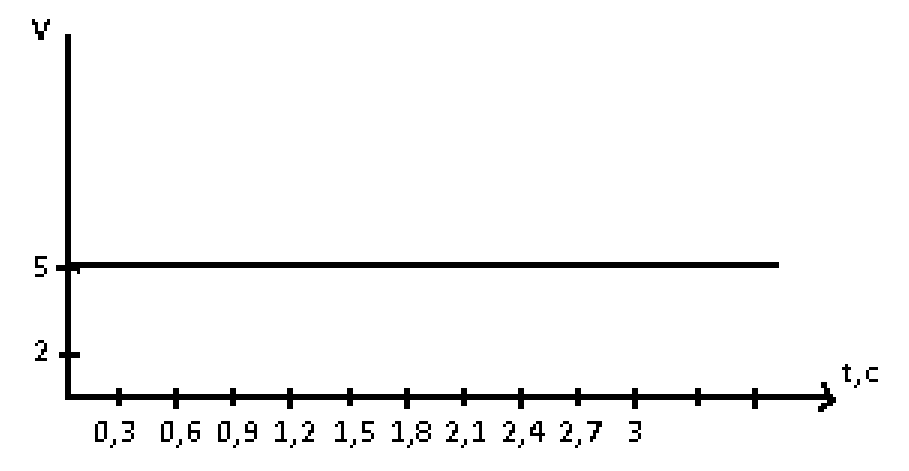иллюстрация примера.

#Маски

Бинарные последовательности можно поставить в соответствие подмножествам какого-то фиксированного множества: если на $i$-той позиции стоит единица, то значит $i$-тый элемент входит множество, а иначе не входит.

Битовые операции таким образом часто используются операций над множествами, представляемыми битовыми мазками — например, в задачах на полный перебор или динамическое программирование.

Выделить i-й бит числа

или . Во втором случае результат будет либо 0, либо $2^i$.

Это часто используется для проверки, принадлежит ли $i$-тый элемент множеству:

Напомним, что нумерация идет с младших бит и начинается с нуля.

Наименьший бит

двоичное представление

В вычислении младший бит (LSB ) является позицией бита в двоичное целое число, дающее значение единиц измерения, то есть определяющее, является ли число четным или нечетным. LSB иногда называют битом младшего разряда или самым правым битом из-за соглашения в позиционной записи о записи менее значимых цифр дальше вправо. Он аналогичен младшей цифре десятичного целого числа, которая является цифрой в позиции единиц (крайняя правая).

Обычно назначают каждый бит — это номер позиции в диапазоне от нуля до N-1, где N — количество битов в используемом двоичном представлении. Обычно это просто показатель степени для соответствующего веса бита в базе 2 (например, в ). Хотя некоторые производители ЦП присваивают номера битов противоположным образом (что не то же самое, что и другой порядок байтов ), сам термин наименее значимый бит остается однозначным как псевдоним для единичного бита.

В более широком смысле наименее значимые биты (множественное число) представляют собой биты числа, ближайшего к младшему разряду и включающего его.

Младшие значащие биты обладают полезным свойством быстрого изменения, если число изменяется даже незначительно. Например, если 1 (двоичный 00000001) добавлен к 3 (двоичный 00000011), результатом будет 4 (двоичный 00000100), а три младших бита изменятся (с 011 на 100). Напротив, три старших бита (MSB) остаются неизменными (от 000 до 000).

Наименьшие значащие биты часто используются в генераторах псевдослучайных чисел, стеганографических инструментах, хэш-функциях и контрольных суммах.

Наименее значимых бит в цифровой стеганографии

В цифровой стеганографии конфиденциальные сообщения могут быть скрыты путем манипулирования и сохранения информации в младших битах изображения или звукового файла. В контексте изображения, если бы пользователь манипулировал последними двумя битами цвета в пикселе, значение цвета изменилось бы не более чем на ± 3 разряда, что, вероятно, будет неразличимо для человеческого глаза. Пользователь может позже восстановить эту информацию, извлекая младшие биты обработанных пикселей, чтобы восстановить исходное сообщение.

Это позволяет скрывать хранение или передачу цифровой информации.

Младший байт

LSB также может означать младший байт . Значение аналогично приведенному выше: это байт (или октет ) в той позиции многобайтового числа, которая имеет наименьшее потенциальное значение. Если значение наименее значимого байта сокращения не очевидно из контекста, его следует указать явно, чтобы избежать путаницы с наименьшим значащим битом.

Чтобы избежать этой двусмысленности, можно использовать менее сокращенные термины «lsbit» или «lsbyte».

Примеры

1. Напишем функции, которые позволяют определять и изменять определённый бит числа

Для того, чтобы узнать, какой бит (1 или 0) стоит на позиции n, воспользуемся логическим умножением.

Пусть имеется число 9

Нужно узнать, выставлен ли бит на позиции 3 (начиная с нуля). Для этого умножим его на число, у которого все биты равны нулю, кроме третьего:

Теперь узнаем значение бита в позиции 6

Таким образом, если мы получаем ответ, равный нулю, то на искомой позиции находится ноль, иначе единица. Чтобы получить число, состоящее из нулей с одним битом на нужной позиции, сдвинем 1 на нужное число бит влево.

#include <stdio.h>
#include <conio.h>
#include <limits.h>

int checkbit(const int value, const int position) {
	int result;
	if ((value & (1 << position)) == 0) {
		result = 0;
	} else {
		result = 1;
	}
	return result;
}

void main() {
	int a = 3;
	size_t len = sizeof(int) * CHAR_BIT;
	size_t i;

	for (i = 0; i < len; i++) {
		printf("%d", checkbit(a, i));
	}

	_getch();
}

Заметьте, что в функции условие записано так

(value & (1 << position)) == 0

Потому что без скобок сначала будет вычислено равенство нулю и только потом выполнено умножение.

value & (1 << position) == 0

Функцию можно упростить

int checkbit(const int value, const int position) {
	return ((value & (1 << position)) != 0);
}

Функция, которая выставляет бит на n-й позиции в единицу.

Известно, что логическое сложение любого бита с 1 будет равно 1. Так что для установки n-го бита нужно логически сложить число с таким, у которого все биты, кроме нужного,
равны нулю. Как получить такое число, уже рассмотрено.

int setbit(const int value, const int position) {
	return (value | (1 << position));
}

Функция, которая устанавливает бит на n-й позиции в ноль.

Для этого нужно, чтобы все биты числа, кроме n-го, не изменились. Умножим число на такое, у которого все биты равны единице, кроме бита под номером n. Например

Чтобы получить такую маску, сначала создадим число с нулями и одной единицей, а потом инвертируем его.

int unsetbit(const int value, const int position) {
	return (value & ~(1 << position));
}

Функция, изменющая значение n-го бита на противоположное.

Для этого воспользуемся функцией исключающего или: применим операцию XOR к числу, которое состоит из одних нулей и одной единицы на месте нужного бита.

int switchbit(const int value, const int position) {
	return (value ^ (1 << position));
}

Проверка

#include <stdio.h>
#include <conio.h>
#include <limits.h>

int checkbit(const int value, const int position) {
	return ((value & (1 << position)) != 0);
}

int setbit(const int value, const int position) {
	return (value | (1 << position));
}

int unsetbit(const int value, const int position) {
	return (value & ~(1 << position));
}

int switchbit(const int value, const int position) {
	return (value ^ (1 << position));
}

void printbits(int n) {
	//CHAR_BIT опеределён в библиотеке limits.h
	//и хранит число бит в байте для данной платформы
	size_t len = sizeof(int)* CHAR_BIT;
	size_t i;
	for (i = 0; i < len; i++) {
		printf("%d", checkbit(n, i));
	}
	printf("\n");
}

void main() {
	int a = 3;
	size_t len = sizeof(int) * CHAR_BIT;
	size_t i;

	printbits(a);
	a = setbit(a, 5);
	printbits(a);
	a = unsetbit(a, 5);
	printbits(a);
	a = switchbit(a, 11);
	printbits(a);
	a = switchbit(a, 11);
	printbits(a);

	_getch();
}

От бита до байта: понятное объяснение единиц измерения информации

Что такое гигабайт? Перед тем как разобраться с вопросом «1 Гб — это много или мало», необходимо понять суть единицы памяти. В работе большинства электронных устройств используется обработка импульсов электрического тока. Этот способ позволяет обрабатывать большой объём информации в короткие сроки и имеет лишь два значения — «Да» или «Нет». Эту минимальную информативную единицу называют битом.

С помощью битов в компьютере задаются все необходимые данные — тексты, картинки, звук и так далее. Чтобы увеличить скорость обработки импульсов, было принято решение разбивать весь поток на группы — один набор из 8 битов стали называть байтом. С развитием технологии требовалось работать со всё большим объёмом данных, из-за чего стали появляться новые деления на более крупные группы. Чтобы упростить процесс понимания количества битов в заданной величине, было принято решение использовать приставки из системы единиц СИ.

В результате этого появились килобиты, мегабайты и другие значения объёма памяти. Но, согласно единой системе СИ, значение каждой приставки представляло собой множитель в виде числа 10 в определённой степени. А компьютерная информация, по причине своей двоичности, представляется в виде двойки в некоторой степени. Из-за этого при точном определении меньшей величины нередко сталкиваются с разногласием.

Несмотря на имеющиеся противоречия в точном определении числа битов, различия значений для приставок с малой разницей несущественны. Так, согласно этим вычислениям, в 1 килобайте содержится не 1000 байт, а 210 — 1024 байта. Сколько в одном гигабайте? Приставка «гига» по системе СИ означает 109, то есть 1 миллиард.

Ближайшая приставка к «гига» — «мега», которая в 103 раз меньше. Но на территории большинства стран мира, включая Россию, точное число байт определяется с использованием двойки в n-ной степени, поэтому ответом на вопрос о том, сколько Мб в 1 Гб, является 1024. Продолжая рассматривать более мелкие значения, вместо умножения на 1000 дальнейшие вычисления производятся с использованием 2 в 10 степени.

Если вы хотите отвечать на вопросы на этом языке, пожалуйста, кликните на кнопку ниже. If you want to answer questions in English, please click button below. Узнать больше о данных, которые собирает Quizzclub или поменять свои настройки приватности сейчас.

Разница только в восприятии. От первого вы ожидаете вернуть то, что было сохранено вами ранее, а второе не подчинялось известному алгоритму кодирования информации и его интерпретация почти невозможна.

Но и в камне есть то, что можно интерпретировать однозначно. Например, радионуклиды, которые позволят определить его точный возраст.

Тема 1: Базовые понятия информатики Урок 6: Объем информации. Скорость передачи Видео Теория Заметили ошибку? Как вы уже знаете, в компьютерной технике используется двоичная система счисления.

Элементарная единица объема информации вне зависимости от ее содержания называется бит.

Основа битовых операций

Обычно используемые числа, такие как 3 и 5, выражаются в десятичной системе, а в основе битовых операций лежит двоичная система. То есть люди используют десятичную систему, а машины используют двоичную систему.Чтобы глубже понять битовые операции, вам необходимо понимать метод преобразования и соответствующие отношения между десятичной системой и двоичной системой.

Двоичный

При преобразовании десятичной дроби в двоичную используется метод «разделить на 2 и взять остаток, расположить в обратном порядке»:

Разделите десятичное число на 2, чтобы получить частное и остаток; Разделите частное на 2, чтобы получить новое частное и остаток; Повторяйте шаги 1 и 2, пока частное не станет 0; принимает остаток, полученный первым, как старший разряд двоичного числа, а затем принимает остаток, полученный позже, как младший разряд двоичного числа, по порядку;

Результатом сортировки является двоичное представление десятичного числа. Например, процесс вычисления десятичного числа 101 в двоичное число выглядит следующим образом:

Обратный порядок означает сортировку от старшего к младшему в двоичной системе. 7-битное двоичное число — 1100101. Если вы хотите преобразовать в 8-битное двоичное число, вам нужно добавить 0 в самую высокую позицию. То есть 8-битное двоичное число десятичного числа равно 01100101.

Полный процесс показан на рисунке ниже: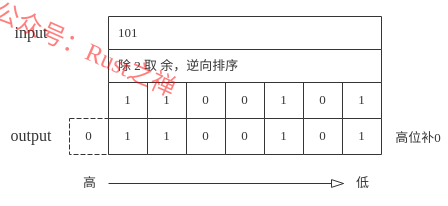 Некоторые пользователи сети составили таблицу общих шестнадцатеричных кодов и кодов ASCII. Содержимое таблицы выглядит следующим образом:

Управляющие символы ASCII

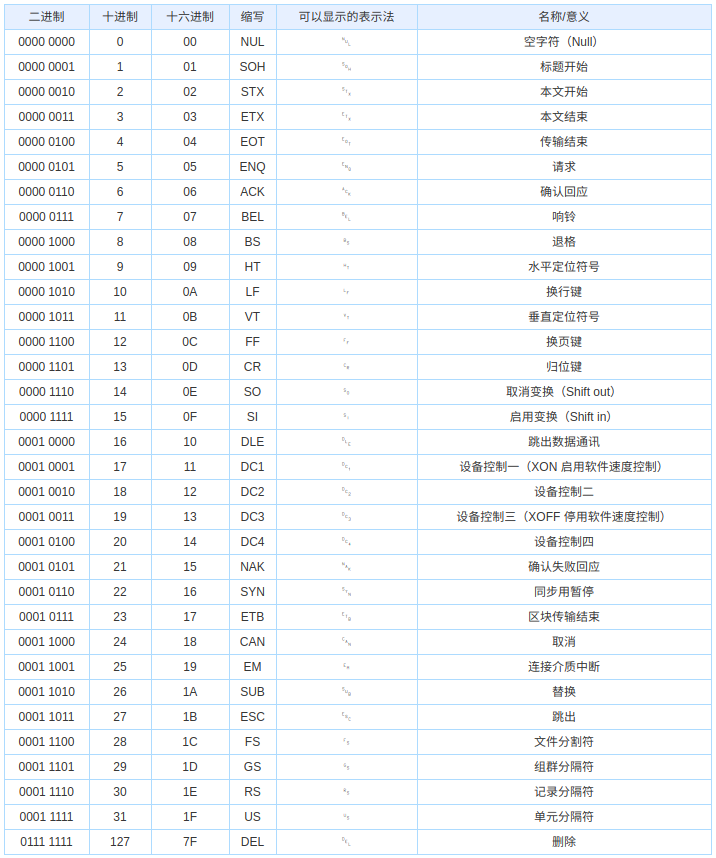Отображаемые символы ASCII

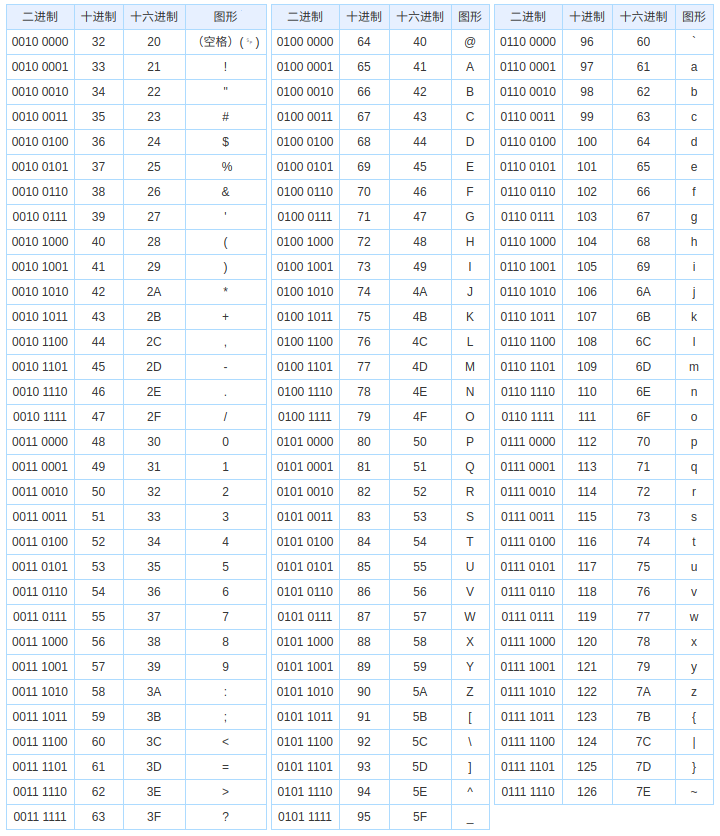
Дополнение

Теперь мы изучили метод преобразования между двоичным и десятичным числами и получили двоичную таблицу сравнения. Но прежде чем мы начнем изучать битовые операторы, нам также необходимо понять, что такое дополнения.

Числовые значения делятся на положительные и отрицательные. Итак, как двоичный файл, содержащий только 0 и 1, представляет положительное и отрицательное?

Люди устанавливают, что старший бит в двоичном формате равен 0 для положительного и 1 для отрицательного. Например, десятичная система, соответствующая 0000 1100, — 12, а десятичная система, соответствующая 1000 1100, — -12. Это представление называется исходным кодом. Но возникла новая проблема: старший бит исходного двоичного файла всегда равен 0. Чтобы указать, что положительное и отрицательное значение равны лишнему 1, при выполнении операции возникнет ошибка. Например, двоичная операция 1 + (-2) выглядит следующим образом:

Это, очевидно, проблематично, и проблема заключается в самой высокой позиции, которая представляет собой положительное и отрицательное. Затем люди придумали дополнение до единицы (0 и 1 в каждой позиции двоичного кода меняются местами, например, дополнение до единицы 0000 1100 равно 1111 0011). На этом этапе расчет будет таким:

На этот раз кажется правильным. Но есть и исключения, давайте посмотрим на 1 + (-1):

Нет разницы между положительным и отрицательным, для решения этой проблемы разработана концепция дополнения. Дополнение должно превратить отрицательное число в положительное число, которое может быть добавлено, поэтому дополнение отрицательного числа = абсолютное значение отрицательного числа инвертируется + 1. Например, дополнение к -1:

Полный процесс получения дополнения -1 показан на рисунке ниже: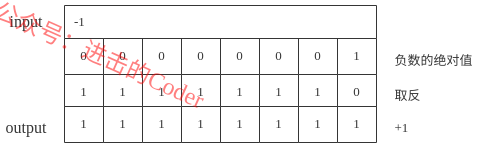 И наоборот, процесс получения исходного кода из дополнения: исходный код = дополнение-1, а затем отрицание. Следует отметить, что в процессе дополнения кода значение самого старшего бита остается неизменным, чтобы гарантировать, что положительный и отрицательный результат не будет ошибочным. Например, процесс вычисления 1 + (-6) и 1 + (-9) выглядит следующим образом:

Следует отметить, что дополнение положительного числа такое же, как и исходный код, и никаких дополнительных операций не требуется. Также можно сказать, что появление дополнения должно решить проблему знака в операции отрицательных чисел.

Бит и биты!

Компьютеры обрабатывают данные иначе, чем люди. Но задумывались ли вы, как на самом деле хранятся эти огромные объёмы данных? Добро пожаловать в компьютеры — их основа: биты. Любая часть информации в большинстве современных вычислительных систем, будь то ваш настольный ПК, мобильный телефон или интеллектуальный экран на вашем умном холодильнике, хранит данные с помощью «битов».

Самый маленький фрагмент информации, который компьютер может «понять» и обработать, — это бит. Но что это немного? Как мы можем оценить бит? На самом деле это очень просто. Представьте, что у вас есть небольшой кусок металла (формы, которая может быть намагничена) и магнит. Если вы намагничиваете кусок металла, мы будем называть это состояние намагниченным или 1. Если мы не намагничиваем кусок металла или возвращаем намагниченный кусок металла в размагниченное состояние, мы назовём такое размагниченное состояние 0.

По сути, это и есть бит: намагниченный или размагниченный кусок металла. Таким образом, казалось бы, что мы не можем хранить много информации в одном бите: только 0 и 1 — два возможных состояния. Давайте вместо этого возьмём восемь бит и посмотрим, что мы можем с этим сделать.

использование

Процессоры с прямым порядком байтов обычно используют нумерацию битов «LSB 0», однако оба соглашения о нумерации битов можно увидеть в машинах с прямым порядком байтов . Некоторые архитектуры, такие как SPARC и Motorola 68000, используют нумерацию битов «LSB 0», в то время как S / 390 , PowerPC и PA-RISC используют «MSB 0».

Рекомендуемый стиль для документов запроса комментариев (RfC) — это нумерация битов «MSB 0».

Нумерация битов обычно прозрачна для программного обеспечения , но некоторые языки программирования, такие как Ada, и языки описания оборудования, такие как VHDL и verilog, позволяют указать соответствующий порядок битов для представления типа данных.